Two Dynamical Scenarios for Binned Master Sample Interpretation
Abstract
1. Introduction
2. Theoretical Furmulation
3. Data Analysis
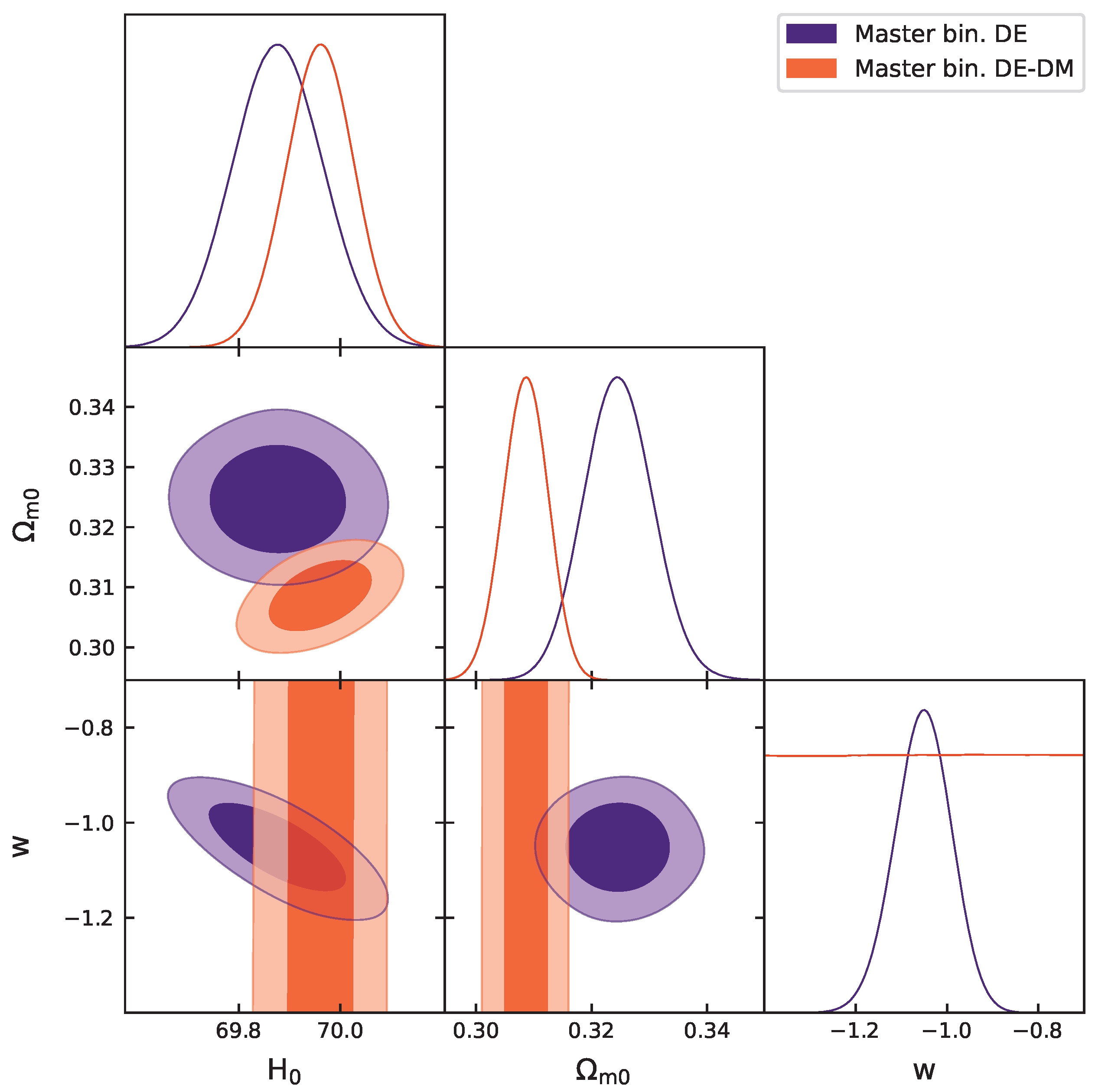
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- de Bernardis, P.; Ade, P.A.R.; Bock, J.J.; Bond, J.R.; Borrill, J.; Boscaleri, A.; Coble, K.; Crill, B.P.; De Gasperis, G.; Farese, P.C.; et al. A flat Universe from high-resolution maps of the cosmic microwave background radiation. Nature 2000, 404, 955–959. [Google Scholar] [CrossRef]
- Bennett, C.L.; Larson, D.; Weiland, J.L.; Jarosik, N.; Hinshaw, G.; Odegard, N.; Smith, K.M.; Hill, R.S.; Gold, B.; Halpern, M.; et al. Nine-year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Final Maps and Results. Astrophys. J. Suppl. Ser. 2013, 208, 20. [Google Scholar] [CrossRef]
- Riess, A.G.; Yuan, W.; Macri, L.M.; Scolnic, D.; Brout, D.; Casertano, S.; Jones, D.O.; Murakami, Y.; Anand, G.S.; Breuval, L.; et al. A comprehensive measurement of the local value of the Hubble constant with 1 km s−1 Mpc−1 uncertainty from the Hubble Space Telescope and the SH0ES team. Astrophys. J. Lett. 2022, 934, L7. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.; Bartolo, N.; Basak, S.; et al. Planck 2018 results-VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Di Valentino, E.; Levi Said, J.; Riess, A.; Pollo, A.; Poulin, V.; Gómez-Valent, A.; Weltman, A.; Palmese, A.; Huang, C.D.; Carsten, v.d.B.; et al. The CosmoVerse White Paper: Addressing observational tensions in cosmology with systematics and fundamental physics. Phys. Dark Universe 2025, 49, 101965. [Google Scholar] [CrossRef]
- Di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the realm of the Hubble tension—A review of solutions. Class. Quantum Gravity 2021, 38, 153001. [Google Scholar] [CrossRef]
- Vagnozzi, S. Seven hints that early-time new physics alone is not sufficient to solve the Hubble tension. Universe 2023, 9, 393. [Google Scholar] [CrossRef]
- Escamilla, L.A.; Fiorucci, D.; Montani, G.; Di Valentino, E. Exploring the Hubble tension with a late time Modified Gravity scenario. Phys. Dark Universe 2024, 46, 101652. [Google Scholar] [CrossRef]
- Montani, G.; Carlevaro, N.; Escamilla, L.A.; Di Valentino, E. Kinetic model for dark energy—dark matter interaction: Scenario for the hubble tension. Phys. Dark Universe 2025, 48, 101848. [Google Scholar] [CrossRef]
- Montani, G.; Carlevaro, N.; Dainotti, M.G. Slow-rolling scalar dynamics as solution for the Hubble tension. Phys. Dark Universe 2024, 44, 101486. [Google Scholar] [CrossRef]
- Montani, G.; De Angelis, M.; Bombacigno, F.; Carlevaro, N. Metric f(R) gravity with dynamical dark energy as a scenario for the Hubble tension. Mon. Not. R. Astron. Soc. Lett. 2023, 527, L156–L161. [Google Scholar] [CrossRef]
- Schiavone, T.; Montani, G.; Bombacigno, F. f(R) gravity in the Jordan frame as a paradigm for the Hubble tension. Mon. Not. R. Astron. Soc. Lett. 2023, 522, L72–L77. [Google Scholar] [CrossRef]
- Schiavone, T.; Montani, G.; Dainotti, M.G.; De Simone, B.; Rinaldi, E.; Lambiase, G. Running Hubble constant from the SNe Ia Pantheon sample? In Proceedings of the 17th Italian-Korean Symposium on Relativistic Astrophysics, Gunsan, Republic of Korea, 2–6 August 2021.
- Nojiri, S.; Odintsov, S.D. Introduction to modified gravity and gravitational alternative for dark energy. eConf 2007, 4, 115–145. [Google Scholar] [CrossRef]
- Silva, E.; Sabogal, M.A.; Scherer, M.; Nunes, R.C.; Di Valentino, E.; Kumar, S. New constraints on interacting dark energy from DESI DR2 BAO observations. Phys. Rev. D 2025, 111, 123511. [Google Scholar] [CrossRef]
- Teixeira, E.M.; Giarè, W.; Hogg, N.B.; Montandon, T.; Poudou, A.; Poulin, V. Implications of distance duality violation for the H_0 tension and evolving dark energy. arXiv 2025, arXiv:2504.10464. [Google Scholar]
- Giarè, W. Inflation, the Hubble tension, and early dark energy: An alternative overview. Phys. Rev. D 2024, 109, 123545. [Google Scholar] [CrossRef]
- Anderson, R.I.; Koblischke, N.W.; Eyer, L. Small-amplitude Red Giants Elucidate the Nature of the Tip of the Red Giant Branch as a Standard Candle. Astrophys. J. Lett. 2024, 963, L43. [Google Scholar] [CrossRef]
- Scolnic, D.; Brout, D.; Carr, A.; Riess, A.G.; Davis, T.M.; Dwomoh, A.; Jones, D.O.; Ali, N.; Charvu, P.; Chen, R.; et al. The Pantheon+ Analysis: The Full Data Set and Light-curve Release. Astrophys. J. 2022, 938, 113. [Google Scholar] [CrossRef]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Brout, D.; Scolnic, D.; Popovic, B.; Riess, A.G.; Carr, A.; Zuntz, J.; Kessler, R.; Davis, T.M.; Hinton, S.; Jones, D.; et al. The Pantheon+ Analysis: Cosmological Constraints. Astrophys. J. 2022, 938, 110. [Google Scholar] [CrossRef]
- Scolnic, D.; Riess, A.G.; Wu, J.; Li, S.; Anand, G.S.; Beaton, R.; Casertano, S.; Anderson, R.I.; Dhawan, S.; Ke, X. CATS: The Hubble Constant from Standardized TRGB and Type Ia Supernova Measurements. Astrophys. J. Lett. 2023, 954, L31. [Google Scholar] [CrossRef]
- Jones, D.O.; Mandel, K.S.; Kirshner, R.P.; Thorp, S.; Challis, P.M.; Avelino, A.; Brout, D.; Burns, C.; Foley, R.J.; Pan, Y.-C.; et al. Cosmological Results from the RAISIN Survey: Using Type Ia Supernovae in the Near Infrared as a Novel Path to Measure the Dark Energy Equation of State. Astrophys. J. 2022, 933, 172. [Google Scholar] [CrossRef]
- Anand, G.S.; Tully, R.B.; Rizzi, L.; Riess, A.G.; Yuan, W. Comparing Tip of the Red Giant Branch Distance Scales: An Independent Reduction of the Carnegie-Chicago Hubble Program and the Value of the Hubble Constant. Astrophys. J. 2022, 932, 15. [Google Scholar] [CrossRef]
- Freedman, W.L. Measurements of the Hubble Constant: Tensions in Perspective. Astrophys. J. 2021, 919, 16. [Google Scholar] [CrossRef]
- Uddin, S.A.; Burns, C.R.; Phillips, M.M.; Suntzeff, N.B.; Freedman, W.L.; Brown, P.J.; Morrell, N.; Hamuy, M.; Krisciunas, K.; Wang, L.; et al. Carnegie Supernova Project-I and -II: Measurements of H0 using Cepheid, TRGB, and SBF Distance Calibration to Type Ia Supernovae. arXiv 2023, arXiv:2308.01875. [Google Scholar]
- Huang, C.D.; Yuan, W.; Riess, A.G.; Hack, W.; Whitelock, P.A.; Zakamska, N.L.; Casertano, S.; Macri, L.M.; Marengo, M.; Menzies, J.W.; et al. The Mira Distance to M101 and a 4% Measurement of H0. Astrophys. J. 2024, 963, 83. [Google Scholar] [CrossRef]
- Li, S.; Riess, A.G.; Casertano, S.; Anand, G.S.; Scolnic, D.M.; Yuan, W.; Breuval, L.; Huang, C.D. Reconnaissance with JWST of the J-region Asymptotic Giant Branch in Distance Ladder Galaxies: From Irregular Luminosity Functions to Approximation of the Hubble Constant. Astrophys. J. 2024, 966, 20. [Google Scholar] [CrossRef]
- Kourkchi, E.; Tully, R.B.; Anand, G.S.; Courtois, H.M.; Dupuy, A.; Neill, J.D.; Rizzi, L.; Seibert, M. Cosmicflows-4: The Calibration of Optical and Infrared Tully–Fisher Relations. Astrophys. J. 2020, 896, 3. [Google Scholar] [CrossRef]
- Schombert, J.; McGaugh, S.; Lelli, F. Using the Baryonic Tully–Fisher Relation to Measure H0. Astron. J. 2020, 160, 71. [Google Scholar] [CrossRef]
- Murakami, Y.S.; Riess, A.G.; Stahl, B.E.; Kenworthy, W.D.; Pluck, D.M.A.; Macoretta, A.; Brout, D.; Jones, D.O.; Scolnic, D.M.; Filippenko, A.V. Leveraging SN Ia spectroscopic similarity to improve the measurement of H0. J. Cosmol. Astropart. Phys. 2023, 11, 046. [Google Scholar] [CrossRef]
- Breuval, L.; Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.M.; Romaniello, M.; Murakami, Y.S.; Scolnic, D.; Anand, G.S.; Soszyński, I. Small Magellanic Cloud Cepheids Observed with the Hubble Space Telescope Provide a New Anchor for the SH0ES Distance Ladder. arXiv 2024, arXiv:2404.08038. [Google Scholar] [CrossRef]
- Balkenhol, L.; Dutcher, D.; Mancini, A.S.; Doussot, A.; Benabed, K.; Galli, S.; Ade, P.A.R.; Anderson, A.J.; Ansarinejad, B.; Archipley, M.; et al. Measurement of the CMB temperature power spectrum and constraints on cosmology from the SPT-3G 2018 TT, TE, and EE dataset. Phys. Rev. D 2023, 108, 023510. [Google Scholar] [CrossRef]
- Aiola, S.; Calabrese, E.; Maurin, L.; Naess, S.; Schmitt, B.L.; Abitbol, M.H.; Addison, G.E.; Ade, P.A.R.; Alonso, D.; Amiri, M.; et al. The Atacama Cosmology Telescope: DR4 Maps and Cosmological Parameters. J. Cosmol. Astropart. Phys. 2020, 12, 047. [Google Scholar] [CrossRef]
- Foidl, H.; Rindler-Daller, T. A proposal to improve the accuracy of cosmological observables and address the Hubble tension problem. Astron. Astrophys. 2024, 686, A210. [Google Scholar] [CrossRef]
- Luongo, O.; Muccino, M. Determining H0 from distance sum rule combining gamma-ray bursts with observational Hubble data and strong gravitational lensing. arXiv 2024, arXiv:2412.18493. [Google Scholar] [CrossRef]
- Shah, R.; Mukherjee, P.; Saha, S.; Garain, U.; Pal, S. Deep Learning Based Recalibration of SDSS and DESI BAO Alleviates Hubble and Clustering Tensions. arXiv 2024, arXiv:2412.14750. [Google Scholar] [CrossRef]
- Verde, L.; Treu, T.; Riess, A.G. Tensions between the early and late Universe. Nat. Astron. 2019, 3, 891–895. [Google Scholar] [CrossRef]
- Freedman, W.L.; Madore, B.F.; Hatt, D.; Hoyt, T.J.; Jang, I.S.; Beaton, R.L.; Burns, C.R.; Lee, M.G.; Monson, A.J.; Neeley, J.R.; et al. The Carnegie-Chicago Hubble Program. VIII. An Independent Determination of the Hubble Constant Based on the Tip of the Red Giant Branch. Astrophys. J. 2019, 882, 34. [Google Scholar] [CrossRef]
- Freedman, W.L.; Madore, B.F.; Hoyt, T.; Jang, I.S.; Beaton, R.; Lee, M.G.; Monson, A.; Neeley, J.; Rich, J. Calibration of the Tip of the Red Giant Branch (TRGB). arXiv 2020, arXiv:2002.01550. [Google Scholar] [CrossRef]
- Soltis, J.; Casertano, S.; Riess, A.G. The Parallax of ω Centauri Measured from Gaia EDR3 and a Direct, Geometric Calibration of the Tip of the Red Giant Branch and the Hubble Constant. Astrophys. J. Lett. 2021, 908, L5. [Google Scholar] [CrossRef]
- Watkins, R.; Allen, T.; Bradford, C.J.; Ramon, A.; Walker, A.; Feldman, H.A.; Cionitti, R.; Al-Shorman, Y.; Kourkchi, E.; Tully, R.B. Analysing the large-scale bulk flow using cosmicflows4: Increasing tension with the standard cosmological model. Mon. Not. R. Astron. Soc. 2023, 524, 1885–1892. [Google Scholar] [CrossRef]
- Luković, V.V.; Haridasu, B.S.; Vittorio, N. Exploring the evidence for a large local void with supernovae Ia data. Mon. Not. R. Astron. Soc. 2020, 491, 2075–2087. [Google Scholar] [CrossRef]
- Lu, W.J.; Qin, Y.P. New constraint of the Hubble constant by proper motions of radio components observed in AGN twin-jets. Res. Astron. Astrophys. 2021, 21, 261. [Google Scholar] [CrossRef]
- Gerardi, F.; Feeney, S.M.; Alsing, J. Unbiased likelihood-free inference of the Hubble constant from light standard sirens. arXiv 2021, arXiv:2104.02728. [Google Scholar] [CrossRef]
- Gray, R.; Messenger, C.; Veitch, J. A Pixelated Approach to Galaxy Catalogue Incompleteness: Improving the Dark Siren Measurement of the Hubble Constant. arXiv 2021, arXiv:2111.04629. [Google Scholar] [CrossRef]
- Li, B.; Shapiro, P.R. Precision cosmology and the stiff-amplified gravitational-wave background from inflation: NANOGrav, Advanced LIGO-Virgo and the Hubble tension. J. Cosmol. Astropart. Phys. 2021, 2021, 024. [Google Scholar] [CrossRef]
- Mozzon, S.; Ashton, G.; Nuttall, L.K.; Williamson, A.R. Does non-stationary noise in LIGO and Virgo affect the estimation of H0? arXiv 2021, arXiv:2110.11731. [Google Scholar]
- Palmese, A.; Bom, C.R.; Mucesh, S.; Hartley, W.G. A standard siren measurement of the Hubble constant using gravitational wave events from the first three LIGO/Virgo observing runs and the DESI Legacy Survey. arXiv 2021, arXiv:2111.06445. [Google Scholar] [CrossRef]
- Zhu, S.; Shu, Y.; Yuan, H.; Fu, J.N.; Gao, J.; Wu, J.; He, X.; Liao, K.; Li, G.; Er, X.; et al. Forecast of Observing Time Delay of Strongly Lensed Quasars with the Muztagh-Ata 1.93 m Telescope. Res. Astron. Astrophys. 2023, 23, 035001. [Google Scholar] [CrossRef]
- Liu, Y.; Oguri, M. Assessing the effect of mass-model assumptions on measuring the Hubble constant from the cluster-lensed supernova Refsdal. Phys. Rev. D 2025, 111, 123506. [Google Scholar] [CrossRef]
- de Jaeger, T.; Galbany, L.; Riess, A.G.; Stahl, B.E.; Shappee, B.J.; Filippenko, A.V.; Zheng, W. A 5 per cent measurement of the Hubble-Lemaître constant from Type II supernovae. Mon. Not. R. Astron. Soc. 2022, 514, 4620–4628. [Google Scholar] [CrossRef]
- Pesce, D.W.; Braatz, J.A.; Reid, M.J.; Riess, A.G.; Scolnic, D.; Condon, J.J.; Gao, F.; Henkel, C.; Impellizzeri, C.M.V.; Kuo, C.Y.; et al. The Megamaser Cosmology Project. XIII. Combined Hubble Constant Constraints. Astrophys. J. Lett. 2020, 891, L1. [Google Scholar] [CrossRef]
- Blakeslee, J.P.; Jensen, J.B.; Ma, C.P.; Milne, P.A.; Greene, J.E. The Hubble Constant from Infrared Surface Brightness Fluctuation Distances. Astrophys. J. 2021, 911, 65. [Google Scholar] [CrossRef]
- Adame, A.G.; Aguilar, J.; Ahlen, S.; Alam, S.; Alexander, D.M.; Alvarez, M.; Alves, O.; Anand, A.; Andrade, U.; Armengaud, E.; et al. DESI 2024 VI: Cosmological constraints from the measurements of baryon acoustic oscillations. J. Cosmol. Astropart. Phys. 2025, 02, 021. [Google Scholar] [CrossRef]
- Abdul-Karim, M.; Aguilar, J.; Ahlen, S.; Alam, S.; Allen, L.; Prieto, C.A.; Alves, O.; Anand, A.; Andrade, U.; Armengaud, E.; et al. DESI DR2 Results II: Measurements of Baryon Acoustic Oscillations and Cosmological Constraints. arXiv 2025, arXiv:2503.14738. [Google Scholar]
- Chevallier, M.; Polarski, D. Accelerating universes with scaling dark matter. Int. J. Mod. Phys. D 2001, 10, 213–223. [Google Scholar] [CrossRef]
- Linder, E.V. Exploring the expansion history of the universe. Phys. Rev. Lett. 2003, 90, 091301. [Google Scholar] [CrossRef] [PubMed]
- Lodha, K.; Calderon, R.; Matthewson, W.; Shafieloo, A.; Ishak, M.; Pan, J.; Garcia-Quintero, C.; Huterer, D.; Valogiannis, G.; Ureña-López, L.; et al. Extended Dark Energy analysis using DESI DR2 BAO measurements. arXiv 2025, arXiv:2503.14743. [Google Scholar]
- Giarè, W.; Mahassen, T.; Di Valentino, E.; Pan, S. An overview of what current data can (and cannot yet) say about evolving dark energy. Phys. Dark Universe 2025, 48, 101906. [Google Scholar] [CrossRef]
- Giarè, W. Dynamical Dark Energy Beyond Planck? Constraints from multiple CMB probes, DESI BAO and Type-Ia Supernovae. arXiv 2024, arXiv:2409.17074. [Google Scholar] [CrossRef]
- Giarè, W.; Najafi, M.; Pan, S.; Di Valentino, E.; Firouzjaee, J.T. Robust preference for Dynamical Dark Energy in DESI BAO and SN measurements. J. Cosmol. Astropart. Phys. 2024, 2024, 035. [Google Scholar] [CrossRef]
- Colgáin, E.Ó.; Dainotti, M.G.; Capozziello, S.; Pourojaghi, S.; Sheikh-Jabbari, M.; Stojkovic, D. Does DESI 2024 Confirm ΛCDM? arXiv 2024, arXiv:2404.08633. [Google Scholar] [CrossRef]
- Ray, S.; Khlopov, M.; Ghosh, P.P.; Mukhopadhyay, U. Phenomenology of Λ-CDM Model: A Possibility of Accelerating Universe with Positive Pressure. Int. J. Theor. Phys. 2011, 50, 939–951. [Google Scholar] [CrossRef]
- Dymnikova, I.; Khlopov, M. Decay of Cosmological Constant as Bose Condensate Evaporation. Mod. Phys. Lett. A 2000, 15, 2305–2314. [Google Scholar] [CrossRef]
- Doroshkevich, A.G.; Khlopov, M.I. Formation of structure in a universe with unstable neutrinos. Mon. Not. RAS 1984, 211, 277–282. [Google Scholar] [CrossRef]
- Dainotti, M.G.; De Simone, B.; Schiavone, T.; Montani, G.; Rinaldi, E.; Lambiase, G. On the Hubble constant tension in the SNe Ia Pantheon sample. Astrophys. J. 2021, 912, 150. [Google Scholar] [CrossRef]
- Dainotti, M.G.; De Simone, B.; Schiavone, T.; Montani, G.; Rinaldi, E.; Lambiase, G.; Bogdan, M.; Ugale, S. On the evolution of the Hubble constant with the SNe Ia pantheon sample and baryon acoustic oscillations: A feasibility study for GRB-cosmology in 2030. Galaxies 2022, 10, 24. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Simone, B.D.; Garg, A.; Kohri, K.; Bashyal, A.; Aich, A.; Mondal, A.; Nagataki, S.; Montani, G.; Jareen, T.; et al. A New Master Supernovae Ia sample and the investigation of the H0 tension. arXiv 2025, arXiv:2501.11772. [Google Scholar]
- Fazzari, E.; Dainotti, M.G.; Montani, G.; Melchiorri, A. The effective running Hubble constant in SNe Ia as a marker for the dark energy nature. arXiv 2025, arXiv:2506.04162. [Google Scholar] [CrossRef]
- Schiavone, T.; Montani, G. Evolution of an effective Hubble constant in f(R) modified gravity. arXiv 2024, arXiv:2408.01410. [Google Scholar]
- Dainotti, M.G.; Bargiacchi, G.; Bogdan, M.; Capozziello, S.; Nagataki, S. On the statistical assumption on the distance moduli of Supernovae Ia and its impact on the determination of cosmological parameters. J. High Energy Astrophys. 2024, 41, 30–41. [Google Scholar] [CrossRef]
- Nicolas, N.; Rigault, M.; Copin, Y.; Graziani, R.; Aldering, G.; Briday, M.; Kim, Y.L.; Nordin, J.; Perlmutter, S.; Smith, M. Redshift evolution of the underlying type Ia supernova stretch distribution. Astron. Astrophys. 2021, 649, A74. [Google Scholar] [CrossRef]
- Freedman, W.L.; Madore, B.F.; Hoyt, T.J.; Jang, I.S.; Lee, A.J.; Owens, K.A. Status Report on the Chicago-Carnegie Hubble Program (CCHP): Measurement of the Hubble Constant Using the Hubble and James Webb Space Telescopes. Astrophys. J. 2025, 985, 203. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Lenart, A.Ł.; Chraya, A.; Sarracino, G.; Nagataki, S.; Fraija, N.; Capozziello, S.; Bogdan, M. The gamma-ray bursts fundamental plane correlation as a cosmological tool. Mon. Not. R. Astron. Soc. 2023, 518, 2201–2240. [Google Scholar] [CrossRef]
- Elizalde, E.; Khurshudyan, M.; Odintsov, S.D. Can we learn from matter creation to solve the H0 tension problem? Eur. Phys. J. C 2024, 84, 782. [Google Scholar] [CrossRef]
- Fazzari, E.; Leo, C.D.; Montani, G.; Martinelli, M.; Melchiorri, A.; Cañas-Herrera, G. Investigating f(R)-Inflation: Background evolution and constraints. arXiv 2025, arXiv:2507.13890. [Google Scholar]
- Scherer, M.; Sabogal, M.A.; Nunes, R.C.; De Felice, A. Challenging ΛCDM: 5σ Evidence for a Dynamical Dark Energy Late-Time Transition. arXiv 2025, arXiv:2504.20664. [Google Scholar] [CrossRef]
- Calvao, M.; Lima, J.; Waga, I. On the thermodynamics of matter creation in cosmology. Phys. Lett. A 1992, 162, 223–226. [Google Scholar] [CrossRef]
- Montani, G. Influence of particle creation on flat and negative curved FLRW universes. Class. Quantum Gravity 2001, 18, 193. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Lenart, A.; Yengejeh, M.G.; Chakraborty, S.; Fraija, N.; Di Valentino, E.; Montani, G. A new binning method to choose a standard set of Quasars. Phys. Dark Universe 2024, 44, 101428. [Google Scholar] [CrossRef]
- Efstathiou, G.; Gratton, S. The evidence for a spatially flat Universe. Mon. Not. R. Astron. Soc. Lett. 2020, 496, L91–L95. [Google Scholar] [CrossRef]
- Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity; Wiley: Hoboken, NJ, USA, 1972. [Google Scholar]
- Nunes, R.C.; Pavón, D. Phantom behavior via cosmological creation of particles. Phys. Rev. D 2015, 91, 063526. [Google Scholar] [CrossRef]
- Amendola, L. Coupled quintessence. Phys. Rev. D 2000, 62, 043511. [Google Scholar] [CrossRef]
- Bolotin, Y.L.; Kostenko, A.; Lemets, O.A.; Yerokhin, D.A. Cosmological evolution with interaction between dark energy and dark matter. Int. J. Mod. Phys. D 2015, 24, 1530007. [Google Scholar] [CrossRef]
- Wang, B.; Abdalla, E.; Atrio-Barandela, F.; Pavón, D. Dark matter and dark energy interactions: Theoretical challenges, cosmological implications and observational signatures. Rep. Prog. Phys. 2016, 79, 096901. [Google Scholar] [CrossRef]
- Wang, B.; Gong, Y.; Abdalla, E. Transition of the dark energy equation of state in an interacting holographic dark energy model. Phys. Lett. B 2005, 624, 141–146. [Google Scholar] [CrossRef]
- Das, S.; Corasaniti, P.S.; Khoury, J. Superacceleration as the signature of a dark sector interaction. Phys. Rev. D 2006, 73, 083509. [Google Scholar] [CrossRef]
- Pan, S.; Chakraborty, S. A cosmographic analysis of holographic dark energy models. Int. J. Mod. Phys. D 2014, 23, 1450092. [Google Scholar] [CrossRef]
- Barrow, J.D.; Clifton, T. Cosmologies with energy exchange. Phys. Rev. D 2006, 73, 103520. [Google Scholar] [CrossRef]
- Amendola, L.; Camargo Campos, G.; Rosenfeld, R. Consequences of dark matter-dark energy interaction on cosmological parameters derived from SNIa data. Phys. Rev. D 2007, 75, 083506. [Google Scholar] [CrossRef]
- He, J.H.; Wang, B. Effects of the interaction between dark energy and dark matter on cosmological parameters. J. Cosmol. Astropart. Phys. 2008, 2008, 010. [Google Scholar] [CrossRef]
- Väliviita, J.; Majerotto, E.; Maartens, R. Large-scale instability in interacting dark energy and dark matter fluids. J. Cosmol. Astropart. Phys. 2008, 2008, 020. [Google Scholar] [CrossRef]
- Yang, W.; Li, H.; Wu, Y.; Lu, J. Cosmological constraints on coupled dark energy. J. Cosmol. Astropart. Phys. 2016, 2016, 007. [Google Scholar] [CrossRef]
- Majerotto, E.; Väliviita, J.; Maartens, R. Adiabatic initial conditions for perturbations in interacting dark energy models. Mon. Not. R. Astron. Soc. 2010, 402, 2344–2354. [Google Scholar] [CrossRef]
- Väliviita, J.; Maartens, R.; Majerotto, E. Observational constraints on an interacting dark energy model. Mon. Not. R. Astron. Soc. 2010, 402, 2355–2368. [Google Scholar] [CrossRef]
- Chimento, L.P. Linear and nonlinear interactions in the dark sector. Phys. Rev. D 2010, 81, 043525. [Google Scholar] [CrossRef]
- He, J.H.; Wang, B.; Abdalla, E. Testing the interaction between dark energy and dark matter via the latest observations. Phys. Rev. D 2011, 83, 063515. [Google Scholar] [CrossRef]
- Chimento, L.P.; Richarte, M.G. Interacting dark sector with transversal interaction. In AIP Conference Proceedings; AIP Publishing LLC: College Park, MD, USA, 2015; Volume 1647, pp. 44–49. [Google Scholar] [CrossRef]
- Costa, A.A.; Xu, X.D.; Wang, B.; Ferreira, E.G.M.; Abdalla, E. Testing the interaction between dark energy and dark matter with Planck data. Phys. Rev. D 2014, 89, 103531. [Google Scholar] [CrossRef]
- Yang, W.; Xu, L. Testing coupled dark energy with large scale structure observation. J. Cosmol. Astropart. Phys. 2014, 2014, 034. [Google Scholar] [CrossRef]
- Nunes, R.C.; Pan, S.; Saridakis, E.N. New constraints on interacting dark energy from cosmic chronometers. Phys. Rev. D 2016, 94. [Google Scholar] [CrossRef]
- D’Amico, G.; Hamill, T.; Kaloper, N. Quantum field theory of interacting dark matter and dark energy: Dark monodromies. Phys. Rev. D 2016, 94, 103526. [Google Scholar] [CrossRef]
- Paliathanasis, A.; Pan, S.; Yang, W. Dynamics of nonlinear interacting dark energy models. Int. J. Mod. Phys. D 2019, 28, 1950161. [Google Scholar] [CrossRef]
- Cheng, G.; Ma, Y.Z.; Wu, F.; Zhang, J.; Chen, X. Testing interacting dark matter and dark energy model with cosmological data. Phys. Rev. D 2020, 102, 043517. [Google Scholar] [CrossRef]
- Zhai, Y.; Giarè, W.; van de Bruck, C.; Valentino, E.D.; Mena, O.; Nunes, R.C. A consistent view of interacting dark energy from multiple CMB probes. J. Cosmol. Astropart. Phys. 2023, 2023, 032. [Google Scholar] [CrossRef]
- Johnson, J.P.; Sangwan, A.; Shankaranarayanan, S. Observational constraints and predictions of the interacting dark sector with field-fluid mapping. J. Cosmol. Astropart. Phys. 2022, 2022, 024. [Google Scholar] [CrossRef]
- Kumar, S. Remedy of some cosmological tensions via effective phantom-like behavior of interacting vacuum energy. Phys. Dark Universe 2021, 33, 100862. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Valentino, E.D.; Nunes, R.C.; Vagnozzi, S.; Mota, D.F. Tale of stable interacting dark energy, observational signatures, and the H0 tension. J. Cosmol. Astropart. Phys. 2018, 2018, 019. [Google Scholar] [CrossRef]
- von Marttens, R.; Casarini, L.; Mota, D.; Zimdahl, W. Cosmological constraints on parametrized interacting dark energy. Phys. Dark Universe 2019, 23, 100248. [Google Scholar] [CrossRef]
- Abbott, T.; Acevedo, M.; Aguena, M.; Alarcon, A.; Allam, S.; Alves, O.; Amon, A.; Andrade-Oliveira, F.; Annis, J. The Dark Energy Survey: Cosmology Results with 1500 New High-redshift Type Ia Supernovae Using the Full 5 yr Data Set. Astrophys. J. Lett. 2024, 973, L14. [Google Scholar] [CrossRef]
- Betoule, M.; Kessler, R.; Guy, J.; Mosher, J.; Hardin, D.; Biswas, R.; Astier, P.; El-Hage, P.; Konig, M.; Kuhlmann, S.; et al. Improved cosmological constraints from a joint analysis of the SDSS-II and SNLS supernova samples. Astron. Astrophys. 2014, 568, A22. [Google Scholar] [CrossRef]
- Torrado, J.; Lewis, A. Cobaya: Code for Bayesian Analysis of hierarchical physical models. J. Cosmol. Astropart. Phys. 2021, 2021, 057. [Google Scholar] [CrossRef]
- Gelman, A.; Rubin, D.B. Inference from iterative simulation using multiple sequences. Stat. Sci. 1992, 7, 457–472. [Google Scholar] [CrossRef]
- Lewis, A. GetDist: A Python package for analysing Monte Carlo samples. arXiv 2019, arXiv:1910.13970. [Google Scholar] [CrossRef]
- Wagenmakers, E.J. A Practical Solution to the Pervasive Problems of p Values. Psychon. Bull. Rev. 2007, 14, 779–804. [Google Scholar] [CrossRef]
- Trotta, R. Bayes in the sky: Bayesian inference and model selection in cosmology. Contemp. Phys. 2008, 49, 71–104. [Google Scholar] [CrossRef]
- Kass, R.E.; Raftery, A.E. Bayes factors. J. Am. Stat. Assoc. 1995, 90, 773–795. [Google Scholar] [CrossRef]
- Jeffreys, H. The Theory of Probability; Oxford Classic Texts in the Physical Sciences; Oxford University Press: Oxford, UK, 1939. [Google Scholar]

| Model | [km ] | ||
|---|---|---|---|
| DE | |||
| DE-DM | − |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montani, G.; Fazzari, E.; Carlevaro, N.; Dainotti, M.G. Two Dynamical Scenarios for Binned Master Sample Interpretation. Entropy 2025, 27, 895. https://doi.org/10.3390/e27090895
Montani G, Fazzari E, Carlevaro N, Dainotti MG. Two Dynamical Scenarios for Binned Master Sample Interpretation. Entropy. 2025; 27(9):895. https://doi.org/10.3390/e27090895
Chicago/Turabian StyleMontani, Giovanni, Elisa Fazzari, Nakia Carlevaro, and Maria Giovanna Dainotti. 2025. "Two Dynamical Scenarios for Binned Master Sample Interpretation" Entropy 27, no. 9: 895. https://doi.org/10.3390/e27090895
APA StyleMontani, G., Fazzari, E., Carlevaro, N., & Dainotti, M. G. (2025). Two Dynamical Scenarios for Binned Master Sample Interpretation. Entropy, 27(9), 895. https://doi.org/10.3390/e27090895









