Description of the Condensed Phases of Water in Terms of Quantum Condensates
Abstract
1. Introduction
2. Quantum Condensates
3. The Dipole States
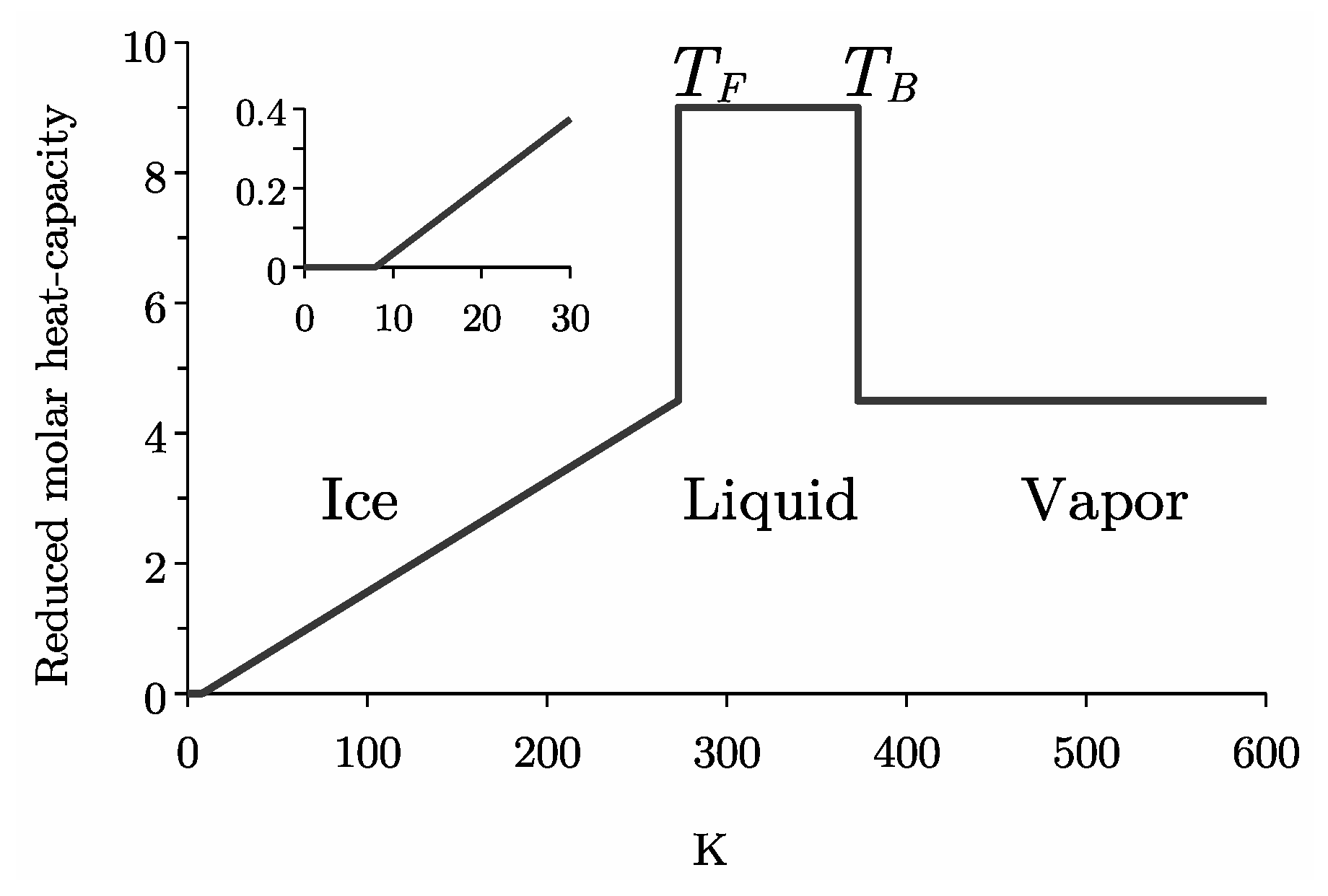
4. The Condensed Phases of Water
4.1. Ice Ih
4.2. Liquid Water
5. Other Phases of Water
5.1. Gaseous Water
5.2. Water Droplets
6. Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Ball, P. Water—An enduring mystery. Nature 2008, 452, 291–292. [Google Scholar] [CrossRef]
- Chaplin, M.F. Structure and properties of water in its various states. In Encyclopedia of Water: Science, Technology, and Society; Maurice, P.A., Ed.; Wiley: Hoboken, NJ, USA, 2019. [Google Scholar]
- Chaplin, M. 2023. Available online: https://water.lsbu.ac.uk/water/ (accessed on 21 July 2025).
- Weingärtner, H.; Chatzidimitriou-Dreismann, C.A. Anomalous H+ and D+ conductance in H2O-D2O mixturs. Nature 1990, 346, 548. [Google Scholar] [CrossRef]
- Chatzidimitriou-Dreismann, C.A.; Krieger, U.K.; Moiler, A.; Stern, M. Evidence of Quantum Correlation Effects of Protons and Deuterons in the Raman Spectra of Liquid H2O-D2O. Phys. Rev. Lett. 1995, 75, 3008–3011. [Google Scholar] [CrossRef]
- Keutsch, F.N.; Saykally, R.J. Water clusters: Untangling the mysteries of the liquid, one molecule at a time. Proc. Natl. Acad. Sci. USA 2001, 98, 10533–10540. [Google Scholar] [CrossRef] [PubMed]
- Bove, L.E.; Klotz, S.; Parciaroni, A.; Sacchetti, F. Anomalous proton dynamics in ice at low temperatures. Phys. Rev. Lett. 2009, 103, 165901. [Google Scholar] [CrossRef] [PubMed]
- Pietropaolo, A.; Senesi, R.; Andreani, C.; Mayers, J. Quantum Effects in Water: Proton Kinetic Energy Maxima in Stable and Supercooled Liquid. Braz. J. Phys. 2009, 39, 318–321. [Google Scholar] [CrossRef]
- Senesi, R.; Romanelli, G.; Adams, M.; Andreani, C. Temperature dependence of the zero point kinetic energy in ice and water above room temperature. Chem. Phys. 2013, 427, 111–116. [Google Scholar] [CrossRef][Green Version]
- Fillaux, F. The quantum phase-transitions of water. Europhys. Lett. 2017, 119, 40008. [Google Scholar] [CrossRef]
- Bernal, J.D.; Fowler, R.H. A Theory of Water and Ionic Solution, with Particular Reference to Hydrogen and Hydroxyl Ions. J. Chem. Phys. 1933, 1, 515–548. [Google Scholar] [CrossRef]
- Pauling, L. The Structure and Entropy of Ice and of Other Crystals with Some Randomness of Atomic Arrangement. J. Am. Chem. Soc. 1935, 57, 2680–2684. [Google Scholar] [CrossRef]
- Benton, O.; Sikora, O.; Shannon, N. Classical and quantum theories of proton disorder in hexagonal water ice. Phys. Rev. B 2016, 93, 125143. [Google Scholar] [CrossRef]
- Stanley, H.E.; Buldyrev, S.V.; Campolat, M.; Havlin, S.; Mishima, O.; Sadr-Lahijani, M.R.; Scala, A.; Starr, F.W. The puzzle of liquid water: A very complex fluid. Phys. D 1999, 133, 453–462. [Google Scholar] [CrossRef]
- Giese, T.J.; York, D.M. Quantum mechanical force fields for condensed phase molecular simulations. J. Phys. Condens. Matter 2017, 29, 383002. [Google Scholar] [CrossRef] [PubMed]
- Ball, P. Water is an active matrix of life for cell and molecular biology. Proc. Natl. Acad. Sci. USA 2017, 19, 13329–13335. [Google Scholar] [CrossRef]
- Smith, S.J.; Lang, B.E.; Liu, S.; Boerio-Goates, J.; Woodfieldt, B.F. Heat capacities and thermodynamic functions of hexagonal ice from T = 0.5 K to T = 38 K. J. Chem. Thermodyn. 2007, 39, 712–716. [Google Scholar] [CrossRef]
- Angeli, C.A.; Oguni, M.; Sichina, W.J. Heat Capacity of Water at Extremes of Supercooling and Superheating. J. Phys. Chem. 1982, 86, 998–1002. [Google Scholar] [CrossRef]
- Verma, M.P. Steam tables for pure water as an ActiveX component in Visual Basic 6.0. Comput. Geosci. 2003, 29, 1155–1163. [Google Scholar] [CrossRef]
- Lishchuk, S.V.; Malomuzh, N.P.; Makhlaichuk, P.V. Contribution of H-bond vibrations to heat capacity of water. Phys. Lett. A 2011, 375, 2656–2660. [Google Scholar] [CrossRef]
- Murphy, D.M.; Koop, T. Review of the vapour pressures of ice and supercooled water for atmospheric applications. Q. J. R. Meteorol. Soc. 2005, 131, 1539–1565. [Google Scholar] [CrossRef]
- Feistel, R.; Wagner, W. A new equation of state for H2O ice Ih. J. Phys. Chem. Ref. Data 2006, 35, 1021–1047. [Google Scholar] [CrossRef]
- Rocher-Casterline, B.E.; Ch’ng, L.C.; Mollner, A.K.; Reisler, H. Communication: Determination of the bond dissociation energy (D0) of the water dimer, (H2O)2, by velocity map imaging. J. Chem. Phys. 2011, 134, 211101–211104. [Google Scholar] [CrossRef]
- Shank, A.; Wang, Y.; Kaledin, A.; Braams, B.J.; Bowman, J.M. Accurate ab initio and “hybrid” potential energy surfaces, intramolecular vibrational energies, and classical IR spectrum of the water dimer. J. Chem. Phys. 2009, 130, 144314. [Google Scholar] [CrossRef]
- Kuhs, W.F.; Lehmann, M.S. The Structure of Ice Ih by Neutron Diffraction. J. Phys. Chem. 1983, 87, 4312–4313. [Google Scholar] [CrossRef]
- Leggett, A.J. Bose-Einstein condensation in the alkali gases: Some fundamental concepts. Rev. Mod. Phys. 2001, 73, 307–356. [Google Scholar] [CrossRef]
- Soper, A.K. The radial distribution functions of water and ice from 220 to 673 K and at pressures up to 400 MPa. Chem. Phys. 2000, 258, 121–137. [Google Scholar] [CrossRef]
- Narten, A.H.; Levy, H.A. Observed Diffraction Pattern and Proposed Models of Liquid Water. Science 1969, 165, 447–454. [Google Scholar] [CrossRef] [PubMed]
- Odutola, J.A.; Hu, T.A.; Prinslow, D.; O’Dell, S.E.; Dyke, T.R. Water dimer tunneling states with K=0. J. Chem. Phys. 1988, 88, 5352–5361. [Google Scholar] [CrossRef]
- Marsh, K.N. (Ed.) Recommended Reference Materials for the Realization of Physicochemical Properties; Blackwell: Oxford, UK, 1987. [Google Scholar]
- Fedorets, A.A.; Frenkel, M.; Shulzinger, E.; Dombrovsky, L.A.; Bormashenko, E.; Nosonovsky, M. Self-assembled levitating clusters of water droplets: Pattern-formation and stability. Sci. Rep. 2017, 7, 1888. [Google Scholar] [CrossRef] [PubMed]
- Fedorets, A.A.; Dombrovsky, L.A.; Ryumin, P.I. Expanding the temperature range for generation of droplet clusters over the locally heated water surface. Int. J. Heat Mass Transf. 2017, 113, 1054–1058. [Google Scholar] [CrossRef]
- Umeki1, T.; Ohata1, M.; Nakanishi, H.; Ichikawa, M. Dynamics of microdroplets over the surface of hot water. Sci. Rep. 2015, 5, 8046. [Google Scholar] [CrossRef]
- Zaitsev, D.V.; Kirichenko, D.P.; Ajaev, V.S.; Kabov1, O.A. Levitation and Self-Organization of Liquid Microdroplets over Dry Heated Substrates. Phys. Rev. Lett. 2017, 119, 094503–094505. [Google Scholar] [CrossRef] [PubMed]
- Ajaev, V.S.; Kabov, O.A. Levitation and Self-Organization of Droplets. Annu. Rev. Fluid Mech. 2021, 53, 203–225. [Google Scholar] [CrossRef]
| Ref. | |||
|---|---|---|---|
| Vapor | [19] | ||
| Liquid | [20] | ||
| Ice Ih | [21,22] | ||
| Ice Ih * | [17] |
| Steam | — | ||
| HDL | |||
| SC | |||
| Ice Ih |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fillaux, F. Description of the Condensed Phases of Water in Terms of Quantum Condensates. Entropy 2025, 27, 885. https://doi.org/10.3390/e27080885
Fillaux F. Description of the Condensed Phases of Water in Terms of Quantum Condensates. Entropy. 2025; 27(8):885. https://doi.org/10.3390/e27080885
Chicago/Turabian StyleFillaux, François. 2025. "Description of the Condensed Phases of Water in Terms of Quantum Condensates" Entropy 27, no. 8: 885. https://doi.org/10.3390/e27080885
APA StyleFillaux, F. (2025). Description of the Condensed Phases of Water in Terms of Quantum Condensates. Entropy, 27(8), 885. https://doi.org/10.3390/e27080885







