Edge States, Bulk Spectra, and Topological Phases of Szegedy’s Quantum Search on a One-Dimensional Cycle with Self-Loops
Abstract
1. Introduction
2. Preliminaries
3. Bulk Spectra and Edge States of the Generalized Three States Quantum Search
3.1. Bulk Spectra of the Generalized 3QWs
3.2. Edge Spectra of the Generalized Three-State Quantum Search
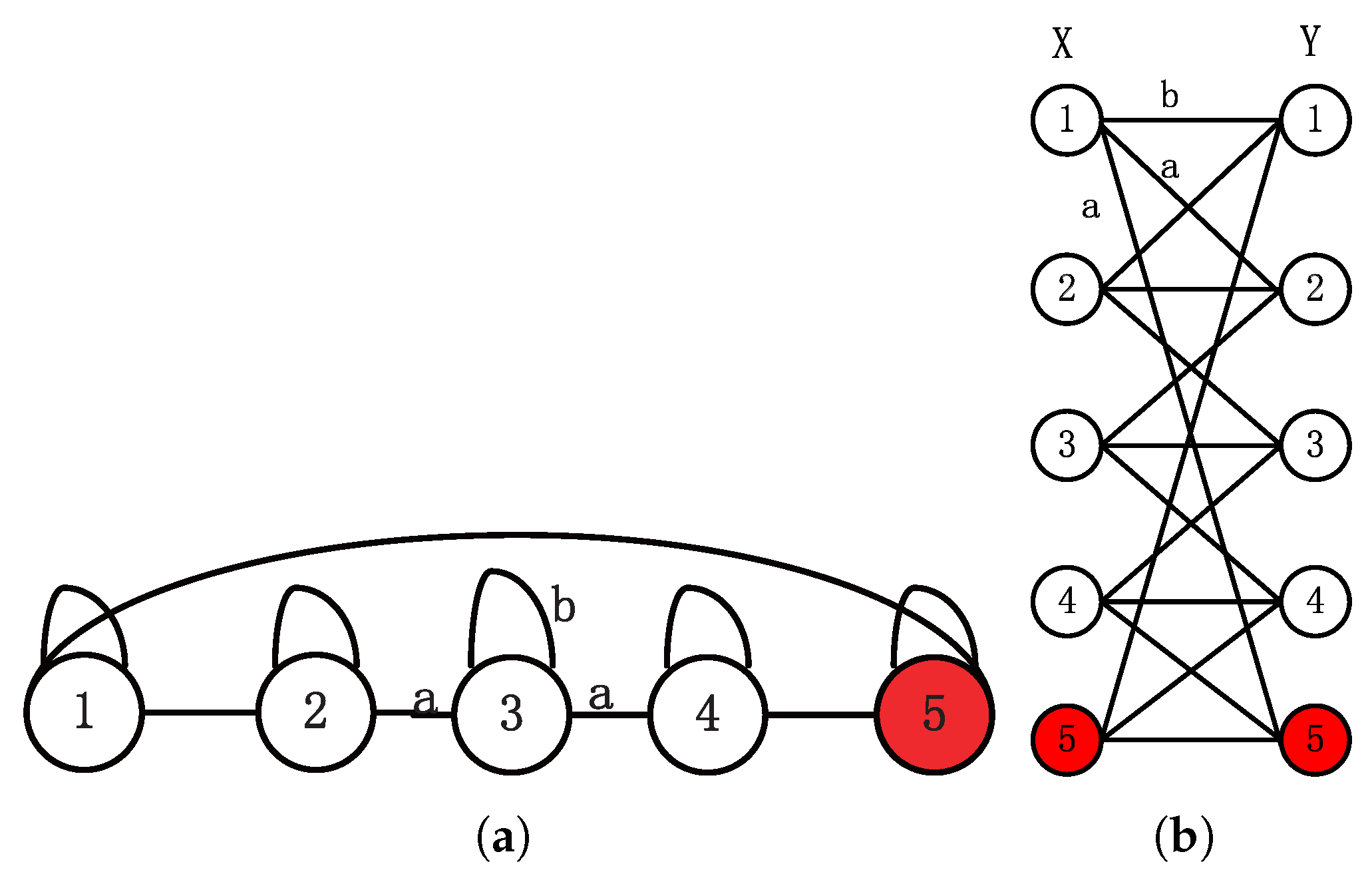
4. Bulk Spectra and Edge States of Szegedy’s Quantum Search on the 1D Cycle with Self-Loops
4.1. Bulk Spectra of Szegedy’s QW
- Thereby, Szegedy’s walk operator in Fourier space is rewritten by the following:
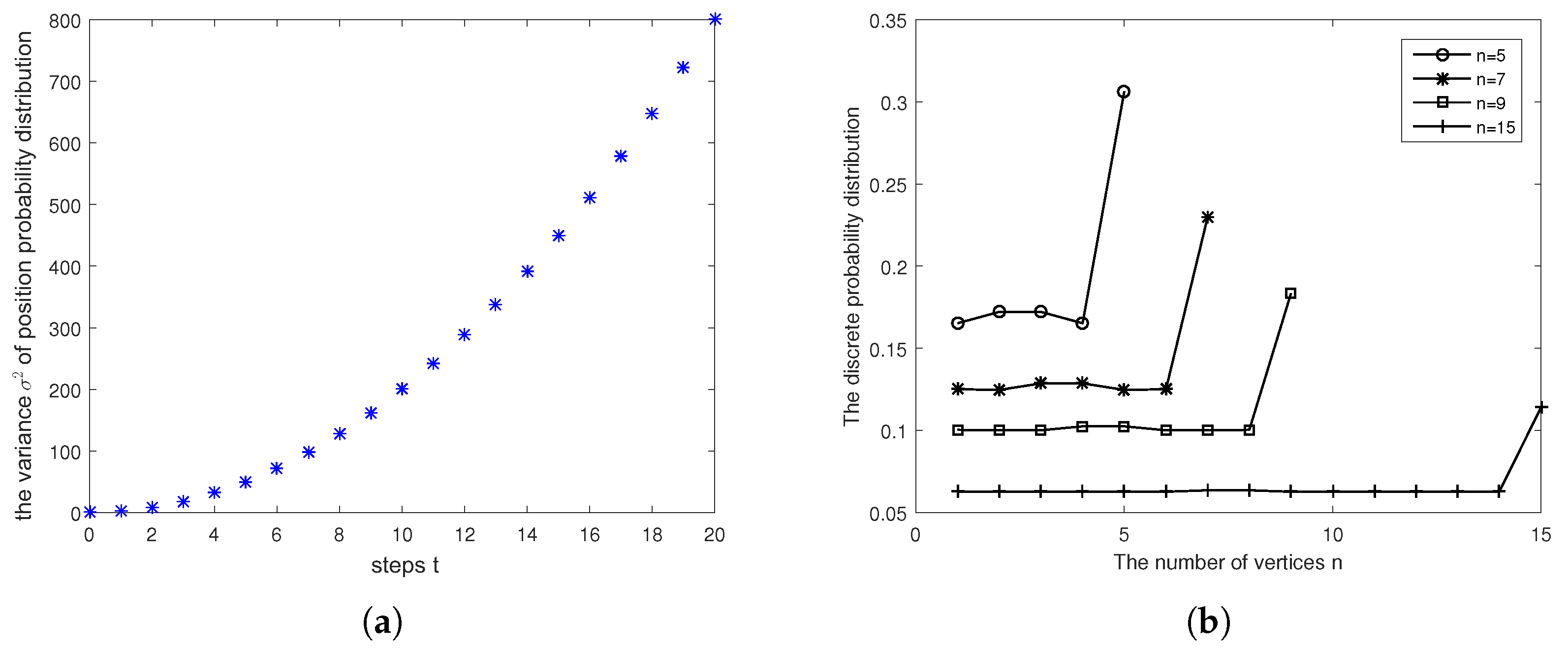
4.2. Edge Spectra of Szegedy’s Quantum Search
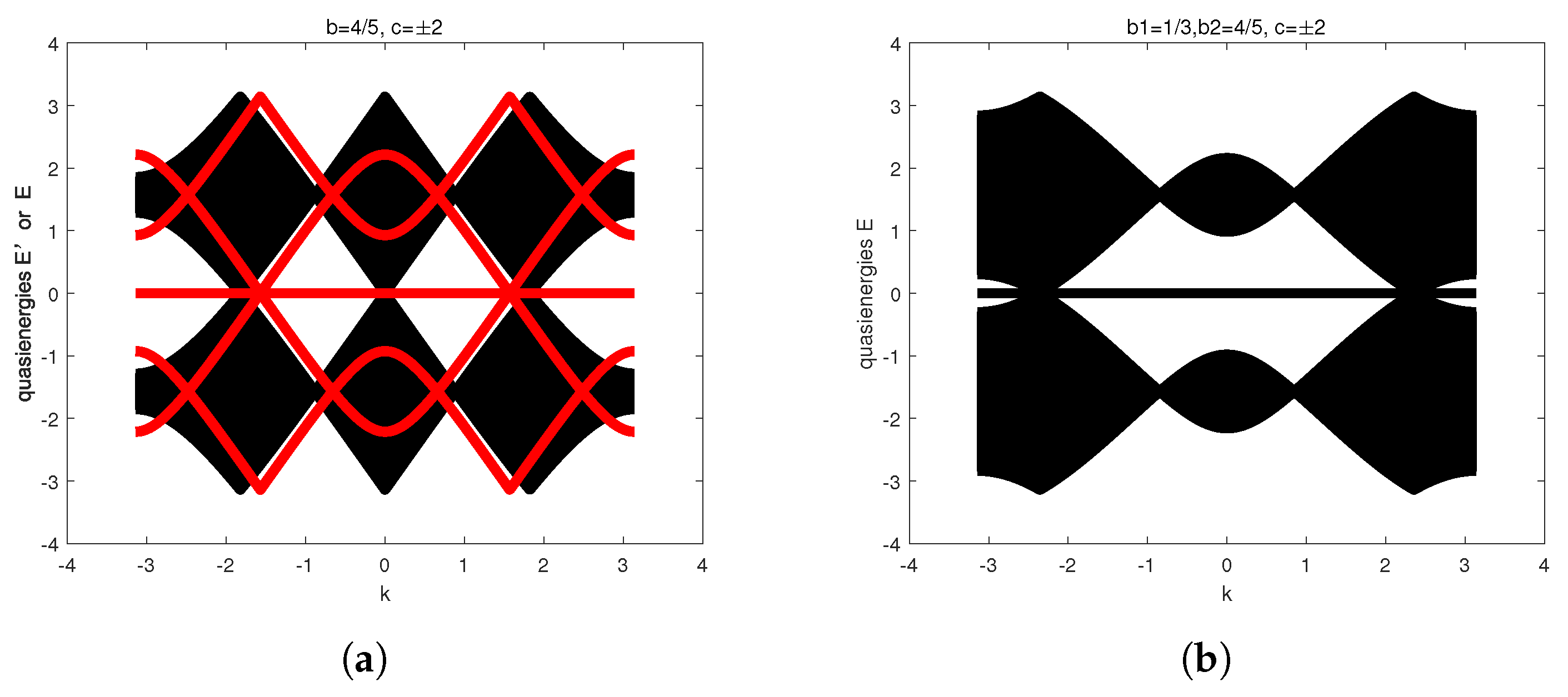
4.3. Bulk Spectra of the Generalized 3QWs with Different Coin Operators as Iterations
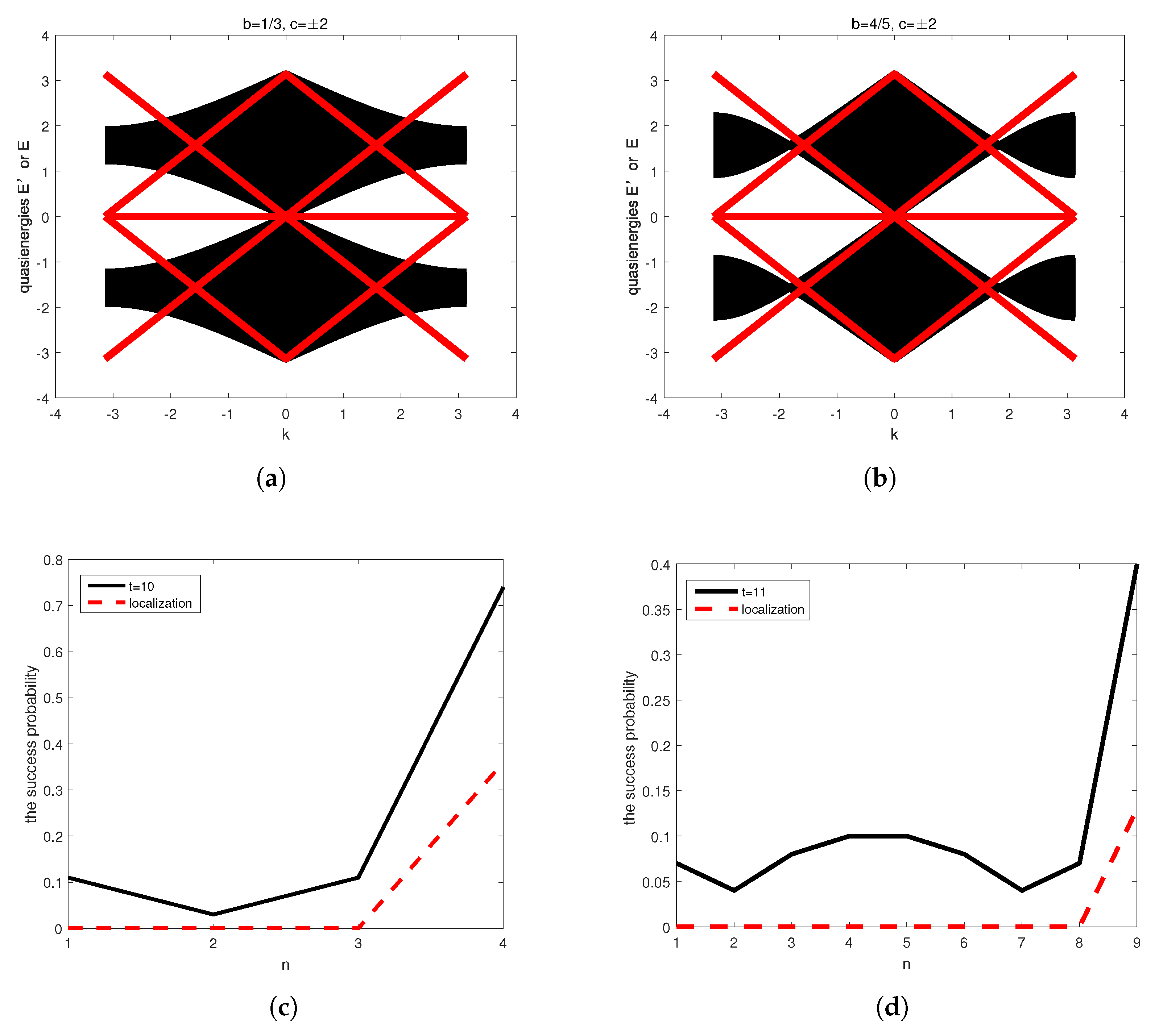
5. Topological Phases
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ambainis, A.; Kempe, J.; Rivosh, A. Coins make quantum walks faster. In Proceedings of the Sixteenth Annual ACM-SIAM Symposium on Discrete Algorithms, Vancouver, BC, Canada, 23–25 January 2005; ACM SIGACT, SIAM: Philadelphia, PA, USA, 2005; pp. 1099–1108. [Google Scholar]
- Cao, H.; Cao, F.; Wang, D. Quantum artificial neural networks with applications. Inf. Sci. 2015, 290, 1–6. [Google Scholar] [CrossRef]
- Inui, N.; Konishi, Y.; Konno, N. Localization of two-dimensional quantum walks. Phys. Rev. A 2004, 69, 052323. [Google Scholar] [CrossRef]
- Kitagawa, T.; Rudner, M.S.; Berg, E.; Demler, E. Exploring topological phases with quantum walks. Phys. Rev. A 2010, 82, 033429. [Google Scholar] [CrossRef]
- Panahiyan, S.; Fritzsche, S. Controllable simulation of topological phases and edge states with quantum walk. Phys. Lett. A 2020, 384, 126828. [Google Scholar] [CrossRef]
- Shenvi, N.; Kempe, J.; Whaley, K.B. Quantum random-walk search algorithm. Phys. Rev. A 2003, 67, 052307. [Google Scholar] [CrossRef]
- Wong, T.G. Grover search with lackadaisical quantum walks. J. Phys. A Math. Theor. 2018, 51, 069501. [Google Scholar] [CrossRef]
- Szegedy, M. Quantum speed-up of Markov chain based algorithms. In Proceedings of the 45th Annual IEEE Symposium on Foundations of Computer Science, Rome, Italy, 17–19 October 2004; pp. 32–41. [Google Scholar] [CrossRef]
- Xu, M.K.; Liu, Z.H.; Chen, H.W.; Zheng, S.H. Localization and discrete probability function of Szegedy’s quantum search on the one-dimensional cycle with self-loops. Quantum Inf. Comput. 2020, 20, 1281–1303. [Google Scholar] [CrossRef]
- Jin, X.; Li, X.; Feng, Y.; Wen, M.; Huang, C.; Yao, Y. RIS-Based Opposite Phase Index Modulation and Its DNN-Assisted Joint Sequence Detection. IEEE Wirel. Commun. Lett. 2023, 12, 1518–1522. [Google Scholar] [CrossRef]
- Asboth, J.K. Symmetries, topological phases, and bound states in the one-dimensional quantum walk. Phys. Rev. B 2012, 86, 195414. [Google Scholar] [CrossRef]
- Obuse, H.; Kawakami, N. Topological phases and delocalization of quantum walks in random environments. Phys. Rev. B 2011, 84, 195139. [Google Scholar] [CrossRef]
- Obuse, H.; Asboth, J.K.; Nishimura, Y.; Kawakami, N. Unveiling hidden topological phases of a one-dimensional Hadamard quantum walk. Phys. Rev. B 2015, 92, 045424. [Google Scholar] [CrossRef]
- Edo, S.; Endo, T.; Konno, N.; Segawa, E.; Takei, M. Limit theorems of a two-phase quantum walk with one defect. Quantum Inf. Comput. 2015, 15, 1373–1396. [Google Scholar]
- Rudner, M.S.; Levitov, L.S. Topological Transition in a Non-Hermitian Quantum Walk. Phys. Rev. Lett. 2009, 102, 065703. [Google Scholar] [CrossRef]
- Zhou, L. Entanglement Phase Transitions in Non-Hermitian Kitaev Chains. Entropy 2024, 26, 272. [Google Scholar] [CrossRef]
- Kitagawa, T.; Berg, E.; Rudner, M.; Demler, E. Topological characterization of periodically driven quantum systems. Phys. Rev. B 2010, 82, 235114. [Google Scholar] [CrossRef]
- He, Y.; Moore, J.; Varma, C.M. Berry phase and anomalous Hall effect in a three-orbital tight-binding Hamiltonian. Phys. Rev. B 2012, 85, 155106. [Google Scholar] [CrossRef]
- Rakovszky, T.; Asboth, J.K. Localization, delocalization, and topological phase transitions in the one-dimensional split-step quantum walk. Phys. Rev. A 2015, 92, 052311. [Google Scholar] [CrossRef]
- Edge, J.M.; Asboth, J.K. Localization, delocalization, and topological transitions in disordered two-dimensional quantum walks. Phys. Rev. B 2015, 91, 104202. [Google Scholar] [CrossRef]
- Asboth, J.K.; Edge, J.M. Edge-state-enhanced transport in a two-dimensional quantum walk. Phys. Rev. A 2015, 91, 022324. [Google Scholar] [CrossRef]
- Wong, T.G. Equivalence of Szegedy’s and coined quantum walks. Quantum Inf. Process. 2017, 16, 215. [Google Scholar] [CrossRef][Green Version]
- Zhu, Y.Q.; Zhang, D.W.; Yan, H.; Xing, D.Y.; Zhu, S.L. Emergent pseudospin-1 Maxwell fermions with a threefold degeneracy in optical lattices. Phys. Rev. A 2017, 96, 033634. [Google Scholar] [CrossRef]
- Tan, X.S.; Zhang, D.W.; Liu, Q.; Xue, G.M.; Yu, H.F.; Zhu, Y.Q.; Yan, H.; Zhu, S.L.; Yu, Y. Topological Maxwell Metal Bands in a Superconducting Qutrit. Phys. Rev. Lett. 2018, 120, 130503. [Google Scholar] [CrossRef] [PubMed]
- Stuart, F.; Andrew, J.D. Enhanced repulsively bound atom pairs in topological optical lattice ladders. Quantum Sci. Technol. 2020, 5, 045017. [Google Scholar] [CrossRef]
- Inui, N.; Konno, N.; Segawa, E. One-dimensional three-state quantum walk. Phys. Rev. E 2005, 72, 056112. [Google Scholar] [CrossRef]
- Endo, T.; Konno, N.; Obuse, H.; Segawa, E. Sensitivity of quantum walks to a boundary of two-dimensional lattices: Approaches based on the CGMV method and topological phases. J. Phys. A Math. Theor. 2017, 50, 455302. [Google Scholar] [CrossRef]
- Xu, M.K.; Liu, Z.H.; Chen, H.W.; Zheng, S.H. Probability and Entanglement Evolutions for Szegedy’s Quantum Search on the One-dimensional Cycle with Self-loops. Quantum Inf. Process. 2021, 20, 51. [Google Scholar] [CrossRef]
- Asboth, J.K.; Obuse, H. Bulk-boundary correspondence for chiral symmetric quantum walks. Phys. Rev. B 2013, 88, 121406. [Google Scholar] [CrossRef]
- Asboth, J.K.; Tarasinski, B.; Delplace, P. Chiral symmetry and bulk-boundary correspondence in periodically driven one-dimensional systems. Phys. Rev. B 2014, 90, 125143. [Google Scholar] [CrossRef]
- Ramachandran, A.; Andreanov, A.; Flach, S. Chiral flat bands: Existence, engineering, and stability. Phys. Rev. B 2017, 96, 161104. [Google Scholar] [CrossRef]
- Wang, K.; Wu, N.; Xu, P.; Song, F.M. One-dimensional lackadaisical quantum walks. J. Phys. A Math. Theor. 2017, 50, 505302. [Google Scholar] [CrossRef]
- Yin, C.H.; Jiang, H.; Li, L.H.; Lu, R.; Chen, S. Geometrical meaning of winding number and its characterization of topological phases in one-dimensional chiral non-Hermitian systems. Phys. Rev. Lett. 2018, 97, 052115. [Google Scholar] [CrossRef]
- Shen, H.T.; Zhen, B.; Fu, L. Topological Band Theory for Non-Hermitian Hamiltonians. Phys. Rev. Lett. 2018, 120, 146402. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.E. Anomalous Edge State in a Non-Hermitian Lattice. Phys. Rev. Lett. 2016, 116, 133903. [Google Scholar] [CrossRef] [PubMed]
- Leykam, D.; Bliokh, K.Y.; Huang, C.L.; Chong, Y.D.; Nori, F. Edge Modes, Degeneracies, and Topological Numbers in Non-Hermitian Systems. Phys. Rev. Lett. 2017, 118, 040401. [Google Scholar] [CrossRef]
- Yao, S.Y.; Wang, Z. Edge States and Topological Invariants of Non-Hermitian Systems. Phys. Rev. Lett. 2018, 121, 086803. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, M.; Li, X.; Wang, X.; Mi, W.; Chen, X. Edge States, Bulk Spectra, and Topological Phases of Szegedy’s Quantum Search on a One-Dimensional Cycle with Self-Loops. Entropy 2025, 27, 623. https://doi.org/10.3390/e27060623
Xu M, Li X, Wang X, Mi W, Chen X. Edge States, Bulk Spectra, and Topological Phases of Szegedy’s Quantum Search on a One-Dimensional Cycle with Self-Loops. Entropy. 2025; 27(6):623. https://doi.org/10.3390/e27060623
Chicago/Turabian StyleXu, Mengke, Xi Li, Xunan Wang, Wanglei Mi, and Xiao Chen. 2025. "Edge States, Bulk Spectra, and Topological Phases of Szegedy’s Quantum Search on a One-Dimensional Cycle with Self-Loops" Entropy 27, no. 6: 623. https://doi.org/10.3390/e27060623
APA StyleXu, M., Li, X., Wang, X., Mi, W., & Chen, X. (2025). Edge States, Bulk Spectra, and Topological Phases of Szegedy’s Quantum Search on a One-Dimensional Cycle with Self-Loops. Entropy, 27(6), 623. https://doi.org/10.3390/e27060623




