Autoencoder-like Sparse Non-Negative Matrix Factorization with Structure Relationship Preservation
Abstract
1. Introduction
2. Related Work
2.1. Non-Negative Matrix Factorization (NMF)
2.2. Robust Non-Negative Matrix Factorization (RNMF)
2.3. Graph Regularized Non-Negative Matrix Factorization (GNMF)
3. Methodology
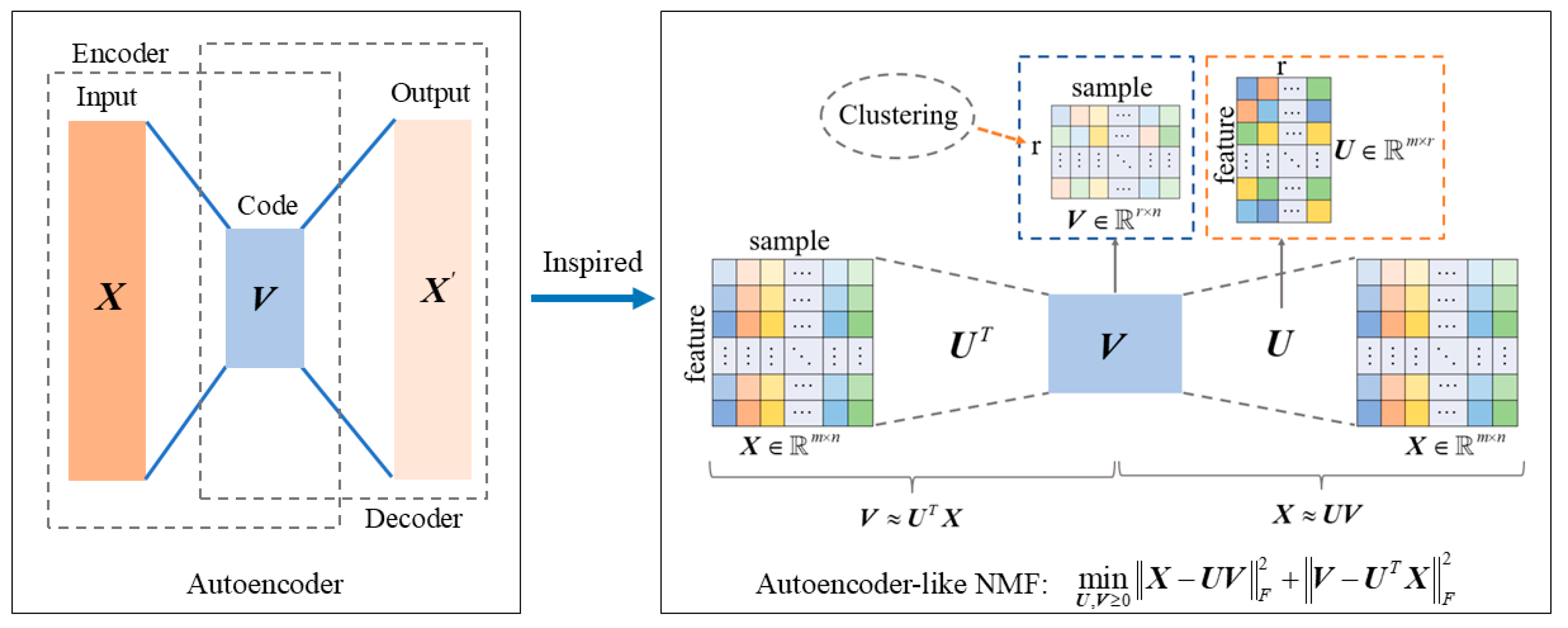
3.1. Autoencoder-like Non-Negative Matrix Factorization
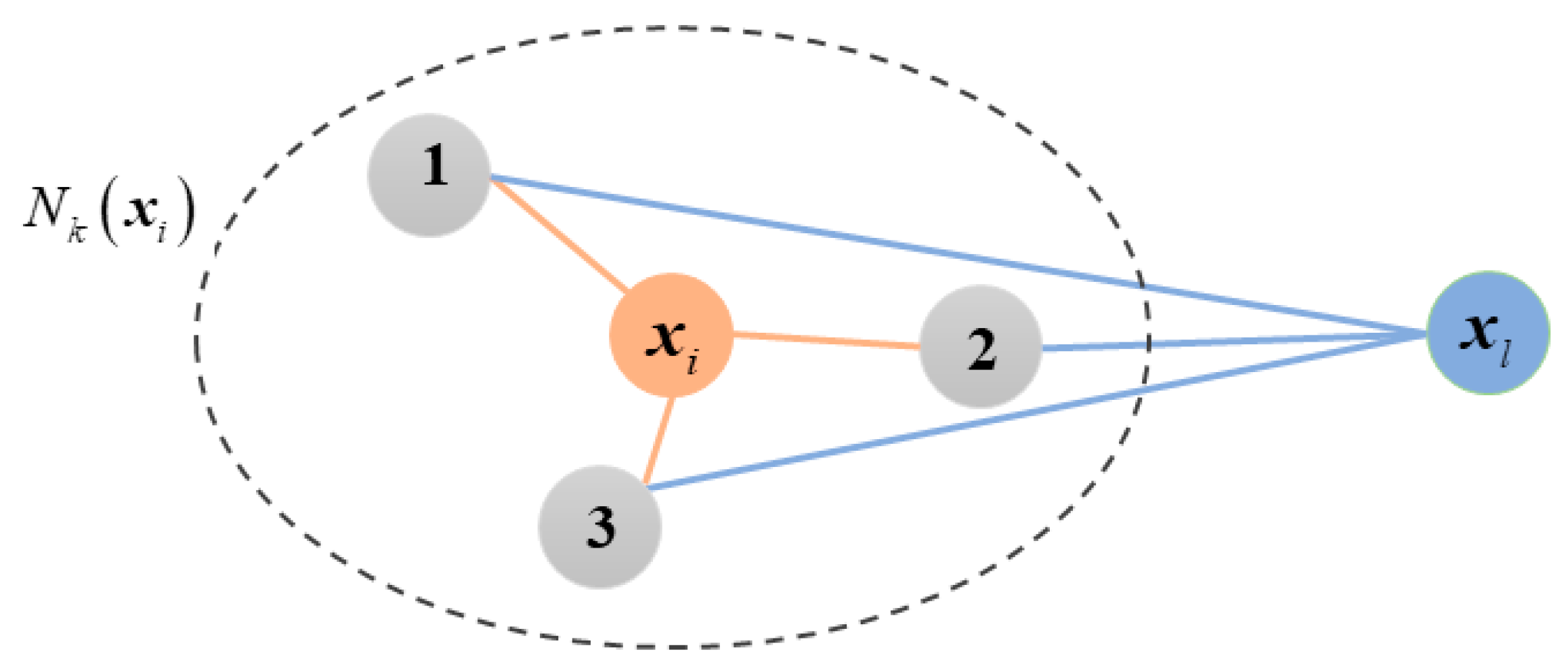
3.2. High-Order Graph Regularization
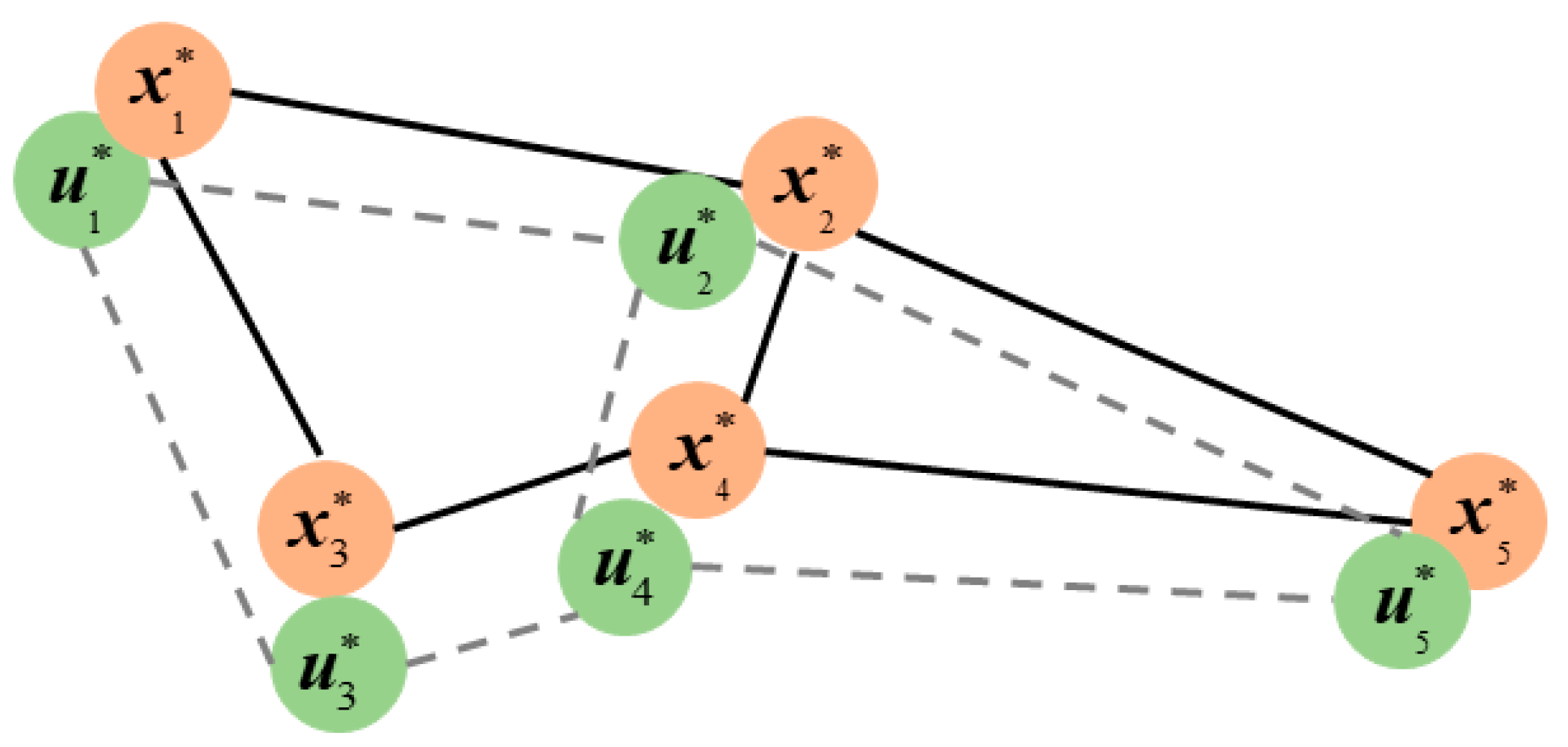
3.3. Feature Relationship Preservation
3.4. Sparsity of Coefficient Matrix
3.5. Objective Function
3.6. Optimization Algorithm
3.7. Convergence Analysis
| Algorithm 1 ASNMF-SRP |
| Input: Initial matrix , number of classes , neighborhood parameter , regularization parameters , and , balance parameters and parameter , threshold , maximum iterations . Output: Basis matrix and coefficient matrix . 1. Initialization: , Randomly generate basis matrix and coefficient matrix ; 2. Obtain optimal Laplacian matrix according to Equations (11)–(17); 3. For 4. ; 5. ; 6. if and Break and return (,); 7. End if 8. End for |
3.8. Time Complexity Analysis
4. Experiments
4.1. Dataset
4.2. Clustering Performance Evaluation Metrics
4.2.1. Clustering Accuracy (ACC)
4.2.2. Adjusted Rand Index (ARI)
4.2.3. Normalized Mutual Information (NMI)
4.2.4. Clustering Purity (PUR)
4.3. Comparison Algorithms and Parameter Settings
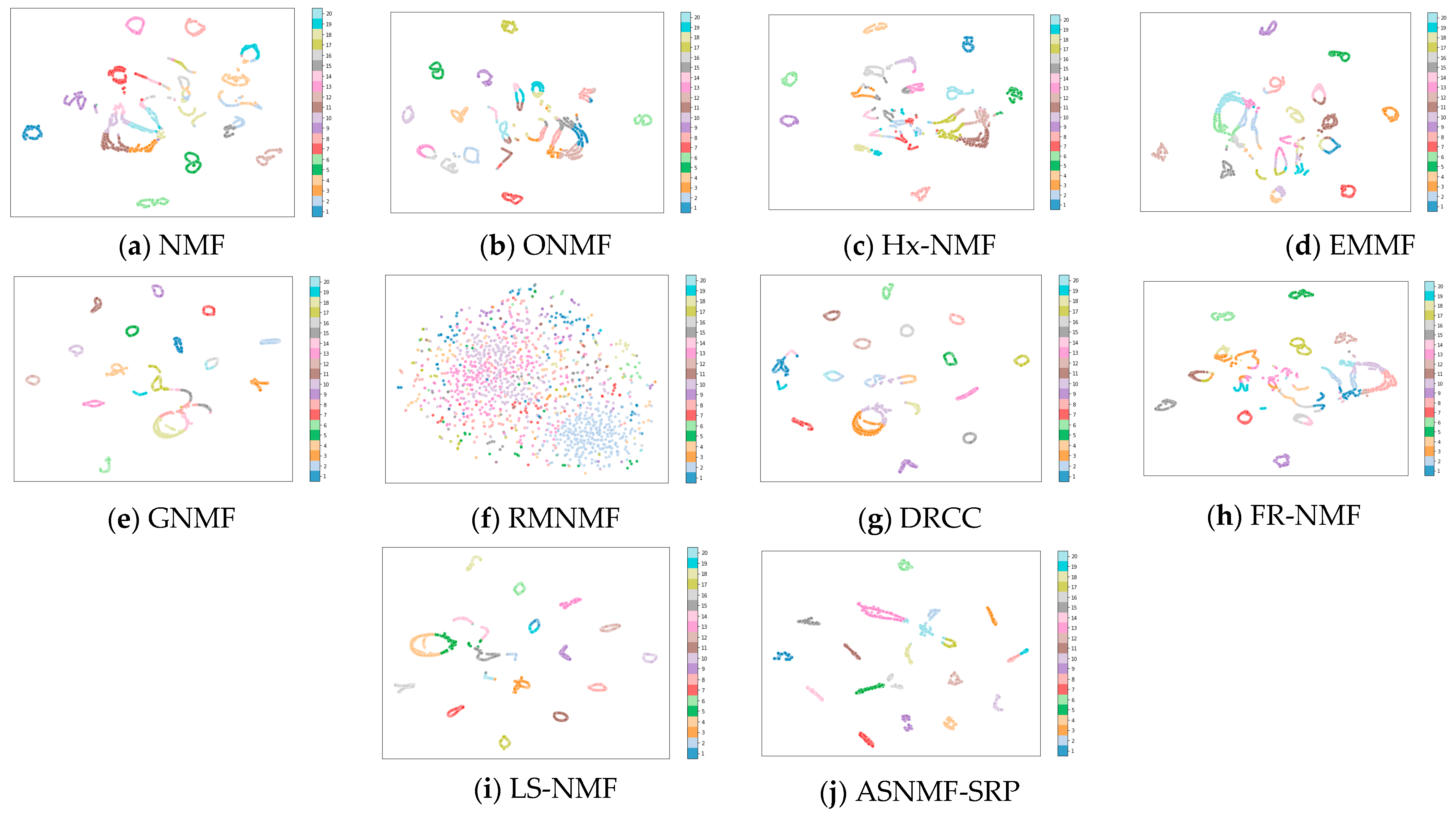
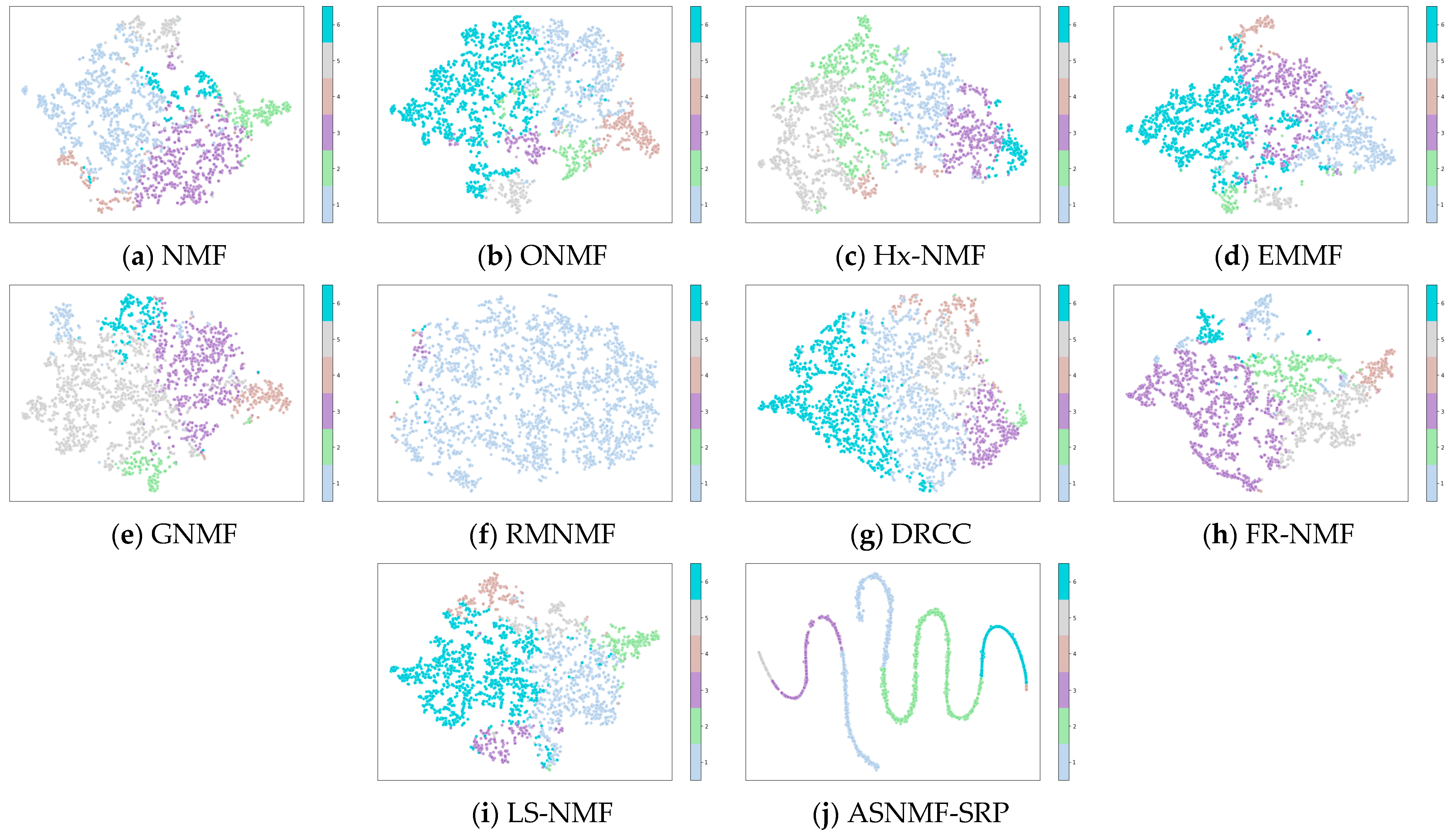
4.4. Results and Analysis
4.5. Analysis of the Impact of Autoencoder-like NMF on Clustering Performance
4.6. Analysis of the Impact of Higher-Order Graph Regularization on Clustering Performance
4.7. Robustness Analysis of ASNMF-SRP
4.8. Parameter Sensitivity Analysis
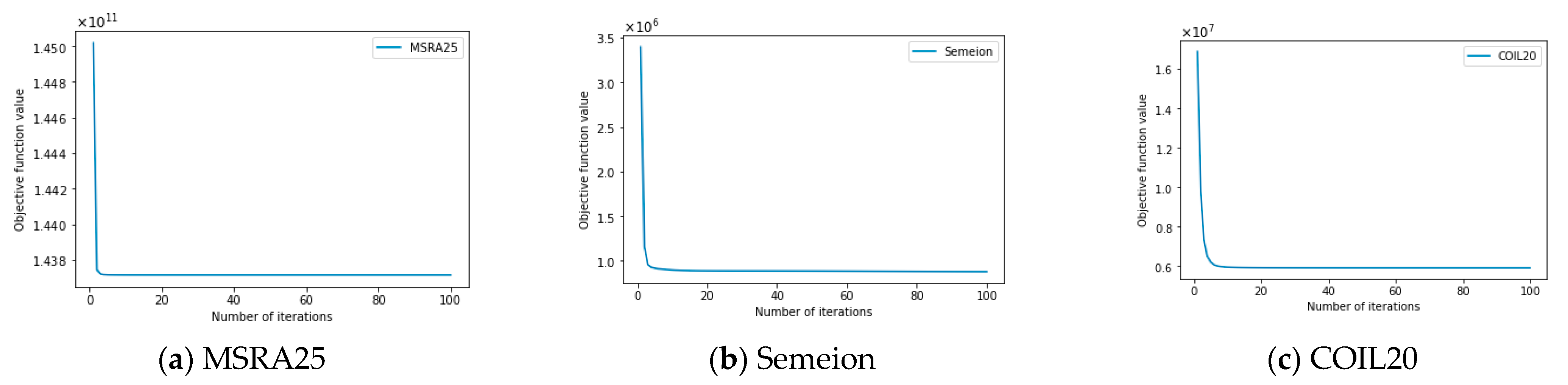
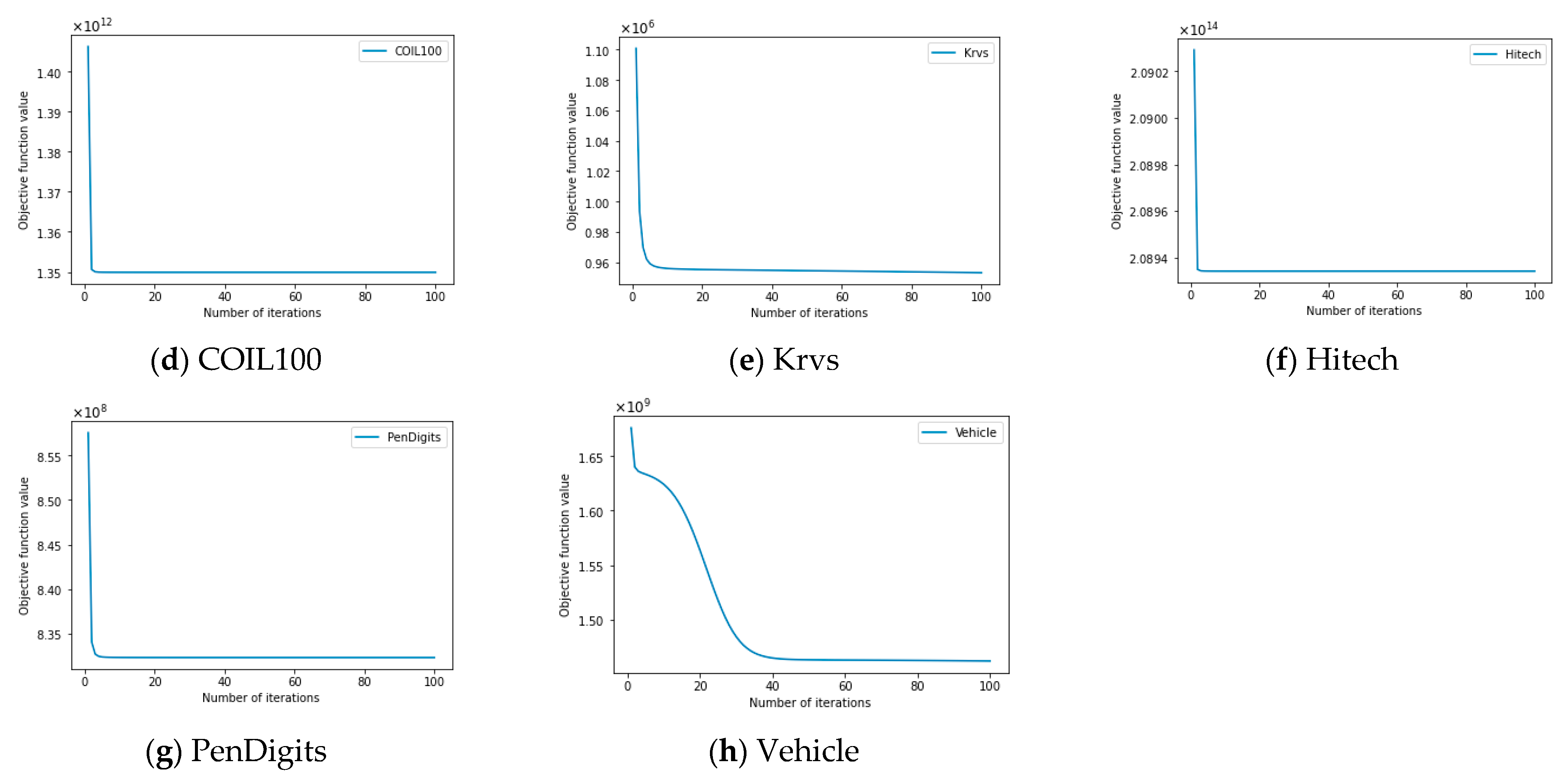
4.9. Empirical Convergence
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kim, S.; Shin, W.; Kim, H.W. Predicting online customer purchase: The integration of customer characteristics and browsing patterns. Decis. Support Syst. 2024, 177, 114105. [Google Scholar] [CrossRef]
- Zeng, Y.; Chen, J.; Pan, Z.; Yu, W.; Yang, Y. Integrating single-cell multi-omics data through self-supervised clustering. Appl. Soft Comput. 2025, 169, 112541. [Google Scholar] [CrossRef]
- Mardani, K.; Maghooli, K.; Farokhi, F. Segmentation of coronary arteries from X-ray angiographic images using density based spatial clustering of applications with noise (DBSCAN). Biomed. Signal Process. Control 2025, 101, 107175. [Google Scholar] [CrossRef]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, Y.; Levine, M.D.; Yuan, X.; Wang, L. Multisensor video fusion based on higher order singular value decomposition. Inf. Fusion 2015, 24, 54–71. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef]
- Hoyer, P.O. Non-negative matrix factorization with sparseness constraints. J. Mach. Learn. Res. 2004, 5, 1457–1469. [Google Scholar] [CrossRef]
- Kong, D.; Ding, C.; Huang, H. Robust Nonnegative Matrix Factorization Using L21-norm. In Proceedings of the 20th ACM International Conference on Information and Knowledge Management, Glasgow, UK, 24–28 October 2011; pp. 673–682. [Google Scholar] [CrossRef]
- Ding, C.; Li, T.; Peng, W. Orthogonal nonnegative matrix t-factorizations for clustering. In Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Philadelphia, PA, USA, 20–23 August 2006; pp. 126–135. [Google Scholar] [CrossRef]
- Belkin, M.; Niyogi, P.; Sindhwani, V. Manifold Regularization: A Geometric Framework for Learning from Labeled and Unlabeled Examples. J. Mach. Learn. Res. 2006, 7, 2399–2434. [Google Scholar]
- Cai, D.; He, X.; Han, J.; Huang, T.S. Graph Regularized Nonnegative Matrix Factorization for Data Representation. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 1548–1560. [Google Scholar] [CrossRef]
- Wu, B.; Wang, E.; Zhu, Z.; Chen, W.; Xiao, P. Manifold NMF with L2,1 norm for clustering. Neurocomputing 2018, 273, 78–88. [Google Scholar] [CrossRef]
- Li, X.; Cui, G.; Dong, Y. Graph Regularized Non-Negative Low-Rank Matrix Factorization for Image Clustering. IEEE Trans. Cybern. 2017, 47, 3840–3853. [Google Scholar] [CrossRef]
- Liu, Z.; Zhu, F.; Xiong, H.; Chen, X.; Pelusi, D.; Vasilakos, A.V. Graph regularized discriminative nonnegative matrix factorization. Eng. Appl. Artif. Intell. 2025, 139, 109629. [Google Scholar] [CrossRef]
- Huang, S.; Xu, Z.; Zhao, K.; Ren, Y. Regularized nonnegative matrix factorization with adaptive local structure learning. Neurocomputing 2020, 382, 196–209. [Google Scholar] [CrossRef]
- Ren, X.; Yang, Y. Semi-supervised symmetric non-negative matrix factorization with graph quality improvement and constraints. Appl. Intell. 2025, 55, 397. [Google Scholar] [CrossRef]
- Mohammadi, M.; Berahmand, K.; Azizi, S.; Sheikhpour, R.; Khosravi, H. Semi-Supervised Adaptive Symmetric Nonnegative Matrix Factorization for Multi-View Clustering. IEEE Trans. Netw. Sci. Eng. 2025; early access. [Google Scholar] [CrossRef]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. Adv. Neural Inf. Process. Syst. 2016, 29, 3844–3852. [Google Scholar] [CrossRef]
- Wang, D.; Ren, F.; Zhuang, Y.; Liang, C. Robust high-order graph learning for incomplete multi-view clustering. Expert Syst. Appl. 2025, 280, 127580. [Google Scholar] [CrossRef]
- Zhan, S.; Jiang, H.; Shen, D. Co-regularized optimal high-order graph embedding for multi-view clustering. Pattern Recogn. 2025, 157, 110892. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, H.; Zhao, S. Auto-encoder based dimensionality reduction. Neurocomputing 2016, 184, 232–242. [Google Scholar] [CrossRef]
- Chen, Y.; Qu, G.; Zhao, J. Orthogonal graph regularized non-negative matrix factorization under sparse constraints for clustering. Expert Syst. Appl. 2024, 249, 123797. [Google Scholar] [CrossRef]
- Meng, Y.; Shang, R.; Jiao, L.; Zhang, W.; Yang, S. Dual-graph regularized non-negative matrix factorization with sparse and orthogonal constraints. Eng. Appl. Artif. Intell. 2018, 69, 24–35. [Google Scholar] [CrossRef]
- Peng, C.; Zhang, Y.; Chen, Y.; Kang, Z.; Chen, C.; Cheng, Q. Log-based sparse nonnegative matrix factorization for data representation. Knowl.-Based Syst. 2022, 251, 109127. [Google Scholar] [CrossRef]
- Xiong, W.; Ma, Y.; Zhang, C.; Liu, S. Dual graph-regularized sparse robust adaptive non-negative matrix factorization. Expert Syst. Appl. 2025, 281, 127594. [Google Scholar] [CrossRef]
- Shang, F.; Jiao, L.C.; Wang, F. Graph dual regularization non-negative matrix factorization for co-clustering. Pattern Recognit. 2012, 45, 2237–2250. [Google Scholar] [CrossRef]
- Gu, Q.; Zhou, J. Co-clustering on manifolds. In Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Paris, France, 28 June–1 July 2009; pp. 359–368. [Google Scholar] [CrossRef]
- Hedjam, R.; Abdesselam, A.; Melgani, F. NMF with feature relationship preservation penalty term for clustering problems. Pattern Recognit. 2021, 112, 107814. [Google Scholar] [CrossRef]
- Salahian, N.; Tab, F.A.; Seyedi, S.A.; Chavoshinejad, J. Deep Autoencoder-like NMF with Contrastive Regularization and Feature Relationship Preservation. Expert Syst. Appl. 2023, 214, 119051. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Algorithms for non-negative matrix factorization. In Proceedings of the 14th International Conference on Neural Information Processing Systems, Denver, CO, USA, 1 January 2000; pp. 535–541. [Google Scholar]
- Sun, B.J.; Shen, H.; Gao, J.; Ouyang, W.; Cheng, X. A non-negative symmetric encoder-decoder approach for community detection. In Proceedings of the 2017 ACM Conference on Information and Knowledge Management, New York, NY, USA, 6–10 November 2017; pp. 597–606. [Google Scholar] [CrossRef]
- Li, T.; Zhang, R.; Yao, Y.; Liu, Y.; Ma, J.; Tang, J. Graph regularized autoencoding-inspired non-negative matrix factorization for link prediction in complex networks using clustering information and biased random walk. J. Supercomput. 2024, 80, 14433–14469. [Google Scholar] [CrossRef]
- Zhang, H.; Kou, G.; Peng, Y.; Zhang, B. Role-aware random walk for network embedding. Inf. Sci. 2024, 652, 119765. [Google Scholar] [CrossRef]
- Hosein, M.; Massoud, B.Z.; Christian, J. A Fast Approach for Overcomplete Sparse Decomposition Based on Smoothed l~(0) Norm. IEEE Trans. Signal Process. 2009, 57, 289–301. [Google Scholar] [CrossRef]
- Lu, X.; Wu, H.; Yuan, Y.; Yan, P.; Li, X. Manifold Regularized Sparse NMF for Hyperspectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2815–2826. [Google Scholar] [CrossRef]
- Meng, Y.; Shang, R.; Jiao, L.; Zhang, W.; Yuan, Y.; Yang, S. Feature selection based dual-graph sparse non-negative matrix factorization for local discriminative clustering. Neurocomputing 2018, 290, 87–99. [Google Scholar] [CrossRef]
- Wang, J.; Wang, L.; Nie, F.; Li, X. A novel formulation of trace ratio linear discriminant analysis. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 5568–5578. [Google Scholar] [CrossRef]
- Wang, Q.; He, X.; Jiang, X.; Li, X. Robust Bi-stochastic Graph Regularized Matrix Factorization for Data Clustering. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 390–403. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Li, X. Entropy Minimizing Matrix Factorization. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 9209–9222. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Nie, F.; Huang, H.; Ding, C.H.Q. Robust Manifold Nonnegative Matrix Factorization. ACM Trans. Knowl. Discov. Data 2013, 8, 11. [Google Scholar] [CrossRef]





| No. | Method | Introduction to Sparsity Method |
|---|---|---|
| 1 | -norm [34] | denotes the number of non-zero elements in . |
| 2 | -norm [35] | |
| 3 | -norm [22] | |
| 4 | -norm [36] | |
| 5 | -(pseudo) norm [24] |
| NO. | Dataset | Samples () | Features () | Classes () | Data Type | Image Size |
|---|---|---|---|---|---|---|
| 1 | MSRA25 | 1799 | 256 | 12 | Face dataset | 16 × 16 |
| 2 | Semeion | 1593 | 256 | 10 | Digit images | 16 × 16 |
| 3 | COIL20 | 1440 | 1024 | 20 | Object images | 32 × 32 |
| 4 | COIL100 | 7200 | 1024 | 100 | Object images | 32 × 32 |
| 5 | Krvs | 3196 | 36 | 2 | Network detection | — |
| 6 | Hitech | 2301 | 2216 | 6 | Technology news | — |
| 7 | PenDigits | 3498 | 16 | 10 | Handwritten digits | — |
| 8 | Vehicle | 846 | 18 | 4 | Vehicle contours | — |
| No. | Dataset | Higher-Order Graph Regularization | Feature Relationship Preservation | Sparse Constraint |
|---|---|---|---|---|
| 1 | MSRA25 | 1000 | 1000 | 0.001 |
| 2 | Semeion | 1 | 100 | 0.0001 |
| 3 | COIL20 | 1000 | 1000 | 0.001 |
| 4 | COIL100 | 1000 | 1000 | 0.001 |
| 5 | Krvs | 100 | 10 | 0.0001 |
| 6 | Hitech | 1000 | 10 | 0.0001 |
| 7 | PenDigits | 100 | 100 | 0.001 |
| 8 | Vehicle | 1 | 1 | 0.001 |
| Algorithm | NMF | ONMF | Hx-NMF | EMMF | GNMF | RMNMF | DRCC | FR-NMF | LS-NMF | ASNMF-SRP | I-P | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dataset | ||||||||||||
| MSRA25 | 0.50842 | 0.49375 | 0.52026 | 0.50592 | 0.53938 | 0.55550 | 0.28974 | 0.51659 | 0.54019 | 0.57904 | 4.24% | |
| ±0.023 | ±0.026 | ±0.029 | ±0.018 | ±0.032 | ±0.034 | ±0.029 | ±0.022 | ±0.022 | ±0.045 | -- | ||
| Semeion | 0.52508 | 0.56959 | 0.50807 | 0.51965 | 0.59209 | 0.27916 | 0.61601 | 0.53540 | 0.60251 | 0.68063 | 10.49% | |
| ±0.042 | ±0.032 | ±0.042 | ±0.040 | ±0.039 | ±0.057 | ±0.037 | ±0.037 | ±0.036 | ±0.050 | -- | ||
| COIL20 | 0.66406 | 0.68531 | 0.65812 | 0.65142 | 0.76844 | 0.24385 | 0.79017 | 0.65028 | 0.77361 | 0.84174 | 6.53% | |
| ±0.029 | ±0.028 | ±0.030 | ±0.019 | ±0.013 | ±0.094 | ±0.034 | ±0.026 | ±0.014 | ±0.012 | -- | ||
| COIL100 | 0.47026 | 0.49159 | 0.46877 | 0.47882 | 0.48738 | 0.41235 | 0.46099 | 0.47044 | 0.48306 | 0.64173 | 30.54% | |
| ±0.014 | ±0.011 | ±0.012 | ±0.018 | ±0.014 | ±0.012 | ±0.014 | ±0.015 | ±0.011 | ±0.010 | -- | ||
| Krvs | 0.51909 | 0.53742 | 0.52223 | 0.52137 | 0.53082 | 0.51810 | 0.55594 | 0.52552 | 0.53387 | 0.56813 | 2.19% | |
| ±0.003 | ±0.012 | ±0.002 | ±0.003 | ±0.012 | ±0.007 | ±0.004 | ±0.023 | ±0.015 | ±0.003 | -- | ||
| Hitech | 0.23385 | 0.23375 | 0.23403 | 0.23544 | 0.23105 | 0.26273 | 0.24087 | 0.22603 | 0.23268 | 0.25367 | −3.45% | |
| ±0.002 | ±0.005 | ±0.008 | ±0.004 | ±0.004 | ±0.001 | ±0.004 | ±0.007 | ±0.002 | ±0.002 | -- | ||
| PenDigits | 0.66216 | 0.70729 | 0.68092 | 0.66630 | 0.67973 | 0.65183 | 0.73119 | 0.66791 | 0.68533 | 0.80442 | 10.02% | |
| ±0.036 | ±0.048 | ±0.040 | ±0.038 | ±0.053 | ±0.037 | ±0.043 | ±0.034 | ±0.052 | ±0.032 | -- | ||
| Vehicle | 0.38794 | 0.43777 | 0.40142 | 0.39096 | 0.44397 | 0.35916 | 0.41194 | 0.43570 | 0.44368 | 0.45236 | 1.89% | |
| ±0.019 | ±0.002 | ±0.026 | ±0.021 | ±0.008 | ±0.003 | ±0.017 | ±0.023 | ±0.009 | ±0.002 | -- | ||
| Algorithm | NMF | ONMF | Hx-NMF | EMMF | GNMF | RMNMF | DRCC | FR-NMF | LS-NMF | ASNMF-SRP | I-P | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dataset | ||||||||||||
| MSRA25 | 0.34575 | 0.32933 | 0.35734 | 0.33482 | 0.40605 | 0.40058 | 0.12013 | 0.35562 | 0.40596 | 0.44662 | 9.99% | |
| ±0.026 | ±0.027 | ±0.027 | ±0.020 | ±0.037 | ±0.034 | ±0.023 | ±0.019 | ±0.034 | ±0.052 | -- | ||
| Semeion | 0.31198 | 0.35051 | 0.30655 | 0.31134 | 0.44280 | 0.11855 | 0.41651 | 0.31943 | 0.45921 | 0.48809 | 6.29% | |
| ±0.033 | ±0.024 | ±0.031 | ±0.030 | ±0.032 | ±0.047 | ±0.026 | ±0.029 | ±0.030 | ±0.034 | -- | ||
| COIL20 | 0.57989 | 0.62582 | 0.57627 | 0.57069 | 0.74160 | 0.16450 | 0.73372 | 0.56682 | 0.74234 | 0.80244 | 8.10% | |
| ±0.026 | ±0.023 | ±0.034 | ±0.026 | ±0.018 | ±0.093 | ±0.036 | ±0.024 | ±0.016 | ±0.007 | -- | ||
| COIL100 | 0.39584 | 0.44157 | 0.39549 | 0.40697 | 0.42371 | 0.30329 | 0.39167 | 0.39709 | 0.42067 | 0.53573 | 21.32% | |
| ±0.016 | ±0.014 | ±0.017 | ±0.019 | ±0.010 | ±0.015 | ±0.016 | ±0.012 | ±0.011 | ±0.016 | -- | ||
| Krvs | 0.00107 | 0.00579 | 0.00158 | 0.00147 | 0.00393 | −0.00038 | 0.01201 | 0.00410 | 0.00505 | 0.01814 | 51.04% | |
| ±0.000 | ±0.004 | ±0.000 | ±0.000 | ±0.003 | ±0.001 | ±0.002 | ±0.006 | ±0.005 | ±0.002 | -- | ||
| Hitech | −0.00095 | 0.00092 | 0.00021 | 0.00034 | −0.00041 | 0.00016 | 0.00252 | 0.00066 | −0.00049 | 0.00689 | 173.41% | |
| ±0.001 | ±0.001 | ±0.001 | ±0.001 | ±0.001 | ±0.001 | ±0.002 | ±0.001 | ±0.001 | ±0.000 | -- | ||
| PenDigits | 0.52361 | 0.55428 | 0.52352 | 0.52329 | 0.54137 | 0.50238 | 0.57474 | 0.52889 | 0.55809 | 0.68487 | 19.16% | |
| ±0.029 | ±0.040 | ±0.037 | ±0.022 | ±0.045 | ±0.049 | ±0.037 | ±0.024 | ±0.039 | ±0.035 | -- | ||
| Vehicle | 0.08169 | 0.12462 | 0.09207 | 0.08322 | 0.13103 | 0.06364 | 0.09691 | 0.11321 | 0.13221 | 0.12014 | −9.13% | |
| ±0.013 | ±0.003 | ±0.018 | ±0.018 | ±0.009 | ±0.004 | ±0.014 | ±0.012 | ±0.007 | ±0.001 | -- | ||
| Algorithm | NMF | ONMF | Hx-NMF | EMMF | GNMF | RMNMF | DRCC | FR-NMF | LS-NMF | ASNMF-SRP | I-P | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dataset | ||||||||||||
| MSRA25 | 0.56935 | 0.56296 | 0.57773 | 0.55467 | 0.65111 | 0.60295 | 0.23745 | 0.57715 | 0.64613 | 0.71512 | 9.83% | |
| ±0.021 | ±0.028 | ±0.023 | ±0.021 | ±0.031 | ±0.029 | ±0.033 | ±0.017 | ±0.031 | ±0.026 | -- | ||
| Semeion | 0.44162 | 0.48847 | 0.44312 | 0.44938 | 0.60790 | 0.20171 | 0.54014 | 0.44938 | 0.61489 | 0.63282 | 2.92% | |
| ±0.025 | ±0.020 | ±0.026 | ±0.023 | ±0.020 | ±0.074 | ±0.018 | ±0.022 | ±0.019 | ±0.021 | -- | ||
| COIL20 | 0.76112 | 0.79591 | 0.76067 | 0.75423 | 0.88538 | 0.31375 | 0.89131 | 0.75546 | 0.88500 | 0.91529 | 2.69% | |
| ±0.015 | ±0.010 | ±0.018 | ±0.017 | ±0.012 | ±0.131 | ±0.011 | ±0.015 | ±0.012 | ±0.006 | -- | ||
| COIL100 | 0.75258 | 0.76835 | 0.75400 | 0.75646 | 0.77226 | 0.70061 | 0.74641 | 0.73117 | 0.76948 | 0.83835 | 8.56% | |
| ±0.005 | ±0.005 | ±0.006 | ±0.006 | ±0.004 | ±0.009 | ±0.006 | ±0.005 | ±0.004 | ±0.003 | |||
| Krvs | 0.00060 | 0.00397 | 0.00091 | 0.00094 | 0.00265 | 0.00203 | 0.00818 | 0.00592 | 0.00352 | 0.01250 | 52.81% | |
| ±0.000 | ±0.003 | ±0.000 | ±0.000 | ±0.002 | ±0.003 | ±0.001 | ±0.006 | ±0.003 | ±0.001 | -- | ||
| Hitech | 0.00799 | 0.00989 | 0.00854 | 0.01049 | 0.00865 | 0.00558 | 0.01203 | 0.00786 | 0.00799 | 0.01935 | 60.85% | |
| ±0.001 | ±0.002 | ±0.002 | ±0.001 | ±0.002 | ±0.001 | ±0.002 | ±0.002 | ±0.002 | ±0.000 | -- | ||
| PenDigits | 0.68251 | 0.69332 | 0.66576 | 0.67684 | 0.69751 | 0.64294 | 0.69615 | 0.68480 | 0.70953 | 0.80120 | 12.92% | |
| ±0.022 | ±0.019 | ±0.026 | ±0.018 | ±0.027 | ±0.043 | ±0.016 | ±0.021 | ±0.018 | ±0.021 | -- | ||
| Vehicle | 0.11678 | 0.19000 | 0.13648 | 0.12714 | 0.19062 | 0.08408 | 0.14858 | 0.16404 | 0.19181 | 0.18544 | −3.32% | |
| ±0.014 | ±0.006 | ±0.019 | ±0.018 | ±0.015 | ±0.005 | ±0.019 | ±0.018 | ±0.013 | ±0.000 | -- | ||
| Algorithm | NMF | ONMF | Hx-NMF | EMMF | GNMF | RMNMF | DRCC | FR-NMF | LS-NMF | ASNMF-SRP | I-P | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dataset | ||||||||||||
| MSRA25 | 0.52985 | 0.52176 | 0.53755 | 0.52287 | 0.56587 | 0.57918 | 0.30698 | 0.53849 | 0.56651 | 0.61479 | 6.15% | |
| ±0.021 | ±0.023 | ±0.025 | ±0.020 | ±0.026 | ±0.027 | ±0.030 | ±0.017 | ±0.025 | ±0.035 | -- | ||
| Semeion | 0.53763 | 0.58804 | 0.53431 | 0.53807 | 0.63726 | 0.28738 | 0.63625 | 0.54862 | 0.64369 | 0.69739 | 8.34% | |
| ±0.036 | ±0.025 | ±0.030 | ±0.031 | ±0.024 | ±0.061 | ±0.027 | ±0.028 | ±0.026 | ±0.031 | -- | ||
| COIL20 | 0.69135 | 0.71340 | 0.68628 | 0.67997 | 0.80715 | 0.24903 | 0.82802 | 0.67753 | 0.80892 | 0.86455 | 4.41% | |
| ±0.024 | ±0.023 | ±0.021 | ±0.021 | ±0.017 | ±0.095 | ±0.017 | ±0.023 | ±0.018 | ±0.011 | -- | ||
| COIL100 | 0.52663 | 0.54705 | 0.52816 | 0.53379 | 0.54654 | 0.47951 | 0.51849 | 0.51637 | 0.54247 | 0.69599 | 27.23% | |
| ±0.013 | ±0.010 | ±0.011 | ±0.013 | ±0.012 | ±0.012 | ±0.012 | ±0.012 | ±0.009 | ±0.006 | -- | ||
| Krvs | 0.52245 | 0.53742 | 0.52289 | 0.52261 | 0.53137 | 0.52237 | 0.55594 | 0.53360 | 0.53387 | 0.56813 | 2.19% | |
| ±0.000 | ±0.012 | ±0.001 | ±0.000 | ±0.011 | ±0.000 | ±0.004 | ±0.016 | ±0.015 | ±0.003 | -- | ||
| Hitech | 0.26693 | 0.27034 | 0.26758 | 0.27017 | 0.26877 | 0.26380 | 0.27099 | 0.26788 | 0.26606 | 0.28525 | 5.26% | |
| ±0.003 | ±0.003 | ±0.003 | ±0.003 | ±0.003 | ±0.001 | ±0.004 | ±0.005 | ±0.003 | ±0.001 | -- | ||
| PenDigits | 0.69262 | 0.72340 | 0.69447 | 0.69118 | 0.70675 | 0.67226 | 0.73872 | 0.69626 | 0.71256 | 0.81095 | 9.78% | |
| ±0.026 | ±0.031 | ±0.031 | ±0.026 | ±0.035 | ±0.035 | ±0.029 | ±0.024 | ±0.035 | ±0.023 | -- | ||
| Vehicle | 0.39285 | 0.43777 | 0.40573 | 0.39681 | 0.44397 | 0.37145 | 0.41832 | 0.43853 | 0.44368 | 0.45236 | 1.89% | |
| ±0.015 | ±0.002 | ±0.020 | ±0.018 | ±0.008 | ±0.005 | ±0.020 | ±0.022 | ±0.009 | ±0.002 | -- | ||
| Dataset | ACC | ARI | NMI | PUR | ||||
|---|---|---|---|---|---|---|---|---|
| ASNMF-SRP-1 | ASNMF-SRP | ASNMF-SRP-1 | ASNMF-SRP | ASNMF-SRP-1 | ASNMF-SRP | ASNMF-SRP-1 | ASNMF-SRP | |
| MSRA25 | 0.49680 | 0.57904 | 0.33356 | 0.44662 | 0.55612 | 0.71512 | 0.51656 | 0.61479 |
| ±0.021 | ±0.045 | ±0.016 | ±0.052 | ±0.019 | ±0.026 | ±0.019 | ±0.035 | |
| Semeion | 0.64724 | 0.68063 | 0.48198 | 0.48809 | 0.64292 | 0.63282 | 0.68908 | 0.69739 |
| ±0.010 | ±0.050 | ±0.007 | ±0.034 | ±0.010 | ±0.021 | ±0.011 | ±0.031 | |
| COIL20 | 0.80552 | 0.84174 | 0.76313 | 0.80244 | 0.88651 | 0.91529 | 0.83587 | 0.86455 |
| ±0.015 | ±0.012 | ±0.017 | ±0.007 | ±0.008 | ±0.006 | ±0.013 | ±0.011 | |
| COIL100 | 0.48007 | 0.64173 | 0.40311 | 0.53573 | 0.73255 | 0.83835 | 0.52556 | 0.69599 |
| ±0.009 | ±0.010 | ±0.011 | ±0.016 | ±0.005 | ±0.003 | ±0.007 | ±0.006 | |
| Krvs | 0.52839 | 0.56813 | 0.00393 | 0.01814 | 0.00396 | 0.01250 | 0.53339 | 0.56813 |
| ±0.017 | ±0.003 | ±0.004 | ±0.002 | ±0.004 | ±0.001 | ±0.012 | ±0.003 | |
| Hitech | 0.23301 | 0.25367 | 0.00014 | 0.00689 | 0.00893 | 0.01935 | 0.26847 | 0.28525 |
| ±0.005 | ±0.002 | ±0.001 | ±0.000 | ±0.001 | ±0.000 | ±0.003 | ±0.001 | |
| PenDigits | 0.66533 | 0.80442 | 0.53130 | 0.68487 | 0.68684 | 0.80120 | 0.69495 | 0.81095 |
| ±0.040 | ±0.032 | ±0.030 | ±0.035 | ±0.020 | ±0.021 | ±0.026 | ±0.023 | |
| Vehicle | 0.44746 | 0.45236 | 0.13445 | 0.12014 | 0.20032 | 0.18544 | 0.44888 | 0.45236 |
| ±0.004 | ±0.002 | ±0.003 | ±0.001 | ±0.008 | ±0.000 | ±0.006 | ±0.002 | |
| Dataset | ACC | ARI | NMI | PUR | ||||
|---|---|---|---|---|---|---|---|---|
| ASNMF-SRP-2 | ASNMF-SRP | ASNMF-SRP-2 | ASNMF-SRP | ASNMF-SRP-2 | ASNMF-SRP | ASNMF-SRP-2 | ASNMF-SRP | |
| MSRA25 | 0.57518 | 0.57904 | 0.44437 | 0.44662 | 0.72012 | 0.71512 | 0.61354 | 0.61479 |
| ±0.032 | ±0.045 | ±0.038 | ±0.052 | ±0.019 | ±0.026 | ±0.025 | ±0.035 | |
| Semeion | 0.67803 | 0.68063 | 0.48380 | 0.48809 | 0.62883 | 0.63282 | 0.69567 | 0.69739 |
| ±0.044 | ±0.050 | ±0.029 | ±0.034 | ±0.018 | ±0.021 | ±0.025 | ±0.031 | |
| COIL20 | 0.83865 | 0.84174 | 0.80155 | 0.80244 | 0.91285 | 0.91529 | 0.86194 | 0.86455 |
| ±0.013 | ±0.012 | ±0.008 | ±0.007 | ±0.004 | ±0.006 | ±0.013 | ±0.011 | |
| COIL100 | 0.63818 | 0.64173 | 0.54346 | 0.53573 | 0.83103 | 0.83835 | 0.69085 | 0.69599 |
| ±0.007 | ±0.010 | ±0.014 | ±0.016 | ±0.003 | ±0.003 | ±0.004 | ±0.006 | |
| Krvs | 0.56884 | 0.56813 | 0.01850 | 0.01814 | 0.01274 | 0.01250 | 0.56884 | 0.56813 |
| ±0.000 | ±0.003 | ±0.000 | ±0.002 | ±0.000 | ±0.001 | ±0.000 | ±0.003 | |
| Hitech | 0.24744 | 0.25367 | 0.00424 | 0.00689 | 0.01893 | 0.01935 | 0.27912 | 0.28525 |
| ±0.001 | ±0.002 | ±0.001 | ±0.000 | ±0.000 | ±0.000 | ±0.001 | ±0.001 | |
| PenDigits | 0.79936 | 0.80442 | 0.67517 | 0.68487 | 0.79476 | 0.80120 | 0.80499 | 0.81095 |
| ±0.029 | ±0.032 | ±0.028 | ±0.035 | ±0.017 | ±0.021 | ±0.022 | ±0.023 | |
| Vehicle | 0.45219 | 0.45236 | 0.12018 | 0.12014 | 0.18540 | 0.18544 | 0.45219 | 0.45236 |
| ±0.001 | ±0.002 | ±0.001 | ±0.001 | ±0.001 | ±0.000 | ±0.001 | ±0.002 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, L.; Gao, H. Autoencoder-like Sparse Non-Negative Matrix Factorization with Structure Relationship Preservation. Entropy 2025, 27, 875. https://doi.org/10.3390/e27080875
Zhong L, Gao H. Autoencoder-like Sparse Non-Negative Matrix Factorization with Structure Relationship Preservation. Entropy. 2025; 27(8):875. https://doi.org/10.3390/e27080875
Chicago/Turabian StyleZhong, Ling, and Haiyan Gao. 2025. "Autoencoder-like Sparse Non-Negative Matrix Factorization with Structure Relationship Preservation" Entropy 27, no. 8: 875. https://doi.org/10.3390/e27080875
APA StyleZhong, L., & Gao, H. (2025). Autoencoder-like Sparse Non-Negative Matrix Factorization with Structure Relationship Preservation. Entropy, 27(8), 875. https://doi.org/10.3390/e27080875






