Latent Class Analysis with Arbitrary-Distribution Responses
Abstract
1. Introduction
- Model. We propose a novel, identifiable, and generative statistical model, the arbitrary-distribution latent class model (adLCM), for data with arbitrary-distribution responses, where the responses can be continuous or negative values. Our adLCM allows the elements of an observed response matrix R to be generated from any distribution provided that the population version of R under adLCM enjoys a latent class structure. For example, our adLCM allows R to be generated from Bernoulli, Normal, Poisson, Binomial, Uniform, and Exponential distributions, etc. By considering a specifically designed discrete distribution, our adLCM can also model signed response matrices. For details, please refer to Examples 1–7.
- Algorithm. We develop an easy-to-implement algorithm, spectral clustering with K-means (SCK), to infer latent classes for arbitrary-distribution response matrices generated from arbitrary distribution under the proposed model. Our algorithm is designed based on a combination of two popular techniques: the singular value decomposition (SVD) and the K-means algorithm.
- Theoretical property. We build a theoretical framework to show that SCK enjoys consistent estimation under adLCM. We also provide Examples 1–7 to show that the theoretical performance of the proposed algorithm can be different when the observed response matrices R are generated from different distributions under the proposed model.
- Empirical validation. We conduct extensive simulations to validate our theoretical insights. Additionally, we apply our SCK approach to two real-world personality test datasets with meaningful interpretations.
2. Related Literature
3. Arbitrary-Distribution Latent Class Model
4. A Spectral Method for Parameter Estimation
- The left singular vectors matrix U can be written aswhere X is a matrix.
- U has K distinct rows such that for any two distinct subjects i and that belong to the same extreme latent profile (i.e., ), we have .
- Θ can be written as
- Furthermore, when , for all , and , we have
| Algorithm 1 Ideal SCK |
|
| Algorithm 2 Spectral Clustering with K-means (SCK for short) |
|
5. Theoretical Properties
- , i.e., only takes two values 0 and 1.
- and because is a probability located in and is assumed to be 1.
- because .
- because .
- Let τ be its upper bound 1 and γ be its upper bound ρ, Assumption 1 becomes , which means a sparsity requirement on R because ρ controls the probability of the numbers of ones in R for this case.
- Let γ be its upper bound ρ in Theorem 1, then we haveWe observe that increasing ρ leads to a decrease in SCK’s error rates when is a Bernoulli distribution.
- .
- and because is a probability that has a range in .
- because .
- because .
- Let τ be its upper bound m and γ be its upper bound ρ, then Assumption 1 becomes which provides a lower bound requirement of the scaling parameter ρ.
- Let γ be its upper bound ρ in Theorem 1, then we obtain the exact forms of error bounds for SCK when is a Binomial distribution, and we observe that increasing ρ reduces SCK’s error rates.
- , i.e., is an nonnegative integer.
- and because Poisson distribution can take any positive value for its mean.
- τ is an unknown positive value because we cannot know the exact upper bound of when R is obtained from the Poisson distribution under the adLCM.
- because .
- Let γ be its upper bound ρ, then Assumption 1 becomes which is a lower bound requirement of ρ.
- Let γ be its upper bound ρ in Theorem 1 which obtains the exact forms of error bounds for the SCK algorithm when is a Poisson distribution. It is easy to observe that increasing ρ leads to a decrease in SCK’s error rates.
- , i.e., is a real value.
- and because the mean of Normal distribution can take any value. Note that, unlike the cases when is Bernoulli or Poisson, B can have negative elements for the Normal distribution case.
- Similar to Example 3, τ is an unknown positive value.
- because for Normal distribution.
- Let γ be its exact value , then Assumption 1 becomes which means that should be set larger than for our theoretical analysis.
- Let γ be its exact value in Theorem 1 which provides the exact forms of error bounds for SCK. We observe that increasing the scaling parameter ρ (or decreasing the variance ) reduces SCK’s error rates.
- , i.e., is a positive value.
- and because the mean of Exponential distribution can be any positive value.
- Similar to Example 3, τ is an unknown positive value.
- because for Exponential distribution.
- Let γ be its upper bound , then Assumption 1 becomes , a lower bound requirement of ρ.
- Let γ be its upper bound in Theorem 1; the theoretical bounds demonstrate that ρ vanishes, which indicates that increasing ρ has no significant impact on the error rates of SCK.
- because .
- and because allows to be any positive value.
- τ is an unknown positive value with an upper bound .
- because for Uniform distribution.
- Let γ be its upper bound , then Assumption 1 becomes , a lower bound requirement of ρ.
- Since ρ disappears in the error bounds when we let in Theorem 1, increasing ρ does not significantly influence SCK’s error rates, a conclusion similar to Example 5.
- , i.e., only takes two values −1 and 1.
- and because and are two probabilities which should be in the range . Note that, similar to Example 4, can be negative for the signed response matrix.
- because and .
- because .
- When setting and , Assumption 1 turns to be .
- Setting γ as its upper bound 1 in Theorem 1 gives that increasing ρ reduces SCK’s error rates.
6. Simulation Studies
6.1. Baseline Method
| Algorithm 3 Ideal RMK |
|
| Algorithm 4 Response Matrix with K-means (RMK for short) |
|
6.2. Evaluation Metric
- Hamming error is defined aswhere denotes the collection of all K-by-K permutation matrices. Hamming error falls within the range , and a smaller Hamming error indicates better classification performance.
- Let C be a confusion matrix such that is the number of common subjects between and for . NMI is defined aswhere and . NMI is in the range and the larger it is, the better it is.
- ARI is defined aswhere is a binomial coefficient. ARI falls within the range [−1,1] and the larger it is, the better it is.
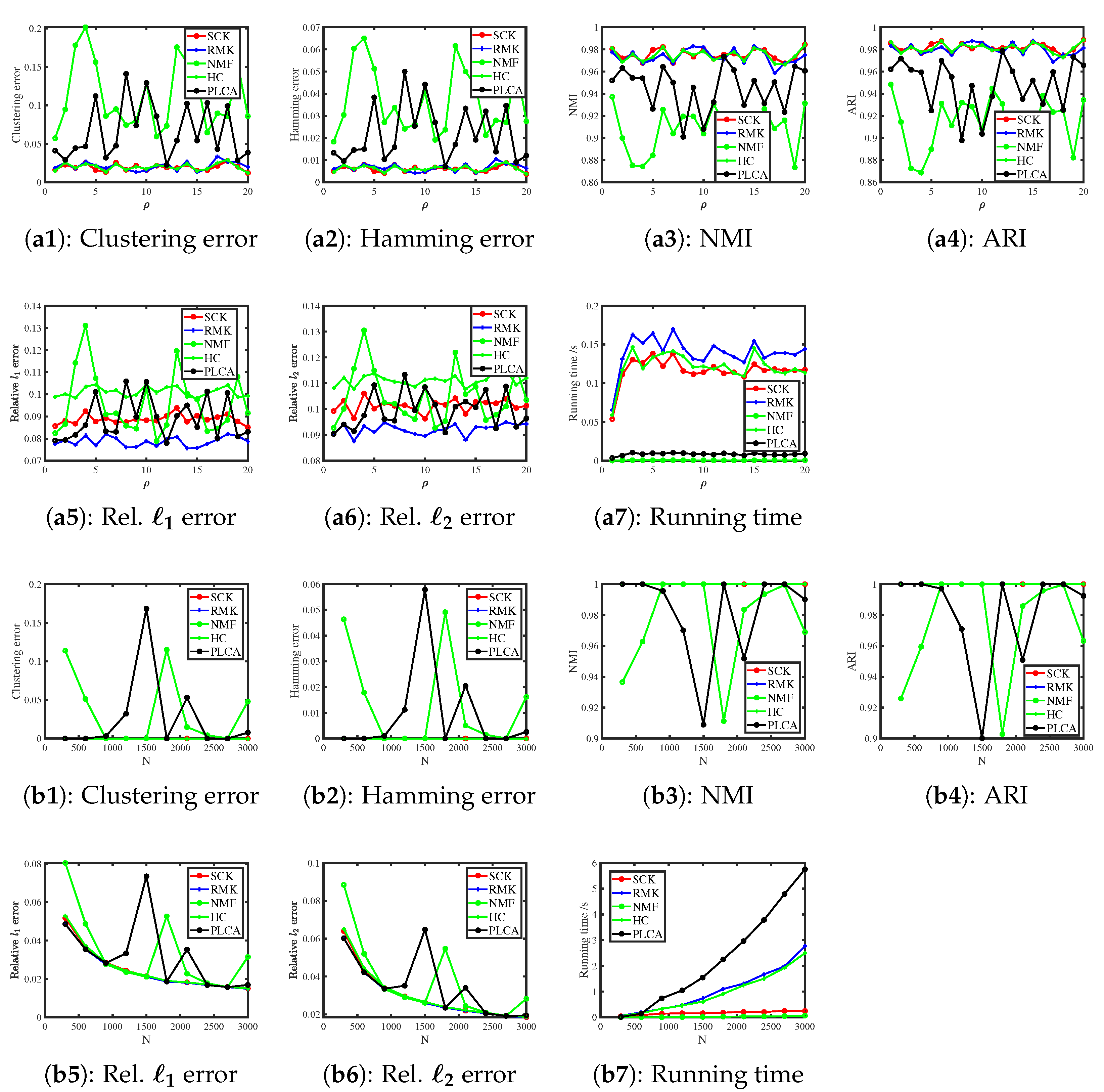
6.3. Synthetic Data
6.3.1. Bernoulli Distribution
6.3.2. Binomial Distribution
6.3.3. Poisson Distribution
6.3.4. Normal Distribution
6.3.5. Exponential Distribution
6.3.6. Uniform Distribution
6.3.7. Signed Response Matrix
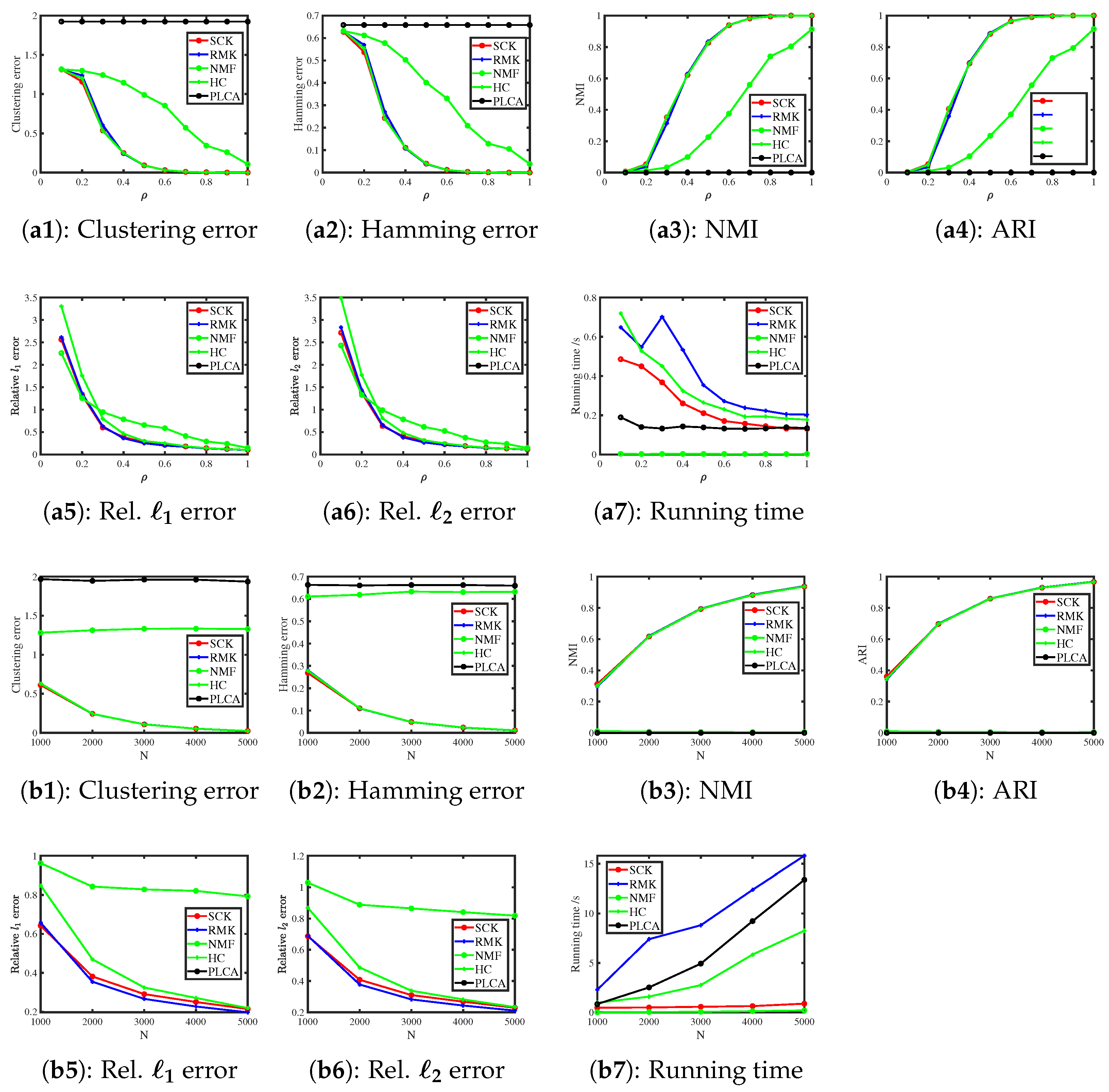
6.3.8. Simulated Arbitrary-Distribution Response Matrices
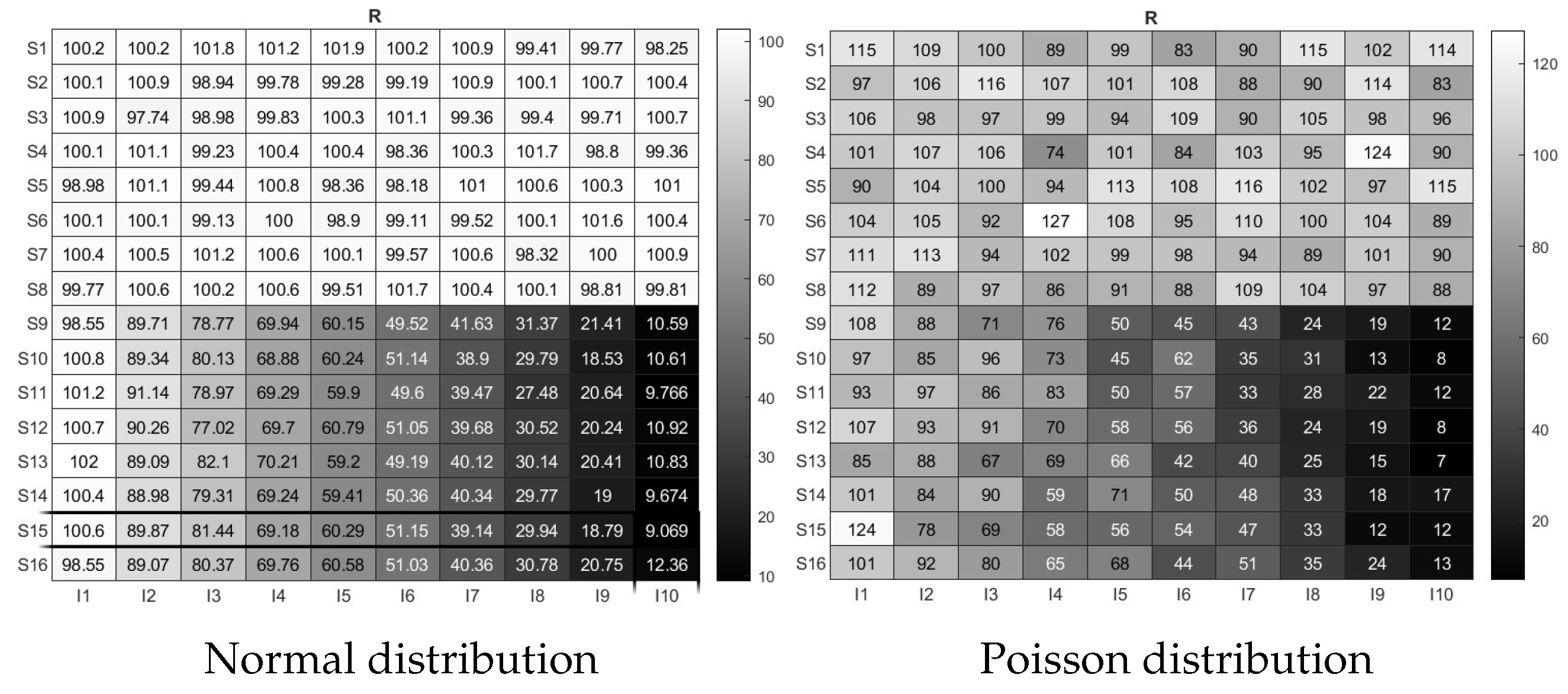
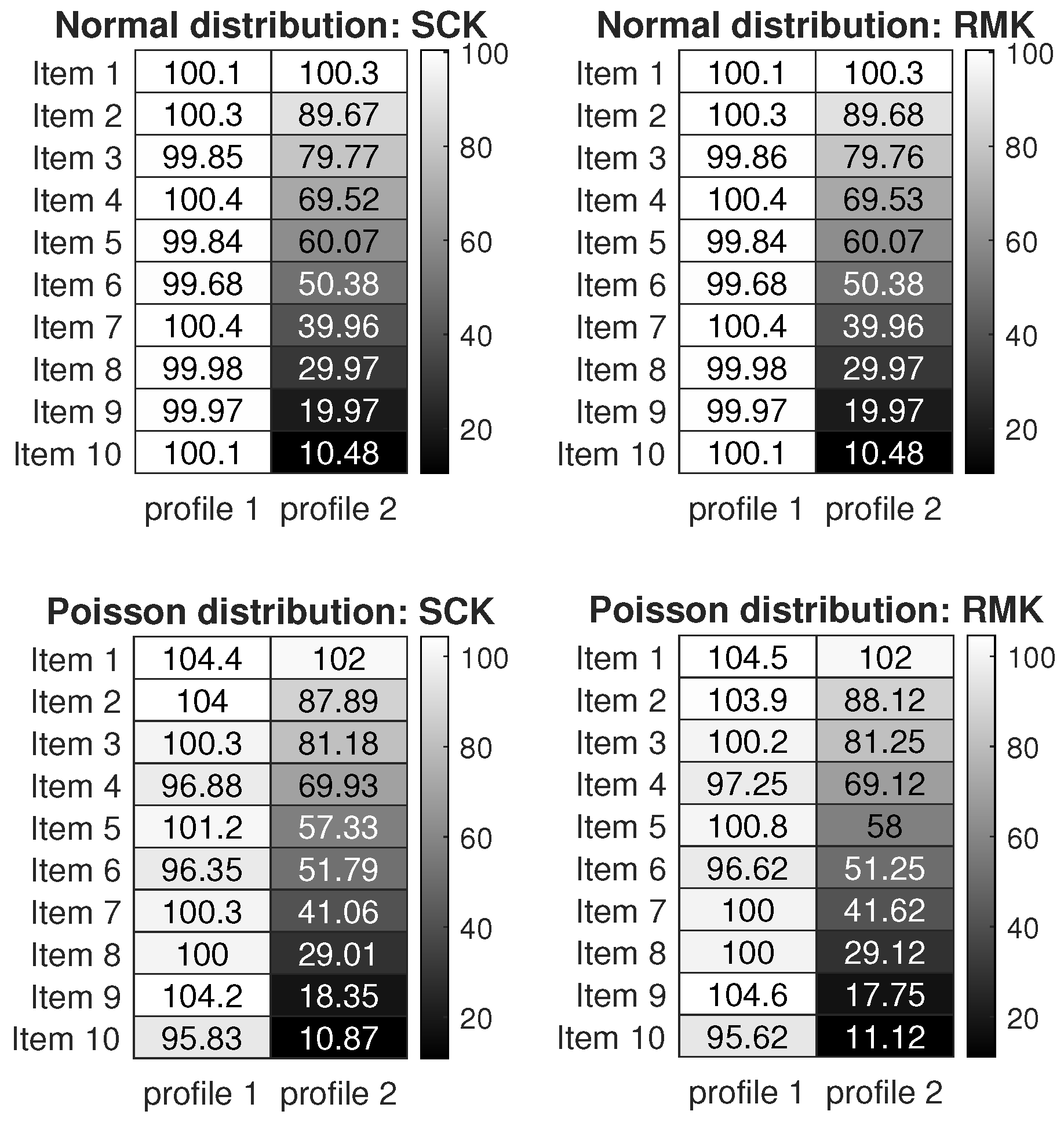
7. Real Data Applications
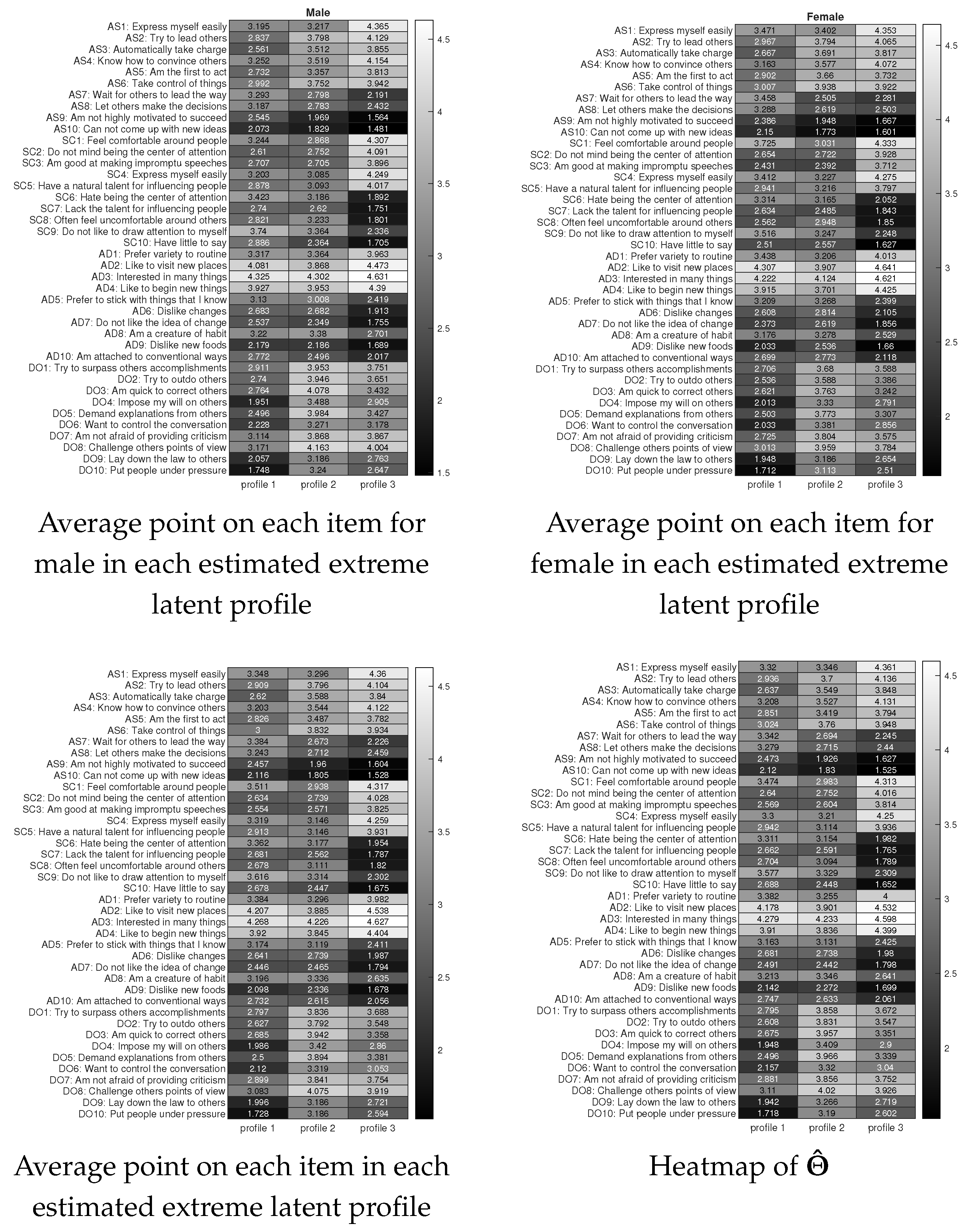
7.1. International Personality Item Pool (IPIP) Personality Test Data
7.2. Big Five Personality Test with Random Number (BFPTRN) Data
8. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Proofs Under adLCM
Appendix A.1. Proof of Proposition 1
Appendix A.2. Proof of Lemma 1
Appendix A.3. Proof of Theorem 1
References
- Dayton, C.M.; Macready, G.B. Concomitant-variable latent-class models. J. Am. Stat. Assoc. 1988, 83, 173–178. [Google Scholar] [CrossRef]
- Hagenaars, J.A.; McCutcheon, A.L. Applied Latent Class Analysis; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Magidson, J.; Vermunt, J.K. Latent class models. In The Sage Handbook of Quantitative Methodology for the Social Sciences; SAGE: Newcastle upon Tyne, UK, 2004; pp. 175–198. [Google Scholar]
- Guo, G.; Zhang, J.; Thalmann, D.; Yorke-Smith, N. Etaf: An extended trust antecedents framework for trust prediction. In Proceedings of the 2014 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM 2014), Beijing, China, 17–20 August 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 540–547. [Google Scholar]
- Harper, F.M.; Konstan, J.A. The movielens datasets: History and context. ACM Trans. Interact. Intell. Syst. (TIIS) 2015, 5, 1–19. [Google Scholar] [CrossRef]
- Meyer, G.J.; Finn, S.E.; Eyde, L.D.; Kay, G.G.; Moreland, K.L.; Dies, R.R.; Eisman, E.J.; Kubiszyn, T.W.; Reed, G.M. Psychological testing and psychological assessment: A review of evidence and issues. Am. Psychol. 2001, 56, 128. [Google Scholar] [CrossRef]
- Silverman, J.J.; Galanter, M.; Jackson-Triche, M.; Jacobs, D.G.; Lomax, J.W.; Riba, M.B.; Tong, L.D.; Watkins, K.E.; Fochtmann, L.J.; Rhoads, R.S.; et al. The American Psychiatric Association practice guidelines for the psychiatric evaluation of adults. Am. J. Psychiatry 2015, 172, 798–802. [Google Scholar] [CrossRef] [PubMed]
- De La Torre, J.; van der Ark, L.A.; Rossi, G. Analysis of clinical data from a cognitive diagnosis modeling framework. Meas. Eval. Couns. Dev. 2018, 51, 281–296. [Google Scholar] [CrossRef]
- Chen, Y.; Li, X.; Zhang, S. Joint maximum likelihood estimation for high-dimensional exploratory item factor analysis. Psychometrika 2019, 84, 124–146. [Google Scholar] [CrossRef]
- Shang, Z.; Erosheva, E.A.; Xu, G. Partial-mastery cognitive diagnosis models. Ann. Appl. Stat. 2021, 15, 1529–1555. [Google Scholar] [CrossRef]
- Poole, K.T. Nonparametric unfolding of binary choice data. Political Anal. 2000, 8, 211–237. [Google Scholar] [CrossRef]
- Clinton, J.; Jackman, S.; Rivers, D. The statistical analysis of roll call data. Am. Political Sci. Rev. 2004, 98, 355–370. [Google Scholar] [CrossRef]
- Bakker, R.; Poole, K.T. Bayesian metric multidimensional scaling. Political Anal. 2013, 21, 125–140. [Google Scholar] [CrossRef]
- Chen, Y.; Ying, Z.; Zhang, H. Unfolding-model-based visualization: Theory, method and applications. J. Mach. Learn. Res. 2021, 22, 548–598. [Google Scholar]
- Martinez-Moya, J.; Feo-Valero, M. Do shippers’ characteristics influence port choice criteria? Capturing heterogeneity by using latent class models. Transp. Policy 2022, 116, 96–105. [Google Scholar] [CrossRef]
- Formann, A.K.; Kohlmann, T. Latent class analysis in medical research. Stat. Methods Med. Res. 1996, 5, 179–211. [Google Scholar] [CrossRef]
- Kongsted, A.; Nielsen, A.M. Latent class analysis in health research. J. Physiother. 2017, 63, 55–58. [Google Scholar] [CrossRef]
- Wu, Z.; Deloria-Knoll, M.; Zeger, S.L. Nested partially latent class models for dependent binary data; estimating disease etiology. Biostatistics 2017, 18, 200–213. [Google Scholar] [CrossRef]
- Van der Heijden, P.G.; Dessens, J.; Bockenholt, U. Estimating the concomitant-variable latent-class model with the EM algorithm. J. Educ. Behav. Stat. 1996, 21, 215–229. [Google Scholar] [CrossRef]
- Smaragdis, P.; Raj, B.; Shashanka, M. Shift-invariant probabilistic latent component analysis. J. Mach. Learn. Res. 2007, 5. [Google Scholar]
- Bakk, Z.; Vermunt, J.K. Robustness of stepwise latent class modeling with continuous distal outcomes. Struct. Equ. Model. Multidiscip. J. 2016, 23, 20–31. [Google Scholar] [CrossRef]
- Chen, H.; Han, L.; Lim, A. Beyond the EM algorithm: Constrained optimization methods for latent class model. Commun. Stat.-Simul. Comput. 2022, 51, 5222–5244. [Google Scholar] [CrossRef]
- Gu, Y.; Xu, G. A joint MLE approach to large-scale structured latent attribute analysis. J. Am. Stat. Assoc. 2023, 118, 746–760. [Google Scholar] [CrossRef]
- Shashanka, M.; Raj, B.; Smaragdis, P. Probabilistic latent variable models as nonnegative factorizations. Comput. Intell. Neurosci. 2008, 2008, 947438. [Google Scholar] [CrossRef]
- Anandkumar, A.; Ge, R.; Hsu, D.; Kakade, S.M.; Telgarsky, M. Tensor decompositions for learning latent variable models. J. Mach. Learn. Res. 2014, 15, 2773–2832. [Google Scholar]
- Zeng, Z.; Gu, Y.; Xu, G. A Tensor-EM Method for Large-Scale Latent Class Analysis with Binary Responses. Psychometrika 2023, 88, 580–612. [Google Scholar] [CrossRef]
- Chen, L.; Gu, Y. A spectral method for identifiable grade of membership analysis with binary responses. Psychometrika 2024, 89, 626–657. [Google Scholar] [CrossRef]
- Qing, H. Finding mixed memberships in categorical data. Inf. Sci. 2024, 676, 120785. [Google Scholar] [CrossRef]
- Lyu, Z.; Chen, L.; Gu, Y. Degree-heterogeneous Latent Class Analysis for high-dimensional discrete data. J. Am. Stat. Assoc. 2025, 1–14. [Google Scholar] [CrossRef]
- Formann, A.K. Constrained latent class models: Theory and applications. Br. J. Math. Stat. Psychol. 1985, 38, 87–111. [Google Scholar] [CrossRef]
- Lindsay, B.; Clogg, C.C.; Grego, J. Semiparametric estimation in the Rasch model and related exponential response models, including a simple latent class model for item analysis. J. Am. Stat. Assoc. 1991, 86, 96–107. [Google Scholar] [CrossRef]
- Zhang, N.L. Hierarchical latent class models for cluster analysis. J. Mach. Learn. Res. 2004, 5, 697–723. [Google Scholar]
- Yang, C.C. Evaluating latent class analysis models in qualitative phenotype identification. Comput. Stat. Data Anal. 2006, 50, 1090–1104. [Google Scholar] [CrossRef]
- Xu, G. Identifiability of restricted latent class models with binary responses. Ann. Stat. 2017, 45, 675–707. [Google Scholar] [CrossRef]
- Xu, G.; Shang, Z. Identifying latent structures in restricted latent class models. J. Am. Stat. Assoc. 2018, 113, 1284–1295. [Google Scholar] [CrossRef]
- Ma, W.; Guo, W. Cognitive diagnosis models for multiple strategies. Br. J. Math. Stat. Psychol. 2019, 72, 370–392. [Google Scholar] [CrossRef]
- Gu, Y.; Xu, G. Partial identifiability of restricted latent class models. Ann. Stat. 2020, 48, 2082–2107. [Google Scholar] [CrossRef]
- Newman, M.E. Analysis of weighted networks. Phys. Rev. E 2004, 70, 056131. [Google Scholar] [CrossRef]
- Derr, T.; Johnson, C.; Chang, Y.; Tang, J. Balance in signed bipartite networks. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management, Beijing, China, 3–7 November 2019; pp. 1221–1230. [Google Scholar]
- Goldberg, K.; Roeder, T.; Gupta, D.; Perkins, C. Eigentaste: A constant time collaborative filtering algorithm. Inf. Retr. 2001, 4, 133–151. [Google Scholar] [CrossRef]
- Gibson, W.A. Three multivariate models: Factor analysis, latent structure analysis, and latent profile analysis. Psychometrika 1959, 24, 229–252. [Google Scholar] [CrossRef]
- Mislevy, R.J.; Verhelst, N. Modeling item responses when different subjects employ different solution strategies. Psychometrika 1990, 55, 195–215. [Google Scholar] [CrossRef]
- Lubke, G.H.; Muthén, B. Investigating population heterogeneity with factor mixture models. Psychol. Methods 2005, 10, 21. [Google Scholar] [CrossRef]
- McLachlan, G.J.; Do, K.A.; Ambroise, C. Analyzing Microarray Gene Expression Data; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Lubke, G.; Muthén, B.O. Performance of factor mixture models as a function of model size, covariate effects, and class-specific parameters. Struct. Equ. Model. Multidiscip. J. 2007, 14, 26–47. [Google Scholar] [CrossRef]
- Kim, Y.; Muthén, B.O. Two-part factor mixture modeling: Application to an aggressive behavior measurement instrument. Struct. Equ. Model. 2009, 16, 602–624. [Google Scholar] [CrossRef]
- Tein, J.Y.; Coxe, S.; Cham, H. Statistical power to detect the correct number of classes in latent profile analysis. Struct. Equ. Model. Multidiscip. J. 2013, 20, 640–657. [Google Scholar] [CrossRef]
- Goodman, L.A. Exploratory Latent Structure Analysis Using Both Identifiable and Unidentifiable Models. Biometrika 1974, 61, 215–231. [Google Scholar] [CrossRef]
- Agresti, A. Categorical Data Analysis; Wiley: New York, NY, USA, 2013. [Google Scholar]
- Forcina, A. Identifiability of extended latent class models with individual covariates. Comput. Stat. Data Anal. 2008, 52, 5263–5268. [Google Scholar] [CrossRef]
- Gyllenberg, M.; Koski, T.; Reilink, E.; Verlaan, M. Non-uniqueness in probabilistic numerical identification of bacteria. J. Appl. Probab. 1994, 31, 542–548. [Google Scholar] [CrossRef]
- Woodbury, M.A.; Clive, J.; Garson Jr, A. Mathematical typology: A grade of membership technique for obtaining disease definition. Comput. Biomed. Res. 1978, 11, 277–298. [Google Scholar] [CrossRef]
- Blei, D.M.; Ng, A.Y.; Jordan, M.I. Latent dirichlet allocation. J. Mach. Learn. Res. 2003, 3, 993–1022. [Google Scholar]
- Dey, K.K.; Hsiao, C.J.; Stephens, M. Visualizing the structure of RNA-seq expression data using grade of membership models. PLoS Genet. 2017, 13, e1006599. [Google Scholar] [CrossRef]
- Ke, Z.T.; Wang, M. Using SVD for topic modeling. J. Am. Stat. Assoc. 2024, 119, 434–449. [Google Scholar] [CrossRef]
- Tolley, H.D.; Manton, K.G. Large sample properties of estimates of a discrete grade of membership model. Ann. Inst. Stat. Math. 1992, 44, 85–95. [Google Scholar] [CrossRef]
- Erosheva, E.A.; Fienberg, S.E.; Joutard, C. Describing disability through individual-level mixture models for multivariate binary data. Ann. Appl. Stat. 2007, 1, 346. [Google Scholar] [CrossRef]
- Gormley, I.; Murphy, T. A grade of membership model for rank data. Bayesian Anal. 2009, 4, 265–295. [Google Scholar] [CrossRef]
- Gu, Y.; Erosheva, E.E.; Xu, G.; Dunson, D.B. Dimension-grouped mixed membership models for multivariate categorical data. J. Mach. Learn. Res. 2023, 24, 1–49. [Google Scholar]
- Massa, P.; Salvetti, M.; Tomasoni, D. Bowling alone and trust decline in social network sites. In Proceedings of the 2009 Eighth IEEE International Conference on Dependable, Autonomic and Secure Computing, Chengdu, China, 12–14 December 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 658–663. [Google Scholar]
- Joseph, A.; Yu, B. Impact of regularization on spectral clustering. Ann. Stat. 2016, 44, 1765–1791. [Google Scholar] [CrossRef]
- Zhou, Z.; Amini, A.A. Analysis of spectral clustering algorithms for community detection: The general bipartite setting. J. Mach. Learn. Res. 2019, 20, 1–47. [Google Scholar]
- Zhang, H.; Guo, X.; Chang, X. Randomized spectral clustering in large-scale stochastic block models. J. Comput. Graph. Stat. 2022, 31, 887–906. [Google Scholar] [CrossRef]
- Mao, X.; Sarkar, P.; Chakrabarti, D. Estimating mixed memberships with sharp eigenvector deviations. J. Am. Stat. Assoc. 2021, 116, 1928–1940. [Google Scholar] [CrossRef]
- Qing, H.; Wang, J. Regularized spectral clustering under the mixed membership stochastic block model. Neurocomputing 2023, 550, 126490. [Google Scholar] [CrossRef]
- Chen, Y.; Chi, Y.; Fan, J.; Ma, C. Spectral methods for data science: A statistical perspective. Found. Trends Mach. Learn. 2021, 14, 566–806. [Google Scholar] [CrossRef]
- Lei, J.; Rinaldo, A. Consistency of spectral clustering in stochastic block models. Ann. Stat. 2015, 43, 215–237. [Google Scholar] [CrossRef]
- Paul, S.; Chen, Y. Spectral and matrix factorization methods for consistent community detection in multi-layer networks. Ann. Stat. 2020, 48, 230–250. [Google Scholar] [CrossRef]
- Lei, J.; Lin, K.Z. Bias-adjusted spectral clustering in multi-layer stochastic block models. J. Am. Stat. Assoc. 2023, 118, 2433–2445. [Google Scholar] [CrossRef]
- Qing, H. Community detection in multi-layer networks by regularized debiased spectral clustering. Eng. Appl. Artif. Intell. 2025, 152, 110627. [Google Scholar] [CrossRef]
- Jin, J.; Ke, Z.T.; Luo, S. Mixed membership estimation for social networks. J. Econom. 2024, 239, 105369. [Google Scholar] [CrossRef]
- Qing, H. Discovering overlapping communities in multi-layer directed networks. Chaos Solitons Fractals 2025, 194, 116175. [Google Scholar] [CrossRef]
- Qing, H. A useful criterion on studying consistent estimation in community detection. Entropy 2022, 24, 1098. [Google Scholar] [CrossRef]
- Jin, J. Fast community detection by SCORE. Ann. Stat. 2015, 43, 57–89. [Google Scholar] [CrossRef]
- Strehl, A.; Ghosh, J. Cluster ensembles—A knowledge reuse framework for combining multiple partitions. J. Mach. Learn. Res. 2002, 3, 583–617. [Google Scholar]
- Danon, L.; Diaz-Guilera, A.; Duch, J.; Arenas, A. Comparing community structure identification. J. Stat. Mech. Theory Exp. 2005, 2005, P09008. [Google Scholar] [CrossRef]
- Bagrow, J.P. Evaluating local community methods in networks. J. Stat. Mech. Theory Exp. 2008, 2008, P05001. [Google Scholar] [CrossRef]
- Luo, W.; Yan, Z.; Bu, C.; Zhang, D. Community detection by fuzzy relations. IEEE Trans. Emerg. Top. Comput. 2017, 8, 478–492. [Google Scholar] [CrossRef]
- Hubert, L.; Arabie, P. Comparing partitions. J. Classif. 1985, 2, 193–218. [Google Scholar] [CrossRef]
- Vinh, N.X.; Epps, J.; Bailey, J. Information theoretic measures for clusterings comparison: Is a correction for chance necessary? In Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, QC, Canada, 14–18 June 2009; pp. 1073–1080. [Google Scholar]
- Rohe, K.; Qin, T.; Yu, B. Co-clustering directed graphs to discover asymmetries and directional communities. Proc. Natl. Acad. Sci. USA 2016, 113, 12679–12684. [Google Scholar] [CrossRef]
- Erosheva, E.A. Comparing latent structures of the grade of membership, Rasch, and latent class models. Psychometrika 2005, 70, 619–628. [Google Scholar] [CrossRef]
- Huang, G.H.; Bandeen-Roche, K. Building an identifiable latent class model with covariate effects on underlying and measured variables. Psychometrika 2004, 69, 5–32. [Google Scholar] [CrossRef]
- Reboussin, B.A.; Ip, E.H.; Wolfson, M. Locally dependent latent class models with covariates: An application to under-age drinking in the USA. J. R. Stat. Soc. Ser. A Stat. Soc. 2008, 171, 877–897. [Google Scholar] [CrossRef]
- Vermunt, J.K. Latent class modeling with covariates: Two improved three-step approaches. Political Anal. 2010, 18, 450–469. [Google Scholar] [CrossRef]
- Di Mari, R.; Bakk, Z.; Punzo, A. A random-covariate approach for distal outcome prediction with latent class analysis. Struct. Equ. Model. Multidiscip. J. 2020, 27, 351–368. [Google Scholar] [CrossRef]
- Bakk, Z.; Di Mari, R.; Oser, J.; Kuha, J. Two-stage multilevel latent class analysis with covariates in the presence of direct effects. Struct. Equ. Model. Multidiscip. J. 2022, 29, 267–277. [Google Scholar] [CrossRef]
- Asparouhov, T.; Hamaker, E.L.; Muthén, B. Dynamic latent class analysis. Struct. Equ. Model. Multidiscip. J. 2017, 24, 257–269. [Google Scholar] [CrossRef]
- Wu, S.; Li, Z.; Zhu, X. A Distributed Community Detection Algorithm for Large Scale Networks Under Stochastic Block Models. Comput. Stat. Data Anal. 2023, 187, 107794. [Google Scholar] [CrossRef]
- Qing, H.; Wang, J. Community detection for weighted bipartite networks. Knowl.-Based Syst. 2023, 274, 110643. [Google Scholar] [CrossRef]
- Tropp, J.A. User-Friendly Tail Bounds for Sums of Random Matrices. Found. Comput. Math. 2012, 12, 389–434. [Google Scholar] [CrossRef]
- Rudelson, M.; Vershynin, R. Smallest singular value of a random rectangular matrix. Commun. Pure Appl. Math. J. Issued Courant Inst. Math. Sci. 2009, 62, 1707–1739. [Google Scholar] [CrossRef]

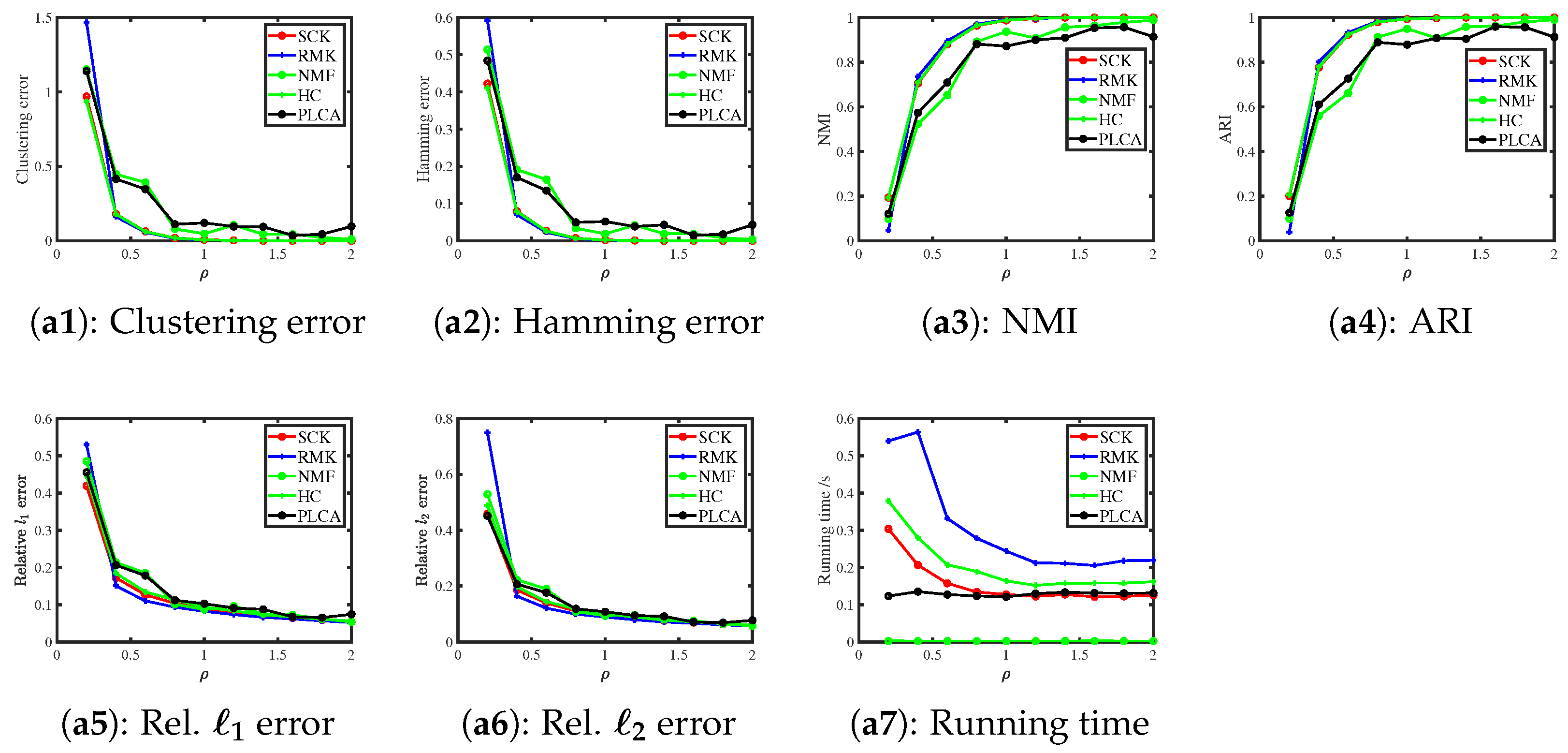
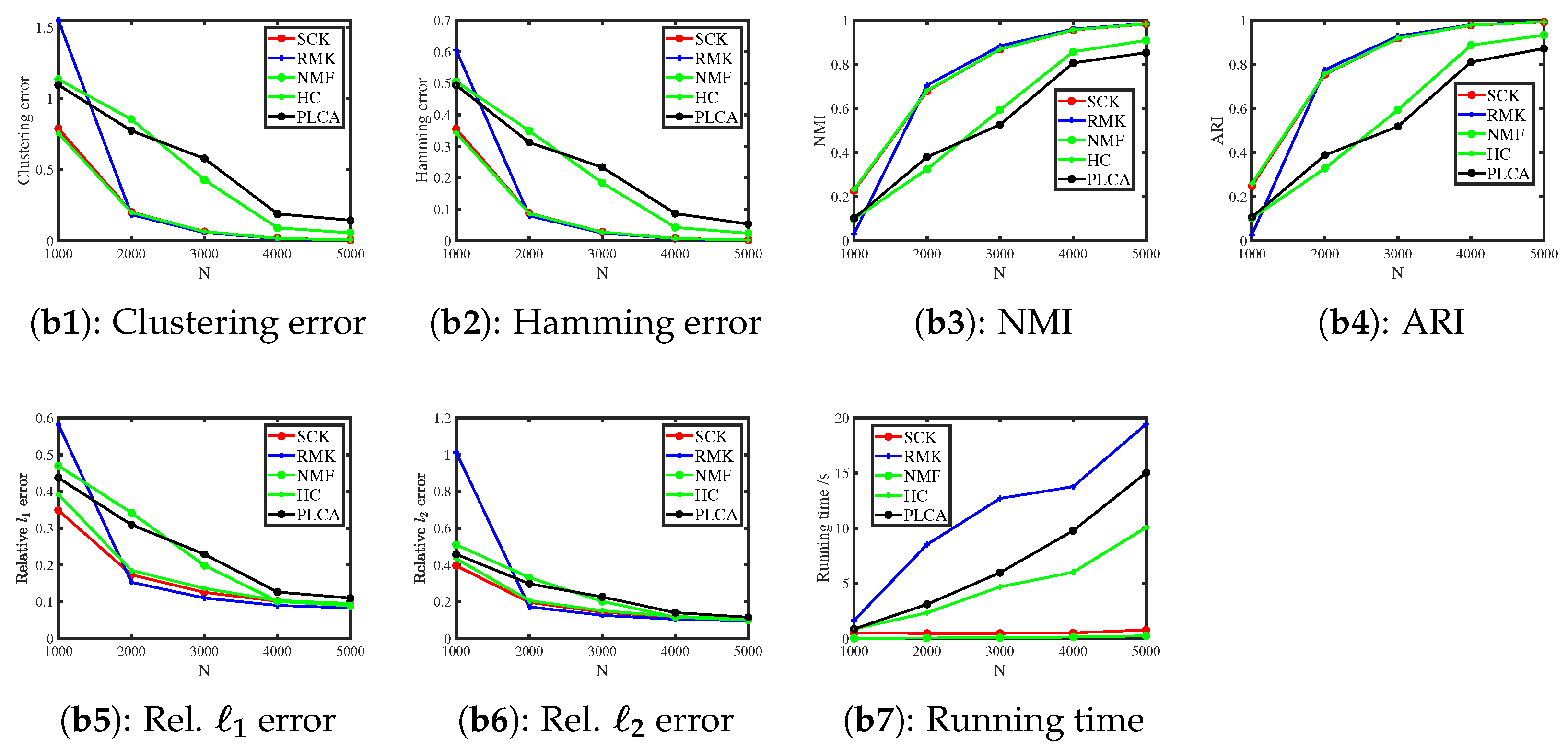
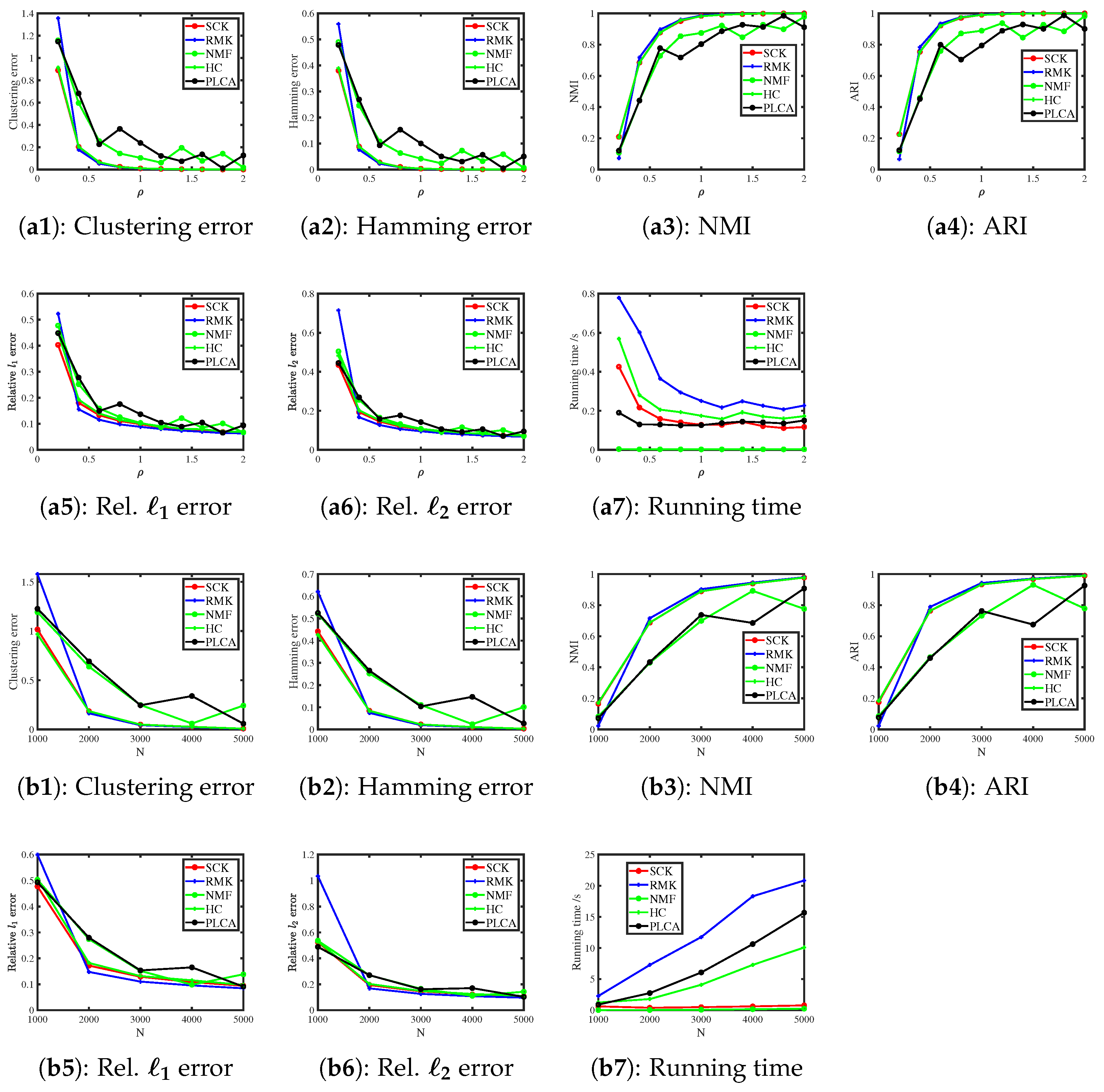

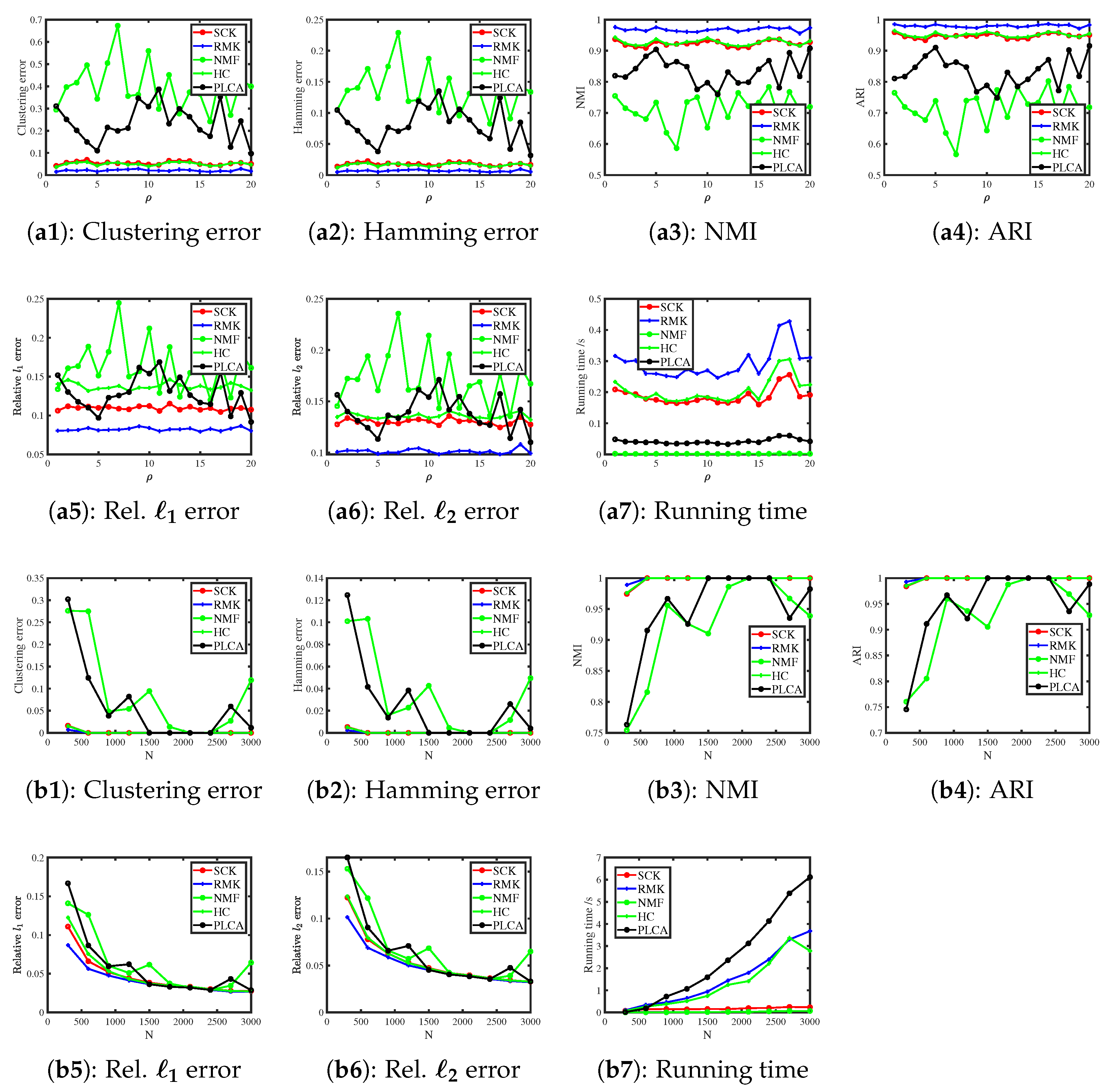


| Method | Clustering | Hamming | NMI | ARI | Rel. | Rel. |
|---|---|---|---|---|---|---|
| Error | Error | Error | Error | |||
| SCK | 0 (0) | 0 (0) | 1.000 (1.000) | 1.000 (1.000) | 0.0024 (0.0254) | 0.0032 (0.0295) |
| RMK | 0 (0) | 0 (0) | 1.000 (1.000) | 1.000 (1.000) | 0.0024 (0.0245) | 0.0032 (0.0295) |
| NMF | 0 (0) | 0 (0) | 1.000 (1.000) | 1.000 (1.000) | 0.0024 (0.0245) | 0.0032 (0.0295) |
| HC | 0 (0) | 0 (0) | 1.000 (1.000) | 1.000 (1.000) | 0.0024 (0.0254) | 0.0032 (0.0307) |
| PLCA | 0 (0) | 0 (0) | 1.000 (1.000) | 1.000 (1.000) | 0.0024 (0.0245) | 0.0032 (0.0295) |
| Statistic | Profile 1 | Profile 2 | Profile 3 |
|---|---|---|---|
| Size | 276 | 226 | 394 |
| # Male | 123 | 129 | 241 |
| # Female | 153 | 97 | 153 |
| Average age (male) | 35.98 | 32.82 | 35.90 |
| Average age (female) | 35.54 | 31.38 | 38.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qing, H.; Xu, X. Latent Class Analysis with Arbitrary-Distribution Responses. Entropy 2025, 27, 866. https://doi.org/10.3390/e27080866
Qing H, Xu X. Latent Class Analysis with Arbitrary-Distribution Responses. Entropy. 2025; 27(8):866. https://doi.org/10.3390/e27080866
Chicago/Turabian StyleQing, Huan, and Xiaofei Xu. 2025. "Latent Class Analysis with Arbitrary-Distribution Responses" Entropy 27, no. 8: 866. https://doi.org/10.3390/e27080866
APA StyleQing, H., & Xu, X. (2025). Latent Class Analysis with Arbitrary-Distribution Responses. Entropy, 27(8), 866. https://doi.org/10.3390/e27080866







