Fast and Robust Optical Cooling via Shortcut to Adiabaticity
Abstract
1. Introduction
2. Preliminaries: Model and Hamiltonian
2.1. RAP Cooling
2.2. Stimulated Adiabatic Passage for Momentum Transfer
3. STA and Optimization
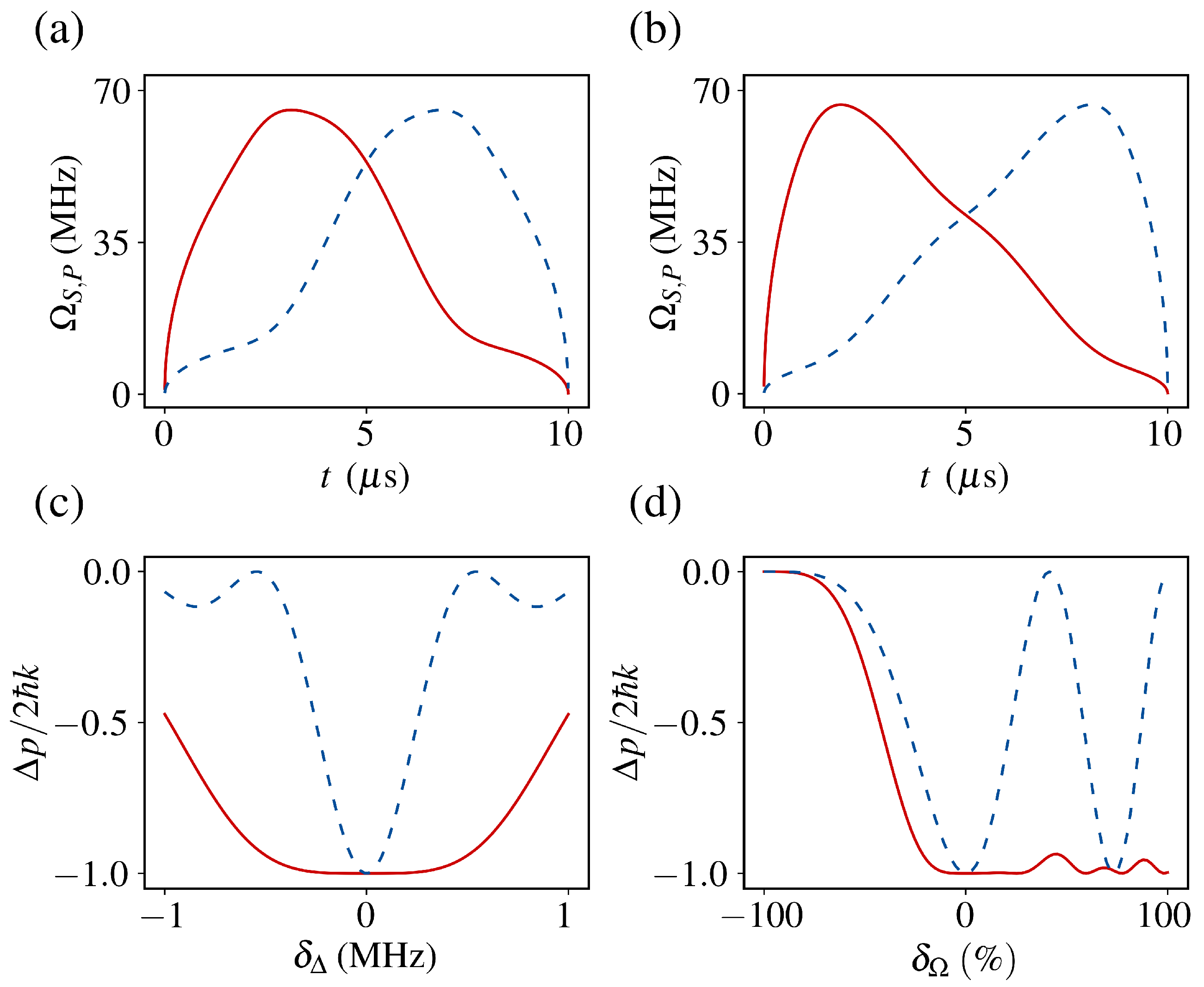
3.1. Inverse Engineering Based on Dynamical Invariants
3.2. Dissipation Analysis
4. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ashkin, A. Atomic-Beam Deflection by Resonance-Radiation Pressure. Phys. Rev. Lett. 1970, 25, 1321–1324. [Google Scholar] [CrossRef]
- Ashkin, A. Applications of laser radiation pressure. Science 1980, 210, 1081–1088. [Google Scholar] [CrossRef] [PubMed]
- Raab, E.L.; Prentiss, M.; Cable, A.; Chu, S.; Pritchard, D.E. Trapping of Neutral Sodium Atoms with Radiation Pressure. Phys. Rev. Lett. 1987, 59, 2631–2634. [Google Scholar] [CrossRef] [PubMed]
- Podlecki, L.; Glover, R.D.; Martin, J.; Bastin, T. Radiation pressure on a two-level atom: An exact analytical approach. J. Opt. Soc. Am. B 2018, 35, 127–132. [Google Scholar] [CrossRef]
- Chu, S. Nobel Lecture: The manipulation of neutral particles. Rev. Mod. Phys. 1998, 70, 685–706. [Google Scholar] [CrossRef]
- Derevianko, A.; Katori, H. Colloquium: Physics of optical lattice clocks. Rev. Mod. Phys. 2011, 83, 331–347. [Google Scholar] [CrossRef]
- Bloom, B.; Nicholson, T.; Williams, J.; Campbell, S.; Bishof, M.; Zhang, X.; Zhang, W.; Bromley, S.; Ye, J. An optical lattice clock with accuracy and stability at the 10–18 level. Nature 2014, 506, 71–75. [Google Scholar] [CrossRef]
- Schumm, T.; Hofferberth, S.; Andersson, L.M.; Wildermuth, S.; Groth, S.; Bar-Joseph, I.; Schmiedmayer, J.; Krüger, P. Matter-wave interferometry in a double well on an atom chip. Nat. Phys. 2005, 1, 57–62. [Google Scholar] [CrossRef]
- Anderson, M.H.; Ensher, J.R.; Matthews, M.R.; Wieman, C.E.; Cornell, E.A. Observation of Bose-Einstein condensation in a dilute atomic vapor. Science 1995, 269, 198–201. [Google Scholar] [CrossRef]
- Davis, K.B.; Mewes, M.O.; Andrews, M.R.; van Druten, N.J.; Durfee, D.S.; Kurn, D.M.; Ketterle, W. Bose-Einstein Condensation in a Gas of Sodium Atoms. Phys. Rev. Lett. 1995, 75, 3969–3973. [Google Scholar] [CrossRef]
- Bradley, C.C.; Sackett, C.A.; Tollett, J.J.; Hulet, R.G. Evidence of Bose-Einstein Condensation in an Atomic Gas with Attractive Interactions. Phys. Rev. Lett. 1995, 75, 1687–1690. [Google Scholar] [CrossRef] [PubMed]
- Esslinger, T.; Sander, F.; Weidemüller, M.; Hemmerich, A.; Hänsch, T.W. Subrecoil Laser Cooling with Adiabatic Transfer. Phys. Rev. Lett. 1996, 76, 2432–2435. [Google Scholar] [CrossRef]
- Aspect, A.; Arimondo, E.; Kaiser, R.; Vansteenkiste, N.; Cohen-Tannoudji, C. Laser cooling below the one-photon recoil energy by velocity-selective coherent population trapping: Theoretical analysis. J. Opt. Soc. Am. B 1989, 6, 2112–2124. [Google Scholar] [CrossRef]
- Chu, S. Cold atoms and quantum control. Nature 2002, 416, 206–210. [Google Scholar] [CrossRef] [PubMed]
- Monroe, C. Quantum information processing with atoms and photons. Nature 2002, 416, 238–246. [Google Scholar] [CrossRef]
- Gross, C.; Bloch, I. Quantum simulations with ultracold atoms in optical lattices. Science 2017, 357, 995–1001. [Google Scholar] [CrossRef]
- Rossi, M.; Mason, D.; Chen, J.; Tsaturyan, Y.; Schliesser, A. Measurement-based quantum control of mechanical motion. Nature 2018, 563, 53–58. [Google Scholar] [CrossRef]
- Cashen, M.; Rivoire, O.; Romanenko, V.; Yatsenko, L.; Metcalf, H. Strong optical forces in frequency-modulated light. Phys. Rev. A 2001, 64, 063411. [Google Scholar] [CrossRef]
- Chieda, M.A.; Eyler, E.E. Prospects for rapid deceleration of small molecules by optical bichromatic forces. Phys. Rev. A 2011, 84, 063401. [Google Scholar] [CrossRef]
- Corder, C.; Arnold, B.; Metcalf, H. Laser Cooling without Spontaneous Emission. Phys. Rev. Lett. 2015, 114, 043002. [Google Scholar] [CrossRef]
- Barker, P.F.; Shneider, M.N. Slowing molecules by optical microlinear deceleration. Phys. Rev. A 2002, 66, 065402. [Google Scholar] [CrossRef]
- Djotyan, G.P.; Bakos, J.S.; Sörlei, Z.; Szigeti, J. Coherent control of atomic quantum states by single frequency-chirped laser pulses. Phys. Rev. A 2004, 70, 063406. [Google Scholar] [CrossRef]
- Torosov, B.T.; Guérin, S.; Vitanov, N.V. High-Fidelity Adiabatic Passage by Composite Sequences of Chirped Pulses. Phys. Rev. Lett. 2011, 106, 233001. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.; Sarma, A.K. Optical dipole force on ladderlike three-level atomic systems induced by few-cycle-pulse laser fields. Phys. Rev. A 2012, 86, 053414. [Google Scholar] [CrossRef][Green Version]
- Miao, X.; Wertz, E.; Cohen, M.G.; Metcalf, H. Strong optical forces from adiabatic rapid passage. Phys. Rev. A 2007, 75, 011402. [Google Scholar] [CrossRef][Green Version]
- Stack, D.; Elgin, J.; Anisimov, P.M.; Metcalf, H. Numerical studies of optical forces from adiabatic rapid passage. Phys. Rev. A 2011, 84, 013420. [Google Scholar] [CrossRef]
- Ivanov, V.S.; Rozhdestvensky, Y.V.; Suominen, K.A. Robust two-dimensional subrecoil Raman cooling by adiabatic transfer in a tripod atomic system. Phys. Rev. A 2012, 86, 033409. [Google Scholar] [CrossRef][Green Version]
- Fang, Y.; Buonocore, E.; Wahl, M.; Metcalf, H. Measurements of velocity-selective resonances from adiabatic rapid passage. Phys. Rev. A 2023, 107, L051101. [Google Scholar] [CrossRef]
- Guéry-Odelin, D.; Ruschhaupt, A.; Kiely, A.; Torrontegui, E.; Martínez-Garaot, S.; Muga, J.G. Shortcuts to adiabaticity: Concepts, methods, and applications. Rev. Mod. Phys. 2019, 91, 045001. [Google Scholar] [CrossRef]
- Chen, X.; Ruschhaupt, A.; Schmidt, S.; del Campo, A.; Guéry-Odelin, D.; Muga, J.G. Fast Optimal Frictionless Atom Cooling in Harmonic Traps: Shortcut to Adiabaticity. Phys. Rev. Lett. 2010, 104, 063002. [Google Scholar] [CrossRef]
- Chen, X.; Lizuain, I.; Ruschhaupt, A.; Guéry-Odelin, D.; Muga, J.G. Shortcut to Adiabatic Passage in Two- and Three-Level Atoms. Phys. Rev. Lett. 2010, 105, 123003. [Google Scholar] [CrossRef]
- Chen, X.; Torrontegui, E.; Muga, J.G. Lewis-Riesenfeld invariants and transitionless quantum driving. Phys. Rev. A 2011, 83, 062116. [Google Scholar] [CrossRef]
- Ruschhaupt, A.; Chen, X.; Alonso, D.; Muga, J.G. Optimally robust shortcuts to population inversion in two-level quantum systems. New J. Phys. 2012, 14, 093040. [Google Scholar] [CrossRef]
- Lu, X.J.; Chen, X.; Ruschhaupt, A.; Alonso, D.; Guérin, S.; Muga, J.G. Fast and robust population transfer in two-level quantum systems with dephasing noise and/or systematic frequency errors. Phys. Rev. A 2013, 88, 033406. [Google Scholar] [CrossRef]
- Daems, D.; Ruschhaupt, A.; Sugny, D.; Guérin, S. Robust Quantum Control by a Single-Shot Shaped Pulse. Phys. Rev. Lett. 2013, 111, 050404. [Google Scholar] [CrossRef] [PubMed]
- Dridi, G.; Liu, K.; Guérin, S. Optimal Robust Quantum Control by Inverse Geometric Optimization. Phys. Rev. Lett. 2020, 125, 250403. [Google Scholar] [CrossRef] [PubMed]
- Bartolotta, J.P.; Reilly, J.T.; Holland, M.J. Speeding up particle slowing using shortcuts to adiabaticity. Phys. Rev. A 2020, 102, 043107. [Google Scholar] [CrossRef]
- Prodan, J.; Migdall, A.; Phillips, W.D.; So, I.; Metcalf, H.; Dalibard, J. Stopping Atoms with Laser Light. Phys. Rev. Lett. 1985, 54, 992–995. [Google Scholar] [CrossRef]
- Phillips, W.D.; Prodan, J.V.; Metcalf, H.J. Laser cooling and electromagnetic trapping of neutral atoms. J. Opt. Soc. Am. B 1985, 2, 1751–1767. [Google Scholar] [CrossRef]
- Ivanov, V.S.; Rozhdestvensky, Y.V.; Suominen, K.A. Theory of robust subrecoil cooling by stimulated Raman adiabatic passage. Phys. Rev. A 2012, 85, 033422. [Google Scholar] [CrossRef]
- Adams, C.S.; Sigel, M.; Mlynek, J. Atom optics. Phys. Rep. 1994, 240, 143–210. [Google Scholar] [CrossRef]
- Lax, M. Quantum noise VII: The rate equations and amplitude noise in lasers. IEEE J. Quantum Electron. 1967, 3, 37–46. [Google Scholar] [CrossRef]
- Li, Y.C.; Chen, X. Shortcut to adiabatic population transfer in quantum three-level systems: Effective two-level problems and feasible counterdiabatic driving. Phys. Rev. A 2016, 94, 063411. [Google Scholar] [CrossRef]
- Du, Y.X.; Liang, Z.T.; Li, Y.C.; Yue, X.X.; Lv, Q.X.; Huang, W.; Chen, X.; Yan, H.; Zhu, S.L. Experimental realization of stimulated Raman shortcut-to-adiabatic passage with cold atoms. Nat. Commun. 2016, 7, 12479. [Google Scholar] [CrossRef]
- Lewis, H.R., Jr.; Riesenfeld, W. An exact quantum theory of the time-dependent harmonic oscillator and of a charged particle in a time-dependent electromagnetic field. J. Math. Phys. 1969, 10, 1458–1473. [Google Scholar] [CrossRef]
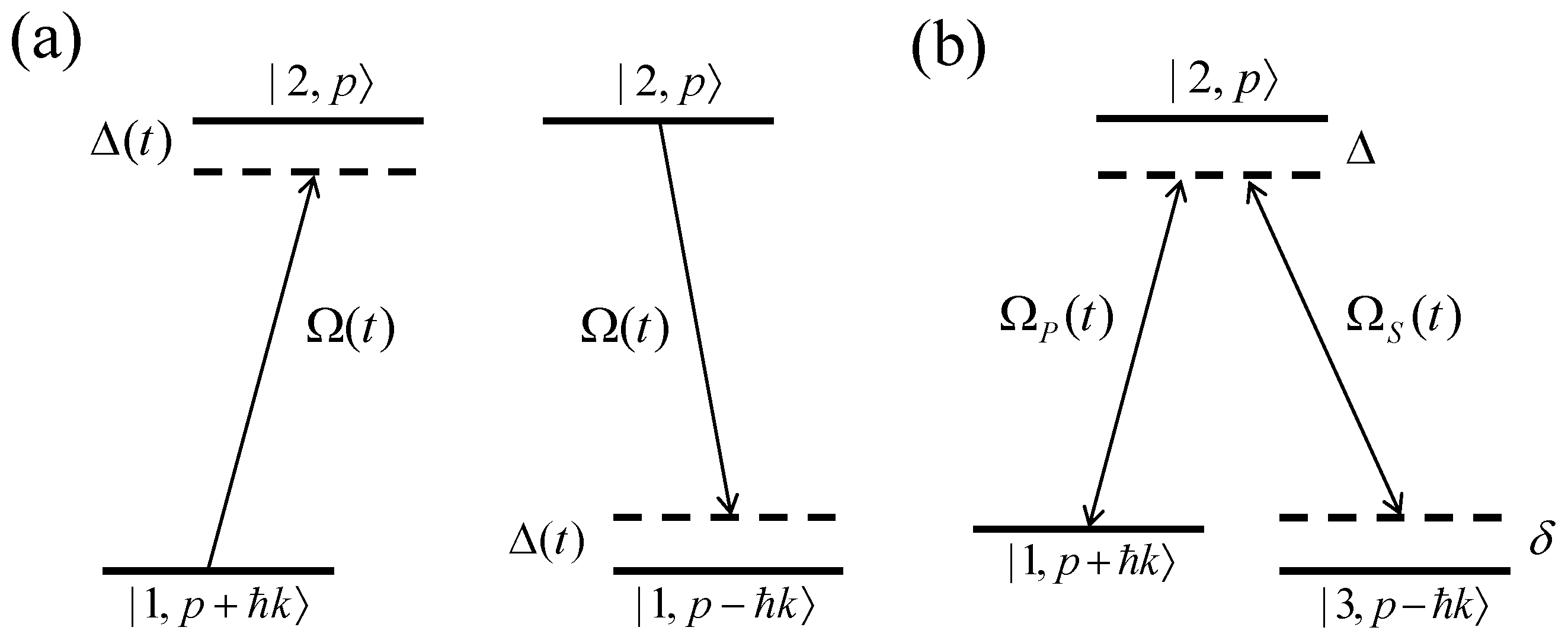


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Lu, J. Fast and Robust Optical Cooling via Shortcut to Adiabaticity. Entropy 2025, 27, 851. https://doi.org/10.3390/e27080851
Wang Z, Lu J. Fast and Robust Optical Cooling via Shortcut to Adiabaticity. Entropy. 2025; 27(8):851. https://doi.org/10.3390/e27080851
Chicago/Turabian StyleWang, Zhiyu, and Jie Lu. 2025. "Fast and Robust Optical Cooling via Shortcut to Adiabaticity" Entropy 27, no. 8: 851. https://doi.org/10.3390/e27080851
APA StyleWang, Z., & Lu, J. (2025). Fast and Robust Optical Cooling via Shortcut to Adiabaticity. Entropy, 27(8), 851. https://doi.org/10.3390/e27080851





