Quantum Coherence and Purity in Dissipative Hydrogen Atoms: Insights from the Lindblad Master Equation
Abstract
1. Introduction
2. The Hamiltonian and Quantum Dynamics
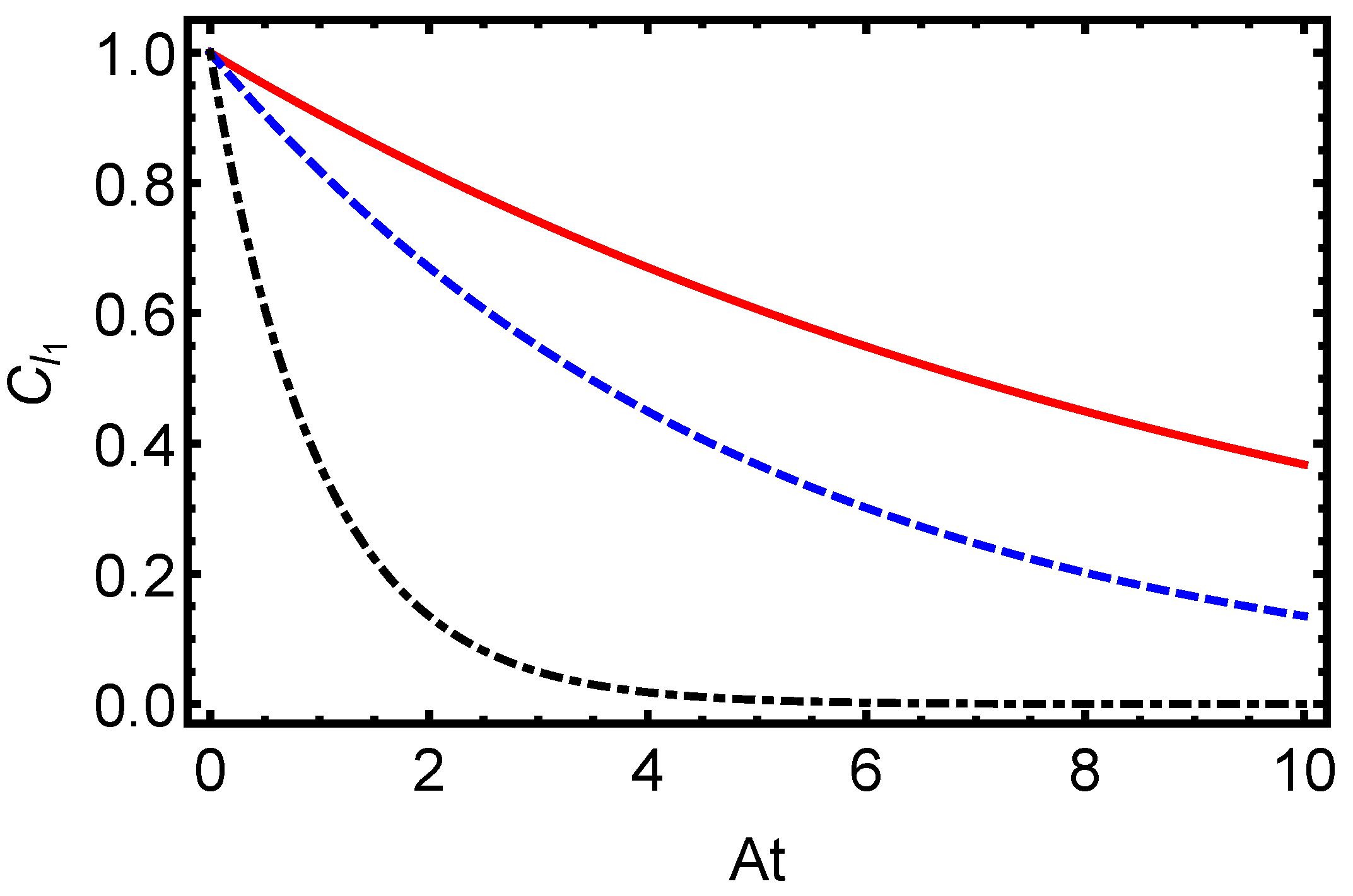
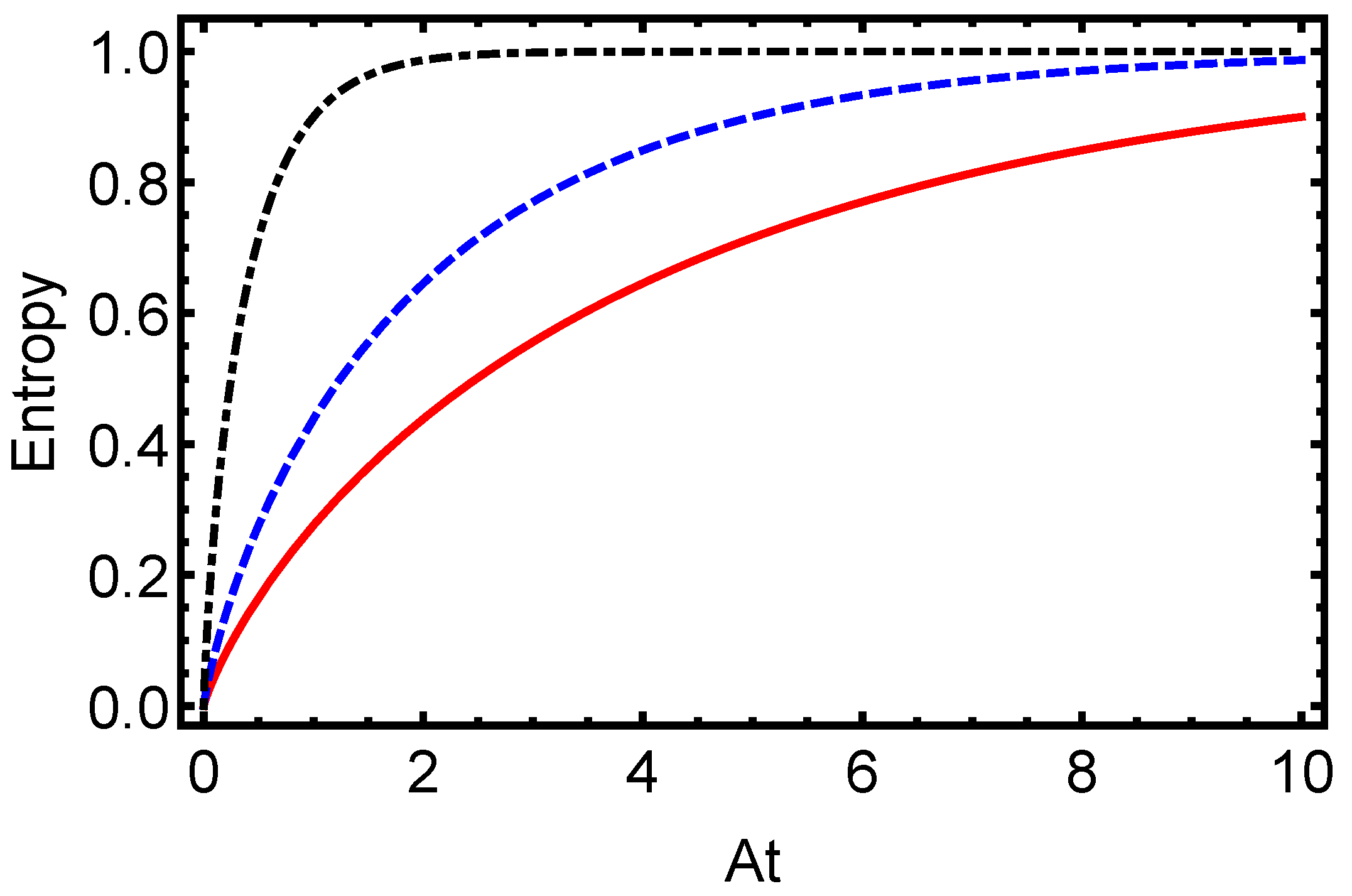
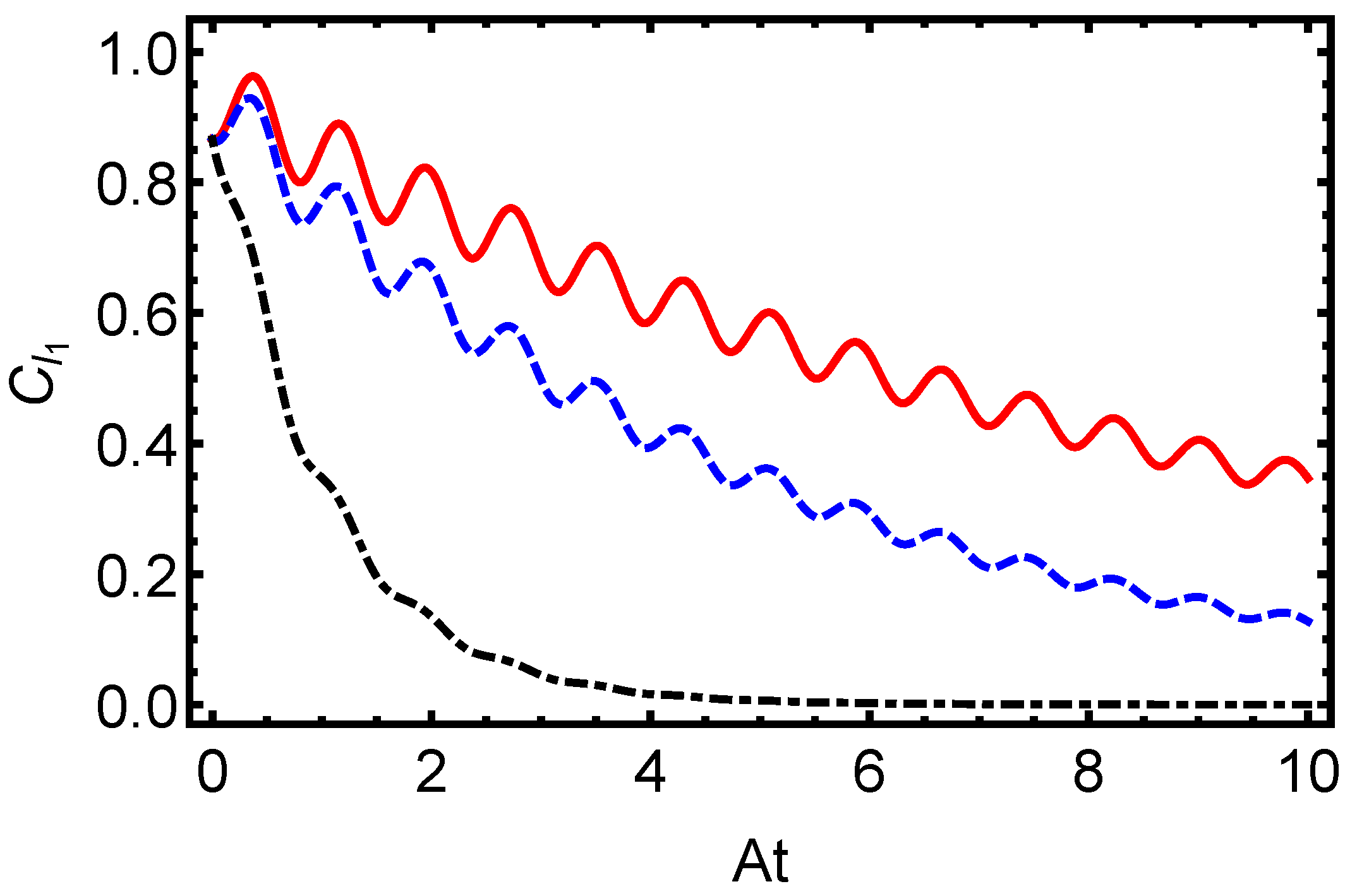
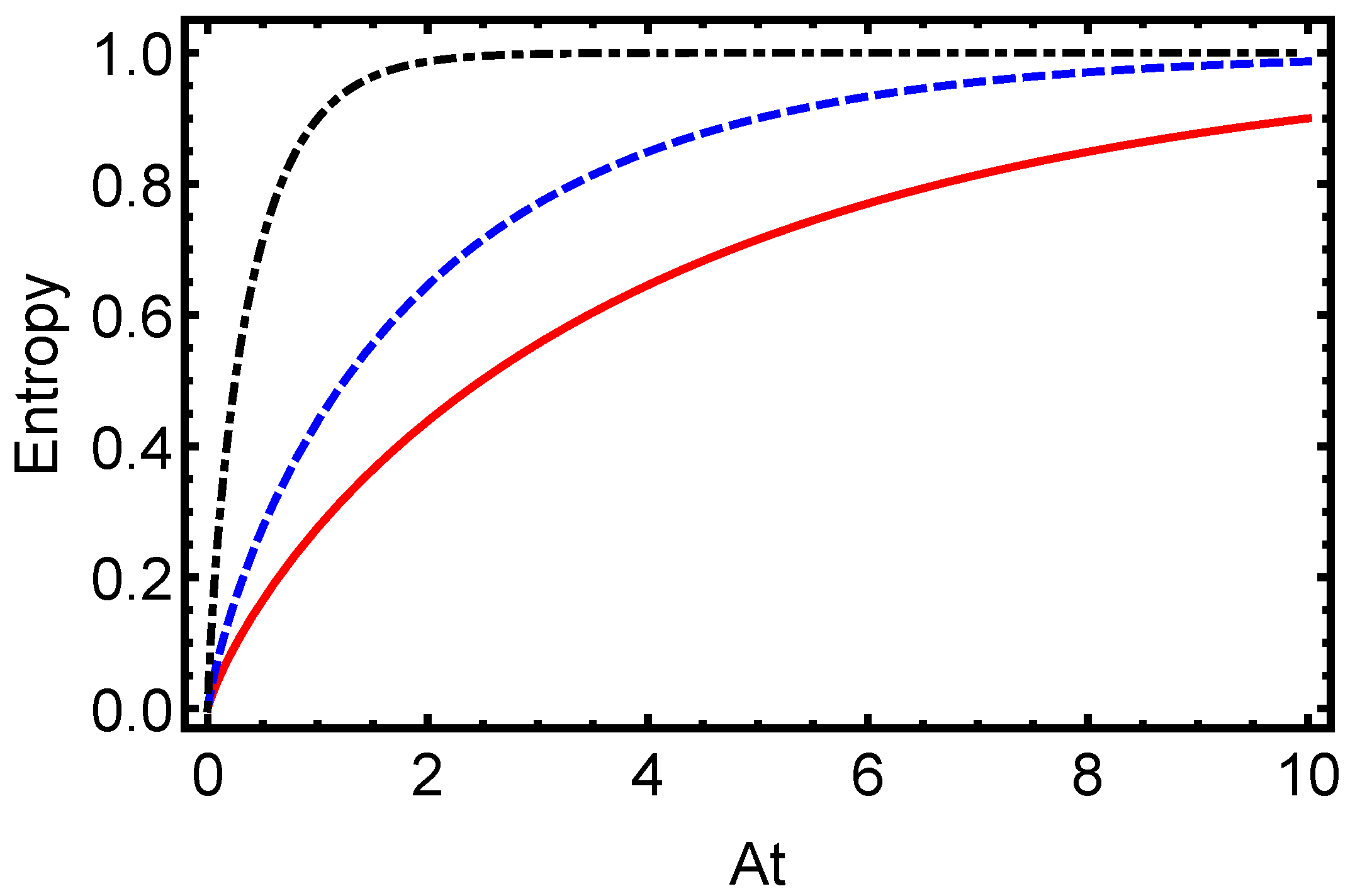
3. Quantum Coherence and Results
- Given the initial state,
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Derivation of the Time-Evolved Density Matrix Elements
References
- Bohr, N. On the constitution of atoms and molecules. Philos. Mag. 1913, 26, 1. [Google Scholar] [CrossRef]
- Bethe, H.; Salpeter, E. Quantum Mechanics of One- and Two-Electron Atoms; Springer: Berlin, Germany, 1957. [Google Scholar]
- Series, G.W. Spectrum of Atomic Hydrogen; Oxford University: New York, NY, USA, 1957. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics: Nonrelativistic Theory; Pergamon: London, UK, 1958. [Google Scholar]
- Sheludiakov, S.; McColgan, P.T.; Lee, D.M.; Khmelenko, V.V.; Järvinen, J.; Ahokas, J.; Vasiliev, S. Polarized Phases of H Atoms Embedded in Solid H2 Films. Phys. Rev. Lett. 2019, 122, 225301. [Google Scholar] [CrossRef] [PubMed]
- Ahokas, J.; Vainio, O.; Novotny, S.; Järvinen, J.; Khmelenko, V.V.; Lee, D.M.; Vasiliev, S. Magnetic resonance study of H atoms in thin films of H2 at temperatures below 1 K. Phys. Rev. B 2010, 81, 104516. [Google Scholar] [CrossRef]
- Ahokas, J.; Järvinen, J.; Khmelenko, V.V.; Lee, D.M.; Vasiliev, S. Exotic Behavior of Hydrogen Atoms in Solid H2 at Temperatures below 1 K. Phys. Rev. Lett. 2006, 97, 095301. [Google Scholar] [CrossRef] [PubMed]
- Bigelow, N.P.; Freed, J.H.; Lee, D.M. Nuclear-spin waves in polarized atomic hydrogen gas: Temperature and density dependence in the hydrodynamic and Knudsen regimes. Phys. Rev. Lett. 1989, 63, 1609. [Google Scholar] [CrossRef]
- Johnson, A.C.; Petta, J.R.; Taylor, J.M.; Yacoby, A.; Lukin, M.D.; Marcus, C.M.; Hanson, M.P.; Gossard, A.C. Triplet–singlet spin relaxation via nuclei in a double quantum dot. Nature 2005, 435, 925. [Google Scholar] [CrossRef]
- Petta, J.R.; Johnson, A.C.; Taylor, J.M.; Laird, E.A.; Yacoby, A.; Lukin, M.D.; Marcus, C.M.; Hanson, M.P.; Gossard, A.C. Coherent manipulation of coupled electron spins in semiconductor quantum dots. Science 2005, 309, 2180. [Google Scholar] [CrossRef]
- Taylor, J.M.; Engel, H.A.; Dür, W.; Yacoby, A.; Marcus, C.M.; Zoller, P.; Lukin, M.D. Fault-tolerant architecture for quantum computation using electrically controlled semiconductor spins. Nat. Phys. 2005, 1, 177. [Google Scholar] [CrossRef]
- Ladd, T.D.; Jelezko, F.; Laflamme, R.; Nakamura, Y.; Monroe, C.; O’Brien, J.L. Quantum computers. Nature 2010, 464, 45. [Google Scholar] [CrossRef] [PubMed]
- Bennett, C.H.; DiVincenzo, D.P. Quantum information and computation. Nature 2000, 404, 247. [Google Scholar] [CrossRef]
- Childress, L.; Gurudev Dutt, M.V.; Taylor, J.M.; Zibrov, A.S.; Jelezko, F.; Wrachtrup, J.; Hemmer, P.R.; Lukin, M.D. Coherent dynamics of coupled electron and nuclear spin qubits in diamond. Science 2006, 314, 281. [Google Scholar] [CrossRef] [PubMed]
- Dutt, M.V.G.; Childress, L.; Jiang, L.; Togan, E.; Maze, J.; Jelezko, F.; Zibrov, A.S.; Hemmer, P.R.; Lukin, M.D. Quantum register based on individual electronic and nuclear spin qubits in diamond. Science 2007, 316, 1312. [Google Scholar] [CrossRef]
- Neumann, P.; Mizuochi, N.; Rempp, F.; Hemmer, P.; Watanabe, H.; Yamasaki, S.; Jacques, V.; Gaebel, T.; Jelezko, F.; Wrachtrup, J. Multipartite entanglement among single spins in diamond. Science 2008, 320, 1326. [Google Scholar] [CrossRef]
- Fuchs, G.D.; Dobrovitski, V.V.; Toyli, D.M.; Heremans, F.J.; Awschalom, D.D. Gigahertz dynamics of a strongly driven single quantum spin. Science 2009, 326, 1520. [Google Scholar] [CrossRef] [PubMed]
- Tommassini, P.; Timmermans, E.; de Toledo Piza, A.F.R. The hydrogen atom as an entangled electron–proton system. Am. J. Phys. 1998, 66, 881. [Google Scholar] [CrossRef]
- Zhu, G.; Du, K.; Li, Y. Electron-nuclear entanglement in hydrogen atom. Phys. A 2005, 346, 295. [Google Scholar] [CrossRef]
- Bartlett, S.D.; Rudolph, T.; Spekkens, R.W. Reference frames, superselection rules, and quantum information. Rev. Mod. Phys. 2007, 79, 555. [Google Scholar] [CrossRef]
- Marvian, I.; Spekkens, R.W. The theory of manipulations of pure state asymmetry: I. Basic tools, equivalence classes and single copy transformations. New J. Phys. 2013, 15, 033001. [Google Scholar] [CrossRef]
- Marvian, I.; Spekkens, R.W. Modes of asymmetry: The application of harmonic analysis to symmetric quantum dynamics and quantum reference frames. Phys. Rev. A 2014, 90, 062110. [Google Scholar] [CrossRef]
- Lloyd, S. Quantum coherence in biological systems. J. Phys. Conf. Ser. 2011, 302, 012037. [Google Scholar] [CrossRef]
- Li, C.-M.; Lambert, N.; Chen, Y.-N.; Chen, G.-Y.; Nori, F. Witnessing quantum coherence: From solid-state to biological systems. Sci. Rep. 2012, 2, 885. [Google Scholar] [CrossRef] [PubMed]
- Lambert, N.; Chen, Y.-N.; Chen, Y.-C.; Li, C.-M.; Chen, G.-Y.; Nori, F. Quantum biology. Nat. Phys. 2013, 9, 10. [Google Scholar] [CrossRef]
- Narasimhachar, V.; Gour, G. Low-temperature thermodynamics with quantum coherence. Nat. Commun. 2015, 6, 7689. [Google Scholar] [CrossRef]
- Aberg, J. Catalytic coherence. Phys. Rev. Lett. 2014, 113, 150402. [Google Scholar] [CrossRef] [PubMed]
- Ćwikliński, P.; Studziński, M.; Horodecki, M.; Oppenheim, J. Limitations on the evolution of quantum coherences: Towards fully quantum second laws of thermodynamics. Phys. Rev. Lett. 2015, 115, 210403. [Google Scholar] [CrossRef] [PubMed]
- Baumgratz, T.; Cramer, M.; Plenio, M.B. Quantifying coherence. Phys. Rev. Lett. 2014, 113, 140401. [Google Scholar] [CrossRef]
- Horodecki, M.; Oppenheim, J.; Winter, A. Partial quantum information. Nature 2005, 436, 673. [Google Scholar] [CrossRef]
- Knill, E.; Laflamme, R. Power of one bit of quantum information. Phys. Rev. Lett. 1998, 81, 5672. [Google Scholar] [CrossRef]
- Deutsch, D.; Jozsa, R. Rapid solution of problems by quantum computation. Proc. R. Soc. Lond. A 1992, 439, 553. [Google Scholar]
- Grover, L.K. Super classical search algorithm to find an element in unsorted array. Phys. Rev. Lett. 1996, 79, 325. [Google Scholar] [CrossRef]
- Marletto, C.; Vedral, V. Gravitationally Induced Entanglement between Two Massive Particles is Sufficient Evidence of Quantum Effects in Gravity. Phys. Rev. Lett. 2017, 119, 040402. [Google Scholar] [CrossRef]
- Hu, M.-L.; Hu, X.; Wang, J.; Peng, Y.; Zhang, Y.-R.; Fan, H. Quantum coherence and geometric quantum discord. Phys. Rep. 2018, 762–764, 1–100. [Google Scholar] [CrossRef]
- Adesso, G.; Bromley, T.R.; Cianciaruso, M. Measures and applications of quantum correlations. J. Phys. A Math. Theor. 2016, 49, 473001. [Google Scholar] [CrossRef]
- Streltsov, A.; Singh, U.; Dhar, H.S.; Bera, M.N.; Adesso, G. Measuring quantum coherence with entanglement. Phys. Rev. Lett. 2015, 115, 020403. [Google Scholar] [CrossRef] [PubMed]
- Winter, A.; Yang, D. Operational resource theory of coherence. Phys. Rev. Lett. 2016, 116, 120404. [Google Scholar] [CrossRef]
- Chitambar, E.; Streltsov, A.; Rana, S.; Bera, M.N.; Adesso, G.; Lewenstein, M. Assisted distillation of quantum coherence. Phys. Rev. Lett. 2016, 116, 070402. [Google Scholar] [CrossRef]
- Yuan, X.; Zhou, H.; Cao, Z.; Ma, X. Intrinsic randomness as a measure of quantum coherence. Phys. Rev. A 2015, 92, 022124. [Google Scholar] [CrossRef]
- Du, S.; Bai, Z.; Qi, X. Coherence measures and optimal conversion for coherent states. Quantum Inf. Comput. 2015, 15, 1307. [Google Scholar] [CrossRef]
- Yao, Y.; Xiao, X.; Ge, L.; Sun, C.P. Quantum coherence in multipartite systems. Phys. Rev. A 2015, 92, 022112. [Google Scholar] [CrossRef]
- Xi, Z.; Li, Y.; Fan, H. Quantum coherence and correlations in quantum system. Sci. Rep. 2015, 5, 10922. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.-R.; Shao, L.-H.; Li, Y.; Fan, H. Quantifying coherence in infinite-dimensional systems. Phys. Rev. A 2016, 93, 012334. [Google Scholar] [CrossRef]
- Xu, J. Quantifying coherence of Gaussian states. Phys. Rev. A 2016, 93, 032111. [Google Scholar] [CrossRef]
- Cheng, S.; Hall, M.J.W. Complementarity relations for quantum coherence. Phys. Rev. A 2015, 92, 042101. [Google Scholar] [CrossRef]
- Yadin, B.; Vedral, V. General framework for quantum macroscopicity in terms of coherence. Phys. Rev. A 2016, 93, 022122. [Google Scholar] [CrossRef]
- Marvian, I.; Spekkens, R.W. Extending Noether’s theorem by quantifying the asymmetry of quantum states. Nat. Commun. 2014, 5, 3821. [Google Scholar] [CrossRef]
- Monras, A.; Chęcinska, A.; Ekert, A. Witnessing quantum coherence in the presence of noise. New J. Phys. 2014, 16, 063041. [Google Scholar] [CrossRef]
- Karpat, G.; Çakmak, B.; Fanchini, F.F. Quantum coherence and uncertainty in the anisotropic XY chain. Phys. Rev. B 2014, 90, 104431. [Google Scholar] [CrossRef]
- Berrada, K.; Bougouffa, S. Robustness of quantum correlations in photonic systems under non-Markovian dephasing: Theoretical analysis in the experimental range. Sci. Rep. 2025, 15, 22260. [Google Scholar] [CrossRef] [PubMed]
- von Neumann, J. Mathematical Foundations of Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1955. [Google Scholar]
- Bromley, T.R.; Cianciaruso, M.; Adesso, G. Frozen quantum coherence. Phys. Rev. Lett. 2015, 114, 210401. [Google Scholar] [CrossRef]
- Hu, M.-L.; Fan, H. Evolution equation for quantum coherence. Sci. Rep. 2016, 6, 29260. [Google Scholar] [CrossRef]
- Styliaris, G.; Venuti, L.C.; Zanardi, P. Coherence-generating power of quantum dephasing processes. Phys. Rev. A 2018, 97, 032304. [Google Scholar] [CrossRef]
- Hu, M.-L.; Fan, H. Quantum coherence of multiqubit states in correlated noisy channels. Sci. China Phys. Mech. Astron. 2020, 63, 230322. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Benatti, F.; Floreanini, R. Open Quantum Systems; Springer: Berlin, Germany, 2003. [Google Scholar]
- Preskill, J. Quantum Information and Computation; Lecture Notes for Physics 229; California Institute of Technology: Pasadena, CA, USA, 1998. [Google Scholar]
- Mintert, F.; Kuś, M.; Buchleitner, A. Concurrence of mixed multipartite quantum states. Phys. Rep. 2005, 415, 207–275. [Google Scholar] [CrossRef]
- Hilt, S.; Lutz, E. System-bath entanglement in quantum thermodynamics. Phys. Rev. A 2009, 79, 010101. [Google Scholar] [CrossRef]
- Pernice, A.; Strunz, W.T. Decoherence and the nature of system-environment correlations. Phys. Rev. A 2011, 84, 062121. [Google Scholar] [CrossRef]
- Iyoda, E.; Kaneko, K.; Sagawa, T. Fluctuation theorem for many-body pure quantum states. Phys. Rev. Lett. 2017, 119, 100601. [Google Scholar] [CrossRef] [PubMed]
- Li, S.-W. Production rate of the system-bath mutual information. Phys. Rev. E 2017, 96, 012139. [Google Scholar] [CrossRef] [PubMed]
- Singh, U.; Bera, M.N.; Dhar, H.S.; Pati, A.K. Maximally coherent mixed states: Complementarity between maximal coherence and mixedness. Phys. Rev. A 2015, 91, 052115. [Google Scholar] [CrossRef]
- Faghihi, M.J.; Tavassoly, M.K. Quantum mutual entropy, coherence and correlation in the presence of phase damping. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 165502. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berrada, K.; Bougouffa, S. Quantum Coherence and Purity in Dissipative Hydrogen Atoms: Insights from the Lindblad Master Equation. Entropy 2025, 27, 848. https://doi.org/10.3390/e27080848
Berrada K, Bougouffa S. Quantum Coherence and Purity in Dissipative Hydrogen Atoms: Insights from the Lindblad Master Equation. Entropy. 2025; 27(8):848. https://doi.org/10.3390/e27080848
Chicago/Turabian StyleBerrada, Kamal, and Smail Bougouffa. 2025. "Quantum Coherence and Purity in Dissipative Hydrogen Atoms: Insights from the Lindblad Master Equation" Entropy 27, no. 8: 848. https://doi.org/10.3390/e27080848
APA StyleBerrada, K., & Bougouffa, S. (2025). Quantum Coherence and Purity in Dissipative Hydrogen Atoms: Insights from the Lindblad Master Equation. Entropy, 27(8), 848. https://doi.org/10.3390/e27080848







