Principal Connection Between Typical Heart Rate Variability Parameters as Revealed by a Comparative Analysis of Their Heart Rate and Age Dependence
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Acquisition and Preprocessing
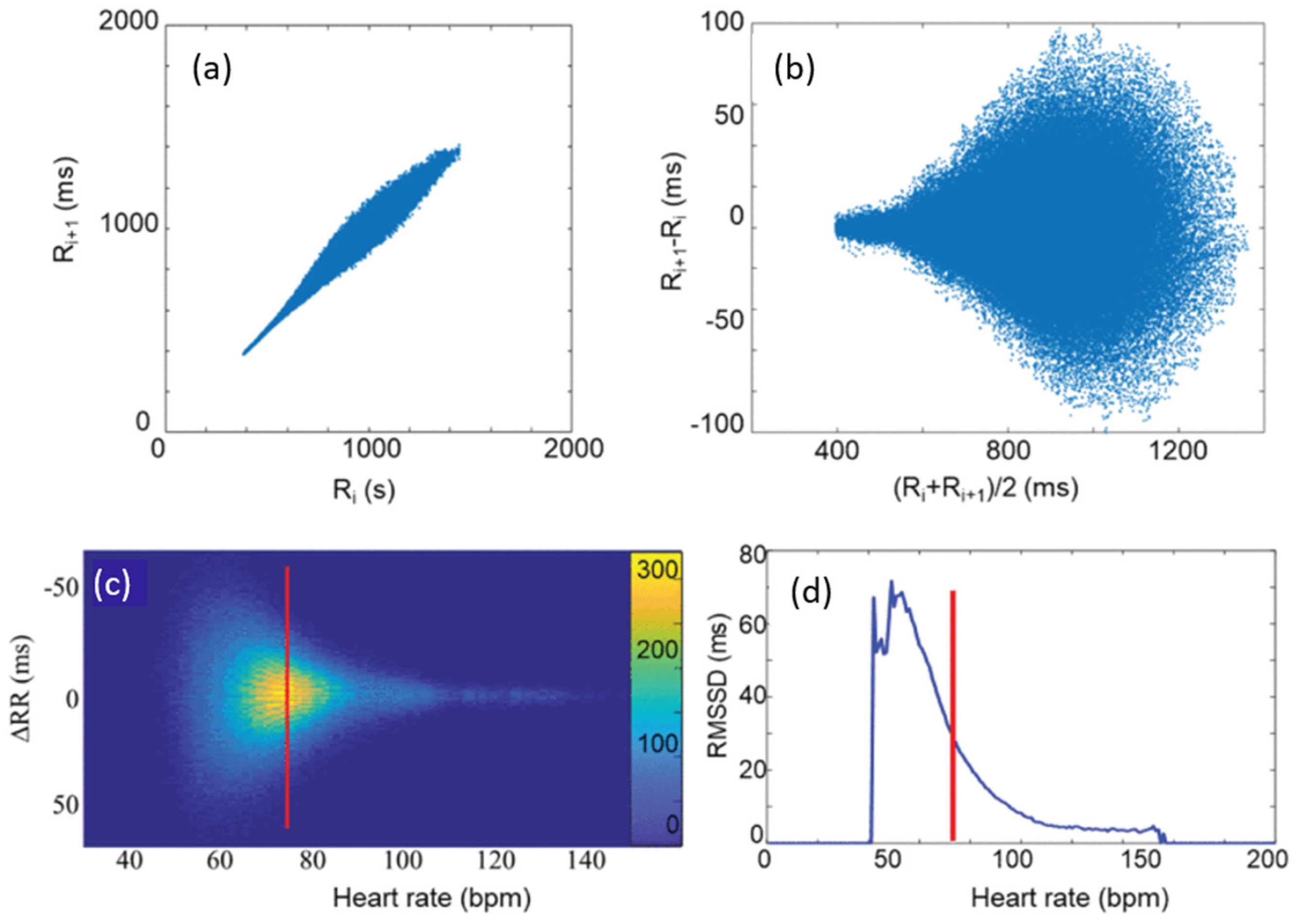
2.2. Modified Poincaré Analysis and M-Curve Construction
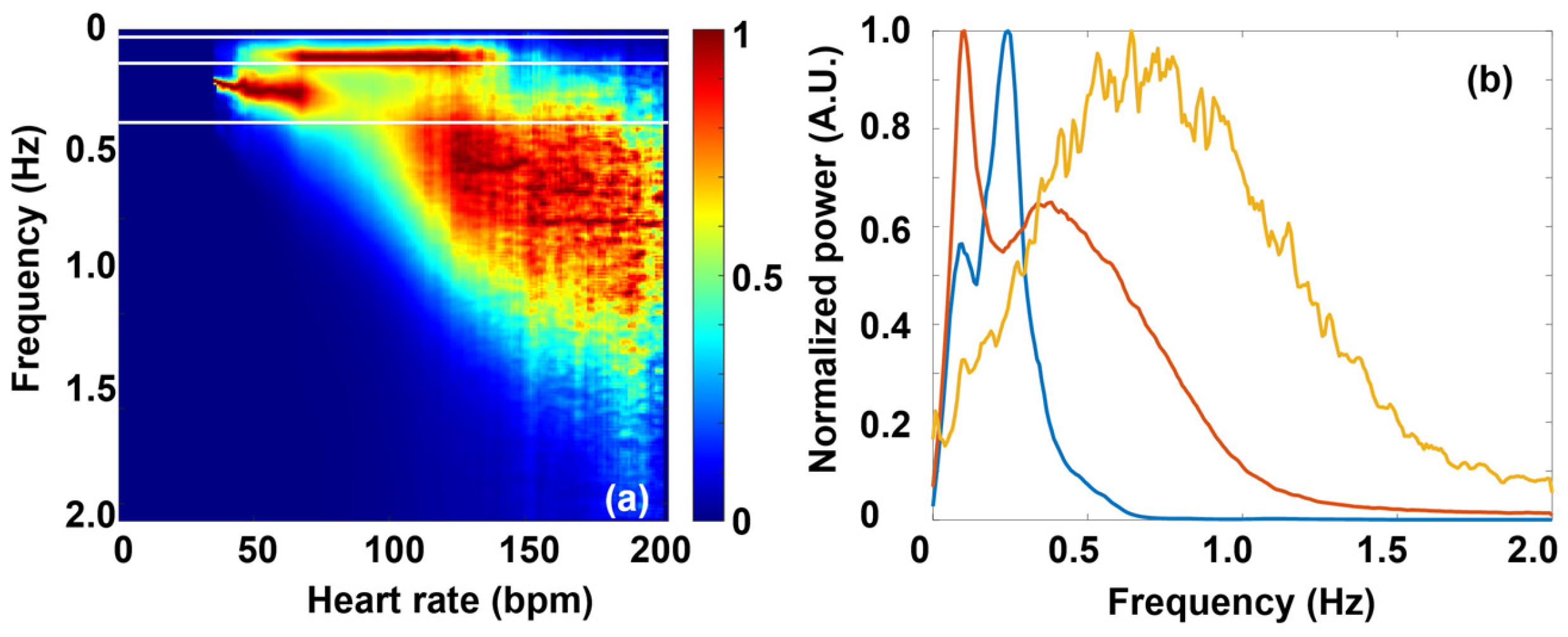
2.3. Spectral Analysis
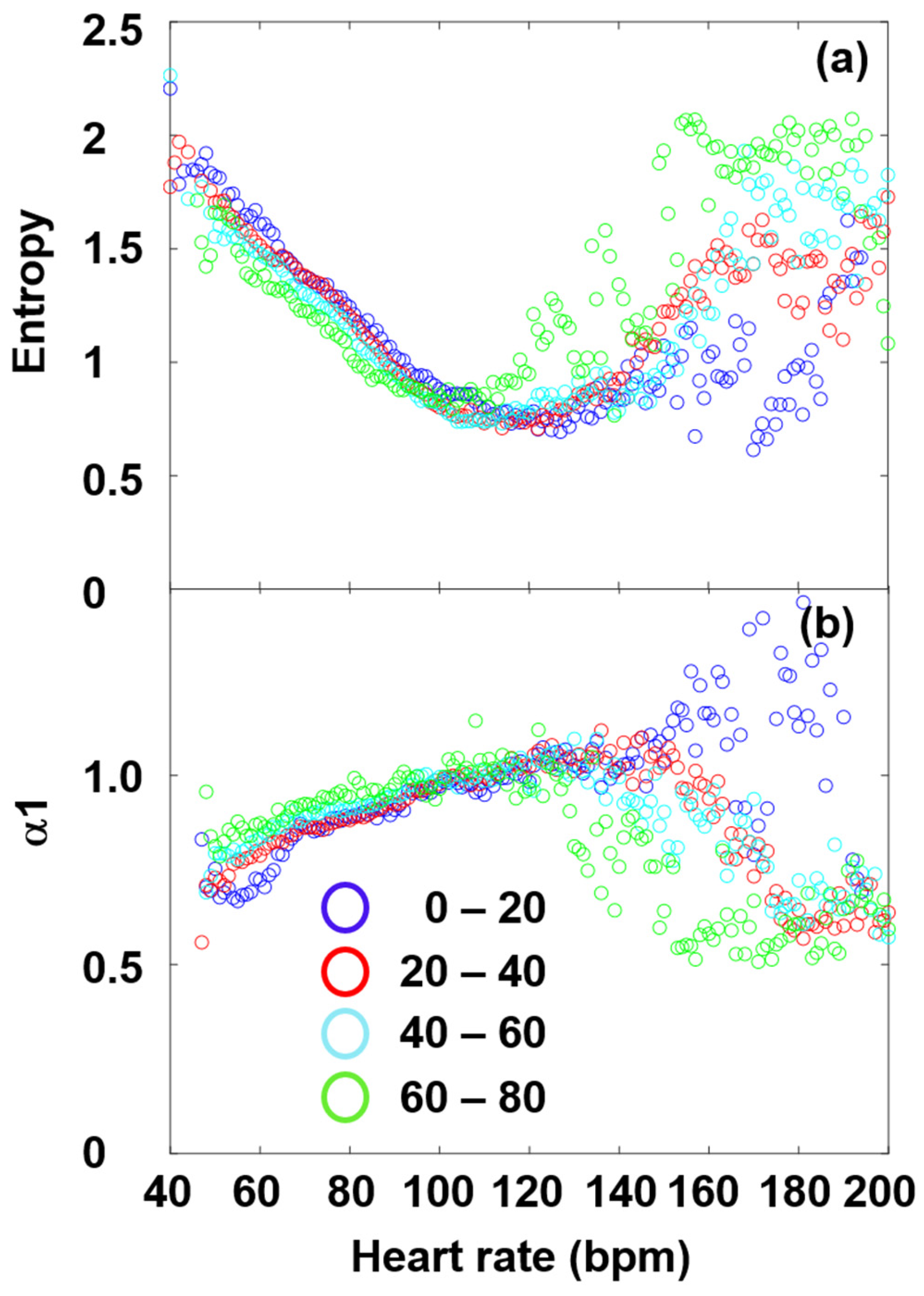
2.4. Nonlinear and Complexity Metrics
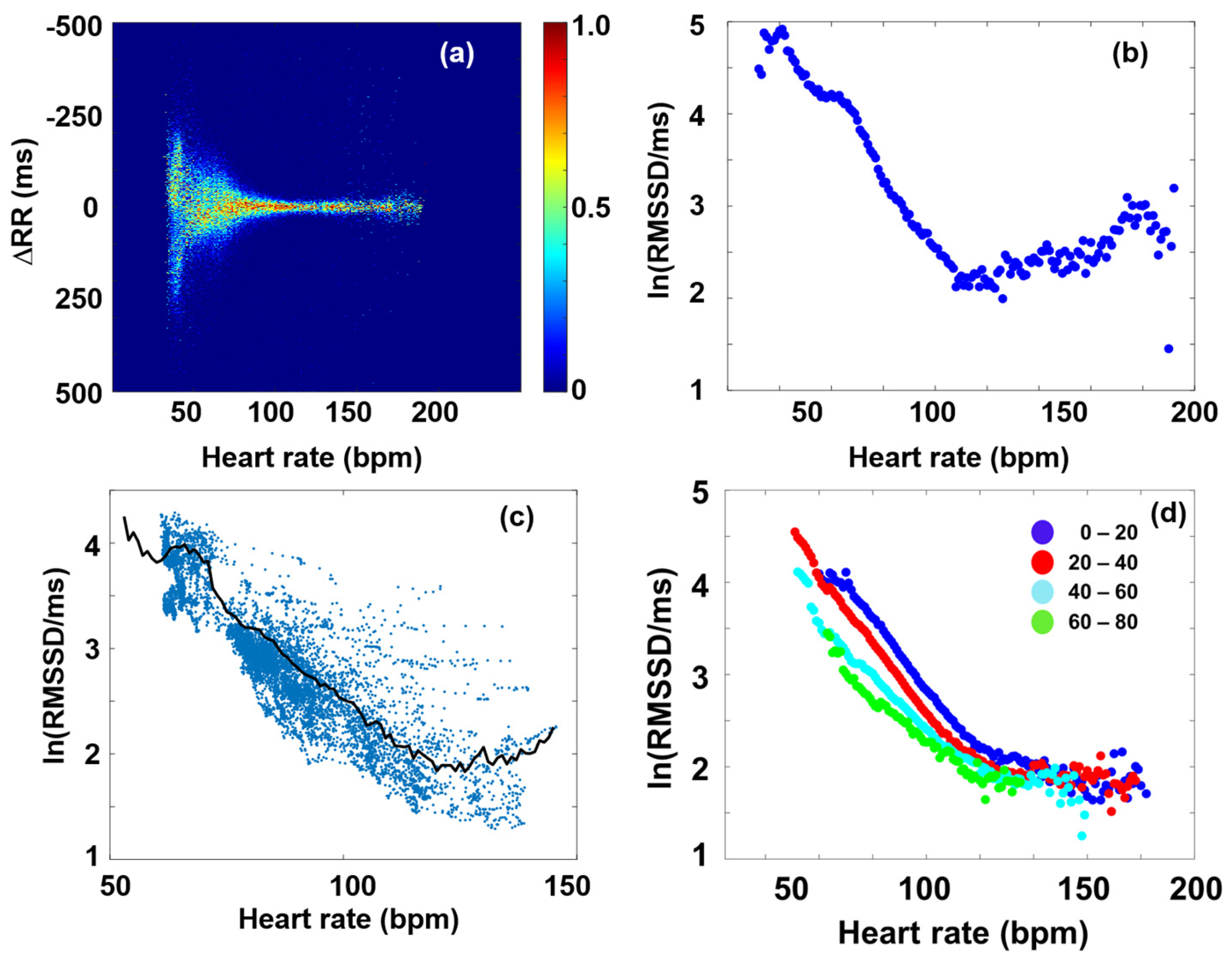
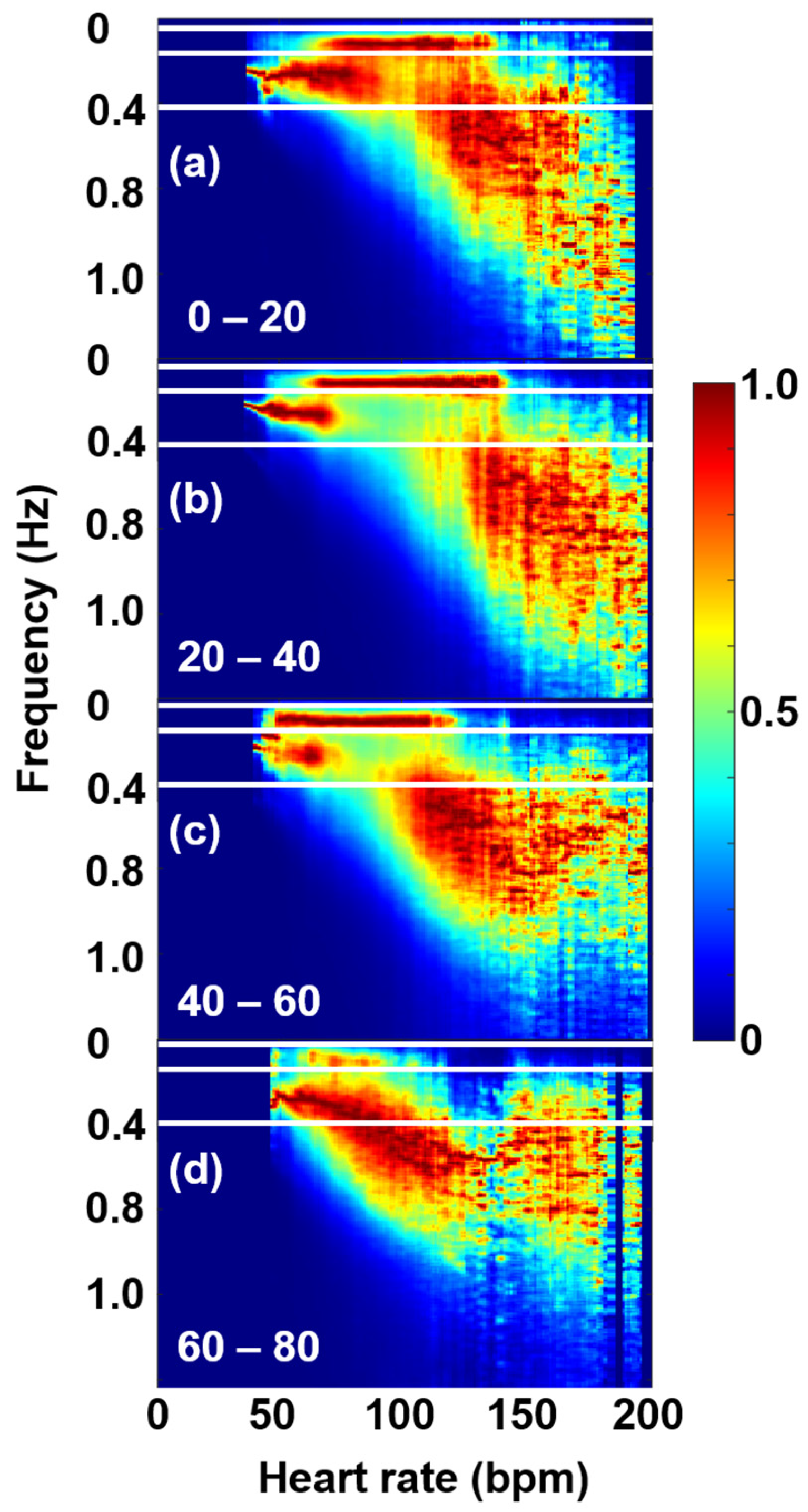
2.5. Age-Cohort Analysis
3. Results and Discussion
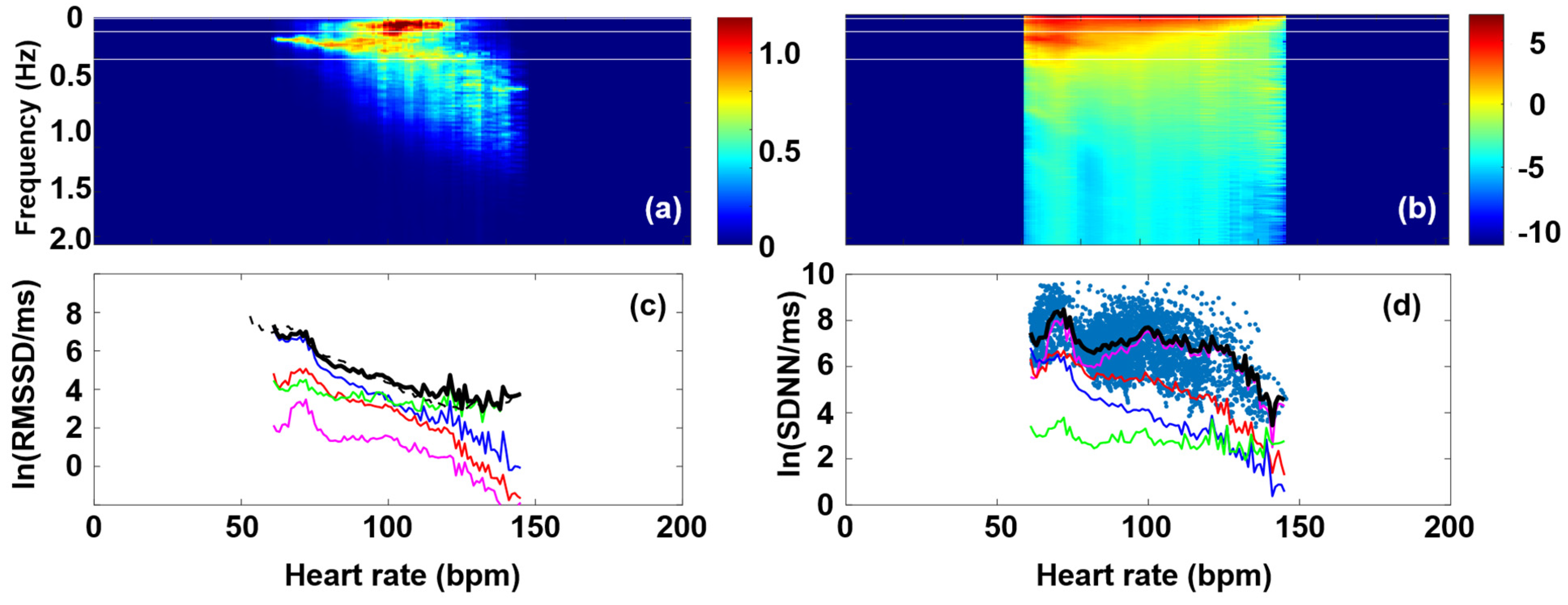
3.1. RMSSD and the Poincaré Plot
3.2. Fourier Components Versus RMSSD and SDNN
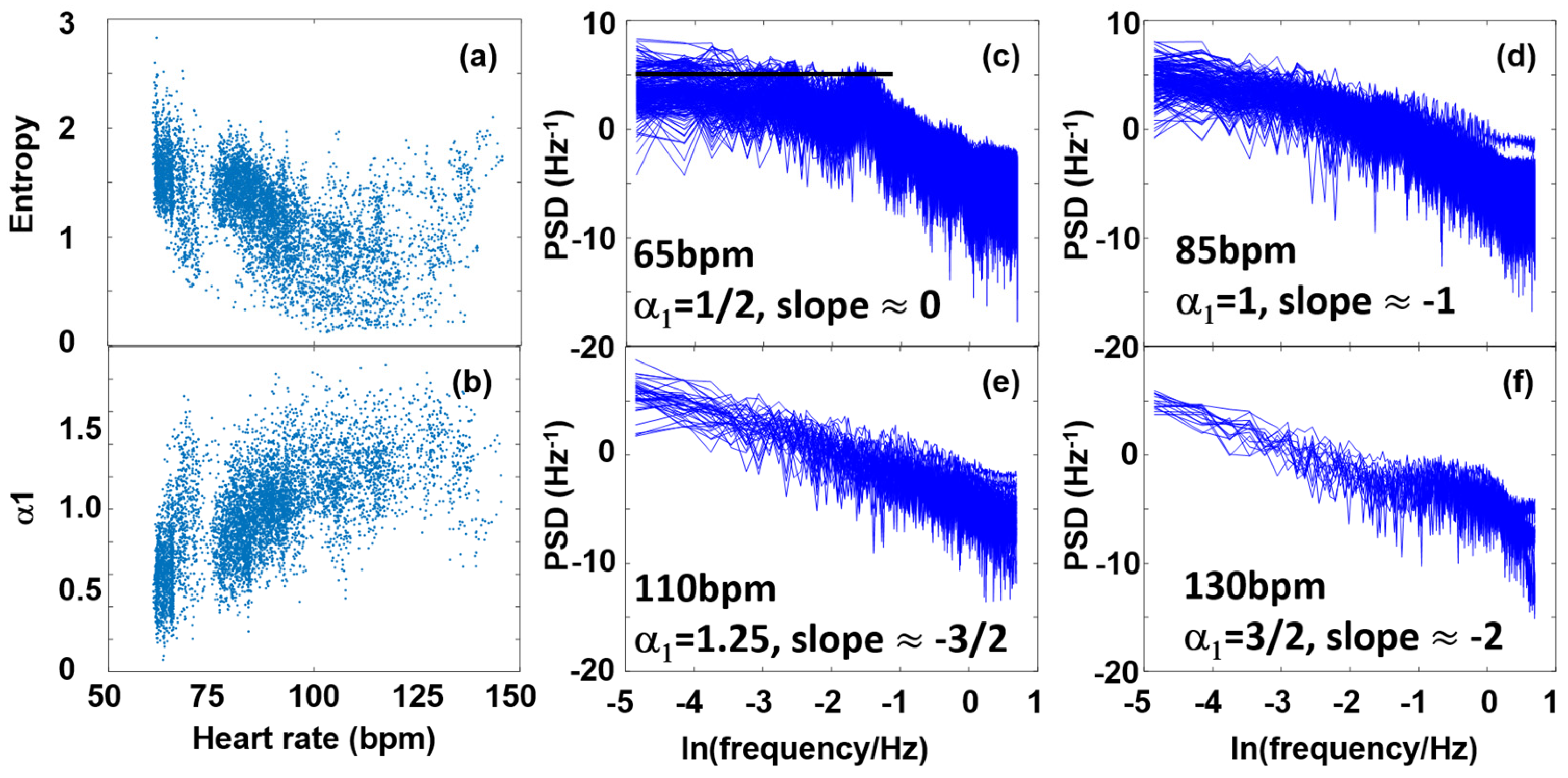
3.3. Fourier Components Versus Nonlinear Measures (DFA and SampEn)
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANS | Autonomic nervous system |
| DFA | Detrended fluctuation analysis |
| ECG | Electrocardiography |
| FFT | Fast Fourier Transform |
| HF | High frequency |
| HR | Heart rate |
| HRV | Heart rate variability |
| LF | Low frequency |
| MC | Master Curve |
| NN | Normal-to-normal RR intervals (NN and RR are used here synonymously) |
| PNS | Parasympathetic nervous system |
| RMSSD | Root mean square of successive differences |
| RR | Length of the RR interval |
| dRR | Length-difference in successive RR intervals |
| SampEn | Sample entropy |
| SDNN | Standard deviation of normal-to-normal RR intervals |
| SNS | Sympathetic nervous system |
| THEW | Telemetric- and Holter-ECG Warehouse |
| VHF | Very high-frequency |
| VLF | Very low-frequency |
References
- Billman, G.E. Heart Rate Variability ? A Historical Perspective. Front. Physiol. 2011, 2, 86. [Google Scholar] [CrossRef]
- Langmár, G.; Sümegi, T.; Fülöp, B.; Pozsgai, L.; Mocsai, T.; Tóth, M.; Racz, L.; Kopper, B.; Dér, A.; Búzás, A.; et al. HRV Alterations During Delayed-Onset Muscle Soreness Inducing Exercise—With Piezo2 Interpretation 2025. eLife 2025, 2025061739. [Google Scholar] [CrossRef]
- Sonkodi, B. LF Power of HRV Could Be the Piezo2 Activity Level in Baroreceptors with Some Piezo1 Residual Activity Contribution. Int. J. Mol. Sci. 2023, 24, 7038. [Google Scholar] [CrossRef] [PubMed]
- Sonkodi, B. Acquired Piezo2 Channelopathy is One Principal Gateway to Pathophysiology. Front. Biosci. 2025, 30, 33389. [Google Scholar] [CrossRef] [PubMed]
- Zeng, W.-Z.; Marshall, K.L.; Min, S.; Daou, I.; Chapleau, M.W.; Abboud, F.M.; Liberles, S.D.; Patapoutian, A. PIEZOs Mediate Neuronal Sensing of Blood Pressure and the Baroreceptor Reflex. Science 2018, 362, 464–467. [Google Scholar] [CrossRef]
- Schiweck, C.; Piette, D.; Berckmans, D.; Claes, S.; Vrieze, E. Heart Rate and High Frequency Heart Rate Variability during Stress as Biomarker for Clinical Depression. A Systematic Review. Psychol. Med. 2019, 49, 200–211. [Google Scholar] [CrossRef]
- Kloter, E.; Barrueto, K.; Klein, S.D.; Scholkmann, F.; Wolf, U. Heart Rate Variability as a Prognostic Factor for Cancer Survival—A Systematic Review. Front. Physiol. 2018, 9, 623. [Google Scholar] [CrossRef]
- Tarvainen, M.P.; Niskanen, J.-P.; Lipponen, J.A.; Ranta-aho, P.O.; Karjalainen, P.A. Kubios HRV—Heart Rate Variability Analysis Software. Comput. Methods Programs Biomed. 2014, 113, 210–220. [Google Scholar] [CrossRef]
- Shaffer, F.; Ginsberg, J.P. An Overview of Heart Rate Variability Metrics and Norms. Front. Public Health 2017, 5, 258. [Google Scholar] [CrossRef]
- Georgieva-Tsaneva, G.N. Time and Frequency Analysis of Heart Rate Variability Data in Heart Failure Patients. Int. J. Adv. Comput. Sci. Appl. 2019, 10, 456–462. [Google Scholar] [CrossRef]
- Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology. Heart Rate Variability: Standards of Measurement, Physiological Interpretation and Clinical Use. Circulation 1996, 93, 1043–1065. [Google Scholar] [CrossRef]
- Stefanovska, A. Physics of the Human Cardiovascular System. Contemp. Phys. 1999, 40, 31–55. [Google Scholar] [CrossRef]
- McClintock, P.V.E.; Stefanovska, A. Noise and Determinism in Cardiovascular Dynamics. Phys. Stat. Mech. Its Appl. 2002, 314, 69–76. [Google Scholar] [CrossRef]
- Stefanovska, A. Coupled Oscillatros: Complex But Not Complicated Cardiovascular and Brain Interactions. IEEE Eng. Med. Biol. Mag. 2007, 26, 25–29. [Google Scholar] [CrossRef]
- Shiogai, Y.; Stefanovska, A.; McClintock, P.V.E. Nonlinear Dynamics of Cardiovascular Ageing. Phys. Rep. 2010, 488, 51–110. [Google Scholar] [CrossRef]
- Rowland Adams, J.; Newman, J.; Stefanovska, A. Distinguishing between Deterministic Oscillations and Noise. Eur. Phys. J. Spec. Top. 2023, 232, 3435–3457. [Google Scholar] [CrossRef]
- Menuet, C.; Ben-Tal, A.; Linossier, A.; Allen, A.M.; Machado, B.H.; Moraes, D.J.A.; Farmer, D.G.S.; Paterson, D.J.; Mendelowitz, D.; Lakatta, E.G.; et al. Redefining Respiratory Sinus Arrhythmia as Respiratory Heart Rate Variability: An International Expert Recommendation for Terminological Clarity. Nat. Rev. Cardiol. 2025, 1–7. [Google Scholar] [CrossRef]
- Hamill, O.P. Pressure Pulsatility Links Cardio-Respiratory and Brain Rhythmicity. J. Integr. Neurosci. 2023, 22, 143. [Google Scholar] [CrossRef]
- Wessel, N.; Voss, A.; Malberg, H.; Ziehmann, C.; Voss, H.U.; Schirdewan, A.; Meyerfeldt, U.; Kurths, J. Nonlinear Analysis of Complex Phenomena in Cardiological Data. Herzschrittmachertherapie Elektrophysiologie 2000, 11, 159–173. [Google Scholar] [CrossRef]
- Porta, A.; Faes, L.; Masé, M.; D’Addio, G.; Pinna, G.D.; Maestri, R.; Montano, N.; Furlan, R.; Guzzetti, S.; Nollo, G.; et al. An Integrated Approach Based on Uniform Quantization for the Evaluation of Complexity of Short-Term Heart Period Variability: Application to 24h Holter Recordings in Healthy and Heart Failure Humans. Chaos Interdiscip. J. Nonlinear Sci. 2007, 17, 015117. [Google Scholar] [CrossRef]
- Catai, A.; Takahashi, A.; Perseguini, N.; Milan, J.; Minatel, V.; Rehder-Santos, P.; Marchi, A.; Bari, V.; Porta, A. Effect of the Postural Challenge on the Dependence of the Cardiovascular Control Complexity on Age. Entropy 2014, 16, 6686–6704. [Google Scholar] [CrossRef]
- Barà, C.; Pernice, R.; Catania, C.A.; Hilal, M.; Porta, A.; Humeau-Heurtier, A.; Faes, L. Comparison of Entropy Rate Measures for the Evaluation of Time Series Complexity: Simulations and Application to Heart Rate and Respiratory Variability. Biocybern. Biomed. Eng. 2024, 44, 380–392. [Google Scholar] [CrossRef]
- Kurths, J.; Voss, A.; Saparin, P.; Witt, A.; Kleiner, H.J.; Wessel, N. Quantitative Analysis of Heart Rate Variability. Chaos Interdiscip. J. Nonlinear Sci. 1995, 5, 88–94. [Google Scholar] [CrossRef]
- Kamen, P.W.; Tonkin, A.M. Application of the Poincaré Plot to Heart Rate Variability: A New Measure of Functional Status in Heart Failure. Aust. N. Z. J. Med. 1995, 25, 18–26. [Google Scholar] [CrossRef] [PubMed]
- Brinkmann, A.E.; Press, S.A.; Helmert, E.; Hautzinger, M.; Khazan, I.; Vagedes, J. Comparing Effectiveness of HRV-Biofeedback and Mindfulness for Workplace Stress Reduction: A Randomized Controlled Trial. Appl. Psychophysiol. Biofeedback 2020, 45, 307–322. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.-G.; Cheon, E.-J.; Bai, D.-S.; Lee, Y.H.; Koo, B.-H. Stress and Heart Rate Variability: A Meta-Analysis and Review of the Literature. Psychiatry Investig. 2018, 15, 235–245. [Google Scholar] [CrossRef] [PubMed]
- Lin, I.-M.; Wang, S.-Y.; Fan, S.-Y.; Peper, E.; Chen, S.-P.; Huang, C.-Y. A Single Session of Heart Rate Variability Biofeedback Produced Greater Increases in Heart Rate Variability Than Autogenic Training. Appl. Psychophysiol. Biofeedback 2020, 45, 343–350. [Google Scholar] [CrossRef]
- Rijken, N.H.; Soer, R.; De Maar, E.; Prins, H.; Teeuw, W.B.; Peuscher, J.; Oosterveld, F.G.J. Increasing Performance of Professional Soccer Players and Elite Track and Field Athletes with Peak Performance Training and Biofeedback: A Pilot Study. Appl. Psychophysiol. Biofeedback 2016, 41, 421–430. [Google Scholar] [CrossRef]
- Billman, G.E. The Effect of Heart Rate on the Heart Rate Variability Response to Autonomic Interventions. Front. Physiol. 2013, 4, 222. [Google Scholar] [CrossRef]
- Billman, G.E. The LF/HF Ratio Does Not Accurately Measure Cardiac Sympatho-Vagal Balance. Front. Physiol. 2013, 4, 26. [Google Scholar] [CrossRef]
- Sacha, J.; Barabach, S.; Statkiewicz-Barabach, G.; Sacha, K.; Müller, A.; Piskorski, J.; Barthel, P.; Schmidt, G. How to Strengthen or Weaken the HRV Dependence on Heart Rate—Description of the Method and Its Perspectives. Int. J. Cardiol. 2013, 168, 1660–1663. [Google Scholar] [CrossRef]
- Monfredi, O.; Lyashkov, A.E.; Johnsen, A.-B.; Inada, S.; Schneider, H.; Wang, R.; Nirmalan, M.; Wisloff, U.; Maltsev, V.A.; Lakatta, E.G.; et al. Biophysical Characterization of the Underappreciated and Important Relationship Between Heart Rate Variability and Heart Rate. Hypertension 2014, 64, 1334–1343. [Google Scholar] [CrossRef] [PubMed]
- Tsuji, H.; Venditti, F.J.; Manders, E.S.; Evans, J.C.; Larson, M.G.; Feldman, C.L.; Levy, D. Determinants of Heart Rate Variability. J. Am. Coll. Cardiol. 1996, 28, 1539–1546. [Google Scholar] [CrossRef] [PubMed]
- Boyett, M.; Wang, Y.; D’Souza, A. CrossTalk Opposing View: Heart Rate Variability as a Measure of Cardiac Autonomic Responsiveness Is Fundamentally Flawed. J. Physiol. 2019, 597, 2599–2601. [Google Scholar] [CrossRef] [PubMed]
- Van Roon, A.M.; Snieder, H.; Lefrandt, J.D.; De Geus, E.J.C.; Riese, H. Parsimonious Correction of Heart Rate Variability for Its Dependency on Heart Rate. Hypertension 2016, 68, e63–e65. [Google Scholar] [CrossRef]
- Platisa, M.M.; Gal, V. Dependence of Heart Rate Variability on Heart Period in Disease and Aging. Physiol. Meas. 2006, 27, 989–998. [Google Scholar] [CrossRef]
- Búzás, A.; Horvath, T.; Der, A. A Novel Approach in Heart-Rate-Variability Analysis Based on Modified Poincaré Plots. IEEE Access 2022, 10, 36606–36615. [Google Scholar] [CrossRef]
- Rudics, E.; Buzás, A.; Pálfi, A.; Szabó, Z.; Nagy, Á.; Hompoth, E.A.; Dombi, J.; Bilicki, V.; Szendi, I.; Dér, A. Quantifying Stress and Relaxation: A New Measure of Heart Rate Variability as a Reliable Biomarker. Biomedicines 2025, 13, 81. [Google Scholar] [CrossRef]
- Platisa, M.M.; Gal, V. Reflection of Heart Rate Regulation on Linear and Nonlinear Heart Rate Variability Measures. Physiol. Meas. 2006, 27, 145–154. [Google Scholar] [CrossRef]
- Platisa, M.M.; Gal, V. Correlation Properties of Heartbeat Dynamics. Eur. Biophys. J. 2008, 37, 1247–1252. [Google Scholar] [CrossRef]
- Platisa, M.M.; Nestorovic, Z.; Damjanovic, S.; Gal, V. Linear and Non-linear Heart Rate Variability Measures in Chronic and Acute Phase of Anorexia Nervosa. Clin. Physiol. Funct. Imaging 2006, 26, 54–60. [Google Scholar] [CrossRef]
- Platisa, M.M.; Mazic, S.; Nestorovic, Z.; Gal, V. Complexity of Heartbeat Interval Series in Young Healthy Trained and Untrained Men. Physiol. Meas. 2008, 29, 439–450. [Google Scholar] [CrossRef] [PubMed]
- Porta, A.; Faes, L.; Bari, V.; Marchi, A.; Bassani, T.; Nollo, G.; Perseguini, N.M.; Milan, J.; Minatel, V.; Borghi-Silva, A.; et al. Effect of Age on Complexity and Causality of the Cardiovascular Control: Comparison between Model-Based and Model-Free Approaches. PLoS ONE 2014, 9, e89463. [Google Scholar] [CrossRef] [PubMed]
- Voss, A.; Heitmann, A.; Schroeder, R.; Peters, A.; Perz, S. Short-Term Heart Rate Variability—Age Dependence in Healthy Subjects. Physiol. Meas. 2012, 33, 1289–1311. [Google Scholar] [CrossRef] [PubMed]
- Voss, A.; Schroeder, R.; Heitmann, A.; Peters, A.; Perz, S. Short-Term Heart Rate Variability—Influence of Gender and Age in Healthy Subjects. PLoS ONE 2015, 10, e0118308. [Google Scholar] [CrossRef]
- Urbančič-Rovan, V.; Meglič, B.; Stefanovska, A.; Bernjak, A.; Ažman-Juvan, K.; Kocijančič, A. Incipient Cardiovascular Autonomic Imbalance Revealed by Wavelet Analysis of Heart Rate Variability in Type 2 Diabetic Patients. Diabet. Med. 2007, 24, 18–26. [Google Scholar] [CrossRef]
- Stefanovska, A.; Bracic Lotric, M.; Strle, S.; Haken, H. The Cardiovascular System as Coupled Oscillators? Physiol. Meas. 2001, 22, 535–550. [Google Scholar] [CrossRef]
- Georgieva-Tsaneva, G.N. Investigation of Heart Rate Variability by Statistical Methods and detrended Fluctuation Analysis. CBU Int. Conf. Proc. 2019, 7, 729–734. [Google Scholar] [CrossRef]
- Georgieva-Tsaneva, G.; Gospodinova, E.; Cheshmedzhiev, K. Examination of Cardiac Activity with ECG Monitoring Using Heart Rate Variability Methods. Diagnostics 2024, 14, 926. [Google Scholar] [CrossRef]
- Gospodinov, M.; Gospodinova, E.; Georgieva-Tsaneva, G. Mathematical Methods of ECG Data Analysis. In Healthcare Data Analytics and Management; Elsevier: Amsterdam, The Netherlands; Academic Press: Cambridge, MA, USA, 2019; pp. 177–209. ISBN 978-0-12-815368-0. [Google Scholar]
- Gospodinova, E.; Lebamovski, P.; Georgieva-Tsaneva, G.; Negreva, M. Evaluation of the Methods for Nonlinear Analysis of Heart Rate Variability. Fractal Fract. 2023, 7, 388. [Google Scholar] [CrossRef]
- Gribbin, B.; Pickering, T.G.; Sleight, P.; Peto, R. Effect of Age and High Blood Pressure on Barorefiex Sensitivity in Man. Circ. Res. 1971, 29, 424–431. [Google Scholar] [CrossRef]
- Monahan, K.D. Effect of Aging on Baroreflex Function in Humans. Am. J. Physiol.-Regul. Integr. Comp. Physiol. 2007, 293, R3–R12. [Google Scholar] [CrossRef] [PubMed]
- Couderc, J.-P. A Unique Digital Electrocardiographic Repository for the Development of Quantitative Electrocardiography and Cardiac Safety: The Telemetric and Holter ECG Warehouse (THEW). J. Electrocardiol. 2010, 43, 595–600. [Google Scholar] [CrossRef] [PubMed]
- Altman, D.G.; Bland, J.M. Measurement in Medicine: The Analysis of Method Comparison Studies. Statistician 1983, 32, 307. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological Time-Series Analysis Using Approximate Entropy and Sample Entropy. Am. J. Physiol.-Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef]
- Magris, M. Detrended Fluctuation Analysis (DFA). MATLAB Central File Exchange. Available online: https://www.mathworks.com/matlabcentral/fileexchange/67889-detrended-fluctuation-analysis-dfa (accessed on 13 March 2022).
- Estévez-Báez, M.; Machado, C.; Montes-Brown, J.; Jas-García, J.; Leisman, G.; Schiavi, A.; Machado-García, A.; Carricarte-Naranjo, C.; Carmeli, E. Very High Frequency Oscillations of Heart Rate Variability in Healthy Humans and in Patients with Cardiovascular Autonomic Neuropathy. In Progress in Medical Research; Pokorski, M., Ed.; Advances in Experimental Medicine and Biology; Springer International Publishing: Cham, Switzerland, 2018; Volume 1070, pp. 49–70. ISBN 978-3-319-89664-9. [Google Scholar]
- Pinhas, I.; Toledo, E.; Aravot, D.; Akselrod, S. Bicoherence Analysis of New Cardiovascular Spectral Components Observed in Heart-Transplant Patients: Statistical Approach for Bicoherence Thresholding. IEEE Trans. Biomed. Eng. 2004, 51, 1774–1783. [Google Scholar] [CrossRef]
- Chang, C.-C.; Hsu, H.-Y.; Hsiao, T.-C. The Interpretation of Very High Frequency Band of Instantaneous Pulse Rate Variability during Paced Respiration. Biomed. Eng. OnLine 2014, 13, 46. [Google Scholar] [CrossRef]
- Li, X.; Xu, T.; Wang, Y.; Hu, Z.; Duan, S.; Peng, C.; Xu, S.; Liu, C.; Li, R.; Deng, Q.; et al. Piezo2 Expressed in Ganglionated Plexi: Potential Therapeutic Target of Atrial Fibrillation. Heart Rhythm 2025. [Google Scholar] [CrossRef]
- Kloth, B.; Mearini, G.; Weinberger, F.; Stenzig, J.; Geertz, B.; Starbatty, J.; Lindner, D.; Schumacher, U.; Reichenspurner, H.; Eschenhagen, T.; et al. Piezo2 Is Not an Indispensable Mechanosensor in Murine Cardiomyocytes. Sci. Rep. 2022, 12, 8193. [Google Scholar] [CrossRef]
- Herraiz-Martínez, A.; Álvarez-García, J.; Llach, A.; Molina, C.E.; Fernandes, J.; Ferrero-Gregori, A.; Rodríguez, C.; Vallmitjana, A.; Benítez, R.; Padró, J.M.; et al. Ageing Is Associated with Deterioration of Calcium Homeostasis in Isolated Human Right Atrial Myocytes. Cardiovasc. Res. 2015, 106, 76–86. [Google Scholar] [CrossRef]
- Bernardi, L.; Keller, F.; Sanders, M.; Reddy, P.S.; Griffith, B.; Meno, F.; Pinsky, M.R. Respiratory Sinus Arrhythmia in the Denervated Human Heart. J. Appl. Physiol. 1989, 67, 1447–1455. [Google Scholar] [CrossRef] [PubMed]
- Bernardi, L.; Salvucci, F.; Suardi, R.; Soldá, P.L.; Calciati, A.; Perlini, S.; Falcone, C.; Ricciardi, L. Evidence for an Intrinsic Mechanism Regulating Heart Rate Variability in the Transplanted and the Intact Heart during Submaximal Dynamic Exercise? Cardiovasc. Res. 1990, 24, 969–981. [Google Scholar] [CrossRef] [PubMed]
- Nagel, M.; Chesler, A.T. PIEZO2 Ion Channels in Proprioception. Curr. Opin. Neurobiol. 2022, 75, 102572. [Google Scholar] [CrossRef] [PubMed]
- Zechini, L.; Camilleri-Brennan, J.; Walsh, J.; Beaven, R.; Moran, O.; Hartley, P.S.; Diaz, M.; Denholm, B. Piezo Buffers Mechanical Stress via Modulation of Intracellular Ca2+ Handling in the Drosophila Heart. Front. Physiol. 2022, 13, 1003999. [Google Scholar] [CrossRef]
- Esler, M.D.; Thompson, J.M.; Kaye, D.M.; Turner, A.G.; Jennings, G.L.; Cox, H.S.; Lambert, G.W.; Seals, D.R. Effects of Aging on the Responsiveness of the Human Cardiac Sympathetic Nerves to Stressors. Circulation 1995, 91, 351–358. [Google Scholar] [CrossRef]
- Iatsenko, D.; Bernjak, A.; Stankovski, T.; Shiogai, Y.; Owen-Lynch, P.J.; Clarkson, P.B.M.; McClintock, P.V.E.; Stefanovska, A. Evolution of Cardiorespiratory Interactions with Age. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371, 20110622. [Google Scholar] [CrossRef]
- Kaplan, W. Advanced Calculus, 4th ed.; 5. Reprint. with Corr.; Addison-Wesley: Reading, MA, USA, 1994; ISBN 978-0-201-57888-1. [Google Scholar]
- Castiglioni, P.; Lazzeroni, D.; Coruzzi, P.; Faini, A. Multifractal-Multiscale Analysis of Cardiovascular Signals: A DFA-Based Characterization of Blood Pressure and Heart-Rate Complexity by Gender. Complexity 2018, 2018, 4801924. [Google Scholar] [CrossRef]
- Jose, A.D.; Collison, D. The Normal Range and Determinants of the Intrinsic Heart Rate in Man. Cardiovasc. Res. 1970, 4, 160–167. [Google Scholar] [CrossRef]
- Singh, V.; Gupta, A.; Sohal, J.S.; Singh, A. A Unified Non-Linear Approach Based on Recurrence Quantification Analysis and Approximate Entropy: Application to the Classification of Heart Rate Variability of Age-Stratified Subjects. Med. Biol. Eng. Comput. 2019, 57, 741–755. [Google Scholar] [CrossRef]
| Parameter | Definition | Mathematical Formula |
|---|---|---|
| RMSSD | Measures short-term HRV based on the square root of the mean of the N − 1 squared differences between adjacent RR intervals. Reflects parasympathetic activity. | |
| SDNN | Standard deviation of all RR intervals. Reflects overall HRV (both sympathetic and parasympathetic). | |
| VLF (Very Low Frequency) | Power in the very low-frequency range (0.0033–0.04 Hz). Linked to thermoregulation, hormones, and other slow-acting regulatory mechanisms. | |
| LF (Low Frequency) | Power in the low-frequency range (0.04–0.15 Hz). Reflects both sympathetic and parasympathetic activity. | |
| HF (High Frequency) | Power in the high-frequency range (0.15–0.40 Hz). Mainly reflects parasympathetic (vagal) activity, associated with respiration. | |
| VHF (Very High Frequency) | Power in the very high-frequency range (>0.4 Hz). May reflect noise or specific physiological phenomena. | |
| Entropy (SampEn, ApEn) | Measures the complexity or unpredictability of RR interval time series. Higher entropy = more complex signal [56] | SampEn(m, r, N) = ln(A/B) in our case |
| DFA (Detrended Fluctuation Analysis) | Detects fractal scaling properties in HRV, capturing long-range correlations. Useful in non-stationary data [57] | (s = 10, 20, …, 100) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Búzás, A.; Sonkodi, B.; Dér, A. Principal Connection Between Typical Heart Rate Variability Parameters as Revealed by a Comparative Analysis of Their Heart Rate and Age Dependence. Entropy 2025, 27, 792. https://doi.org/10.3390/e27080792
Búzás A, Sonkodi B, Dér A. Principal Connection Between Typical Heart Rate Variability Parameters as Revealed by a Comparative Analysis of Their Heart Rate and Age Dependence. Entropy. 2025; 27(8):792. https://doi.org/10.3390/e27080792
Chicago/Turabian StyleBúzás, András, Balázs Sonkodi, and András Dér. 2025. "Principal Connection Between Typical Heart Rate Variability Parameters as Revealed by a Comparative Analysis of Their Heart Rate and Age Dependence" Entropy 27, no. 8: 792. https://doi.org/10.3390/e27080792
APA StyleBúzás, A., Sonkodi, B., & Dér, A. (2025). Principal Connection Between Typical Heart Rate Variability Parameters as Revealed by a Comparative Analysis of Their Heart Rate and Age Dependence. Entropy, 27(8), 792. https://doi.org/10.3390/e27080792







