CurveMark: Detecting AI-Generated Text via Probabilistic Curvature and Dynamic Semantic Watermarking
Abstract
1. Introduction
- We propose a dual-channel detection framework that combines probability curvature analysis with dynamic semantic watermarking and incorporates a Bayesian multi-hypothesis approach to enable detection without prior knowledge of source models, achieving superior detection performance through complementary information channels that address limitations of single-channel approaches.
- We develop a dynamic watermarking strategy using entropy-aware token selection that operates within acceptable rate–distortion bounds while preserving semantic coherence, demonstrating 85–89% channel capacity utilization.
- We provide experimental validation demonstrating 95.4% detection accuracy with minimal quality degradation, demonstrating effective performance for AI-generated text authentication in controlled environments where watermarking protocols can be standardized.
2. Related Work
2.1. Statistical Anomaly Detection in Text
2.2. Information Embedding and Watermarking
2.3. Information-Theoretic Foundations for Detection
2.4. Robustness and Channel Capacity
3. Proposed Methodology
3.1. Watermark Embedding
3.2. Watermark Embedding Algorithm
| Algorithm 1 Information-Theoretic Watermark Embedding |
| Require: prompt, LM, EMB, , , , NGram, k, Ensure: watermarked_text |
|
3.3. Watermark Detection
3.4. Detection Algorithm
| Algorithm 2 Information-Theoretic Feature Extraction and Detection |
| Require: text, LM, EMB, N, , NGram, Classifier, k Ensure: is_watermarked, confidence
|
| Algorithm 3 Bayesian Multi-Hypothesis Detection Framework |
| Require: text, LLM_models = [GPT, LLaMA, PaLM, Claude], watermark_params, usage_priors Ensure: most_likely_source, confidence_score, is_ai_generated
|
4. Experiments and Results Analysis
4.1. Experimental Setup
- 1.
- Multi-Model Synthetic Data: We generate 5000 text samples each from GPT-2 [38], LLaMA-7B (via local deployment), and Vicuna-13B [39] (open-source conversational model) with our watermarking, creating an evaluation across diverse LLM architectures. Text lengths are uniformly distributed between 100–500 tokens to ensure controlled comparison.
- 2.
- WikiText-103 [40]: 10,000 high-quality Wikipedia articles serve as a reference distribution for human-written text, characterized by high lexical diversity and complex information structure.
- 3.
- 4.
- C4 [43]: 10,000 web-crawled text samples provide a diverse, real-world distribution with varying information density and quality.
- 5.
- Cross-Model Generalization: To evaluate the method’s robustness across LLM families, we test the detection of Mistral-7B [44] generated text (2000 samples via local deployment) using models trained on GPT-2 data, representing a realistic scenario where the detection system encounters unknown LLM architectures. For watermark-based evaluation, we generate clean text from target LLMs and post hoc apply our watermarking protocol using the same semantic similarity parameters (, ) to simulate cross-model detection scenarios where detectors encounter differently trained models.
4.2. Performance Results
- 1.
- Improved Mutual Information: CurveMark consistently achieves higher mutual information between predictions and ground truth (0.751–0.812 bits) compared to baselines, validating our dual-channel approach. DetectGPT demonstrates strong performance (0.732–0.786 bits) through probability curvature analysis alone, confirming the effectiveness of information-theoretic features.
- 2.
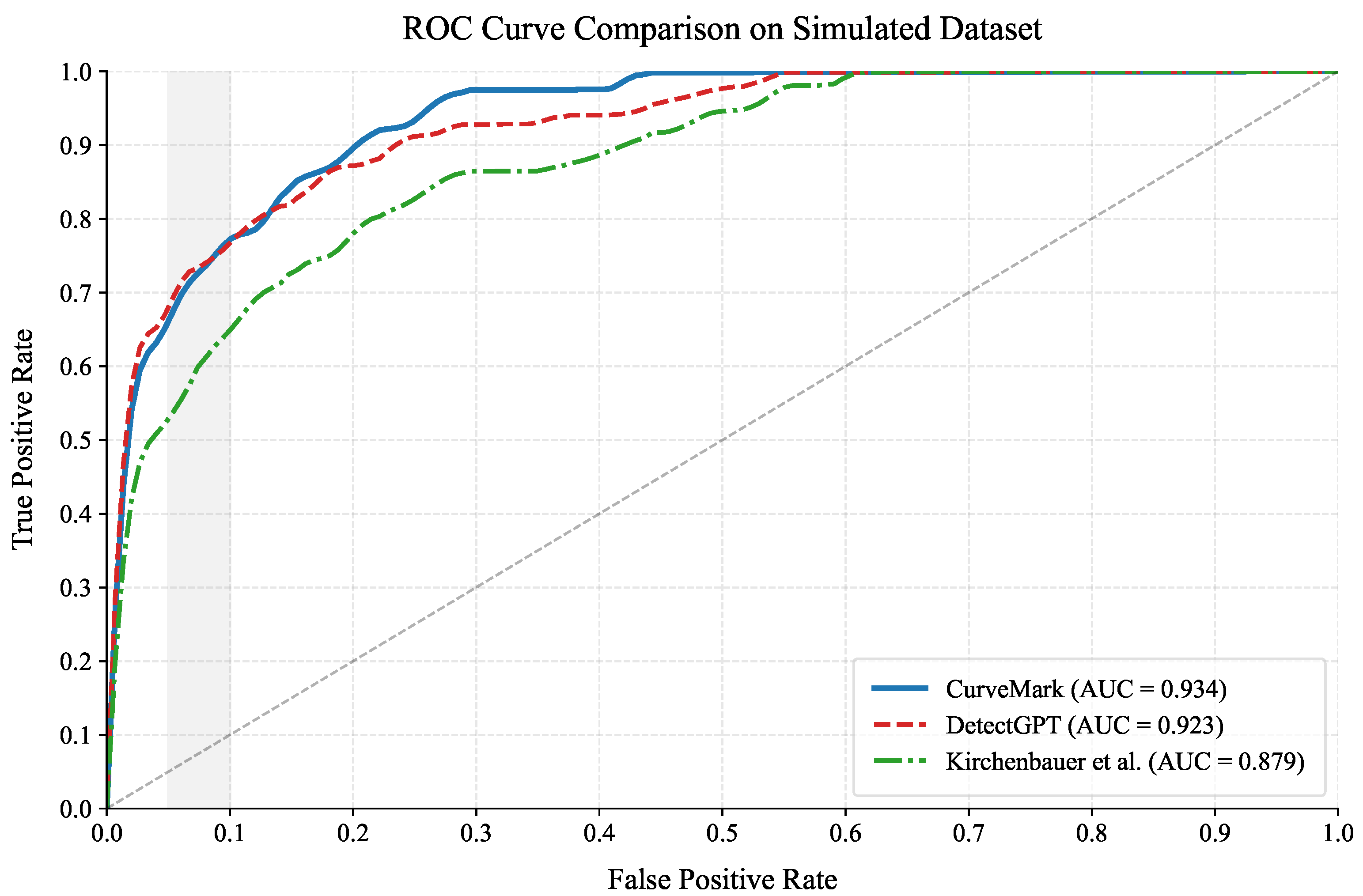
- Enhanced Detection Performance: Our multi-modal approach achieves improved AUC performance on the simulated dataset (0.934) compared to DetectGPT’s single-channel approach (0.923), demonstrating the value of combining intrinsic statistical analysis with explicit watermark signals. DetectGPT demonstrates strong baseline performance (0.732–0.786 bits) through probability curvature analysis alone, but lacks the information redundancy of our dual-channel design.
- 3.
- Efficient Channel Utilization: Our dynamic watermarking achieves 85-89% of theoretical channel capacity, substantially outperforming the static approach of Kirchenbauer et al. [7] (55–62%).
- 4.
- Effective Rate–Distortion Trade-off: CurveMark maintains lower perplexity increases (0.8–1.3) while embedding more information, operating effectively within the rate–distortion trade-off region. DetectGPT’s zero-shot approach requires no watermarking overhead but lacks the information redundancy of our dual-channel design.
4.3. Ablation Study
4.4. Robustness Analysis
4.5. Quality Assessment
4.6. Bayesian Multi-Hypothesis Detection Evaluation
4.7. Failure Case Analysis
5. Discussion
5.1. Interpretation of Key Findings
5.2. Comparison with State-of-the-Art
5.3. Limitations of the Study
5.4. Broader Implications and Future Directions
5.5. Practical Constraints and Deployment Considerations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bakhtin, A.; Gross, S.; Ott, M.; Deng, Y.; Ranzato, M.; Szlam, A. Real or Fake? Learning to Discriminate Machine from Human Generated Text. arXiv 2019, arXiv:1906.03351. [Google Scholar] [CrossRef]
- Zellers, R.; Holtzman, A.; Rashkin, H.; Bisk, Y.; Farhadi, A.; Roesner, F.; Choi, Y. Defending Against Neural Fake News. Adv. Neural Inf. Process. Syst. 2019, 32, 1–15. [Google Scholar]
- Uchendu, A.; Le, T.; Shu, K.; Lee, D. Authorship Attribution for Neural Text Generation. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), Online, 16–20 November 2020; Webber, B., Cohn, T., He, Y., Liu, Y., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2020; pp. 8384–8395. [Google Scholar] [CrossRef]
- Solaiman, I.; Brundage, M.; Clark, J.; Askell, A.; Herbert-Voss, A.; Wu, J.; Radford, A.; Krueger, G.; Kim, J.W.; Kreps, S.; et al. Release Strategies and the Social Impacts of Language Models. arXiv 2019, arXiv:1908.09203. [Google Scholar] [CrossRef]
- Gehrmann, S.; Strobelt, H.; Rush, A.M. GLTR: Statistical Detection and Visualization of Generated Text. arXiv 2019, arXiv:1906.04043. [Google Scholar] [CrossRef]
- Mitchell, E.; Lee, Y.; Khazatsky, A.; Manning, C.D.; Finn, C. DetectGPT: Zero-shot machine-generated text detection using probability curvature. In Proceedings of the International Conference on Machine Learning, PMLR, Honolulu, HI, USA, 23–29 July 2023; pp. 24950–24962. [Google Scholar]
- Kirchenbauer, J.; Geiping, J.; Wen, Y.; Katz, J.; Miers, I.; Goldstein, T. A Watermark for Large Language Models. In Proceedings of the 40th International Conference on Machine Learning, PMLR, Honolulu, HI, USA, 23–29 July 2023; Krause, A., Brunskill, E., Cho, K., Engelhardt, B., Sabato, S., Scarlett, J., Eds.; JMLR: Cambridge, MA, USA, 2023; Volume 202, pp. 17061–17084. [Google Scholar]
- Atallah, M.J.; Raskin, V.; Crogan, M.; Hempelmann, C.; Kerschbaum, F.; Mohamed, D.; Naik, S. Natural language watermarking: Design, analysis, and a proof-of-concept implementation. In Proceedings of the Information Hiding: 4th International Workshop, IH 2001, Pittsburgh, PA, USA, 25–27 April 2001; Proceedings 4. Springer: Berlin/Heidelberg, Germany, 2001; pp. 185–200. [Google Scholar]
- Poje, K.; Brcic, M.; Kovac, M.; Babac, M.B. Effect of Private Deliberation: Deception of Large Language Models in Game Play. Entropy 2024, 26, 524. [Google Scholar] [CrossRef] [PubMed]
- He, H.; Liu, Y.; Wang, Z.; Mao, Y.; Bu, Y. Theoretically Grounded Framework for LLM Watermarking: A Distribution-Adaptive Approach. arXiv 2024, arXiv:2506.06409. [Google Scholar]
- Fang, T.; Jaggi, M.; Argyraki, K. Generating Steganographic Text with LSTMs. arXiv 2017, arXiv:1705.10742. [Google Scholar] [CrossRef]
- Ahvanooey, M.T.; Li, Q.; Hou, J.; Mazraeh, H.D.; Zhang, J. AITSteg: An innovative text steganography technique for hidden transmission of text message via social media. IEEE Access 2018, 6, 65981–65995. [Google Scholar] [CrossRef]
- Iqbal, M.M.; Khadam, U.; Han, K.J.; Han, J.; Jabbar, S. A robust digital watermarking algorithm for text document copyright protection based on feature coding. In Proceedings of the 2019 15th InternationalWireless Communications & Mobile Computing Conference (IWCMC), Tangier, Morocco, 24–28 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1940–1945. [Google Scholar]
- Liu, Y.; Bu, Y. Adaptive Text Watermark for Large Language Models. arXiv 2024, arXiv:2401.13927. [Google Scholar] [CrossRef]
- Wang, Z.; Gu, T.; Wu, B.; Yang, Y. MorphMark: Flexible Adaptive Watermarking for Large Language Models. arXiv 2025, arXiv:2505.11541. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Shannon, C.E. Prediction and entropy of printed English. Bell Syst. Tech. J. 1951, 30, 50–64. [Google Scholar] [CrossRef]
- Brown, T.B.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language Models are Few-Shot Learners. arXiv 2020, arXiv:2005.14165. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Second Edition of the 1991 Original; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Kontoyiannis, I.; Algoet, P.H.; Suhov, Y.M.; Wyner, A.J. Nonparametric entropy estimation for stationary processes and random fields, with applications to English text. IEEE Trans. Inf. Theory 1998, 44, 1319–1327. [Google Scholar] [CrossRef]
- Bentz, C.; Alikaniotis, D.; Cysouw, M.; Ferrer-i Cancho, R. The entropy of words—Learnability and expressivity across more than 1000 languages. Entropy 2017, 19, 275. [Google Scholar] [CrossRef]
- Bender, E.M.; Gebru, T.; McMillan-Major, A.; Shmitchell, S. On the Dangers of Stochastic Parrots: Can Language Models Be Too Big? In Proceedings of the 2021 ACM Conference on Fairness, Accountability, and Transparency (FAccT ’21), New York, NY, USA, 3–10 March 2021; FAccT ’21. pp. 610–623. [Google Scholar] [CrossRef]
- Chowdhery, A.; Narang, S.; Devlin, J.; Bosma, M.; Mishra, G.; Roberts, A.; Barham, P.; Chung, H.W.; Sutton, C.; Gehrmann, S.; et al. PaLM: Scaling Language Modeling with Pathways. J. Mach. Learn. Res. 2023, 24, 1–113. [Google Scholar]
- Krishna, K.; Song, Y.; Karpinska, M.; Wieting, J.; Iyyer, M. Paraphrasing evades detectors of AI-generated text, but retrieval is an effective defense. In Proceedings of the Advances in Neural Information Processing Systems, New Orleans, LA USA, 10–16 December 2023; Naumann, T., Globerson, A., Saenko, K., Hardt, M., Levine, S., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2023; Volume 36, pp. 27469–27500. [Google Scholar]
- Sadasivan, V.S.; Kumar, A.; Balasubramanian, S.; Wang, W.; Feizi, S. Can AI-Generated Text be Reliably Detected? arXiv 2023, arXiv:2303.11156. [Google Scholar]
- Jiang, Y.; Wu, C.; Boroujeny, M.K.; Mark, B.; Zeng, K. StealthInk: A Multi-bit and Stealthy Watermark for Large Language Models. arXiv 2025, arXiv:2506.05502. [Google Scholar]
- Diaa, A.; Aremu, T.; Lukas, N. Optimized Adaptive Attacks against LLM Watermarks. arXiv 2024, arXiv:2410.02440. [Google Scholar]
- Zhang, H.; Edelman, B.L.; Francati, D.; Venturi, D.; Ateniese, G.; Barak, B. Watermarks in the Sand: Impossibility of Strong Watermarking for Language Models. arXiv 2023, arXiv:2311.04378. [Google Scholar]
- Christ, M.; Gunn, S.; Zamir, O. Undetectable Watermarks for Language Models. In Proceedings of the The Thirty Seventh Annual Conference on Learning Theory, PMLR, Edmonton, AB, Canada, 30 June–3 July 2023; pp. 1–53. [Google Scholar]
- Zhao, X.; Wang, Y.X.; Li, L. Provable Robust Watermarking for AI-Generated Text. In Proceedings of the International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Kuditipudi, R.; Thickstun, J.; Hashimoto, T.; Liang, P. Robust Distortion-free Watermarks for Language Models. In Proceedings of the 40th International Conference on Machine Learning, Honolulu, HI, USA, 23–29 July 2023. [Google Scholar]
- Fernandez, P.; Chaffin, A.; Tit, K.; Chizat, V.; Furon, T. Three Bricks to Consolidate Watermarks for Large Language Models. In Proceedings of the 2023 IEEE International Workshop on Information Forensics and Security (WIFS), Nurnberg, Germany, 4–7 December 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar]
- Piet, J.; Sitawarin, C.; Fang, V.; Mu, N.; Wagner, D. Mark My Words: Analyzing and Evaluating Language Model Watermarks. arXiv 2023, arXiv:2312.00273. [Google Scholar] [CrossRef]
- Wu, Y.; Hu, Z.; Guo, J.; Zhang, H.; Huang, H. A Resilient and Accessible Distribution-Preserving Watermark for Large Language Models. arXiv 2023, arXiv:2310.07710. [Google Scholar]
- Hou, A.B.; Zhang, J.; He, T.; Wang, Y.; Chuang, Y.S.; Wang, H.; Shen, L.; Van Durme, B.; Khashabi, D.; Tsvetkov, Y. SemStamp: A Semantic Watermark with Paraphrastic Robustness for Text Generation. arXiv 2023, arXiv:2310.03991. [Google Scholar]
- Pennington, J.; Socher, R.; Manning, C.D. Glove: Global vectors for word representation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; pp. 1532–1543. [Google Scholar]
- Heafield, K. KenLM: Faster and Smaller Language Model Queries. In Proceedings of the Sixth Workshop on Statistical Machine Translation, Edinburgh, UK, 30–31 July 2011; pp. 187–197. [Google Scholar]
- Radford, A.; Wu, J.; Child, R.; Luan, D.; Amodei, D.; Sutskever, I. Language models are unsupervised multitask learners. OpenAI Blog 2019, 1, 9. [Google Scholar]
- Chiang, W.L.; Li, Z.; Lin, Z.; Sheng, Y.; Wu, Z.; Zhang, H.; Zheng, L.; Zhuang, S.; Zhuang, Y.; Gonzalez, J.E.; et al. Vicuna: An Open-Source Chatbot Impressing GPT-4 with 90%* ChatGPT Quality. 2023. Available online: https://lmsys.org/blog/2023-03-30-vicuna/ (accessed on 14 May 2025).
- Merity, S.; Xiong, C.; Bradbury, J.; Socher, R. Pointer Sentinel Mixture Models. arXiv 2016, arXiv:1609.07843. [Google Scholar] [CrossRef]
- Narayan, S.; Cohen, S.B.; Lapata, M. Don’t give me the details, just the summary! Topic-Aware Convolutional Neural Networks for Extreme Summarization. arXiv 2018, arXiv:1808.08745. [Google Scholar]
- Lewis, M.; Liu, Y.; Goyal, N.; Ghazvininejad, M.; Mohamed, A.; Levy, O.; Stoyanov, V.; Zettlemoyer, L. BART: Denoising Sequence-to-Sequence Pre-training for Natural Language Generation, Translation, and Comprehension. arXiv 2019, arXiv:1910.13461. [Google Scholar]
- Raffel, C.; Shazeer, N.; Roberts, A.; Lee, K.; Narang, S.; Matena, M.; Zhou, Y.; Li, W.; Liu, P.J. Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer. J. Mach. Learn. Res. 2020, 21, 1–67. [Google Scholar]
- Jiang, A.Q.; Sablayrolles, A.; Mensch, A.; Bamford, C.; Chaplot, D.S.; de las Casas, D.; Bressand, F.; Lengyel, G.; Lample, G.; Saulnier, L.; et al. Mistral 7B. arXiv 2023, arXiv:2310.06825. [Google Scholar] [CrossRef]
- Shi, Y.; Yang, Y.; Sheng, Q.; Mi, H.; Hu, B.; Xu, C.; Cao, J. PhantomHunter: Detecting Unseen Privately-Tuned LLM-Generated Text via Family-Aware Learning. arXiv 2025, arXiv:2506.15683. [Google Scholar]
- Bhattacharjee, A.; Moraffah, R.; Garland, J.; Liu, H. EAGLE: A Domain Generalization Framework for AI-generated Text Detection. arXiv 2024, arXiv:2403.15690. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, Y.; Bi, Y.; Cao, H.; Lin, Z.; Zhao, Y.; Wu, F. Training-free LLM-generated Text Detection by Mining Token Probability Sequences. arXiv 2024, arXiv:2410.06072. [Google Scholar]



| Method | Dataset | Acc. (± std) | AUC (± std) | MI (± std) | Cap. Util. | PPL Δ |
|---|---|---|---|---|---|---|
| CurveMark | Simulated | 0.954 ± 0.012 | 0.934 ± 0.018 | 0.812 ± 0.025 | 0.89 | 0.8 |
| DetectGPT | Simulated | 0.948 ± 0.015 | 0.923 ± 0.022 | 0.785 ± 0.031 | N/A | N/A |
| Kirchenbauer et al. [7] | Simulated | 0.938 ± 0.019 | 0.879 ± 0.027 | 0.754 ± 0.034 | 0.61 | 1.5 |
| CurveMark | WikiText+GPT-2 | 0.942 ± 0.016 | 0.943 ± 0.019 | 0.785 ± 0.028 | 0.87 | 0.9 |
| DetectGPT | WikiText+GPT-2 | 0.935 ± 0.018 | 0.952 ± 0.015 | 0.771 ± 0.029 | N/A | N/A |
| Kirchenbauer et al. [7] | WikiText+GPT-2 | 0.916 ± 0.023 | 0.842 ± 0.031 | 0.683 ± 0.036 | 0.58 | 1.7 |
| CurveMark | XSum+BART | 0.932 ± 0.014 | 0.952 ± 0.016 | 0.751 ± 0.026 | 0.85 | 1.3 |
| DetectGPT | XSum+BART | 0.925 ± 0.017 | 0.947 ± 0.018 | 0.732 ± 0.032 | N/A | N/A |
| Kirchenbauer et al. [7] | XSum+BART | 0.904 ± 0.021 | 0.817 ± 0.029 | 0.632 ± 0.038 | 0.55 | 2.1 |
| CurveMark | C4+GPT-2 | 0.945 ± 0.013 | 0.961 ± 0.014 | 0.798 ± 0.024 | 0.88 | 0.8 |
| DetectGPT | C4+GPT-2 | 0.941 ± 0.016 | 0.958 ± 0.017 | 0.786 ± 0.027 | N/A | N/A |
| Kirchenbauer et al. [7] | C4+GPT-2 | 0.921 ± 0.020 | 0.854 ± 0.025 | 0.695 ± 0.033 | 0.62 | 1.6 |
| Source Model | Prior Knowledge Required | CurveMark Acc. (AUC) | DetectGPT Acc. (AUC) | Kirchenbauer Acc. (AUC) | Gen. Gap |
|---|---|---|---|---|---|
| GPT-2 (1.5B) | Watermark+LLM | 0.954 (0.934) | 0.948 (0.923) | 0.938 (0.879) | - |
| LLaMA-7B | Watermark+LLM | 0.941 (0.925) | 0.931 (0.912) | 0.915 (0.845) | −1.3% |
| Vicuna-13B | Watermark+LLM | 0.948 (0.935) | 0.938 (0.920) | 0.922 (0.855) | −1.1% |
| Cross-Model Scenarios (Trained on GPT-2, Tested on others): | |||||
| Mistral-7B | None (DetectGPT) | N/A | 0.894 (0.863) | N/A | −5.4% |
| Simulated watermark | 0.863 (0.841) | - | 0.772 (0.718) | −9.1% | |
| LLaMA-7B | None (DetectGPT) | N/A | 0.902 (0.878) | N/A | −4.5% |
| Simulated watermark | 0.851 (0.822) | - | 0.758 (0.702) | −10.3% | |
| Features Removed | Acc. | MI | ΔMI | Info. Loss | Interpretation |
|---|---|---|---|---|---|
| None (Full) | 0.954 | 0.812 | - | - | Baseline |
| Prob. Curvature | 0.875 | 0.543 | −0.269 | 33.1% | Primary channel loss |
| Watermark Metrics | 0.912 | 0.651 | −0.161 | 19.8% | Secondary channel loss |
| Info-Theory Stats | 0.938 | 0.751 | −0.061 | 7.5% | Auxiliary signal loss |
| Perturbation Type | Noise Level | Detection Accuracy | Info. Retained (CurveMark) | ||
|---|---|---|---|---|---|
| CurveMark | DetectGPT | Kirchenbauer | |||
| None | 0% | 0.954 | 0.948 | 0.938 | 100% |
| Synonym Replace | 10% | 0.941 | 0.928 | 0.891 | 94.3% |
| Synonym Replace | 20% | 0.918 | 0.885 | 0.832 | 86.7% |
| Paraphrase | Moderate | 0.902 | 0.832 | 0.785 | 81.2% |
| Paraphrase | Aggressive | 0.867 | 0.751 | 0.694 | 72.5% |
| Dataset | Bits/Token | PPL (Orig.) | PPL (Watermarked) | Distortion/Bit |
|---|---|---|---|---|
| Simulated | 0.41 | 25.3 | 26.1 | 1.95 |
| XSum | 0.38 | 32.5 | 33.8 | 3.42 |
| WikiText | 0.43 | 18.7 | 19.6 * | 2.09 |
| C4 | 0.40 | 22.4 | 23.2 * | 2.00 |
| Task | Accuracy | Confidence (Avg.) | False Pos. Rate | False Neg. Rate | Computation Time (s) |
|---|---|---|---|---|---|
| Human vs AI Detection | 92.1% | 0.847 | 7.3% | 8.5% | 3.2 |
| Source Model Identification | 89.3% | 0.763 | N/A | N/A | 4.1 |
| Watermark Parameter Recovery | 84.7% | 0.692 | N/A | N/A | 4.8 |
| Baseline Comparison: | |||||
| Single-Model CurveMark | 95.4% | 0.912 | 4.2% | 5.8% | 1.8 |
| DetectGPT (Zero-shot) | 94.8% | 0.883 | 5.4% | 4.9% | 2.1 |
| Failure Type | Count | % | Primary Cause | Mitigation |
|---|---|---|---|---|
| Heavily Paraphrased AI Text | 47 | 23.5 | Watermark degradation | Robust encoding |
| Short Text Segments (<50 tokens) | 38 | 19.0 | Insufficient features | Length filtering |
| Human Text with Technical Jargon | 31 | 15.5 | High perplexity similarity | Domain adaptation |
| Cross-domain AI Text | 29 | 14.5 | Distribution shift | Multi-domain training |
| Adversarially Modified Text | 24 | 12.0 | Targeted attacks | Adversarial training |
| Edge Cases (Poetry, Code) | 31 | 15.5 | Format mismatch | Genre-specific models |
| Method | Peak Accuracy | Adversarial Robustness | Channel Utilization | Modular Design | Optimal Use Case |
|---|---|---|---|---|---|
| CurveMark | 95.4% | 94.3% | 89% | Dual-channel | High-precision verification |
| DetectGPT | 94.8% | 85.2% | N/A | Single-channel | Universal screening |
| Kirchenbauer | 93.8% | 78.5% | 61% | Watermark-only | Institutional monitoring |
| PhantomHunter | 92.1% | 81.7% | N/A | ML-based | Multi-domain detection |
| EAGLE | 91.5% | 83.4% | N/A | Adversarial training | Domain adaptation |
| LASTDE | 90.8% | 79.8% | N/A | Large-scale training | Zero-shot detection |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Jiang, X.; Sun, H.; Zhang, Y.; Tong, D. CurveMark: Detecting AI-Generated Text via Probabilistic Curvature and Dynamic Semantic Watermarking. Entropy 2025, 27, 784. https://doi.org/10.3390/e27080784
Zhang Y, Jiang X, Sun H, Zhang Y, Tong D. CurveMark: Detecting AI-Generated Text via Probabilistic Curvature and Dynamic Semantic Watermarking. Entropy. 2025; 27(8):784. https://doi.org/10.3390/e27080784
Chicago/Turabian StyleZhang, Yuhan, Xingxiang Jiang, Hua Sun, Yao Zhang, and Deyu Tong. 2025. "CurveMark: Detecting AI-Generated Text via Probabilistic Curvature and Dynamic Semantic Watermarking" Entropy 27, no. 8: 784. https://doi.org/10.3390/e27080784
APA StyleZhang, Y., Jiang, X., Sun, H., Zhang, Y., & Tong, D. (2025). CurveMark: Detecting AI-Generated Text via Probabilistic Curvature and Dynamic Semantic Watermarking. Entropy, 27(8), 784. https://doi.org/10.3390/e27080784






