Cross-Domain Feature Enhancement-Based Password Guessing Method for Small Samples
Abstract
1. Introduction
- Enhancing the corpus: To address sample limitations, additional personal data, topics, regional corpora, password fragments, and other relevant information can be incorporated. In 2016, Wang et al. [8] introduced a targeted online password guessing framework based on user personal information, which combines seven probabilistic attack models to enhance guessing efficiency in scenarios with limited samples. In 2019, Bi et al. [9] developed a topic-based PCFG model that integrates user interests, cultural backgrounds, and other topic-related data to lessen dependence on leaked password information. In 2021, Gan et al. [10] introduced a corpus-based password guessing approach that leverages extensive corpora to make up for the scarcity of words in smaller training sets, thus enhancing password guessing efficiency in such contexts. In 2022, Chen [11] suggested generating guessing rules that can be adapted for longer passwords by examining the corpus transfer characteristics of shorter ones. That same year, Han et al. [12] tackled the challenge of traditional methods that depend on large datasets by proposing a parameterized hybrid guessing framework (hyPassGu). This framework merges the strengths of various techniques, including probabilistic context-free grammar (PCFG) and Markov models, along with model pruning and optimal guessing number allocation strategies to create effective guessing sets with minimal data. However, while these methods can produce relatively comprehensive password guessing dictionaries, they are heavily dependent on corpus information, and research shows that acquiring relevant corpus data can be difficult in real-world applications.
- Feature extraction approach: This method involves using AI models to identify additional potential features to make up for a lack of samples. Significant advancements have been made in neural password models. For instance, PassGAN [13] was the first to apply generative adversarial networks to understand the underlying distribution of passwords. Following this, models like FLA [14] and Transformer-based approaches [15], including discussions around PassGPT, have been able to capture intricate long-range dependencies in passwords through more advanced architectures. In 2022, Geng [16] introduced a small-sample password guessing model that employs multi-task learning, which reduces the dependence on a single large sample set by sharing feature representations across different datasets. Additionally, transfer learning techniques have emerged as a crucial strategy for tackling the small-sample issue.Melicher et al. [17] were pioneers in showing that pre-training recurrent neural networks (RNNs) or gated recurrent units (GRUs) on extensive leaked datasets allows the general knowledge of password structures to be transferred and adapted to new, smaller contexts. In 2023, Wang et al. [18] introduced the Pass2Edit algorithm, which utilizes GRU to understand the effects of password modification actions. With just one previous password from the user, it can produce a high-hit-rate guessing sequence, achieving a 24.2% hit rate for regular users within 100 attempts. In the same year, Wei [19] employed a pre-trained model to extract general features from a large leaked dataset and apply them to a small-sample context, enhancing the model’s adaptability to specific user demographics, while feature extraction methods can offer robust solutions for various complex issues, the high training costs and low efficiency they involve present significant challenges that researchers and developers need to tackle.
- This study introduces a methodology for evaluating the similarity of password sets through the structural probability vectorization of these sets, enabling a quantitative analysis of the degree of similarity among various password collections. The findings indicate that this approach can reliably quantify the similarity between a limited sample of password sets within a specific domain and a publicly available compromised set, provided that the size of the set exceeds 150;
- This study validates the hypothesis that a greater degree of similarity between and B correlates with an increased hit rate of on the test set associated with B. Experimental results indicate that the hit rate for password guessing is enhanced by as much as 32% compared to training conducted with B;
- The impact of the guessing hit rate is particularly pronounced when there is a low degree of similarity between and B. Empirical findings indicate that when the similarity index between and B falls below 0.6, the application of this method can enhance the guessing hit rate by a maximum of 10.52%;
- Our approach leverages password set similarity to transfer the most relevant features from publicly leaked datasets to the intra-site small-sample password set. This effectively addresses the issue of insufficient feature extraction in traditional intra-site methods under small-sample conditions, thereby significantly improving the password guessing hit rate in a simple yet efficient manner.
2. Background Knowledge
2.1. Probabilistic Context-Free Grammar
2.2. Cosine Similarity
- A and B represent two vectors for which the computation of similarity is to be conducted, respectively;
- and represent the ith eigenvalues associated with their respective eigenvectors;
- The notation and represents the Euclidean norms of the vectors A and B, respectively.
3. Algorithmic Progression
- The password set , which bears resemblance to B, has the capacity to significantly enhance the password characteristics associated with B.
- The pertinence of password features to the target region can be improved by enhancing the relevant features of B in ;
- Assumption 1 can expand the features, and Assumption 2 can enhance the features, and the combination of the two can improve the hit rate of password guessing in the target region.
- (1)
- Conduct a statistical analysis of the password dataset utilizing the probabilistic context-free grammar (PCFG) methodology. This analysis should yield a probability list detailing the structural components of the passwords, as well as a probability dictionary for the fragments within the password set;
- (2)
- Similarity computation involves converting the probability list of password structures from a given password set into a corresponding structure vector. Subsequently, the cosine similarity is calculated between the structure vectors of the password sets, serving as a measure of similarity between these sets. The objective is to identify the publicly leaked password set, denoted as , that exhibits the highest degree of similarity;
- (3)
- Feature enhancement: Enhance the structure of B in the password structure probability list of and the fragment of B in the password fragment probability dictionary.
- (4)
- Password generation: generate a guess password set based on the password structure probability list and password fragment probability dictionary of after feature enhancement.
3.1. Password Analysis
3.2. Similarity Calculation
- First, the structural characteristics are derived for each password set within the collections B and A through the process of model training, resulting in the generation of a structural probability list for each password set;
- Then, the structural features of a password set in A, which is to be measured for structural similarity, are concatenated with the structural features of B to get the length of the proposed vector and the meaning of each component.
- The structural probabilities of and B are subsequently incorporated into the vector file in accordance with the sequential interpretations of the components. Ultimately, this process yields the structural feature vectors associated with and B.
- Ultimately, the cosine similarity is computed for the derived vectors utilizing the formula outlined in Section 2.2, in order to assess the structural similarity between and B. The vector exhibiting the highest degree of similarity is designated as .
3.3. Feature Enhancement
| Algorithm 1: Procedure for Enhancing Structural Features |
| Input: : Probability distribution of ; : Probability distribution of B; : Enhancement strength parameter Output: : Enhanced probability distribution 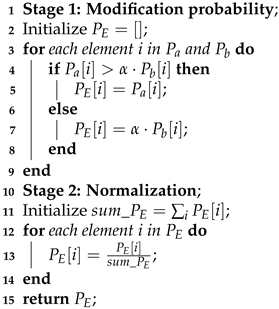 |
3.4. Password Generation
4. Experiments and Analysis of Results
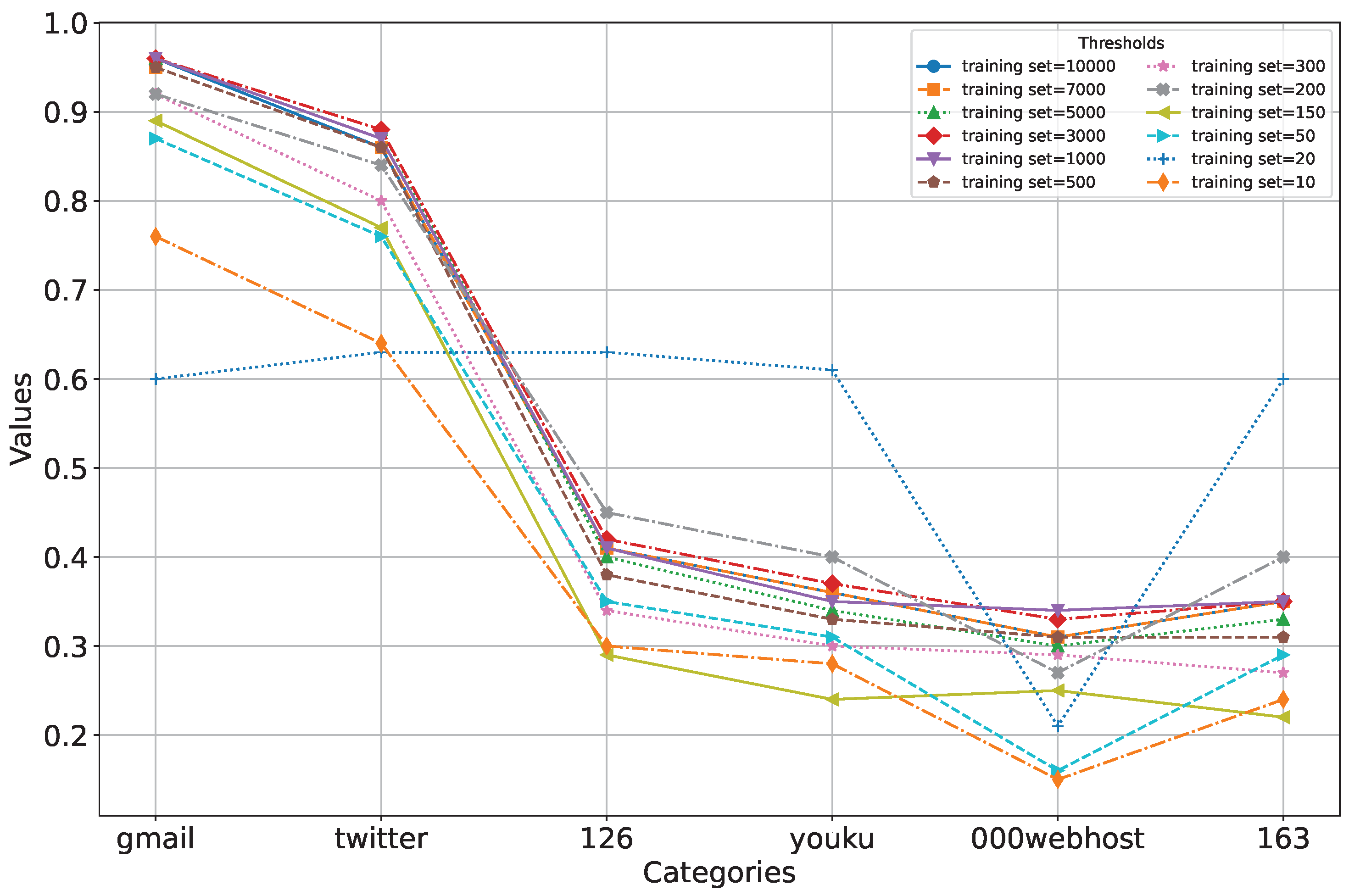
- Data Constraint Evaluation: Assess the data constraints for similarity metrics and quantitatively establish the minimum sample size threshold required for stable similarity metrics within a small-sample password set B;
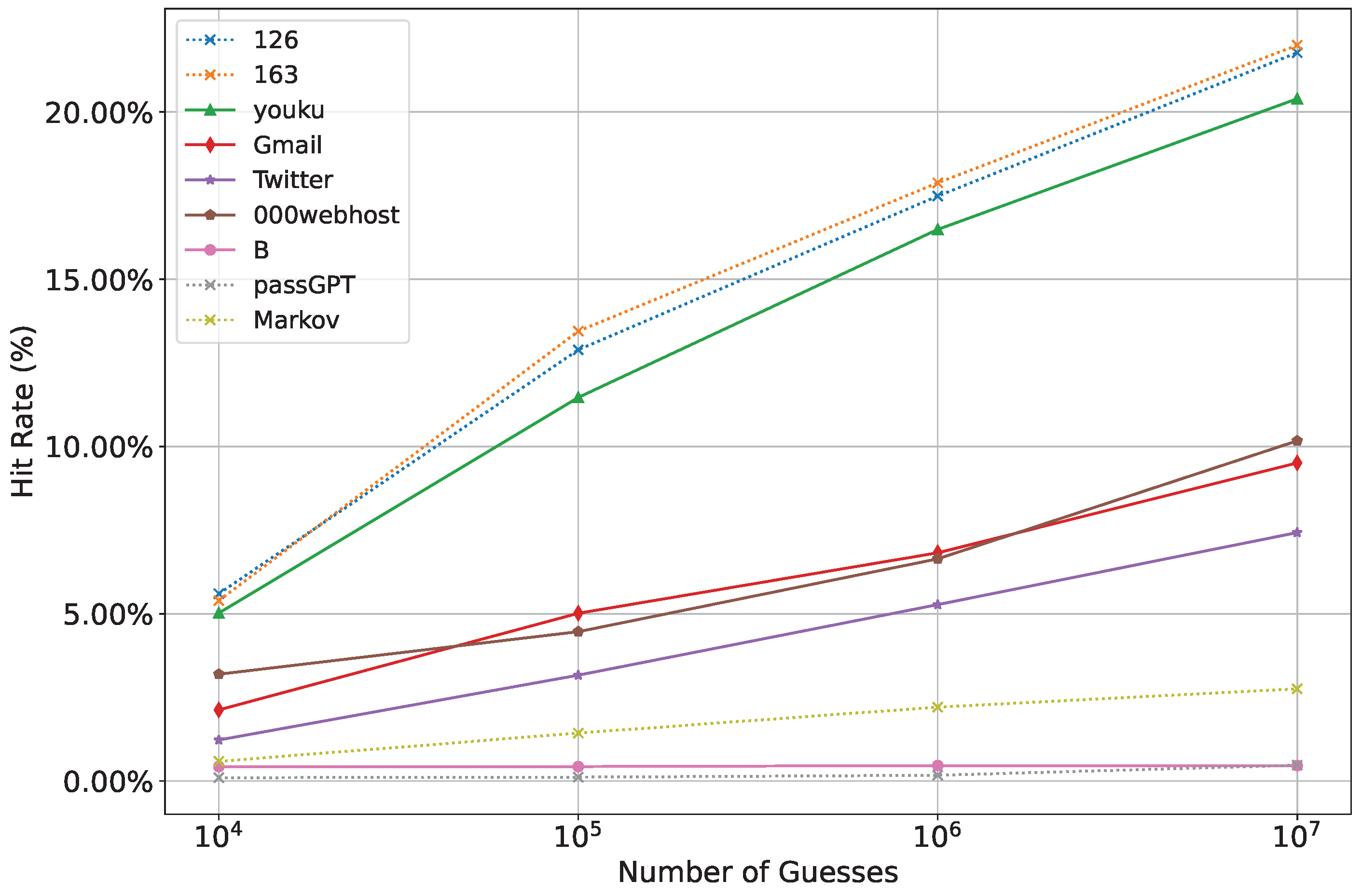
- The core hypothesis is to verify whether an increase in similarity between and B corresponds with an increase in the guessing hit rate of the training-generated password set, thereby confirming the positive correlation between similarity and hit rate.
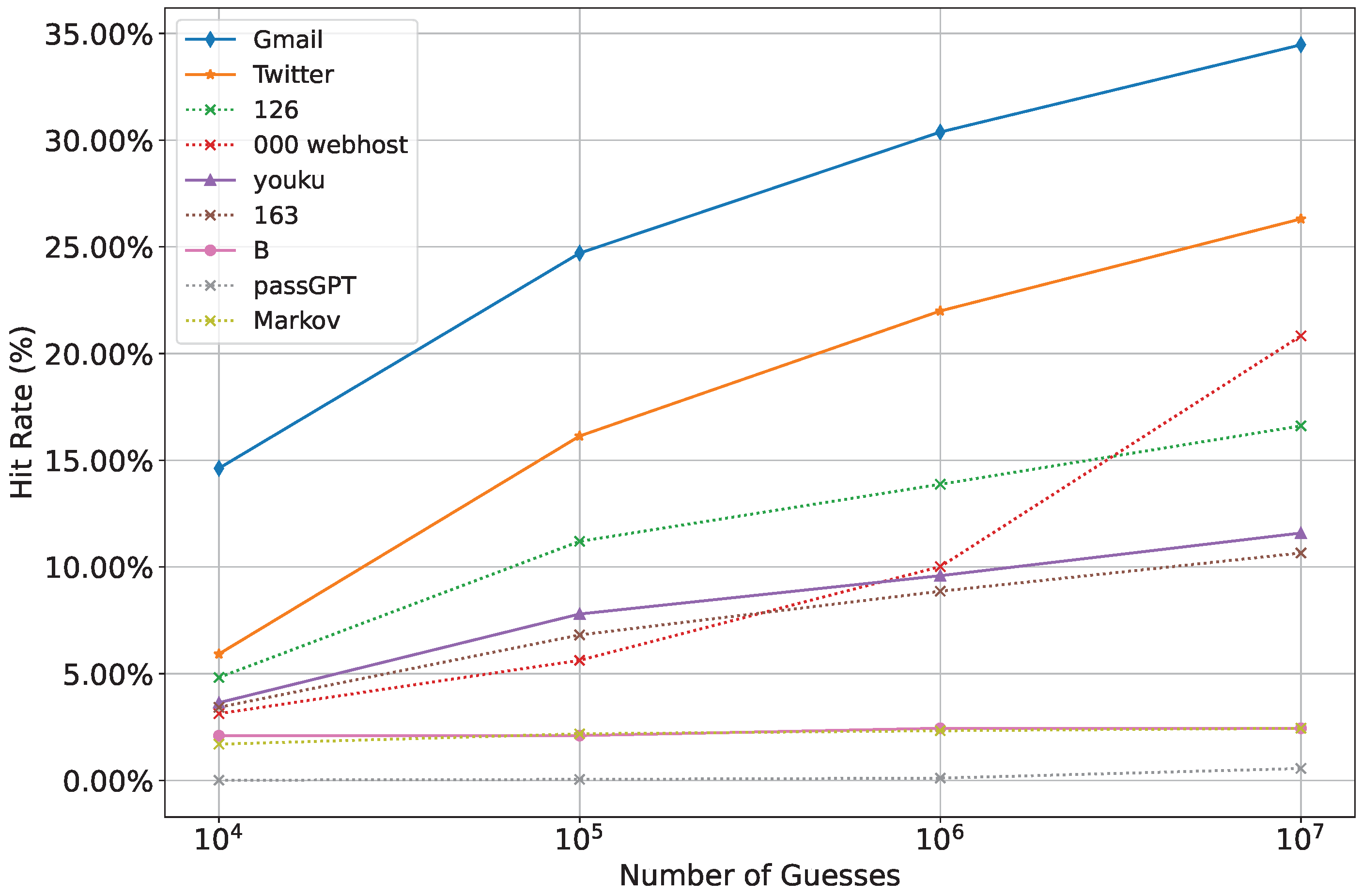
- Analyzing the Impact of Feature Enhancement: This study examines the varying effects of feature enhancement on different sets of similar passwords.
4.1. Data Sets
4.2. Evaluation Indicators
- indicates the number of test passphrases included in the generated passphrase guessing dictionary.
- indicates the total number of test passwords.
4.3. Experiment 1: Evaluation of Data Constraints for Similarity Metrics
4.4. Experiment 2: Verifying the Positive Correlation Between Similarity and Hit Rate
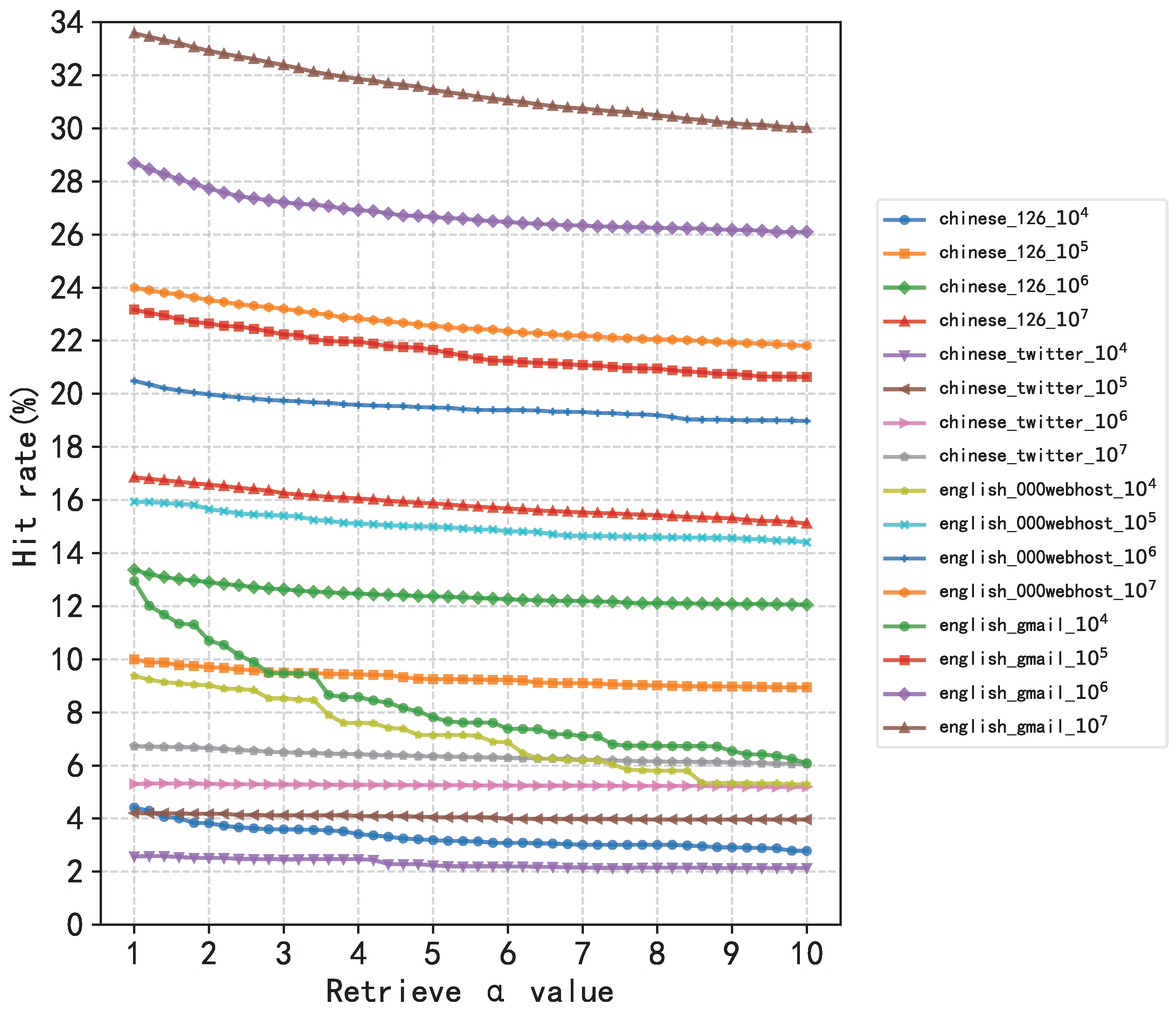
4.5. Experiment 3: Feature Enhancement and Effect Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Ji, S.; Yang, S.; Hu, X.; Han, W.; Li, Z.; Beyah, R. Zero-Sum Password Cracking Game: A Large-Scale Empirical Study on the Crackability, Correlation, and Security of Passwords. IEEE Trans. Dependable Secur. Comput. 2017, 14, 550–564. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, J.; Xu, M.; Zhang, H.; Han, W. #Segments: A Dominant Factor of Password Security to Resist against Data-driven Guessing. Comput. Secur. 2022, 121, 102848. [Google Scholar] [CrossRef]
- Su, X.; Zhu, X.; Li, Y.; Li, Y.; Chen, C.; Esteves-Veríssimo, P. PagPassGPT: Pattern Guided Password Guessing via Generative Pretrained Transformer. In Proceedings of the 2024 54th Annual IEEE/IFIP International Conference on Dependable Systems and Networks (DSN), Brisbane, Australia, 24–27 June 2024; pp. 429–442. [Google Scholar] [CrossRef]
- Deng, G.; Yu, X.; Guo, H. Efficient Password Guessing Based on a Password Segmentation Approach. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Xie, J.; Cheng, H.; Zhu, R.; Wang, P.; Liang, K. WordMarkov: A New Password Probability Model of Semantics. In Proceedings of the 2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 22–27 May 2022; pp. 3034–3038. [Google Scholar] [CrossRef]
- Zou, Y.; Wang, D. Advances in Password Guessing Research. J. Cryptogr. (Chin. Engl. Ed.) 2024, 11, 67–100. [Google Scholar] [CrossRef]
- Xie, Z.; Shi, F.; Zhang, M.; Rao, Z.; Zhou, Y.; Ji, X. Similarities: The Key Factors Influencing Cross-Site Password Guessing Performance. Electronics 2025, 14, 945. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, Z.; Wang, P.; Yan, J.; Huang, X. Targeted Online Password Guessing: An Underestimated Threat. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security (CCS), Vienna, Austria, 24–28 October 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 1242–1254. [Google Scholar] [CrossRef]
- Bi, H.; Tan, R.; Zhao, J.; Li, Y. Research on a Password Guessing Model Based on Topic PCFG. Inf. Netw. Secur. 2019, 8, 1–7. [Google Scholar]
- Gan, X.; Chen, M.; Li, D.; Wu, Z.; Han, W.; Chen, H. Corpora-based Password Guessing: An Efficient Approach for Small Training Sets. In Proceedings of the 2021 IEEE 4th International Conference on Electronics and Communication Engineering (ICECE), Xi’an, China, 17–19 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 311–319. [Google Scholar]
- Chen, M. Research and Application of Password Guessing Rule Extension Method. Master’s Thesis, South China University of Technology, Guangzhou, China, 2022. [Google Scholar]
- Han, W.; Zhang, J.; Xu, M.; Wang, C.; Zhang, H.; He, Z.; Chen, H. Parametric Mixed Password Guessing Method. Comput. Res. Dev. 2022, 59, 2708–2722. [Google Scholar]
- Hitaj, B.; Gasti, P.; Ateniese, G.; Perez-Cruz, F. Passgan: A deep learning approach for password guessing. In Proceedings of the 17th International Conference on Applied Cryptography and Network Security, ACNS 2019, Bogota, Colombia, 5–7 June 2019; Springer International Publishing: Cham, Switzerland, 2019; pp. 217–237. [Google Scholar]
- Yu, F.; Martin, M.V. GNPassGAN: Improved generative adversarial networks for trawling offline password guessing. In Proceedings of the 2022 IEEE European Symposium on Security and Privacy Workshops (EuroS&PW), Genoa, Italy, 6–10 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 10–18. [Google Scholar]
- Rando, J.; Perez-Cruz, F.; Hitaj, B. Passgpt: Password modeling and (guided) generation with large language models. In Proceedings of the European Symposium on Research in Computer Security, The Hague, The Netherlands, 25–29 September 2023; Springer Nature Switzerland: Cham, Switzerland, 2023; pp. 164–183. [Google Scholar]
- Geng, Y. Research on Small Sample Password Set Guessing Model Based on Multi-Task Learning. Master’s Thesis, Xi’an University of Electronic Science and Technology, Xi’an, China, 2022. [Google Scholar]
- Melicher, W.; Ur, B.; Segreti, S.M.; Komanduri, S.; Bauer, L.; Christin, N.; Cranor, L.F. Fast, lean, and accurate: Modeling password guessability using neural networks. In Proceedings of the 25th USENIX Security Symposium (USENIX Security 16), Austin, TX, USA, 10–12 August 2016; pp. 175–191. [Google Scholar]
- Wang, D.; Zou, Y.; Xiao, Y.-A.; Ma, S.; Chen, X. Pass2Edit: A Multi-Step Generative Model for Guessing Edited Passwords. In Proceedings of the 32nd USENIX Security Symposium (USENIX Security 23), Anaheim, CA, USA, 9–11 August 2023. [Google Scholar]
- Yu, H. Research on Password Guessing Model Based on Digital Semantics. Master’s Thesis, East China Normal University, Shanghai, China, 2023. [Google Scholar]
- Tianya, China’s Biggest Online Forum 40 Million Users Data Leaked [EB/OL]. (2011-12). Available online: https://thehackernews.com/2011/12/tianya-chinas-biggest-online-forum-40.html (accessed on 15 March 2025).
- Train Ticket Website Leaks User Info [EB/OL]. 2014. Available online: https://www.globaltimes.cn/content/898706.shtml (accessed on 15 March 2025).
- Taylor, C. Twitch Resets All User Passwords After Suffering Data Breach [EB/OL]. 2015. Available online: https://techcrunch.com/2015/03/23/twitch-passwords-data-breach-hack/ (accessed on 15 March 2025).
- Twitter Data Breach and 10 Billion Password Leak Details [EB/OL]. 2016. Available online: https://www.cybersecurity-insiders.com/twitter-data-breach-and-10-billion-password-leak-details/ (accessed on 15 March 2025).
- Hackers Steal 6 Million User Accounts for Cash-for-Surveys Site [EB/OL]. 2017. Available online: https://www.vice.com/en/article/hackers-steal-6-million-user-accounts-for-cash-for-surveys-site/ (accessed on 15 March 2025).




| Name | Sample Content | Training Set | Test Set |
|---|---|---|---|
| Small Command Set | |||
| 12306 | 500 | 69,500 | |
| 12306 | 300 | 69,700 | |
| 12306 | 200 | 69,800 | |
| 12306 | 150 | 69,850 | |
| 12306 | 50 | 69,950 | |
| 12306 | 20 | 69,980 | |
| 12306 | 10 | 69,990 | |
| cashcraete | 500 | 69,500 | |
| cashcraete | 300 | 69,700 | |
| cashcraete | 200 | 69,800 | |
| cashcraete | 150 | 69,850 | |
| cashcraete | 50 | 69,950 | |
| cashcraete | 20 | 69,980 | |
| cashcraete | 10 | 69,990 | |
| Large-scale Command Cluster | |||
| 126 | 70,000 | \ | |
| 163 | 70,000 | \ | |
| youku | 70,000 | \ | |
| Gmail | 70,000 | \ | |
| 70,000 | \ | ||
| 000webhost | 70,000 | \ | |
| Similarity | ||
|---|---|---|
| 126 | 0.74 | 0.29 |
| 163 | 0.72 | 0.22 |
| youku | 0.63 | 0.24 |
| Gmail | 0.52 | 0.89 |
| 0.36 | 0.77 | |
| 000webhost | 0.35 | 0.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Li, J.; Liu, X.; Li, B.; Hou, M.; Yu, W.; Li, Y.; Liu, W. Cross-Domain Feature Enhancement-Based Password Guessing Method for Small Samples. Entropy 2025, 27, 752. https://doi.org/10.3390/e27070752
Liu C, Li J, Liu X, Li B, Hou M, Yu W, Li Y, Liu W. Cross-Domain Feature Enhancement-Based Password Guessing Method for Small Samples. Entropy. 2025; 27(7):752. https://doi.org/10.3390/e27070752
Chicago/Turabian StyleLiu, Cheng, Junrong Li, Xiheng Liu, Bo Li, Mengsu Hou, Wei Yu, Yujun Li, and Wenjun Liu. 2025. "Cross-Domain Feature Enhancement-Based Password Guessing Method for Small Samples" Entropy 27, no. 7: 752. https://doi.org/10.3390/e27070752
APA StyleLiu, C., Li, J., Liu, X., Li, B., Hou, M., Yu, W., Li, Y., & Liu, W. (2025). Cross-Domain Feature Enhancement-Based Password Guessing Method for Small Samples. Entropy, 27(7), 752. https://doi.org/10.3390/e27070752






