Statistical Mechanics of Linear k-mer Lattice Gases: From Theory to Applications
Abstract
1. Introduction
2. Thermodynamic Functions of Lattice Gases of Polyatomics in One Dimension: Multilayer Adsorption
Multilayer Adsorption of Dimers
3. Thermodynamic Functions of Lattice Gases of Polyatomics in Two Dimensions: Analytical Approaches for Single Species and Mixtures
3.1. Two-Dimensional Model of Non-Interacting Structured Particles: More Recent Approximations from Our Group
3.1.1. Extension to Higher Dimensions of the Exact Thermodynamic Functions in One Dimension ()
3.1.2. Fractional Statistics Thermodynamic Theory of Adsorption of Polyatomics ()
3.1.3. Occupation Balance Approximation ()
3.1.4. Semi-Empirical Adsorption Model for Polyatomics ()
3.1.5. Brief Introduction to Multiple Exclusion Statistics
3.2. Two-Dimensional Model of Non-Interacting (k-mer–l-mer) Binary Mixtures
3.2.1. Approximation
3.2.2. Approximation
3.2.3. Approximation
3.3. Multilayer Adsorption in the Presence of Multisite Occupancy: Theoretical Approach for 2D Substrates
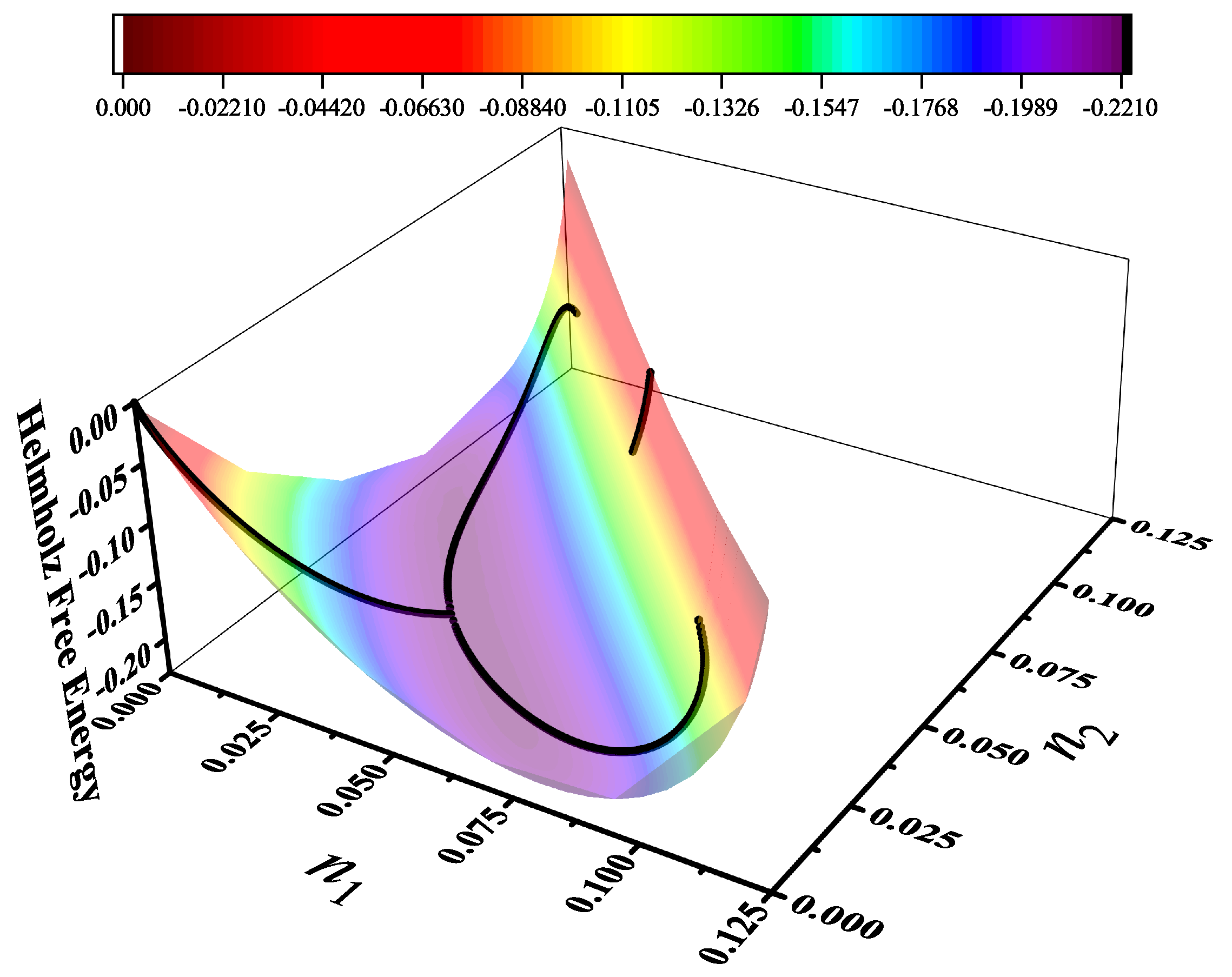
4. Two-Dimensional Lattice Gases of Interacting Polyatomics
4.1. Mean-Field Approximation for Interacting k-mers Adsorbed onto 2D Substrates
4.2. Quasi-Chemical Approximation for Interacting k-mers Adsorbed onto 2D Substrates
General Expression of the Thermodynamic Functions in Terms of the Configurational Factor
4.3. Quasi-Chemical Approximation for Interacting Mixtures Adsorbed onto 2D Substrates
- (1)
- (2)
- (3)
- (4)
5. Latest Developments, Part I: Multiple Exclusion Statistics for Spatially Correlated Single Species
5.1. Multiple Exclusion Statistics Formalism
5.2. States Counting Ansatz: Density of States
5.3. Density of States Parameters
5.4. Lambert Function
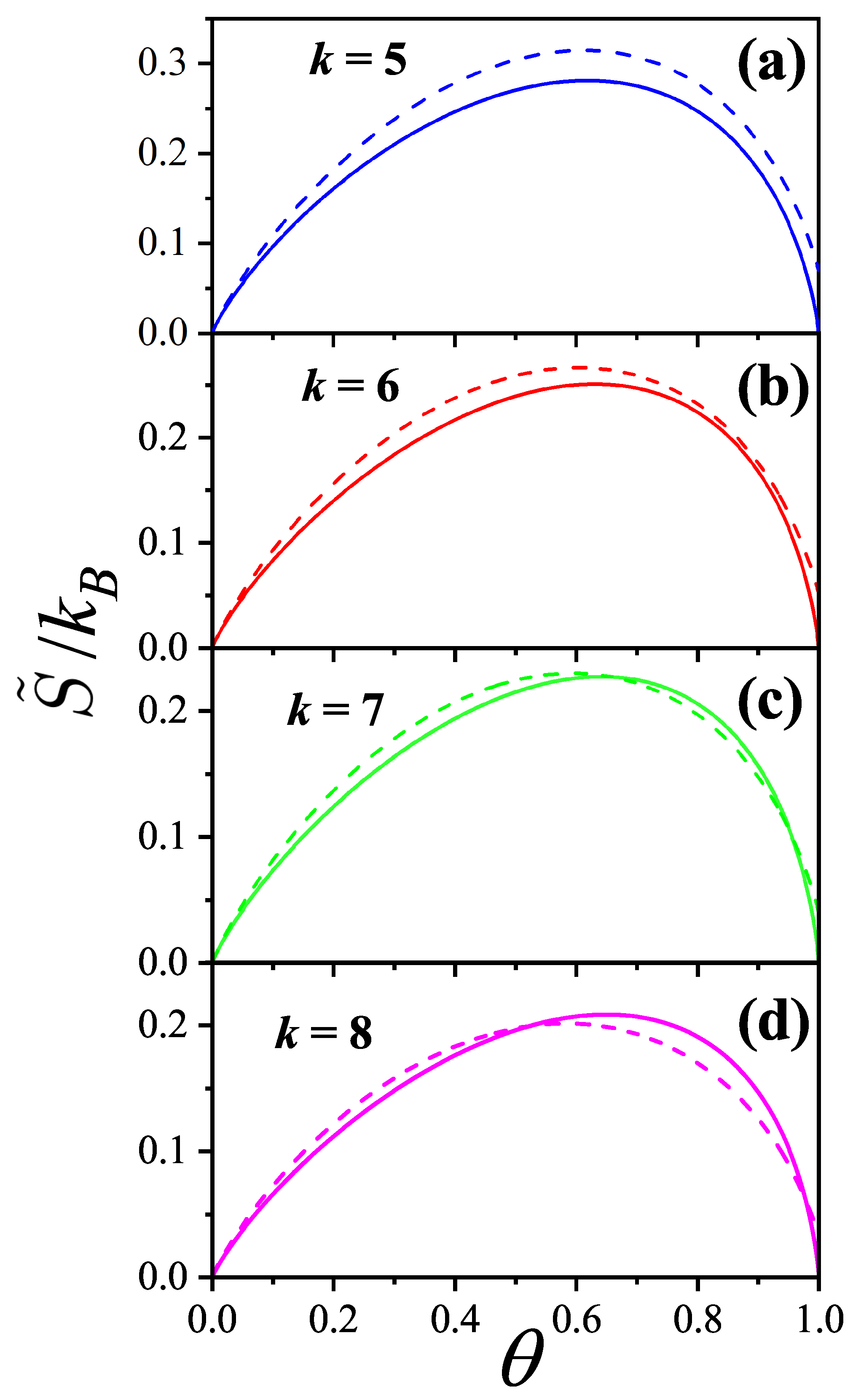
5.5. Entropy of k-mers on Square Lattices: Orientational Phase Transitions
5.6. Exclusion Spectrum Functions
5.7. Adsorption of Polyatomics: Relationships Between Exclusion Functions, Thermodynamic Observables, and Adsorption Field Topology
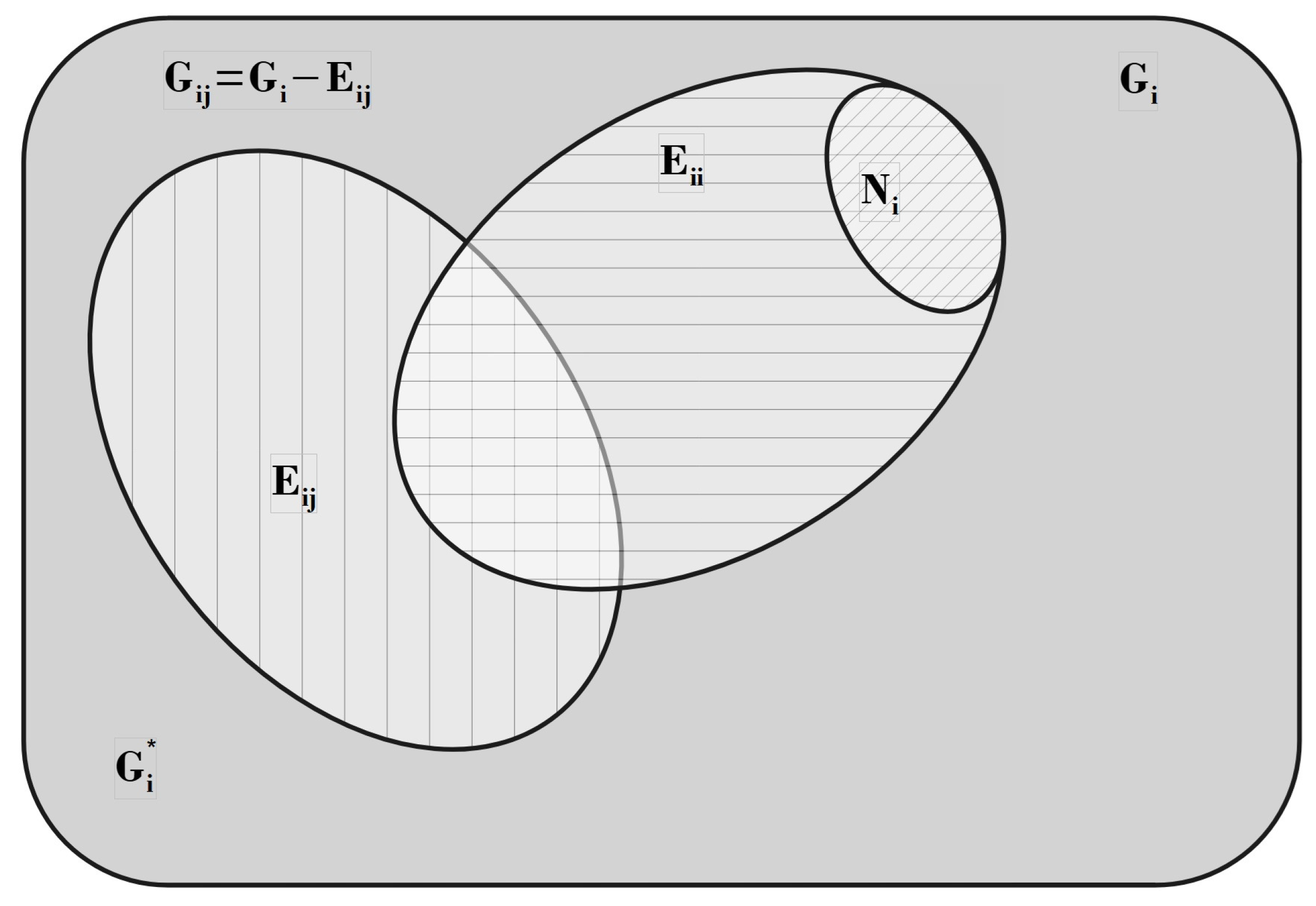
6. Latest Developments, Part II: Multiple Exclusion Statistics Formulation for Mixtures
6.1. State-Counting Approximation and Density of States for Mixtures with Multiple State Exclusion
6.2. Statistical Thermodynamics of Mixtures
6.3. State Exclusion Spectrum Functions: Determination of Exclusion Correlation Parameters
6.4. The k-mers Problem as a Mixture Model: Basic Definitions
7. Applications
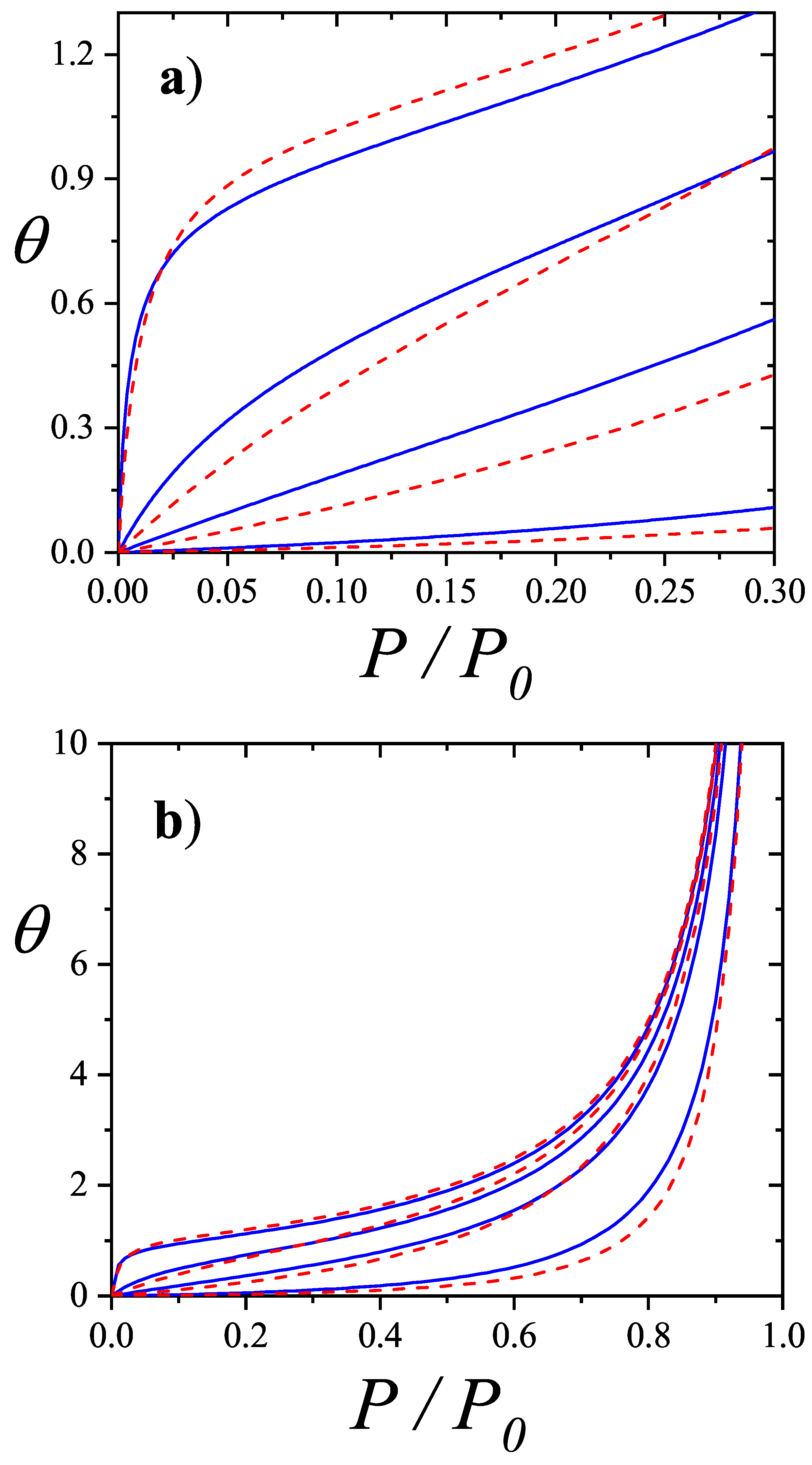
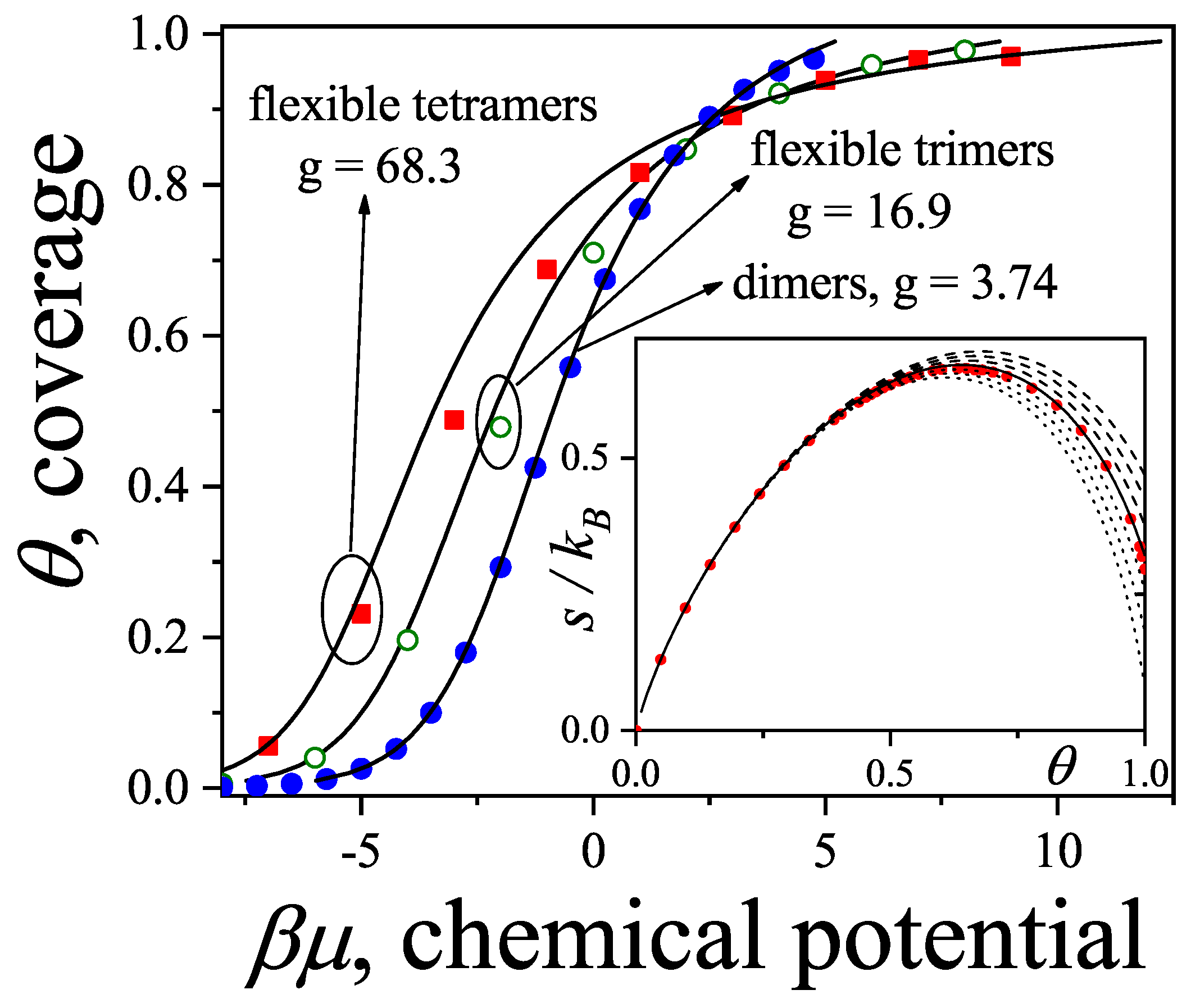
7.1. Two-Dimensional Adsorption: Comparison Between Theory and Monte Carlo Simulations
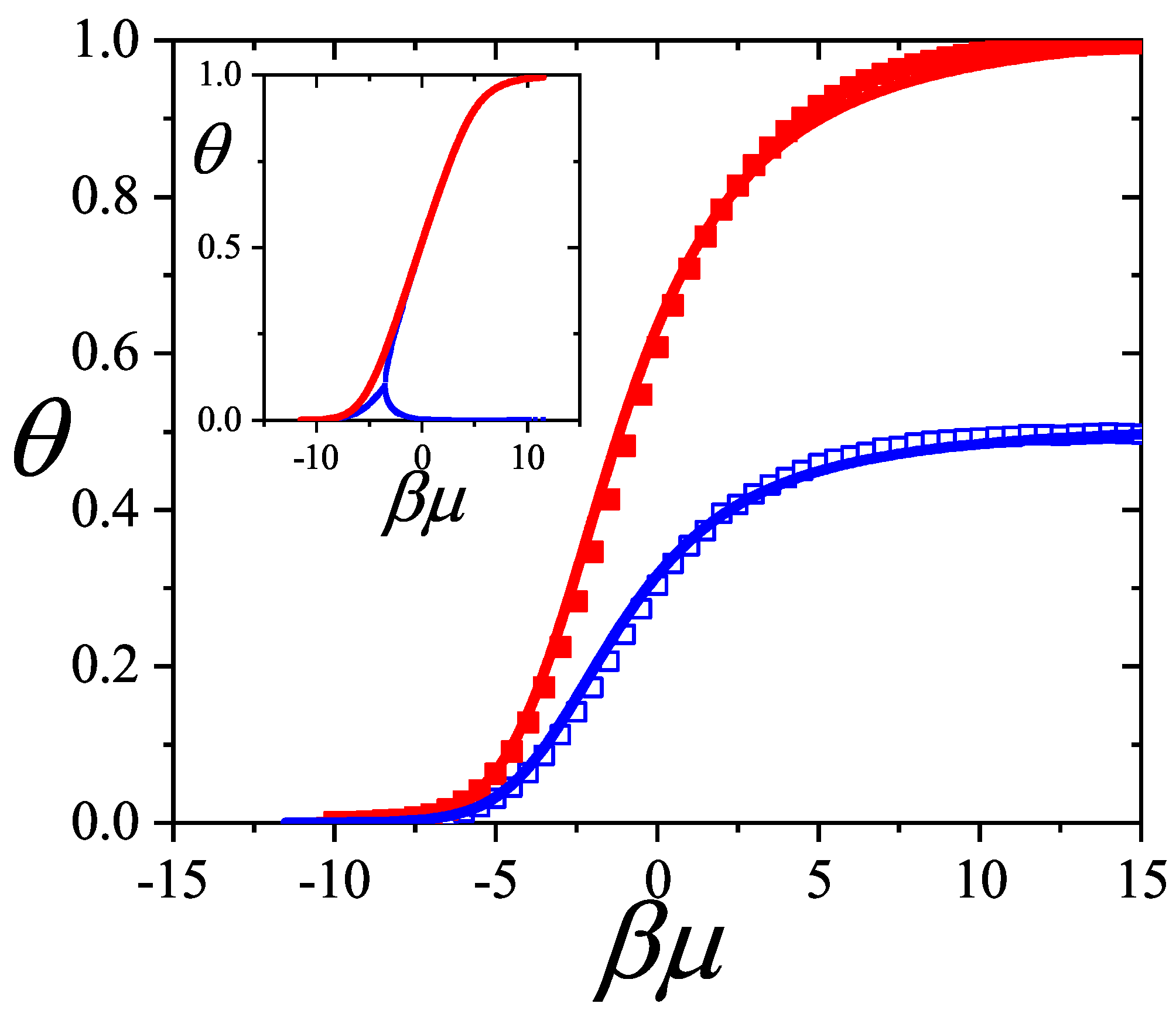
7.2. Two-Dimensional Adsorption of Binary Mixtures: Comparison Between Theory and Monte Carlo Simulations
7.3. Two-Dimensional Adsorption of Interacting k-mers: Comparison Between Theory and Monte Carlo Simulations
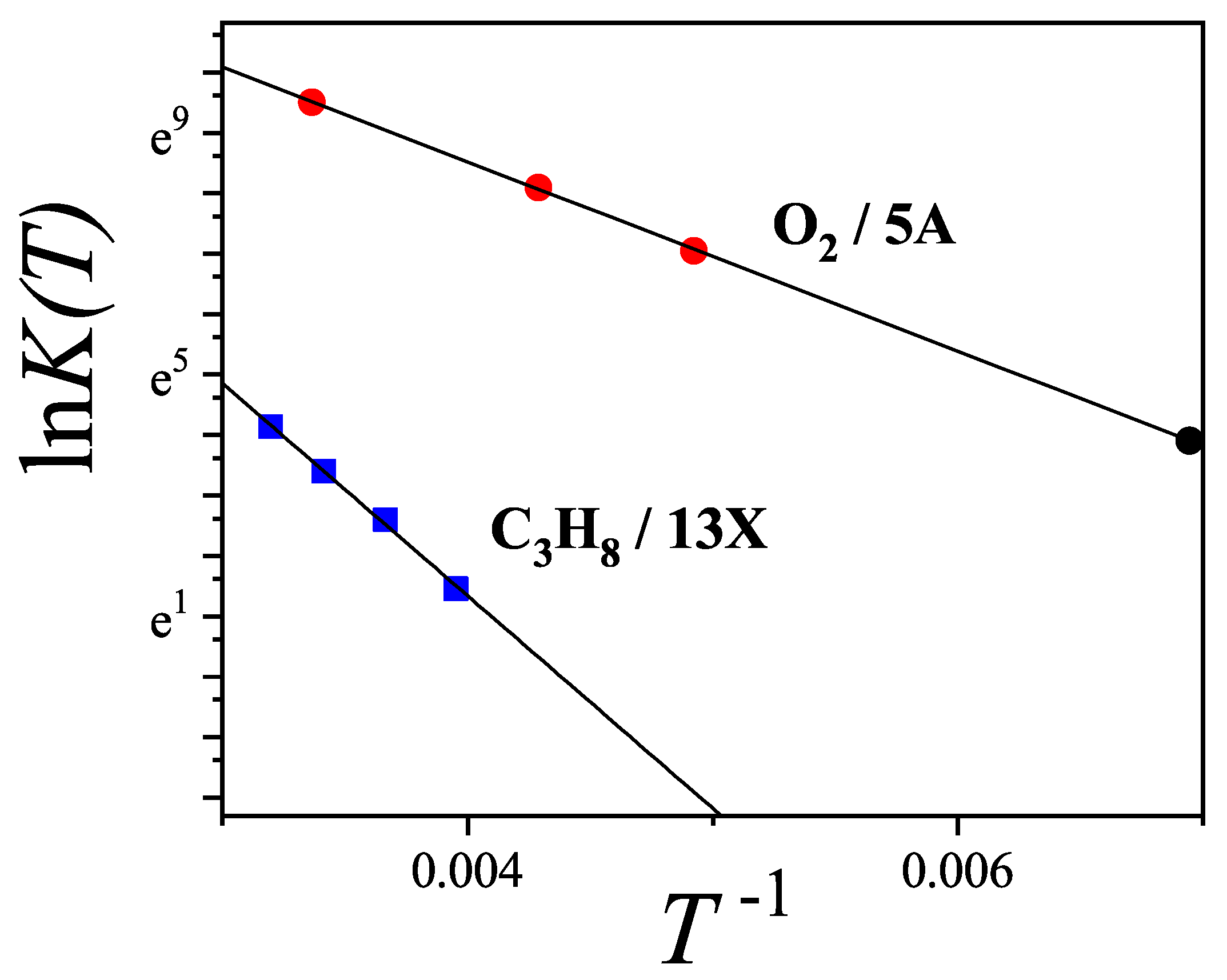
7.4. Application of to the Adsorption of and in Zeolites 13X and 5A: Determination of the Adsorption Configuration

| System | k | m | g | D (%) | |||||
|---|---|---|---|---|---|---|---|---|---|
| 2 | 2 | 4 | 3.10 | 0.72 | 5.60 | ||||
| 3 | 1 | 3 | 5.75 | 6.94 | 1.27 | 2.08 |


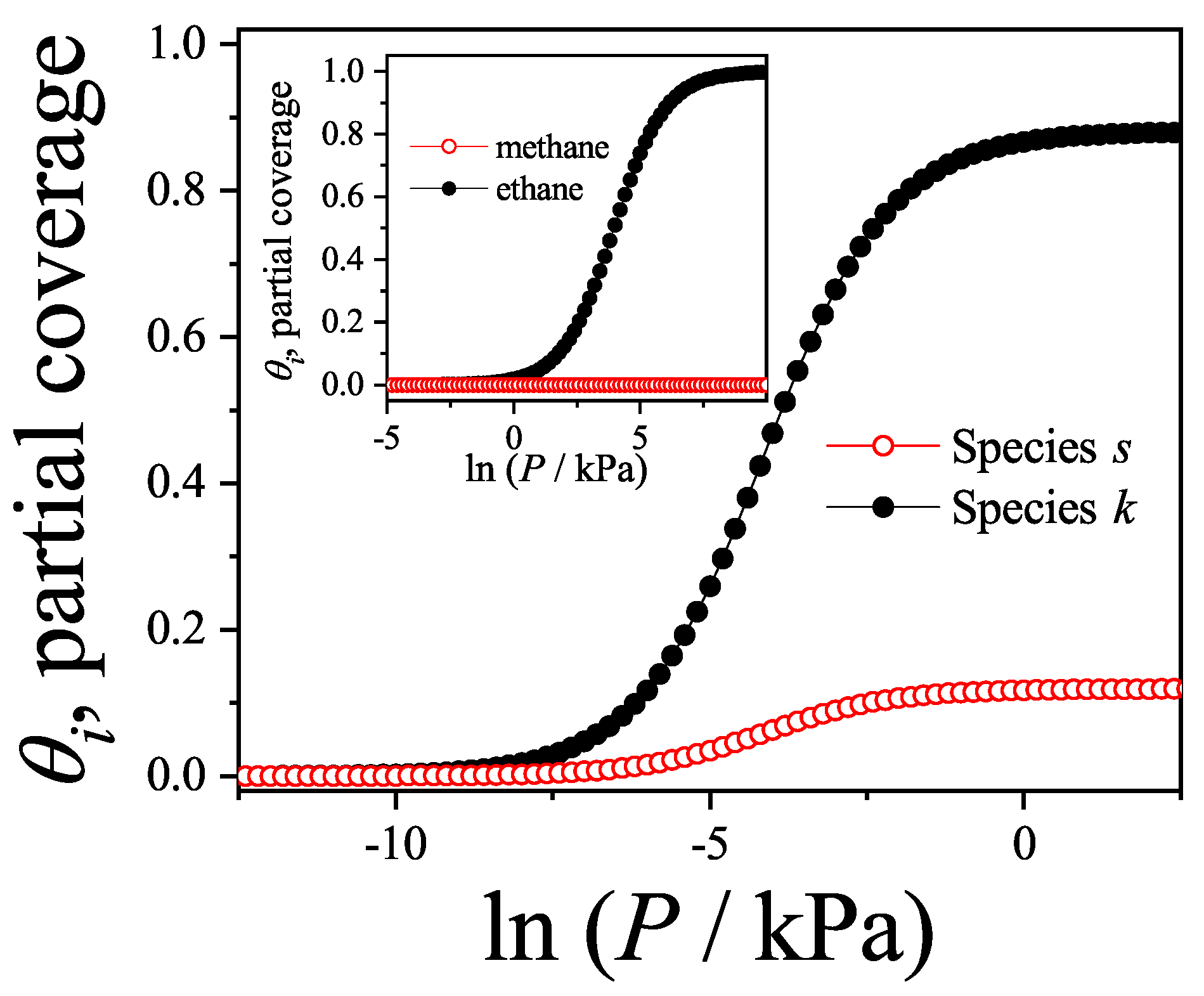
7.5. Adsorption of Methane–Ethane Mixtures in Zeolites: Reversal Adsorption Phenomena
7.6. Alkanes Adsorbed in Carbon Nanotube Bundles: Surface Area Characterization
- (1)
- In this first approach (procedure A), we used the one-dimensional MBET equations for all four adsorbates to account for the linear geometry of the molecules. For methane, we employed the standard BET equation, which corresponds to the MBET expression for monomers. For ethane, we applied the exact 1-D MBET formula for dimers [Equation (270)]. For propane and butane, we utilized the same dimer equation but adjusted its parameters to fit the experimental data in the low-pressure, low-coverage regime—specifically, the same region typically used in BET analysis.Using Procedure A, the calculated specific surface areas for ethane, propane, and butane were consistently higher than those obtained using the BET method. In addition to producing improved results, this method remains relatively straightforward to implement.However, we also observed a consistent trend: as the length of the alkane chain increases, the derived specific surface area decreases. This behavior is illustrated in Figure 6, which includes data obtained from both this and other approaches.Although not perfect, the results from Procedure A represent a clear enhancement over the standard BET approach.
- (2)
- The second strategy (procedure B) involved fitting the isotherm data for all four adsorbates to the approximate MBET expression developed for the two-dimensional case [Equation (137) in Section 3.3]:In this formulation, is a constant that reflects both the interaction strength between the adsorbate and the substrate, as well as the connectivity of the adsorption lattice. The parameter k denotes the number of units in the k-mer molecule.The experimental adsorption isotherms were fitted to this model using the appropriate k value for each adsorbate—1 for methane, 2 for ethane, 3 for propane, and 4 for butane—within the same low-pressure range typically employed for BET analysis. Figure 45 shows the fit obtained for butane, which demonstrates excellent agreement with the data; similarly accurate fits were achieved for the other three alkanes. The fits yielded values for the monolayer capacity, , which were subsequently used to compute the specific surface area of the sample.
7.7. Crystal Growth from Aqueous Solution in the Presence of Structured Impurities
- HCOOH: Equation (283) was employed as the fitting model, with and treated as the adjustable parameter.
- COOH: The fit was performed using Equation (284), corresponding to , with optimized.
- COOH: Equation (285) was selected for this case, with and fitted accordingly.
- COOH: Equation (286) served as the fitting function, with and as the fitting parameter.
7.8. Application to k-mer Phase Transitions
7.8.1. Basic Definitions
7.8.2. Entropy Surface, Equilibrium Path, and Order Parameter
7.8.3. Generalized Density of States Function in Multiple Exclusion Statistics
7.8.4. Nematic-Phase Density Branches and Phase Transitions
7.8.5. State Exclusion Spectrum Functions of k-mers: Coverage Dependence
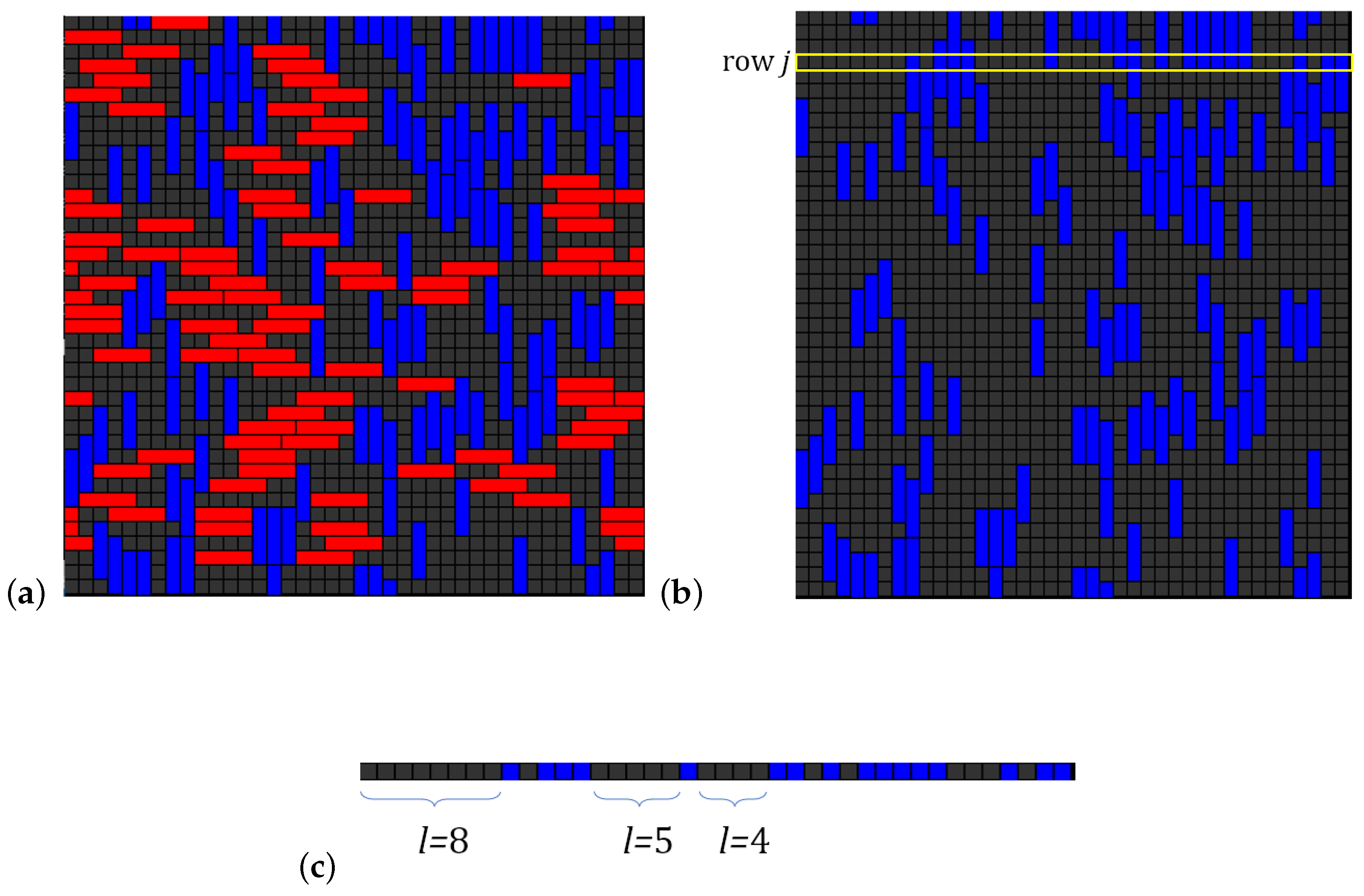
8. Monte Carlo Simulation Method Applied to the Problem of Adsorption with Multisite Occupancy
8.1. Metropolis MC Algorithms for Adsorption of Interacting k-mers
8.1.1. Grand Canonical Ensemble
- (i)
- Specify the chemical potential and the temperature T.
- (ii)
- Randomly select a linear group of k adjacent sites.
- (iii)
- If all the k sites chosen in step are vacant, a rod insertion is attempted with probability . If instead the selected sites are fully occupied by segments of the same k-mer, a removal (desorption) attempt is made with probability . In any other scenario, the attempt is rejected. Here, and correspond to the transition probabilities for increasing or decreasing the particle count from N to or , respectively. According to the Metropolis algorithm [199], these probabilities are defined as , where represents the change in the system’s Hamiltonian between the final and initial configurations.
- (iv)
- Repeat steps () and () a total of M times.
8.1.2. Canonical Ensemble
- (i)
- Define the system temperature T.
- (ii)
- Fix the surface coverage by placing linear molecules onto the lattice, each occupying k adjacent sites.
- (iii)
- Randomly choose one k-mer and a linear sequence of k unoccupied lattice sites. Once their positions are determined, an exchange of their occupancy states is attempted. The acceptance of this move follows the Metropolis criterion [199]:where represents the energy difference between the final and initial configurations.
- (iv)
- Select a k-mer at random and attempt a movement to neighboring sites. This movement may be either a translational shift along the molecule’s axis or a reptation move involving rotation around one of its units. These diffusion steps are governed by the Metropolis rule and are essential for ensuring that the system relaxes toward equilibrium within practical simulation timeframes.
- (v)
- Repeat steps (iii) and (iv) a total of M times.
8.2. Parallel Tempering MC Algorithm for Adsorption of Interacting k-mers
8.2.1. Replica-Update
8.2.2. Replica-Exchange
8.3. Parallel Tempering MC Algorithm for Adsorption of Binary Mixtures of Interacting Species of Polyatomics
8.3.1. Replica-Update
8.3.2. Replica-Exchange
8.4. Improving the Update Algorithm Through the Use of Lists of Full and Empty k-tuples
8.5. Non-Local Update Kundu’s Algorithm for Adsorption of Non-Interacting Large k-mers (Only Excluded Volume Interaction)
8.6. Thermodynamic Integration Method in Canonical Ensemble: Artificial Hamiltonian Method
9. Conclusions and Future Perspectives
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Model and Reference | Mathematical Form of the Adsorption Isotherm |
|---|---|
| 1D lattice, non-interacting k-mers, exact solution [20] | |
| Flory–Huggins approximation, -connectivity lattice, non-interacting flexible k-mers [6,7] | |
| Flory–Huggins approximation, -connectivity lattice, non-interacting linear k-mers [6,7,16] | |
| Guggenheim–DiMarzio approximation, -connectivity lattice, non-interacting linear k-mers [9,10] | |
| approximation, -connectivity lattice, non-interacting linear k-mers [16,20] | |
| approximation, -connectivity lattice, non-interacting linear k-mers [12,13] | |
| approximation, -connectivity lattice, non-interacting linear k-mers [11,16] |
| Model and Reference | Mathematical Form of the Partial Adsorption Isotherms |
|---|---|
| 1D lattice, exact solution [100] | |
| approximation, -connectivity lattice [97,98] | |
| approximation, -connectivity lattice [97,98] | |
| approximation, -connectivity lattice [97,98] |
| Model and Reference | Mathematical Form of the Adsorption Isotherm |
|---|---|
| 1D lattice, dimers (), exact solution [101,102] | |
| Non-interacting k-mers, -connectivity lattice [101,102] |
|
| Model and Reference | Mathematical Form of the Adsorption Isotherm |
|---|---|
| 1D lattice, exact solution [30,31] | |
| Mean-field approximation, -connectivity lattice [30,31] | |
| Quasi-chemical approximation, -connectivity lattice [30,31] |
| Model and Reference | Mathematical Form of the Partial Adsorption Isotherms |
|---|---|
| 1D lattice, exact solution [113] | See Section 4.3, deriving the final equations of the partial adsorption isotherms requires the use of a standard mathematical software program |
| Quasi-chemical approximation, -connectivity lattice [113] | See Section 4.3, deriving the final equations of the partial adsorption isotherms requires the use of a standard mathematical software program |
| Model and Reference | Mathematical Form of the Adsorption Isotherm |
|---|---|
| ME Statistics. General form [17,18,19] | |
| ME Statistics. Simplified form assuming vanishing entropy at full coverage () [18] | |
| ME Statistics. Mean-field approximation | Replace in above equations; is interaction energy per particle at full coverage |
| Method/Algorithm and Reference | Main Features |
|---|---|
| Metropolis MC algorithm, grand canonical ensemble [20,142,198] | The state of the system is modified in one of two ways: by adsorbing a particle onto the substrate or desorbing it from the substrate |
| Metropolis MC algorithm, canonical ensemble [94,198] | Thermodynamic equilibrium is achieved using Kawasaki dynamics, extended to accommodate polyatomic species. One k-mer and a linear sequence of k unoccupied lattice sites are randomly selected. Once their positions are determined, an exchange of their occupancy states is attempted |
| Parallel tempering MC algorithm for single adsorption [200,201] | Starting from a compound system of R non-interacting replicas of the system under study, each of them associated to a different gas pressure . There are two simulation steps: replica-update and replica-exchange. The first basically involves selecting one of the R replicas and applying the Metropolis algorithm to it. The second involves the random selection of two replicas and the intent of exchanging their states with a given probability |
| Parallel tempering MC algorithm for multicomponent adsorption [97,200,201] | The above algorithm for single adsorption can be applied to the case of mixtures of two or more species. In order to simulate the adsorption of a binary mixture (i.e., k-mers and l-mers), the application of the Metropolis algorithm must be preceded by the random selection with equal probability of one of the possible species |
| Update algorithm through the use of lists of k-tuples [102] | The updating process (replica-update), through application of the Metropolis rule, involves the random selection of a linear k-tuple. The use of lists of full and empty k-tuples allows this selection to be carried out in a rejection-free manner, which significantly improves the performance of the process |
| Non-local update Kundu’s algorithm [17,18,19,63,129,137] | The number of particles on the lattice is allowed to fluctuate through non-local changes; i.e, insertion and deletion of many k-mers at a time (in contrast to the standard Metropolis rule used in previous algorithms) |
| Thermodynamic integration method [94,95,202,203,204,205] | Free energy and entropy cannot be directly calculated using MC simulations. However, the thermodynamic integration method enables the estimation of entropy through the numerical integration of adsorption isotherms or other thermodynamic quantities, provided that the entropy of a reference state is known |
| Artificial Hamiltonian (AH) method [94,95] | Through the AH method, starting from the original system of interest, an artificial system that enables calculation of the entropy of the reference state can be constructed |
References
- Onsager, L. The effects of shape on the interaction of colloidal particles. Ann. N. Y. Acad. Sci. 1949, 51, 627–659. [Google Scholar] [CrossRef]
- Kasteleyn, P. The statistics of dimers on a lattice I. The number of dimer arrangements on a quadratic lattice. Physica 1961, 27, 1209–1225. [Google Scholar] [CrossRef]
- Baxter, R.J. Hard hexagons: Exact solution. J. Phys. A Math. Gen. 1980, 13, L61–L70. [Google Scholar] [CrossRef]
- Frenkel, D.; Eppenga, R. Evidence for algebraic orientational order in a two-dimensional hard-core nematic. Phys. Rev. A 1985, 31, 1776–1787. [Google Scholar] [CrossRef]
- Khandkar, D.; Barma, M. Orientational correlations and the effect of spatial gradients in the equilibrium steady state of hard rods in two dimensions: A study using deposition-evaporation kinetics. Phys. Rev. E 2005, 72, 051717. [Google Scholar] [CrossRef]
- Flory, P.J. Thermodynamics of High Polymer Solutions. J. Chem. Phys. 1942, 10, 51–61. [Google Scholar] [CrossRef]
- Huggins, M.L. Some properties of solutions of long-chain compounds. J. Chem. Phys. 1942, 46, 151–158. [Google Scholar] [CrossRef]
- Des Cloizeaux, J.; Jannink, G. Polymers in Solution. Their Modelling and Structure; Clarendon Press: Oxford, UK, 1990. [Google Scholar] [CrossRef]
- DiMarzio, E.A. Statistics of Orientation Effects in Linear Polymer Molecules. J. Chem. Phys. 1961, 35, 658–669. [Google Scholar] [CrossRef]
- Guggenheim, E.A. Statistical Thermodynamics of Mixtures with Zero Energies of Mixing. Proc. R. Soc. A 1944, A183, 203–212. [Google Scholar] [CrossRef]
- Romá, F.; Riccardo, J.L.; Ramirez-Pastor, A.J. Semiempirical Model for Adsorption of Polyatomics. Langmuir 2006, 22, 3192–3197. [Google Scholar] [CrossRef]
- Riccardo, J.L.; Romá, F.; Ramirez-Pastor, A.J. Fractional Statistical Theory of Adsorption of Polyatomics. Phys. Rev. Lett. 2004, 93, 186101. [Google Scholar] [CrossRef] [PubMed]
- Riccardo, J.L.; Romá, F.; Ramirez-Pastor, A.J. Generalized statistical description of adsorption of polyatomics. Appl. Surf. Sci. 2005, 252, 505–511. [Google Scholar] [CrossRef]
- Haldane, F.D.M. “Fractional statistics” in arbitrary dimensions: A generalization of the Pauli principle. Phys. Rev. Lett. 1991, 67, 937–940. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.S. Statistical distribution for generalized ideal gas of fractional-statistics particles. Phys. Rev. Lett. 1994, 73, 922–925. [Google Scholar] [CrossRef]
- Riccardo, J.L.; Romá, F.; Ramirez-Pastor, A.J. Adsorption of polyatomics: Theoretical approaches in model systems and applications. Int. J. Mod. Phys. B 2006, 20, 4709–4778. [Google Scholar] [CrossRef]
- Riccardo, J.J.; Riccardo, J.L.; Ramirez-Pastor, A.J.; Pasinetti, P.M. Multiple Exclusion Statistics. Phys. Rev. Lett. 2019, 123, 020602. [Google Scholar] [CrossRef]
- Riccardo, J.J.; Pasinetti, P.M.; Ramirez-Pastor, A.J.; Riccardo, J.L. Exclusion statistics for structured particles on topologically correlated states. I. Single species lattice gases. Phys. Rev. E 2025, 111, 014122. [Google Scholar] [CrossRef]
- Riccardo, J.J.; Pasinetti, P.M.; Ramirez-Pastor, A.J.; Riccardo, J.L. Exclusion statistics for structured particles on topologically correlated states. II. Multicomponent lattice gases. Phys. Rev. E 2025, 111, 014123. [Google Scholar] [CrossRef]
- Ramirez-Pastor, A.J.; Eggarter, T.P.; Pereyra, V.; Riccardo, J.L. Statistical thermodynamics and transport of linear adsorbates. Phys. Rev. B 1999, 59, 11027–11036. [Google Scholar] [CrossRef]
- Kasteleyn, P. Dimer Statistics and Phase Transitions. J. Math. Phys. 1963, 4, 287–293. [Google Scholar] [CrossRef]
- Temperley, H.N.V.; Fisher, M.E. Dimer problem in statistical mechanics—An exact result. Philos. Mag. 1961, 6, 1061–1063. [Google Scholar] [CrossRef]
- Fisher, M.E. Statistical mechanics of dimers on a plane lattice. Phys. Rev. 1961, 124, 1664–1672. [Google Scholar] [CrossRef]
- Phares, A.J.; Wunderlich, F.J.; Grumbine, D.W.; Curley, J.D. The entropy curves for interacting dimers on a square lattice. Phys. Lett. A 1993, 173, 365–368. [Google Scholar] [CrossRef]
- Phares, A.J.; Wunderlich, F.J. Thermodynamics of dimers on a rectangular L×M×N lattice. J. Math. Phys. 1985, 26, 2491–2499. [Google Scholar] [CrossRef]
- Phares, A.J.; Wunderlich, F.J. Thermodynamics and Molecular Freedom of Dimers on Plane Triangular Lattices. J. Math. Phys. 1986, 27, 1099–1109. [Google Scholar] [CrossRef]
- Phares, A.J.; Wunderlich, F.J. Thermodynamics and Molecular Freedom of Dimers on Plane Honeycomb and Kagomé Lattices. Nuovo C. B 1988, 301, 653–686. [Google Scholar] [CrossRef]
- Rżysko, W.; Patrykiejew, A.; Binder, K. Phase transitions in a two-dimensional lattice gas model of orientable diatomic molecules. Phys. Rev. B 2005, 72, 165416. [Google Scholar] [CrossRef]
- Wu, F.Y. Dimers on two-dimensional lattices. Int. J. Mod. Phys. B 2006, 20, 5357–5371. [Google Scholar] [CrossRef]
- Dávila, M.; Romá, F.; Riccardo, J.L.; Ramirez-Pastor, A.J. Quasi-chemical approximation for polyatomics: Statistical thermodynamics of adsorption. Surf. Sci. 2006, 600, 2011–2025. [Google Scholar] [CrossRef]
- Dávila, M.; Riccardo, J.L.; Ramirez-Pastor, A.J. Fractional statistical theory and use of quasi-chemical approximation for adsorption of interacting k-mers. Surf. Sci. 2009, 603, 683–689. [Google Scholar] [CrossRef]
- Marczewski, A.W.; Derylo-Marczewska, M.; Jaroniec, M. Energetic heterogeneity and molecular size effects in physical adsorption on solid surfaces. J. Colloid Interface Sci. 1986, 109, 310–324. [Google Scholar] [CrossRef]
- Nitta, T.; Kuro-Oka, M.; Katayama, T. An adsorption isotherm of multi-site occupancy model for heterogeneous surface. J. Chem. Eng. Jpn. 1984, 17, 45–52. [Google Scholar] [CrossRef]
- Nitta, T.; Yamaguchi, A.J. A hybrid isotherm equation for mobile molecules adsorbed on heterogeneous surface of random topography. J. Chem. Eng. Jpn. 1992, 25, 420–426. [Google Scholar] [CrossRef]
- Rudziński, W.; Lajtar, L.; Zaja̧c, J.; Wolfram, E.; Pászli, I. Ideal adsorption from binary liquid mixtures on heterogeneous solid surfaces: Equations for excess isotherms and heats of immersion. J. Colloid Interface Sci. 1983, 96, 339–359. [Google Scholar] [CrossRef]
- Rudziński, W.; Zaja̧c, J.; Hsu, C.C. Excess isotherms and heats of immersion in monolayer adsorption from binary liquid mixtures on strongly heterogeneous solid surfaces. J. Colloid Interface Sci. 1985, 103, 528–541. [Google Scholar] [CrossRef]
- Rudziński, W.; Everett, D.H. Adsorption of Gases on Heterogeneous Surfaces; Academic Press: London, UK, 1992. [Google Scholar] [CrossRef]
- Lebowitz, J.L.; Penrose, O. Rigorous Treatment of the Van Der Waals–Maxwell Theory of the Liquid–Vapor Transition. J. Math. Phys. 1966, 7, 98–113. [Google Scholar] [CrossRef]
- Lebowitz, J.L.; Penrose, O. Analytic and clustering properties of thermodynamic functions and distribution functions for classical lattice and continuum systems. Commun. Math. Phys. 1968, 11, 99–124. [Google Scholar] [CrossRef]
- Lebowitz, J.L.; Mazel, A.; Presutti, E. Liquid–Vapor Phase Transitions for Systems with Finite-Range Interactions. J. Stat. Phys. 1999, 94, 955–1025. [Google Scholar] [CrossRef]
- Mladek, B.M.; Gottwald, D.; Kahl, G.; Neumann, M.; Likos, C.N. Formation of Polymorphic Cluster Phases for a Class of Models of Purely Repulsive Soft Spheres. Phys. Rev. Lett. 2006, 96, 045701. [Google Scholar] [CrossRef]
- Finken, R.; Hansen, J.-P.; Kahl, G.; Louis, A.A. Phase separation of a multiple occupancy lattice gas. J. Phys. A 2004, 37, 577–590. [Google Scholar] [CrossRef]
- Likos, C.N. Soft matter with soft particles. Soft Matter 2006, 2, 478–498. [Google Scholar] [CrossRef] [PubMed]
- Craven, G.T.; Popov, A.V.; Hernandez, R. Stochastic dynamics of penetrable rods in one dimension: Occupied volume and spatial order. J. Chem. Phys. 2013, 138, 244901. [Google Scholar] [CrossRef] [PubMed]
- Craven, G.T.; Popov, A.V.; Hernandez, R. Structure of a Tractable Stochastic Mimic of Soft Particles. Soft Matter 2014, 10, 5350–5361. [Google Scholar] [CrossRef] [PubMed]
- Craven, G.T.; Popov, A.V.; Hernandez, R. Effective Surface Coverage of Coarse-Grained Soft Matter. J. Phys. Chem. B 2014, 118, 14092–14102. [Google Scholar] [CrossRef]
- Craven, G.T.; Popov, A.V.; Hernandez, R. Stochastic dynamics of penetrable rods in one dimension: Entangled dynamics and transport properties. J. Chem. Phys. 2015, 142, 154906. [Google Scholar] [CrossRef]
- Verberkmoes, A.; Nienhuis, B. Triangular Trimers on the Triangular Lattice: An Exact Solution. Phys. Rev. Lett. 1999, 83, 3986–3989. [Google Scholar] [CrossRef]
- Bellemans, A.; Nigam, R.K. Phase Transitions in Two-Dimensional Lattice Gases of Hard-Square Molecules. J. Chem. Phys. 1967, 46, 2922–2935. [Google Scholar] [CrossRef]
- Bellemans, A.; Nigam, R.K. Phase Transitions in the Hard-Square Lattice Gas. Phys. Rev. Lett. 1966, 16, 1038–1039. [Google Scholar] [CrossRef]
- Ree, F.H.; Chesnut, D.A. Phase Transition of a Hard-Core Lattice Gas. The Square Lattice with Nearest-Neighbor Exclusion. J. Chem. Phys. 1966, 45, 3983–4003. [Google Scholar] [CrossRef]
- Ramola, K.; Dhar, D. High-activity perturbation expansion for the hard square lattice gas. Phys. Rev. E 2012, 86, 031135. [Google Scholar] [CrossRef]
- Nath, T.; Dhar, D.; Rajesh, R. Stability of columnar order in assemblies of hard rectangles or squares. Europhys. Lett. 2016, 114, 10003. [Google Scholar] [CrossRef]
- Nath, T.; Rajesh, R. The high density phase of the k-NN hard core lattice gas model. J. Stat. Mech. 2016, 073203. [Google Scholar] [CrossRef]
- Mandal, D.; Nath, T.; Rajesh, R. Estimating the critical parameters of the hard square lattice gas model. J. Stat. Mech. 2017, 043201. [Google Scholar] [CrossRef]
- Szabelski, P.; Zysko, W.R.; Panczyk, T.; Ghijsens, E.; Tahara, K.; Tobe, Y.; Feyter, S.D. Self-assembly of molecular tripods in two dimensions: Structure and thermodynamics from computer simulations. RSC Adv. 2013, 3, 25159–25165. [Google Scholar] [CrossRef]
- Ruth, D.; Toral, R.; Holz, D.; Rickman, J.; Gunton, J. Impact of surface interactions on the phase behavior of Y-shaped molecules. Thin Solid Films 2015, 597, 188–192. [Google Scholar] [CrossRef]
- Mandal, D.; Nath, T.; Rajesh, R. Phase transitions in a system of hard Y-shaped particles on the triangular lattice. Phys. Rev. E 2018, 97, 032131. [Google Scholar] [CrossRef]
- Mao, L.; Harris, H.H.; Stine, K.J. Simple Lattice Simulation of Chiral Discrimination in Monolayers. J. Chem. Inf. Comput. Sci. 2002, 42, 1179–1184. [Google Scholar] [CrossRef]
- Barnes, B.C.; Siderius, D.W.; Gelb, L.D. Structure, Thermodynamics, and Solubility in Tetromino Fluids. Langmuir 2009, 25, 6702–6716. [Google Scholar] [CrossRef]
- Kundu, J.; Rajesh, R. Phase transitions in systems of hard rectangles with non-integer aspect ratio. Eur. Phys. J. B 2015, 88, 133. [Google Scholar] [CrossRef]
- Kundu, J.; Rajesh, R. Asymptotic behavior of the isotropic-nematic and nematic-columnar phase boundaries for the system of hard rectangles on a square lattice. Phys. Rev. E 2015, 91, 012105. [Google Scholar] [CrossRef]
- Kundu, J.; Rajesh, R. Phase transitions in a system of hard rectangles on the square lattice. Phys. Rev. E 2014, 89, 052124. [Google Scholar] [CrossRef] [PubMed]
- Nath, T.; Kundu, J.; Rajesh, R. High-Activity Expansion for the Columnar Phase of the Hard Rectangle Gas. J. Stat. Phys. 2015, 160, 1173–1197. [Google Scholar] [CrossRef]
- Gurin, P.; Varga, S.; González-Pinto, M.; Martínez-Ratón, Y.; Velasco, E. Ordering of hard rectangles in strong confinement. J. Chem. Phys. 2017, 146, 134503. [Google Scholar] [CrossRef]
- Rodrigues, N.T.; Stilck, J.F.; Oliveira, T.J. Entropy of fully packed rigid rods on generalized Husimi trees: A route to the square-lattice limit. Phys. Rev. E 2022, 105, 024132. [Google Scholar] [CrossRef]
- Dhar, D.; Rajesh, R.; Stilck, J.F. Hard rigid rods on a Bethe-like lattice. Phys. Rev. E 2011, 84, 011140. [Google Scholar] [CrossRef]
- Kundu, J.; Rajesh, R. Reentrant disordered phase in a system of repulsive rods on a Bethe-like lattice. Phys. Rev. E 2013, 88, 012134. [Google Scholar] [CrossRef]
- Dantas, W.G.; Oliveira, T.J.; Stilck, J.F.; Prellberg, T. Grand-canonical solution of semiflexible self-avoiding trails on the Bethe lattice. Phys. Rev. E 2017, 95, 022132. [Google Scholar] [CrossRef]
- Clark, A. The Theory of Adsorption and Catalysis; Academic Press: New York, NY, USA, 1970. [Google Scholar][Green Version]
- Gregg, S.J.; Sing, K.S.W. Adsorption, Surface Area, and Porosity; Academic Press: New York, NY, USA, 1991. [Google Scholar][Green Version]
- Adamson, A.W. Physical Chemistry of Surfaces; John Wiley and Sons: New York, NY, USA, 1990. [Google Scholar][Green Version]
- Steele, W.A. The Interaction of Gases with Solid Surfaces; Pergamon Press: New York, NY, USA, 1974. [Google Scholar][Green Version]
- Frenkel, J. Kinetic Theory of Liquids; Dover Reprint: New York, NY, USA, 1955. [Google Scholar][Green Version]
- Halsey, G.D. Physical Adsorption on Non-Uniform Surfaces. J. Chem. Phys. 1948, 16, 931–937. [Google Scholar] [CrossRef]
- Hill, T.L. Theory of Physical Adsorption. Adv. Catal. 1952, 4, 211–258. [Google Scholar] [CrossRef]
- McMillan, W.G.; Teller, E. The Role of Surface Tension in Multilayer Gas Adsorption. J. Chem. Phys. 1951, 19, 25–32. [Google Scholar] [CrossRef]
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of Gases in Multimolecular Layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- Pierce, C.; Ewing, B. Areas of Uniform Graphite Surfaces. J. Phys. Chem. 1964, 68, 2562–2568. [Google Scholar] [CrossRef]
- Hill, T.L. An Introduction to Statistical Thermodynamics; Addison-Wesley: Reading, MA, USA, 1960. [Google Scholar][Green Version]
- Patrykiejew, A.; Sokolowski, S. Statistical mechanics of adsorption of polyatomic molecules on solid surfaces. Adv. Colloid Interface Sci. 1989, 30, 203–334. [Google Scholar] [CrossRef]
- Koningsveld, R.; Stockmayer, W.H.; Nies, E. Polymer Phase Diagrams; Oxford University Press: Oxford, UK, 2001. [Google Scholar] [CrossRef]
- de Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University Press: London, UK, 1979. [Google Scholar]
- Gujrati, P.D. Ordering Field, Order Parameter, and Self-Avoiding Walks. Phys. Rev. Lett. 1984, 53, 2453–2456. [Google Scholar] [CrossRef]
- Gujrati, P.D. Bethe or Bethe-like Lattice Calculations Are More Reliable Than Conventional Mean-Field Calculations. Phys. Rev. Lett. 1995, 74, 809–812. [Google Scholar] [CrossRef]
- Gujrati, P.D.; Chhajer, M. New statistical mechanical treatment of systems near surfaces. I. Theory and principles. J. Chem. Phys. 1997, 106, 5599–5614. [Google Scholar] [CrossRef]
- De Los Rios, P.; Lise, S.; Pelizzola, A. Bethe approximation for self-interacting lattice trees. Europhys. Lett. 2001, 53, 176–182. [Google Scholar] [CrossRef]
- Binder, K. Critical Behavior at Surfaces. In Phase Transitions and Critical Phenomena; Domb, C., Lebowitz, J., Eds.; Academic Press: New York, NY, USA, 1983; Volume 8, pp. 1–144. [Google Scholar]
- Gujrati, P.D. On the absence of the completely ordered phase in the Flory model of semi-flexible linear polymers. J. Phys. A Math. Gen. 1980, 13, L437–L442. [Google Scholar] [CrossRef]
- Gujrati, P.D.; Goldstein, M. On the validity of the Flory–Huggins approximation for semiflexible chains. J. Chem. Phys. 1981, 74, 2596–2603. [Google Scholar] [CrossRef]
- Gujrati, P.D. Lower bounds on entropy for polymer chains on a square and a cubic lattice. J. Stat. Phys. 1982, 28, 441–472. [Google Scholar] [CrossRef]
- Ramirez-Pastor, A.J.; Pereyra, V.D.; Riccardo, J.L. Statistical Thermodynamics of Linear Adsorbates in Low Dimensions: Application to Adsorption on Heterogeneous Surfaces. Langmuir 1999, 15, 5707–5712. [Google Scholar] [CrossRef]
- Romá, F.; Ramirez-Pastor, A.J.; Riccardo, J.L. Multisite Occupancy Adsorption: Comparative Study of New Different Analytical Approaches. Langmuir 2003, 19, 6770–6777. [Google Scholar] [CrossRef]
- Romá, F.; Ramirez-Pastor, A.J.; Riccardo, J.L. Configurational Entropy in k-mer Adsorption. Langmuir 2000, 16, 9406–9409. [Google Scholar] [CrossRef]
- Romá, F.; Ramirez-Pastor, A.J.; Riccardo, J.L. Configurational entropy for adsorbed linear species (k-mers). J. Chem. Phys. 2001, 114, 10932–10937. [Google Scholar] [CrossRef]
- Maltz, A.; Mola, E.E. Pair site occupation probability for one-dimensional array of dumbbells. J. Math. Phys. 1981, 22, 1746–1748. [Google Scholar] [CrossRef]
- Matoz-Fernandez, D.A.; Dávila, M.; Pasinetti, P.M.; Ramirez-Pastor, A.J. A semiempirical model for adsorption of binary mixtures. Phys. Chem. Chem. Phys. 2014, 15, 24063–24068. [Google Scholar] [CrossRef]
- Matoz-Fernandez, D.A.; Ramirez-Pastor, A.J. Adsorption preference reversal phenomenon frommultisite-occupancy theory for two-dimensional lattices. Chem. Phys. Lett. 2014, 610–611, 131–134. [Google Scholar] [CrossRef]
- Peterson, H.T.; Martire, D.E.; Cotter, M.A. Lattice model for a binary mixture of hard rods of different lengths. Application to solute induced nematic→isotropic transitions. J. Chem. Phys. 1974, 61, 3547–3555. [Google Scholar] [CrossRef]
- Dávila, M.; Riccardo, J.L.; Ramirez-Pastor, A.J. Exact statistical thermodynamics of alkane binary mixtures in zeolites: New interpretation of the adsorption preference reversal phenomenon from multisite-occupancy theory. Chem. Phys. Lett. 2009, 477, 402–405. [Google Scholar] [CrossRef]
- Riccardo, J.L.; Ramirez-Pastor, A.J.; Romá, F. Multilayer Adsorption with Multisite Occupancy: An Improved Isotherm for Surface Characterization. Langmuir 2002, 18, 2130–2134. [Google Scholar] [CrossRef]
- Romá, F.; Ramirez-Pastor, A.J.; Riccardo, J.L. A new theoretical approach to multilayer adsorption of polyatomics. Surf. Sci. 2005, 583, 213–228. [Google Scholar] [CrossRef]
- Patrykiejew, A.; Sokolowski, S.; Binder, K. Phase transitions in adsorbed layers formed on crystals of square and rectangular surface lattice. Surf. Sci. Rep. 2000, 37, 207–344. [Google Scholar] [CrossRef]
- Plischke, M.; Bergersen, B. Equilibrium Statistical Physics; Prentice Hall: Upper Saddle River, NJ, USA, 1989. [Google Scholar] [CrossRef]
- Goldenfeld, N. Lectures on Phase Transitions and the Renormalization Group; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar] [CrossRef]
- Yeomans, J.M. Statistical Mechanics of Phase Transitions; Clarendon Press: Oxford, UK, 1992. [Google Scholar]
- Friedli, S.; Velenik, Y. Statistical Mechanics of Lattice Systems: A Concrete Mathematical Introduction; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar] [CrossRef]
- Ising, E. Beitrag zur Theorie des Ferromagnetismus. Z. Phys. 1925, 31, 253–258. [Google Scholar] [CrossRef]
- Domb, C. Series Expansions for Lattice Models. In Phase Transitions and Critical Phenomena; Domb, C., Green, M.S., Eds.; Academic Press: London, UK, 1974; Volume 3, pp. 1–95. [Google Scholar]
- Fisher, M.E. The theory of equilibrium critical phenomena. Rep. Prog. Phys. 1967, 30, 615–730. [Google Scholar] [CrossRef]
- Onsager, L. Crystal Statistics. I. A Two-Dimensional Model with an Order-Disorder Transition. Phys. Rev. 1944, 65, 117–149. [Google Scholar] [CrossRef]
- Bethe, H.A. Statistical theory of superlattices. Proc. R. Soc. A 1935, A150, 552–575. [Google Scholar] [CrossRef]
- Dávila, M.; Pasinetti, P.M.; Matoz-Fernandez, D.A.; Ramirez-Pastor, A.J. Quasi-chemical approximation for polyatomic mixtures. Phys. Chem. Chem. Phys. 2016, 18, 24912–24921. [Google Scholar] [CrossRef]
- Quiroga, E.; Ramirez-Pastor, A.J. Statistical thermodynamics of molecules with multiple adsorption states: Application to protein adsorption. Chem. Phys. Lett. 2013, 556, 330–335. [Google Scholar] [CrossRef]
- Bruscolini, P.; Buzano, C.; Pelizzola, A.; Pretti, M. Bethe approximation for a model of polymer solvation. Chem. Phys. Lett. 2001, 64, 050801(R). [Google Scholar] [CrossRef]
- Dhar, D.; Rajesh, R. Entropy of fully packed hard rigid rods on d-dimensional hypercubic lattices. Phys. Rev. E 2021, 103, 042130. [Google Scholar] [CrossRef]
- Rodrigues, L.R.; Stilck, J.F.; Dantas, W.G. Entropy of rigid k-mers on a square lattice. Phys. Rev. E 2023, 107, 014115. [Google Scholar] [CrossRef] [PubMed]
- Flory, P.J. Molecular Size Distribution in Three Dimensional Polymers. I. Gelation. J. Am. Chem. Soc. 1941, 63, 3083–3090. [Google Scholar] [CrossRef]
- De Los Rios, P.; Caldarelli, G. Cold and Warm Swelling of Hydrophobic Polymers. Phys. Rev. E 2001, 63, 031802. [Google Scholar] [CrossRef] [PubMed]
- Lambert, J.H. Observationes variae in mathesin puram. Acta Helv.-Phys.-Math.-Anatonico-Bot.-Medica 1758, 3, 128–168. [Google Scholar]
- Scott, T.C.; Aubert-Frécon, M.; Grotendorst, J. New approach for the electronic energies of the hydrogen molecular ion. Chem. Phys. 2006, 324, 323–338. [Google Scholar] [CrossRef]
- Scott, T.C.; Lüchow, A.; Bressanini, D.; Morgan, J.D. Nodal surfaces of helium atom eigenfunctions. Phys. Rev. A 2007, 75, 060101(R). [Google Scholar] [CrossRef]
- Farrugi, P.S.; Mann, R.B.; Scott, T.C. N-body gravity and the Schrödinger equation. Class. Quantum Grav. 2007, 24, 4647–4659. [Google Scholar] [CrossRef]
- Ghosh, A.; Dhar, D. On the orientational ordering of long rods on a lattice. Eur. Phys. Lett. 2007, 78, 20003. [Google Scholar] [CrossRef]
- Matoz-Fernandez, D.A.; Linares, D.H.; Ramirez-Pastor, A.J. Determination of the critical exponents for the isotropic-nematic phase transition in a system of long rods on two-dimensional lattices: Universality of the transition. Eur. Phys. Lett. 2008, 82, 50007. [Google Scholar] [CrossRef]
- Matoz-Fernandez, D.A.; Linares, D.H.; Ramirez-Pastor, A.J. Critical behavior of long straight rigid rods on two-dimensional lattices: Theory and Monte Carlo simulations. J. Chem. Phys. 2008, 128, 214902. [Google Scholar] [CrossRef]
- Matoz-Fernandez, D.A.; Linares, D.H.; Ramirez-Pastor, A.J. Critical behavior of long linear k-mers on honeycomb lattices. Physica A 2008, 387, 6513–6525. [Google Scholar] [CrossRef]
- Disertori, M.; Giuliani, A. The Nematic Phase of a System of Long Hard Rods. Commun. Math. Phys. 2013, 323, 143–175. [Google Scholar] [CrossRef]
- Kundu, J.; Rajesh, R.; Dhar, D.; Stilck, J.F. Nematic-disordered phase transition in systems of long rigid rods on two-dimensional lattices. Phys. Rev. E 2013, 87, 032103. [Google Scholar] [CrossRef]
- Chatelain, C.; Gendiar, A. Absence of logarithmic divergence of the entanglement entropies at the phase transitions of a 2D classical hard rod model. Eur. Phys. J. B 2020, 93, 134. [Google Scholar] [CrossRef]
- Vogel, E.E.; Saravia, G.; Ramirez-Pastor, A.J. Phase transitions in a system of long rods on two-dimensional lattices by means of information theory. Phys. Rev. E 2017, 96, 062133. [Google Scholar] [CrossRef]
- Vogel, E.E.; Saravia, G.; Ramirez-Pastor, A.J.; Pasinetti, M. Alternative characterization of the nematic transition in deposition of rods on two-dimensional lattices. Phys. Rev. E 2020, 101, 022104. [Google Scholar] [CrossRef]
- Shah, A.; Dhar, D.; Rajesh, R. Phase transition from nematic to high-density disordered phase in a system of hard rods on a lattice. Phys. Rev. E 2022, 105, 034103. [Google Scholar] [CrossRef]
- Pasinetti, P.M.; Ramirez-Pastor, A.J.; Vogel, E.E.; Saravia, G. Entropy-driven phases at high coverage adsorption of straight rigid rods on two-dimensional square lattices. Phys. Rev. E 2021, 104, 054136. [Google Scholar] [CrossRef]
- Centres, P.M.; Ramirez-Pastor, A.J. Configurational entropy of adsorbed rigid rods: Theory and Monte Carlo simulations. Physica A 2009, 388, 2001–2019. [Google Scholar] [CrossRef]
- De La Cruz Feliz, N.M.; De La Cruz Félix, N.; Quiroga, E.; Riccardo, J.J.; Riccardo, J.L.; Ramirez Pastor, A.J. Fractional Statistics Description Applied to Adsorption of Trimers on Triangular Lattices. in preparation.
- Kundu, J.; Rajesh, R.; Dhar, D.; Stilck, J.F. A Monte Carlo Algorithm for Studying Phase Transition in Systems of Hard Rigid Rods. AIP Conf. Proc. 2012, 1447, 113–114. [Google Scholar] [CrossRef]
- Nath, T. Phase Behaviour and Ordering in Hard Core Lattice Gas Models. PhD. Thesis, The Institute of Mathematical Sciences, Chennai, India, 2016. PHYS10201104002. Available online: http://www.hbni.ac.in/phdthesis/phys/PHYS10201104002.pdf (accessed on 8 May 2025).
- Costa, E.; Sotelo, J.; Calleja, G.; Marron, C. Adsorption of binary and ternary hydrocarbon gas mixtures on activated carbon: Experimental determination and theoretical prediction of the ternary equilibrium data. AIChE J. 1981, 27, 5–12. [Google Scholar] [CrossRef]
- Chaer Nascimento, M.A. Theoretical Aspects of Heterogeneous Catalysis; Kluwer Academic Publishers: Boston, MA, USA, 2002. [Google Scholar]
- Ramirez-Pastor, A.J.; Riccardo, J.L.; Pereyra, V.D. Monte Carlo study of dimer adsorption at monolayer on square lattices. Surf. Sci. 1998, 411, 294–302. [Google Scholar] [CrossRef]
- González, J.E.; Ramirez-Pastor, A.J.; Pereyra, V.D. Adsorption of Dimer Molecules on Triangular and Honeycomb Lattices. Langmuir 2001, 17, 6974–6980. [Google Scholar] [CrossRef]
- Tarek, M.; Kahn, R.; Cohen de Lara, E. Modelization of experimental isotherms of n-alkanes in NaX zeolite. Zeolites 1995, 15, 67–72. [Google Scholar] [CrossRef]
- Miller, G.W.; Knaebel, K.S.; Ikels, K.G. Equilibria of nitrogen, oxygen, argon, and air in molecular sieve 5A. AIChE J. 1987, 33, 194–201. [Google Scholar] [CrossRef]
- Danner, R.P.; Wenzel, L.A. Adsorption of carbon monoxide-nitrogen, carbon monoxide-oxygen, and oxygen-nitrogen mixtures on synthetic zeolites. AIChE J. 1969, 15, 515–520. [Google Scholar] [CrossRef]
- Ramirez-Pastor, A.J.; Nazzarro, M.S.; Riccardo, J.L.; Zgrablich, G. Dimer physisorption on heterogeneous substrates. Surf. Sci. 1995, 341, 249–261. [Google Scholar] [CrossRef]
- Razmus, D.; Hall, C. Prediction of Gas Adsorption in 5A Zeolites Using Monte Carlo Simulation. AIChE J. 1991, 37, 769–779. [Google Scholar] [CrossRef]
- Abdul-Reham, H.B.; Loughlin, K.F. Quaternary, Ternary, Binary, and Pure Component Sorption on Zeolites. 1. Light Alkanes on Linde S-115 Silicalite at Moderate to High Pressures. Ind. Eng. Chem. Res. 1990, 29, 1525–1535. [Google Scholar] [CrossRef]
- Du, Z.; Manos, G.; Vlugt, T.J.H.; Smit, B. Molecular simulation of adsorption of short linear alkanes and their mixtures in silicalite. AIChE J. 1998, 44, 1756–1764. [Google Scholar] [CrossRef]
- Krishna, R.; Smit, B.; Calero, S. Entropy effects during sorption of alkanes in zeolites. Chem. Soc. Rev. 2002, 31, 185–194. [Google Scholar] [CrossRef] [PubMed]
- Macedonia, M.; Maginn, E.J. Pure and binary component sorption equilibria of light hydrocarbons in the zeolite silicalite from grand canonical Monte Carlo simulations. Fluid Phase Equilibria 1999, 158–160, 19–27. [Google Scholar] [CrossRef]
- Denayer, J.F.M.; Ocakoglu, R.; Huybrechts, W.; Dejonckheere, B.; Jacobs, P.; Calero, S.; Krishna, R.; Smit, B.; Baron, G.V.; Martens, J.A. High-pressure liquid phase hydroconversion of heptane/nonane mixtures on Pt/HY zeolite catalyst. J. Catal. 2003, 220, 66–73. [Google Scholar] [CrossRef]
- Krishna, R.; Baur, R. Modelling Issues in Zeolite Based Separation Processes. Sep. Purif. Technol. 2003, 33, 213–254. [Google Scholar] [CrossRef]
- Cabral, V.F.; Castier, M.; Tavares, F.W. Adsorption equilibrium of light hydrocarbon mixtures by Monte Carlo simulation. Braz. J. Chem. Eng. 2007, 24, 597–610. [Google Scholar] [CrossRef]
- Smit, B.; Maesen, T.L.M. Molecular Simulations of Zeolites: Adsorption, Diffusion, and Shape Selectivity. Chem. Rev. 2008, 108, 4125–4184. [Google Scholar] [CrossRef]
- Jiang, J.; Sandler, S.I.; Schenk, M.; Smit, B. Adsorption and separation of linear and branched alkanes on carbon nanotube bundles from configurational-bias Monte Carlo simulation. Phys. Rev. B 2005, 72, 045447. [Google Scholar] [CrossRef]
- Jiang, J.; Sandler, S.I. Monte Carlo Simulation for the Adsorption and Separation of Linear and Branched Alkanes in IRMOF-1. Langmuir 2006, 22, 5702–5707. [Google Scholar] [CrossRef]
- Khettar, A.; Jalili, S.E.; Dunne, L.J.; Manos, G.; Du, Z. Monte-Carlo simulation and mean-field theory interpretation of adsorption preference reversal in isotherms of alkane binary mixtures in zeolites at elevated pressures. Chem. Phys. Lett. 2002, 362, 414–418. [Google Scholar] [CrossRef]
- Dunne, L.J.; Manos, G.; Du, Z. Exact statistical mechanical one-dimensional lattice model of alkane binary mixture adsorption in zeolites and comparision with Monte-Carlo simulations. Chem. Phys. Lett. 2003, 377, 551–556. [Google Scholar] [CrossRef]
- Lide, D.R. CRC Handbook of Chemistry and Physics, 88th ed.; Internet Version 2008; CRC Press/Taylor and Francis: Boca Raton, FL, USA, 2008. [Google Scholar]
- Ungerer, P.; Tavitian, B.; Boutin, A. Applications of Molecular Simulation in the Oil and Gas Industry: Monte Carlo Methods; Editions Technip: Paris, France, 2005. [Google Scholar]
- Silva, J.A.C.; Rodrigues, A.E. Multisite Multisite Langmuir model applied to the interpretation of sorption of n- paraffins in 5A zeolite. Ind. Eng. Chem. Res. 1999, 38, 2434–2438. [Google Scholar] [CrossRef]
- Romá, F.; Riccardo, J.L.; Ramirez-Pastor, A.J. Statistical Thermodynamics Models for Polyatomic Adsorbates: Application to Adsorption of n-Paraffins in 5A Zeolite. Langmuir 2005, 21, 2454–2459. [Google Scholar] [CrossRef] [PubMed]
- Chiang, I.W.; Brinson, B.E.; Smalley, R.E.; Margrave, J.L.; Hauge, R.H. Purification and Characterization of Single-Wall Carbon Nanotubes. J. Phys. Chem. B 2001, 105, 1157–1161. [Google Scholar] [CrossRef]
- Kuznetsova, A.; Mawhinney, D.B.; Naumenko, V.; Yates, J.T., Jr.; Liu, J.; Smalley, R.E. Enhancement of adsorption inside of single-walled nanotubes: Opening the entry ports. Chem. Phys. Lett. 2000, 321, 292–296. [Google Scholar] [CrossRef]
- Kuznetsova, A.; Yates, J.T., Jr.; Liu, J.; Smalley, R.E. Physical adsorption of xenon in open single walled carbon nanotubes: Observation of a quasi-one-dimensional confined Xe phase. J. Chem. Phys. 2000, 112, 9590–9598. [Google Scholar] [CrossRef]
- Shi, W.; Johnson, J.K. Gas Adsorption on Heterogeneous Single-Walled Carbon Nanotube Bundles. Phys. Rev. Lett. 2003, 91, 155504. [Google Scholar] [CrossRef]
- LaBrosse, M.R.; Shi, W.; Johnson, J.K. Adsorption of Gases in Carbon Nanotubes: Are Defect Interstitial Sites Important? Langmuir 2008, 24, 9430–9439. [Google Scholar] [CrossRef]
- Shrestha, P.; Alkhafaji, M.T.; Lukowitz, M.M.; Yang, G.; Migone, A.D. Adsorption Studies on Boron Nitride Substrates. Langmuir 1994, 10, 3244–3249. [Google Scholar] [CrossRef]
- Vora, P.; Sinha, S.K.; Crawford, R.K. Neutron-Diffraction Study of Phases of CD4 Monolayer Films on Graphite. Phys. Rev. Lett. 1979, 43, 704–708. [Google Scholar] [CrossRef]
- Newton, J.C.; Taub, H. Neutron diffraction study of the S2 monolayer phase of ethane physisorbed on graphite. Surf. Sci. 1996, 364, 273–278. [Google Scholar] [CrossRef]
- Matthies, B.; Herwig, K.W.; Taub, H. Acceleration schemes for ab initio molecular-dynamics simulations and electronic-structure calculations. Bull. Am. Phys. Soc. 1994, 39, 455. [Google Scholar]
- Emmett, P.H.; Brunauer, S. The Use of Low Temperature van der Waals Adsorption Isotherms in Determining the Surface Area of Iron Synthetic Ammonia Catalysts. J. Am. Chem. Soc. 1937, 59, 1553–1564. [Google Scholar] [CrossRef]
- Rouquerol, F.; Rouquerol, J.; Sing, K. Adsorption by Powders and Porous Solids; Academic Press: London, UK, 1999; Electronic version; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar] [CrossRef]
- Talapatra, S.; Migone, A.D. Adsorption of methane on bundles of closed-ended single-wall carbon nanotubes. Phys. Rev. B 2002, 65, 045416. [Google Scholar] [CrossRef]
- Rawat, D.S.; Furuhashi, T.; Migone, A.D. Study of a Butane Monolayer Adsorbed on Single-Walled Carbon Nanotubes. Langmuir 2009, 25, 973–976. [Google Scholar] [CrossRef]
- Krungleviciute, V.; Heroux, L.; Talapatra, S.; Migone, A.D. Gas Adsorption on HiPco nanotubes: Surface Area Determinations, and Neon Second Layer Data. Nano Lett. 2004, 24, 1133–1137. [Google Scholar] [CrossRef]
- Mullin, J.W. Crystallization; Butterworth-Heinemann: Oxford, UK, 2001. [Google Scholar]
- Meenan, P.A.; Anderson, S.R.; Klug, D.L. The influence of impurities and solvents on crystallization. In Handbook of Industrial Crystallization; Myerson, A.S., Ed.; Butterworth-Heinemann: Boston, MA, USA, 2002; pp. 67–100. [Google Scholar] [CrossRef]
- Chianese, A.; Kramer, H.J.M. Industrial Crystallization Process Monitoring and Control; John Wiley & Sons, Inc.: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Buckley, H.E. Crystal Growth; Wiley: New York, NY, USA, 1951. [Google Scholar]
- Bienfait, M.R.; Boistelle, R.; Kern, R. Croissance cristalline et adsorption. In Adsorption et Croissance Cristalline; Kern, R., Ed.; CNRS: Paris, France, 1965; pp. 207–266. [Google Scholar]
- Simon, B.; Boistelle, R. Crystal growth from low temperature solutions. J. Crystal Growth 1981, 52, 779–788. [Google Scholar] [CrossRef]
- Sangwal, K. Effect of impurities on the processes of crystal growth. J. Crystal Growth 1993, 128, 1236–1244. [Google Scholar] [CrossRef]
- Sangwal, K. Effects of impurities on crystal growth processes. Prog. Cryst. Growth Charact. 1996, 32, 3–43. [Google Scholar] [CrossRef]
- Kubota, N.; Yokota, M.; Doki, N.; Guzman, L.A.; Sasaki, S. A Mathematical Model for Crystal Growth Rate Hysteresis Induced by Impurity. Cryst. Growth Des. 2003, 3, 397–402. [Google Scholar] [CrossRef]
- Bliznakov, G.M. Über die Wachstumsformen der Kristalle und den Einfluß der Adsorption auf die lineare Kristallisationsgeschwindigkeit. Bull. Acad. Sci. Bulg. Ser. Phys. 1954, 4, 135–152. [Google Scholar]
- Bliznakov, G.M.; Kirkova, E. A study of the effect of sulfate ions on the growth of sodium chlorate crystals. Krist. Und Tech. 1969, 4, 331–336. [Google Scholar] [CrossRef]
- Bliznakov, G.M. Die kristalltracht und die adsorption fremder beimischungen. Fortschr. Min. 1958, 36, 149–191. [Google Scholar]
- Bliznakov, G.M. Method of Investigating the Adsorption on the Active Centers. In Adsorption et Croissance Cristalline; Kern, R., Ed.; CNRS: Paris, France, 1965; pp. 291–310. [Google Scholar]
- Cabrera, N.; Vermilyea, D.A. The Growth of Crystals from Solutions. In Growth and Perfection of Crystals; Doremus, R.H., Roberts, B.W., Turnbull, D., Eds.; Wiley: New York, NY, USA, 1958; pp. 393–408. [Google Scholar]
- Davey, R.J.; Mullin, J.W. Growth of the {100} faces of ammonium dihydrogen phosphate crystals in the presence of ionic species. J. Cryst. Growth 1974, 26, 45–51. [Google Scholar] [CrossRef]
- Kubota, N.; Mullin, J.W. A kinetic model for crystal growth from aqueous solution in the presence of impurity. J. Cryst. Growth 1995, 152, 203–208. [Google Scholar] [CrossRef]
- Langmuir, I. The adsorption of gases on plane surfaces of glass, mica, and platinum in 5A zeolite pellets. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef]
- Ilevbare, G.A.; Liu, H.; Edgarb, K.J.; Taylor, L.S. Inhibition of solution crystal growth of ritonavir by cellulose polymers - factors influencing polymer effectiveness. Cryst. Eng. Comm. 2012, 14, 6503–6514. [Google Scholar] [CrossRef]
- Bliznakov, G.M.; Nikolaeva, R.D. Über den Einfluß der aliphatischen Carbonsauren auf die Wachstumsgeschwindigkeit von KBr-Kristallen. Krist. Und Tech. 1967, 2, 161–166. [Google Scholar] [CrossRef]
- Linares, D.H.; Romá, F.; Ramirez-Pastor, A.J. Entropy-driven phase transition in a system of long rods on a square lattice. J. Stat. Mech. 2008, P03013. [Google Scholar] [CrossRef]
- Nicholson, D.; Parsonage, N.G. Computer Simulation and the Statistical Mechanics of Adsorption; Academic Press: London, UK, 1982. [Google Scholar]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.W.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Hukushima, K.; Nemoto, K. Exchange Monte Carlo Method and Application to Spin Glass Simulations. J. Phys. Soc. Jpn. 1996, 65, 1604–1608. [Google Scholar] [CrossRef]
- Hartmann, A.H.; Rieger, H. Monte Carlo Methods. In Optimization Algorithms in Physics; Hartmann, A.H., Rieger, H., Eds.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2006; pp. 260–262. Available online: https://onlinelibrary.wiley.com/doi/book/10.1002/3527600876 (accessed on 8 May 2025).
- Binder, K. Applications of the Monte Carlo method in statistical physics. In Topics in Current Physics; Binder, K., Ed.; Springer: Berlin/Heidelberg, Germany, 1984; Volume 36, pp. 1–36. Available online: https://link.springer.com/book/10.1007/978-3-642-51703-7 (accessed on 8 May 2025).
- Hansen, J.P.; Verlet, L. Phase Transitions of the Lennard-Jones System. Phys. Rev. 1969, 184, 151–161. [Google Scholar] [CrossRef]
- Binder, K. Static and dynamic critical phenomena of the two-dimensionalq-state Potts model. J. Stat. Phys. 1981, 24, 69–86. [Google Scholar] [CrossRef]
- Binder, K. Critical Properties from Monte Carlo Coarse Graining and Renormalization. Phys. Rev. Lett. 1981, 47, 693–696. [Google Scholar] [CrossRef]
- Ma, S.K. Calculation of entropy from data of motion. J. Stat. Phys. 1981, 26, 221–240. [Google Scholar] [CrossRef]
- Alexandrowicz, Z.J. Stochastic Models for the Statistical Description of Lattice Systems. J. Chem. Phys. 1971, 55, 2765–2779. [Google Scholar] [CrossRef]
- Meirovitch, H. Calculation of entropy with computer simulation methods. Chem. Phys. Lett. 1977, 45, 389–392. [Google Scholar] [CrossRef]
- Valleau, J.P.; Card, D.N. Monte Carlo Estimation of the Free Energy by Multistage Sampling. J. Chem. Phys. 1972, 57, 5457–5462. [Google Scholar] [CrossRef]
- Torrie, G.M.; Valleau, J.P. Monte Carlo free energy estimates using non-Boltzmann sampling: Application to the sub-critical Lennard-Jones fluid. Chem. Phys. Lett. 1974, 28, 578–581. [Google Scholar] [CrossRef]
- Torrie, G.M.; Valleau, J.P. Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar] [CrossRef]
- Torrie, G.M.; Valleau, J.P. Monte Carlo study of a phase-separating liquid mixture by umbrella sampling. J. Chem. Phys. 1977, 66, 1402–1408. [Google Scholar] [CrossRef]
- Salsburg, Z.W.; Jacobsen, J.; Fickett, W.; Wood, W.W. Application of the Monte Carlo Method to the Lattice-Gas Model. I. Two-Dimensional Triangular Lattice. J. Chem. Phys. 1959, 30, 65–72. [Google Scholar] [CrossRef]
- de Koning, M.; Antonelli, A.; Yip, S. Optimized Free-Energy Evaluation Using a Single Reversible-Scaling Simulation. Phys. Rev. Lett. 1999, 83, 3973–3977. [Google Scholar] [CrossRef]









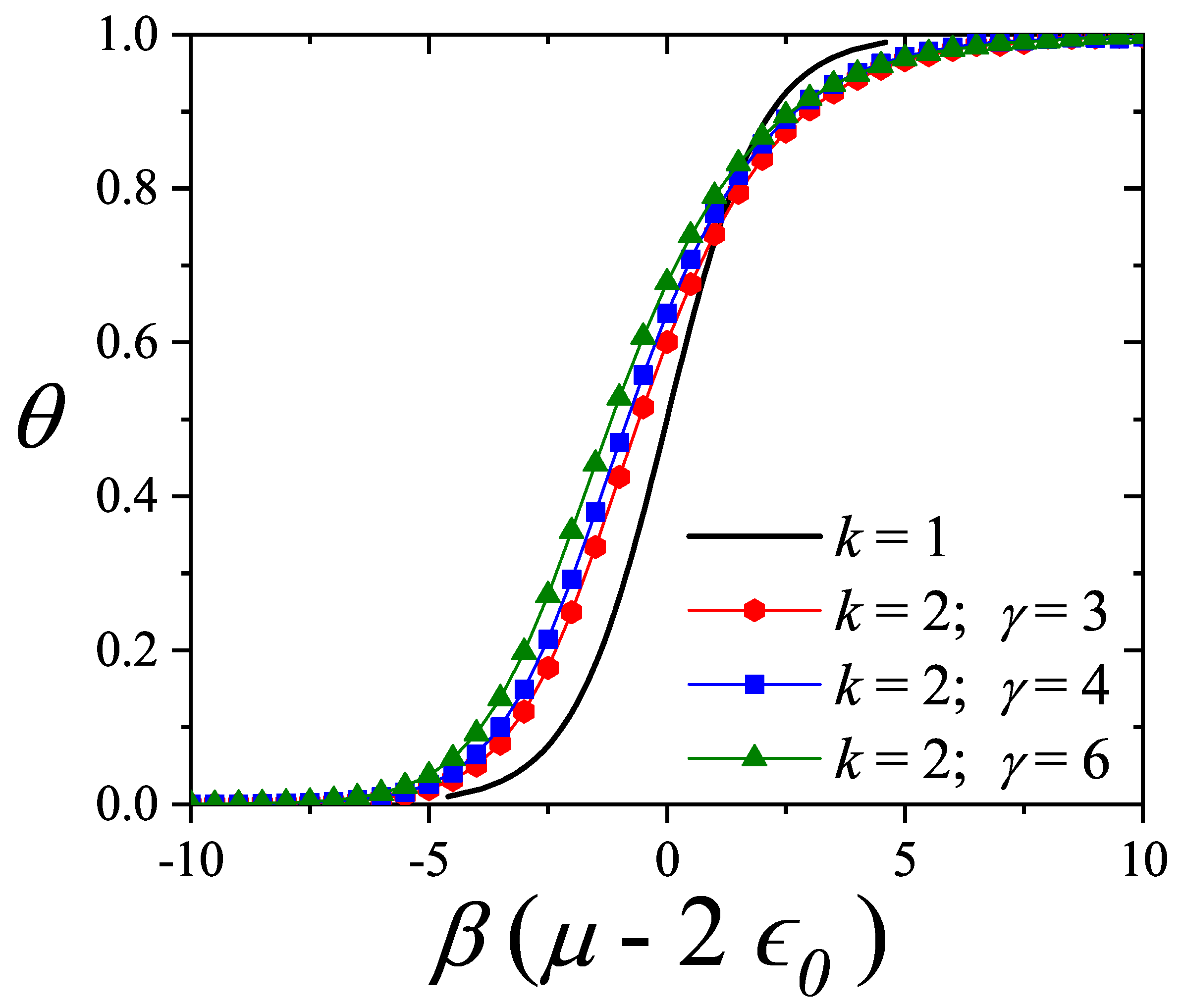


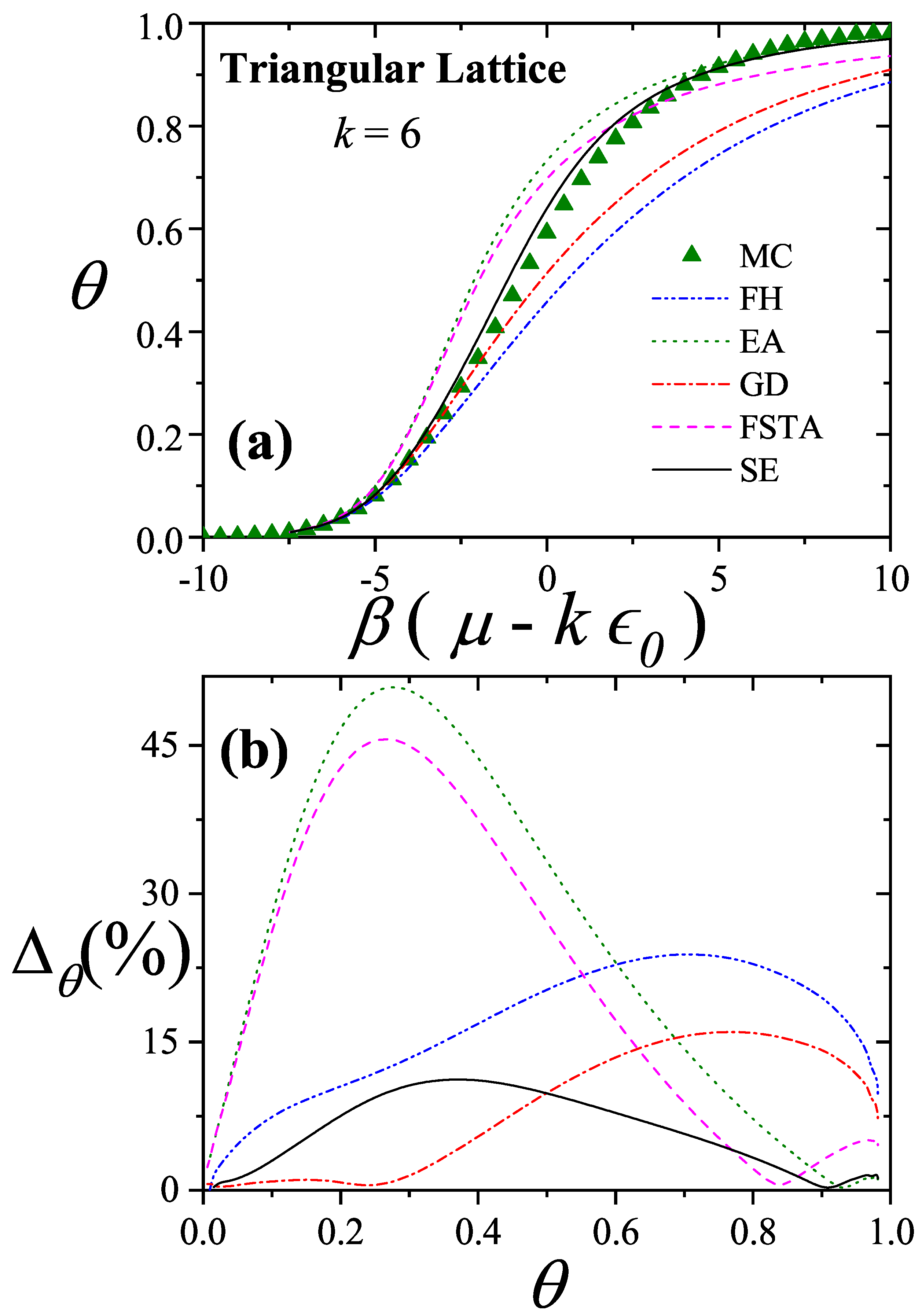


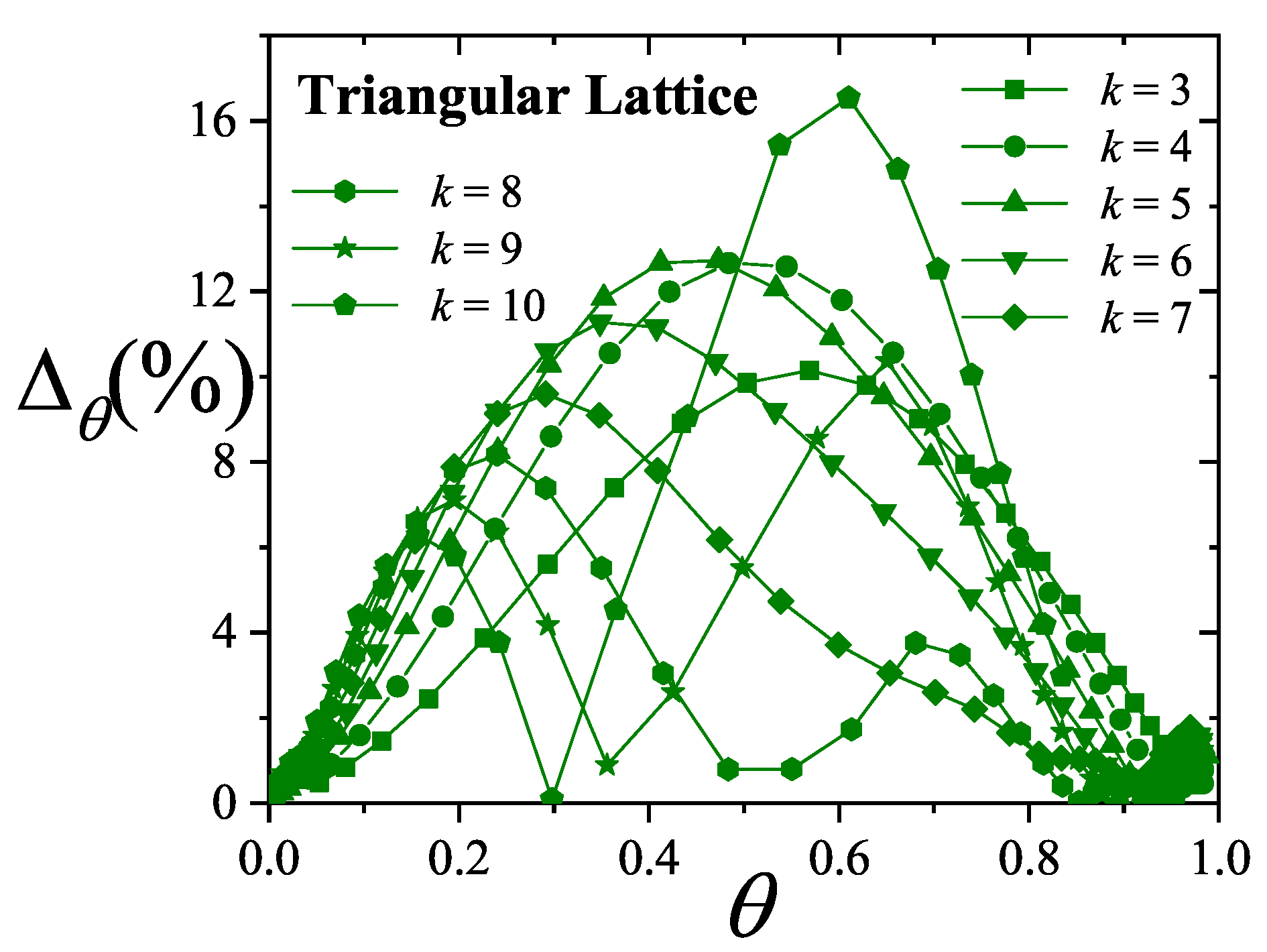

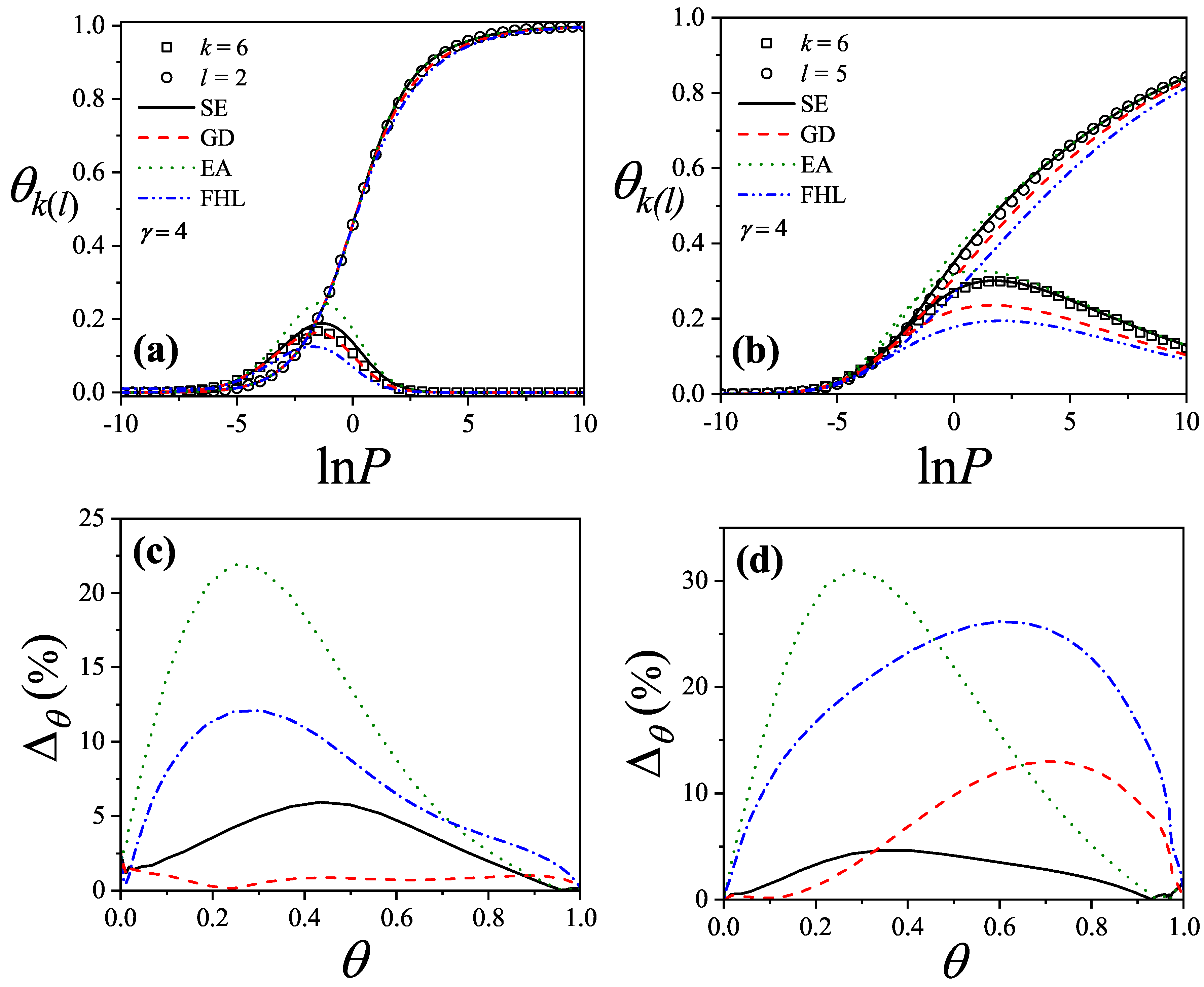







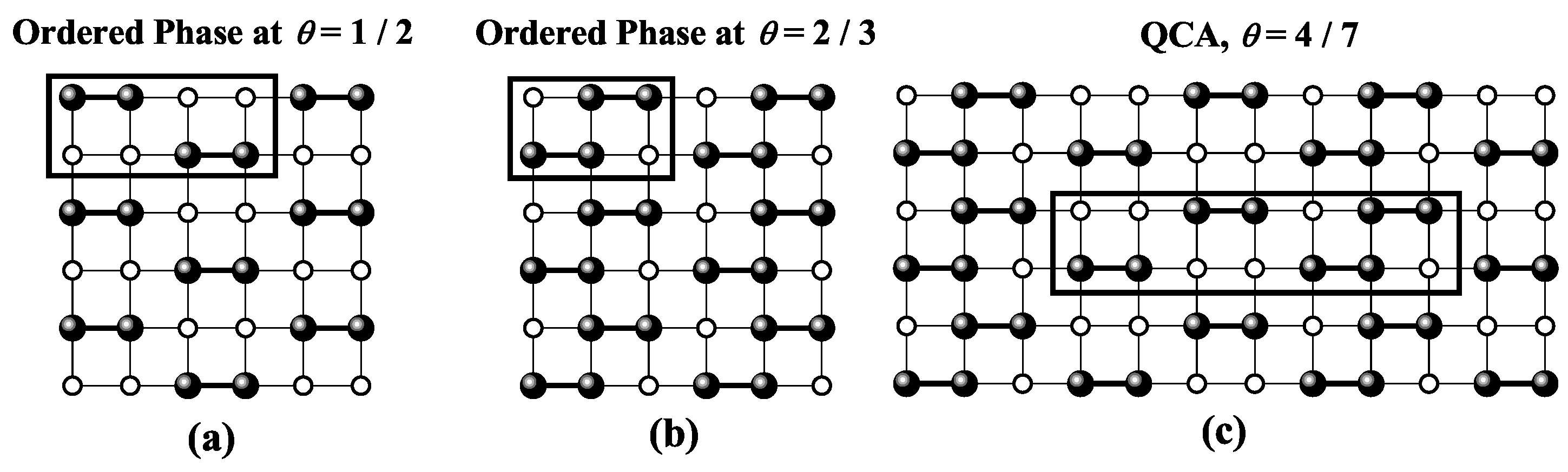
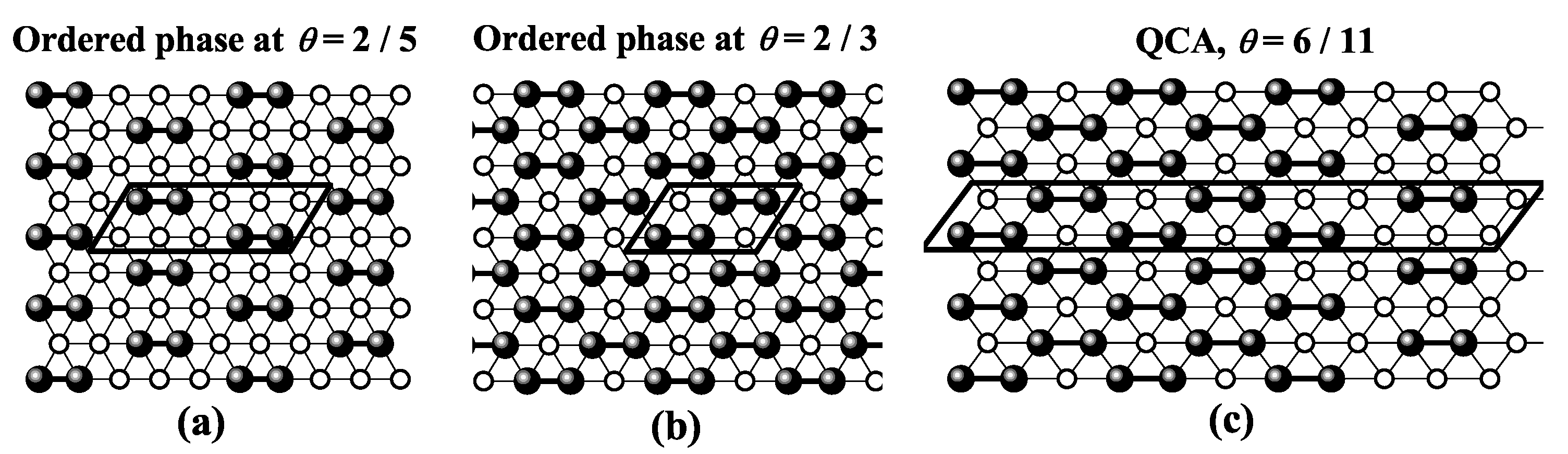





















| / | / | |
|---|---|---|
| (mol./g) | 0.41 | 0.41 |
| () | 3.5 | 0.48 |
| () | 1.6 | 0.6 |
| Sample | Type | Weight (g) | Gas | Area/mol on Graphite () | Isotherm Temp (K) |
|---|---|---|---|---|---|
| SWNTs | HiPco | 0.1727 | methane | 15.4 [170] | 77 |
| SWNTs | HiPco | 0.325 | ethane | 21 [171] | 165 |
| SWNTs | HiPco | 0.325 | propane | 28.8 [172] | 190 |
| SWNTs | HiPco | 0.325 | butane | 32.7 [171] | 220 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riccardo, J.J.; Pasinetti, P.M.; Riccardo, J.L.; Ramirez-Pastor, A.J. Statistical Mechanics of Linear k-mer Lattice Gases: From Theory to Applications. Entropy 2025, 27, 750. https://doi.org/10.3390/e27070750
Riccardo JJ, Pasinetti PM, Riccardo JL, Ramirez-Pastor AJ. Statistical Mechanics of Linear k-mer Lattice Gases: From Theory to Applications. Entropy. 2025; 27(7):750. https://doi.org/10.3390/e27070750
Chicago/Turabian StyleRiccardo, Julian Jose, Pedro Marcelo Pasinetti, Jose Luis Riccardo, and Antonio Jose Ramirez-Pastor. 2025. "Statistical Mechanics of Linear k-mer Lattice Gases: From Theory to Applications" Entropy 27, no. 7: 750. https://doi.org/10.3390/e27070750
APA StyleRiccardo, J. J., Pasinetti, P. M., Riccardo, J. L., & Ramirez-Pastor, A. J. (2025). Statistical Mechanics of Linear k-mer Lattice Gases: From Theory to Applications. Entropy, 27(7), 750. https://doi.org/10.3390/e27070750







