Pre-Warning for the Remaining Time to Alarm Based on Variation Rates and Mixture Entropies
Abstract
1. Introduction
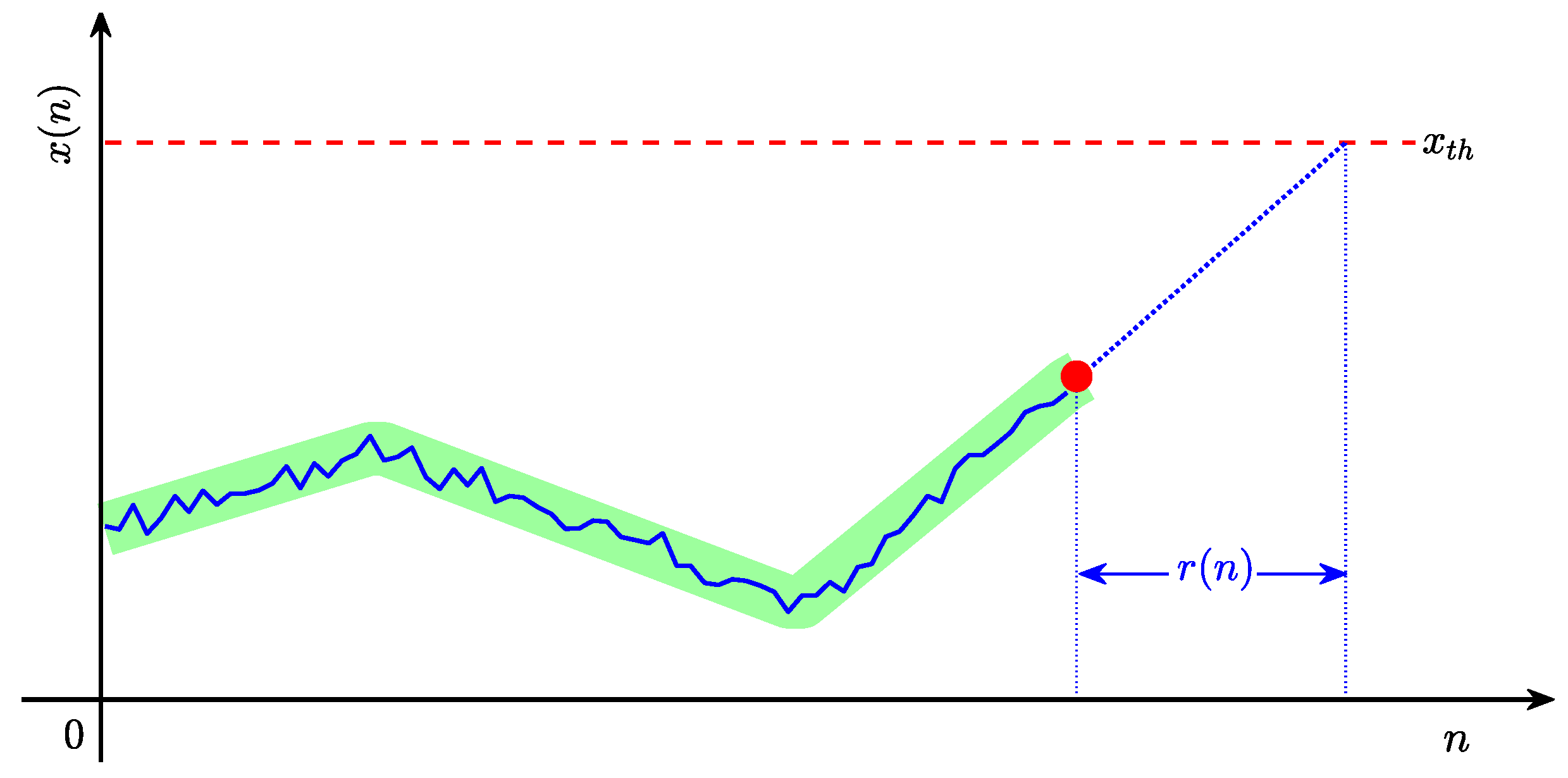
2. Problem Description
3. The Proposed Method
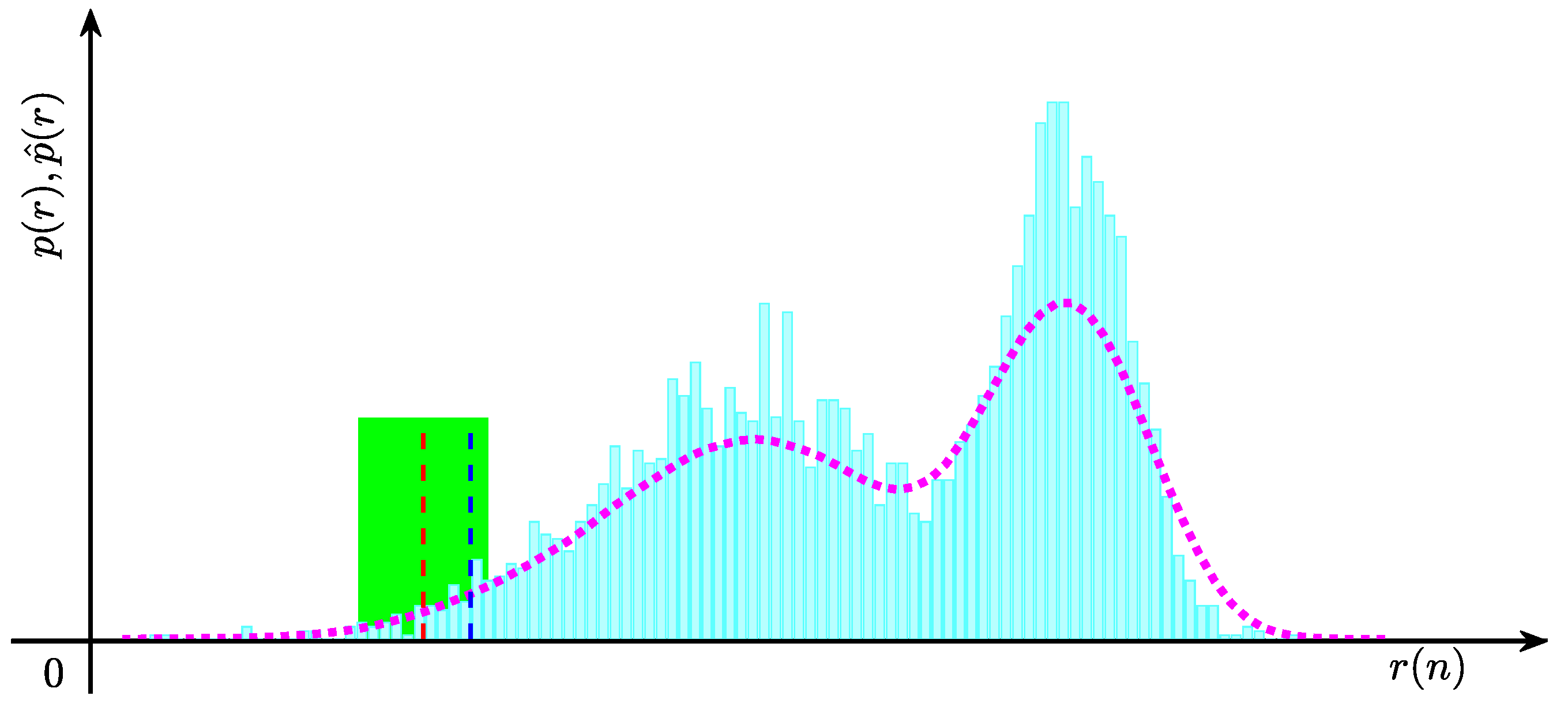
3.1. Determining the Optimal Pre-Warning Threshold
3.2. Extracting Features from an Historical Data Sequence
3.3. Generating Pre-Warnings by Combining the Mixture Entropies
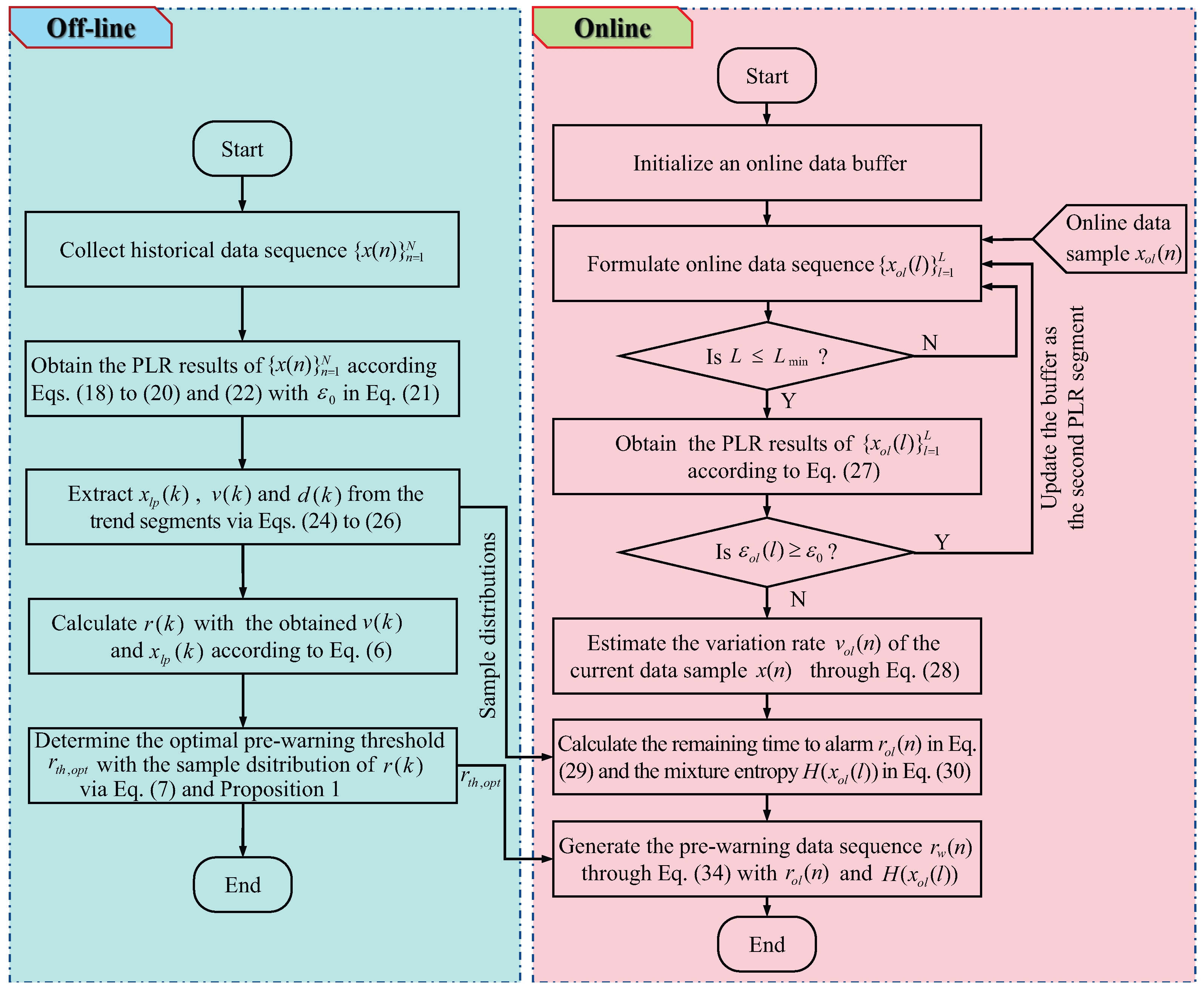
3.4. Summary of the Proposed Method
| Algorithm 1: Pre-warning for the remaining time to alarm |
 |
4. Examples
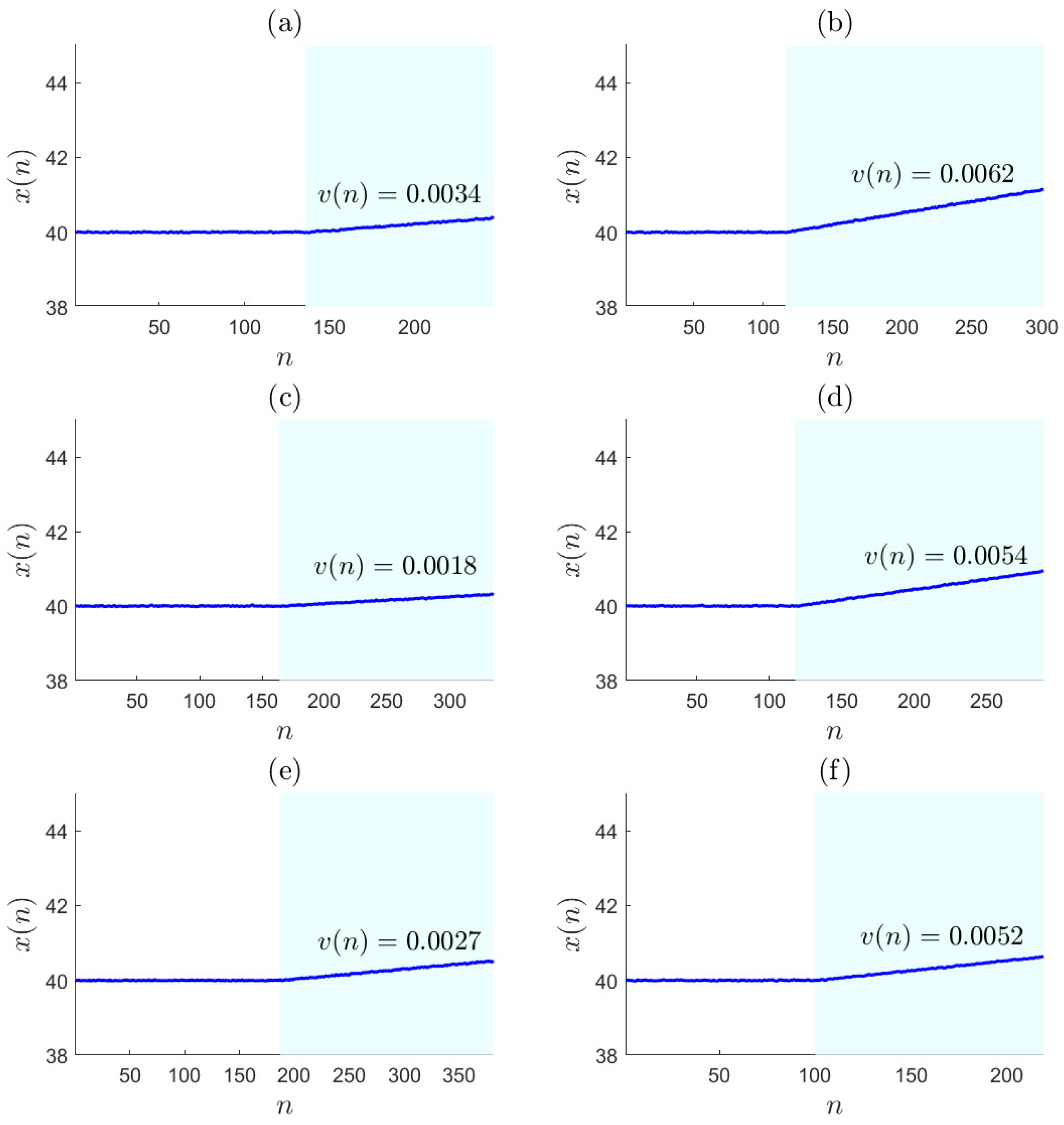
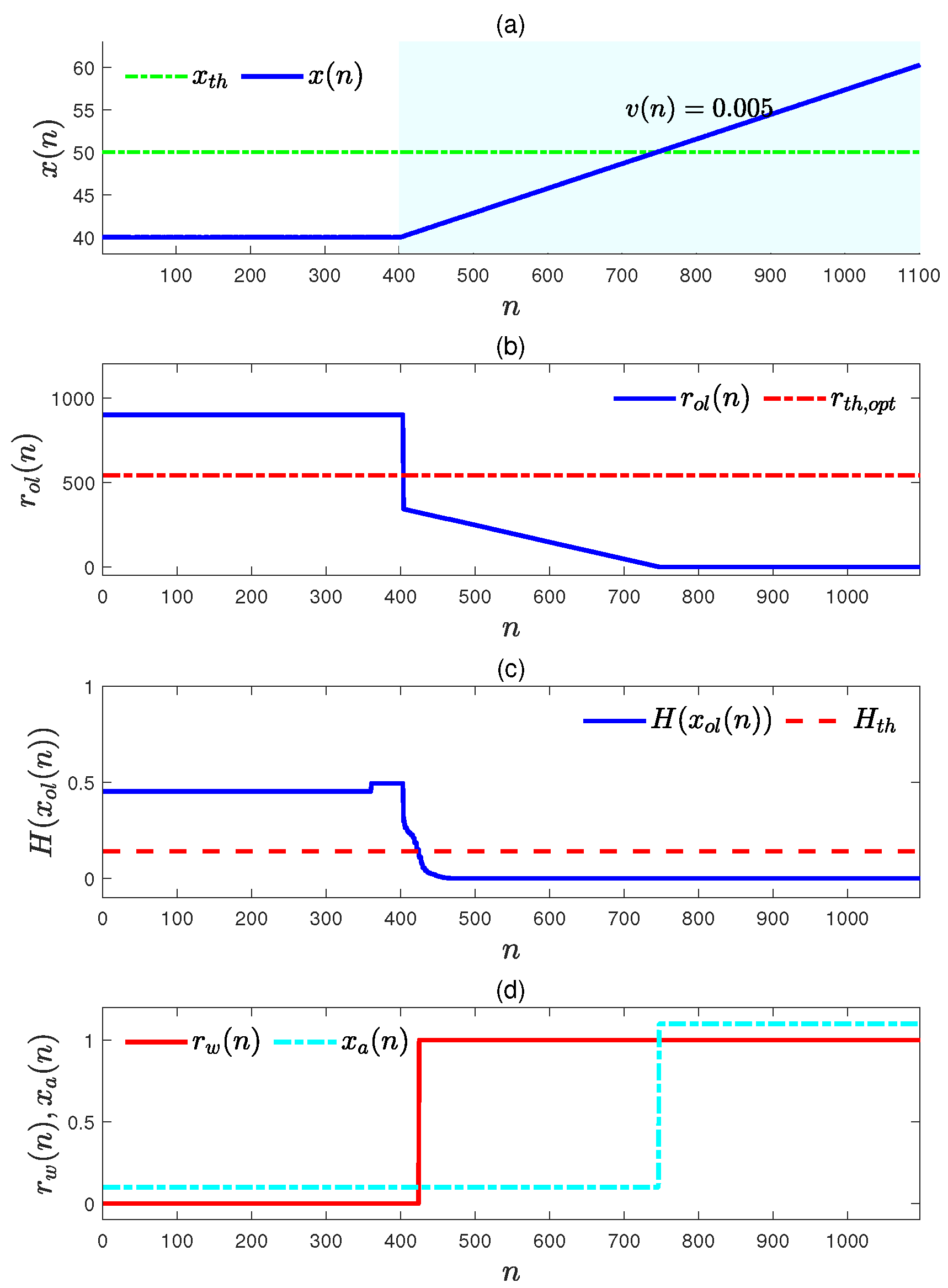
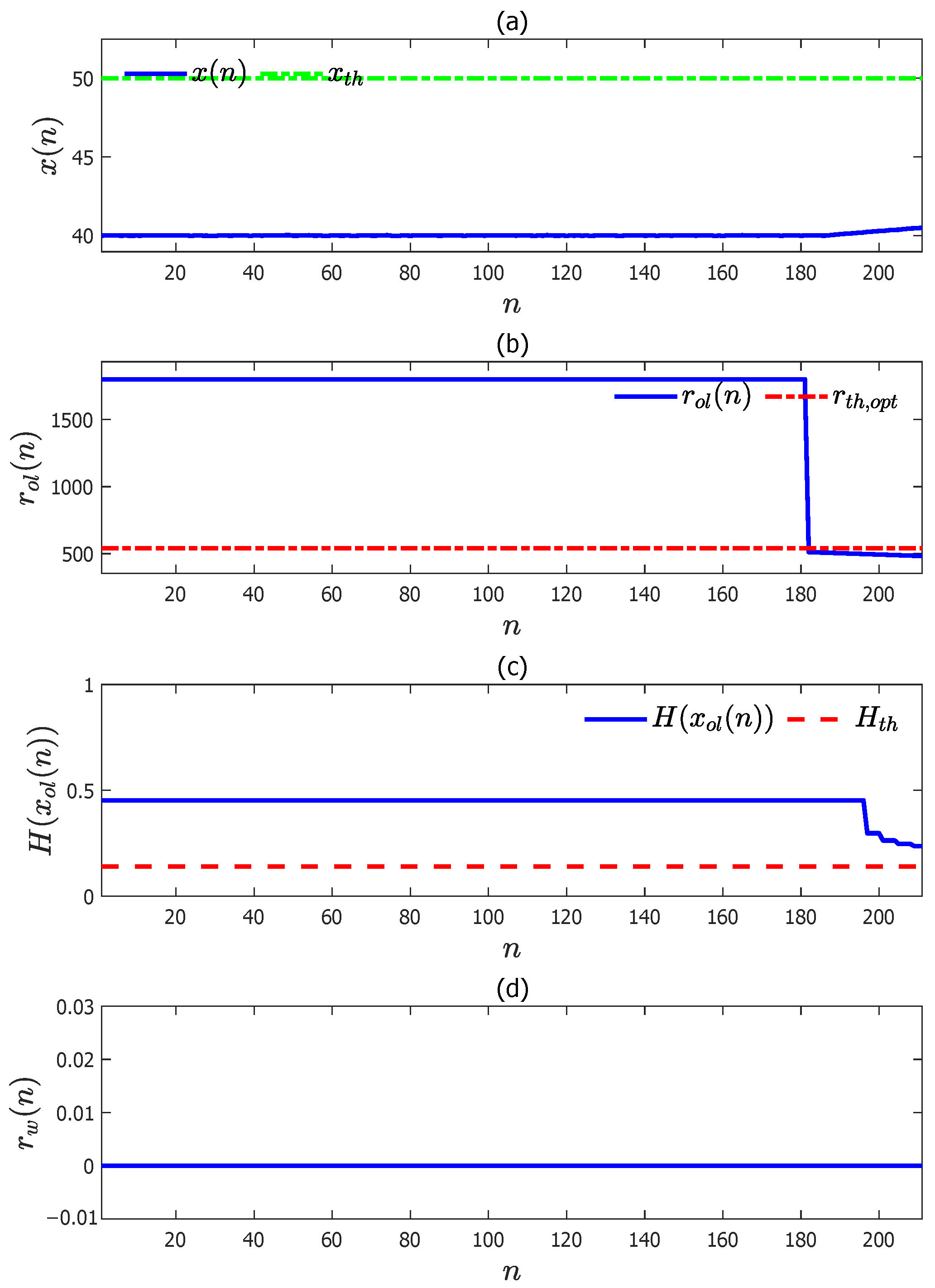
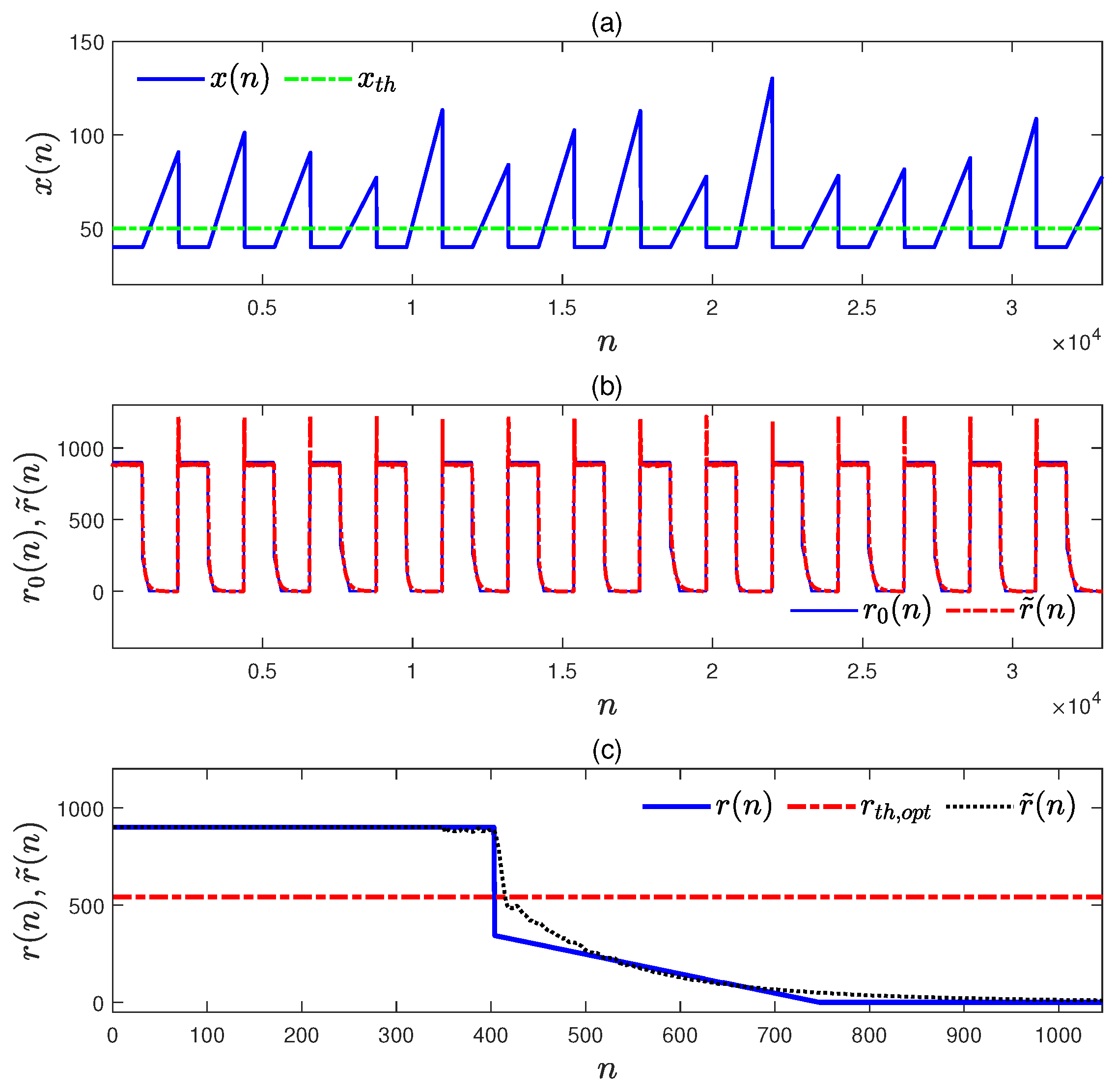
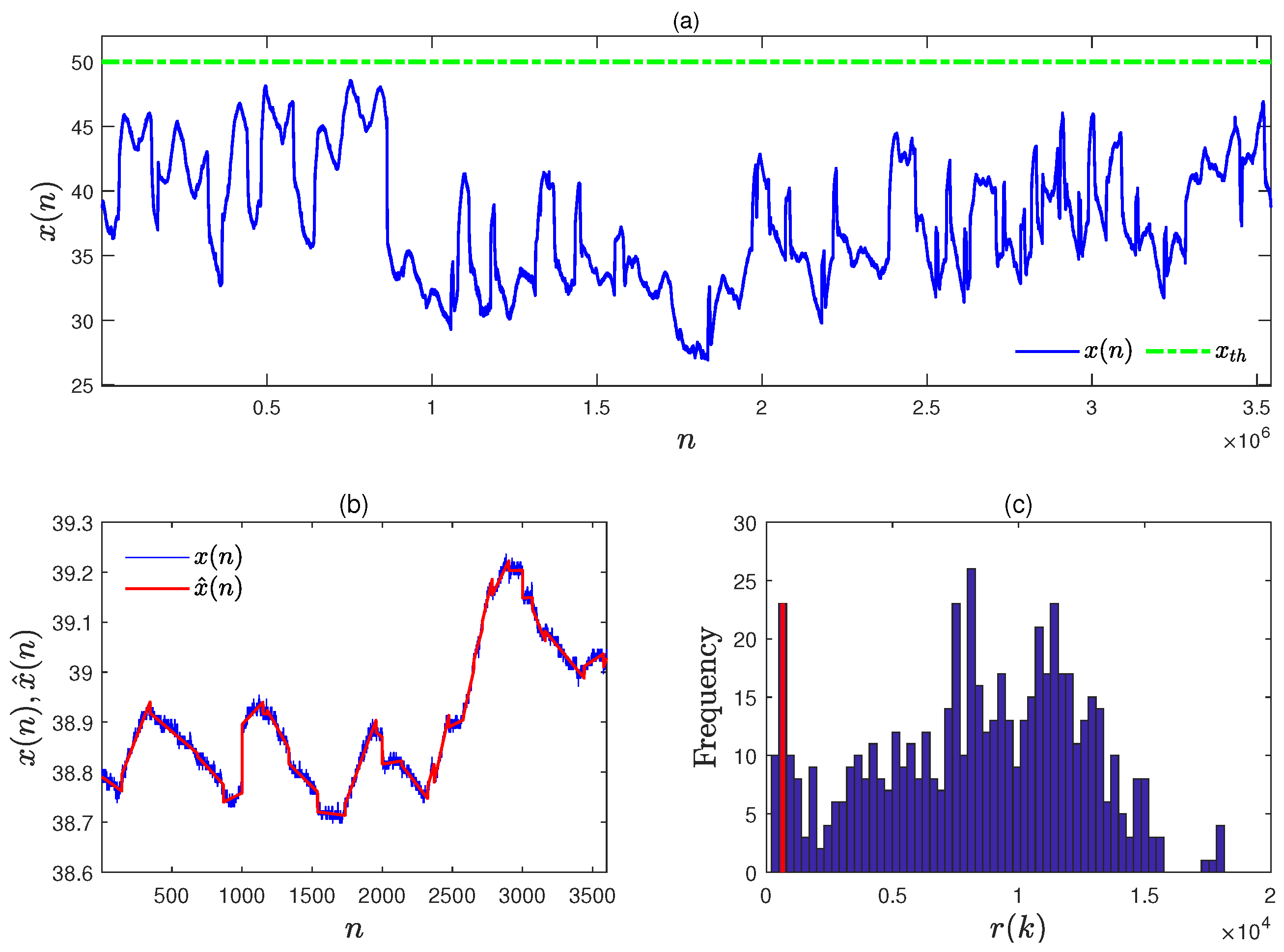
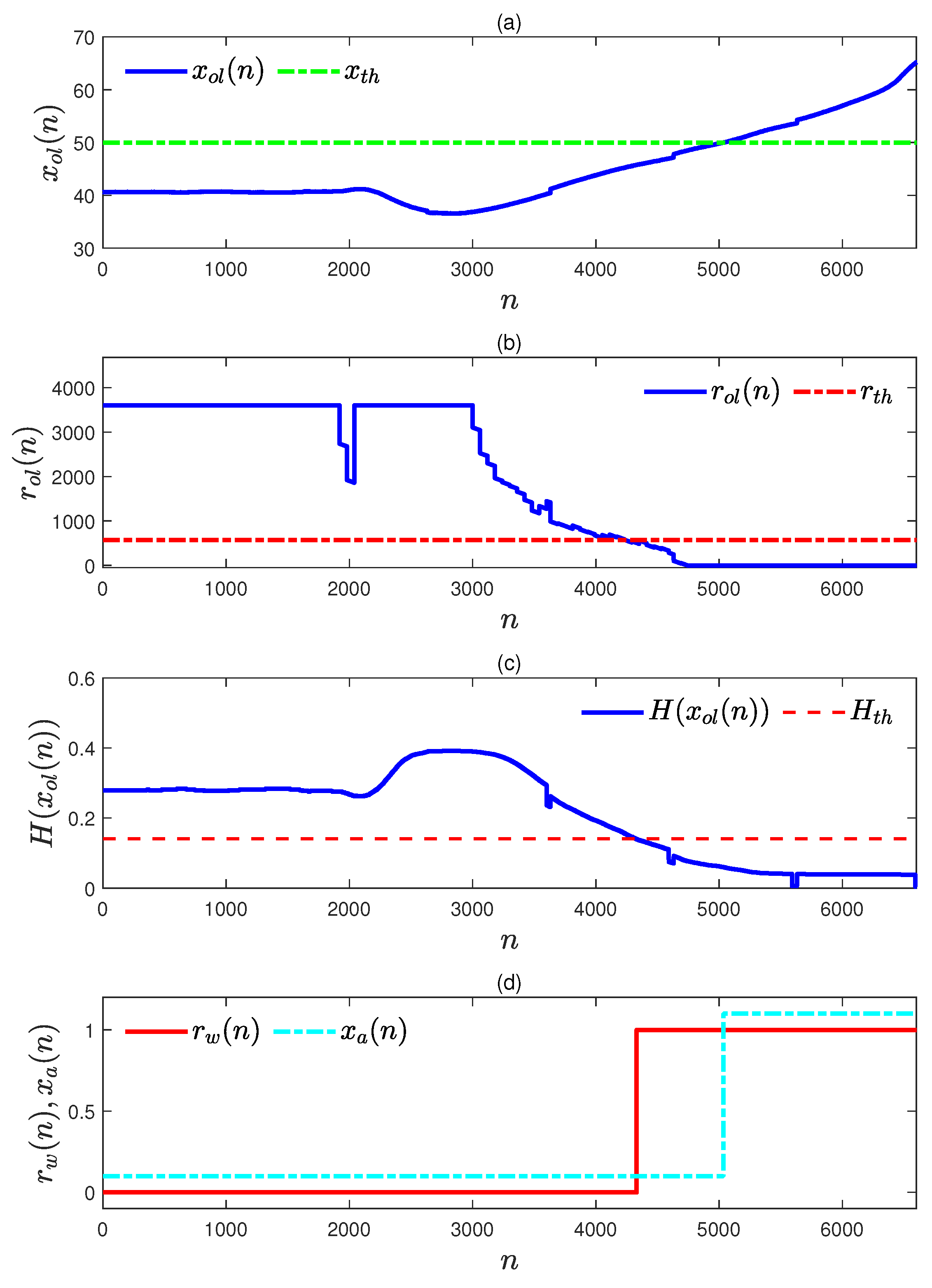
4.1. Numerical Example A
4.2. Numerical Example B
4.3. Numerical Example C
4.4. Numerical Example D
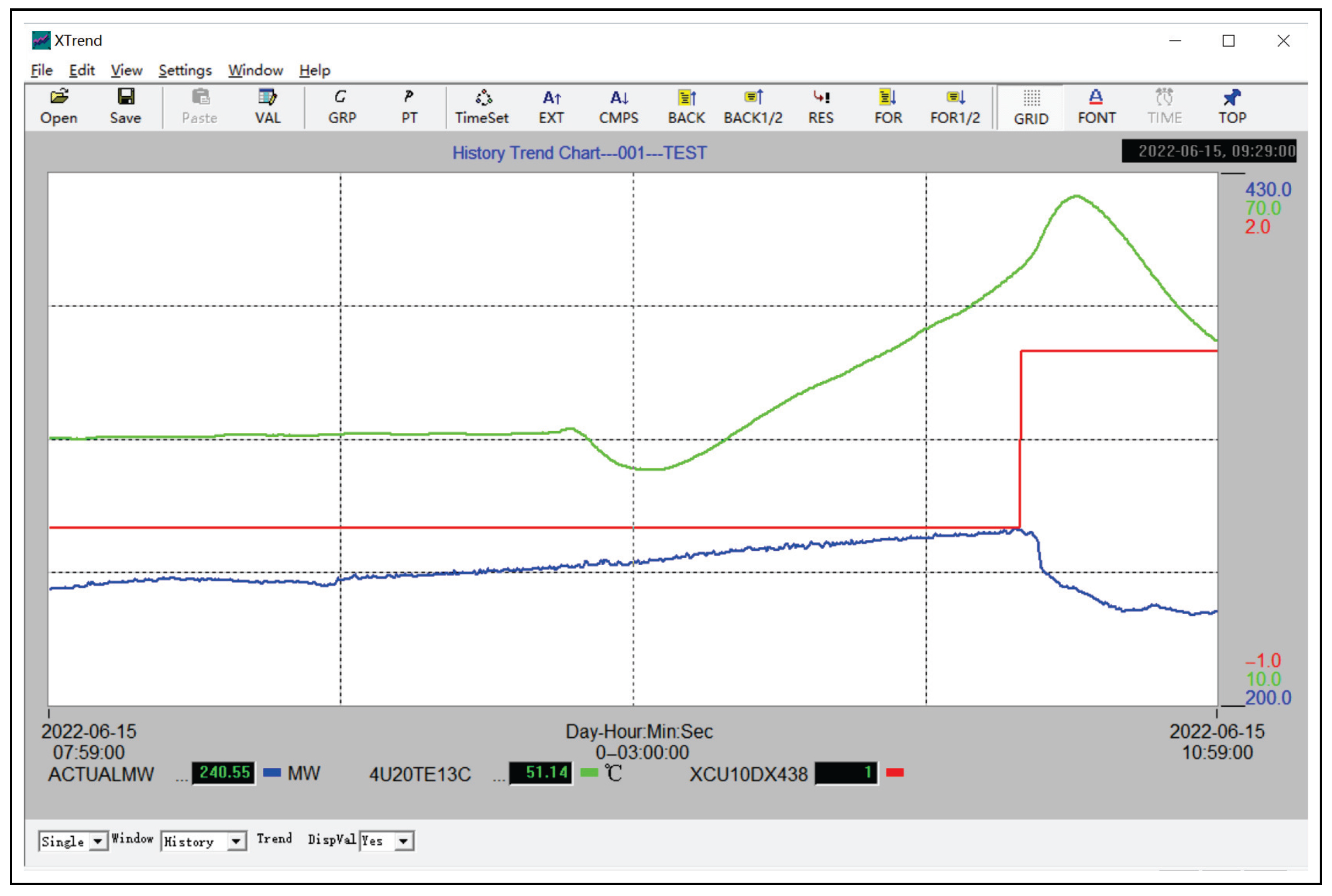
4.5. Industrial Example
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PLR | piecewise linear representation |
| CNN–LSTM | convolutional neural network–long short-term memory |
References
- Wang, J.; Yang, F.; Chen, T.; Shah, S.L. An overview of industrial alarm systems: Main causes for alarm overloading, research status, and open problems. IEEE Trans. Autom. Sci. Eng. 2016, 13, 1045–1061. [Google Scholar] [CrossRef]
- Mustaf, F.E.; Ahmed, I.; Basit, A.; Alvi, U.; Malik, S.H.; Mahmood, A.; Ali, P.R. A review on effective alarm management systems for industrial process control: Barriers and opportunities. Int. J. Crit. Infrastruct. Prot. 2023, 41, 100599. [Google Scholar] [CrossRef]
- Rothenberg, D. Alarm Management for Process Control; Momentum Press: New York, NY, USA, 2009; pp. 24–27. [Google Scholar]
- Wang, J.; Hu, W.; Chen, T. Intelligent Industrial Alarm Systems–Advanced Analysis and Design Methods; Springer: Singapore, 2024. [Google Scholar]
- ANSI/ISA-18. 2; Management of Alarm Systems for the Process Industries. ISA (International Society of Automation): Durham, NC, USA, 2016.
- Dorgo, G.; Tandari, F.; Szabó, T.; Palazoglu, A.; Abonyi, J. Quality vs. quantity of alarm messages–How to measure the performance of an alarm system. Chem. Eng. Res. Des. 2021, 173, 63–80. [Google Scholar] [CrossRef]
- Engineering Equipment and Materials Users Association. EEMUA-191: Alarm Systems—A Guide to Design, Management and Procurement; Engineering Equipment and Materials Users Association: London, UK, 2013. [Google Scholar]
- Gao, H.; Wei, C.; Huang, W.; Gao, X. Design of multivariate alarm trippoints for industrial processes based on causal model. Chem. Eng. Res. Des. 2021, 60, 9128–9140. [Google Scholar] [CrossRef]
- Luo, Y.; Gopaluni, B.; Cao, L.; Wang, Y.; Cheng, J. Adaptive online optimization of alarm thresholds using multilayer Bayesian networks and active transfer entropy. Control Eng. Pract. 2023, 137, 105534. [Google Scholar] [CrossRef]
- Xu, X.; Weng, X.; Xu, D.; Xu, H.; Hu, Y.; Li, J. Evidence updating with static and dynamical performance analyses for industrial alarm system design. ISA Trans. 2020, 99, 110–122. [Google Scholar] [CrossRef] [PubMed]
- Kaced, R.; Kouadri, A.; Baiche, K.; Bensmail, A. Multivariate nuisance alarm management in chemical processes. J. Loss Prev. Process Ind. 2021, 72, 104548. [Google Scholar] [CrossRef]
- Raei, R.; Izadi, I.; Kamali, M. Performance analysis of up/down counters in alarm design. Process Saf. Environ. Protect. 2023, 170, 877–885. [Google Scholar] [CrossRef]
- Zhang, X.; Hu, W.; Yang, F. Detection of cause-effect relations based on information granulation and transfer entropy. Entropy 2022, 24, 212. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Liu, J.; Yang, X.; Wu, Z.; Wei, Y.; Xu, Z.; Wen, J. Fault root cause analysis based on Liang–Kleeman information flow and graphical lasso. Entropy 2025, 27, 213. [Google Scholar] [CrossRef] [PubMed]
- Shirshahi, A.; Aliyari-Shoorehdeli, M. Diagnosing root causes of faults based on alarm flood classification using transfer entropy and multi-sensor fusion approaches. Process Saf. Environ. Protect. 2024, 181, 469–479. [Google Scholar] [CrossRef]
- Beebe, D.; Ferrer, S.; Logerot, D. The connection of peak alarm rates to plant incidents and what you can do to minimize. Process Saf. Prog. 2013, 32, 72–77. [Google Scholar] [CrossRef]
- Kamil, M.Z.; Khan, F.; Amyotte, P.; Ahmed, S. Multi-source heterogeneous data integration for incident likelihood analysis. Comput. Chem. Eng. 2024, 185, 108677. [Google Scholar] [CrossRef]
- Osarogiagbon, A.U.; Khan, F.; Venkatesan, R.; Gillard, P. Review and analysis of supervised machine learning algorithms for hazardous events in drilling operations. Process Saf. Environ. Protect. 2021, 147, 367–384. [Google Scholar] [CrossRef]
- Djeziri, M.A.; Benmoussa, S.; Benbouzid, M.E. Data-driven approach augmented in simulation for robust fault prognosis. Eng. Appl. Artif. Intell. 2019, 86, 154–164. [Google Scholar] [CrossRef]
- Peng, J.; Andreas, K.; Wang, D.; Niu, Z.; Zhi, F.; Wang, J.; Liu, X.; Jivka, O. A systematic review of data-driven approaches to fault diagnosis and early warning. J. Intell. Manuf. 2023, 34, 3277–3304. [Google Scholar]
- Qu, Z.; Feng, H.; Zeng, Z.; Zhuge, J.; Jin, S. A SVM-based pipeline leakage detection and pre-warning system. Measurement 2010, 43, 513–519. [Google Scholar] [CrossRef]
- Jiang, D.; Gong, J.; Garg, A. Design of early warning model based on time series data for production safety. Measurement 2017, 101, 62–71. [Google Scholar] [CrossRef]
- Zhang, L.; Cai, S.; Hu, J. An adaptive pre-warning method based on trend monitoring: Application to an oil refining process. Measurement 2019, 139, 163–176. [Google Scholar] [CrossRef]
- Jin, S.; Si, F.; Dong, Y.; Ren, S. Data-driven modelling for online fault pre-warning in thermal power plant using incremental Gaussian mixture regression. Can. J. Chem. Eng. 2024, 102, 1497–1508. [Google Scholar] [CrossRef]
- He, S.; Hou, W.; Chen, Z.; Liu, H.; Wang, J.; Cheng, P. Early warning model based on support vector machine ensemble algorithm. J. Oper. Res. Soc. 2025, 76, 411–425. [Google Scholar] [CrossRef]
- Wang, Y.; Li, F.; Lv, M.; Wang, T.; Wang, X. A multi-index fusion adaptive cavitation feature extraction for hydraulic turbine cavitation detection. Entropy 2025, 27, 443. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.; Gao, D.; Zhao, F.; Yang, Q. Early warning method for charging thermal runaway of electric vehicle lithium-ion battery based on charging network. Sci. Rep. 2025, 15, 7895. [Google Scholar] [CrossRef] [PubMed]
- Cai, S.; Palazoglu, A.; Zhang, L.; Hu, J. Process alarm prediction using deep learning and word embedding methods. ISA Trans. 2019, 85, 274–283. [Google Scholar] [CrossRef] [PubMed]
- Geng, Z.; Chen, N.; Han, Y.; Ma, B. An improved intelligent early warning method based on MWSPCA and its application in complex chemical processes. Can. J. Chem. Eng. 2020, 98, 1307–1318. [Google Scholar] [CrossRef]
- Sun, Y.; Hua, Y.; Wang, E.; Li, N.; Ma, S.; Zhang, L.; Hu, Y. A temperature-based fault pre-warning method for the dry-type transformer in the offshore oil platform. Int. J. Electr. Power Energy Syst. 2020, 123, 106218. [Google Scholar] [CrossRef]
- Arunthavanathan, R.; Khan, F.; Ahmed, S.; Imtiaz, S. A deep learning model for process fault prognosis. Process Saf. Environ. Protect. 2021, 154, 467–479. [Google Scholar] [CrossRef]
- Mamudu, A.; Khan, F.; Zendehboudi, S.; Adedigba, S. Dynamic risk modeling of complex hydrocarbon production systems. Process Saf. Environ. Protect. 2021, 151, 71–84. [Google Scholar] [CrossRef]
- Kopbayev, A.; Khan, F.; Yang, M.; Halim, S.Z. Gas leakage detection using spatial and temporal neural network model. Process Saf. Environ. Protect. 2022, 160, 968–975. [Google Scholar] [CrossRef]
- He, J.; Xiao, Y.; Huang, L.; Li, A.; Chen, Y.; Ma, Y.; Li, W.; Liu, D.; Zhan, Y. Application of leakage pre-warning system for hazardous chemical storage tank based on YOLOv3-prePReLU algorithm. J. Loss Prev. Process Ind. 2022, 80, 104905. [Google Scholar] [CrossRef]
- Han, S.; Hua, Y.; Lin, Y.; Yao, L.; Wang, Z.; Zheng, Z.; Yang, J.; Zhao, C.; Zheng, C.; Gao, X. Fault diagnosis of regenerative thermal oxidizer system via dynamic uncertain causality graph integrated with early anomaly detection. Process Saf. Environ. Protect. 2023, 179, 724–734. [Google Scholar] [CrossRef]
- Song, Z.; Huang, X.; Ji, C.; Zhang, Y. Deformable YOLOX: Detection and rust warning method of transmission line connection fittings based on image processing technology. IEEE Trans. Instrum. Meas. 2023, 72, 1–21. [Google Scholar] [CrossRef]
- Ali, H.; Zhang, Z.; Gao, F. Multiscale monitoring of industrial chemical process using wavelet-entropy aided machine learning approach. Process Saf. Environ. Protect. 2023, 180, 1053–1075. [Google Scholar] [CrossRef]
- Fu, Y.; Zhao, Z.; Lin, P. Multiscale entropy-based feature extraction for the detection of instability inception in axial compressors. Entropy 2024, 26, 48. [Google Scholar] [CrossRef] [PubMed]
- Sharma, K.K.; Krishna, H. Asymptotic sampling distribution of inverse coefficient-of-variation and its applications. IEEE Trans. Reliab. 1994, 43, 630–633. [Google Scholar] [CrossRef]
- Bernardo, J.M. Reference analysis. Handb. Stat. 2005, 25, 17–90. [Google Scholar]
- Fortuin, V. Priors in Bayesian deep learning: A review. Int. Stat. Rev. 2022, 90, 563–591. [Google Scholar] [CrossRef]
- Keogh, E.; Chu, S.; Hart, D.; Pazzani, M. Segmenting time series: A survey and novel approach. Data Min. Time Ser. Databases 2004, 57, 1–22. [Google Scholar]
- Seber, G.A.; Lee, A.J. Linear Regression Analysis, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2003; p. 41. [Google Scholar]
- Wang, J.; Yang, Z.; Wei, M.; Gao, S.; Zhao, Y. Static gain estimation for automatic generation control systems from historical ramp responses. IEEE Trans. Control Syst. Technol. 2020, 29, 1831–1838. [Google Scholar] [CrossRef]
- Chatterjee, S.; Hadi, A.S. Regression Analysis by Example; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009; pp. 13–16. [Google Scholar]
- Keogh, E.; Chu, S.; Hart, D.; Pazzani, M. An online algorithm for segmenting time series. In Proceedings of the 2001 IEEE International Conference on Data Mining, San Jose, CA, USA, 29 November 2001; pp. 289–296. [Google Scholar]
- Zhang, Z.; Wang, J.; Qi, Y. Selection of alarm deadbands and delay timers with their connections based on risk indicators for removing nuisance alarms. Control Eng. Pract. 2024, 153, 106113. [Google Scholar] [CrossRef]
- Brooks, R.; Thorpe, R.; Wilson, J. A new method for defining and managing process alarms and for correcting process operation when an alarm occurs. J. Hazard. Mater. 2004, 115, 169–174. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Wang, J.; Li, H.; Gao, S. Pre-Warning for the Remaining Time to Alarm Based on Variation Rates and Mixture Entropies. Entropy 2025, 27, 736. https://doi.org/10.3390/e27070736
Yang Z, Wang J, Li H, Gao S. Pre-Warning for the Remaining Time to Alarm Based on Variation Rates and Mixture Entropies. Entropy. 2025; 27(7):736. https://doi.org/10.3390/e27070736
Chicago/Turabian StyleYang, Zijiang, Jiandong Wang, Honghai Li, and Song Gao. 2025. "Pre-Warning for the Remaining Time to Alarm Based on Variation Rates and Mixture Entropies" Entropy 27, no. 7: 736. https://doi.org/10.3390/e27070736
APA StyleYang, Z., Wang, J., Li, H., & Gao, S. (2025). Pre-Warning for the Remaining Time to Alarm Based on Variation Rates and Mixture Entropies. Entropy, 27(7), 736. https://doi.org/10.3390/e27070736





