Time-Resolved Information-Theoretic and Spectral Analysis of fNIRS Signals from Multi-Channel Prototypal Device
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset Description and Pre-Processing
2.2. Time-Resolved Information Measures
2.3. Spectral Analysis of fNIRS Signals
2.4. Data Analysis and Statistical Validation
3. Results
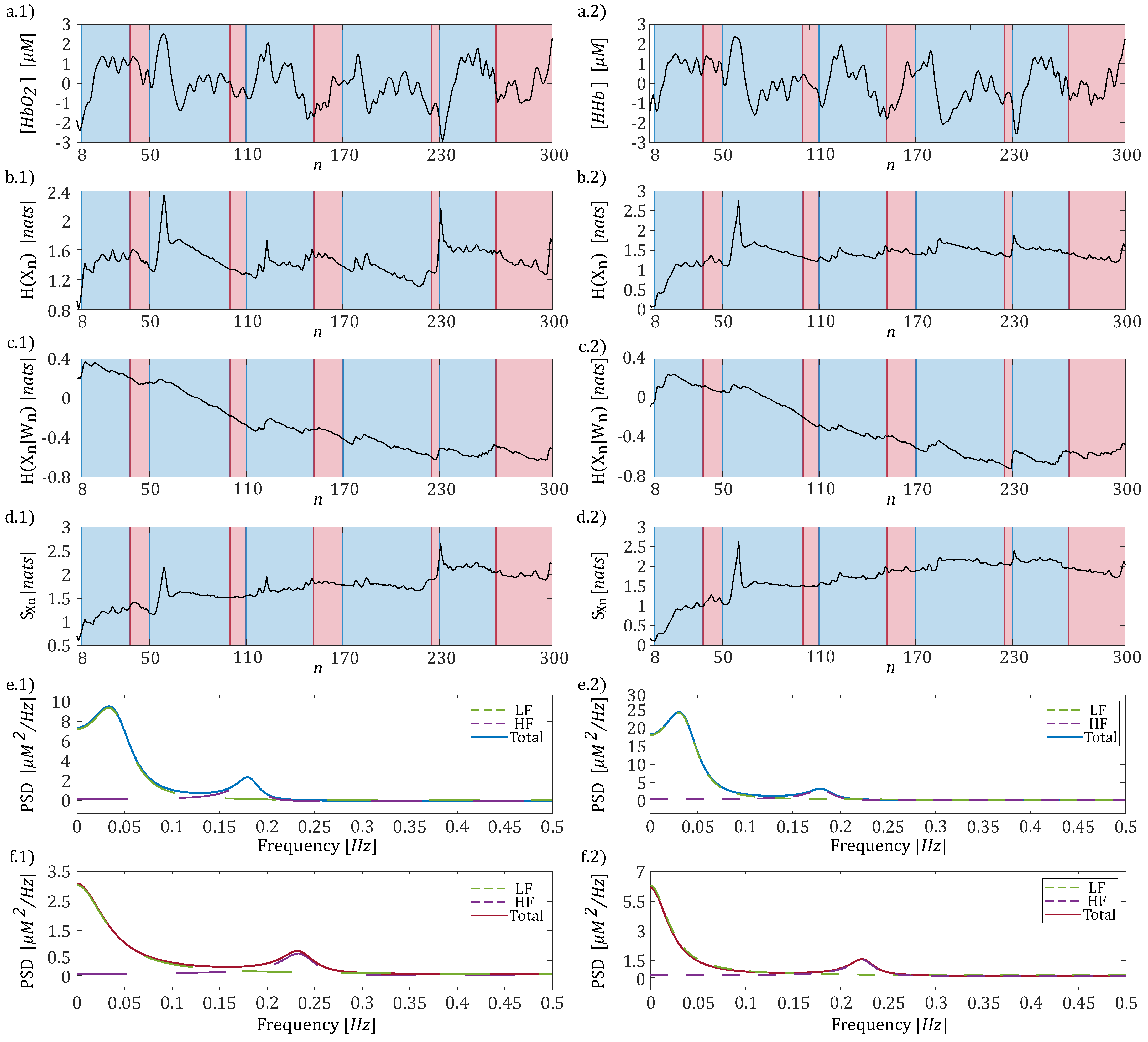
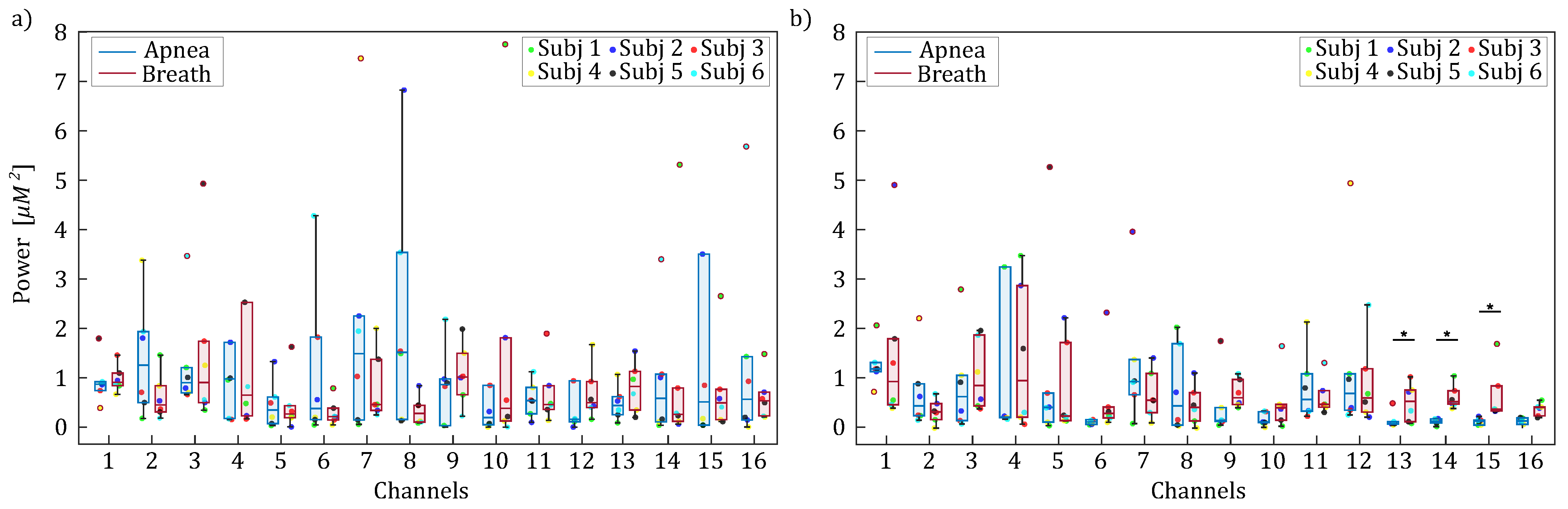
3.1. Frequency Specific Analysis of fNIRS Signals
3.2. Time-Resolved Information-Theoretic Measures
4. Discussion
Final Remarks and Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nosrati, R.; Lin, S.; Ramadeen, A.; Monjazebi, D.; Dorian, P.; Toronov, V. Cerebral hemodynamics and metabolism during cardiac arrest and cardiopulmonary resuscitation using hyperspectral near infrared spectroscopy. Circ. J. 2017, 81, 879–887. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, M.; Quaresima, V. A brief review on the history of human functional near-infrared spectroscopy (fNIRS) development and fields of application. Neuroimage 2012, 63, 921–935. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, M.; Mottola, L.; Quaresima, V. Principles, techniques, and limitations of near infrared spectroscopy. Can. J. Appl. Physiol. 2004, 29, 463–487. [Google Scholar] [CrossRef] [PubMed]
- Chiarelli, A.M.; Perpetuini, D.; Croce, P.; Greco, G.; Mistretta, L.; Rizzo, R.; Vinciguerra, V.; Romeo, M.F.; Zappasodi, F.; Merla, A.; et al. Fiberless, multi-channel fNIRS-EEG system based on silicon photomultipliers: Towards sensitive and ecological mapping of brain activity and neurovascular coupling. Sensors 2020, 20, 2831. [Google Scholar] [CrossRef]
- Kassab, A.; Le Lan, J.; Tremblay, J.; Vannasing, P.; Dehbozorgi, M.; Pouliot, P.; Gallagher, A.; Lesage, F.; Sawan, M.; Nguyen, D.K. Multichannel Wearable f NIRS-EEG System for Long-Term Clinical Monitoring; Technical Report; Wiley Online Library: New York, NY, USA, 2018. [Google Scholar]
- Barut, Ç.; Kızıltan, E.; Gelir, E.; Köktürk, F. Advanced analysis of finger-tapping performance: A preliminary study. Balk. Med. J. 2013, 2013, 167–171. [Google Scholar] [CrossRef]
- Eggebrecht, A.T.; White, B.R.; Ferradal, S.L.; Chen, C.; Zhan, Y.; Snyder, A.Z.; Dehghani, H.; Culver, J.P. A quantitative spatial comparison of high-density diffuse optical tomography and fMRI cortical mapping. Neuroimage 2012, 61, 1120–1128. [Google Scholar] [CrossRef]
- Vendrell, P.; Junqué, C.; Pujol, J.; Jurado, M.A.; Molet, J.; Grafman, J. The role of prefrontal regions in the Stroop task. Neuropsychologia 1995, 33, 341–352. [Google Scholar] [CrossRef]
- Lloyd-Fox, S.; Blasi, A.; Elwell, C. Illuminating the developing brain: The past, present and future of functional near infrared spectroscopy. Neurosci. Biobehav. Rev. 2010, 34, 269–284. [Google Scholar] [CrossRef]
- Wolf, M.; Ferrari, M.; Quaresima, V. Progress of near-infrared spectroscopy and topography for brain and muscle clinical applications. J. Biomed. Opt. 2007, 12, 062104. [Google Scholar]
- Scholkmann, F.; Kleiser, S.; Metz, A.J.; Zimmermann, R.; Pavia, J.M.; Wolf, U.; Wolf, M. A review on continuous wave functional near-infrared spectroscopy and imaging instrumentation and methodology. Neuroimage 2014, 85, 6–27. [Google Scholar] [CrossRef]
- Tachtsidis, I.; Scholkmann, F. False positives and false negatives in functional near-infrared spectroscopy: Issues, challenges, and the way forward. Neurophotonics 2016, 3, 031405. [Google Scholar] [CrossRef] [PubMed]
- Guerouah, Z.; Lin, S.; Toronov, V. Measurement of adult human brain responses to breath-holding by multi-distance hyperspectral near-infrared spectroscopy. Appl. Sci. 2021, 12, 371. [Google Scholar] [CrossRef]
- Strangman, G.E.; Li, Z.; Zhang, Q. Depth sensitivity and source-detector separations for near infrared spectroscopy based on the Colin27 brain template. PLoS ONE 2013, 8, e66319. [Google Scholar] [CrossRef]
- Haeussinger, F.B.; Heinzel, S.; Hahn, T.; Schecklmann, M.; Ehlis, A.C.; Fallgatter, A.J. Simulation of near-infrared light absorption considering individual head and prefrontal cortex anatomy: Implications for optical neuroimaging. PLoS ONE 2011, 6, e26377. [Google Scholar] [CrossRef]
- Scarpa, F.; Cutini, S.; Scatturin, P.; Dell’Acqua, R.; Sparacino, G. Bayesian filtering of human brain hemodynamic activity elicited by visual short-term maintenance recorded through functional near-infrared spectroscopy (fNIRS). Opt. Express 2010, 18, 26550–26568. [Google Scholar] [CrossRef]
- Pinti, P.; Tachtsidis, I.; Hamilton, A.; Hirsch, J.; Aichelburg, C.; Gilbert, S.; Burgess, P.W. The present and future use of functional near-infrared spectroscopy (fNIRS) for cognitive neuroscience. Ann. N. Y. Acad. Sci. 2020, 1464, 5–29. [Google Scholar] [CrossRef]
- Ivanov, P.C. The new field of network physiology: Building the human physiolome. Front. Netw. Physiol. 2021, 1, 711778. [Google Scholar] [CrossRef]
- Bröhl, T.; von Wrede, R.; Lehnertz, K. Impact of biological rhythms on the importance hierarchy of constituents in time-dependent functional brain networks. Front. Netw. Physiol. 2023, 3, 1237004. [Google Scholar] [CrossRef]
- Bashan, A.; Bartsch, R.P.; Kantelhardt, J.W.; Havlin, S.; Ivanov, P.C. Network physiology reveals relations between network topology and physiological function. Nat. Commun. 2012, 3, 702. [Google Scholar] [CrossRef]
- Kandimalla, M.; Lim, S.; Thakkar, J.; Dewan, S.; Kang, D.; In, M.H.; Jo, H.J.; Jang, D.P.; Nedelska, Z.; Lapid, M.I.; et al. Cardiorespiratory Dynamics in the Brain: Review on the Significance of Cardiovascular and Respiratory Correlates in functional MRI signal. NeuroImage 2025, 306, 121000. [Google Scholar] [CrossRef]
- Minati, L.; Kress, I.U.; Visani, E.; Medford, N.; Critchley, H.D. Intra-and extra-cranial effects of transient blood pressure changes on brain near-infrared spectroscopy (NIRS) measurements. J. Neurosci. Methods 2011, 197, 283–288. [Google Scholar] [CrossRef] [PubMed]
- Sütterlin, S.; Schroijen, M.; Constantinou, E.; Smets, E.; Van den Bergh, O.; Van Diest, I. Breath holding duration as a measure of distress tolerance: Examining its relation to measures of executive control. Front. Psychol. 2013, 4, 483. [Google Scholar] [CrossRef] [PubMed]
- Antonacci, Y.; Barà, C.; Zaccaro, A.; Ferri, F.; Pernice, R.; Faes, L. Time-varying information measures: An adaptive estimation of information storage with application to brain-heart interactions. Front. Netw. Physiol. 2023, 3, 1242505. [Google Scholar] [CrossRef] [PubMed]
- Azami, H.; Faes, L.; Escudero, J.; Humeau-Heurtier, A.; Silva, L.E. Entropy analysis of univariate biomedical signals: Review and comparison of methods. In Frontiers in Entropy Across the Disciplines: Panorama of Entropy: Theory, Computation, and Applications; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2023; pp. 233–286. [Google Scholar]
- Zhang, J.; Chen, H.; Fang, F.; Liao, W. Quantitative analysis of asymmetrical cortical activity based on power spectrum changes. Brain Topogr. 2010, 23, 257–268. [Google Scholar] [CrossRef]
- Minati, L.; Jones, C.L.; Gray, M.A.; Medford, N.; Harrison, N.A.; Critchley, H.D. Emotional modulation of visual cortex activity: A functional near-infrared spectroscopy study. Neuroreport 2009, 20, 1344–1350. [Google Scholar] [CrossRef]
- Tachtsidis, I.; Tisdall, M.; Delpy, D.T.; Smith, M.; Elwell, C.E. Measurement of cerebral tissue oxygenation in young healthy volunteers during acetazolamide provocation: A transcranial Doppler and near-infrared spectroscopy investigation. In Proceedings of the Oxygen Transport to Tissue XXIX; Springer: Berlin/Heidelberg, Germany, 2008; pp. 389–396. [Google Scholar]
- Cui, W.; Kumar, C.; Chance, B. Experimental study of migration depth for the photons measured at sample surface. In Proceedings of the Time-Resolved Spectroscopy and Imaging of Tissues; SPIE: Bellingham, WA, USA, 1991; Volume 1431, pp. 180–191. [Google Scholar]
- Strangman, G.; Boas, D.A.; Sutton, J.P. Non-invasive neuroimaging using near-infrared light. Biol. Psychiatry 2002, 52, 679–693. [Google Scholar] [CrossRef]
- Fishburn, F.A.; Ludlum, R.S.; Vaidya, C.J.; Medvedev, A.V. Temporal derivative distribution repair (TDDR): A motion correction method for fNIRS. Neuroimage 2019, 184, 171–179. [Google Scholar] [CrossRef]
- Delpy, D.T.; Cope, M.; van der Zee, P.; Arridge, S.; Wray, S.; Wyatt, J. Estimation of optical pathlength through tissue from direct time of flight measurement. Phys. Med. Biol. 1988, 33, 1433. [Google Scholar] [CrossRef]
- Nollo, G.; Faes, L.; Pellegrini, B.; Porta, A.; Antolini, R. Synchronization index for quantifying nonlinear causal coupling between RR interval and systolic arterial pressure after myocardial infarction. In Proceedings of the Computers in Cardiology 2000. Vol.27 (Cat. 00CH37163), Cambridge, MA, USA, 24–27 September 2000; IEEE: Piscataway, NJ, USA; pp. 143–146. [Google Scholar]
- Antonacci, Y.; Barà, C.; de Felice, G.; Sferlazza, A.; Pernice, R.; Faes, L. Exploring transient neurophysiological states through local and time-varying measures of Information Dynamics. Appl. Math. Comput. 2025, 500, 129437. [Google Scholar] [CrossRef]
- Antonacci, Y.; Bara, C.; Sparacino, L.; Mijatovic, G.; Minati, L.; Faes, L. A Method for the Time-Frequency Analysis of High-Order Interactions in Non-Stationary Physiological Networks. arXiv 2025, arXiv:2503.12421. [Google Scholar]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Barà, C.; Pernice, R.; Catania, C.A.; Hilal, M.; Porta, A.; Humeau-Heurtier, A.; Faes, L. Comparison of entropy rate measures for the evaluation of time series complexity: Simulations and application to heart rate and respiratory variability. Biocybern. Biomed. Eng. 2024, 44, 380–392. [Google Scholar] [CrossRef]
- Lizier, J.T.; Prokopenko, M.; Zomaya, A.Y. A framework for the local information dynamics of distributed computation in complex systems. In Guided Self-Organization: Inception; Springer: Berlin/Heidelberg, Germany, 2014; pp. 115–158. [Google Scholar]
- Barnett, L.; Barrett, A.B.; Seth, A.K. Granger causality and transfer entropy are equivalent for Gaussian variables. Phys. Rev. Lett. 2009, 103, 238701. [Google Scholar] [CrossRef]
- Haykin, S.S. Adaptive Filter Theory; Pearson Education: Noida, India, 2002. [Google Scholar]
- Baselli, G.; Porta, A.; Rimoldi, O.; Pagani, M.; Cerutti, S. Spectral decomposition in multichannel recordings based on multivariate parametric identification. IEEE Trans. Biomed. Eng. 1997, 44, 1092–1101. [Google Scholar] [CrossRef]
- Lütkepohl, H. New Introduction to Multiple Time Series Analysis; Springer Science & Business Media: New York, NY, USA, 2005. [Google Scholar]
- Antonacci, Y.; Toppi, J.; Pietrabissa, A.; Anzolin, A.; Astolfi, L. Measuring connectivity in linear multivariate processes with penalized regression techniques. IEEE Access 2024, 12, 30638–30652. [Google Scholar] [CrossRef]
- Sparacino, L.; Antonacci, Y.; Barà, C.; Švec, D.; Javorka, M.; Faes, L. A method to assess linear self-predictability of physiologic processes in the frequency domain: Application to beat-to-beat variability of arterial compliance. Front. Netw. Physiol. 2024, 4, 1346424. [Google Scholar] [CrossRef]
- Sullivan, G.M.; Feinn, R. Using effect size—Or why the P value is not enough. J. Grad. Med. Educ. 2012, 4, 279–282. [Google Scholar] [CrossRef]
- Chance, B.; Zhuang, Z.; UnAh, C.; Alter, C.; Lipton, L. Cognition-activated low-frequency modulation of light absorption in human brain. Proc. Natl. Acad. Sci. USA 1993, 90, 3770–3774. [Google Scholar] [CrossRef]
- Elwell, C.; Springett, R.; Hillman, E.; Delpy, D.T. Oscillations in cerebral haemodynamics: Implications for functional activation studies. In Oxygen Transport to Tissue XXI; Springer: Berlin/Heidelberg, Germany, 1999; pp. 57–65. [Google Scholar]
- Emir, U.E.; Ozturk, C.; Akin, A. Multimodal investigation of fMRI and fNIRS derived breath hold BOLD signals with an expanded balloon model. Physiol. Meas. 2007, 29, 49. [Google Scholar] [CrossRef]
- Akin, A.; Emir, U.E.; Kalsin, S.; Sayli, O. Frequency components in breath holding experiments. In Proceedings of the Optical Tomography and Spectroscopy of Tissue VI; SPIE: Bellingham, WA, USA, 2005; Volume 5693, pp. 172–178. [Google Scholar]
- Tachtsidis, I.; Leung, T.S.; Chopra, A.; Koh, P.H.; Reid, C.B.; Elwell, C.E. False positives in functional nearinfrared topography. In Oxygen Transport to Tissue XXX; Springer: Berlin/Heidelberg, Germany, 2009; pp. 307–314. [Google Scholar]
- Kastrup, A.; Krüger, G.; Neumann-Haefelin, T.; Moseley, M.E. Assessment of cerebrovascular reactivity with functional magnetic resonance imaging: Comparison of CO2 and breath holding. Magn. Reson. Imaging 2001, 19, 13–20. [Google Scholar] [CrossRef]
- Zhang, R.; Zuckerman, J.H.; Levine, B.D. Spontaneous fluctuations in cerebral blood flow: Insights from extended-duration recordings in humans. Am. J. -Physiol.-Heart Circ. Physiol. 2000, 278, H1848–H1855. [Google Scholar] [CrossRef] [PubMed]
- Morelli, M.S.; Vanello, N.; Callara, A.L.; Hartwig, V.; Maestri, M.; Bonanni, E.; Emdin, M.; Passino, C.; Giannoni, A. Breath-hold task induces temporal heterogeneity in electroencephalographic regional field power in healthy subjects. J. Appl. Physiol. 2021, 130, 298–307. [Google Scholar] [CrossRef] [PubMed]
- Parkes, M. Breath-holding and its breakpoint. Exp. Physiol. 2006, 91, 1–15. [Google Scholar] [CrossRef]
- Eckberg, D.L. Human sinus arrhythmia as an index of vagal cardiac outflow. J. Appl. Physiol. 1983, 54, 961–966. [Google Scholar] [CrossRef]
- Hakimi, N.; Shahbakhti, M.; Sappia, S.; Horschig, J.M.; Bronkhorst, M.; Floor-Westerdijk, M.; Valenza, G.; Dudink, J.; Colier, W.N. Estimation of respiratory rate from functional near-infrared spectroscopy (fNIRS): A new perspective on respiratory interference. Biosensors 2022, 12, 1170. [Google Scholar] [CrossRef]
- Obrig, H.; Neufang, M.; Wenzel, R.; Kohl, M.; Steinbrink, J.; Einhäupl, K.; Villringer, A. Spontaneous low frequency oscillations of cerebral hemodynamics and metabolism in human adults. Neuroimage 2000, 12, 623–639. [Google Scholar] [CrossRef]
- Näsi, T.; Virtanen, J.; Noponen, T.; Toppila, J.; Salmi, T.; Ilmoniemi, R.J. Spontaneous hemodynamic oscillations during human sleep and sleep stage transitions characterized with near-infrared spectroscopy. PLoS ONE 2011, 6, e25415. [Google Scholar] [CrossRef]
- Tachtsidis, I.; Elwell, C.E.; Leung, T.S.; Lee, C.W.; Smith, M.; Delpy, D.T. Investigation of cerebral haemodynamics by near-infrared spectroscopy in young healthy volunteers reveals posture-dependent spontaneous oscillations. Physiol. Meas. 2004, 25, 437. [Google Scholar] [CrossRef]
- Barà, C.; Zaccaro, A.; Antonacci, Y.; Dalla Riva, M.; Busacca, A.; Ferri, F.; Faes, L.; Pernice, R. Local and global measures of information storage for the assessment of heartbeat-evoked cortical responses. Biomed. Signal Process. Control 2023, 86, 105315. [Google Scholar] [CrossRef]
- Antonacci, Y.; Barà, C.; Sparacino, L.; Pirovano, I.; Mastropietro, A.; Rizzo, G.; Faes, L. Spectral Information Dynamics of Cortical Signals Uncover the Hierarchical Organization of the Human Brain’s Motor Network. IEEE Trans. Biomed. Eng. 2024, 72, 1655–1664. [Google Scholar] [CrossRef]
- Tak, S.; Polimeni, J.R.; Wang, D.J.; Yan, L.; Chen, J.J. Associations of resting-state fMRI functional connectivity with flow-BOLD coupling and regional vasculature. Brain Connect. 2015, 5, 137–146. [Google Scholar] [CrossRef] [PubMed]
- Holton, P.; Huang, Y.; Bahuri, N.F.A.; Boccard, S.; Hyam, J.A.; Paterson, D.J.; Dorrington, K.L.; Aziz, T.Z.; Moosavi, S.H.; Green, A.L. Differential responses to breath-holding, voluntary deep breathing and hypercapnia in left and right dorsal anterior cingulate. Exp. Physiol. 2021, 106, 726–735. [Google Scholar] [CrossRef] [PubMed]
- Ronca, V.; Babiloni, F.; Aricò, P. A Novel Mutual Information-based Approach for Neurophysiological Characterization of Sense of Presence in Virtual Reality. IEEE Trans. Biomed. Eng. 2025. [Google Scholar] [CrossRef] [PubMed]
- Giorgi, A.; Ronca, V.; Vozzi, A.; Aricò, P.; Borghini, G.; Capotorto, R.; Tamborra, L.; Simonetti, I.; Sportiello, S.; Petrelli, M.; et al. Neurophysiological mental fatigue assessment for developing user-centered Artificial Intelligence as a solution for autonomous driving. Front. Neurorobot. 2023, 17, 1240933. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Franzone, I.; Antonacci, Y.; Giuliano, F.; Pernice, R.; Busacca, A.; Faes, L.; Giaconia, G.C. Time-Resolved Information-Theoretic and Spectral Analysis of fNIRS Signals from Multi-Channel Prototypal Device. Entropy 2025, 27, 694. https://doi.org/10.3390/e27070694
Franzone I, Antonacci Y, Giuliano F, Pernice R, Busacca A, Faes L, Giaconia GC. Time-Resolved Information-Theoretic and Spectral Analysis of fNIRS Signals from Multi-Channel Prototypal Device. Entropy. 2025; 27(7):694. https://doi.org/10.3390/e27070694
Chicago/Turabian StyleFranzone, Irene, Yuri Antonacci, Fabrizio Giuliano, Riccardo Pernice, Alessandro Busacca, Luca Faes, and Giuseppe Costantino Giaconia. 2025. "Time-Resolved Information-Theoretic and Spectral Analysis of fNIRS Signals from Multi-Channel Prototypal Device" Entropy 27, no. 7: 694. https://doi.org/10.3390/e27070694
APA StyleFranzone, I., Antonacci, Y., Giuliano, F., Pernice, R., Busacca, A., Faes, L., & Giaconia, G. C. (2025). Time-Resolved Information-Theoretic and Spectral Analysis of fNIRS Signals from Multi-Channel Prototypal Device. Entropy, 27(7), 694. https://doi.org/10.3390/e27070694







