Entropy Alternatives for Equilibrium and Out-of-Equilibrium Systems
Abstract
1. Introduction and Background
2. Methodology and Definitions
2.1. Shannon Entropy
2.2. Mutability
2.3. Functions
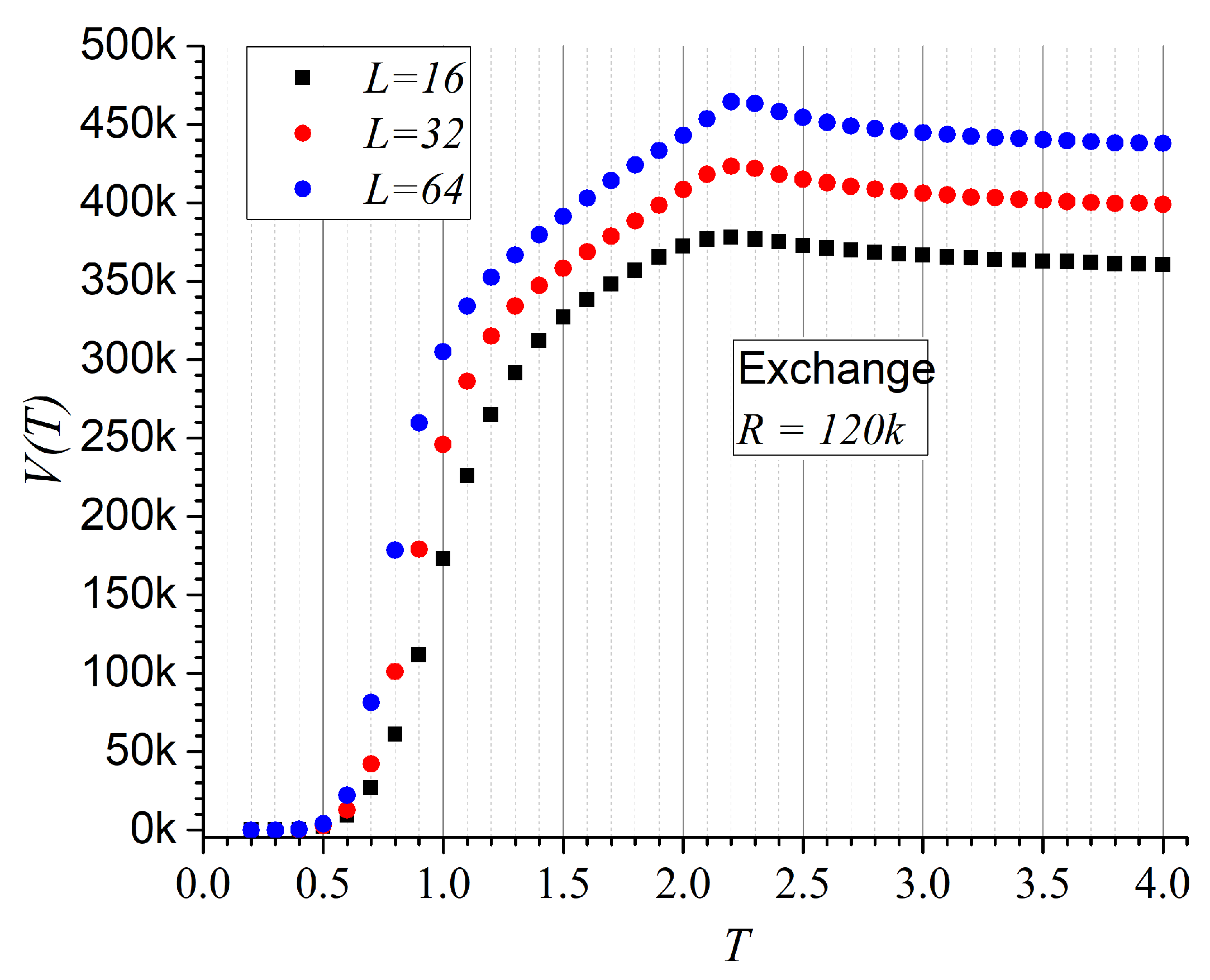
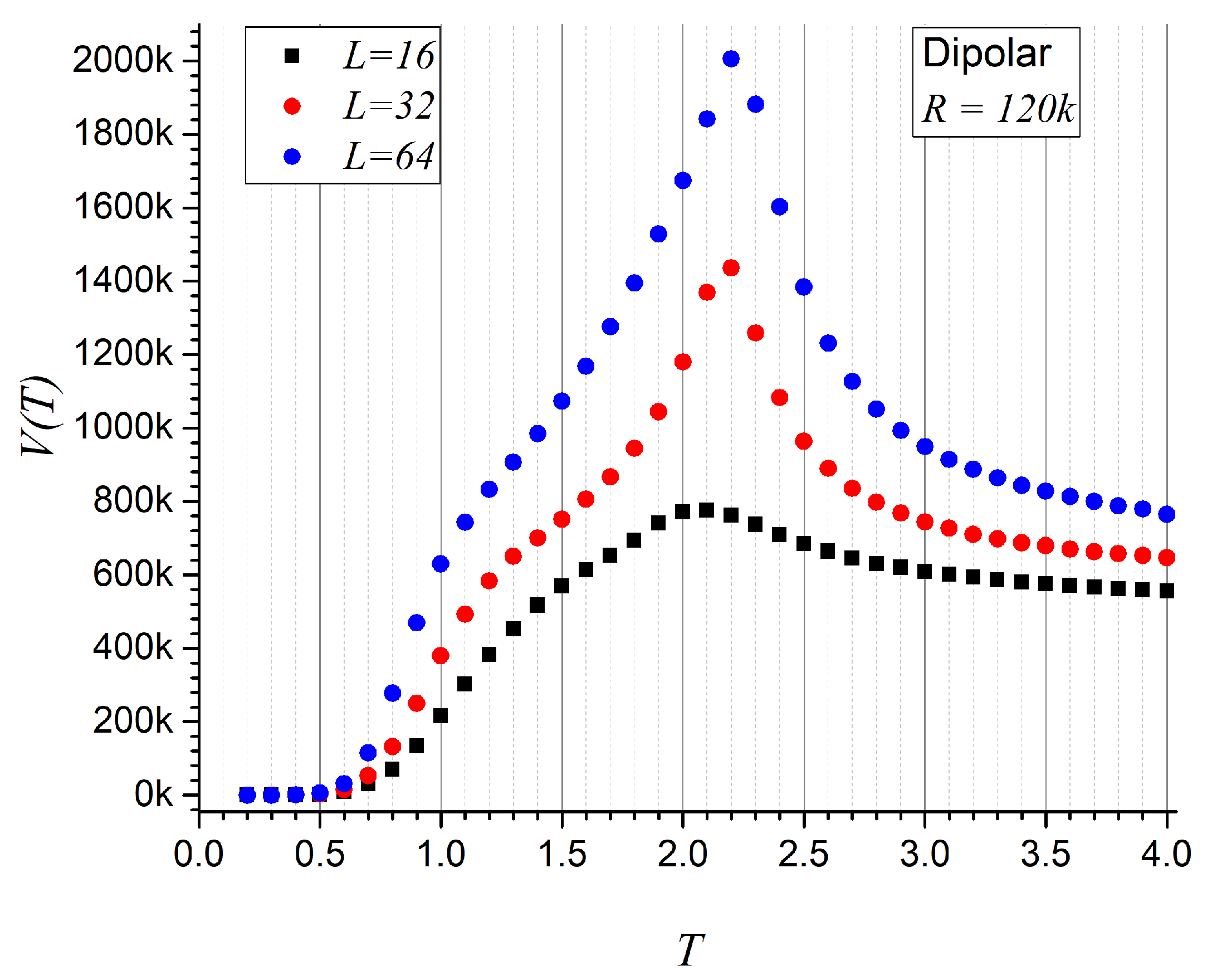
- Non-repeatability V, defined directly by the compressed weight: .
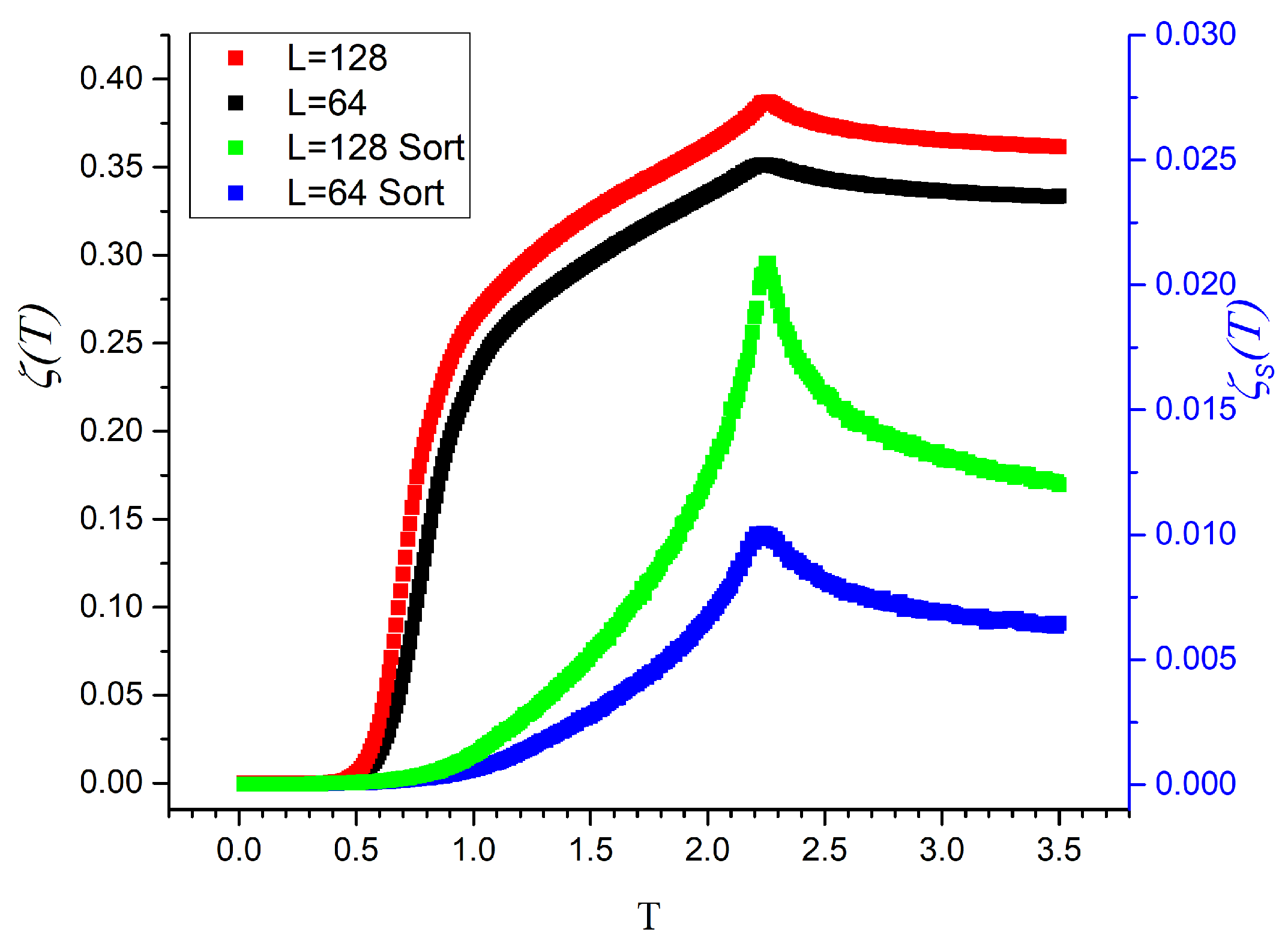
- Regular mutability , given by Equation (7). This function allows reversibility since the map generated by wlzip stores the locations of the values along the original chain of data.
- Sorted mutability , given by Equation (8). This function does not allow the recovery of the original data sequence.
- Shannon entropy H, given by Equation (2). This function does not allow the recovery of the original data sequence.
3. Systems Under Study and Theoretical Basis
- (1)
- First system: Square spin lattice. At a given temperature T, the system’s energy is computed using the appropriate Hamiltonian, as detailed below. The time evolution is simulated via a Monte Carlo (MC) procedure [50,51,52,53] in which, at each time step t, a spin (or magnetic moment) is randomly selected and temporarily flipped. The resulting energy difference (defined as the energy before minus the energy after the flip) is evaluated. If , the flip is accepted unconditionally and is updated. If , the flip is accepted with a probability governed by the Metropolis criterion.This process is carried out over MC steps at each temperature to ensure equilibration (with R defined per case). A subsequent sequence of MC steps is then used to collect data: every 20 MC steps, the value of a relevant observable is recorded, yielding a total of R entries. The most probable value of the observable is taken as its average over these R measurements. The temperature is then updated as , with , unless otherwise specified.
- (1a)
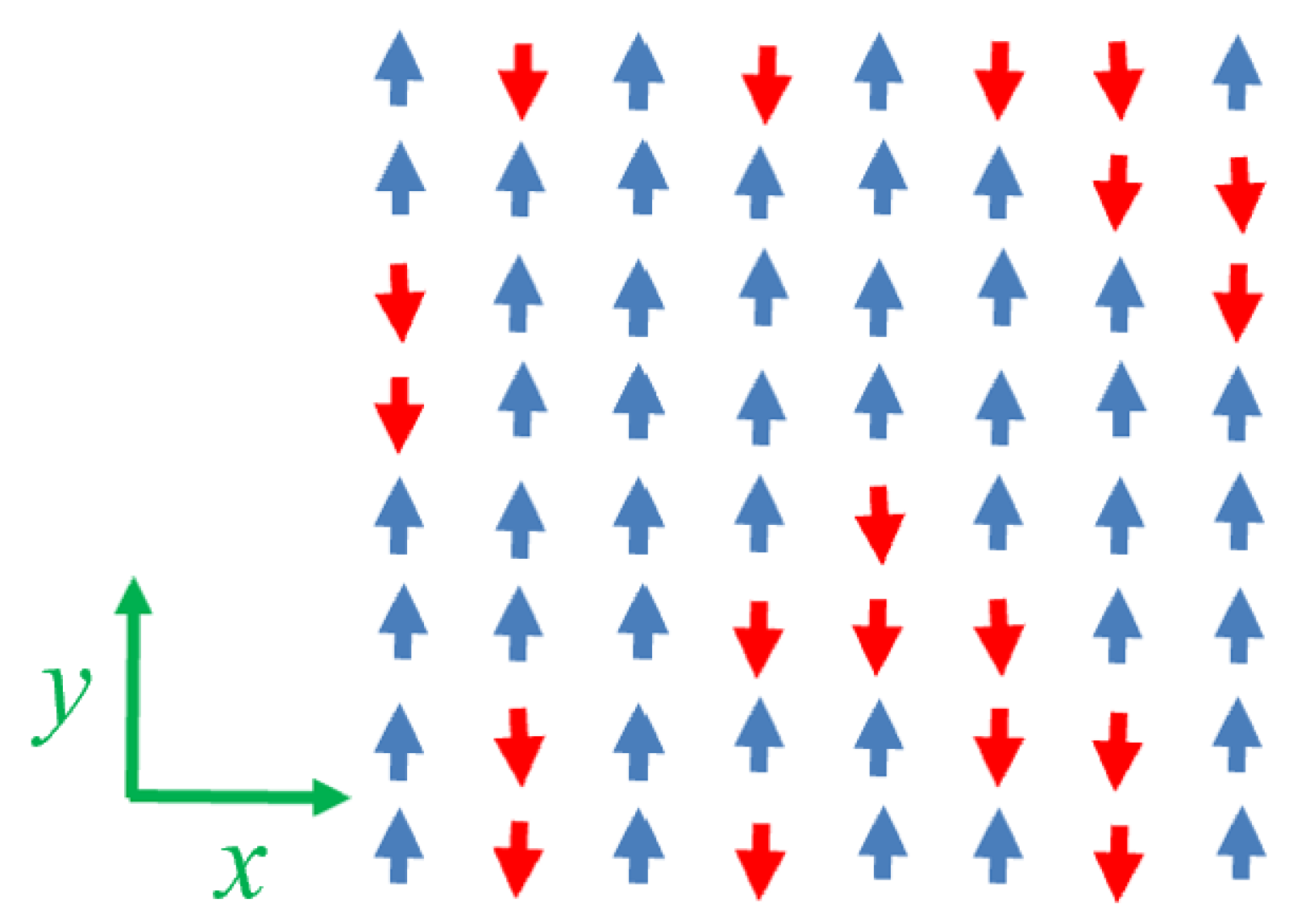
- Ising magnets. In this case, the magnetic moments can take values (aligned with ) or (aligned with ). Only nearest-neighbor interactions are considered, described by the standard exchange Hamiltonian [54,55,56]:where the summation is over all nearest-neighbor pairs, and denotes a ferromagnetic coupling constant. Indices and denote distinct lattice sites. Free boundary conditions are imposed, which are particularly suitable for modeling nanoscale systems.
- (1b)
- Dipolar magnets. In this configuration, narrow ferromagnets with strong shape anisotropy are positioned at the vertices of the same square lattice and aligned along the y-axis. These magnets are treated as point dipoles, assuming their physical size is much smaller than the lattice spacing. Their interactions are mediated by the demagnetizing field, modeled via dipole–dipole interactions. The Hamiltonian contribution, , due to a dipole interacting with all other dipoles , is given by [39,40,41,42,43]where is the vector from site to , and is its unit vector. The total Hamiltonian is obtained by summing over contributions, avoiding double counting. This is equivalent to summing over all dipole pairs. The notation is retained for consistency with the exchange model.
- (2)
- Second system: Seismic activity. The United States Geological Survey (USGS) provides a comprehensive catalog of seismic events in the United States. From this database, we extract a time series of earthquake magnitudes exceeding a given threshold (typically M 1.5) within a predefined geographical “rectangle” and depth range. Two specific regions are considered:
- (2a)
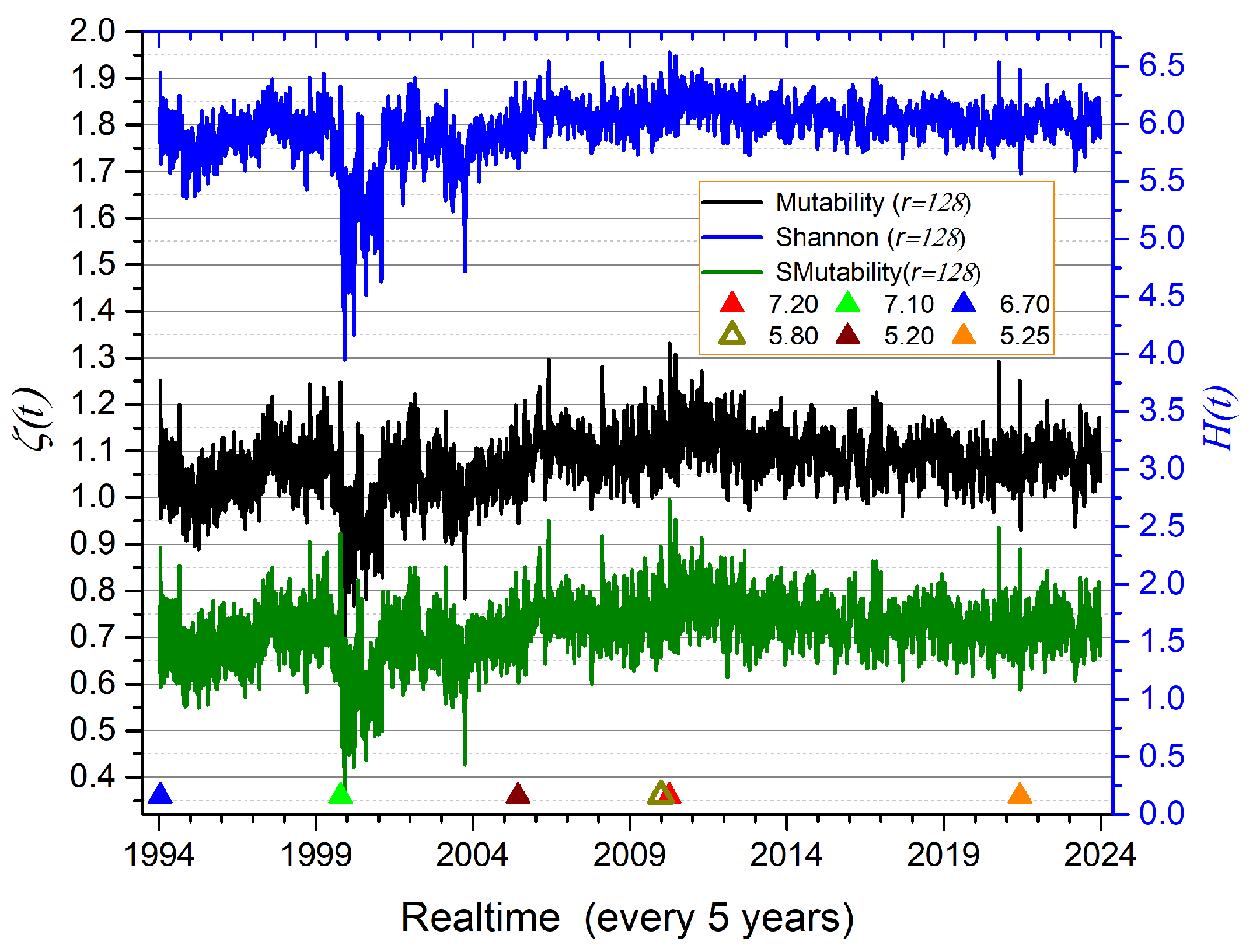
- California seismicity. Data is selected from the region bounded by longitudes 115° W to 119° W and latitudes 31° N to 35° N, with depths limited to 35 km. The data extraction spans the period from 1 January 1994 to 31 December 2023, resulting in a total of 131,459 seismic events. This region includes the M 7.2 El Mayor–Cucapah earthquake of 4 April 2010.
- (2b)
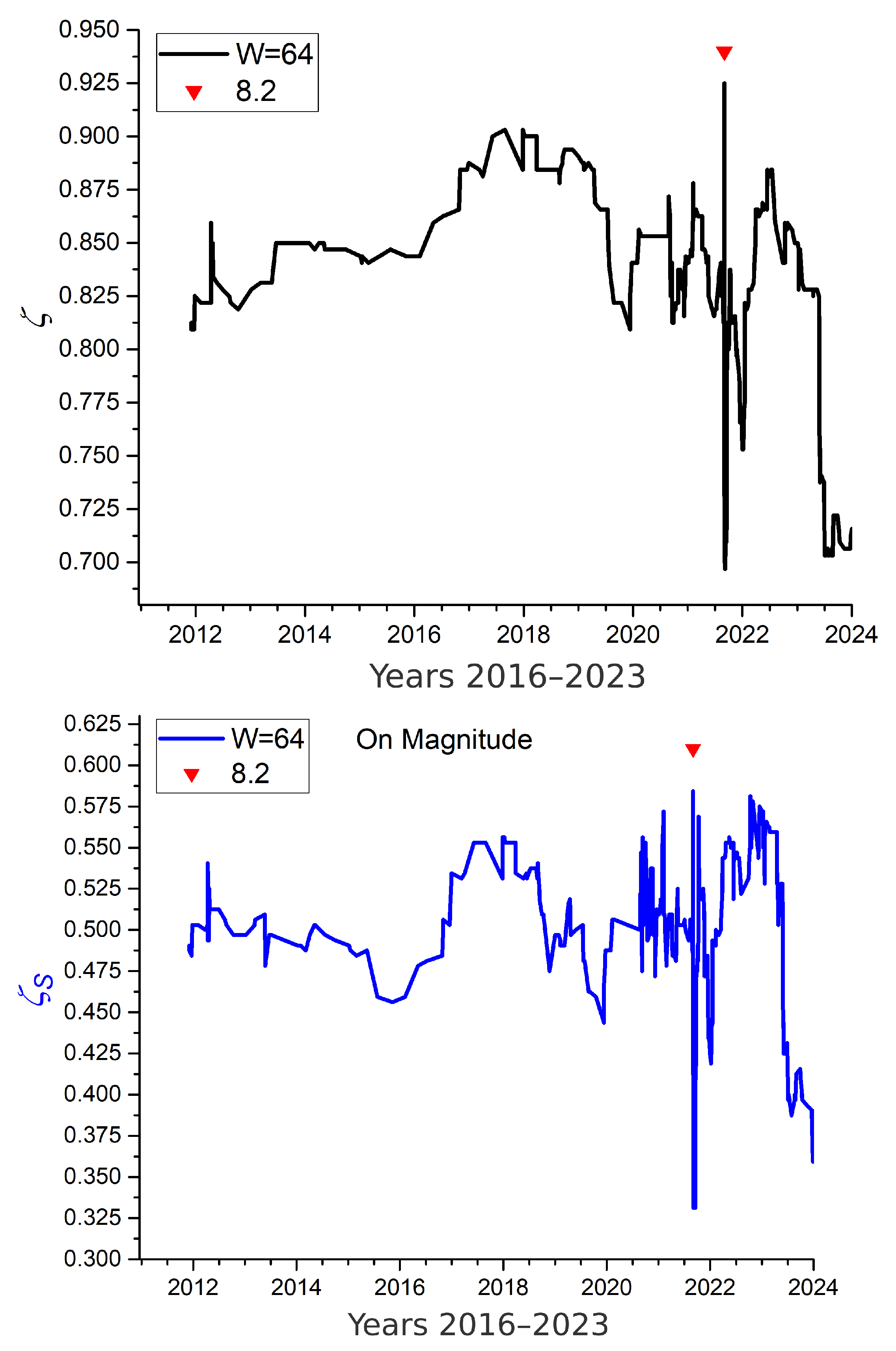
- Alaska seismicity. Data is extracted from a smaller region defined by longitudes 157.3° W to 158.2° W and latitudes 54.5° N to 55.5° N, down to depths of 70 km. The time span from 1 January 2020 to 31 December 2023 includes 629 recorded earthquakes. This region is notable for recent intense seismic activity, including the M 8.2 Chignik earthquake of 29 July 2021. Due to the relatively low number of events, this dataset presents an opportunity to test information-theoretic methods under sparse data conditions.
4. Results and Discussion
- The similarity of the three curves confirms the connection between Shannon entropy and mutability.
- Major earthquakes tend to coincide with upward spikes in the curves; however, the converse is not always true—some spikes are not linked to single large events, indicating the possible influence of local activity or seismic swarms.
- Mutability curves more clearly reveal the undulating trends in the data.
- Downward behavior associated with aftershock regimes is better captured by mutability curves.
- Mutability exhibits richer texture than Shannon entropy, with greater amplitude and clearer resolution of consecutive segments.
- Sorted mutability provides slightly more detail than regular mutability—for example, the downward triplet near 1995, sharper peaks around 2010, and broader oscillation ranges within the same vertical span.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tsallis, C. Entropy. Encyclopedia 2022, 2, 264–300. [Google Scholar] [CrossRef]
- Wehrl, A. General properties of entropy. Rev. Mod. Phys. 1978, 50, 221. [Google Scholar] [CrossRef]
- Greiner, W.; Neise, L.; Stöcker, H. Thermodynamics and Statistical Mechanics; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Callen, H.B.; Scott, H. Thermodynamics and an Introduction to Thermostatistics; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Zanchini, E.; Beretta, G.P. Recent progress in the definition of thermodynamic entropy. Entropy 2014, 16, 1547–1570. [Google Scholar] [CrossRef]
- Gyftopoulos, E.P.; Cubukcu, E. Entropy: Thermodynamic definition and quantum expression. Phys. Rev. E 1997, 55, 3851. [Google Scholar] [CrossRef]
- Clausius, R. The Mechanical Theory of Heat: With its Applications to the Steam-Engine and to Physical Properties of Bodies; John van Voorst: London, UK, 1865. [Google Scholar]
- Lebon, G. History of entropy and the second law of thermodynamics in classical thermodynamics. Entropy 2019, 21, 562. [Google Scholar]
- Pérez, R. A historical review of entropy: From Clausius to black hole thermodynamics. Rev. Mex. Física 2013, 59, 432–442. [Google Scholar]
- Zemansky, M.W.; Dittman, R.H. Heat and Thermodynamics, 7th ed.; Classic Textbook with Historical Discussion on Clausius’ Entropy; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Buchdahl, H. Entropy and the second law: Interpretation and policy. Am. J. Phys. 1966, 34, 839–845. [Google Scholar]
- Pathria, R.; Beale, P.D. Statistical Mechanics, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Reichl, L.E. A Modern Course in Statistical Physics, 2nd ed.; Wiley-VCH: New York, NY, USA, 1998. [Google Scholar]
- Huang, K. Statistical Mechanics, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1987. [Google Scholar]
- Landau, L.; Lifshitz, E. Statistical Physics, Part 1, 3rd ed.; Pergamon Press: Oxford, UK, 1980. [Google Scholar]
- Gibbs, J.W. Elementary Principles in Statistical Mechanics; Yale University Press: New Haven, CT, USA, 1902. [Google Scholar]
- Boltzmann, L. Über die Beziehung zwischen dem zweiten Hauptsatze der mechanischen Wärmetheorie und der Wahrscheinlichkeitsrechnung respektive den Sätzen über das Wärmegleichgewicht. Wien Berichte 1877, 76, 373–435. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Urbana, IL, USA, 1949. [Google Scholar]
- Pierce, J.R. An Introduction to Information Theory: Symbols, Signals and Noise. Am. J. Phys. 1961, 29, 504–505. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley-Interscience: New York, NY, USA, 1991. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Vogel, E.E.; Saravia, G. Information theory applied to econophysics: Stock market behaviors. Eur. Phys. J. B 2014, 87, 177. [Google Scholar] [CrossRef]
- Vogel, E.; Saravia, G.; Astete, J.; Díaz, J.; Riadi, F. Information theory as a tool to improve individual pensions: The Chilean case. Phys. A Stat. Mech. Appl. 2015, 424, 372–382. [Google Scholar] [CrossRef]
- Negrete, O.A.; Vargas, P.; Peña, F.J.; Saravia, G.; Vogel, E.E. Entropy and Mutability for the q-state Clock Model in Small Systems. Entropy 2018, 20, 933. [Google Scholar] [CrossRef]
- Negrete, O.A.; Vargas, P.; Peña, F.J.; Saravia, G.; Vogel, E.E. Short-range Berezinskii-Kosterlitz-Thouless phase characterization for the q-state clock model. Entropy 2021, 23, 1019. [Google Scholar] [CrossRef]
- Vogel, E.; Saravia, G.; Ramirez-Pastor, A.J.; Pasinetti, M. Alternative characterization of the nematic transition in deposition of rods on two-dimensional lattices. Phys. Rev. E 2020, 101, 022104. [Google Scholar] [CrossRef]
- Vogel, E.; Saravia, G.; Kobe, S.; Schuster, R. Onshore versus offshore capacity factor and reliability for wind energy production in Germany: 2010–2022. Energy Sci. Eng. 2024, 12, 2198–2208. [Google Scholar] [CrossRef]
- Contreras, D.J.; Vogel, E.E.; Saravia, G.; Stockins, B. Derivation of a measure of systolic blood pressure mutability: A novel information theory-based metric from ambulatory blood pressure tests. J. Am. Soc. Hypertens. 2016, 10, 217–223. [Google Scholar] [CrossRef]
- Pasten, D.; Saravia, G.; Vogel, E.E.; Posadas, A. Information theory and earthquakes: Depth propagation seismicity in northern Chile. Chaos Solitons Fractals 2022, 165, 112874. [Google Scholar] [CrossRef]
- Pasten, D.; Vogel, E.E.; Saravia, G.; Posadas, A.; Sotolongo, O. Tsallis entropy and mutability to characterize seismic sequences: The case of 2007–2014 northern Chile earthquakes. Entropy 2023, 25, 1417. [Google Scholar] [CrossRef]
- Posadas, A.; Pasten, D.; Vogel, E.E.; Saravia, G. Earthquake hazard characterization by using entropy: Application to northern Chilean earthquakes. Nat. Hazards Earth Syst. Sci. 2023, 23, 1911–1920. [Google Scholar] [CrossRef]
- Vogel, E.E.; Pastén, D.; Saravia, G.; Aguilera, M.; Posadas, A. 2021 Alaska earthquake: Entropy approach to its precursors and aftershock regimes. Nat. Hazards Earth Syst. Sci. 2024, 24, 3895–3906. [Google Scholar] [CrossRef]
- Caitano, R.; Ramirez-Pastor, A.; Vogel, E.; Saravia, G. Competition analysis of grain flow versus clogging by means of information theory. Granul. Matter 2024, 26, 77. [Google Scholar] [CrossRef]
- Ising, E. Beitrag zur Theorie des Ferromagnetismus. Z. Phys. 1925, 31, 253–258. [Google Scholar] [CrossRef]
- Onsager, L. Crystal Statistics. I. A Two-Dimensional Model with an Order-Disorder Transition. Phys. Rev. 1944, 65, 117–149. [Google Scholar] [CrossRef]
- Yeomans, J.M. Statistical Mechanics of Phase Transitions; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- Brush, S.G. History of the Lenz-Ising model. Rev. Mod. Phys. 1967, 39, 883–893. [Google Scholar] [CrossRef]
- MacIsaac, A.B.; Whitehead, J.P.; Robinson, M.C.; De’Bell, K. A model of magnetic ordering in two-dimensional dipolar systems. Phys. Rev. B 1995, 51, 16033–16044. [Google Scholar] [CrossRef]
- De’Bell, K.; MacIsaac, A.B.; Whitehead, J.P. Dipolar effects in magnetic thin films and quasi-two-dimensional systems. Rev. Mod. Phys. 2000, 72, 225–257. [Google Scholar] [CrossRef]
- Garel, T.; Doniach, S. Phase transitions with spontaneous modulation—The dipolar Ising ferromagnet. Phys. Rev. B 1982, 26, 325–329. [Google Scholar] [CrossRef]
- Vaterlaus, A.; Stamm, C.; Maier, U.; Pescia, D.; Egger, W.; Beutler, T.; Wermelinger, J.; Melchior, H. Spin relaxation in the two-dimensional dipolar Ising ferromagnet Fe/W(001). Phys. Rev. Lett. 2000, 84, 2247–2250. [Google Scholar] [CrossRef]
- Telo da Gama, M.M.; Bortz, M.L.; Branco, N.S. Stripe phases in two-dimensional Ising models with competing interactions. Phys. Rev. E 2002, 66, 046123. [Google Scholar] [CrossRef]
- Bostrom, A.; McBride, S.K.; Becker, J.S.; Goltz, J.D.; de Groot, R.M.; Peek, L.; Terbush, B.; Dixon, M. Great expectations for earthquake early warnings on the United States West Coast. Int. J. Disaster Risk Reduct. 2022, 82, 103296. [Google Scholar] [CrossRef]
- Qu, R.; Ji, Y.; Zhu, W.; Zhao, Y.; Zhu, Y. Fast and slow earthquakes in Alaska: Implications from a three-dimensional thermal regime and slab metamorphism. Appl. Sci. 2022, 12, 11139. [Google Scholar] [CrossRef]
- Cortez, V.; Saravia, G.; Vogel, E. Phase diagram and reentrance for the 3D Edwards–Anderson model using information theory. J. Magn. Magn. Mater. 2014, 372, 173–180. [Google Scholar] [CrossRef]
- Vogel, E.; Saravia, G.; Cortez, L. Data compressor designed to improve recognition of magnetic phases. Phys. A Stat. Mech. Appl. 2012, 391, 1591–1601. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics: Approaching a Complex World; Springer: New York, NY, USA, 2009; Volume 1. [Google Scholar]
- Sotolongo-Costa, O.; Posadas, A. Fragment-asperity interaction model for earthquakes. Phys. Rev. Lett. 2004, 92, 048501. [Google Scholar] [CrossRef]
- Binder, K.; Heermann, D.W. Monte Carlo Simulation in Statistical Physics: An Introduction, 1st ed.; Springer: Berlin, Germany, 1986. [Google Scholar] [CrossRef]
- Landau, D.P.; Binder, K. Monte Carlo simulations in statistical physics: From basic principles to advanced applications. Phys. Rep. 2001, 349, 1–57. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Newman, M.E.J.; Barkema, G.T. Monte Carlo Methods in Statistical Physics; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Newell, G.F.; Montroll, E.W. On the theory of the Ising model of ferromagnetism. Rev. Mod. Phys. 1953, 25, 353. [Google Scholar] [CrossRef]
- Zandvliet, H.J.; Hoede, C. Spontaneous magnetization of the square 2D Ising lattice with nearest-and weak next-nearest-neighbour interactions. Phase Transit. 2009, 82, 191–196. [Google Scholar] [CrossRef][Green Version]
- Dixon, J.; Tuszyński, J.; Carpenter, E. Analytical expressions for energies, degeneracies and critical temperatures of the 2D square and 3D cubic Ising models. Phys. A Stat. Mech. Appl. 2005, 349, 487–510. [Google Scholar] [CrossRef]


| i | M | Map of M | Map of | |||
|---|---|---|---|---|---|---|
| 1 | 1.7 | 1.7 0 10 12 9 | 4 | 0.12500 | 1.5 | 1.5 0,2 |
| 2 | 2.7 | 2.7 1 | 1 | 0.03125 | 1.5 | 1.6 2,4 |
| 3 | 1.5 | 1.5 2,2 | 2 | 0.06250 | 1.6 | 1.7 7,4 |
| 4 | 1.5 | 1.8 4 | 1 | 0.03125 | 1.6 | 1.8 11 |
| 5 | 1.8 | 1.6 5 2 2 4,2 | 5 | 0.15625 | 1.6 | 1.9 12,3 |
| 6 | 1.6 | 2.4 8 15 3 | 3 | 0.09375 | 1.6 | 2.0 15 |
| 7 | 1.9 | 2.0 11 | 1 | 0.03125 | 1.6 | 2.2 16,3 |
| 8 | 1.6 | 2.2 12 9 9 | 3 | 0.09375 | 1.7 | 2.3 19 |
| 9 | 2.4 | 3.9 15 2 | 2 | 0.06250 | 1.7 | 2.4 20,3 |
| 10 | 1.6 | 5.4 16 | 1 | 0.03125 | 1.7 | 2.6 23,2 |
| 11 | 1.7 | 2.9 18,2 | 2 | 0.06250 | 1.7 | 2.7 25 |
| 12 | 2.0 | 1.9 6 18 5 | 3 | 0.09375 | 1.8 | 2.9 26,2 |
| 13 | 2.2 | 2.6 20 8 | 2 | 0.06250 | 1.9 | 3.4 28 |
| 14 | 1.6 | 3.4 25 | 1 | 0.03125 | 1.9 | 3.9 29,2 |
| 15 | 1.6 | 2.3 27 | 1 | 0.03125 | 1.9 | 5.4 31 |
| 16 | 3.9 | 2.0 | ||||
| 17 | 5.4 | 2.2 | ||||
| 18 | 3.9 | 2.2 | ||||
| 19 | 2.9 | 2.2 | ||||
| 20 | 2.9 | 2.3 | ||||
| 21 | 2.6 | 2.4 | ||||
| 22 | 2.2 | 2.4 | ||||
| 23 | 1.7 | 2.4 | ||||
| 24 | 2.4 | 2.6 | ||||
| 25 | 1.9 | 2.6 | ||||
| 26 | 3.4 | 2.7 | ||||
| 27 | 2.4 | 2.9 | ||||
| 28 | 2.3 | 2.9 | ||||
| 29 | 2.6 | 3.4 | ||||
| 30 | 1.9 | 3.9 | ||||
| 31 | 2.2 | 3.9 | ||||
| 32 | 1.7 | 5.4 | ||||
| 0.944 | 0.594 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vogel, E.E.; Peña, F.J.; Saravia, G.; Vargas, P. Entropy Alternatives for Equilibrium and Out-of-Equilibrium Systems. Entropy 2025, 27, 689. https://doi.org/10.3390/e27070689
Vogel EE, Peña FJ, Saravia G, Vargas P. Entropy Alternatives for Equilibrium and Out-of-Equilibrium Systems. Entropy. 2025; 27(7):689. https://doi.org/10.3390/e27070689
Chicago/Turabian StyleVogel, Eugenio E., Francisco J. Peña, Gonzalo Saravia, and Patricio Vargas. 2025. "Entropy Alternatives for Equilibrium and Out-of-Equilibrium Systems" Entropy 27, no. 7: 689. https://doi.org/10.3390/e27070689
APA StyleVogel, E. E., Peña, F. J., Saravia, G., & Vargas, P. (2025). Entropy Alternatives for Equilibrium and Out-of-Equilibrium Systems. Entropy, 27(7), 689. https://doi.org/10.3390/e27070689









