Factor Graph-Based Online Bayesian Identification and Component Evaluation for Multivariate Autoregressive Exogenous Input Models †
Abstract
1. Introduction
- We derive a message-passing algorithm for exact recursive Bayesian inference in MARX models, maintaining full posterior distributions while ensuring computational efficiency.
- We extend the inference framework to predict future system outputs that explicitly account for parameter uncertainty, improving robustness for real-time applications.
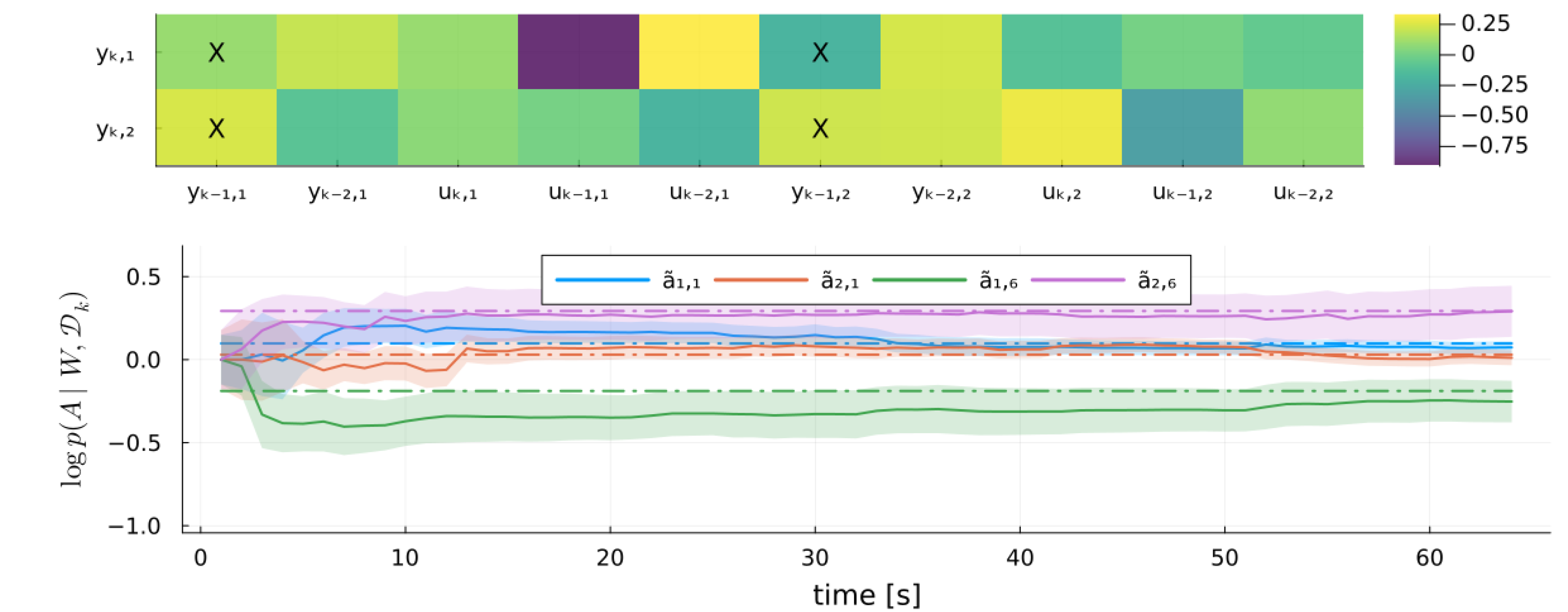
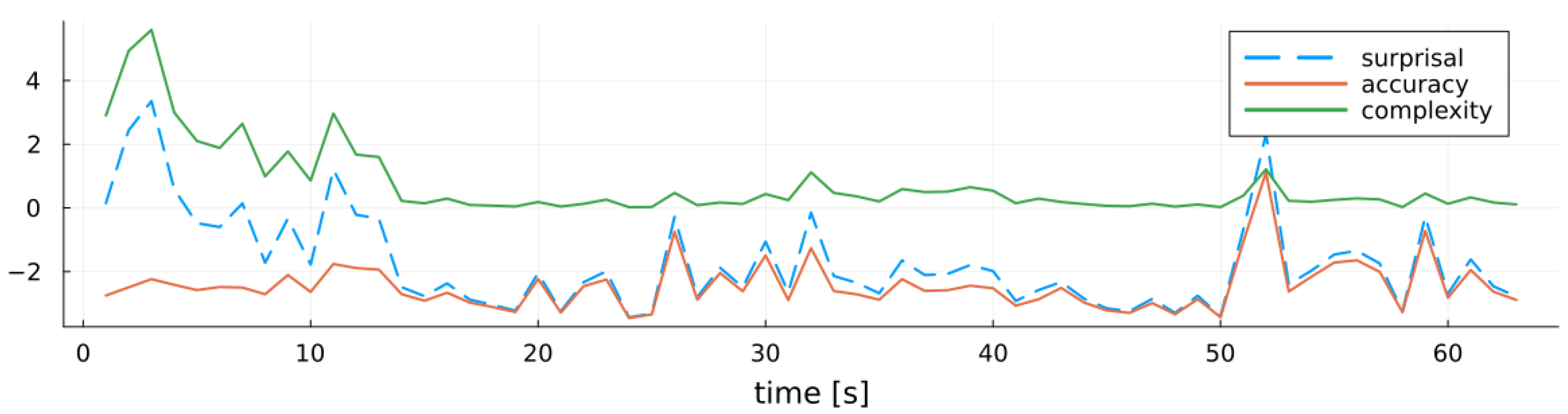
- We introduce a novel model evaluation method by decomposing the negative log-model evidence (surprisal) into contributions from individual nodes and edges in the factor graph, providing insights into uncertainty and learning dynamics.
- We demonstrate the effectiveness of our approach through empirical evaluations on (i) a synthetic MARX system with known parameters for verification, and (ii) two synthetic dynamical systems with unknown parameters: a double mass-spring-damper system and a nonlinear double pendulum system.
2. Problem Statement
3. Model Specification
Factor Graph
4. Inference
4.1. Parameter Estimation
4.2. Output Prediction
5. Model Evaluation
5.1. MARX Model Evidence and Surprisal
5.2. MARX Variational Free Energy
6. Experiments
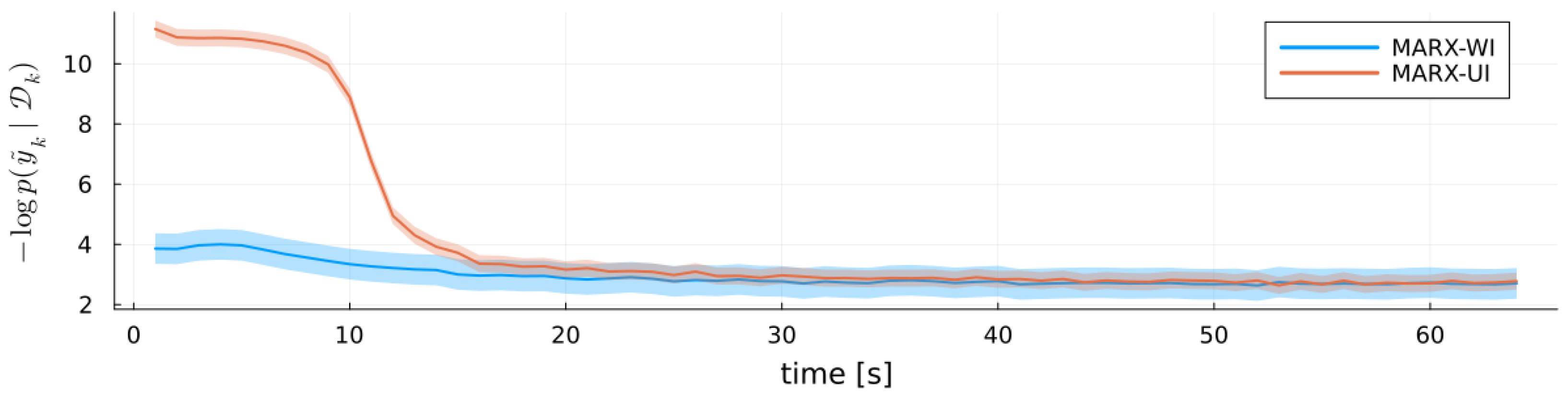
6.1. Baseline Estimator
6.2. Verification
6.3. Validation
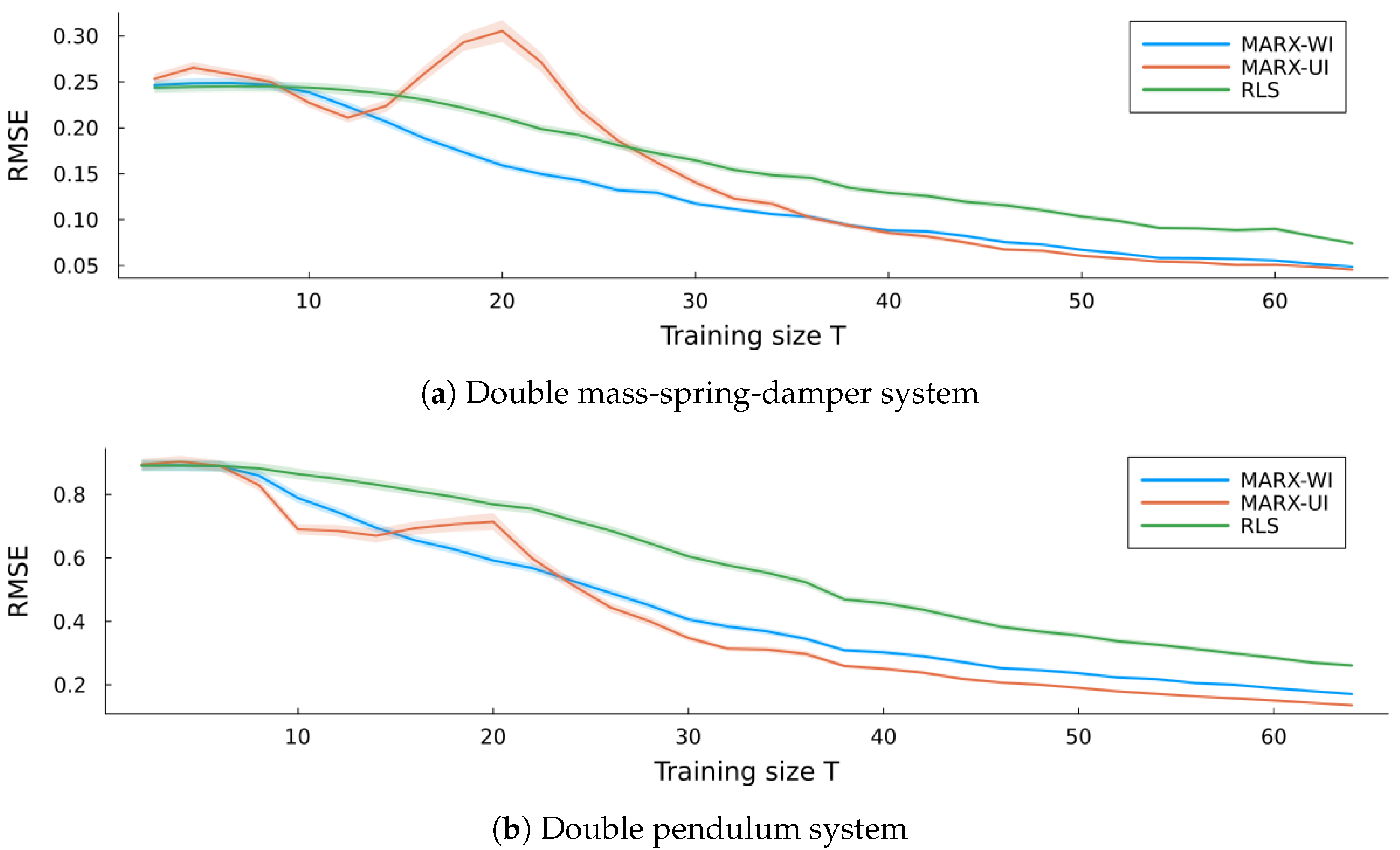
6.3.1. Linear System: Double Mass-Spring-Damper
6.3.2. Nonlinear System: Double Pendulum
6.3.3. Results
7. Discussion
7.1. Computational Efficiency
7.2. Limitations
7.3. Future Work
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MARX | multivariate autoregressive models with exogenous inputs |
| MARX-UI | MARX model with uninformative prior |
| MARX-WI | MARX model with weakly informative prior |
| VFE | variational free energy |
| BFE | Bethe Free Energy |
| RLS | recursive least squares |
| RMSE | Root Mean Square Error |
| ODE | Ordinary Differential Equation |
| KL | Kullback–Leibler |
Appendix A. Parameter Estimation
Appendix B. Backwards Message from Likelihood
Appendix C. Product of Matrix Normal Wishart Distributions
Appendix D. Marginalization over A
Appendix E. Marginalization over W
Appendix F. Cross-Entropy of a Matrix Normal Wishart Relative to a Matrix Normal Wishart
Appendix G. Entropy of a Matrix Normal Wishart
Appendix H. KL-Divergence of a Matrix Normal Wishart from a Matrix Normal Wishart
Appendix I. Cross-Entropy of a Matrix Normal Wishart Relative to a Multivariate Normal
References
- Nisslbeck, T.N.; Kouw, W.M. Online Bayesian system identification in multivariate autoregressive models via message passing. (accepted). In Proceedings of the European Control Conference, Thessaloniki, Greece, 24–27 June 2025; IEEE: New York, NY, USA, 2025. [Google Scholar]
- Tiao, G.C.; Zellner, A. On the Bayesian estimation of multivariate regression. J. R. Stat. Soc. Ser. B 1964, 26, 277–285. [Google Scholar] [CrossRef]
- Hannan, E.J.; McDougall, A.; Poskitt, D.S. Recursive estimation of autoregressions. J. R. Stat. Soc. Ser. B 1989, 51, 217–233. [Google Scholar] [CrossRef]
- Karlsson, S. Forecasting with Bayesian vector autoregression. Handb. Econ. Forecast. 2013, 2, 791–897. [Google Scholar]
- Nisslbeck, T.N.; Kouw, W.M. Coupled autoregressive active inference agents for control of multi-joint dynamical systems. In Proceedings of the International Workshop on Active Inference, Oxford, UK, 9–11 September 2024; Springer: Berlin/Heidelberg, Germany, 2024. [Google Scholar]
- Barber, D. Bayesian Reasoning and Machine Learning; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Hecq, A.; Issler, J.V.; Telg, S. Mixed causal–noncausal autoregressions with exogenous regressors. J. Appl. Econom. 2020, 35, 328–343. [Google Scholar] [CrossRef]
- Penny, W.; Harrison, L. Multivariate autoregressive models. In Statistical Parametric Mapping: The Analysis of Functional Brain Images; Academic Press: Amsterdam, The Netherlands, 2007; pp. 534–540. [Google Scholar]
- Shaarawy, S.M.; Ali, S.S. Bayesian identification of multivariate autoregressive processes. Commun. Stat. Methods 2008, 37, 791–802. [Google Scholar] [CrossRef]
- Chaloner, K.; Verdinelli, I. Bayesian experimental design: A review. Stat. Sci. 1995, 10, 273–304. [Google Scholar] [CrossRef]
- Williams, G.; Drews, P.; Goldfain, B.; Rehg, J.M.; Theodorou, E.A. Information-theoretic model predictive control: Theory and applications to autonomous driving. IEEE Trans. Robot. 2018, 34, 1603–1622. [Google Scholar] [CrossRef]
- Kschischang, F.R.; Frey, B.J.; Loeliger, H.A. Factor graphs and the sum-product algorithm. IEEE Trans. Inf. Theory 2001, 47, 498–519. [Google Scholar] [CrossRef]
- Şenöz, İ.; van de Laar, T.; Bagaev, D.; de Vries, B. Variational message passing and local constraint manipulation in factor graphs. Entropy 2021, 23, 807. [Google Scholar] [CrossRef]
- Hoffmann, C.; Rostalski, P. Linear optimal control on factor graphs—a message passing perspective. IFAC-PapersOnLine 2017, 50, 6314–6319. [Google Scholar] [CrossRef]
- Loeliger, H.A.; Dauwels, J.; Hu, J.; Korl, S.; Ping, L.; Kschischang, F.R. The factor graph approach to model-based signal processing. Proc. IEEE 2007, 95, 1295–1322. [Google Scholar] [CrossRef]
- Cox, M.; van de Laar, T.; de Vries, B. A factor graph approach to automated design of Bayesian signal processing algorithms. Int. J. Approx. Reason. 2019, 104, 185–204. [Google Scholar] [CrossRef]
- Palmieri, F.A.; Pattipati, K.R.; Di Gennaro, G.; Fioretti, G.; Verolla, F.; Buonanno, A. A unifying view of estimation and control using belief propagation with application to path planning. IEEE Access 2022, 10, 15193–15216. [Google Scholar] [CrossRef]
- Forney, G.D. Codes on graphs: Normal realizations. IEEE Trans. Inf. Theory 2001, 47, 520–548. [Google Scholar] [CrossRef]
- Le, F.; Srivatsa, M.; Reddy, K.K.; Roy, K. Using graphical models as explanations in deep neural networks. In Proceedings of the IEEE International Conference on Mobile Ad-Hoc and Smart Systems, Monterey, CA, USA, 4–7 November 2019; pp. 283–289. [Google Scholar]
- Lecue, F. On the role of knowledge graphs in explainable AI. Semant. Web 2020, 11, 41–51. [Google Scholar] [CrossRef]
- Yedidia, J.S.; Freeman, W.T.; Weiss, Y. Bethe free energy, Kikuchi approximations, and belief propagation algorithms. Adv. Neural Inf. Process. Syst. 2001, 13. Available online: https://merl.com/publications/docs/TR2001-16.pdf (accessed on 8 June 2025).
- Zhang, Y.; Xu, W.; Liu, A.; Lau, V. Message Passing Based Wireless Federated Learning via Analog Message Aggregation. In Proceedings of the IEEE/CIC International Conference on Communications in China, Hangzhou, China, 7–9 August 2024; pp. 2161–2166. [Google Scholar]
- Bagaev, D.; de Vries, B. Reactive message passing for scalable Bayesian inference. Sci. Program. 2023, 2023, 6601690. [Google Scholar] [CrossRef]
- Podusenko, A.; Kouw, W.M.; de Vries, B. Message passing-based inference for time-varying autoregressive models. Entropy 2021, 23, 683. [Google Scholar] [CrossRef]
- Kouw, W.M.; Podusenko, A.; Koudahl, M.T.; Schoukens, M. Variational message passing for online polynomial NARMAX identification. In Proceedings of the American Control Conference, Atlanta, GA, USA, 8–10 June 2022; IEEE: New York, NY, USA, 2022; pp. 2755–2760. [Google Scholar]
- Petersen, K.B.; Pedersen, M.S. The matrix cookbook. Tech. Univ. Den. 2008, 7, 510. [Google Scholar]
- Soch, J.; Allefeld, C.; Faulkenberry, T.J.; Pavlovic, M.; Petrykowski, K.; Sarıtaş, K.; Balkus, S.; Kipnis, A.; Atze, H.; Martin, O.A. The Book of Statistical Proofs (Version 2023). 2024. Available online: https://zenodo.org/records/10495684 (accessed on 8 June 2025).
- Gupta, A.K.; Nagar, D.K. Matrix Variate Distributions; Chapman and Hall/CRC: Boca Raton, FL, USA, 2018. [Google Scholar]
- Särkkä, S. Bayesian Filtering and Smoothing; Cambridge University Press: London, UK; New York, NY, USA, 2013. [Google Scholar]
- Lopes, M.T.; Castello, D.A.; Matt, C.F.T. A Bayesian inference approach to estimate elastic and damping parameters of a structure subjected to vibration tests. In Proceedings of the Inverse Problems, Design and Optimization Symposium, Joao Pessoa, Brazil, 25–27 August 2010. [Google Scholar]
- Winn, J.; Bishop, C.M.; Jaakkola, T. Variational message passing. J. Mach. Learn. Res. 2005, 6, 661–694. [Google Scholar]
- Dauwels, J.; Korl, S.; Loeliger, H.A. Particle methods as message passing. In Proceedings of the IEEE International Symposium on Information Theory, Seattle, DC, USA, 9–14 July 2006; pp. 2052–2056. [Google Scholar]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Smith, R.; Friston, K.J.; Whyte, C.J. A step-by-step tutorial on active inference and its application to empirical data. J. Math. Psychol. 2022, 107, 102632. [Google Scholar] [CrossRef] [PubMed]
- Blei, D.M.; Kucukelbir, A.; McAuliffe, J.D. Variational inference: A review for statisticians. J. Am. Stat. Assoc. 2017, 112, 859–877. [Google Scholar] [CrossRef]
- Parr, T.; Pezzulo, G.; Friston, K.J. Active Inference: The Free Energy Principle in Mind, Brain, and Behavior; MIT Press: Cambridge, MA, USA, 2022. [Google Scholar]
- Friston, K.; Da Costa, L.; Sajid, N.; Heins, C.; Ueltzhöffer, K.; Pavliotis, G.A.; Parr, T. The free energy principle made simpler but not too simple. Phys. Rep. 2023, 1024, 1–29. [Google Scholar] [CrossRef]
- Yedidia, J.S.; Freeman, W.T.; Weiss, Y. Constructing free-energy approximations and generalized belief propagation algorithms. IEEE Trans. Inf. Theory 2005, 51, 2282–2312. [Google Scholar] [CrossRef]
- Proakis, J.G. Digital Signal Processing: Principles Algorithms and Applications; Pearson Education India: Noida, India, 2001. [Google Scholar]
- Robertson, D.G.E.; Dowling, J.J. Design and responses of Butterworth and critically damped digital filters. J. Electromyogr. Kinesiol. 2003, 13, 569–573. [Google Scholar] [CrossRef]
- Smith, J.O. Introduction to Digital Filters: With Audio Applications; Smith, J., Ed.; W3K Publishing: San Francisco, CA, USA, 2008; Volume 2. [Google Scholar]
- Zumbahlen, H. (Ed.) Linear Circuit Design Handbook; Newnes: Oxford, UK, 2011. [Google Scholar]
- Mello, R.G.; Oliveira, L.F.; Nadal, J. Digital Butterworth filter for subtracting noise from low magnitude surface electromyogram. Comput. Methods Programs Biomed. 2007, 87, 28–35. [Google Scholar] [CrossRef]
- Damgaard, M.R.; Pedersen, R.; Bak, T. Study of variational inference for flexible distributed probabilistic robotics. Robotics 2022, 11, 38. [Google Scholar] [CrossRef]
- Tedeschini, B.C.; Brambilla, M.; Nicoli, M. Message passing neural network versus message passing algorithm for cooperative positioning. IEEE Trans. Cogn. Commun. Netw. 2023, 9, 1666–1676. [Google Scholar] [CrossRef]
- Ta, D.N.; Kobilarov, M.; Dellaert, F. A factor graph approach to estimation and model predictive control on unmanned aerial vehicles. In Proceedings of the International Conference on Unmanned Aircraft Systems, Orlando, FL, USA, 27–30 May 2014; IEEE: New York, NY, USA, 2014; pp. 181–188. [Google Scholar]
- Castaldo, F.; Palmieri, F.A. A multi-camera multi-target tracker based on factor graphs. In Proceedings of the IEEE International Symposium on Innovations in Intelligent Systems and Applications, Alberobello, Italy, 23–25 June 2014; IEEE: New York, NY, USA, 2014; pp. 131–137. [Google Scholar]
- van Erp, B.; Bagaev, D.; Podusenko, A.; Şenöz, İ.; de Vries, B. Multi-agent trajectory planning with NUV priors. In Proceedings of the American Control Conference, Toronto, ON, Canada, 10–12 July 2024; IEEE: New York, NY, USA, 2024; pp. 2766–2771. [Google Scholar]
- Assimakis, N.; Adam, M.; Douladiris, A. Information filter and Kalman filter comparison: Selection of the faster filter. In Proceedings of the Information Engineering, Chongqing, China, 26–28 October 2012; Volume 2, pp. 1–5. [Google Scholar]
- Cover, T.M. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]


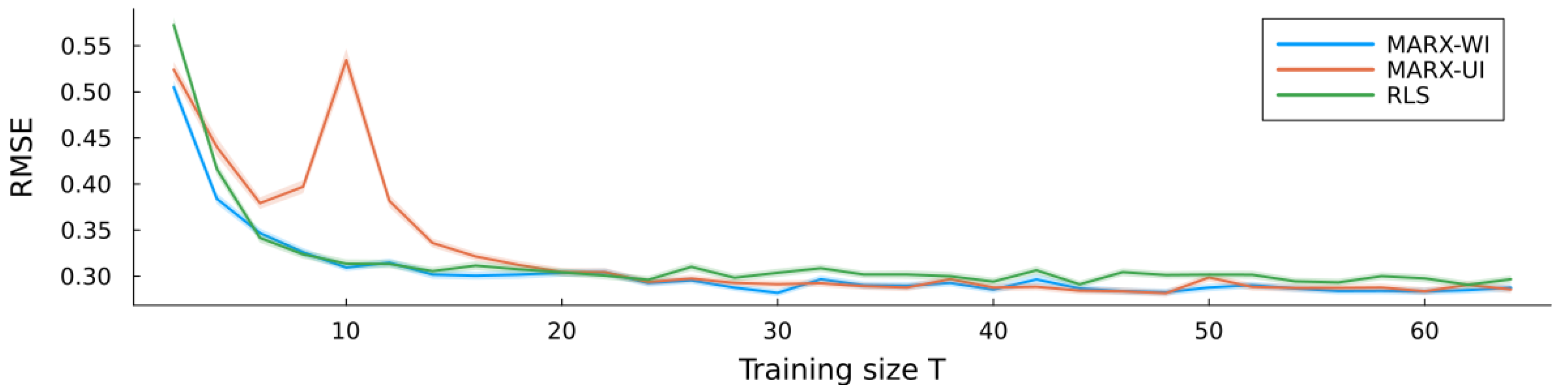
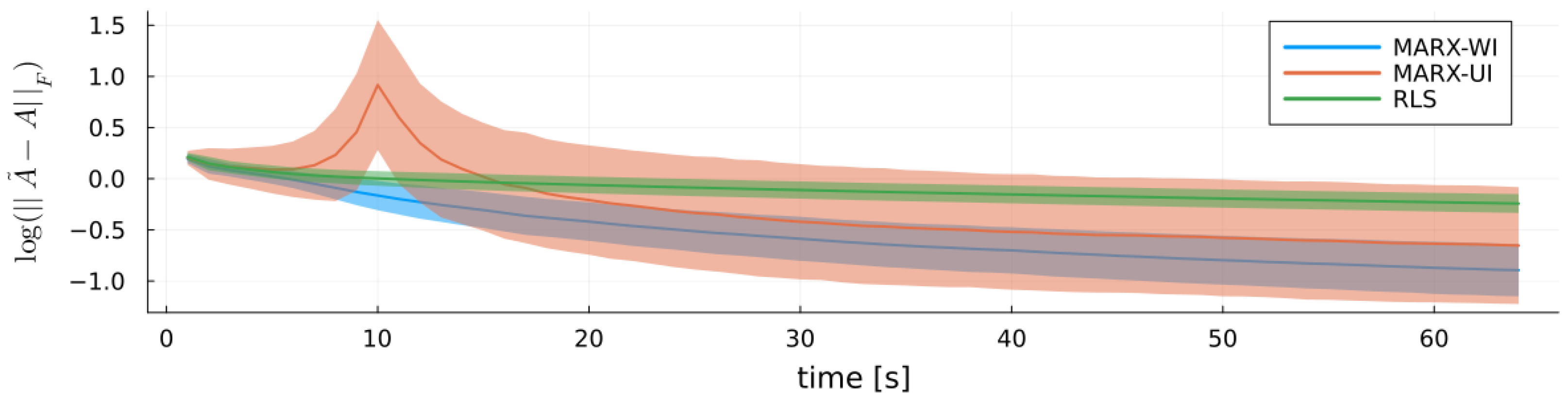

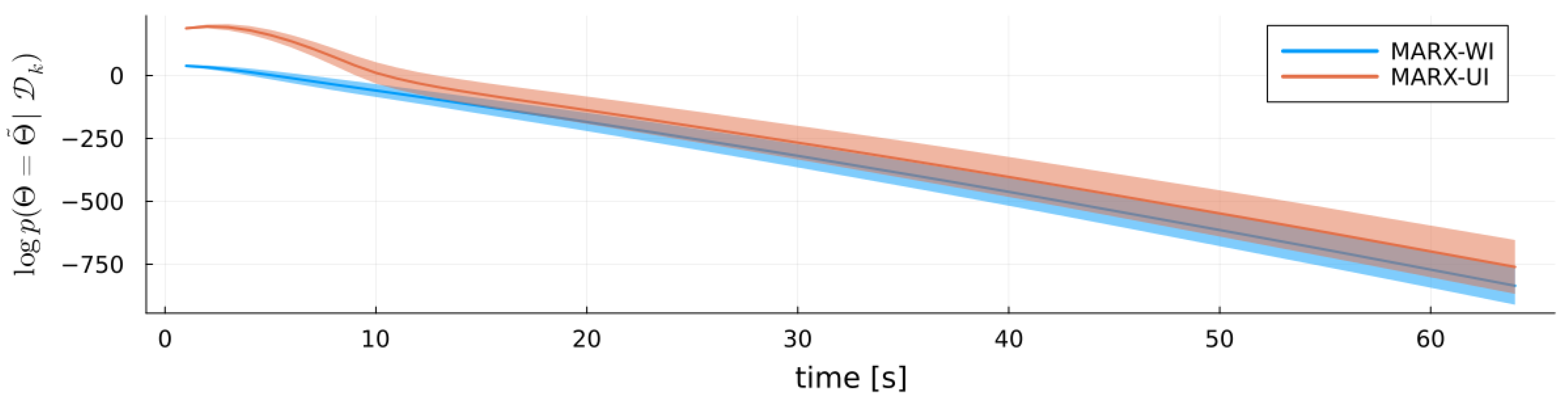
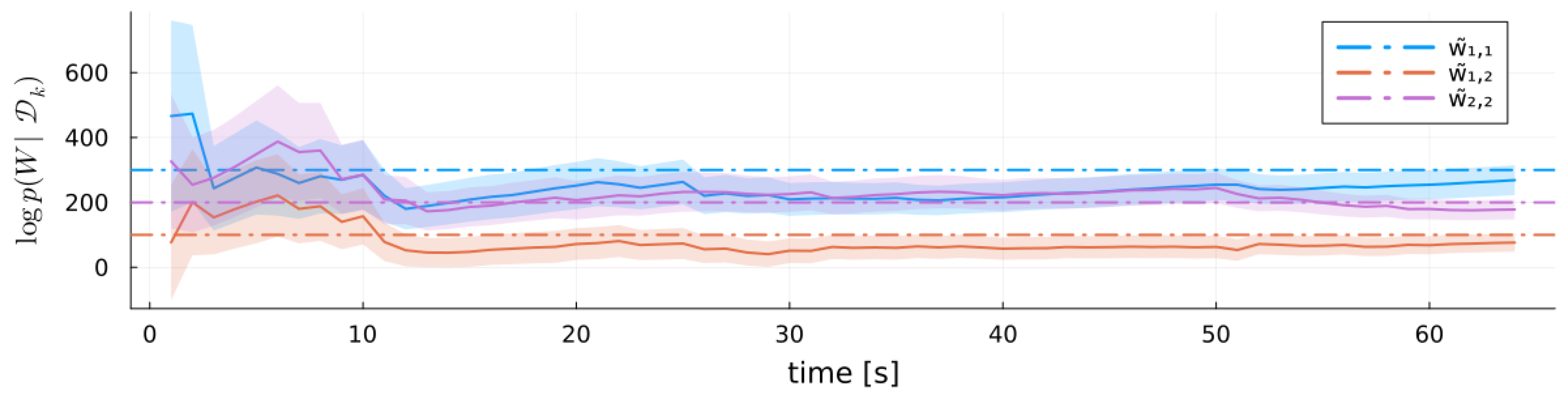


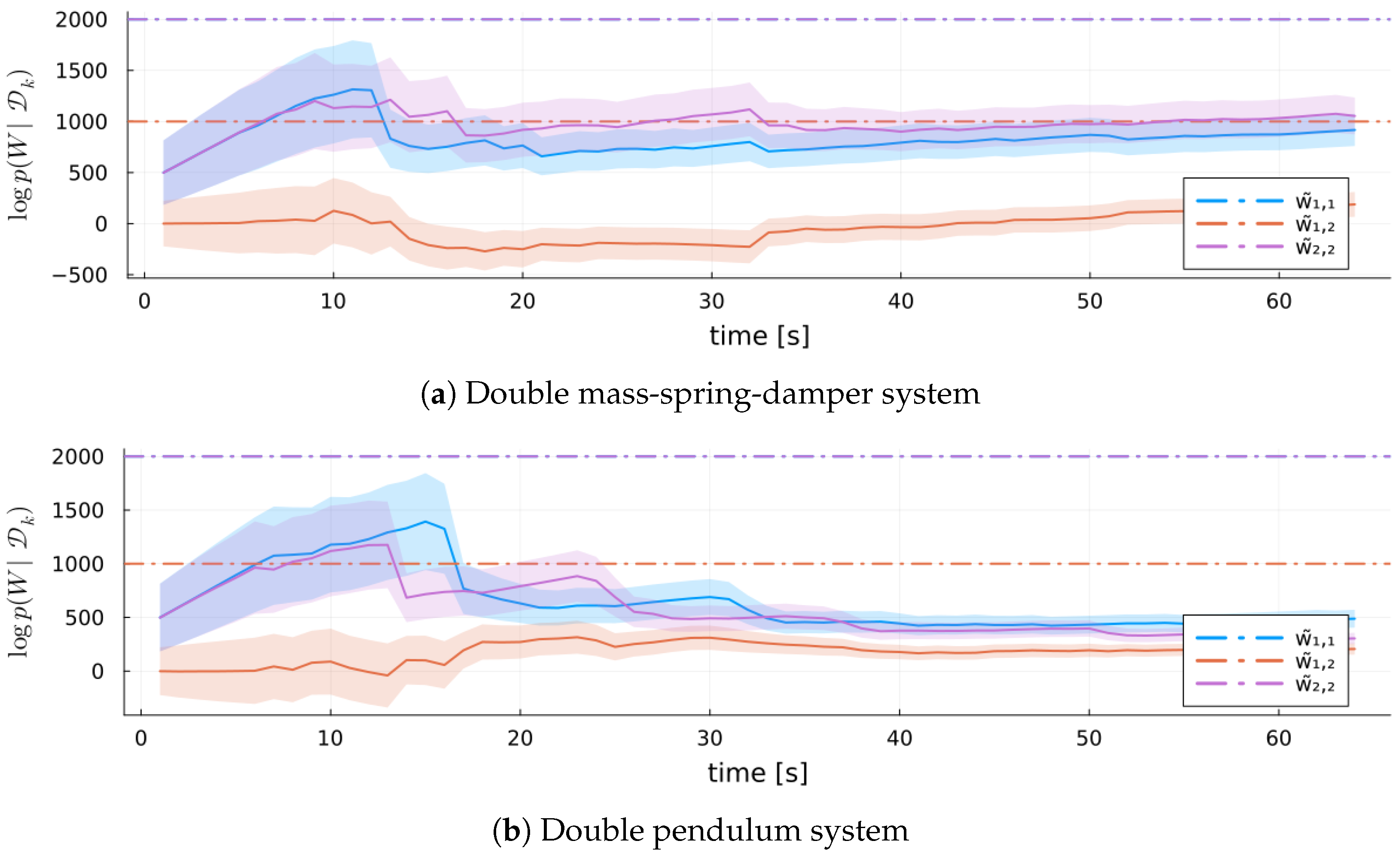
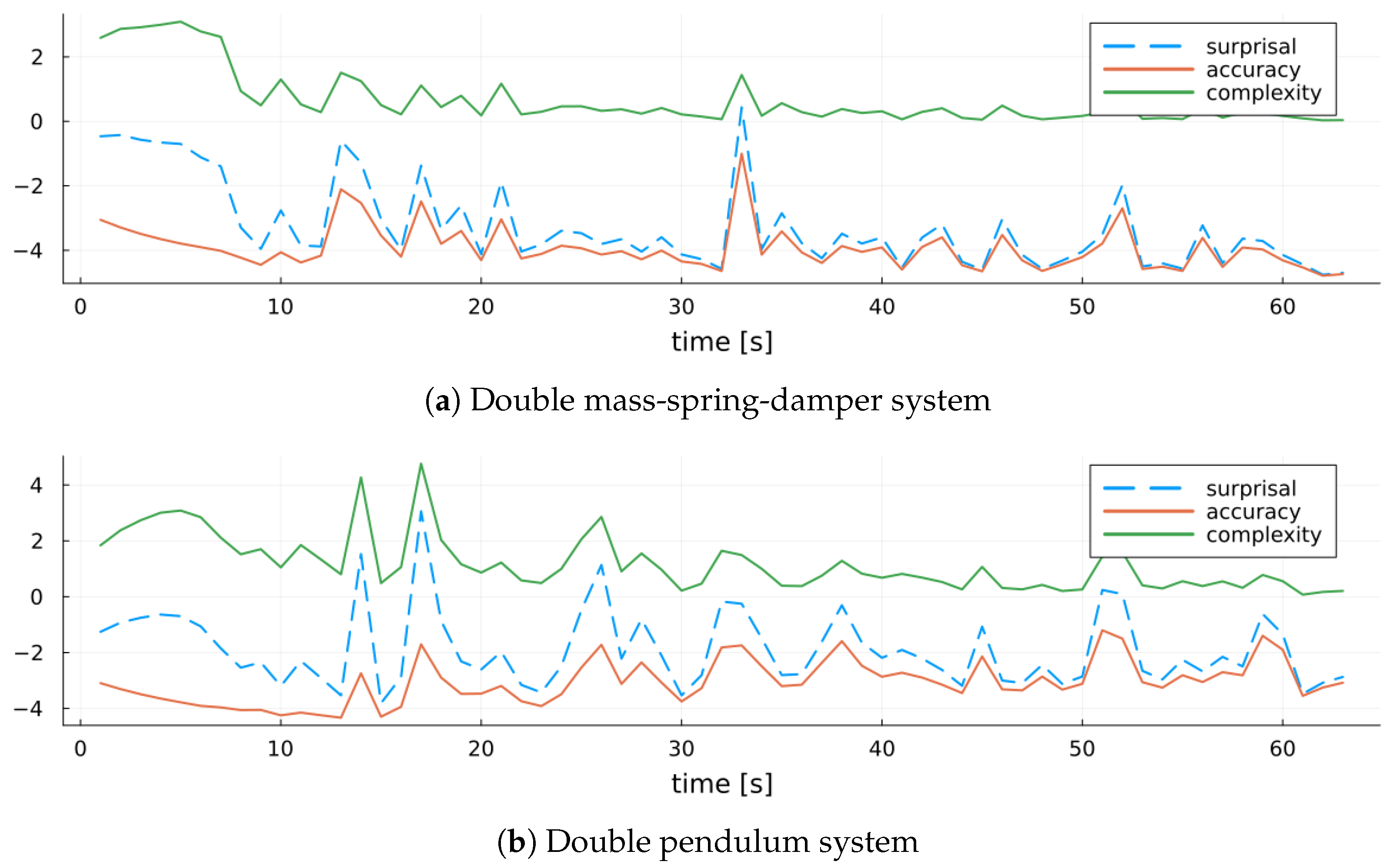
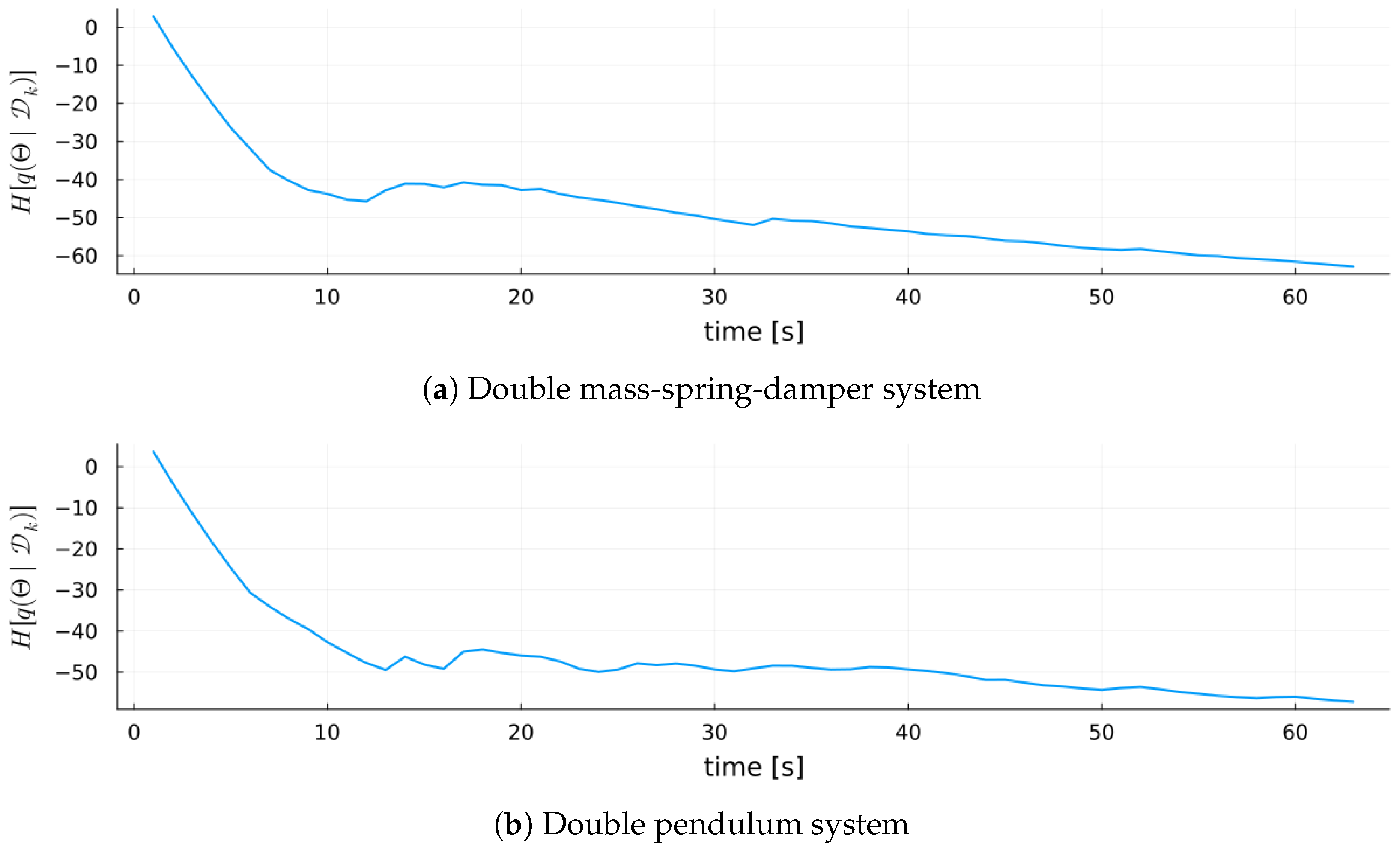
| Uninformative | ||||
| Weakly informative |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nisslbeck, T.N.; Kouw, W.M. Factor Graph-Based Online Bayesian Identification and Component Evaluation for Multivariate Autoregressive Exogenous Input Models. Entropy 2025, 27, 679. https://doi.org/10.3390/e27070679
Nisslbeck TN, Kouw WM. Factor Graph-Based Online Bayesian Identification and Component Evaluation for Multivariate Autoregressive Exogenous Input Models. Entropy. 2025; 27(7):679. https://doi.org/10.3390/e27070679
Chicago/Turabian StyleNisslbeck, Tim N., and Wouter M. Kouw. 2025. "Factor Graph-Based Online Bayesian Identification and Component Evaluation for Multivariate Autoregressive Exogenous Input Models" Entropy 27, no. 7: 679. https://doi.org/10.3390/e27070679
APA StyleNisslbeck, T. N., & Kouw, W. M. (2025). Factor Graph-Based Online Bayesian Identification and Component Evaluation for Multivariate Autoregressive Exogenous Input Models. Entropy, 27(7), 679. https://doi.org/10.3390/e27070679







