Entropy in the Assessment of the Labour Market Situation in the Context of the Survival Analysis Methods
Abstract
1. Introduction
2. Entropy in the Survival Analysis
2.1. Basic Functions in the Survival Analysis
- —probability density function of random variable T.
- —cumulative distribution function.
2.2. Entropy in the Assessment of Uncertainty of Life Expectancy
- The age at which the death occurred.
- Distribution of possible life expectancies at the age of death.
- When there is an age-related change in the probability of death, this change affects the entire life expectancy distribution. Some lifetimes become more likely and others less likely than before the change. The net effect on the lifetime entropy is difficult to estimate.
- Individual decisions on, e.g., insurance depend on life expectancy and the magnitude of life expectancy risk. A question arises—how do mortality shocks (for instance, epidemics) affect life expectancy and lifetime entropy?
- In the world’s economies, mortality shocks may affect various life periods differently. It is therefore important to examine how the relationship between lifetime entropy and mortality shocks changes with age.
- —survival function.
- —probability density.
- —the cumulative distribution function;
- —probability density;
- —the reversed failure rate of T or reversed hazard function.
2.3. Entropy for the Exponential Distribution of Survival Time
- The distribution of survival time can be estimated.
- Estimated parameters provide clinically meaningful estimates of effect.
- Residuals can represent the difference between observed and estimated values of time.
- Full maximum likelihood can be used to estimate parameters.
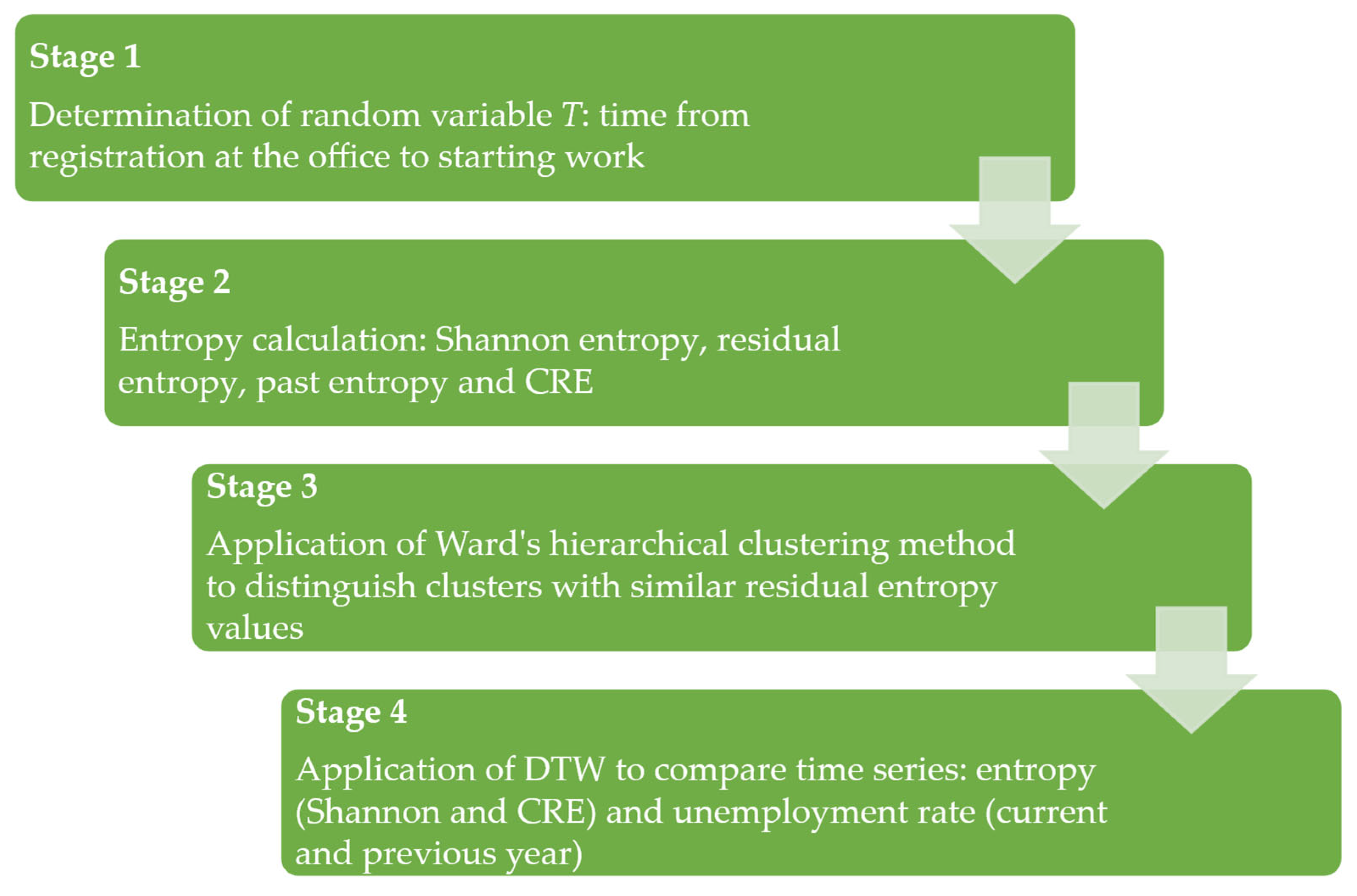
3. Data and Research Methodology
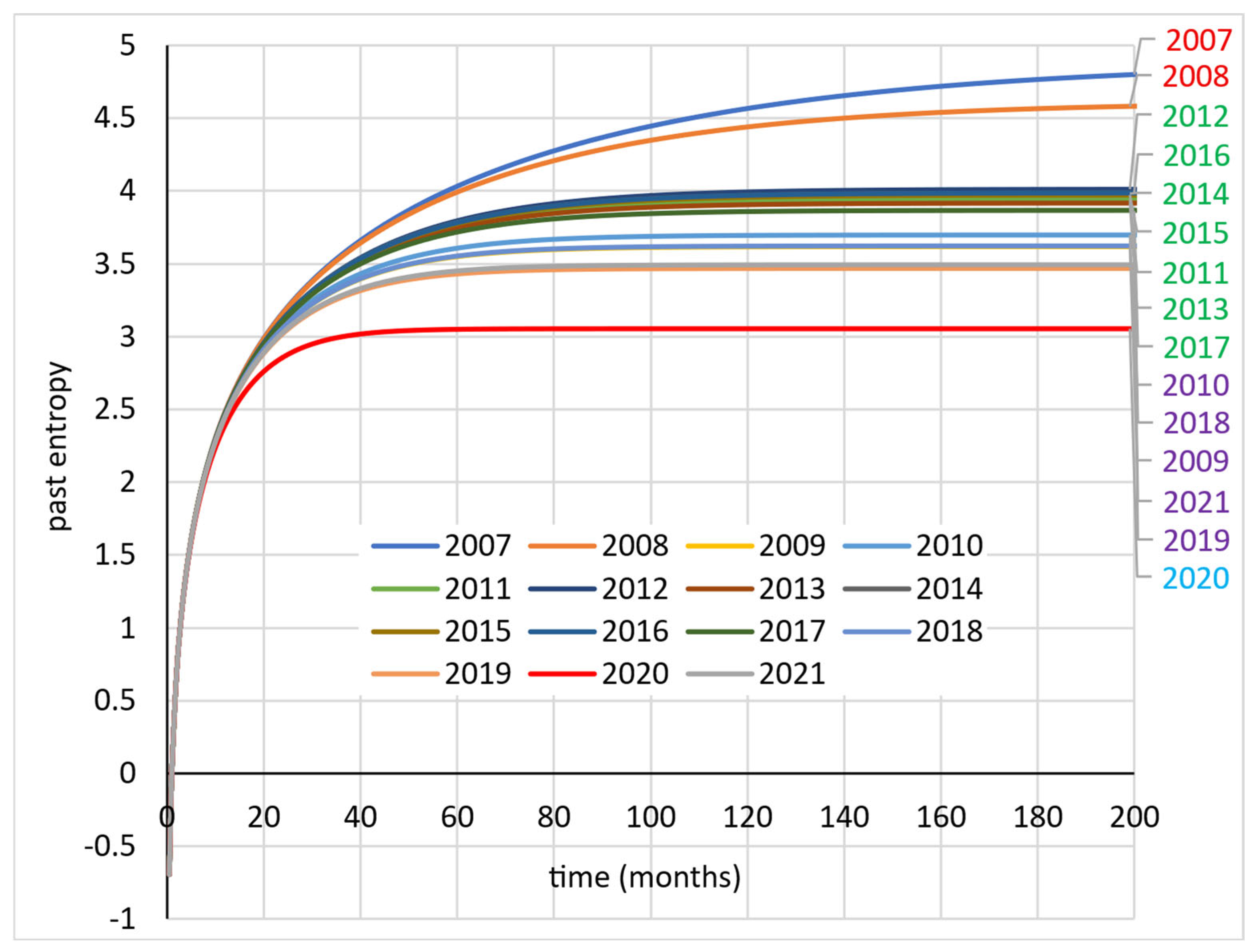
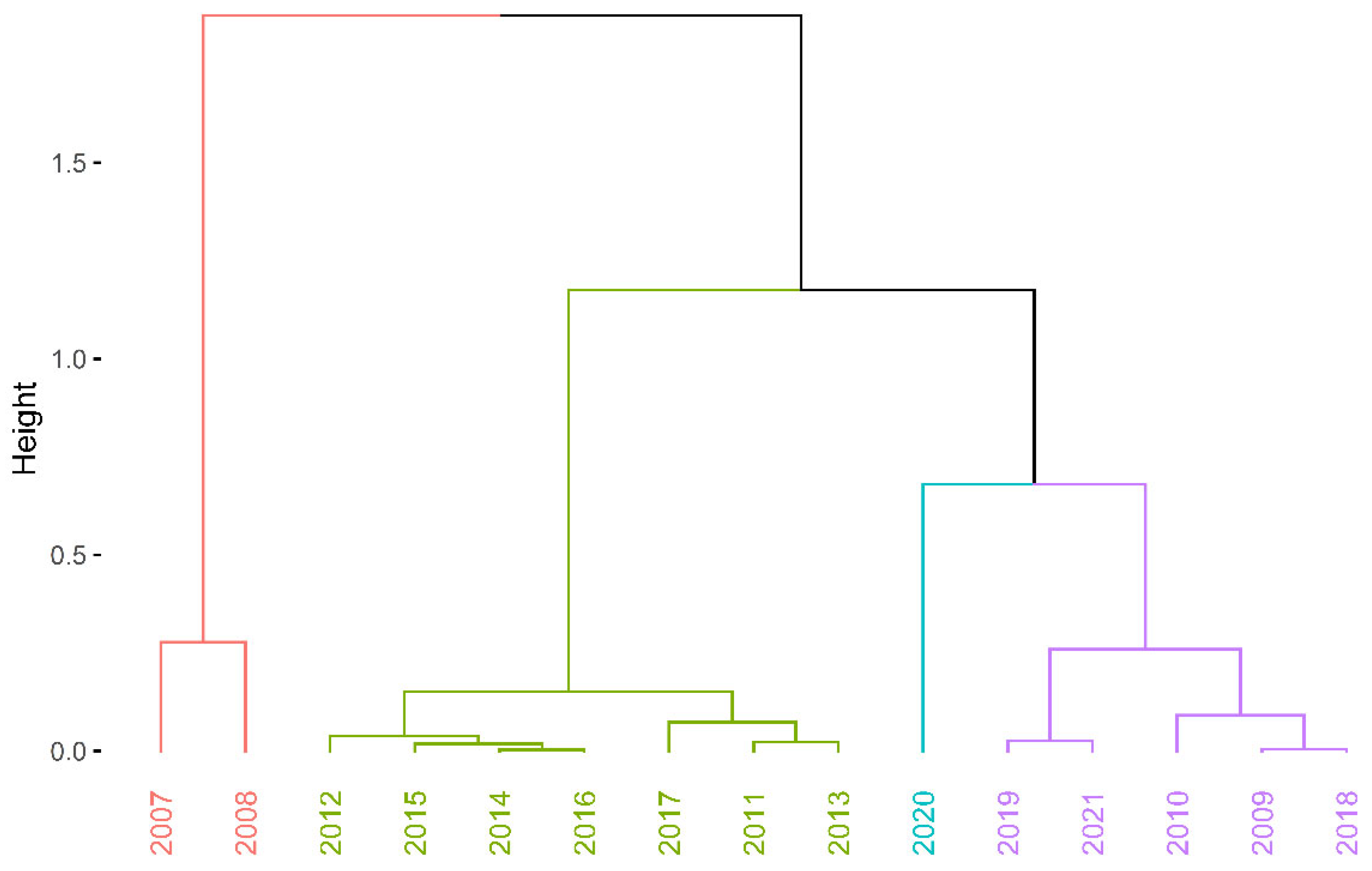
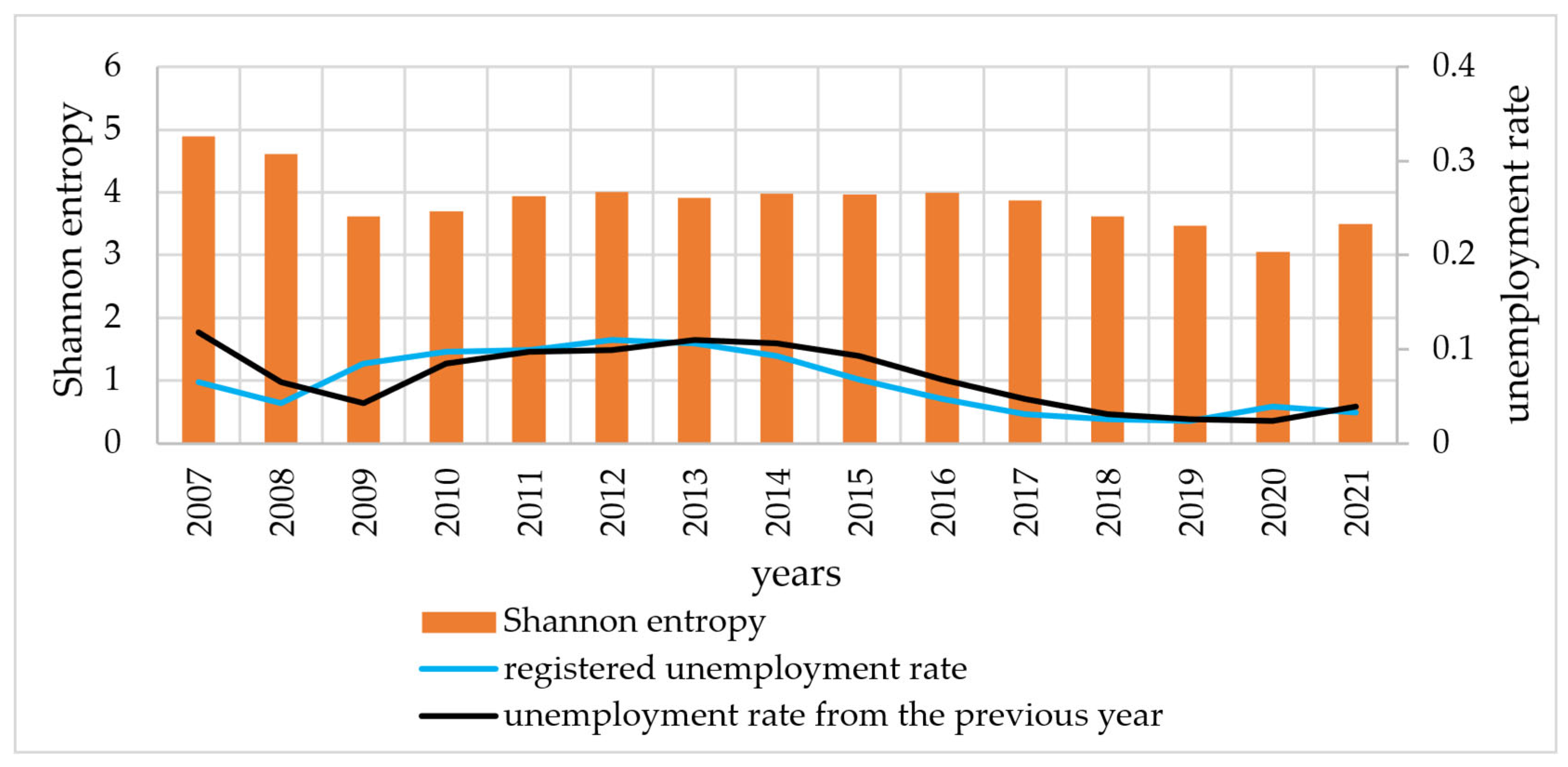
4. Results
- Cluster 1—years 2007–2008—high entropy.
- Cluster 2—years 2011–2016—medium high entropy.
- Cluster 3—years 2009–2010, 2017–2019, and 2021—medium low entropy.
- Cluster 4—year 2020—low entropy.
5. Discussion
6. Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Zografos, K.; Nadarajah, S. Survival exponential entropies. IEEE Trans. Inf. Theory 2005, 51, 1239–1246. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–432. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
- Boateng, E.; Asafo-Adjei, E.; Gatsi, J.G.; Gherghina, Ş.C.; Simionescu, L.N. Multifrequency-based non-linear approach to analyzing implied volatility transmission across global financial markets. Oeconomia Copernic. 2022, 13, 699–743. [Google Scholar] [CrossRef]
- Karas, M.; Režňáková, M. A novel approach to estimating the debt capacity of European SMEs. Equilibrium. Q. J. Econ. Econ. Policy 2023, 18, 551–581. [Google Scholar] [CrossRef]
- Remeikienė, R.; Ligita, G.; Fedajev, A.; Raistenskis, E.; Krivins, A. Links between crime and economic development: EU classification. Equilibrium. Q. J. Econ. Econ. Policy 2022, 17, 909–938. [Google Scholar] [CrossRef]
- Brodny, J.; Tutak, M. The level of implementing sustainable development goal “Industry, innovation and infrastructure” of Agenda 2030 in the European Union countries: Application of MCDM methods. Oeconomia Copernic. 2023, 14, 47–102. [Google Scholar] [CrossRef]
- Olbryś, J. Entropy-Based Applications in Economics, Finance, and Management. Entropy 2022, 24, 1468. [Google Scholar] [CrossRef]
- Meyer, P.; Ponthière, G. Human Lifetime Entropy in a Historical Perspective (1750–2014). Cliometrica 2020, 14, 129–167. [Google Scholar] [CrossRef]
- Meyer, P.; Ponthiere, G. Threshold ages for the relation between lifetime entropy and mortality risk. Math. Soc. Sci. 2020, 108, 1–7. [Google Scholar] [CrossRef]
- Wiener, N. Cybernetics or Control and Communication in the Animal and the Machine; MIT Press: Cambridge, UK, 1965. [Google Scholar]
- Hill, G. The entropy of the survival curve: An alternative measure. Can. Stud. Popul. 1993, 20, 43–57. [Google Scholar] [CrossRef]
- Meyer, B.D. Unemployment Insurance and Unemployment Spells. Econometrica 1990, 58, 757–782. [Google Scholar] [CrossRef]
- Babucea, A.G.; Danacica, D.-E. Using Kaplan-Meier Curves for Preliminary Evaluation the Duration of Unemployment Spells. Ann. Univ. “Constantin Brancusi’ Targu Jiu 2007, 2, 33–38. [Google Scholar] [CrossRef][Green Version]
- Markowicz, I. Duration analysis of firms–cohort tables and hazard function. Int. J. Bus. Soc. Res. 2015, 5, 36–47. [Google Scholar] [CrossRef]
- Box-Steffensmeier, J.M.; Zorn, C.J.W. Duration Models and Proportional Hazards in Political Science. Am. J. Political Sci. 2001, 45, 972–988. [Google Scholar] [CrossRef]
- Box-Steffensmeier, J.M.; Reiter, D.; Zorn, C.J.W. Nonproportional Hazards and Event History Analysis in International Relations. J. Confl. Resolut. 2003, 47, 33–53. [Google Scholar] [CrossRef]
- Box-Steffensmeier, J.M.; Bradford, S.J. Event History Modeling A Guide for Social Scientists; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Bieszk-Stolorz, B.; Dmytrów, K. Evaluation of Changes on World Stock Exchanges in Connection with the SARS-CoV-2 Pandemic. Survival Analysis Methods. Risks 2021, 9, 121. [Google Scholar] [CrossRef]
- Landmesser, J. The survey of economic activity of people in rural areas-the analysis using the econometric hazard models. Acta Univ. Lodziensis. Folia Oeconomica 2009, 228, 363–370. [Google Scholar]
- Sączewska-Piotrowska, A. Poverty duration of households of the self-employed. Econometrics 2015, 1, 44–55. [Google Scholar] [CrossRef][Green Version]
- Wycinka, E. Competing risk models of default in the presence of early repayments. Econometrics 2019, 23, 99–120. [Google Scholar] [CrossRef]
- Putek-Szeląg, E.; Gdakowicz, A. Application of Duration Analysis Methods in the Study of the Exit of a Real Estate Sale Offer from the Offer Database System. In Data Analysis and Classification. Methods and Applications; Jajuga, K., Najman, K., Walesiak, M., Eds.; Springer: Cham, Switzerland, 2021; pp. 153–169. [Google Scholar] [CrossRef]
- Batóg, J.; Batóg, B. Economic Performance Paths of CEE Countries and the EU-27 in 2000–2022. Folia Oeconomica Stetin. 2023, 23, 45–66. [Google Scholar] [CrossRef]
- Musa, H.; Rech, F.; Yan, C.; Musova, Z. The Deterioration of Financial Ratios During the Covid-19 Pandemic: Does Corporate Governance Matter? Folia Oeconomica Stetin. 2022, 22, 219–242. [Google Scholar] [CrossRef]
- Foo, J.; Witkowska, D. The 2020 COVID-19 Financial Crisis Impact on the European Stock Markets and Economies. A Preliminary Analysis. Folia Oeconomica Stetin. 2024, 24, 22–40. [Google Scholar] [CrossRef]
- Di Crescenzo, A.; Paolillo, L. Analysis and applications of the residual varentropy of random lifetimes. Probab. Eng. Inf. Sci. 2021, 35, 680–698. [Google Scholar] [CrossRef]
- Di Crescenzo, A.; Toomaj, A. Extension of the past lifetime and its connection to the cumulative entropy. J. Appl. Probab. 2015, 52, 1156–1174. [Google Scholar] [CrossRef]
- Ebrahimi, N.; Pellerey, F. New partial ordering of survival functions based on the notion of uncertainty. J. Appl. Probab. 1995, 32, 202–211. [Google Scholar] [CrossRef]
- Kleinbaum, D.G.; Klein, M. Survival Analysis a Self-Learning Text, 2nd ed.; Springer: New York, NY, USA, 2005. [Google Scholar]
- Aalen, O.O.; Borgan, Ø.; Gjessing, H.K. Survival and Event History Analysis: A Process Point of View; Springer: New York, NY, USA, 2008. [Google Scholar]
- Kaplan, E.L.; Meier, P. Nonparametric estimation from incomplete observations. J. Amer. Statist. Assoc. 1958, 53, 457–481. [Google Scholar] [CrossRef]
- Nelson, W. Hazard plotting for incomplete failure data. J. Qual. Technol 1969, 1, 27–52. [Google Scholar] [CrossRef]
- Nelson, W. Theory and applications of hazard plotting for censored failure data. Technometrics 1972, 14, 945–965. [Google Scholar] [CrossRef]
- Aalen, O. Nonparametric inference for a family of counting processes. Ann. Stat. 1978, 6, 701–726. [Google Scholar] [CrossRef]
- Cox, D.R. Regression models and life tables (with discussion). J. R. Statist. Soc. B 1972, 34, 187–220. [Google Scholar] [CrossRef]
- Pierce, J.R. An Introduction to Information Theory: Symbols, Signals & Noise; Dover Publications: New York, NY, USA, 1980. [Google Scholar]
- Keyfitz, N.; Caswell, H. Applied Mathematical Demography; Springer: New York, NY, USA, 2005. [Google Scholar]
- Fernandez, O.E.; Beltrán-Sánchez, H. The entropy of the life table: A reappraisal. Theor. Popul. Biol. 2015, 104, 26–45. [Google Scholar] [CrossRef] [PubMed]
- Keyfitz, N. What difference would it make if cancer were eradicated? An examination of the Taeuber paradox. Demography 1977, 14, 411–418. [Google Scholar] [CrossRef]
- Rajesh, G.; Abdul-Sathar, E.I.; Maya, R.; Muraleedharan Nair, K.R. Nonparametric estimation of the residual entropy function with censored dependent data. Braz. J. Probab. Stat. 2015, 29, 866–877. [Google Scholar] [CrossRef]
- Ebrahimi, N. How to Measure Uncertainty in the Residual Life Time Distribution. Indian J. Stat. Ser. A (1961–2002) 1996, 58, 48–56. [Google Scholar]
- Tenreiro Machado, J.A.; Lopes, A.M. Entropy analysis of human death uncertainty. Nonlinear Dyn. 2021, 104, 3897–3911. [Google Scholar] [CrossRef]
- Di Crescenzo, A.; Longobardi, M. A measure of discrimination between past lifetime distributions. Stat. Probab. Lett. 2004, 67, 173–182. [Google Scholar] [CrossRef]
- Habib, A.; Alahyani, M. Entropy for Past Residual Life Time Distributions. Am. J. Theor. Appl. Stat. 2015, 3, 118–124. [Google Scholar] [CrossRef][Green Version]
- Di Crescenzo, A.D.; Longobardi, M. Entropy based measure of uncertainty in past life time distributions. J. Appl. Probab. 2002, 39, 434–440. [Google Scholar] [CrossRef]
- Chandra, N.K.; Roy, D. Some results on reversed hazard rate. Probab. Eng. Informational Sci. 2001, 15, 95–102. [Google Scholar] [CrossRef]
- Nair, K.R.M.; Rajesh, G. Characterization of probability distributions using the residual entropy function. J. Indian Stat. Assoc. 1998, 36, 157–166. [Google Scholar]
- Smitha, S.; Kattumannil, S.K. Entropy generating function for past lifetime and its properties. arXiv 2023, arXiv:2312.02177. [Google Scholar] [CrossRef]
- Di Crescenzo, M.; Longobardi, M. On weighted residual and past entropies. Sci. Math. Jpn. 2006, 64, 255–266. [Google Scholar] [CrossRef]
- Ebrahimi, N.; Kirmani, S.N.U.A. Some results on ordering of survival functions through uncertainty. Stat. Probab. Lett. 1996, 29, 167–176. [Google Scholar] [CrossRef]
- Shrahili, M.; El-Saeed, A.R.; Hassan, A.S.; Elbatal, I.; Elgarhy, M. Estimation of Entropy for Log-Logistic Distribution under Progressive Type II Censoring. J. Nanomater. 2022, 2022, 2739606. [Google Scholar] [CrossRef]
- Rao, M.; Chen, Y.; Vemuri, B.C.; Wang, F. Cumulative residual entropy: A new measure of information. IEEE Trans. Inform. Theory 2004, 50, 1220–1228. [Google Scholar] [CrossRef]
- Wang, F.; Vemuri, B.C.; Rao, M.; Chen, Y. A New & Robust Information Theoretic Measure and Its Application to Image Alignment. In Information Processing in Medical Imaging. IPMI 2003. Lecture Notes in Computer Science; Taylor, C., Noble, J.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2732, pp. 388–400. [Google Scholar] [CrossRef]
- Abbasnejad, M.; Arghami, N.R.; Morgenthaler, S.; Borzadaran, G.M. On the dynamic survival entropy. Stat. Probab. Lett. 2010, 80, 1962–1971. [Google Scholar] [CrossRef]
- Rezaei, R.; Yari, G. Keyfitz entropy: Investigating some mathematical properties and its application for estimating survival function in life table. Math. Sci. 2021, 15, 229–240. [Google Scholar] [CrossRef]
- Zhang, Z. Parametric regression model for survival data: Weibull regression model as an example. Ann. Transl. Med. 2016, 4, 484. [Google Scholar] [CrossRef]
- Stevenson, M. An Introduction to Survival Analysis; EpiCentre, IVABS, Massey University: Palmerston North, New Zealand, 2007. [Google Scholar]
- Montaseri, M.; Charati, J.Y.; Espahbodi, F. Application of Parametric Models to a Survival Analysis of Hemodialysis Patients. Nephrourol. Mon. 2016, 8, e28738. [Google Scholar] [CrossRef]
- Gross, A.J. Applications in Survival Analysis. In Exponential Distribution: Theory, Methods and Applications; Balakrishnan, K., Basu, A.P., Eds.; Gordon and Breach: Amsterdam, The Netherlands, 1995; pp. 498–508. [Google Scholar]
- Landmesser, J.M. Econometric analysis of unemployment duration using hazard models. Stud. Ekon. 2009, 1–2, 79–92. [Google Scholar]
- Güell, M.; Lafuente, C. Revisiting the determinants of unemployment duration: Variance decomposition à la ABS in Spain. Labour Econ. 2022, 78, 102233. [Google Scholar] [CrossRef]
- Basha, L.; Gjika, E. Accelerated failure time models in analyzing duration of employment. J. Phys. Conf. Ser. 2022, 2287, 012014. [Google Scholar] [CrossRef]
- Sachlas, A.; Papaioannou, T. Residual and Past Entropy in Actuarial Science and Survival Models. Methodol. Comput. Appl. Probab. 2014, 16, 79–99. [Google Scholar] [CrossRef]
- Hooda, D.S.; Sharma, D.K. Exponential survival entropies and their properties. Adv. Math. Sci. Appl. 2010, 20, 265–279. [Google Scholar]
- Bellman, R.; Kalaba, R. On adaptive control processes. IEEE Trans. Autom. Control. 1959, 4, 1–9. [Google Scholar] [CrossRef]
- Rabiner, L.; Rosenberg, A.; Levinson, S. Considerations in dynamic time warping algorithms for discrete word recognition. IEEE Trans. Acoust. Speech Signal. Process 1978, 26, 575–582. [Google Scholar] [CrossRef]
- Sakoe, H.; Chiba, S. Dynamic programming algorithm optimization for spoken word recognition. IEEE Trans. Acoust. Speech Signal. Process 1978, 26, 43–49. [Google Scholar] [CrossRef]
- Myers, C.S.; Rabiner, L.R. A comparative study of several dynamic time-warping algorithms for connected word recognition. Bell Syst. Tech. J. 1981, 60, 1389–1409. [Google Scholar] [CrossRef]
- Sankoff, D.; Kruskal, J. (Eds.) Time Warps, String Edits, and Macromolecules: The Theory and Practice of Sequence Comparison; Addison-Wesley: Reading, MA, USA, 1983. [Google Scholar]
- Müller, M. Information Retrieval for Music and Motion; Springer-Verlag: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Aach, J.; Church, G.M. Aligning gene expression time series with time warping algorithms. Bioinformatics 2001, 17, 495–508. [Google Scholar] [CrossRef]
- Arici, T.; Celebi, S.; Aydin, A.S.; Temiz, T.T. Robust gesture recognition using feature pre-processing and weighted dynamic time warping. Multimed. Tools. Appl. 2014, 72, 3045–3062. [Google Scholar] [CrossRef]
- Stübinger, J. Statistical arbitrage with optimal causal paths on high-frequency data of the S&P 500. Quant. Financ. 2019, 19, 921–935. [Google Scholar] [CrossRef]
- Dmytrów, K.; Landmesser, J.; Bieszk-Stolorz, B. The Connections between COVID-19 and the Energy Commodities Prices: Evidence through the Dynamic Time Warping Method. Energies 2021, 14, 4024. [Google Scholar] [CrossRef]
- Bieszk-Stolorz, B.; Dmytrów, K. Assessment of the Similarity of the Situation in the EU Labour Markets and Their Changes in the Face of the COVID-19 Pandemic. Sustainability 2022, 14, 3646. [Google Scholar] [CrossRef]
- Aghabozorgi, S.; Shirkhorshidi, A.S.; Wah, T.Y. Time-series clustering—A decade review. Inf. Syst. 2015, 53, 16–38. [Google Scholar] [CrossRef]
- Ward, J.H. Hierarchical Grouping to Optimize an Objective Function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2025; Available online: https://www.R-project.org (accessed on 20 February 2025).
- Charrad, M.; Ghazzali, N.; Boiteau, V.; Niknafs, A. NbClust: An R Package for Determining the Relevant Number of Clusters in a Data Set. J. Stat. Softw. 2014, 61, 1–36. [Google Scholar] [CrossRef]
- Oh, G.; Kim, H.Y.; Ahn, S.W.; Kwak, W. Analyzing the financial crisis using the entropy density function. Phys. A Stat. Mech. Its Appl. 2015, 419, 464–469. [Google Scholar] [CrossRef]
- Anagnoste, S.; Caraiani, P. The Impact of Financial and Macroeconomic Shocks on the Entropy of Financial Markets. Entropy 2019, 21, 316. [Google Scholar] [CrossRef]
- Hou, Y.; Liu, F.; Gao, J.; Cheng, C.; Song, C. Characterizing Complexity Changes in Chinese Stock Markets by Permutation Entropy. Entropy 2017, 19, 514. [Google Scholar] [CrossRef]
- Caraiani, P. Modeling the Comovement of Entropy between Financial Markets. Entropy 2018, 20, 417. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wang, X. COVID-19 and financial market efficiency: Evidence from an entropy-based analysis. Financ. Res. Lett. 2021, 42, 101888. [Google Scholar] [CrossRef] [PubMed]
- Olbryś, J.; Majewska, E. Regularity in Stock Market Indices within Turbulence Periods: The Sample Entropy Approach. Entropy 2022, 24, 921. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez, R.A.; Cáceres-Hernández, J.J. Information, entropy, value, and price formation: An econophysical perspective. Phys. A Stat. Mech. Appl. 2018, 512, 74–85. [Google Scholar] [CrossRef]
- Popkov, A.Y.; Popkov, Y.S.; van Wissen, L. Positive dynamic systems with entropy operator: Application to labour market modelling. Eur. J. Oper. Res. 2005, 164, 811–828. [Google Scholar] [CrossRef]
- Symeonaki, M. A Relative Entropy Measure of Divergences in Labour Market Outcomes by Educational Attainment. In Quantitative Methods in Demography. The Springer Series on Demographic Methods and Population Analysis; Skiadas, C.H., Skiadas, C., Eds.; Springer: Cham, Switzerland, 2022; Volume 52, pp. 351–358. [Google Scholar] [CrossRef]
- Attaran, M. Industrial diversity and economic performance in U.S. areas. Ann. Reg. Sci. 1986, 20, 44–54. [Google Scholar] [CrossRef]
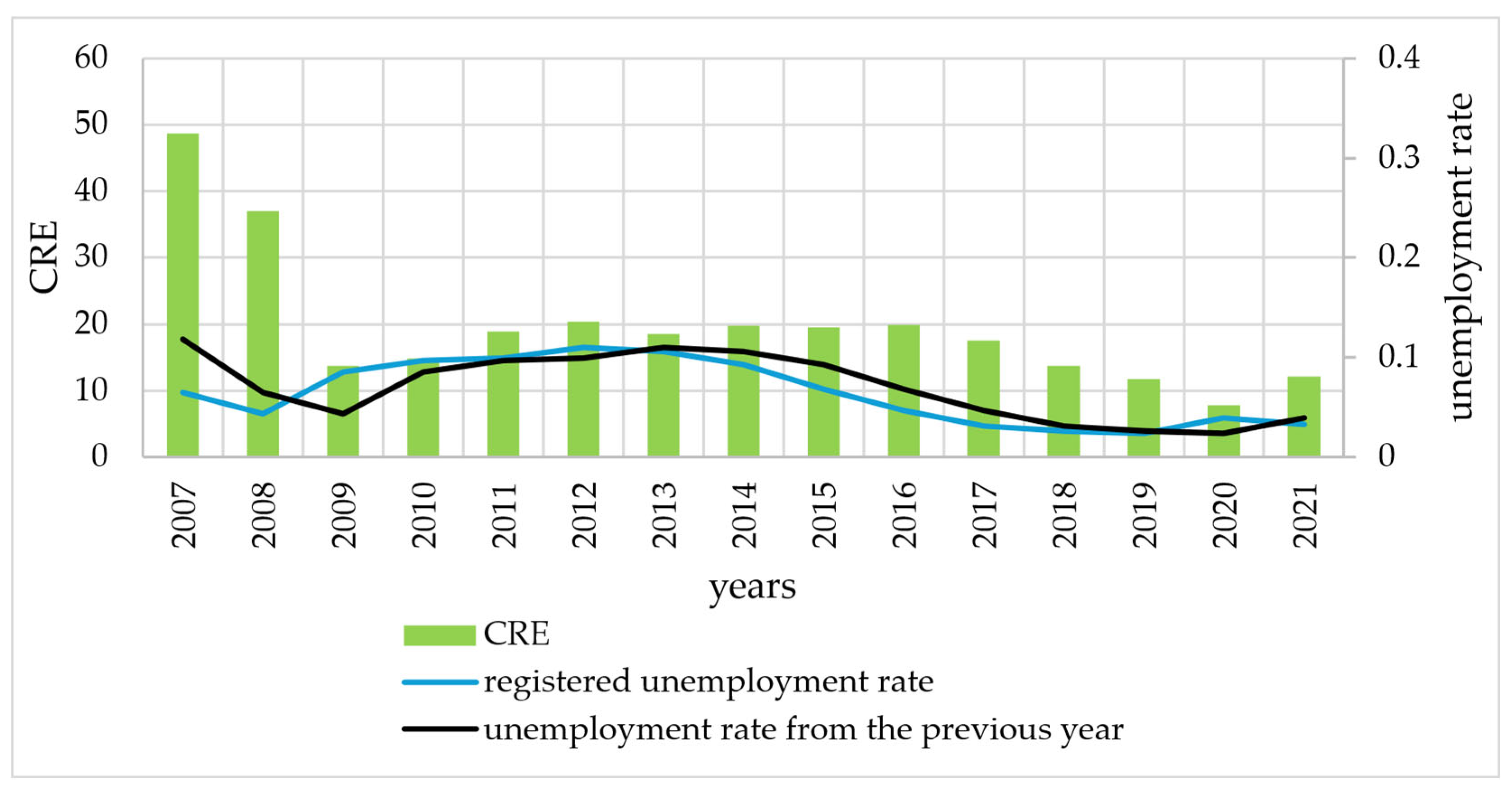
| Years | Number of De-Registered Persons | Average Duration of Registration (Months) | Registered Unemployment Rate in Poland (%) | ||
|---|---|---|---|---|---|
| Total | for Work | Total | for Work | ||
| 2007 | 23,745 | 8185 | 12.5 | 13.8 | 11.2 |
| 2008 | 17,232 | 5434 | 11.7 | 9.8 | 9.5 |
| 2009 | 19,398 | 6992 | 4.9 | 4.2 | 12.1 |
| 2010 | 17,613 | 7259 | 6.1 | 6.3 | 12.4 |
| 2011 | 15,194 | 5950 | 7.4 | 7. 6 | 12.5 |
| 2012 | 15,570 | 6020 | 7.9 | 7.7 | 13.4 |
| 2013 | 23,762 | 10,979 | 8.5 | 7.5 | 13.4 |
| 2014 | 24,443 | 10,956 | 8.9 | 8.0 | 11.4 |
| 2015 | 25,568 | 11,019 | 8.4 | 7.4 | 9.7 |
| 2016 | 23,447 | 9897 | 8.4 | 6.6 | 8.2 |
| 2017 | 19,697 | 7888 | 7.0 | 5.6 | 6.6 |
| 2018 | 14,873 | 6180 | 5.7 | 4.8 | 5.8 |
| 2019 | 12,680 | 5636 | 5.3 | 4.1 | 5.2 |
| 2020 | 7772 | 5383 | 5.4 | 4.4 | 6.3 |
| 2021 | 8878 | 5621 | 7.7 | 6.3 | 5.8 |
| Years | Parameter λ | Shannon Entropy/ Residual Entropy | CRE |
|---|---|---|---|
| 2007 | 0.0205 | 4.8867 | 48.7489 |
| 2008 | 0.0271 | 4.6096 | 36.9525 |
| 2009 | 0.0729 | 3.6186 | 13.7169 |
| 2010 | 0.0672 | 3.6994 | 14.8704 |
| 2011 | 0.0528 | 3.9405 | 18.9253 |
| 2012 | 0.0492 | 4.0127 | 20.3431 |
| 2013 | 0.0541 | 3.9176 | 18.4971 |
| 2014 | 0.0505 | 3.9854 | 19.7953 |
| 2015 | 0.0512 | 3.9714 | 19.5200 |
| 2016 | 0.0504 | 3.9885 | 19.8554 |
| 2017 | 0.0570 | 3.8652 | 17.5523 |
| 2018 | 0.0726 | 3.6225 | 13.7695 |
| 2019 | 0.0848 | 3.4671 | 11.7878 |
| 2020 | 0.1283 | 3.0532 | 7.7926 |
| 2021 | 0.0827 | 3.4923 | 12.0895 |
| Types of Entropy | Registered Unemployment Rate | Previous Year’s Unemployment Rate |
|---|---|---|
| DTW distances | ||
| Shannon entropy | 12.325 | 9.898 |
| CRE | 14.034 | 10.328 |
| Median shifts | ||
| Shannon entropy | 1 | 0 |
| CRE | 1 | 1 |
| Mean shifts | ||
| Shannon entropy | 0.700 | 0.000 |
| CRE | 0.792 | 0.440 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bieszk-Stolorz, B. Entropy in the Assessment of the Labour Market Situation in the Context of the Survival Analysis Methods. Entropy 2025, 27, 665. https://doi.org/10.3390/e27070665
Bieszk-Stolorz B. Entropy in the Assessment of the Labour Market Situation in the Context of the Survival Analysis Methods. Entropy. 2025; 27(7):665. https://doi.org/10.3390/e27070665
Chicago/Turabian StyleBieszk-Stolorz, Beata. 2025. "Entropy in the Assessment of the Labour Market Situation in the Context of the Survival Analysis Methods" Entropy 27, no. 7: 665. https://doi.org/10.3390/e27070665
APA StyleBieszk-Stolorz, B. (2025). Entropy in the Assessment of the Labour Market Situation in the Context of the Survival Analysis Methods. Entropy, 27(7), 665. https://doi.org/10.3390/e27070665







