Enhanced Video Anomaly Detection Through Dual Triplet Contrastive Loss for Hard Sample Discrimination
Abstract
1. Introduction
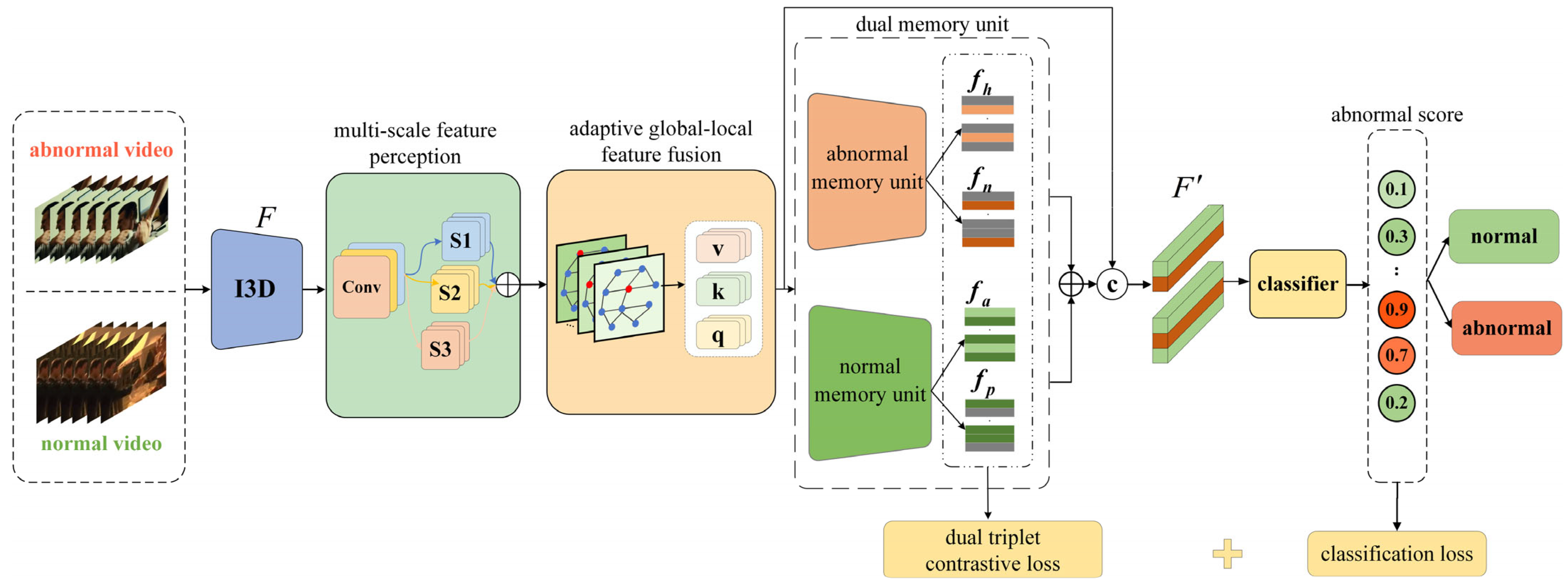
- A dual-triplet contrastive loss strategy is proposed to enhance the distinction between hard samples and abnormal features. This strategy extracts four types of sample features through dual memory units to enhance the distinction between hard samples and abnormal features.
- A multi-scale feature perception module is designed to capture feature information at different levels through a parallel multi-branch convolutional structure, and a learnable channel attention mechanism is utilized to fuse these features, thereby enhancing the discriminative ability of the model.
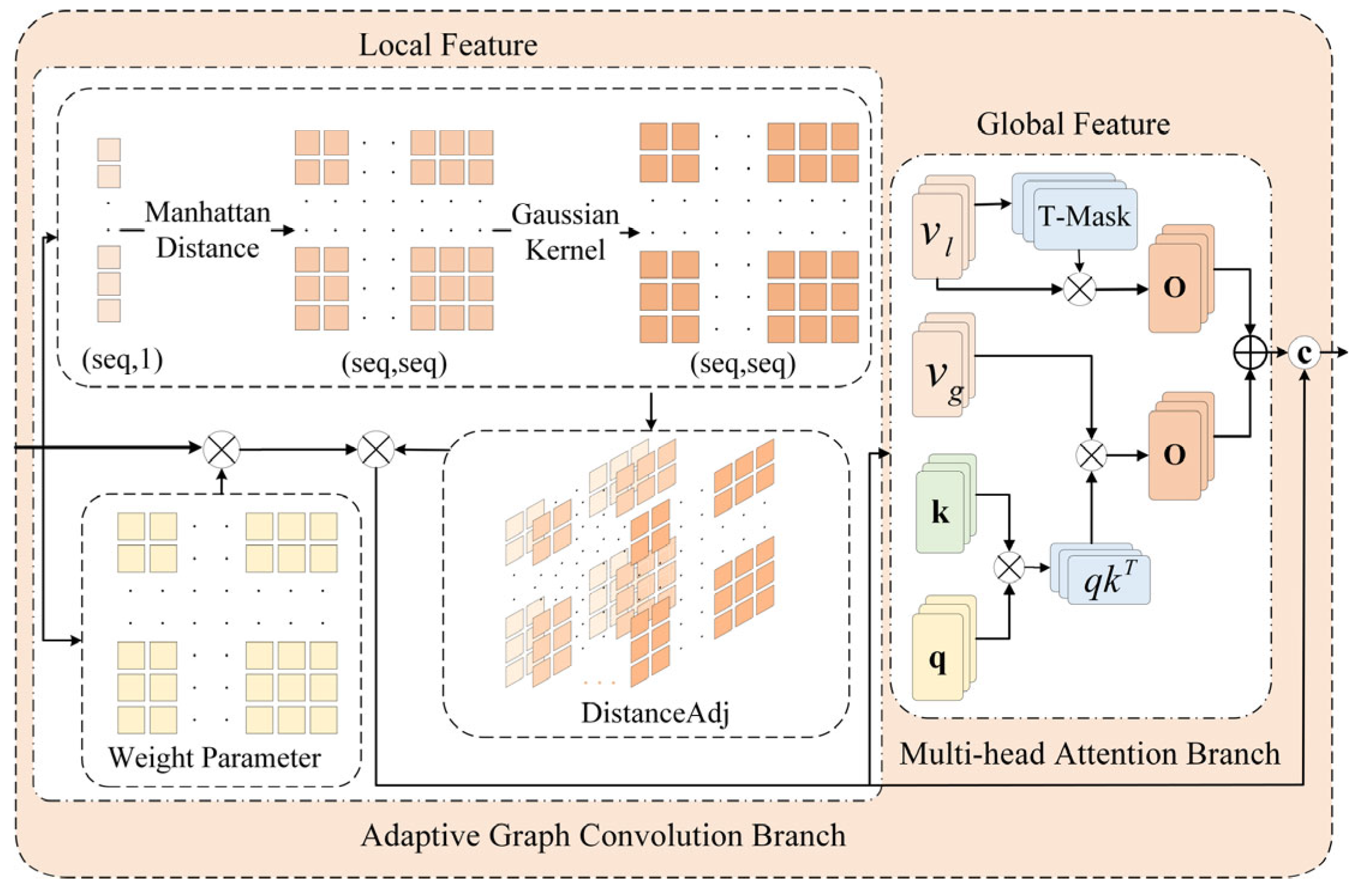
- An adaptive global–local feature fusion module is constructed, which employs two types of branch structures to separately capture global dynamic patterns and local fine-grained features, and a feature fusion strategy is implemented to achieve complementary feature enhancement.
2. Related Work
2.1. Multi-Scale Feature Extraction
2.2. Local–Global Relationship Modeling
2.3. Loss Function Constraint Strategy
3. Proposed Method
3.1. Multi-Scale Feature Perception
3.2. Adaptive Global–Local Feature Fusion
3.3. Dual Triplet Contrastive Loss
3.4. Overall Loss Functions
4. Experiments
4.1. Datasets and Evaluation Metrics
4.2. Implementation Details
4.3. Comparison Study
4.3.1. Comparison with SOTA Methods
4.3.2. Comparative Study of Feature Extraction Methods
4.4. Ablation Study
4.4.1. Effectiveness of Different Components
4.4.2. Effectiveness of Different Loss
4.4.3. Different Fusion Strategies
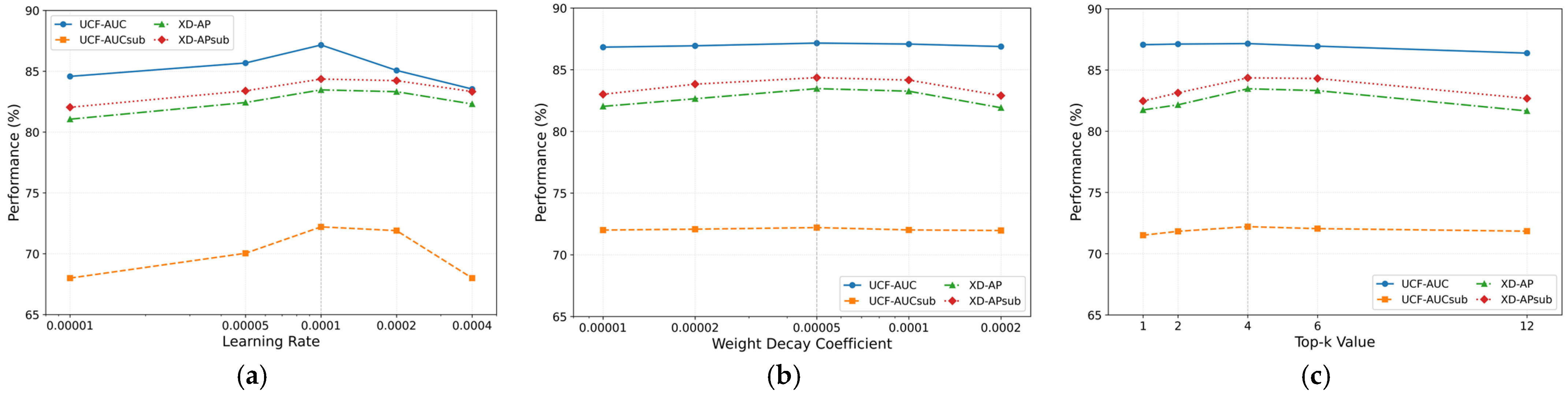
4.5. Hyperparameter Sensitivity Analysis
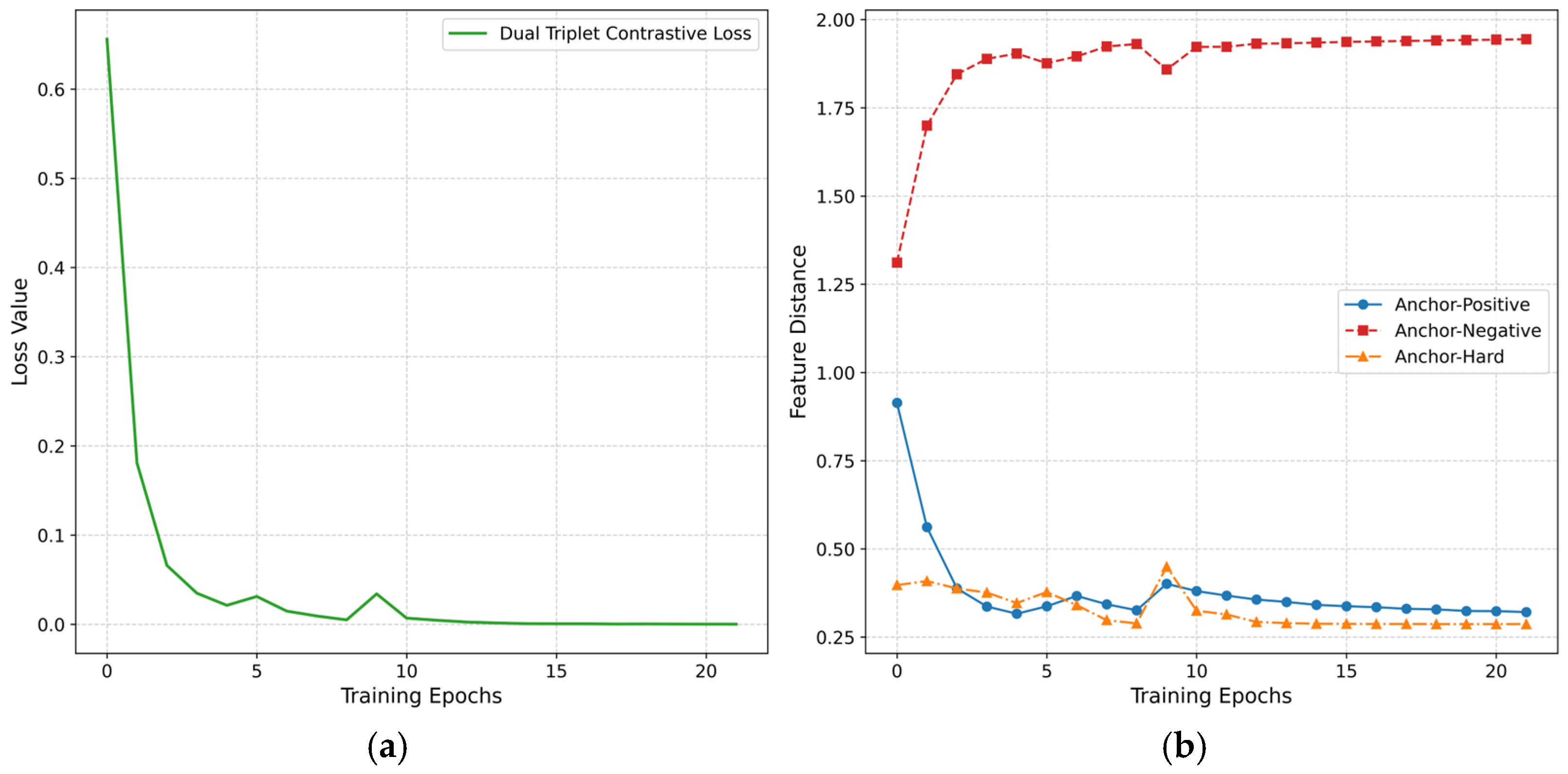
4.6. Training Trajectory Analysis on Feature Distance Evolution
4.7. Qualitative Results
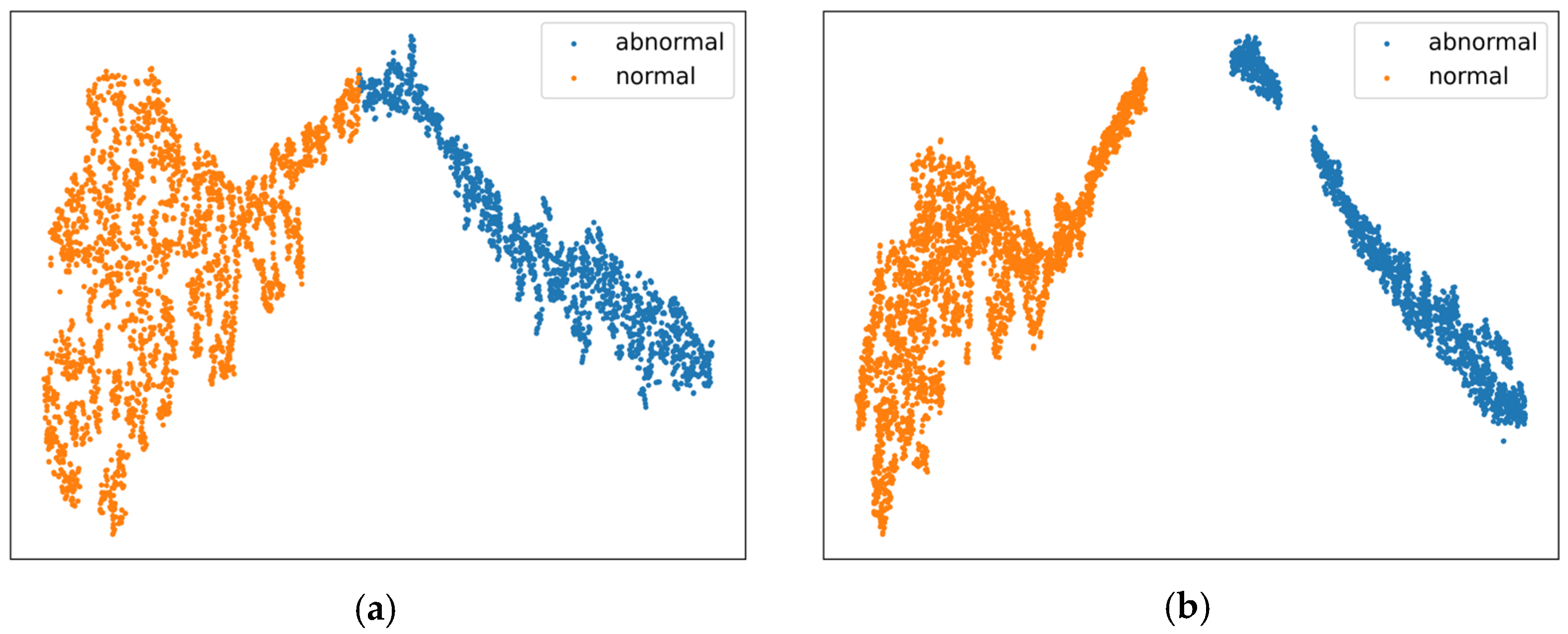
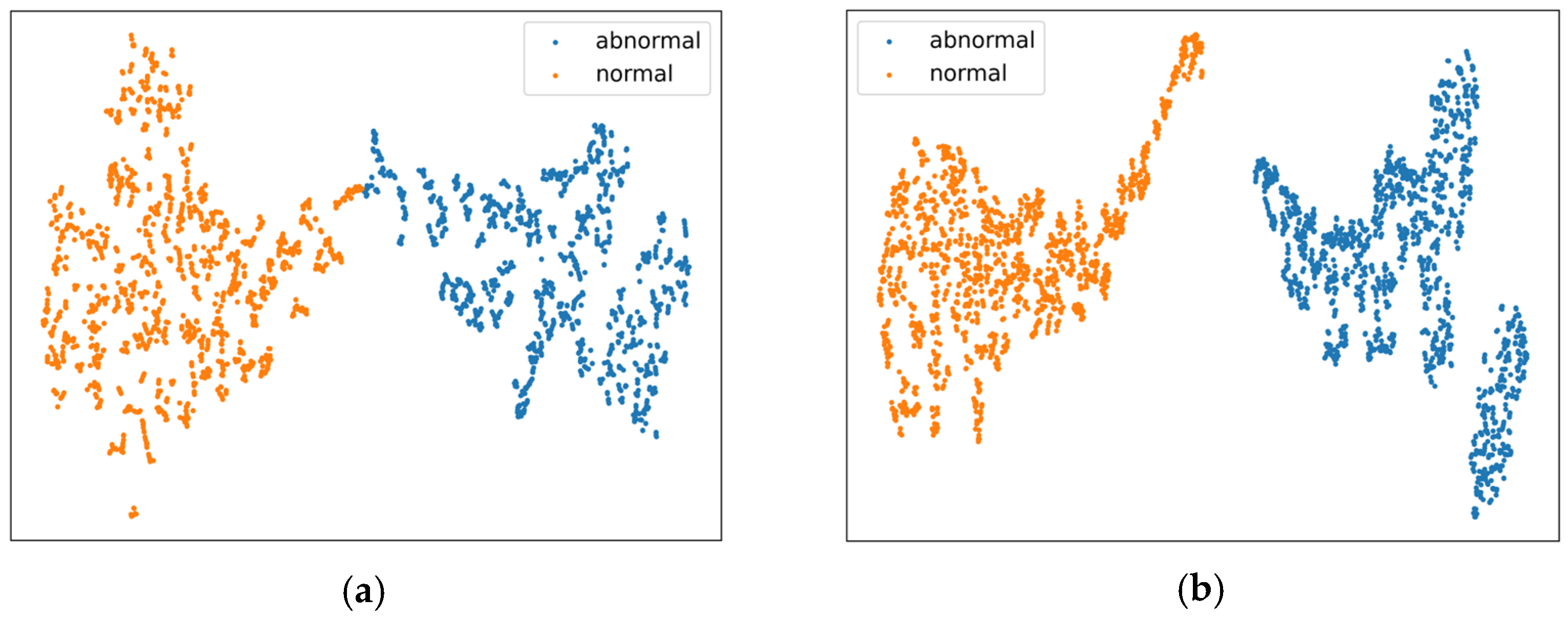
4.7.1. Feature Distribution Analysis via t-SNE
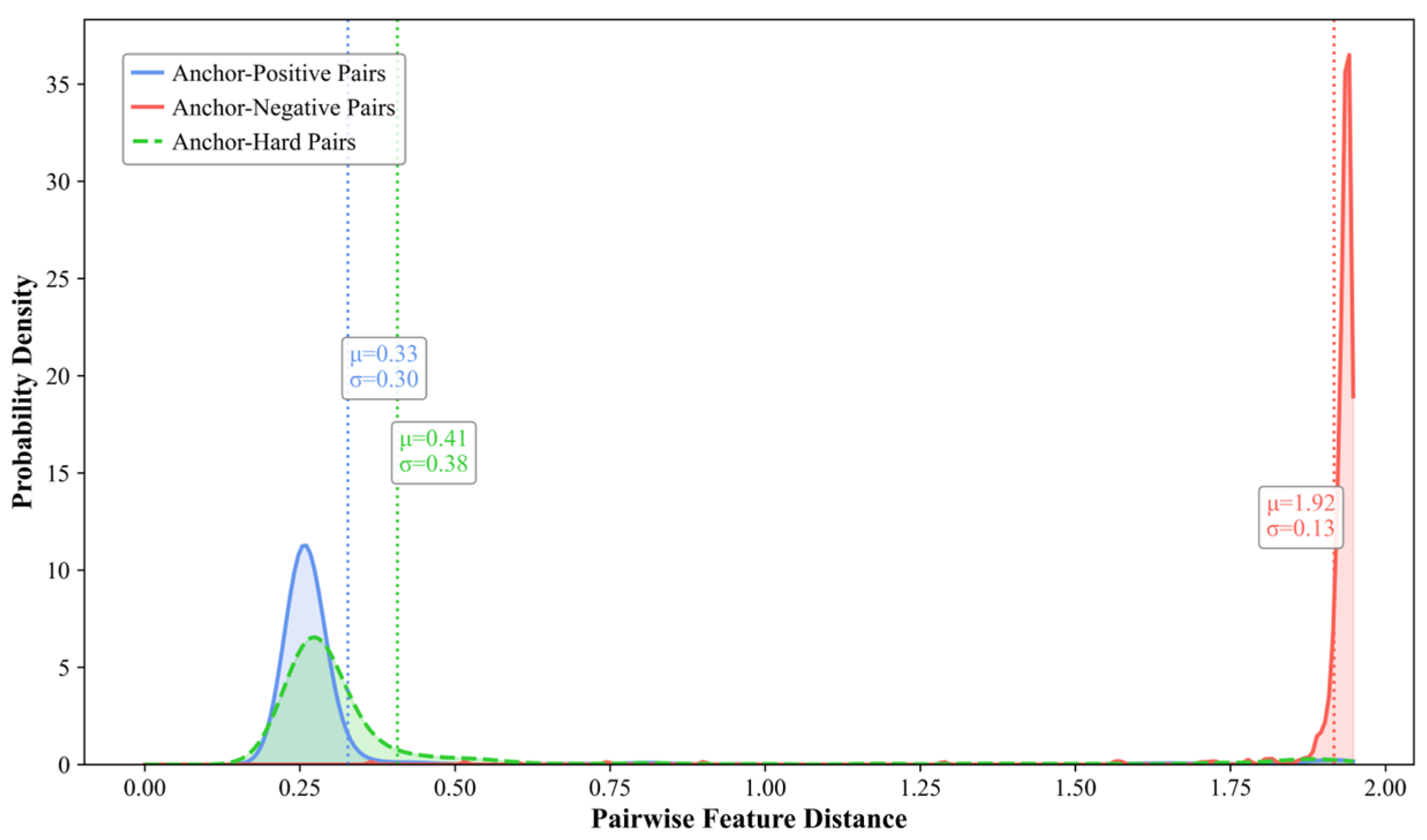
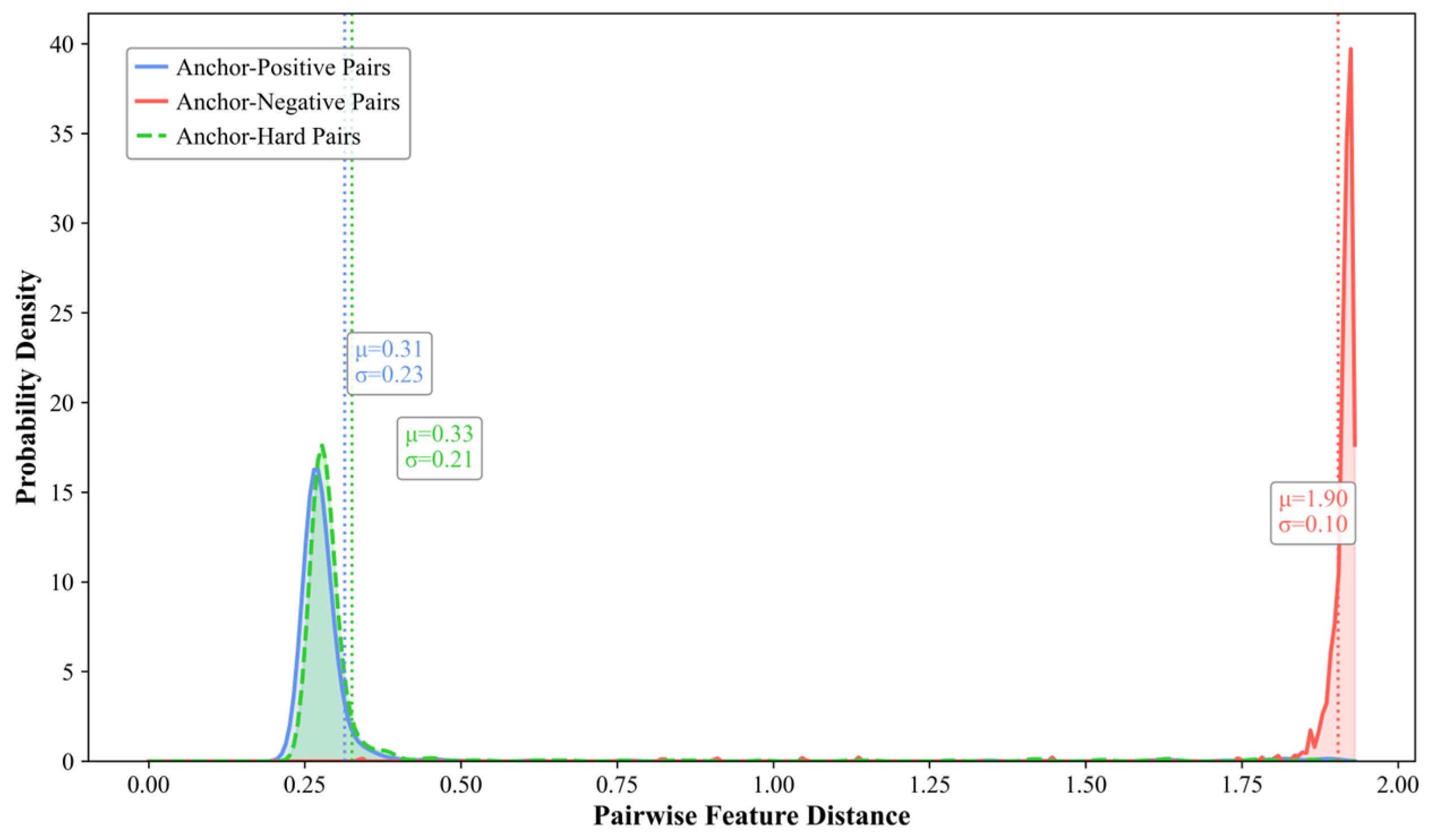
4.7.2. Distribution of Pairwise Sample Distances
4.7.3. Anomaly Scores
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Li, W.; Mahadevan, V.; Vasconcelos, N. Anomaly detection and localization in crowded scenes. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 36, 18–32. [Google Scholar]
- Wu, P.; Pan, C.; Yan, Y.; Pang, G.; Wang, P.; Zhang, Y. Deep learning for video anomaly detection: A review. arXiv 2024, arXiv:2409.05383. [Google Scholar]
- Sultani, W.; Chen, C.; Shah, M. Real-world anomaly detection in surveillance videos. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 6479–6488. [Google Scholar]
- Zhou, Y.; Qu, Y.; Xu, X.; Shen, F.; Song, J.; Shen, H. BatchNorm-based Weakly Supervised Video Anomaly Detection. arXiv 2023, arXiv:2311.15367. [Google Scholar] [CrossRef]
- Pu, Y.; Wu, X.; Yang, L.; Wang, S. Learning prompt-enhanced context features for weakly-supervised video anomaly detection. IEEE Trans. Image Process. 2024, 33, 4923–4936. [Google Scholar] [CrossRef] [PubMed]
- Dang, Y.; Chen, J.; Chen, P.; Gao, N.; Huan, R.; Zhao, D. Generate anomalies from normal: A partial pseudo-anomaly augmented approach for video anomaly detection. Vis. Comput. 2024, 41, 3843–3852. [Google Scholar] [CrossRef]
- Zhang, L.; Li, S.; Luo, X.; Liu, X.; Zhang, R. Video anomaly detection with both normal and anomaly memory modules. Vis. Comput. 2024, 41, 3003–3015. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, Z.; Zhang, B.; Fok, W.; Qi, X.; Wu, Y.C. Mgfn: Magnitude-contrastive glance-and-focus network for weakly-supervised video anomaly detection. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, No. 1. pp. 387–395. [Google Scholar]
- Robinson, J.; Chuang, C.Y.; Sra, S.; Jegelka, S. Contrastive learning with hard negative samples. arXiv 2020, arXiv:2010.04592. [Google Scholar]
- Zhang, H.; Li, Z.; Yang, J.; Wang, X.; Guo, C.; Feng, C. Revisiting Hard Negative Mining in Contrastive Learning for Visual Understanding. Electronics 2023, 12, 4884. [Google Scholar] [CrossRef]
- Zhao, Y.; Shu, Q. Debiased hybrid contrastive learning with hard negative mining for unsupervised person re-identification. Digit. Signal Process. 2025, 156, 104826. [Google Scholar] [CrossRef]
- Gong, Y.; Wang, C.; Dai, X.; Yu, S.; Xiang, L.; Wu, J. Multi-scale continuity-aware refinement network for weakly supervised video anomaly detection. In Proceedings of the 2022 IEEE International Conference on Multimedia and Expo (ICME), Taipei, Taiwan, 18–22 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar]
- Ristea, N.C.; Madan, N.; Ionescu, R.T.; Nasrollahi, K.; Khan, F.S.; Moeslund, T.B.; Shah, M. Self-supervised predictive convolutional attentive block for anomaly detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 13576–13586. [Google Scholar]
- Gong, S.; Chen, Y. Video action recognition based on spatio-temporal feature pyramid module. In Proceedings of the 2020 13th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 12–13 December 2020; IEEE: Piscataway, NJ, USA, 2022; pp. 338–341. [Google Scholar]
- Tian, Y.; Pang, G.; Chen, Y.; Singh, R.; Verjans, J.W.; Carneiro, G. Weakly-supervised video anomaly detection with robust temporal feature magnitude learning. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 4975–4986. [Google Scholar]
- Purwanto, D.; Chen, Y.T.; Fang, W.H. Dance with self-attention: A new look of conditional random fields on anomaly detection in videos. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 173–183. [Google Scholar]
- Rahimpour, S.M.; Kazemi, M.; Moallem, P.; Safayani, M. Video anomaly detection based on attention and efficient spatio-temporal feature extraction. Vis. Comput. 2024, 40, 6825–6841. [Google Scholar] [CrossRef]
- Pu, Y.; Wu, X. Locality-aware attention network with discriminative dynamics learning for weakly supervised anomaly detection. In Proceedings of the 2022 IEEE International Conference on Multimedia and Expo ICME, Taipei, Taiwan, 18–22 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar]
- Naji, Y.; Setkov, A.; Loesch, A.; Gouiffès, M.; Audigier, R. Spatio-temporal predictive tasks for abnormal event detection in videos. In Proceedings of the 2022 18th IEEE International Conference on Advanced Video and Signal Based Surveillance (AVSS), Madrid, Spain, 29 November–2 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–8. [Google Scholar]
- Li, S.; Liu, F.; Jiao, L. Self-training multi-sequence learning with transformer for weakly supervised video anomaly detection. In Proceedings of the AAAI Conference on Artificial Intelligence, Online, 22 February–1 March 2022; Volume 36, No. 2. pp. 1395–1403. [Google Scholar]
- Cao, C.; Zhang, X.; Zhang, S.; Wang, P.; Zhang, Y. Adaptive graph convolutional networks for weakly supervised anomaly detection in videos. IEEE Signal Process. Lett. 2022, 29, 2497–2501. [Google Scholar] [CrossRef]
- Wu, P.; Liu, J.; Shi, Y.; Sun, Y.; Shao, F.; Wu, Z.; Yang, Z. Not only look, but also listen: Learning multimodal violence detection under weak supervision. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 322–339. [Google Scholar]
- Zhang, J.; Qing, L.; Miao, J. Temporal convolutional network with complementary inner bag loss for weakly supervised anomaly detection. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 4030–4034. [Google Scholar]
- Wan, B.; Fang, Y.; Xia, X.; Mei, J. Weakly supervised video anomaly detection via center-guided discriminative learning. In Proceedings of the 2020 IEEE International Conference on Multimedia and Expo (ICME), Online, 6–10 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Yu, S.; Wang, C.; Mao, Q.; Li, Y.; Wu, J. Cross-epoch learning for weakly supervised anomaly detection in surveillance videos. IEEE Signal Process. Lett. 2021, 28, 2137–2141. [Google Scholar] [CrossRef]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A simple framework for contrastive learning of visual representations. In Proceedings of the International Conference on Machine Learning, Online, 12–18 July 2020; pp. 1597–1607. [Google Scholar]
- Doersch, C.; Gupta, A.; Efros, A.A. Unsupervised visual representation learning by context prediction. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1422–1430. [Google Scholar]
- Zhou, H.; Yu, J.; Yang, W. Dual memory units with uncertainty regulation for weakly supervised video anomaly detection. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, No. 3. pp. 3769–3777. [Google Scholar]
- Cho, M.; Kim, M.; Hwang, S.; Park, C.; Lee, K.; Lee, S. Look around for anomalies: Weakly-supervised anomaly detection via context-motion relational learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 12137–12146. [Google Scholar]
- Tan, W.; Yao, Q.; Liu, J. Overlooked video classification in weakly supervised video anomaly detection. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2024; pp. 202–210. [Google Scholar]
- Wu, J.C.; Hsieh, H.Y.; Chen, D.J.; Fuh, C.S.; Liu, T.L. Self-supervised sparse representation for video anomaly detection. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer Nature: Cham, Switzerland, 2022; pp. 729–745. [Google Scholar]
- Zhang, C.; Li, G.; Qi, Y.; Wang, S.; Qing, L.; Huang, Q.; Yang, M.H. Exploiting completeness and uncertainty of pseudo labels for weakly supervised video anomaly detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 16271–16280. [Google Scholar]
- Karim, H.; Doshi, K.; Yilmaz, Y. Real-time weakly supervised video anomaly detection. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2024; pp. 6848–6856. [Google Scholar]
- Wu, P.; Zhou, X.; Pang, G.; Sun, Y.; Liu, J.; Wang, P.; Zhang, Y. Open-vocabulary video anomaly detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 18297–18307. [Google Scholar]
- Wu, P.; Liu, J. Learning causal temporal relation and feature discrimination for anomaly detection. IEEE Trans. Image Process. 2021, 30, 3513–3527. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Kim, H.; Kim, M.; Kim, D.; Sohn, K. Normality guided multiple instance learning for weakly supervised video anomaly detection. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 2–7 January 2023; pp. 2665–2674. [Google Scholar]
- Javed, M.H.; Li, T.; Yu, Z.; Hussain, A.; Rajeh, T.M.; Zhang, F. Pyramidal temporal frame prediction for efficient anomalous event detection in smart surveillance systems. Knowl.-Based Syst. 2023, 282, 111111. [Google Scholar] [CrossRef]
- Tahira, N.J.; Park, J.R.; Lim, S.J.; Park, J.S. YOLOv5 based Anomaly Detection for Subway Safety Management Using Dilated Convolution. J. Korean Soc. Ind. Converg. 2023, 26, 217–223. [Google Scholar]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Chen, W.; Ma, K.T.; Yew, Z.J.; Hur, M.; Khoo, D.A.A. TEVAD: Improved video anomaly detection with captions. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 5549–5559. [Google Scholar]




| Method | Feature | AP (%) |
|---|---|---|
| RTFM [15] | I3D-RGB | 77.81 |
| MSL [20] | VideoSwin-RGB | 78.59 |
| S3R [31] | I3D-RGB | 80.26 |
| MGFN [8] | VideoSwin-RGB | 80.11 |
| CMRL [29] | I3D-RGB | 81.30 |
| CUPL [32] | I3D-RGB | 81.43 |
| DMU [28] | I3D-RGB | 79.85 |
| REWARD-E2E [33] | Uniformer-RGB | 80.30 |
| Tan et al. [30] | I3D-RGB | 82.10 |
| Ours | I3D-RGB | 83.47 |
| Method | Feature | AUC (%) |
|---|---|---|
| RTFM [15] | I3D-RGB | 84.30 |
| CTR [35] | I3D-RGB | 84.89 |
| MSL [20] | VideoSwin-RGB | 85.62 |
| S3R [31] | I3D-RGB | 85.99 |
| DMU [28] | I3D-RGB | 86.01 |
| Park et al. [36] | I3D-RGB | 85.63 |
| OPVAD [34] | CLIP-RGB | 86.05 |
| CMRL [29] | I3D-RGB | 86.10 |
| CUPL [32] | I3D-RGB | 86.22 |
| Ours | I3D-RGB | 87.16 |
| Module | UCF (%) | XD (%) | GFLOPs | TFLOPs/s | Params (M) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AUC | AP | AUCsub | APsub | FAR | AUC | AP | AUCsub | APsub | FAR | ||||
| PTFP | 84.14 | 21.07 | 62.61 | 23.60 | 1.63 | 93.34 | 80.18 | 80.59 | 81.34 | 0.93 | 2.14 | 3.47 | 10.90 |
| DMC | 85.56 | 37.07 | 68.82 | 39.46 | 0.99 | 94.27 | 82.84 | 83.12 | 83.69 | 0.56 | 2.05 | 3.22 | 10.23 |
| Our | 87.16 | 34.14 | 72.21 | 36.61 | 0.71 | 94.40 | 83.47 | 83.81 | 84.36 | 0.45 | 1.84 | 3.92 | 9.18 |
| Module | Dataset | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| UCF (%) | XD (%) | ||||||||||||
| MFP | AGLF | Clsin | Mdual | AUC | AP | AUCsub | APsub | FAR | AUC | AP | AUCsub | APsub | FAR |
| 85.78 | 31.85 | 70.29 | 34.59 | 1.36 | 93.10 | 79.85 | 81.02 | 81.46 | 1.22 | ||||
| √ | 86.19 | 32.94 | 70.33 | 35.36 | 1.34 | 93.88 | 81.92 | 82.22 | 82.97 | 0.41 | |||
| √ | 85.90 | 32.81 | 69.92 | 35.29 | 1.26 | 93.71 | 81.26 | 82.28 | 82.52 | 0.94 | |||
| √ | 83.02 | 29.64 | 67.09 | 33.43 | 2.03 | 91.32 | 77.97 | 80.13 | 79.62 | 1.89 | |||
| √ | 85.50 | 31.91 | 69.51 | 34.69 | 0.70 | 93.29 | 80.46 | 81.32 | 81.85 | 0.40 | |||
| √ | √ | 85.63 | 32.94 | 70.72 | 35.88 | 1.04 | 93.77 | 81.35 | 81.84 | 82.31 | 0.49 | ||
| √ | √ | 86.11 | 32.54 | 70.07 | 34.93 | 1.21 | 93.65 | 80.61 | 81.51 | 81.68 | 0.97 | ||
| √ | √ | 85.81 | 33.14 | 70.34 | 35.85 | 0.75 | 90.13 | 81.92 | 82.22 | 82.97 | 0.41 | ||
| √ | √ | √ | 84.86 | 31.35 | 69.93 | 34.72 | 1.91 | 91.29 | 80.73 | 80.52 | 81.64 | 1.76 | |
| √ | √ | √ | 87.16 | 34.14 | 72.21 | 36.61 | 0.71 | 94.40 | 83.47 | 83.81 | 84.36 | 0.45 | |
| Module | Dataset | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| UCF (%) | XD (%) | ||||||||||||
| Lcls | L(a,p,n) | L(a,h,n) | Ldual | AUC | AP | AUCsub | APsub | FAR | AUC | AP | AUCsub | APsub | FAR |
| √ | 82.71 | 26.03 | 59.40 | 27.30 | 1.67 | 94.12 | 81.79 | 81.65 | 82.19 | 0.90 | |||
| √ | √ | 86.11 | 32.54 | 70.07 | 34.93 | 0.89 | 93.90 | 82.07 | 81.26 | 81.73 | 0.56 | ||
| √ | √ | 83.06 | 29.24 | 61.18 | 30.59 | 0.83 | 94.01 | 82.40 | 80.96 | 81.33 | 0.52 | ||
| √ | √ | 87.16 | 34.14 | 72.21 | 36.61 | 0.71 | 94.40 | 83.47 | 83.81 | 84.36 | 0.45 | ||
| Fusion Strategy | UCF (%) | XD (%) | Params (k) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| AUC | AP | AUCsub | APsub | FAR | AUC | AP | AUCsub | APsub | FAR | ||
| AGC branch | 84.21 | 31.76 | 65.84 | 33.45 | 2.08 | 92.91 | 79.95 | 82.04 | 81.72 | 1.96 | _ |
| MA branch | 85.99 | 34.27 | 70.99 | 36.93 | 2.63 | 93.84 | 81.28 | 81.95 | 82.18 | 1.79 | _ |
| CrossAttention | 81.17 | 24.14 | 58.26 | 25.71 | 2.40 | 91.50 | 72.19 | 73.27 | 72.63 | 1.83 | 1048.6 |
| ElementwiseMultiply | 85.58 | 34.70 | 71.18 | 37.52 | 1.21 | 92.83 | 81.36 | 83.21 | 83.75 | 1.67 | 0 |
| Addition | 86.35 | 35.53 | 71.53 | 38.36 | 0.95 | 94.01 | 82.38 | 82.47 | 83.45 | 0.53 | 0 |
| GatedFusion | 87.16 | 34.14 | 72.21 | 36.61 | 0.71 | 94.40 | 83.47 | 83.81 | 84.36 | 0.45 | 524.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, C.; Meng, S.; Wang, R. Enhanced Video Anomaly Detection Through Dual Triplet Contrastive Loss for Hard Sample Discrimination. Entropy 2025, 27, 655. https://doi.org/10.3390/e27070655
Niu C, Meng S, Wang R. Enhanced Video Anomaly Detection Through Dual Triplet Contrastive Loss for Hard Sample Discrimination. Entropy. 2025; 27(7):655. https://doi.org/10.3390/e27070655
Chicago/Turabian StyleNiu, Chunxiang, Siyu Meng, and Rong Wang. 2025. "Enhanced Video Anomaly Detection Through Dual Triplet Contrastive Loss for Hard Sample Discrimination" Entropy 27, no. 7: 655. https://doi.org/10.3390/e27070655
APA StyleNiu, C., Meng, S., & Wang, R. (2025). Enhanced Video Anomaly Detection Through Dual Triplet Contrastive Loss for Hard Sample Discrimination. Entropy, 27(7), 655. https://doi.org/10.3390/e27070655





