Fisher Information and the Dynamics of Multicellular Ageing
Abstract
:1. Introduction
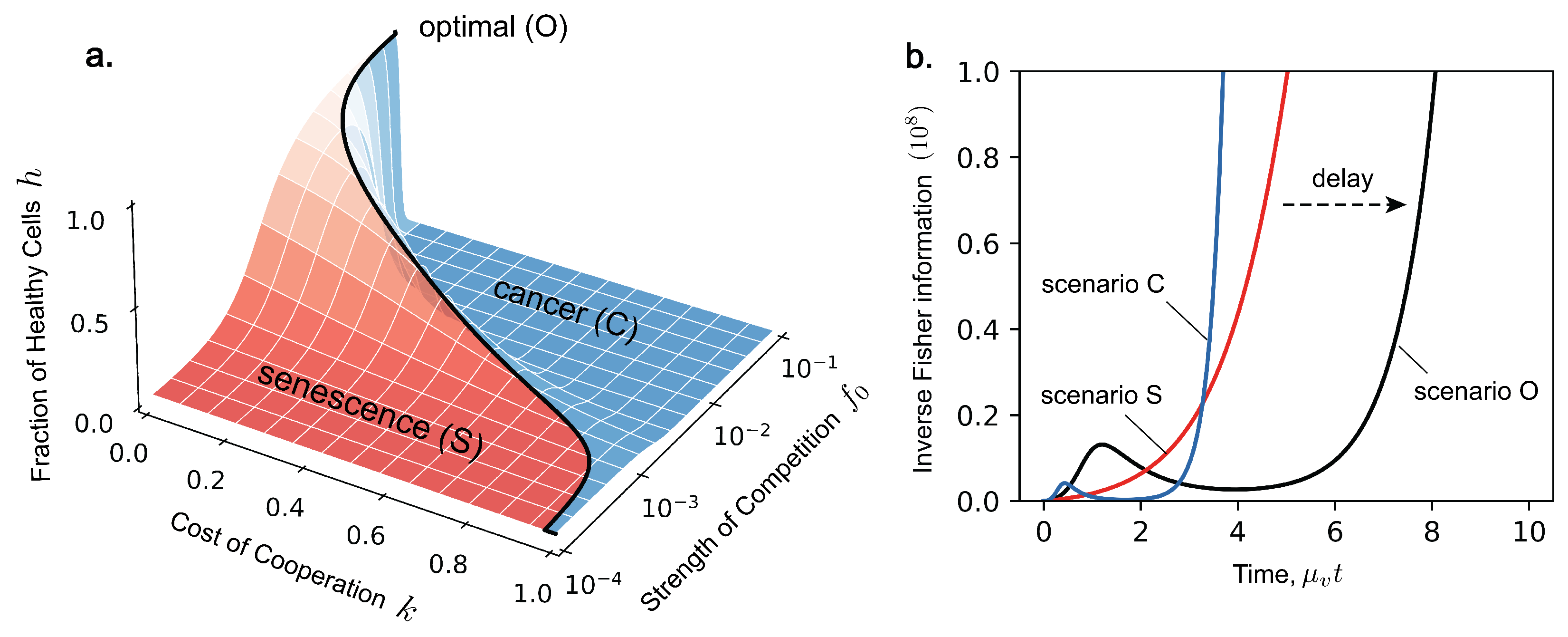
2. Ageing as Optimal Competition
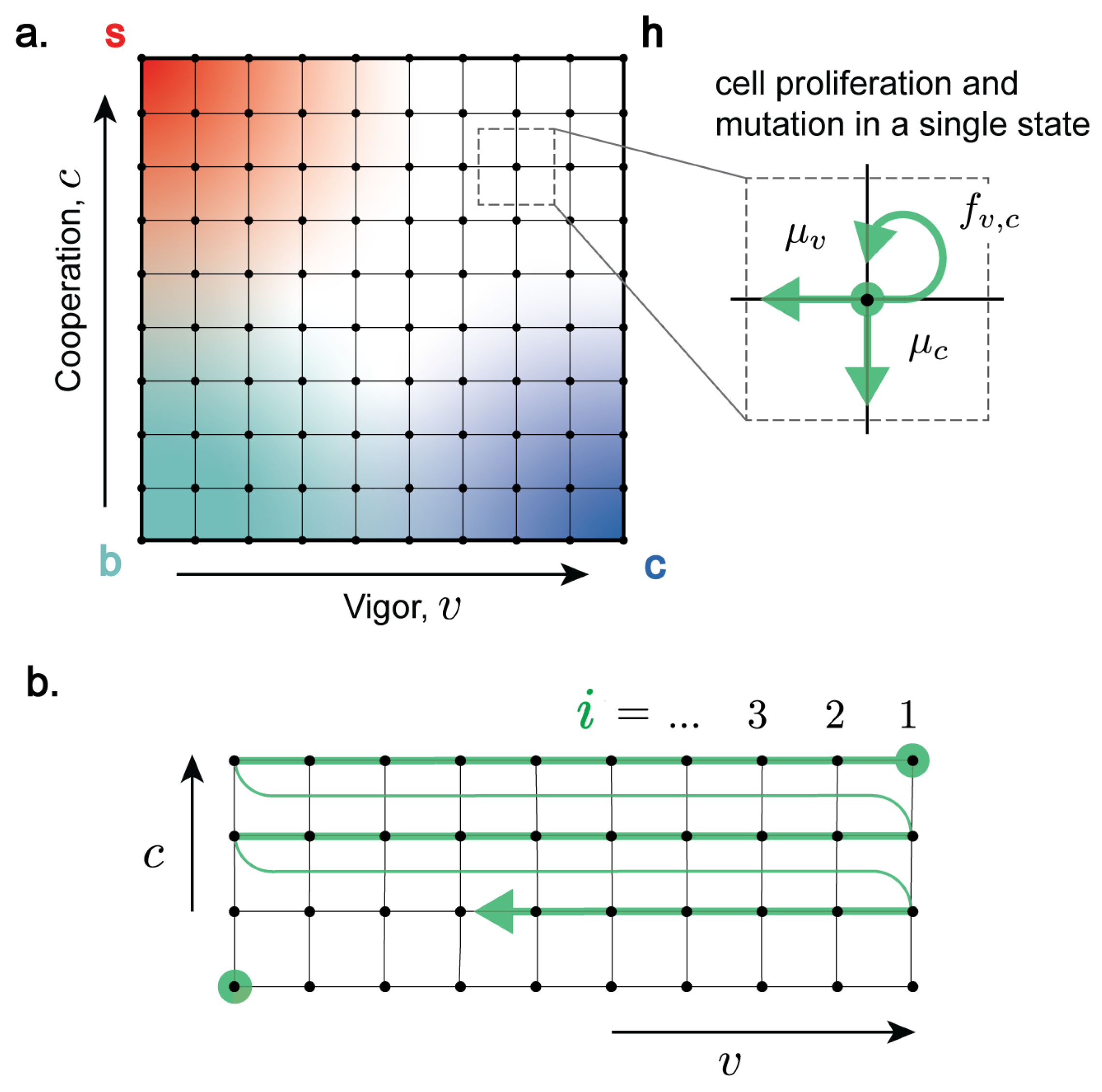
3. Master Equation for the Dynamics of Multicellular Ageing
Time Evolution of Cell Fractions and the Inevitability of Multicellular Ageing
4. Lagrangian Formulation of Master Equation
5. Link to Fisher Information
6. Fisher Information and Statistical Inference
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Rewriting Master Equation as Effective Replicator Equation
Appendix B. Derivation of Lagrangian
References
- Aktipis, C.A.; Boddy, A.M.; Jansen, G.; Hibner, U.; Hochberg, M.E.; Maley, C.C.; Wilkinson, G.S. Cancer across the tree of life: Cooperation and cheating in multicellularity. Philos. Trans. R. Soc. Biol. Sci. 2015, 370, 20140219. [Google Scholar] [CrossRef] [PubMed]
- Aktipis, A. Principles of cooperation across systems: From human sharing to multicellularity and cancer. Evol. Appl. 2016, 9, 17–36. [Google Scholar] [CrossRef]
- Michod, R.E. Darwinian Dynamics: Evolutionary Transitions in Fitness and Individuality; Princeton University Press: Princeton, NJ, USA, 2000. [Google Scholar]
- Knoll, A.H. The multiple origins of complex multicellularity. Annu. Rev. Earth Planet. Sci. 2011, 39, 217–239. [Google Scholar] [CrossRef]
- Kaiser, C.A.; Krieger, M.; Lodish, H.; Berk, A. Medical Cell Biology; WH Freeman: New York, NY, USA, 2007. [Google Scholar]
- Michod, R.E.; Roze, D. Cooperation and conflict in the evolution of multicellularity. Heredity 2001, 86, 1. [Google Scholar] [CrossRef] [PubMed]
- Hynes, R.O. The evolution of metazoan extracellular matrix. J. Cell Biol. 2012, 196, 671–679. [Google Scholar] [CrossRef]
- Harman, D. The aging process. Proc. Natl. Acad. Sci. USA 1981, 78, 7124–7128. [Google Scholar] [CrossRef]
- Vural, D.C.; Morrison, G.; Mahadevan, L. Aging in complex interdependency networks. Phys. Rev. E 2014, 89, 022811. [Google Scholar] [CrossRef]
- Sun, E.D.; Michaels, T.C.; Mahadevan, L. Optimal control of aging in complex networks. Proc. Natl. Acad. Sci. USA 2020, 117, 20404–20410. [Google Scholar] [CrossRef]
- Taneja, S.; Mitnitski, A.B.; Rockwood, K.; Rutenberg, A.D. Dynamical network model for age-related health deficits and mortality. Phys. Rev. E 2016, 93, 022309. [Google Scholar] [CrossRef]
- Farrell, S.G.; Mitnitski, A.B.; Rockwood, K.; Rutenberg, A.D. Network model of human aging: Frailty limits and information measures. Phys. Rev. E 2016, 94, 052409. [Google Scholar] [CrossRef]
- Fulop, T.; Larbi, A.; Witkowski, J.M.; McElhaney, J.; Loeb, M.; Mitnitski, A.; Pawelec, G. Aging, frailty and age-related diseases. Biogerontology 2010, 11, 547–563. [Google Scholar] [CrossRef] [PubMed]
- Nelson, P.; Masel, J. Intercellular competition and the inevitability of multicellular aging. Proc. Natl. Acad. Sci. USA 2017, 114, 12982–12987. [Google Scholar] [CrossRef]
- Vijg, J. Somatic mutations and aging: A re-evaluation. Mutat. Res. Mol. Mech. Mutagen. 2000, 447, 117–135. [Google Scholar] [CrossRef]
- Campisi, J. Aging, cellular senescence, and cancer. Annu. Rev. Physiol. 2013, 75, 685–705. [Google Scholar] [CrossRef] [PubMed]
- Van Deursen, J.M. The role of senescent cells in ageing. Nature 2014, 509, 439. [Google Scholar] [CrossRef]
- van Neerven, S.M.; Vermeulen, L. Cell competition in development, homeostasis and cancer. Nat. Rev. Mol. Cell Biol. 2023, 24, 221–236. [Google Scholar] [CrossRef]
- Baillon, L.; Basler, K. Reflections on cell competition. In Proceedings of the Seminars in Cell & Developmental Biology; Elsevier: Amsterdam, The Netherlands, 2014; Volume 32, pp. 137–144. [Google Scholar]
- Wodarz, D. Effect of stem cell turnover rates on protection against cancer and aging. J. Theor. Biol. 2007, 245, 449–458. [Google Scholar] [CrossRef]
- Biteau, B.; Karpac, J.; Supoyo, S.; DeGennaro, M.; Lehmann, R.; Jasper, H. Lifespan extension by preserving proliferative homeostasis in Drosophila. PLoS Genet. 2010, 6, e1001159. [Google Scholar] [CrossRef] [PubMed]
- Chalmers, A.D.; Whitley, P.; Vivarelli, S.; Wagstaff, L.; Piddini, E. Cell wars: Regulation of cell survival and proliferation by cell competition. Essays Biochem. 2012, 53, 69–82. [Google Scholar] [CrossRef]
- Moreno, E.; Basler, K. dMyc transforms cells into super-competitors. Cell 2004, 117, 117–129. [Google Scholar] [CrossRef]
- Hanahan, D.; Weinberg, R.A. Hallmarks of cancer: The next generation. Cell 2011, 144, 646–674. [Google Scholar] [CrossRef] [PubMed]
- Tenen, D.G. Disruption of differentiation in human cancer: AML shows the way. Nat. Rev. Cancer 2003, 3, 89. [Google Scholar] [CrossRef]
- Cancer: The Transforming Power of Cell Competition. Curr. Biol. 2016, 26, R164–R166. [CrossRef] [PubMed]
- Hausser, J.; Alon, U. Tumour heterogeneity and the evolutionary trade-offs of cancer. Nat. Rev. Cancer 2020, 20, 247–257. [Google Scholar] [CrossRef]
- Goodell, M.A.; Rando, T.A. Stem cells and healthy aging. Science 2015, 350, 1199–1204. [Google Scholar] [CrossRef]
- Wen, T.; Cheong, K.H.; Lai, J.W.; Koh, J.M.; Koonin, E.V. Extending the lifespan of multicellular organisms via periodic and stochastic intercellular competition. Phys. Rev. Lett. 2022, 128, 218101. [Google Scholar] [CrossRef] [PubMed]
- Wagner, G.P. The power of negative [theoretical] results. Proc. Natl. Acad. Sci. USA 2017, 114, 12851–12852. [Google Scholar] [CrossRef]
- Cheong, K.H.; Koh, J.M.; Jones, M.C. Multicellular survival as a consequence of Parrondo’s paradox. Proc. Natl. Acad. Sci. USA 2018, 115, E5258–E5259. [Google Scholar] [CrossRef]
- Mitteldorf, J.; Fahy, G.M. Questioning the inevitability of aging. Proc. Natl. Acad. Sci. USA 2018, 115, E558. [Google Scholar] [CrossRef]
- Michaels, T.C.; Mahadevan, L. Optimal intercellular competition in senescence and cancer. Proc. R. Soc. A 2023, 479, 20230204. [Google Scholar] [CrossRef]
- Raju, V.; Krishnaprasad, P. A variational problem on the probability simplex. In Proceedings of the 2018 IEEE Conference on Decision and Control (CDC), Miami Beach, FL, USA, 17–19 December 2018; pp. 3522–3528. [Google Scholar]
- Raju, V.; Krishnaprasad, P. Lie algebra structure of fitness and replicator control. arXiv 2020, arXiv:2005.09792. [Google Scholar]
- Frank, S.A. Simple unity among the fundamental equations of science. Philos. Trans. R. Soc. Biol. Sci. 2020, 375. [Google Scholar] [CrossRef] [PubMed]
- Price, G.R. Extension of covariance selection mathematics. Ann. Hum. Genet. 1972, 35, 485–490. [Google Scholar] [CrossRef] [PubMed]
- Zegers, P. Fisher information properties. Entropy 2015, 17, 4918–4939. [Google Scholar] [CrossRef]
- Frank, S.A. The Price equation program: Simple invariances unify population dynamics, thermodynamics, probability, information and inference. Entropy 2018, 20, 978. [Google Scholar] [CrossRef]
- Kim, E.J. Information Geometry, Fluctuations, Non-Equilibrium Thermodynamics, and Geodesics in Complex Systems. Entropy 2021, 23, 1393. [Google Scholar] [CrossRef]
- Lu, Y.R.; Tian, X.; Sinclair, D.A. The information theory of aging. Nature Aging 2023, 3, 1486–1499. [Google Scholar] [CrossRef]
- Ramakrishnan, N.; Pillai, S.R.B.; Padinhateeri, R. High fidelity epigenetic inheritance: Information theoretic model predicts threshold filling of histone modifications post replication. PLoS Comput. Biol. 2022, 18, e1009861. [Google Scholar] [CrossRef]
- Aristov, V.V.; Karnaukhov, A.V.; Buchelnikov, A.S.; Levchenko, V.F.; Nechipurenko, Y.D. The Degradation and Aging of Biological Systems as a Process of Information Loss and Entropy Increase. Entropy 2023, 25, 1067. [Google Scholar] [CrossRef]
- Szilard, L. On the nature of the aging process. Proc. Natl. Acad. Sci. USA 1959, 45, 30–45. [Google Scholar] [CrossRef]
- López-Otín, C.; Blasco, M.A.; Partridge, L.; Serrano, M.; Kroemer, G. Hallmarks of aging: An expanding universe. Cell 2023, 186, 243–278. [Google Scholar] [CrossRef]
- Cagan, A.; Baez-Ortega, A.; Brzozowska, N.; Abascal, F.; Coorens, T.H.H.; Sanders, M.A.; Lawson, A.R.J.; Harvey, L.M.R.; Bhosle, S.; Jones, D.; et al. Somatic Mutation Rates Scale with Lifespan across Mammals. Nature 2022, 604, 517–524. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.H.; Hayano, M.; Griffin, P.T.; Amorim, J.A.; Bonkowski, M.S.; Apostolides, J.K.; Salfati, E.L.; Blanchette, M.; Munding, E.M.; Bhakta, M.; et al. Loss of epigenetic information as a cause of mammalian aging. Cell 2023, 186, 305–326. [Google Scholar] [CrossRef] [PubMed]
- Frank, S.A. Natural selection maximizes Fisher information. J. Evol. Biol. 2009, 22, 231–244. [Google Scholar] [CrossRef] [PubMed]
- Bertucci-Richter, E.M.; Parrott, B.B. The rate of epigenetic drift scales with maximum lifespan across mammals. Nat. Commun. 2023, 14, 7731. [Google Scholar] [CrossRef]
- Bell, C.G.; Lowe, R.; Adams, P.D.; Baccarelli, A.A.; Beck, S.; Bell, J.T.; Christensen, B.C.; Gladyshev, V.N.; Heijmans, B.T.; Horvath, S.; et al. DNA methylation aging clocks: Challenges and recommendations. Genome Biol. 2019, 20, 249. [Google Scholar] [CrossRef]
- Meyer, D.H.; Schumacher, B. Aging clocks based on accumulating stochastic variation. Nat. Aging 2024, 4, 871–885. [Google Scholar] [CrossRef]
- Horvath, S.; Raj, K. DNA methylation-based biomarkers and the epigenetic clock theory of ageing. Nat. Rev. Genet. 2018, 19, 371–384. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hale, Z.F.; Cánez, G.A.; Michaels, T.C.T. Fisher Information and the Dynamics of Multicellular Ageing. Entropy 2025, 27, 638. https://doi.org/10.3390/e27060638
Hale ZF, Cánez GA, Michaels TCT. Fisher Information and the Dynamics of Multicellular Ageing. Entropy. 2025; 27(6):638. https://doi.org/10.3390/e27060638
Chicago/Turabian StyleHale, Zachary F., Gonzalo A. Cánez, and Thomas C. T. Michaels. 2025. "Fisher Information and the Dynamics of Multicellular Ageing" Entropy 27, no. 6: 638. https://doi.org/10.3390/e27060638
APA StyleHale, Z. F., Cánez, G. A., & Michaels, T. C. T. (2025). Fisher Information and the Dynamics of Multicellular Ageing. Entropy, 27(6), 638. https://doi.org/10.3390/e27060638





