Approaches for Reducing Expert Burden in Bayesian Network Parameterization
Abstract
:1. Introduction
1.1. Related Works
1.2. What to Expect in This Paper
2. Methodology
2.1. Data
2.1.1. Elicited Data
Pollinator Abundance (PA)
Food Security (FS)
Polar Bears (PB)
2.1.2. Simulated Data
- Equal and low (EqL): The same low correlation () is set between each parent node and the child node.
- Equal and high (EqH): The same high(er) correlation () is set between each parent node and the child node.
- Increasing (Incr): The correlations between the parent nodes and the child node increases, with values of , , and for the three parent–child pairs, respectively.
- Outlier (Out): The correlation between one parent node and the child node is significantly higher than the correlation between the other parent nodes and the child node, with values of 0.1, 0.1, and 0.9 for the three parent nodes, respectively.
2.2. InterBeta
2.2.1. Method
- 1.
- The mean () and variance () are derived from the multinomial distribution, and the alpha () and beta () parameters are then calculated using the method of moments [11].
- 2.
- The and parameters are iteratively adjusted using Gaussian noise, accepting only those mutations that improve the Kullback–Leibler (KL) divergence between the discretized fitted beta distribution and the original elicited multinomial distribution. This process typically converges within 1000 iterations [11].
2.2.2. Versions
2.2.3. Extensions
2.3. Other CPT Construction Methods
2.3.1. Ranked Nodes Method
2.3.2. Functional Interpolation
2.4. Performance Metrics
2.4.1. Kullback–Leibler Divergence
2.4.2. Percentage of Agreement
2.4.3. Burden
3. Results
3.1. Comparison
3.2. InterBeta Extensions
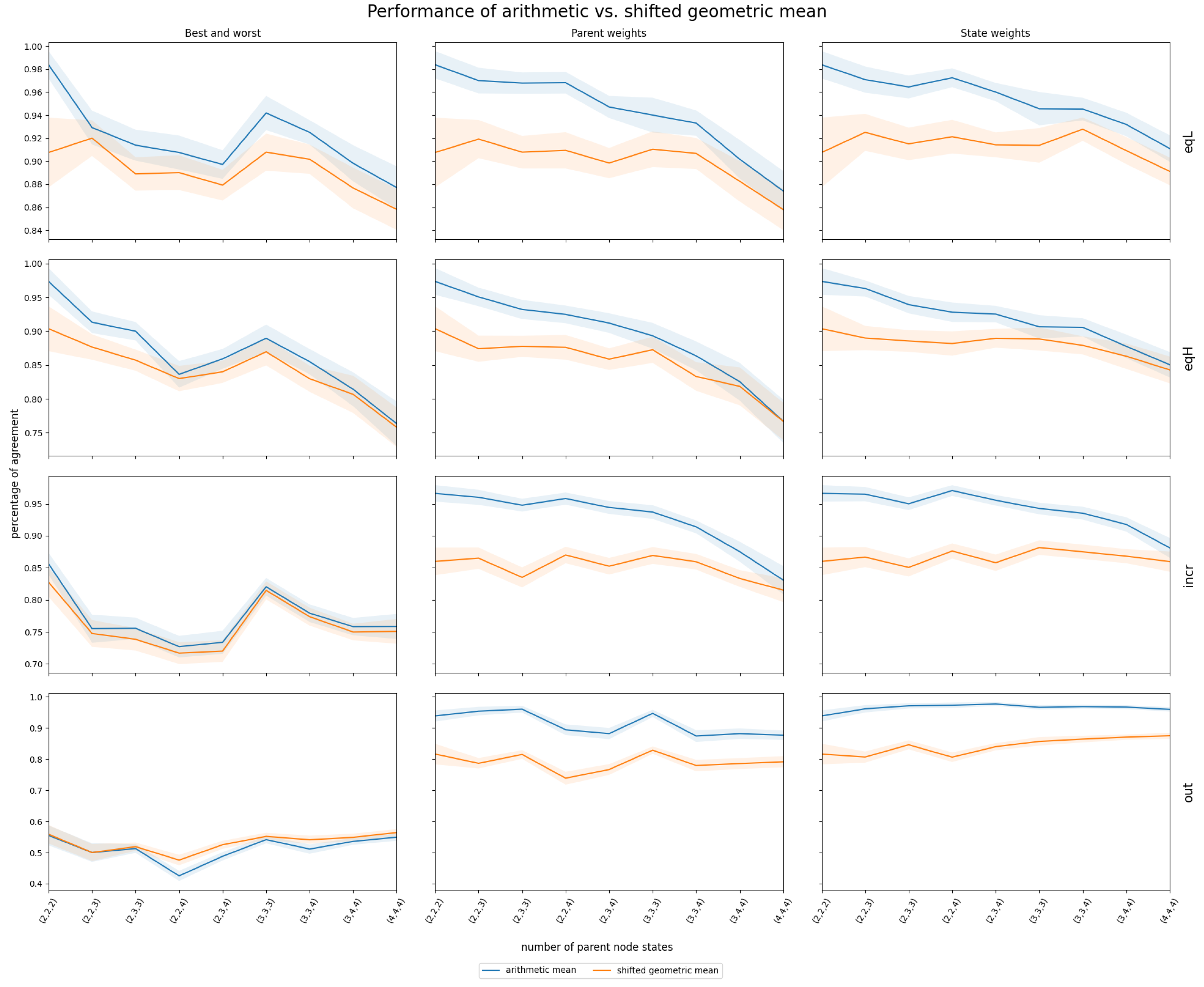
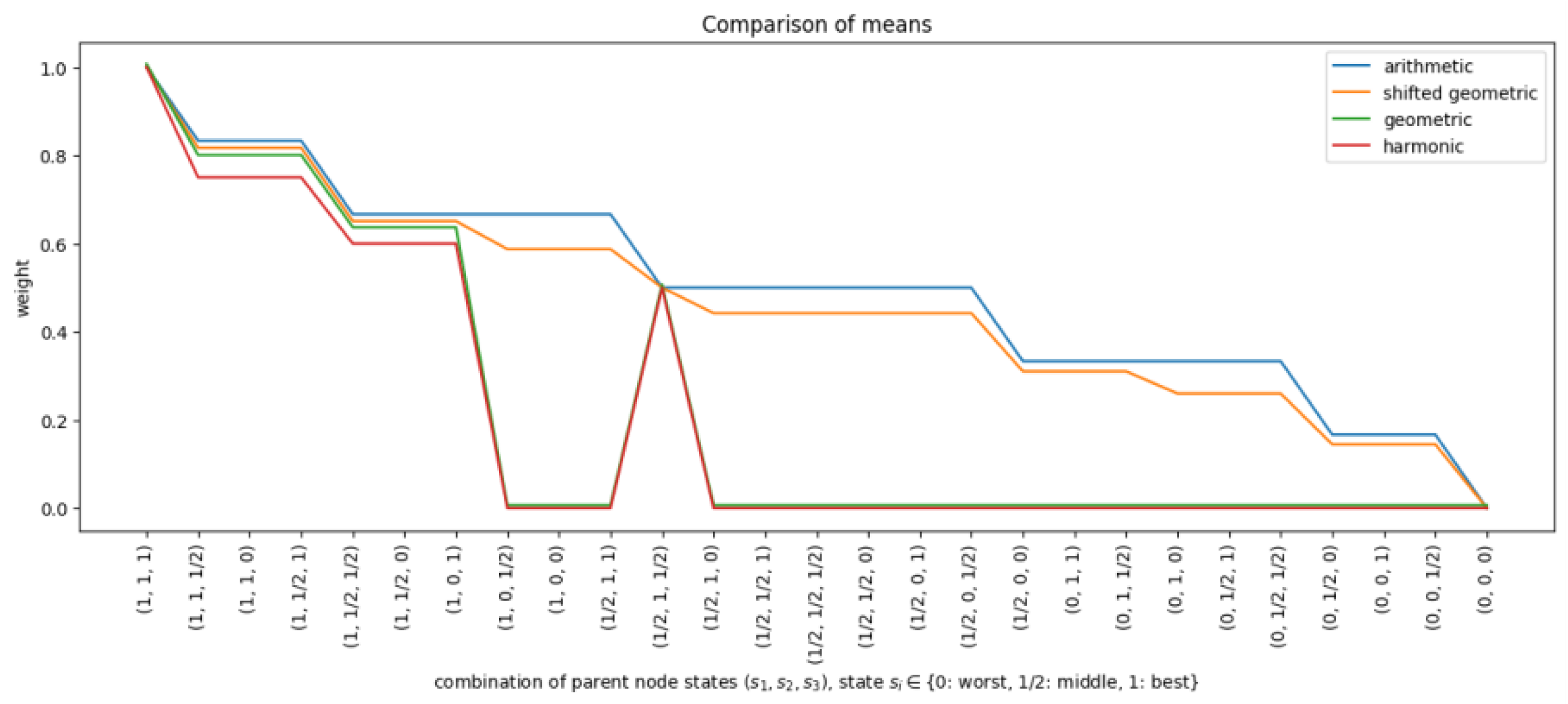
3.2.1. Shifted Geometric Mean
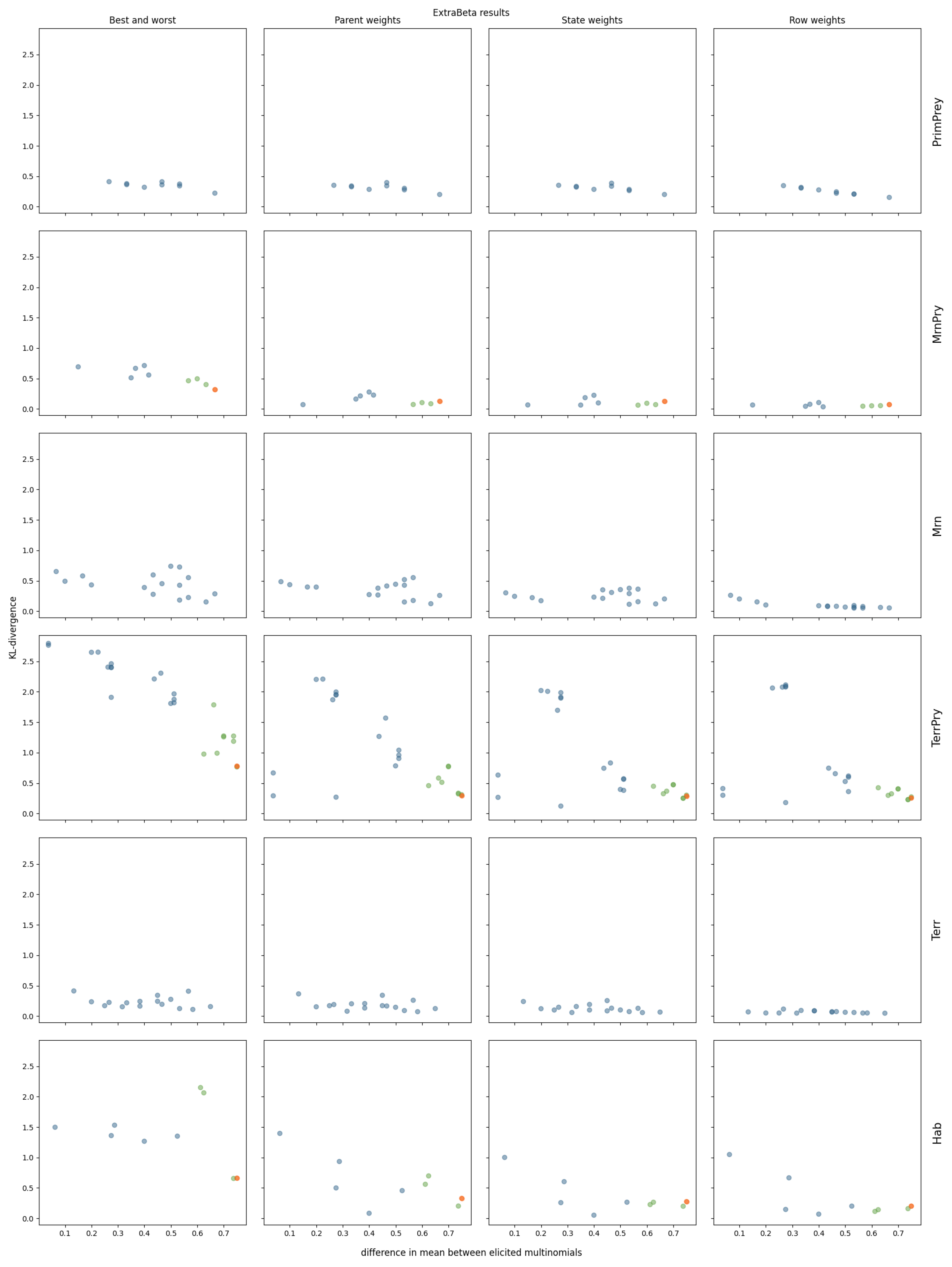
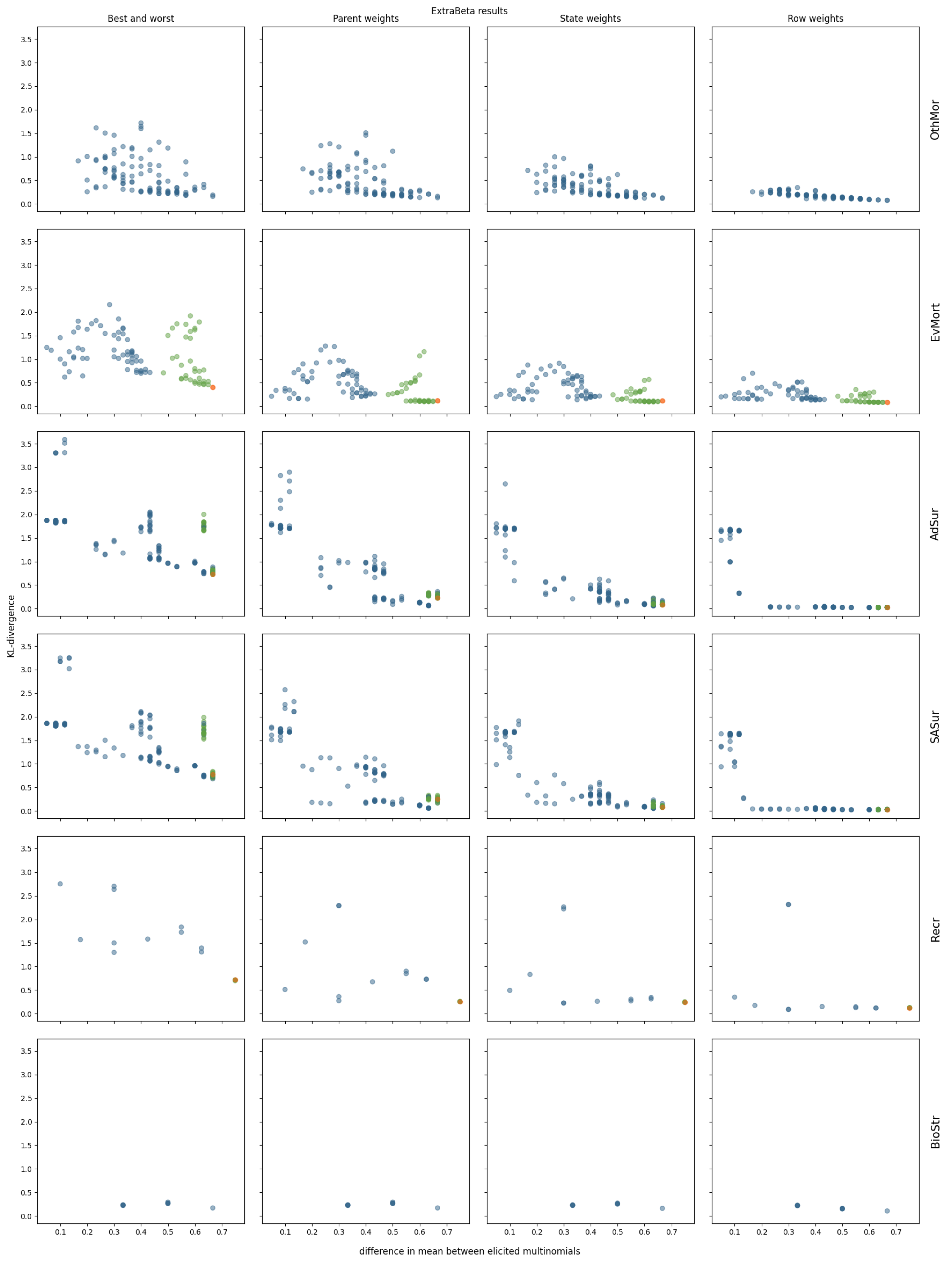
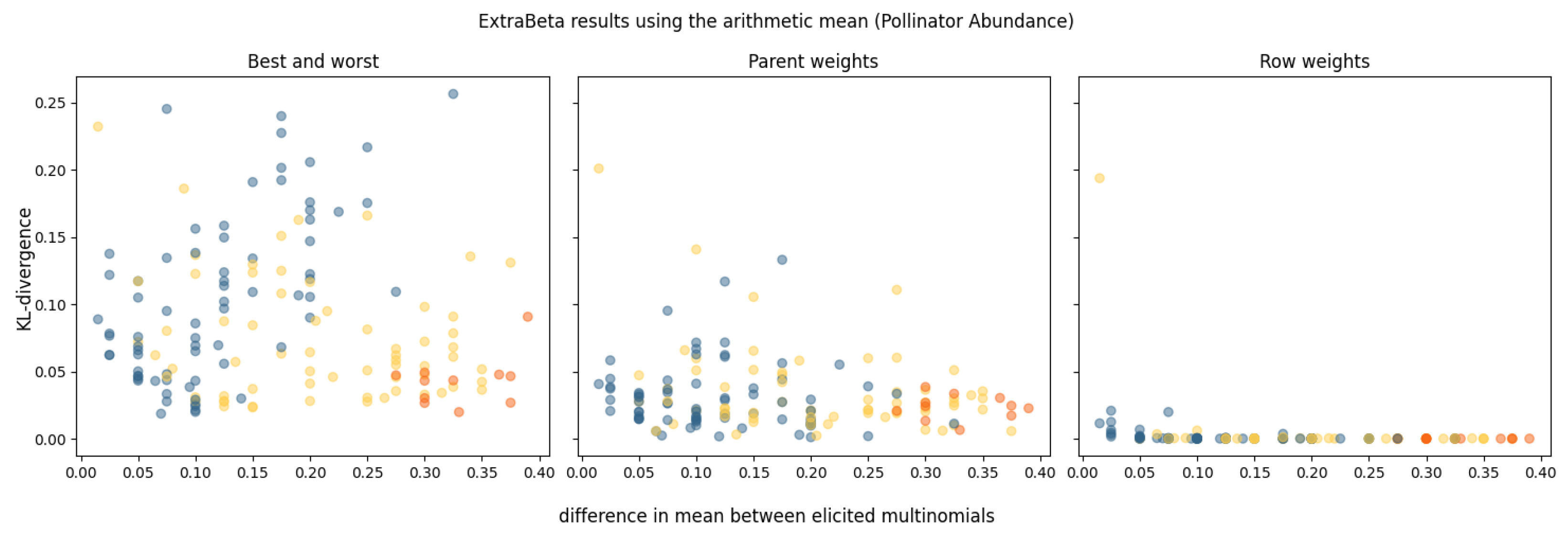
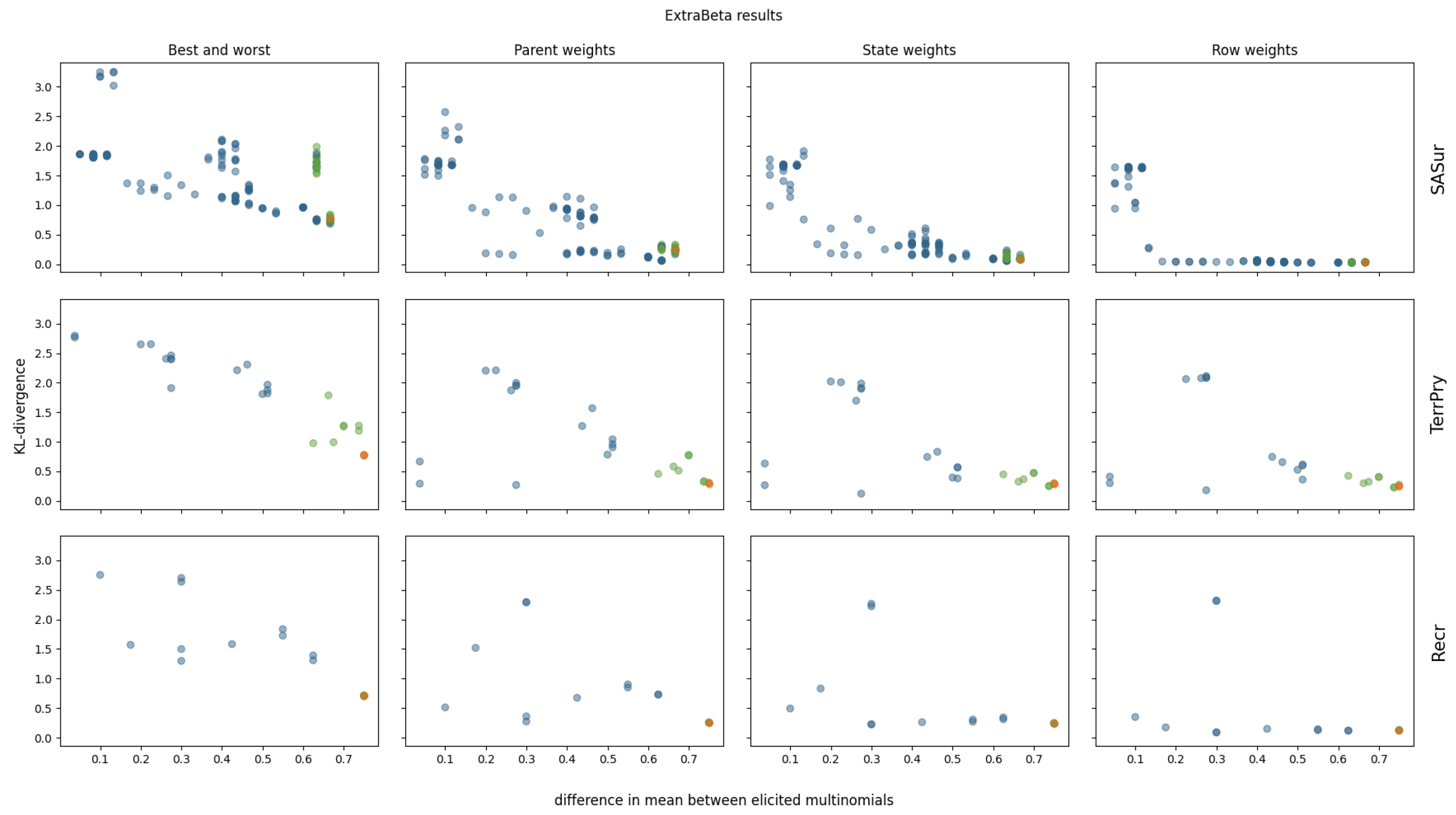
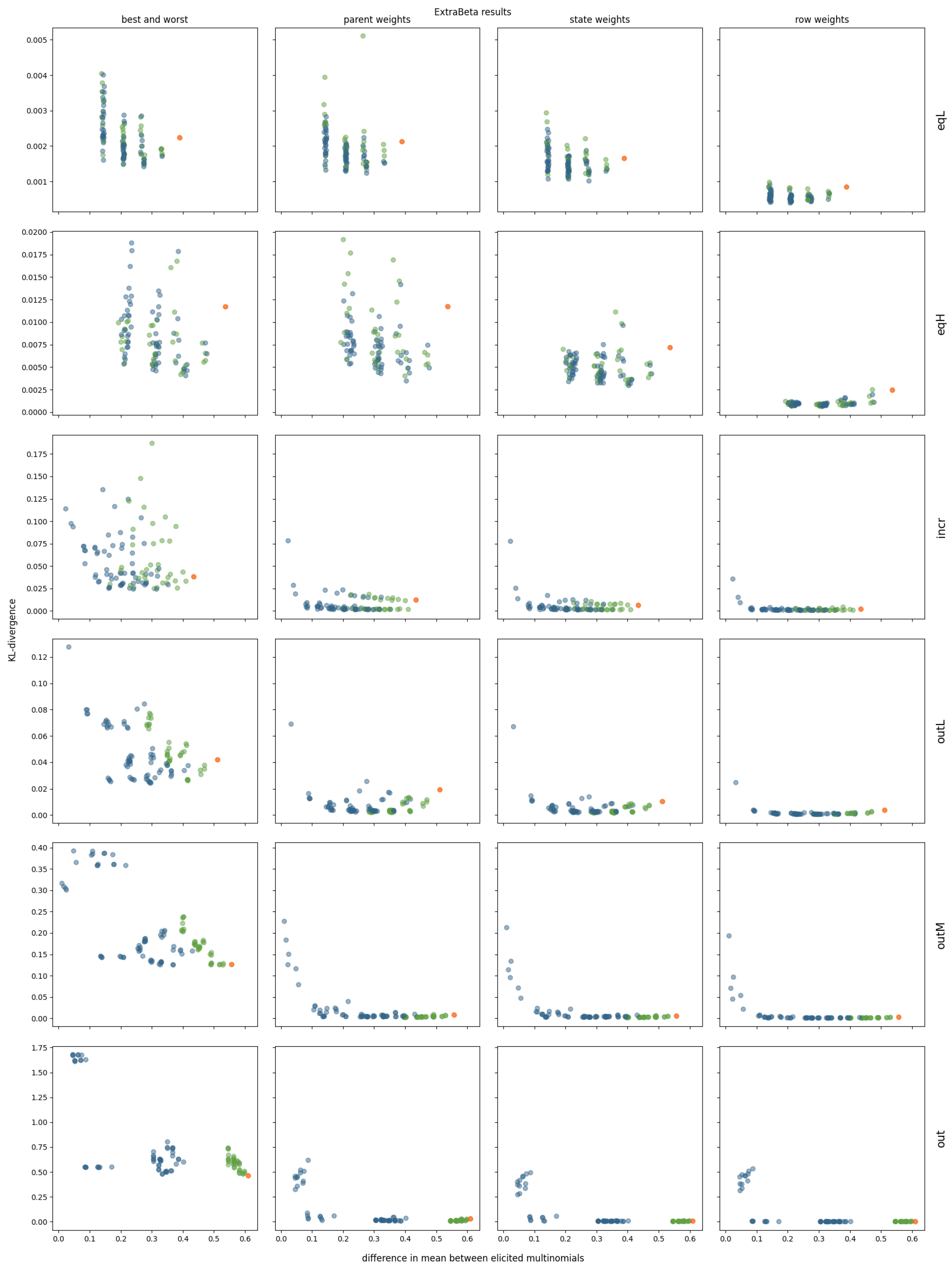
3.2.2. ExtraBeta
4. Discussion
Recommendations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

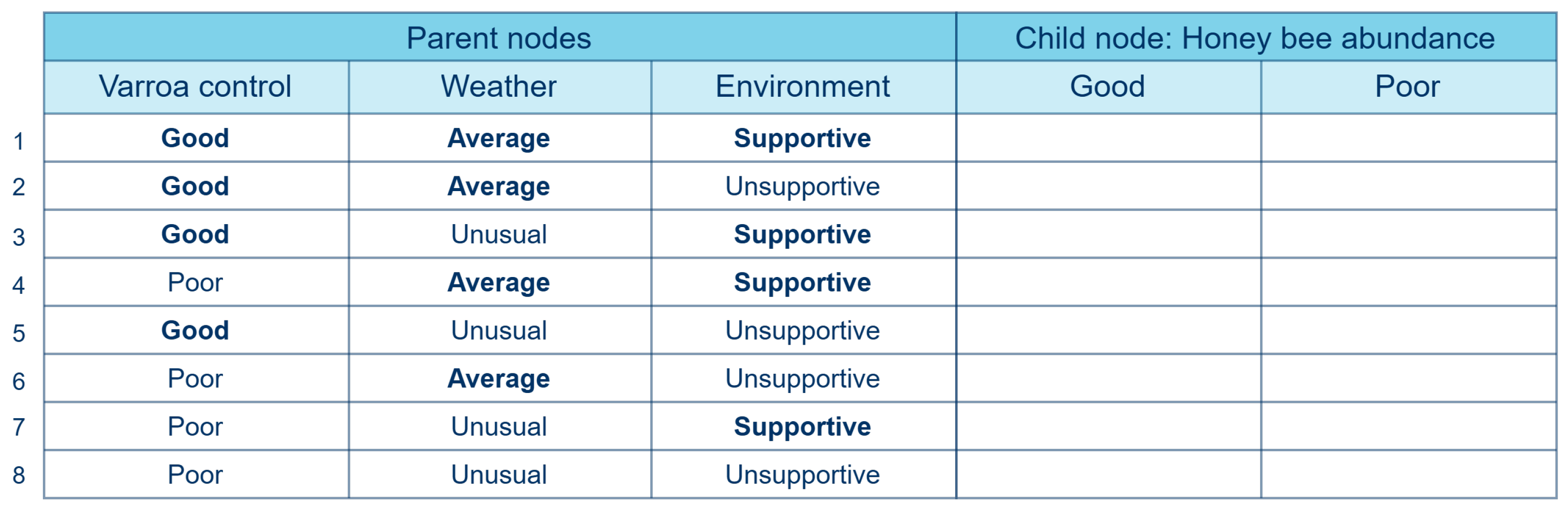

| CPT | RNM | Functional Interpolation | |||
|---|---|---|---|---|---|
| (KL div. / % Agreement) | Original | AutoRNM | Normal | t-Normal | Beta |
| Polar bears Ice | 0.3509/56.9 | 0.2833/54.2 | 0.2996/61.1 | 0.3769/70.8 | 0.2501/62.5 |
| Polar bears Disturb | 0.1205/60.5 | 0.1547/48.1 | 0.0913/80.2 | 0.1525/85.2 | 0.0912/80.2 |
| Polar bears CumPop | 0.2119/72.2 | 0.2324/72.2 | 0.2163/75.0 | 1.5414/55.6 | 0.2015/75.0 |
| Polar bears AFBod | 0.186/91.7 | 0.2327/97.2 | 0.3125/69.4 | 0.6553/50.0 | 0.1522/91.7 |
| Polar bears SASur | 0.3026/63.9 | 0.3204/72.2 | 0.4699/63.9 | 0.8802/61.1 | 0.1005/94.4 |
| Polar bears AdSur | 0.3113/63.9 | 0.3312/72.2 | 0.5344/63.9 | 0.8427/55.6 | 0.124/94.4 |
| Polar bears OthMor | 0.148/77.8 | 0.181/70.4 | 0.1712/74.1 | 0.2521/74.1 | 0.1061/85.2 |
| Polar bears EvMort | 0.1332/100.0 | 0.1518/100.0 | 0.1833/92.6 | 0.3768/66.7 | 0.1031/92.6 |
| Polar bears TerrPry | 0.22/100.0 | 0.2745/100.0 | 0.4597/62.5 | 0.9088/50.0 | 0.2109/100.0 |
| Polar bears Recr | 0.2418/100.0 | 0.2596/100.0 | 0.6192/75.0 | 0.7533/58.3 | 0.2718/91.7 |
| Polar bears Mrn | 0.138/50.0 | 0.1412/75.0 | 0.1911/75.0 | 0.4872/75.0 | 0.1008/91.7 |
| Polar bears Hab | 0.417/55.6 | 0.4197/55.6 | 0.178/77.8 | 0.9017/55.6 | 0.1474/77.8 |
| Polar bears Terr | 0.0923/91.7 | 0.0999/91.7 | 0.0846/91.7 | 0.6179/75.0 | 0.1288/91.7 |
| Polar bears PrimPrey | 0.1983/77.8 | 0.227/77.8 | 0.2511/100.0 | 0.2791/66.7 | 0.2115/77.8 |
| Polar bears MrnPry | 0.0862/88.9 | 0.1425/88.9 | 0.0594/100.0 | 0.5905/77.8 | 0.0688/88.9 |
| Polar bears BioStr | 0.1472/77.8 | 0.1633/77.8 | 0.2262/66.7 | 0.2582/66.7 | 0.1417/77.8 |
| Food security EWDM | 0.1843/66.7 | 0.1851/66.7 | 0.1043/91.7 | 0.0631/91.7 | 0.0171/91.7 |
| Food security PWDM | 0.1863/50.0 | 0.1752/58.3 | 0.1005/75.0 | 0.109/66.7 | 0.0242/66.7 |
| Food security 1 | 0.188/66.7 | 0.1733/58.3 | 0.1221/75.0 | 0.1558/66.7 | 0.0237/66.7 |
| Food security 2 | 0.2108/58.3 | 0.1848/41.7 | 0.1238/75.0 | 0.1073/66.7 | 0.0284/66.7 |
| Food security 3 | 0.2005/50.0 | 0.1697/75.0 | 0.1299/66.7 | 0.1831/58.3 | 0.0816/58.3 |
| Food security 4 | 0.1903/66.7 | 0.2223/58.3 | 0.0852/100.0 | 0.0758/75.0 | 0.0235/83.3 |
| Food security 5 | 0.4594/41.7 | 0.4761/66.7 | 0.5775/66.7 | 0.1192/100.0 | 0.028/100.0 |
| Pollinator abundance EWDM | 0.0032/100.0 | 0.0031/100.0 | 0.0/100.0 | 0.0/100.0 | 0.0/100.0 |
| Pollinator abundance 1 | 0.01/100.0 | 0.0099/100.0 | 0.0/100.0 | 0.0/100.0 | 0.0/100.0 |
| Pollinator abundance 2 | 0.0094/100.0 | 0.0082/100.0 | 0.0/100.0 | 0.0/87.5 | 0.0/100.0 |
| Pollinator abundance 3 | 0.0088/100.0 | 0.0083/100.0 | 0.0/100.0 | 0.0/87.5 | 0.0/100.0 |
| Pollinator abundance 4 | 0.004/100.0 | 0.0027/100.0 | 0.0/100.0 | 0.0/100.0 | 0.0/100.0 |
| Pollinator abundance 5 | 0.0201/87.5 | 0.0161/100.0 | 0.0/100.0 | 0.0/100.0 | 0.0/100.0 |
| Pollinator abundance 6 | 0.0043/100.0 | 0.0054/100.0 | 0.0/100.0 | 0.0/100.0 | 0.0/100.0 |
| Pollinator abundance 7 | 0.0166/75.0 | 0.0153/87.5 | 0.0/100.0 | 0.0/100.0 | 0.0/100.0 |
| Pollinator abundance 8 | 0.0247/75.0 | 0.0238/75.0 | 0.0/100.0 | 0.0/87.5 | 0.0/100.0 |
| Pollinator abundance 9 | 0.0219/87.5 | 0.0201/75.0 | 0.0/100.0 | 0.0/100.0 | 0.0/100.0 |
| Pollinator abundance 10 | 0.0086/100.0 | 0.0071/100.0 | 0.0/100.0 | 0.0/100.0 | 0.0/100.0 |
| CPT | InterBeta | |||
|---|---|---|---|---|
| (KL div. / % Agreement) | Best–Worst Rows | Parent Weights | State Weights | Row Weights |
| Polar bears Ice | 0.2284/70.8 | 0.1347/76.4 | 0.1158/73.6 | 0.0337/81.9 |
| Polar bears Disturb | 0.1885/75.3 | 0.1885/75.3 | 0.1853/72.8 | 0.1346/67.9 |
| Polar bears CumPop | 0.3701/63.9 | 0.3554/72.2 | 0.3407/77.8 | 0.2367/88.9 |
| Polar bears AFBod | 0.704/47.2 | 0.2047/97.2 | 0.1799/97.2 | 0.1324/97.2 |
| Polar bears SASur | 0.6735/58.3 | 0.2423/75.0 | 0.0792/97.2 | 0.0298/100.0 |
| Polar bears AdSur | 0.6897/58.3 | 0.201/80.6 | 0.0753/97.2 | 0.0256/100.0 |
| Polar bears OthMor | 0.1616/77.8 | 0.133/77.8 | 0.1188/77.8 | 0.0766/85.2 |
| Polar bears EvMort | 0.4037/55.6 | 0.1105/100.0 | 0.1096/100.0 | 0.084/92.6 |
| Polar bears TerrPry | 0.7762/62.5 | 0.2977/100.0 | 0.2896/100.0 | 0.258/100.0 |
| Polar bears Recr | 0.7226/58.3 | 0.2264/100.0 | 0.149/100.0 | 0.1165/91.7 |
| Polar bears Mrn | 0.2361/83.3 | 0.2015/83.3 | 0.1302/100.0 | 0.0545/100.0 |
| Polar bears Hab | 0.6701/55.6 | 0.3285/66.7 | 0.2724/77.8 | 0.1915/88.9 |
| Polar bears Terr | 0.1646/91.7 | 0.1394/91.7 | 0.0612/83.3 | 0.0478/100.0 |
| Polar bears PrimPrey | 0.2239/66.7 | 0.2021/100.0 | 0.2019/100.0 | 0.1528/88.9 |
| Polar bears MrnPry | 0.341/66.7 | 0.1533/88.9 | 0.1445/88.9 | 0.0707/100.0 |
| Polar bears BioStr | 0.1641/77.8 | 0.1641/77.8 | 0.1602/88.9 | 0.1063/77.8 |
| Food security EWDM | 0.1819/66.7 | 0.0288/91.7 | 0.0285/91.7 | 0.0221/91.7 |
| Food security PWDM | 0.1987/41.7 | 0.0273/83.3 | 0.0272/83.3 | 0.0184/75.0 |
| Food security 1 | 0.1756/50.0 | 0.0477/75.0 | 0.0381/75.0 | 0.0163/75.0 |
| Food security 2 | 0.1982/50.0 | 0.0348/91.7 | 0.0348/91.7 | 0.0247/75.0 |
| Food security 3 | 0.2111/66.7 | 0.1114/91.7 | 0.1054/91.7 | 0.0638/83.3 |
| Food security 4 | 0.2164/50.0 | 0.0346/75.0 | 0.0342/75.0 | 0.0214/83.3 |
| Food security 5 | 0.2759/75.0 | 0.11/100.0 | 0.0307/100.0 | 0.0233/100.0 |
| Pollinator abundance EWDM | 0.0164/87.5 | 0.0027/100.0 | 0.0027/100.0 | 0.0/100.0 |
| Pollinator abundance 1 | 0.0265/87.5 | 0.0133/100.0 | 0.0133/100.0 | 0.0/100.0 |
| Pollinator abundance 2 | 0.0374/87.5 | 0.0063/100.0 | 0.0063/100.0 | 0.0/100.0 |
| Pollinator abundance 3 | 0.0132/87.5 | 0.0097/87.5 | 0.0097/87.5 | 0.0/100.0 |
| Pollinator abundance 4 | 0.041/87.5 | 0.0031/100.0 | 0.0031/100.0 | 0.0/100.0 |
| Pollinator abundance 5 | 0.0391/100.0 | 0.024/100.0 | 0.024/100.0 | 0.0/100.0 |
| Pollinator abundance 6 | 0.0405/87.5 | 0.0141/100.0 | 0.0141/100.0 | 0.0/100.0 |
| Pollinator abundance 7 | 0.0235/100.0 | 0.012/100.0 | 0.012/100.0 | 0.0/100.0 |
| Pollinator abundance 8 | 0.042/87.5 | 0.0218/87.5 | 0.0218/87.5 | 0.0/100.0 |
| Pollinator abundance 9 | 0.0318/87.5 | 0.0206/87.5 | 0.0206/87.5 | 0.0/100.0 |
| Pollinator abundance 10 | 0.0553/87.5 | 0.0046/100.0 | 0.0046/100.0 | 0.0/100.0 |
| CPT | InterBeta with Elicited Middle Rows | |||
|---|---|---|---|---|
| (KL div. / % Agreement) | Best, Worst, Mid | Parent Weights | State Weights | Row Weights |
| Polar bears Ice | 1.0349/66.7 | 0.6539/80.6 | 0.3214/69.4 | 0.0636/83.3 |
| Polar bears Disturb | 1.2857/75.3 | 1.2857/75.3 | 1.27/75.3 | 0.6246/82.7 |
| Polar bears CumPop | 0.7845/66.7 | 0.4828/63.9 | 0.4663/66.7 | 0.1197/86.1 |
| Polar bears AFBod | 1.7942/47.2 | 0.3596/97.2 | 0.1425/88.9 | 0.0584/91.7 |
| Polar bears SASur | 1.6724/58.3 | 0.2478/88.9 | 0.223/97.2 | 0.0337/100.0 |
| Polar bears AdSur | 1.6483/58.3 | 0.299/88.9 | 0.2623/97.2 | 0.0277/100.0 |
| Polar bears OthMor | 0.8206/77.8 | 0.7762/77.8 | 0.7429/77.8 | 0.2117/92.6 |
| Polar bears EvMort | 1.312/55.6 | 0.3012/100.0 | 0.3003/100.0 | 0.1189/96.3 |
| Polar bears TerrPry | 1.6725/56.2 | 0.0618/100.0 | 0.0524/100.0 | 0.0441/100.0 |
| Polar bears Recr | 1.702/50.0 | 0.4709/100.0 | 0.1893/100.0 | 0.0501/100.0 |
| Polar bears Mrn | 0.6355/75.0 | 0.5673/91.7 | 0.3914/91.7 | 0.0722/100.0 |
| Polar bears Hab | 1.3242/55.6 | 0.075/88.9 | 0.0667/88.9 | 0.0584/100.0 |
| Polar bears Terr | 0.496/91.7 | 0.3498/91.7 | 0.3084/100.0 | 0.1547/100.0 |
| Polar bears PrimPrey | 1.0344/66.7 | 0.6767/100.0 | 0.6757/100.0 | 0.3311/77.8 |
| Polar bears MrnPry | 1.0919/66.7 | 0.2235/88.9 | 0.2043/100.0 | 0.0347/100.0 |
| Polar bears BioStr | 0.8446/77.8 | 0.7387/77.8 | 0.7387/77.8 | 0.3464/77.8 |
References
- Kyrimi, E.; McLachlan, S.; Dube, K.; Neves, M.R.; Fahmi, A.; Fenton, N. A comprehensive scoping review of Bayesian networks in healthcare: Past, present and future. Artif. Intell. Med. 2021, 117, 2050–2061. [Google Scholar] [CrossRef]
- European Commission and Directorate-General for Research and Innovation; Cooke, R.M.; Goossens, L.J.H. Procedures Guide for Structured Expert Judgment; Publications Office of EU: Luxembourg, 2000. [Google Scholar]
- Di Zio, M.; Scanu, M.; Coppola, L.; Luzi, O.; Ponti, A. Bayesian networks for imputation. J. R. Stat. Soc. Ser. A Stat. Soc. 2004, 167, 309–322. [Google Scholar] [CrossRef]
- Hruschka, E.R.; Hruschka, E.R.; Ebecken, N.F.F. Bayesian networks for imputation in classification problems. J. Intell. Inf. Syst. 2007, 29, 231–252. [Google Scholar] [CrossRef]
- Niloofar, P.; Ganjali, M. A new multivariate imputation method based on Bayesian networks. J. Appl. Stat. 2014, 41, 501–518. [Google Scholar] [CrossRef]
- Brown, B.B. Delphi Process: A Methodology Used for the Elicitation of Opinions of Experts; RAND Corporation: Santa Monica, CA, USA, 1968. [Google Scholar]
- Cooke, R.M. Experts in Uncertainty: Opinion and Subjective Probability in Science; Oxford University Press: Cary, NC, USA, 1991. [Google Scholar]
- Hanea, A.M.; McBride, M.F.; Burgman, M.A.; Wintle, B.C.; Fidler, F.; Flander, L.; Twardy, C.R.; Manning, B.; Mascaro, S. Investigate Discuss Estimate Aggregate for structured expert judgement. Int. J. Forecast. 2017, 33, 267–279. [Google Scholar] [CrossRef]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems; Morgan Kaufmann: Burlington, MA, USA, 1988. [Google Scholar]
- Fenton, N.E.; Neil, M.; Caballero, J.G. Using Ranked Nodes to Model Qualitative Judgments in Bayesian Networks. IEEE Trans. Knowl. Data Eng. 2007, 192, 1241–1251. [Google Scholar] [CrossRef]
- Mascaro, S.; Woodberry, O. A flexible method for parameterizing ranked nodes in Bayesian networks using Beta distributions. Risk Anal. 2022, 42, 1179–1195. [Google Scholar] [CrossRef]
- Podofillini, L.; Mkrtchyan, L.; Dang, V.N. Aggregating Expert-Elicited Error Probabilities to Build HRA Models; CRC Press: Boca Raton, FL, USA, 2014; pp. 1119–1128. [Google Scholar]
- Knochenhauer, M.; Swaling, V.H.; Dedda, F.D.; Hansson, F.; Sjökvist, S.; Sunnegaerd, K. Using Bayesian Belief Network (BBN) Modelling for Rapid Source Term Prediction. Final Report; Nordisk Kernesikkerhedsforskning: Roskilde, Denmark, 2013. [Google Scholar]
- Mkrtchyan, L.; Podofillini, L.; Dang, N.V. Methods for building Conditional Probability Tables of Bayesian Belief Networks from limited judgment: An evaluation for Human Reliability Application Reliab. Eng. Syst. Saf. 2016, 151, 93–112. [Google Scholar] [CrossRef]
- Zio, E.; Mustafayeva, M.; Montanaro, A. A Bayesian belief network model for the risk assessment and management of premature screen-out during hydraulic fracturing. Reliab. Eng. Syst. Saf. 2022, 218, 108094. [Google Scholar] [CrossRef]
- Zagorecki, A.; Druzdzel, M.J. Knowledge engineering for Bayesian networks: How common are noisy-MAX distributions in practice. IEEE Trans. Syst. Man Cybern. Part A Syst. Humans 2013, 43, 186–195. [Google Scholar] [CrossRef]
- Yanore, L.; Sok, J.; Lansink, A.O. Do Dutch farmers invest in expansion despite increased policy uncertainty? A participatory Bayesian network approach. Agribusiness 2023, 40, 93–115. [Google Scholar] [CrossRef]
- Chen, G.; Li, G.; Xie, M.; Xu, Q.; Zhang, G. A probabilistic analysis method based on Noisy-OR gate Bayesian network for hydrogen leakage of proton exchange membrane fuel cell. Reliab. Eng. Syst. Saf. 2024, 243, 109862. [Google Scholar] [CrossRef]
- Ji, C.; Su, X.; Qin, Z.; Nawaz, A. Probability Analysis of Construction Risk based on Noisy-OR Gate Bayesian Networks. Reliab. Eng. Syst. Saf. 2022, 217, 107974. [Google Scholar] [CrossRef]
- Wisse, B.W.; Van Gosliga, S.P.; Van Elst, N.P.; Barros, A.I. Relieving the elicitation burden of Bayesian Belief Networks. In Proceedings of the Sixth UAI Bayesian Modelling Applications Workshop, Helsinki, Finland, 9 July 2008. [Google Scholar]
- Cain, J. Planning Improvements in Natural Resources Management Guidelines for Using Bayesian Networks to Support the Planning and Management of Development Programmes in the Water Sector and Beyond; CEH: Wallingford, UK, 2001. [Google Scholar]
- Røed, W.; Mosleh, A.; Vinnem, J.E.; Aven, T. On the use of the hybrid causal logic method in offshore risk analysis. Reliab. Eng. Syst. Saf. 2009, 94, 445–4555. [Google Scholar] [CrossRef]
- Freire, A.; Perkusich, M.; Saraiva, R.; Almeida, H.; Perkusich, A. A Bayesian networks-based approach to assess and improve the teamwork quality of agile teams. Inf. Softw. Technol. 2018, 100, 119–132. [Google Scholar] [CrossRef]
- Sakib, N.; Hossain, N.U.I.; Nur, F.; Talluri, S.; Jaradat, R.; Lawrence, J.M. An assessment of probabilistic disaster in the oil and gas supply chain leveraging Bayesian belief network. Int. J. Prod. Econ. 2021, 235, 108107. [Google Scholar] [CrossRef]
- Kaya, R.; Yet, B. Building Bayesian networks based on DEMATEL for multiple criteria decision problems: A supplier selection case study. Expert Syst. Appl. 2019, 134, 234–248. [Google Scholar] [CrossRef]
- Aulia, R.; Tan, H.; Sriramula, S. Dynamic reliability analysis for residual life assessment of corroded subsea pipelines. Ships Offshore Struct. 2021, 16, 410–422. [Google Scholar] [CrossRef]
- Barons, M.J.; Mascaro, S.; Hanea, A.M. Balancing the Elicitation Burden and the Richness of Expert Input When Quantifying Discrete Bayesian Networks. Risk Anal. 2022, 42, 1196–1234. [Google Scholar] [CrossRef]
- Blomaard, B.P.M. Approaches to Reduce Bayesian Network Parametrization. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 11 July 2024. Available online: https://repository.tudelft.nl/record/uuid:36c6db20-8531-4f62-9462-1c46b52c3111 (accessed on 27 May 2025).
- Barons, M.J.; Hanea, A.M.; Wright, S.K.; Baldock, K.R.C.; Wilfert, L.; Chandler, D.; Datta, S.; Fannon, J.; Hartfield, C.; Lucas, A.; et al. Assessment of the response of pollinator abundance to environmental pressures using structured expert elicitation. J. Apic. Res. 2018, 57, 593–604. [Google Scholar] [CrossRef]
- Kleve, S.; Barons, M.J. A structured expert judgement elicitation approach: How can it inform sound intervention decision-making to support household food security? Public Health Nutr. 2019, 24, 2050–2061. [Google Scholar] [CrossRef] [PubMed]
- Atwood, T.C.; Marcot, B.G.; Douglas, D.C.; Amstrup, S.C.; Rode, K.D.; Durner, G.M.; Bromaghin, J.F. Forecasting the relative influence of environmental and anthropogenic stressors on polar bears. Ecosphere 2016, 7, e01370. [Google Scholar] [CrossRef]
- Barons, M.J.; Wright, S.K.; Smith, J.Q. Eliciting Probabilistic Judgements for Integrating Decision Support Systems. In Elicitation: The Science and Art of Structuring Judgement; Dias, L.C., Morton, A., Quigley, J., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 445–478. [Google Scholar]
- Hanea, A.; Kurowicka, D. Mixed Non-Parametric Continuous and Discrete Bayesian Belief Nets. Adv. Math. Model. Reliab. 2008, 1, 9–16. [Google Scholar]
- Nešlehová, J. On rank correlation measures for non-continuous random variables. J. Multivar. Anal. 2007, 98, 544–567. [Google Scholar] [CrossRef]
- Das, B. Generating Conditional Probabilities for Bayesian Networks: Easing the Knowledge Acquisition Problem. arXiv 2004, arXiv:cs/0411034. [Google Scholar]



| InterBeta Version | # Parameters | Additional Assumptions |
|---|---|---|
| Row weights | Beta distribution with linearly interpolated parameters between best and worst rows. | |
| Parent state weights | No parental synergy (i.e., increased combined effects of parent nodes). | |
| Parent weights | Uniformly increasing influence of states for each parent. | |
| Best–worst rows | Equal weights for each parent node. | |
| Default | 0 | Beta(4,1), Beta(1,4) to model best and worst rows. |
| Mean KL Divergence | Percentage of Agreement | Number of Elicited Parameters | ||
|---|---|---|---|---|
| InterBeta | Best–worst rows | 0.23 | 70.8% | 8 |
| Parent weights | 0.13 | 76.4% | 11 | |
| State weights | 0.12 | 73.6% | 18 | |
| Row weights | 0.03 | 81.9% | 78 | |
| InterBeta with elicited middle rows | Best–worst rows | 1.03 | 66.7% | 12 |
| Parent weights | 0.65 | 80.6% | 15 | |
| State weights | 0.32 | 69.4% | 22 | |
| Row weights | 0.06 | 83.3% | 82 | |
| Functional Interpolation | Normal | 0.30 | 61.1% | 32 |
| Truncated normal | 0.38 | 70.8% | 32 | |
| Alpha/beta | 0.25 | 62.5% | 32 | |
| RNM | 0.35 | 56.9% | 16 | |
| AutoRNM | 0.28 | 54.2% | 32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blomaard, B.P.M.; Nane, G.F.; Hanea, A.M. Approaches for Reducing Expert Burden in Bayesian Network Parameterization. Entropy 2025, 27, 579. https://doi.org/10.3390/e27060579
Blomaard BPM, Nane GF, Hanea AM. Approaches for Reducing Expert Burden in Bayesian Network Parameterization. Entropy. 2025; 27(6):579. https://doi.org/10.3390/e27060579
Chicago/Turabian StyleBlomaard, Bodille P. M., Gabriela F. Nane, and Anca M. Hanea. 2025. "Approaches for Reducing Expert Burden in Bayesian Network Parameterization" Entropy 27, no. 6: 579. https://doi.org/10.3390/e27060579
APA StyleBlomaard, B. P. M., Nane, G. F., & Hanea, A. M. (2025). Approaches for Reducing Expert Burden in Bayesian Network Parameterization. Entropy, 27(6), 579. https://doi.org/10.3390/e27060579









