MEFL: Meta-Equilibrize Federated Learning for Imbalanced Data in IoT
Abstract
1. Introduction
- We propose MEFL based on meta-learning with Gradient Descent Preservation (GDP), which enhances personalization by leveraging client-specific data distribution and neutralizes gradient bias introduced by accumulated local training.
- We introduce an equilibrized optimizing aggregation algorithm based on gradient variance weighting (MEFL-EOA). Thereby, it effectively balances the impact of each client’s updates by assigning higher weights to clients with more consistent and reliable gradients.
- Comprehensive experimental results demonstrate that the performance of the proposed method is faster in convergence and achieves higher accuracy than the baselines. MEFL achieves an optimal balance between personalization and generalization capabilities.
2. Related Work
2.1. Personalized Federated Learning
2.2. Mate Learning
3. Preliminaries
3.1. Personalized FL Model
3.2. Problem Formulation
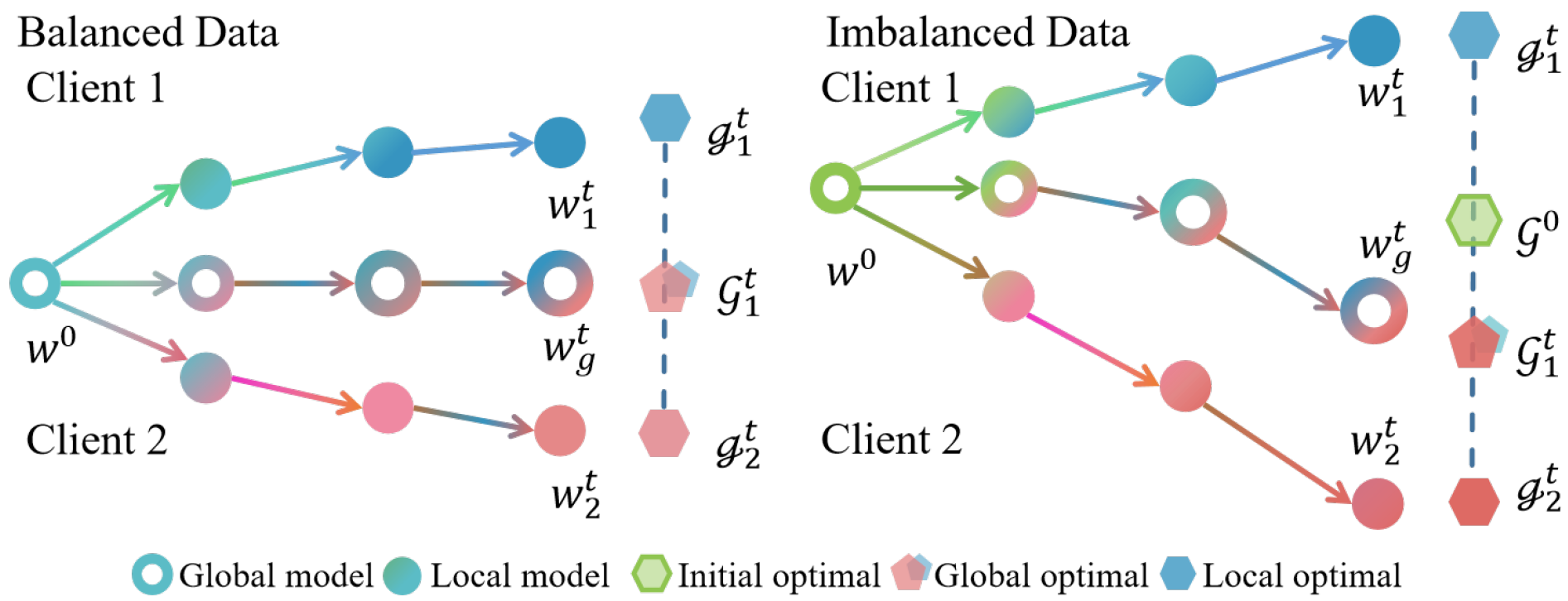
3.3. Gradient Bias
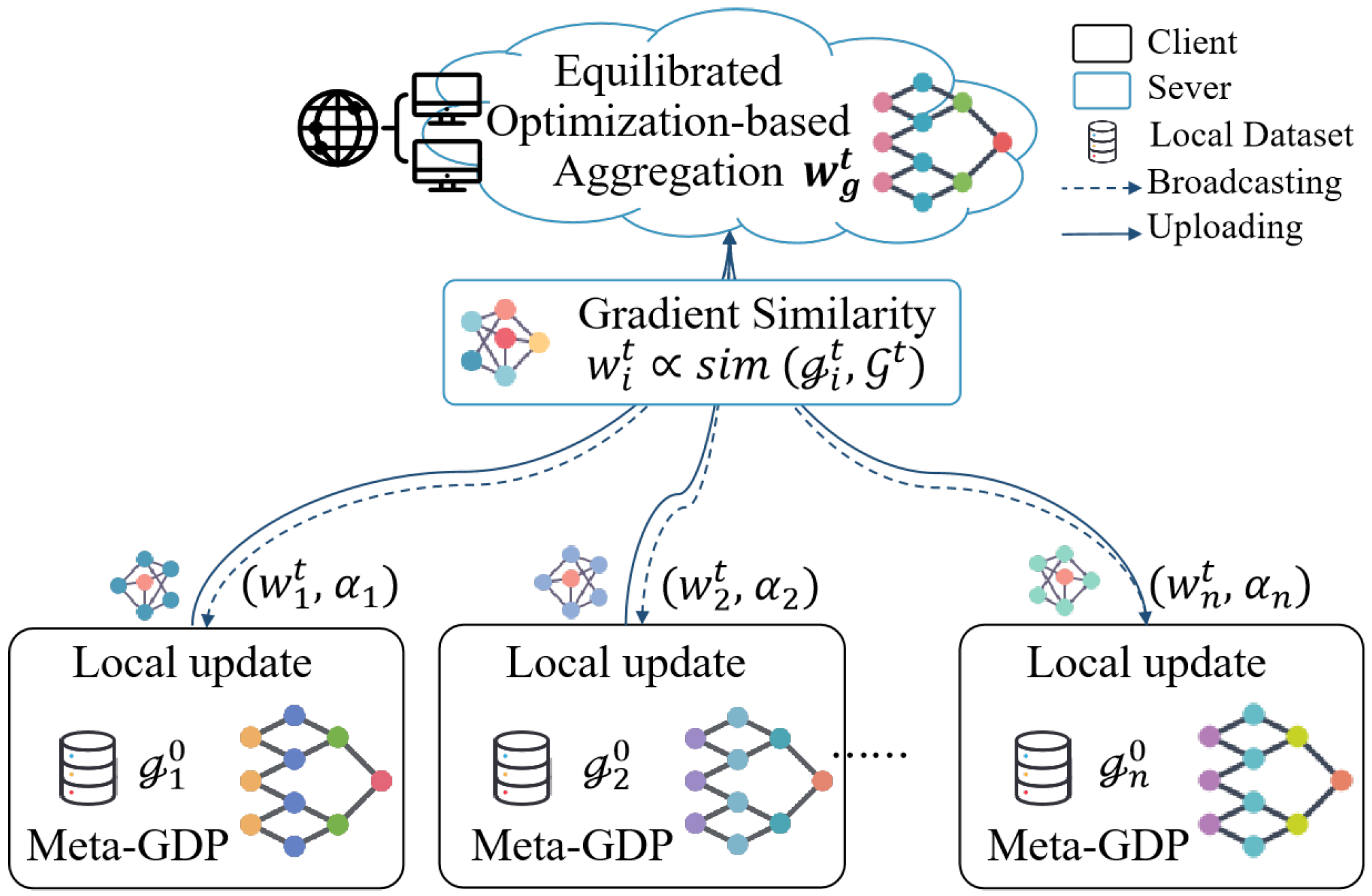
4. Method
4.1. Architecture of MEFL
4.2. Meta-Learning with Gradient Descent Preservation
| Algorithm 1: Meta-GDP: Personalized update algorithms based on meta-learning with gradient descent preservation. |
 |
4.3. Equilibrized Optimizing Aggregation
| Algorithm 2: MEFL-EOA: Meta-Equilibrated Federated Learning with Equilibrated Optimization Aggregation. |
 |
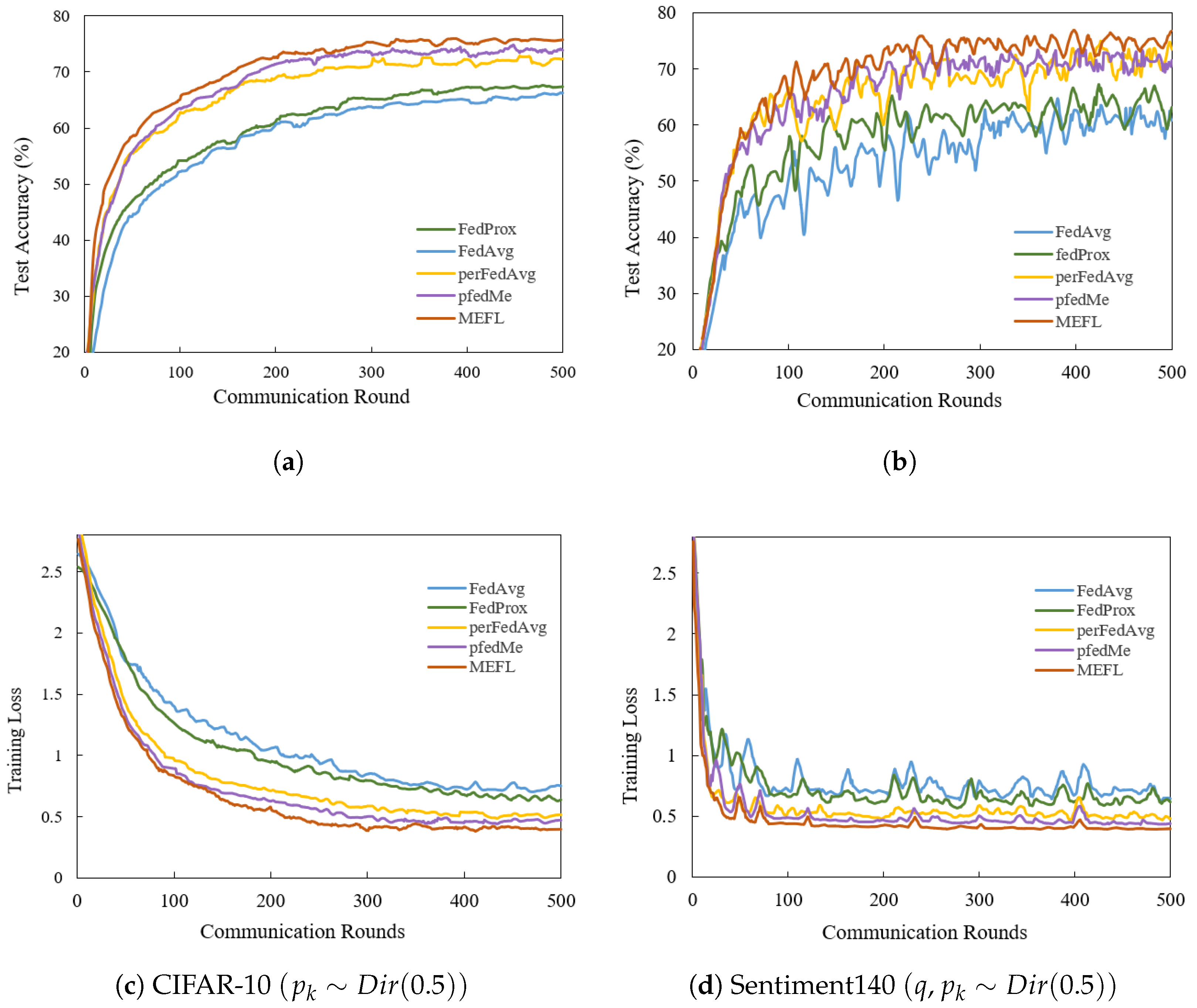
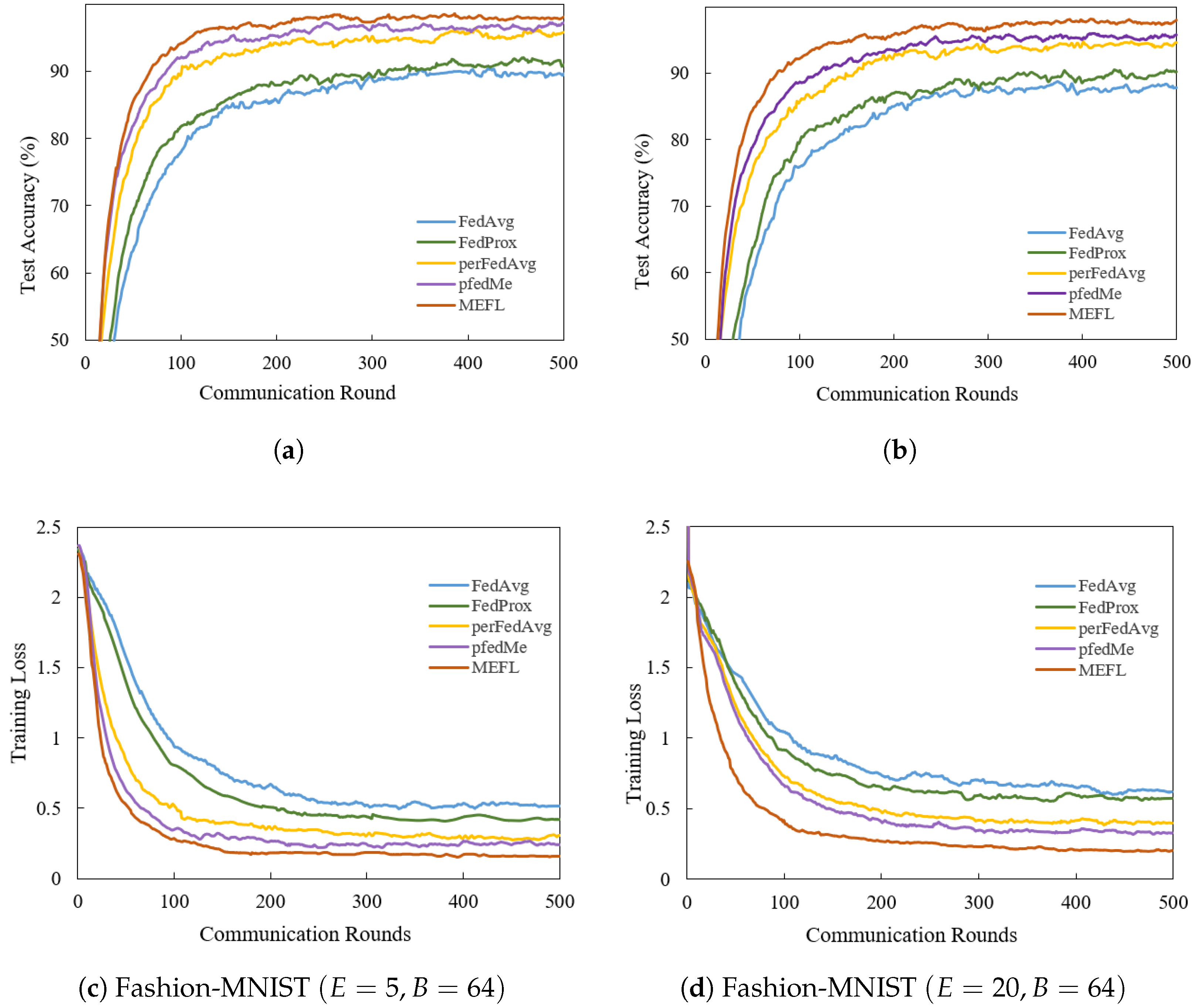
5. Results
5.1. Experimental Setup
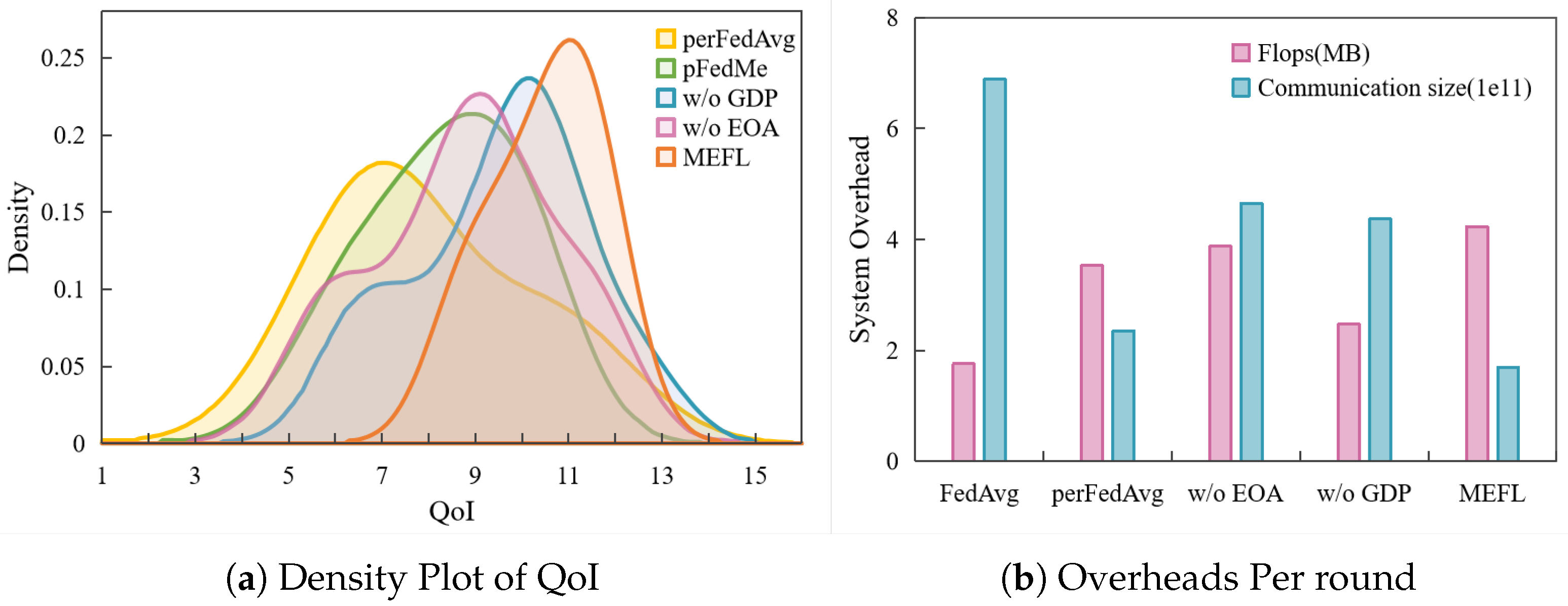
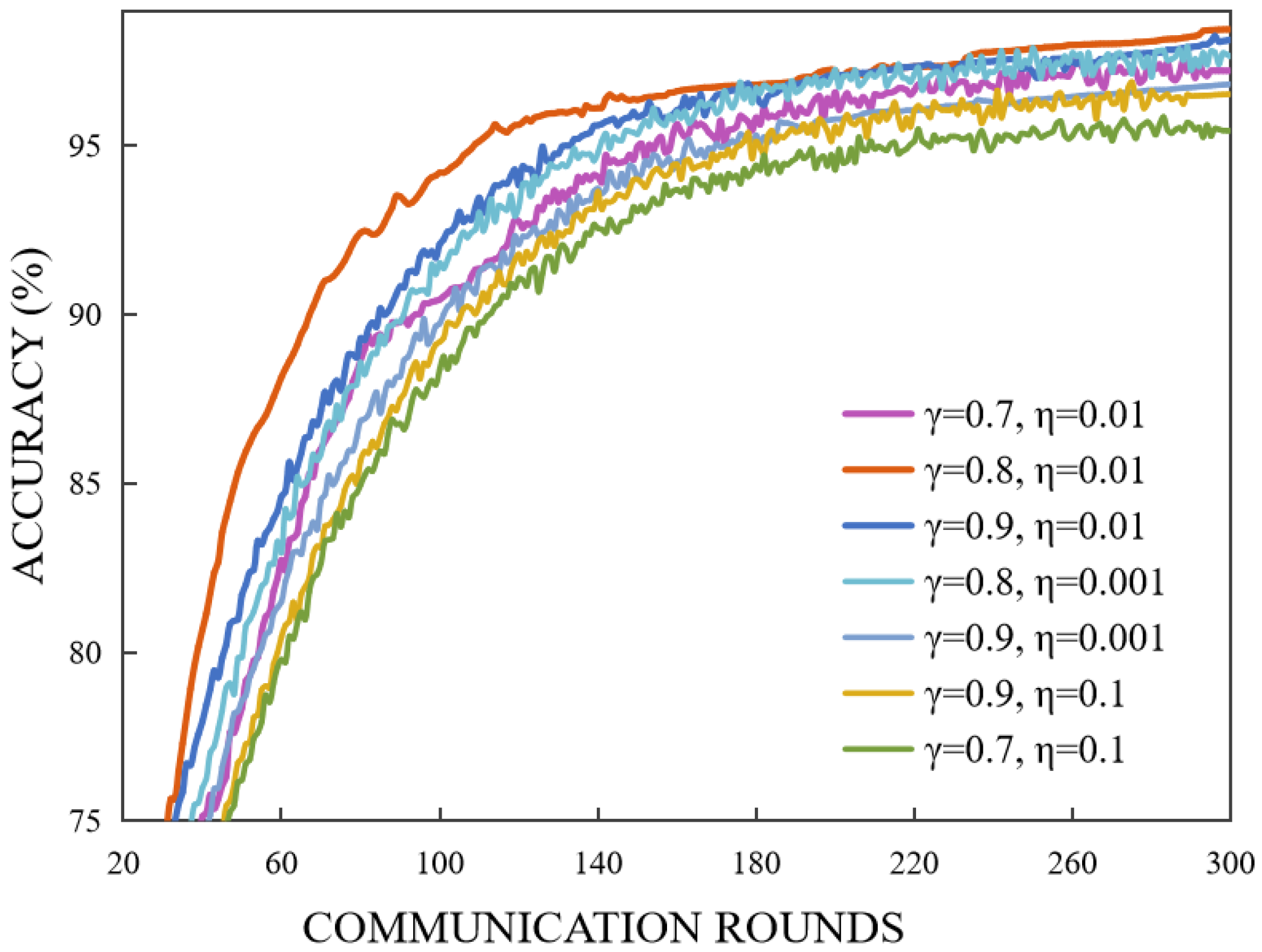
5.2. Evaluation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Gruetzemacher, R.; Whittlestone, J. The transformative potential of artificial intelligence. Futures 2022, 135, 102884. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, M.; Wang, H.; Cui, Z.; Zhang, W. An efficient interval many-objective evolutionary algorithm for cloud task scheduling problem under uncertainty. Inf. Sci. 2022, 583, 56–72. [Google Scholar] [CrossRef]
- Li, L.; Fan, Y.; Tse, M.; Lin, K.Y. A review of applications in federated learning. Comput. Ind. Eng. 2020, 149, 106854. [Google Scholar] [CrossRef]
- Nguyen, D.C.; Ding, M.; Pathirana, P.N.; Seneviratne, A.; Li, J.; Poor, H.V. Federated learning for internet of things: A comprehensive survey. IEEE Commun. Surv. Tutor. 2021, 23, 1622–1658. [Google Scholar] [CrossRef]
- Sharma, V.; You, I.; Andersson, K.; Palmieri, F.; Rehmani, M.H.; Lim, J. Security, Privacy and Trust for Smart Mobile- Internet of Things (M-IoT): A Survey. IEEE Access 2020, 8, 167123–167163. [Google Scholar] [CrossRef]
- Cai, X.; Hu, Z.; Chen, J. A many-objective optimization recommendation algorithm based on knowledge mining. Inf. Sci. 2020, 537, 148–161. [Google Scholar] [CrossRef]
- Wen, J.; Zhang, Z.; Lan, Y.; Cui, Z.; Cai, J.; Zhang, W. A survey on federated learning: Challenges and applications. Int. J. Mach. Learn. Cybern. 2023, 14, 513–535. [Google Scholar] [CrossRef]
- Rieke, N.; Hancox, J.; Li, W.; Milletari, F.; Roth, H.R.; Albarqouni, S.; Bakas, S.; Galtier, M.N.; Landman, B.A.; Maier-Hein, K.; et al. The future of digital health with federated learning. NPJ Digit. Med. 2020, 3, 119. [Google Scholar] [CrossRef]
- Pfitzner, B.; Steckhan, N.; Arnrich, B. Federated learning in a medical context: A systematic literature review. ACM Trans. Internet Technol. (TOIT) 2021, 21, 1–31. [Google Scholar] [CrossRef]
- Zhang, C.; Xie, Y.; Bai, H.; Yu, B.; Li, W.; Gao, Y. A survey on federated learning. Knowl.-Based Syst. 2021, 216, 106775. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, M.; Lai, L.; Suda, N.; Civin, D.; Chandra, V. Federated learning with non-iid data. arXiv 2018, arXiv:1806.00582. [Google Scholar] [CrossRef]
- Duan, M.; Liu, D.; Chen, X.; Liu, R.; Tan, Y.; Liang, L. Self-balancing federated learning with global imbalanced data in mobile systems. IEEE Trans. Parallel Distrib. Syst. 2020, 32, 59–71. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Q.; Liang, H.; Joshi, G.; Poor, H.V. Tackling the objective inconsistency problem in heterogeneous federated optimization. Adv. Neural Inf. Process. Syst. 2020, 33, 7611–7623. [Google Scholar]
- Karimireddy, S.P.; Kale, S.; Mohri, M.; Reddi, S.; Stich, S.; Suresh, A.T. Scaffold: Stochastic controlled averaging for federated learning. In Proceedings of the International Conference on Machine Learning, Virtual Event, 13–18 July 2020; pp. 5132–5143. [Google Scholar]
- Tan, A.Z.; Yu, H.; Cui, L.; Yang, Q. Towards personalized federated learning. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 9587–9603. [Google Scholar] [CrossRef]
- Li, T.; Sahu, A.K.; Talwalkar, A.; Smith, V. Federated Learning: Challenges, Methods, and Future Directions. arXiv 2019, arXiv:1908.07873. [Google Scholar] [CrossRef]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, Ft. Lauderdale, FL, USA, 20–22 April 2017; pp. 1273–1282. [Google Scholar]
- Nguyen, D.C.; Pham, Q.V.; Pathirana, P.N.; Ding, M.; Seneviratne, A.; Lin, Z.; Dobre, O.; Hwang, W.J. Federated learning for smart healthcare: A survey. ACM Comput. Surv. (Csur) 2022, 55, 1–37. [Google Scholar] [CrossRef]
- Geyer, R.C.; Klein, T.; Nabi, M. Differentially private federated learning: A client level perspective. arXiv 2017, arXiv:1712.07557. [Google Scholar]
- Collins, L.; Hassani, H.; Mokhtari, A.; Shakkottai, S. Exploiting shared representations for personalized federated learning. In Proceedings of the International Conference on Machine Learning, Virtual, 18–24 July 2021; pp. 2089–2099. [Google Scholar]
- Deng, Y.; Kamani, M.M.; Mahdavi, M. Adaptive personalized federated learning. arXiv 2020, arXiv:2003.13461. [Google Scholar]
- Mothukuri, V.; Khare, P.; Parizi, R.M.; Pouriyeh, S.; Dehghantanha, A.; Srivastava, G. Federated-learning-based anomaly detection for IoT security attacks. IEEE Internet Things J. 2021, 9, 2545–2554. [Google Scholar] [CrossRef]
- Imteaj, A.; Thakker, U.; Wang, S.; Li, J.; Amini, M.H. A survey on federated learning for resource-constrained IoT devices. IEEE Internet Things J. 2021, 9, 1–24. [Google Scholar] [CrossRef]
- Zhang, T.; Gao, L.; He, C.; Zhang, M.; Krishnamachari, B.; Avestimehr, A.S. Federated learning for the internet of things: Applications, challenges, and opportunities. IEEE Internet Things Mag. 2022, 5, 24–29. [Google Scholar] [CrossRef]
- Konečnỳ, J.; Richtárik, P. Semi-stochastic gradient descent methods. Front. Appl. Math. Stat. 2017, 3, 9. [Google Scholar] [CrossRef]
- Zhuo, H.H.; Feng, W.; Lin, Y.; Xu, Q.; Yang, Q. Federated deep reinforcement learning. arXiv 2019, arXiv:1901.08277. [Google Scholar]
- Yang, H.H.; Liu, Z.; Quek, T.Q.; Poor, H.V. Scheduling policies for federated learning in wireless networks. IEEE Trans. Commun. 2019, 68, 317–333. [Google Scholar] [CrossRef]
- Zhou, X.; Yang, Q.; Zheng, X.; Liang, W.; Wang, K.I.K.; Ma, J.; Pan, Y.; Jin, Q. Personalized federated learning with model-contrastive learning for multi-modal user modeling in human-centric metaverse. IEEE J. Sel. Areas Commun. 2024, 42, 817–831. [Google Scholar] [CrossRef]
- Yao, Z.; Liu, J.; Xu, H.; Wang, L.; Qian, C.; Liao, Y. Ferrari: A personalized federated learning framework for heterogeneous edge clients. IEEE Trans. Mob. Comput. 2024, 23, 10031–10045. [Google Scholar] [CrossRef]
- Yang, X.; Huang, W.; Ye, M. Fedas: Bridging inconsistency in personalized federated learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 11986–11995. [Google Scholar]
- Hospedales, T.; Antoniou, A.; Micaelli, P.; Storkey, A. Meta-learning in neural networks: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 5149–5169. [Google Scholar] [CrossRef]
- Chen, F.; Luo, M.; Dong, Z.; Li, Z.; He, X. Federated meta-learning with fast convergence and efficient communication. arXiv 2018, arXiv:1802.07876. [Google Scholar]
- Mishra, N.; Rohaninejad, M.; Chen, X.; Abbeel, P. A simple neural attentive meta-learner. arXiv 2017, arXiv:1707.03141. [Google Scholar]
- Santoro, A.; Bartunov, S.; Botvinick, M.; Wierstra, D.; Lillicrap, T. Meta-learning with memory-augmented neural networks. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1842–1850. [Google Scholar]
- Jamal, M.A.; Qi, G.J. Task agnostic meta-learning for few-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 11719–11727. [Google Scholar]
- Wang, S.; Fu, X.; Ding, K.; Chen, C.; Chen, H.; Li, J. Federated few-shot learning. In Proceedings of the 29th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Long Beach, CA, USA, 6–10 August 2023; pp. 2374–2385. [Google Scholar]
- Asghari, A.; Ghodrati Amiri, G.; Darvishan, E.; Asghari, A. A novel approach for structural damage detection using multi-headed stacked deep ensemble learning. J. Vib. Eng. Technol. 2024, 12, 4209–4224. [Google Scholar] [CrossRef]
- Ghosh, A.; Chung, J.; Yin, D.; Ramchandran, K. An efficient framework for clustered federated learning. Adv. Neural Inf. Process. Syst. 2020, 33, 19586–19597. [Google Scholar] [CrossRef]
- Jiang, Y.; Konečnỳ, J.; Rush, K.; Kannan, S. Improving federated learning personalization via model agnostic meta learning. arXiv 2019, arXiv:1909.12488. [Google Scholar]
- Nichol, A.; Schulman, J. Reptile: A scalable metalearning algorithm. arXiv 2018, arXiv:1803.02999. [Google Scholar]
- Li, Z.; Zhou, F.; Chen, F.; Li, H. Meta-sgd: Learning to learn quickly for few-shot learning. arXiv 2017, arXiv:1707.09835. [Google Scholar]
- Pillutla, K.; Kakade, S.M.; Harchaoui, Z. Robust aggregation for federated learning. IEEE Trans. Signal Process. 2022, 70, 1142–1154. [Google Scholar] [CrossRef]
- Vettoruzzo, A.; Bouguelia, M.R.; Rögnvaldsson, T. Personalized federated learning with contextual modulation and meta-learning. In Proceedings of the 2024 SIAM International Conference on Data Mining (SDM), Houston, TX, USA, 18–20 April 2024; pp. 842–850. [Google Scholar]
- Tu, J.; Huang, J.; Yang, L.; Lin, W. Personalized federated learning with layer-wise feature transformation via meta-learning. ACM Trans. Knowl. Discov. Data 2024, 18, 1–21. [Google Scholar] [CrossRef]
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-mnist: A novel image dataset for benchmarking machine learning algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images. 2009. Available online: https://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf (accessed on 18 April 2025).
- Kiritchenko, S.; Zhu, X.; Mohammad, S.M. Sentiment analysis of short informal texts. J. Artif. Intell. Res. 2014, 50, 723–762. [Google Scholar] [CrossRef]
- Cohen, G.; Afshar, S.; Tapson, J.; Van Schaik, A. EMNIST: Extending MNIST to handwritten letters. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 2921–2926. [Google Scholar]
- Hsu, T.M.H.; Qi, H.; Brown, M. Measuring the effects of non-identical data distribution for federated visual classification. arXiv 2019, arXiv:1909.06335. [Google Scholar]
- Li, T.; Sahu, A.K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; Smith, V. Federated optimization in heterogeneous networks. Proc. Mach. Learn. Syst. 2020, 2, 429–450. [Google Scholar]
- Fallah, A.; Mokhtari, A.; Ozdaglar, A. Personalized federated learning: A meta-learning approach. arXiv 2020, arXiv:2002.07948. [Google Scholar]
- Dinh, C.T.; Tran, N.; Nguyen, J. Personalized federated learning with moreau envelopes. Adv. Neural Inf. Process. Syst. 2020, 33, 21394–21405. [Google Scholar]
- Divi, S.; Lin, Y.S.; Farrukh, H.; Celik, Z.B. New metrics to evaluate the performance and fairness of personalized federated learning. arXiv 2021, arXiv:2107.13173. [Google Scholar]
| Notations | Description |
|---|---|
| i | Index of client, total number of clients N. |
| t | Global communication round index, total number T. |
| Local update step (epochs) index per round, total number E. | |
| P | Sample fraction of data used as a support set for each client. |
| Global model parameters at round t, at the beginning. | |
| Local model parameters on client i after local update steps in round t. | |
| Gradient of local model on client in round T. | |
| The estimated global gradient aggregated from previous rounds. | |
| The similarity score of client i, with cosine similarity between local model parameter and global gradient vectors. | |
| The weight of contribution in global aggregation. | |
| Local meta learning rate: inner adaptation rate, meta update rate. | |
| Global learning rate. | |
| EMA smoothing factor. | |
| Variance smoothing factor. |
| Dataset | P | FedAvg | EOA | GDP | MEFL |
|---|---|---|---|---|---|
| 76.15 ± 1.77 | |||||
| CIFAR-10 | 76.26 ± 1.28 | ||||
| 76.58 ± 0.85 | |||||
| Fashion- | 97.46 ± 0.32 | ||||
| MNIST | 97.63 ± 0.27 | ||||
| (Non-IID) | 97.82 ± 0.22 | ||||
| Fashion- | 99.54 ± 0.17 | ||||
| MNIST | 99.61 ± 0.03 | ||||
| (IID) | 99.59 ± 0.05 |
| Methods | ||||
|---|---|---|---|---|
| FedAvg | 88.93 ± 1.25 | 89.53 ± 0.83 | 89.12 ± 0.94 | 88.76 ± 1.02 |
| FedProx | 90.41 ± 0.93 | 91.54 ± 0.76 | 90.32 ± 0.81 | 89.83 ± 0.85 |
| pfedMe | 96.45 ± 0.62 | 97.83 ± 0.32 | 96.83 ± 0.47 | 96.54 ± 0.34 |
| perFedAvg | 94.95 ± 0.78 | 96.12 ± 0.42 | 95.26 ± 0.48 | 94.39 ± 0.38 |
| MEFL | 97.86 ± 0.32 | 98.21 ± 0.15 | 97.96 ± 0.21 | 97.53 ± 0.17 |
| Methods | Communication Rounds | Convergence Accuracy | ||
|---|---|---|---|---|
| 70% | 85% | 90% | ||
| FedAvg | 65 | 175 | 463 | 90.18% ± 1.02% |
| GDP | 31 | 58 | 185 | 96.37% ± 0.36% |
| EOA | 33 | 62 | 196 | 96.31% ± 0.43% |
| MEFL | 25 | 47 | 68 | 98.03% ± 0.23% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, J.; Gao, Y.; Li, X.; Jia, J. MEFL: Meta-Equilibrize Federated Learning for Imbalanced Data in IoT. Entropy 2025, 27, 553. https://doi.org/10.3390/e27060553
Tang J, Gao Y, Li X, Jia J. MEFL: Meta-Equilibrize Federated Learning for Imbalanced Data in IoT. Entropy. 2025; 27(6):553. https://doi.org/10.3390/e27060553
Chicago/Turabian StyleTang, Jialu, Yali Gao, Xiaoyong Li, and Jia Jia. 2025. "MEFL: Meta-Equilibrize Federated Learning for Imbalanced Data in IoT" Entropy 27, no. 6: 553. https://doi.org/10.3390/e27060553
APA StyleTang, J., Gao, Y., Li, X., & Jia, J. (2025). MEFL: Meta-Equilibrize Federated Learning for Imbalanced Data in IoT. Entropy, 27(6), 553. https://doi.org/10.3390/e27060553






