Bootstrap Confidence Intervals for Multiple Change Points Based on Two-Stage Procedures
Abstract
1. Introduction
2. Multiple Change Point Detection Based on Two-Stage Procedures
- 1.
- When , the change point coincides with the pre-specified cut-point and . The regression coefficients corresponding to the three segments are denoted by , and are equal to , , and , respectively. The segment that contains the change point can be identified by .
- 1.
2.1. Segment Selection
| Algorithm 1 OGA + HDIC + Trim |
| Require: response vector , regressor matrix . Initialzation: set , and . While do Compute and update ; Compute via , where ; Compute via . end Compute the minimum of HDIC via |
2.2. Refining
3. Bootstrap Confidence Intervals for Multiple Change Points
- 1.
- We generate a bootstrap sample by randomly sampling residuals from the set as in (11);
- 2.
- We apply the two-stage procedure and compute the local maximizer obtained as in (12) for each estimated segment;
- 3.
- For a given bootstrap sample size B, we repeat Steps 1-2 B times and record , , where .
4. Theoretical Validity of the Bootstrap Confidence Intervals
5. Simulation
5.1. Detection of Multiple Change Points
5.2. Bootstrap CIs
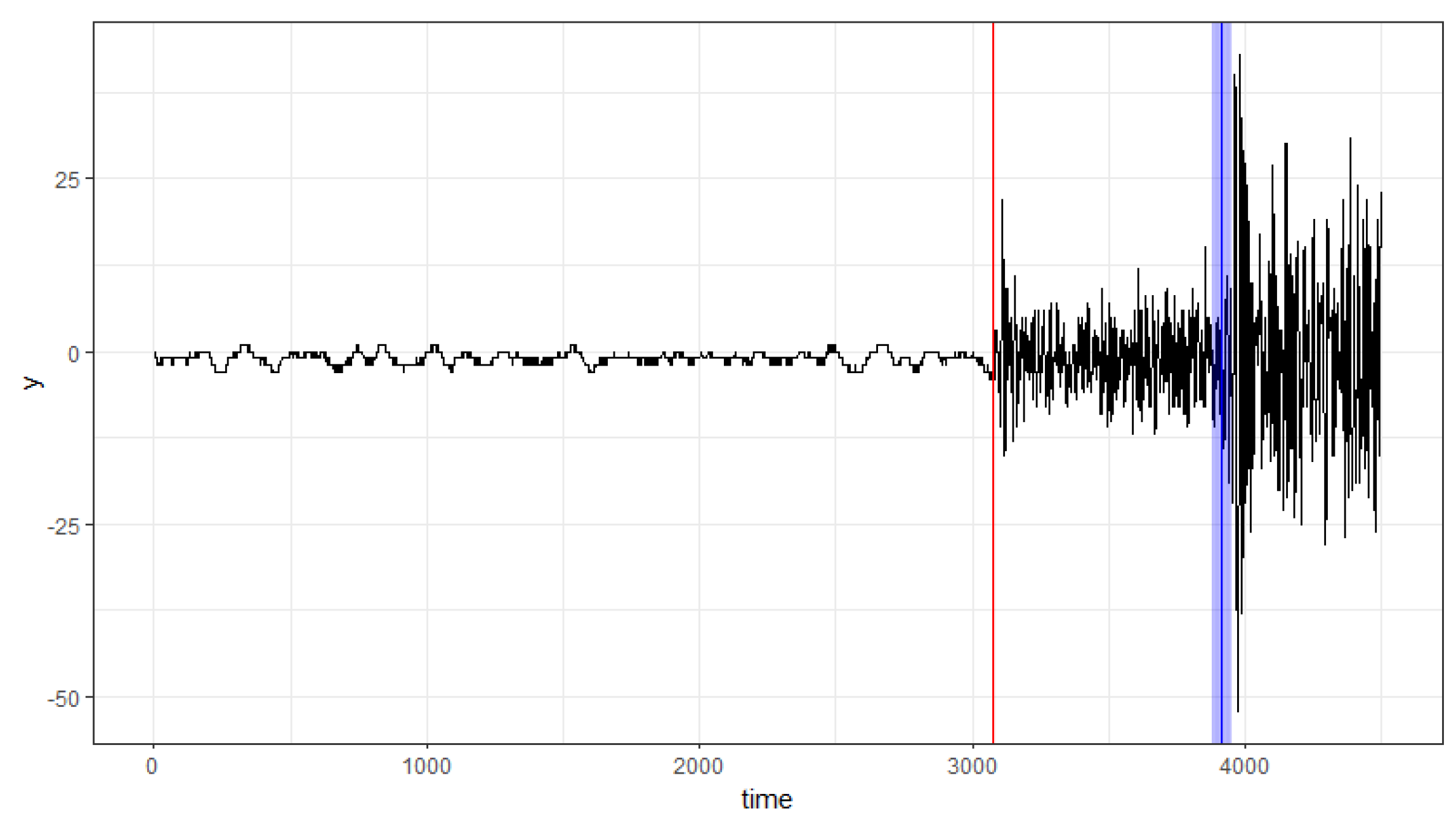
6. Empirical Application
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Haynes, K.; Eckley, I.A.; Fearnhead, P. Computationally efficient changepoint detection for a range of penalties. J. Comput. Graph. Stat. 2017, 26, 134–143. [Google Scholar] [CrossRef]
- Picard, F.; Robin, S.; Lavielle, M.; Vaisse, C.; Daudin, J.J. A statistical approach for array CGH data analysis. BMC Bioinform. 2005, 6, 27. [Google Scholar] [CrossRef]
- Li, J.; Fearnhead, P.; Fryzlewicz, P.; Wang, T. Automatic change-point detection in time series via deep learning. J. R. Stat. Soc. Ser. B Stat. Methodol. 2024, 86, 273–285. [Google Scholar] [CrossRef]
- Killick, R.; Fearnhead, P.; Eckley, I.A. Optimal detection of changepoints with a linear computational cost. J. Am. Stat. Assoc. 2012, 107, 1590–1598. [Google Scholar] [CrossRef]
- Bai, J.; Perron, P. Estimating and testing linear models with multiple structural changes. Econometrica 1998, 66, 47–78. [Google Scholar] [CrossRef]
- Bai, J.; Perron, P. Computation and analysis of multiple structural change models. J. Appl. Econom. 2003, 18, 1–22. [Google Scholar] [CrossRef]
- Davis, R.A.; Lee, T.C.M.; Rodriguez-Yam, G.A. Structural break estimation for nonstationary time series models. J. Am. Stat. Assoc. 2006, 101, 223–239. [Google Scholar] [CrossRef]
- Harchaoui, Z.; Lévy-Leduc, C. Multiple change-point estimation with a total variation penalty. J. Am. Stat. Assoc. 2010, 105, 1480–1493. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Jin, B.; Wu, Y.; Shi, X. Consistent two-stage multiple change-point detection in linear models. Can. J. Stat. 2016, 44, 161–179. [Google Scholar] [CrossRef]
- Zou, H. The adaptive lasso and its oracle properties. J. Am. Stat. Assoc. 2006, 101, 1418–1429. [Google Scholar] [CrossRef]
- Fan, J.; Li, R. Variable Selection via Nonconcave Penalized Likelihood and its Oracle Properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Zhang, C. Nearly unbiased variable selection under minimax concave penalty. Ann. Stat. 2010, 38, 894–942. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Jin, B. Multi-threshold accelerated failure time model. Ann. Stat. 2018, 46, 2657–2682. [Google Scholar] [CrossRef]
- Eichinger, B.; Kirch, C. A MOSUM procedure for the estimation of multiple random change points. Bernoulli 2018, 24, 526–564. [Google Scholar] [CrossRef]
- Fang, X.; Li, J.; Siegmund, D. Segmentation and estimation of change-point models: False positive control and confidence regions. Ann. Stat. 2020, 48, 1615–1647. [Google Scholar] [CrossRef]
- Antoch, J.; Hušková, M.; Veraverbeke, N. Change-point problem and bootstrap. J. Nonparametr. Stat. 1995, 5, 123–144. [Google Scholar] [CrossRef]
- Dumbgen, L. The asymptotic behavior of some nonparametric change-point estimators. Ann. Stat. 1991, 19, 1471–1495. [Google Scholar] [CrossRef]
- Hušková, M.; Kirch, C. Bootstrapping confidence intervals for the change-point of time series. J. Time Ser. Anal. 2008, 29, 947–972. [Google Scholar] [CrossRef]
- Cho, H.; Kirch, C. Bootstrap confidence intervals for multiple change points based on moving sum procedures. Comput. Stat. Data Anal. 2022, 175, 107552. [Google Scholar] [CrossRef]
- Lv, J.; Fan, Y. A unified approach to model selection and sparse recovery using regularized least squares. Ann. Stat. 2009, 37, 3498–3528. [Google Scholar] [CrossRef]
- Ing, C.K.; Lai, T.L. A stepwise regression method and consistent model selection for high-dimensional sparse linear models. Stat. Sin. 2011, 21, 1473–1513. [Google Scholar] [CrossRef]
- Jin, B.; Shi, X.; Wu, Y. A novel and fast methodology for simultaneous multiple structural break estimation and variable selection for nonstationary time series models. Stat. Comput. 2013, 23, 221–231. [Google Scholar] [CrossRef]
- White, H. Maximum likelihood estimation of misspecified models. Econom. J. Econom. Soc. 1982, 50, 1–25. [Google Scholar] [CrossRef]
- Flynn, C.J.; Hurvich, C.M.; Simonoff, J.S. Efficiency for regularization parameter selection in penalized likelihood estimation of misspecified models. J. Am. Stat. Assoc. 2013, 108, 1031–1043. [Google Scholar] [CrossRef]
- Bai, J. Estimation of a change point in multiple regression models. Rev. Econ. Stat. 1997, 79, 551–563. [Google Scholar] [CrossRef]
- Takanami, T.; Kitagawa, G. Estimation of the arrival times of seismic waves by multivariate time series model. Ann. Inst. Stat. Math. 1991, 43, 407–433. [Google Scholar] [CrossRef]
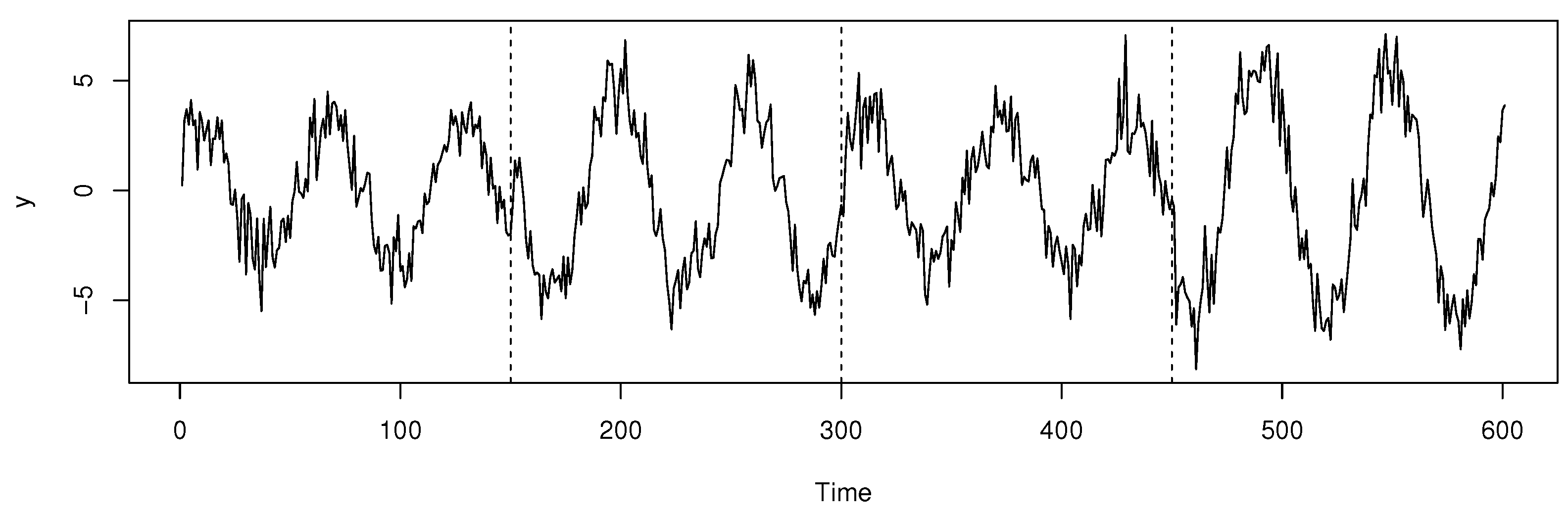
| Method | |||||
|---|---|---|---|---|---|
| TSPoga,wald | 90.70 | 98.50 | 96.80 | 97.80 | |
| Mean | 150.34 | 300.41 | 449.77 | ||
| SE | 1.66 | 2.31 | 2.22 | ||
| TSMCDlasso | 72.60 | 95.20 | 95.80 | 96.40 | |
| Mean | 150.61 | 300.43 | 450.16 | ||
| SE | 2.42 | 2.31 | 2.19 |
| % | ||||
|---|---|---|---|---|
| 90 | 93.80 | 91.80 | 93.80 | 91.00 |
| 95 | 96.80 | 95.80 | 95.80 | 95.60 |
| Change Point | 95% Bootstrap CIs | 90% Bootstrap CIs |
|---|---|---|
| 3074 | [3072, 3084] | [3073, 3080] |
| 3914 | [3877, 3952] | [3882, 3948] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, L.; Jin, B.; Wu, Y.; Wang, F. Bootstrap Confidence Intervals for Multiple Change Points Based on Two-Stage Procedures. Entropy 2025, 27, 537. https://doi.org/10.3390/e27050537
Hou L, Jin B, Wu Y, Wang F. Bootstrap Confidence Intervals for Multiple Change Points Based on Two-Stage Procedures. Entropy. 2025; 27(5):537. https://doi.org/10.3390/e27050537
Chicago/Turabian StyleHou, Li, Baisuo Jin, Yuehua Wu, and Fangwei Wang. 2025. "Bootstrap Confidence Intervals for Multiple Change Points Based on Two-Stage Procedures" Entropy 27, no. 5: 537. https://doi.org/10.3390/e27050537
APA StyleHou, L., Jin, B., Wu, Y., & Wang, F. (2025). Bootstrap Confidence Intervals for Multiple Change Points Based on Two-Stage Procedures. Entropy, 27(5), 537. https://doi.org/10.3390/e27050537







