Integrating Human Mobility Models with Epidemic Modeling: A Framework for Generating Synthetic Temporal Contact Networks
Abstract
1. Introduction
2. Related Work
2.1. Temporal Contact Networks
2.2. Epidemic Simulation Frameworks
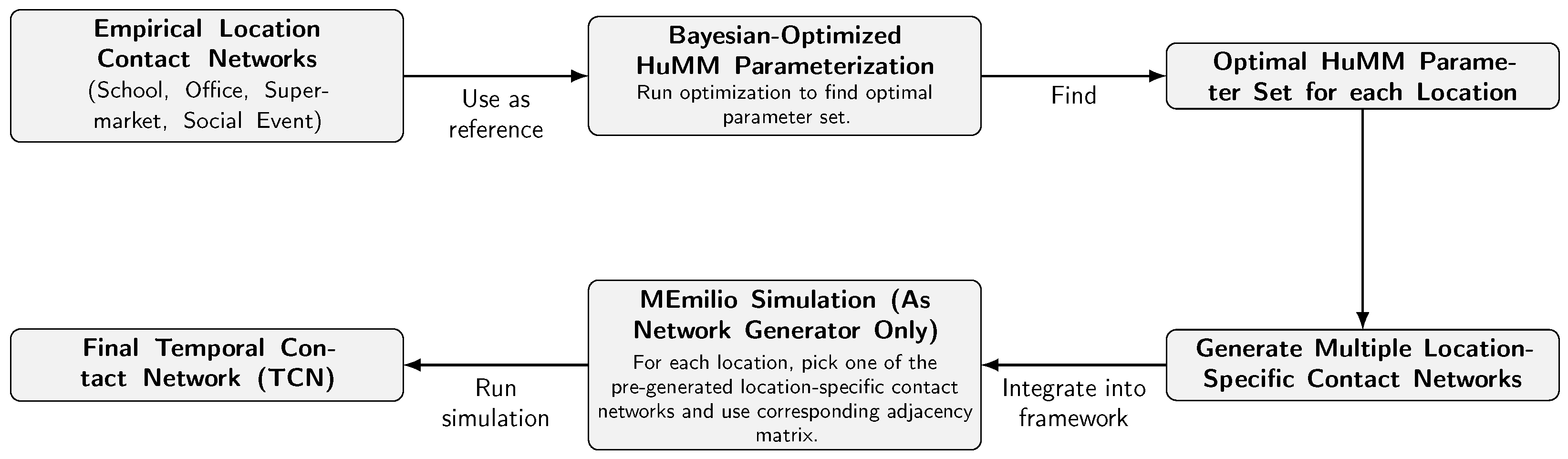
3. Methodology
3.1. MEmilio Simulation Framework
3.2. Bayesian-Optimized Human Mobility Models
3.2.1. Bayesian Optimization Strategy
- : the absolute difference in the peak number of infections;
- : the relative difference in the timing of these peaks;
- : the relative difference in the total number of edges;
- : the difference in the contact duration distributions (measured via the Kolmogorov–Smirnov statistic).
3.2.2. Parameter Space
- Movement shapes, which controls whether individuals tend to move short distances with occasional long trips, following a power-law distribution, or have more uniform travel patterns.
- Pause dynamics, describing how long individuals tend to remain in a given spot before continuing movement.
- Spatial clustering, indicating whether individuals are likely to cluster in default sub-spaces and how strongly they gravitate back to these spaces.
3.2.3. Stochastic Repetitions and Final Selection
3.3. Integration of Bayesian-Optimized HuMMs into MEmilio
4. Contact Network Generation
4.1. Household Composition and Demographic Setup
4.2. Location Capacities and Variation
4.2.1. Schools and Workplaces
4.2.2. Supermarkets and Social Events
4.2.3. Households
4.3. Experimental Setup
4.3.1. Scaling Population Size
4.3.2. Scaling Location Capacity
5. Temporal Contact Network Analysis
5.1. Impact of Scaling Population Size
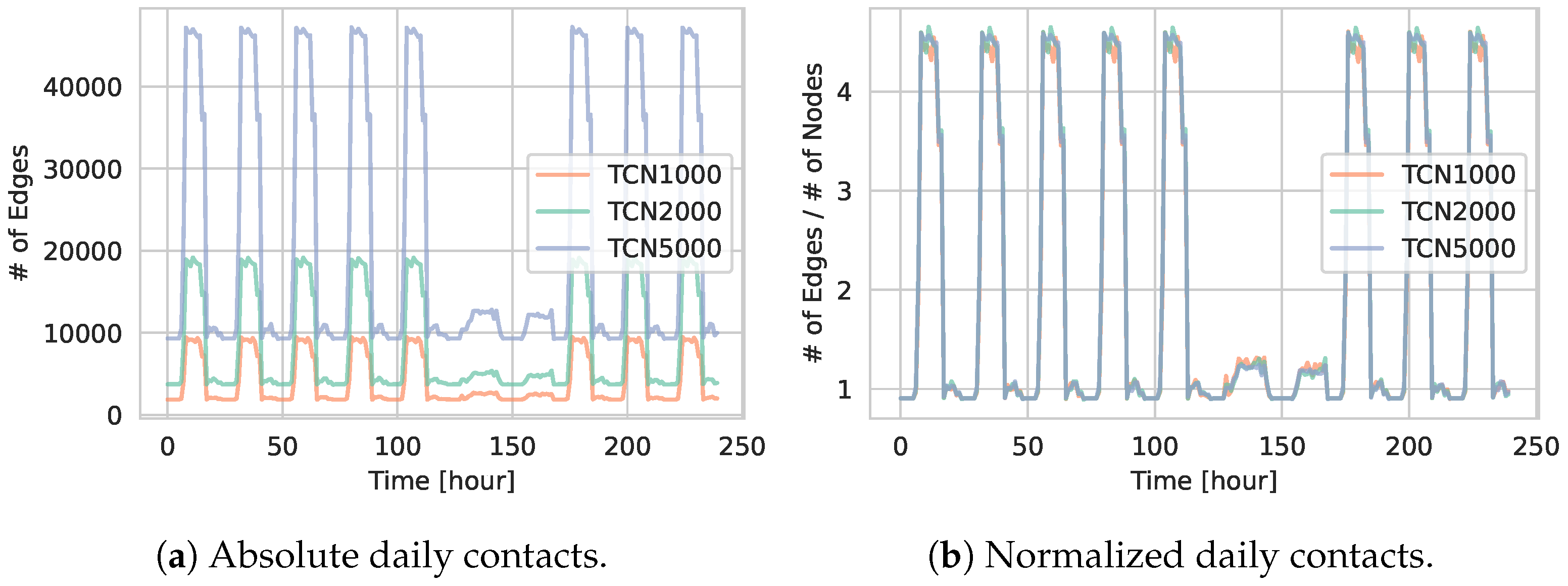
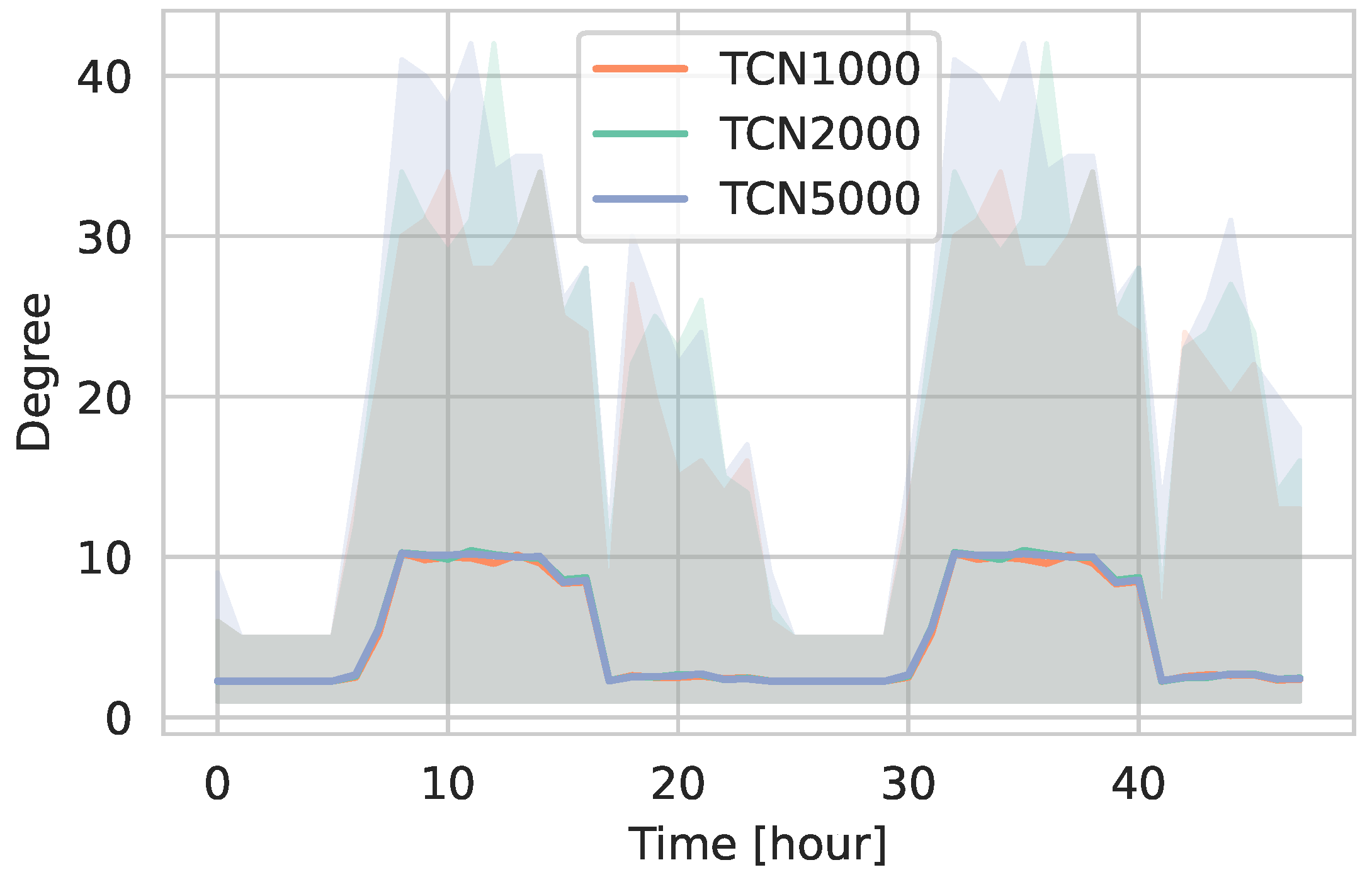
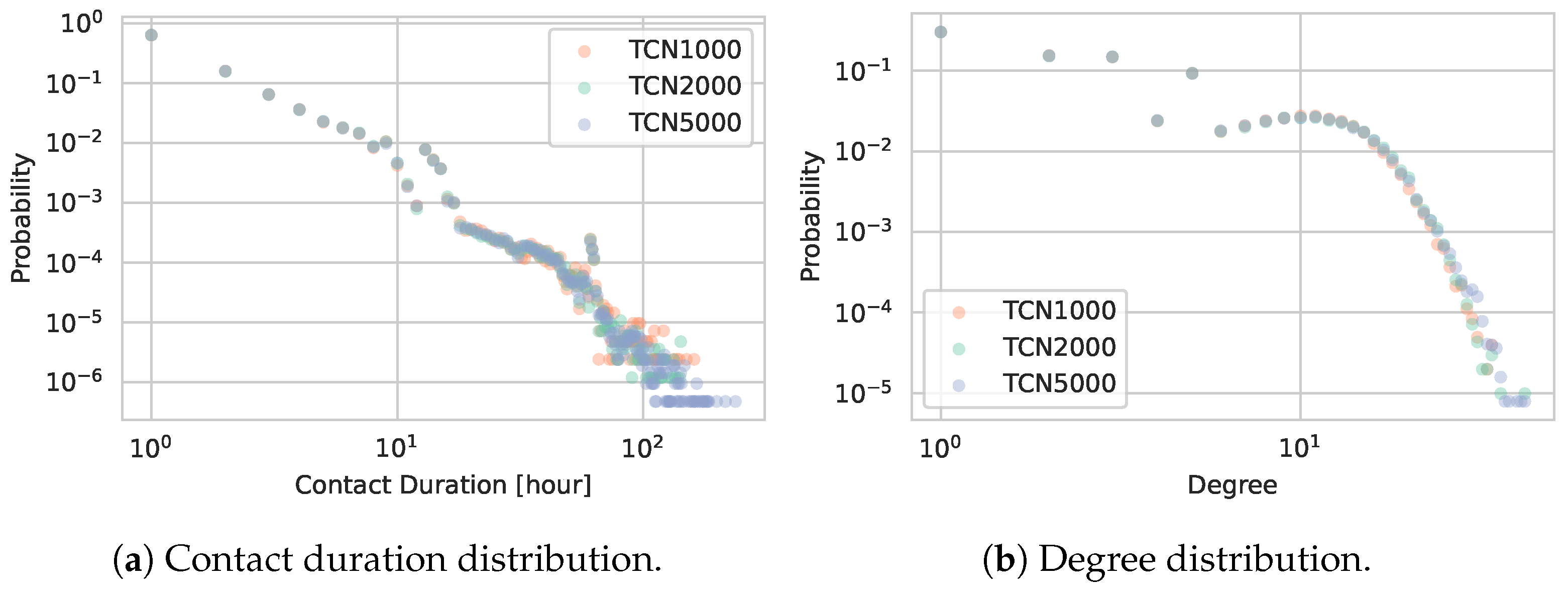
5.1.1. Network Statistics
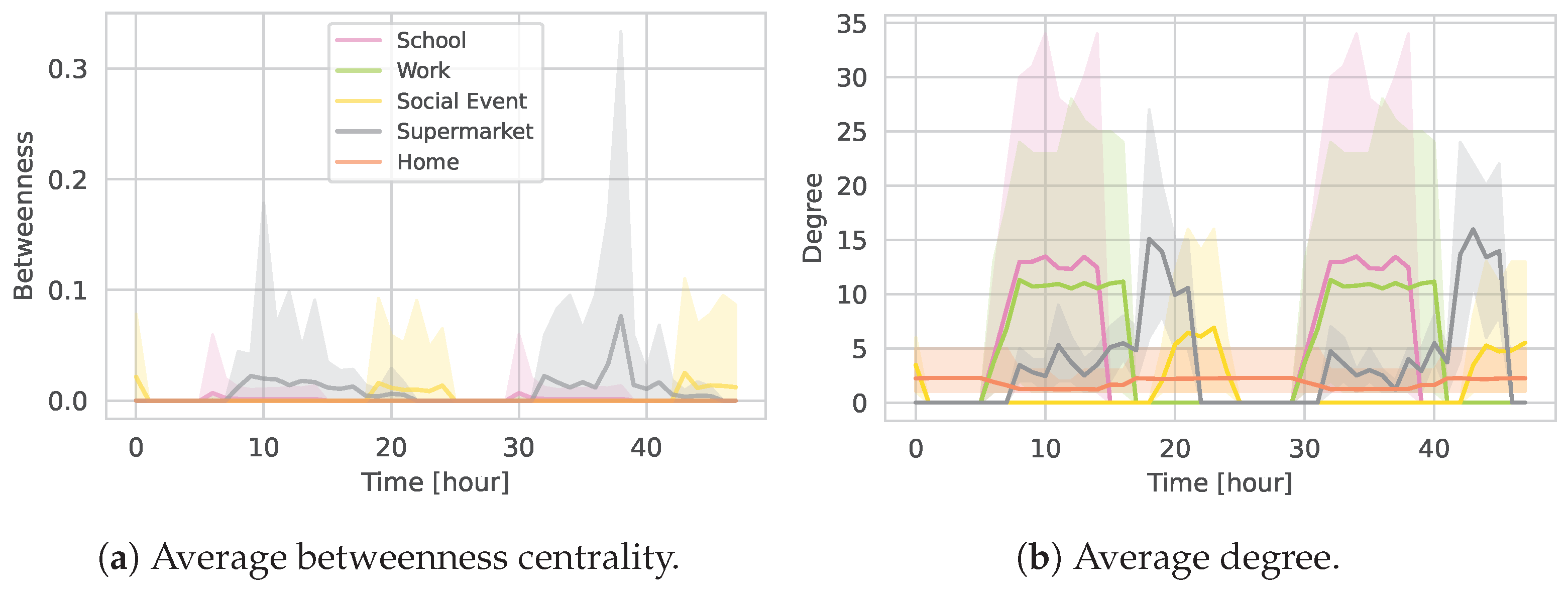
5.1.2. Daily Contact Patterns
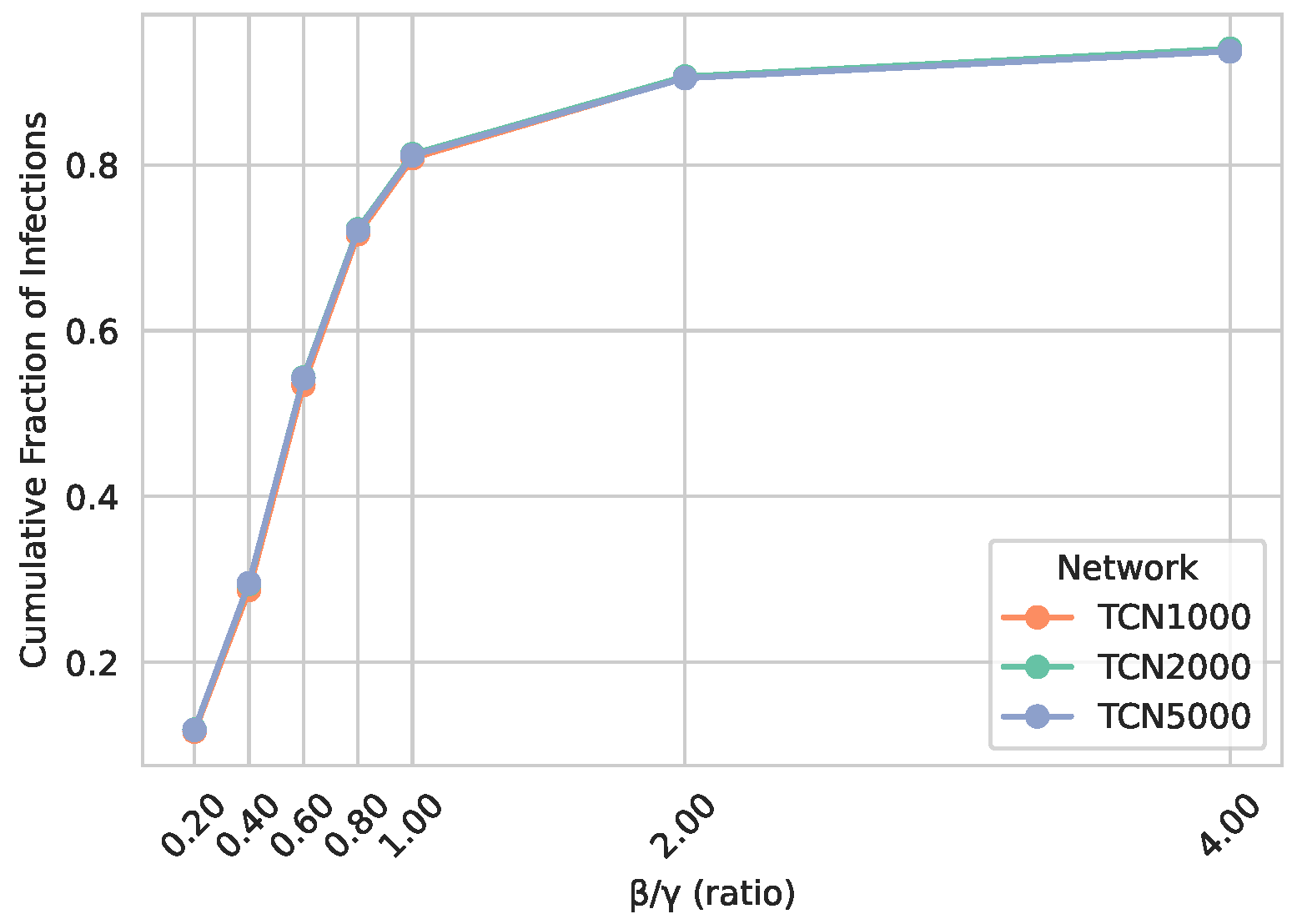
5.1.3. Epidemic Spreading
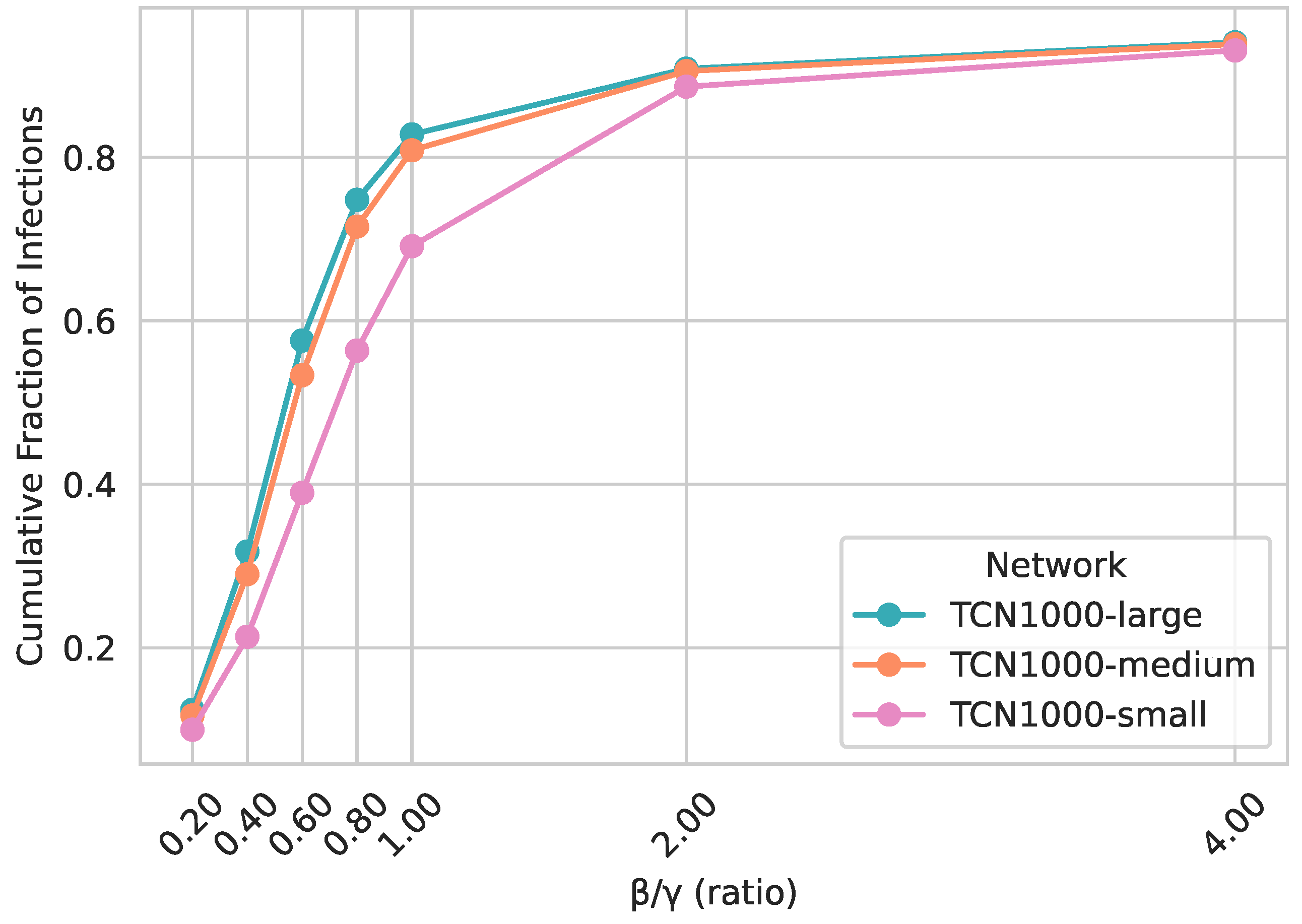
5.2. Impact of Scaling Location Capacity
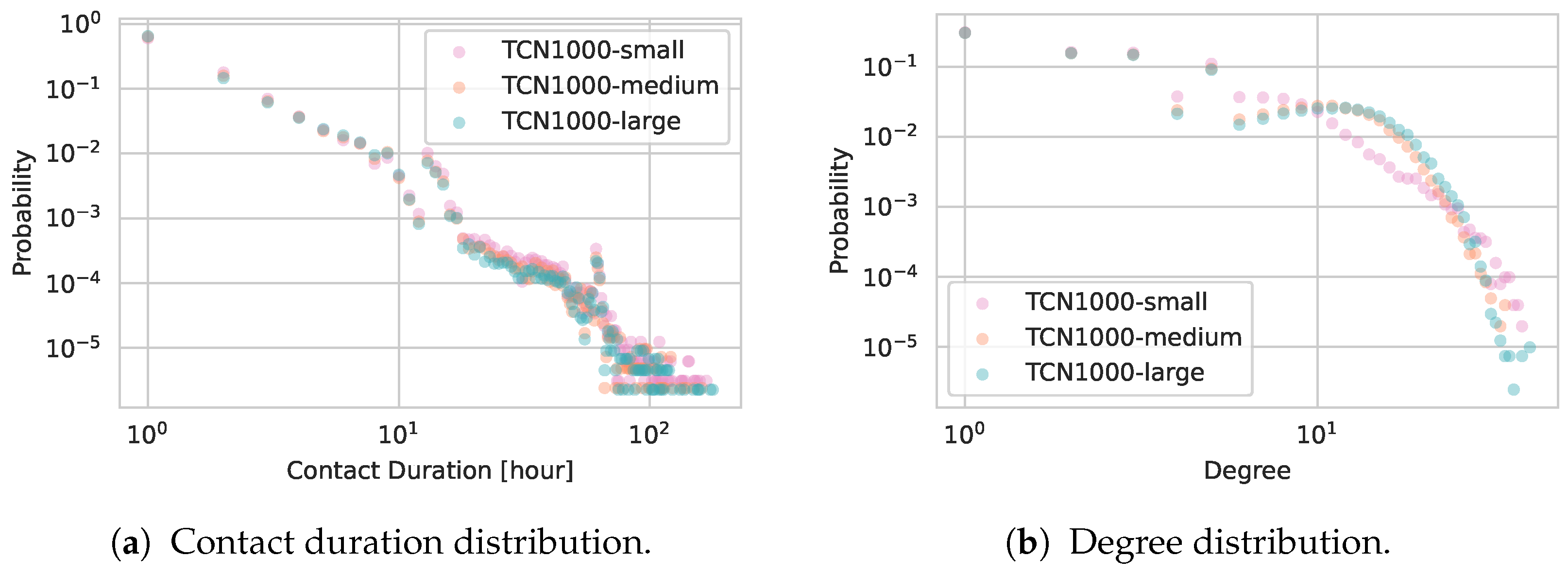
5.2.1. Network Statistics
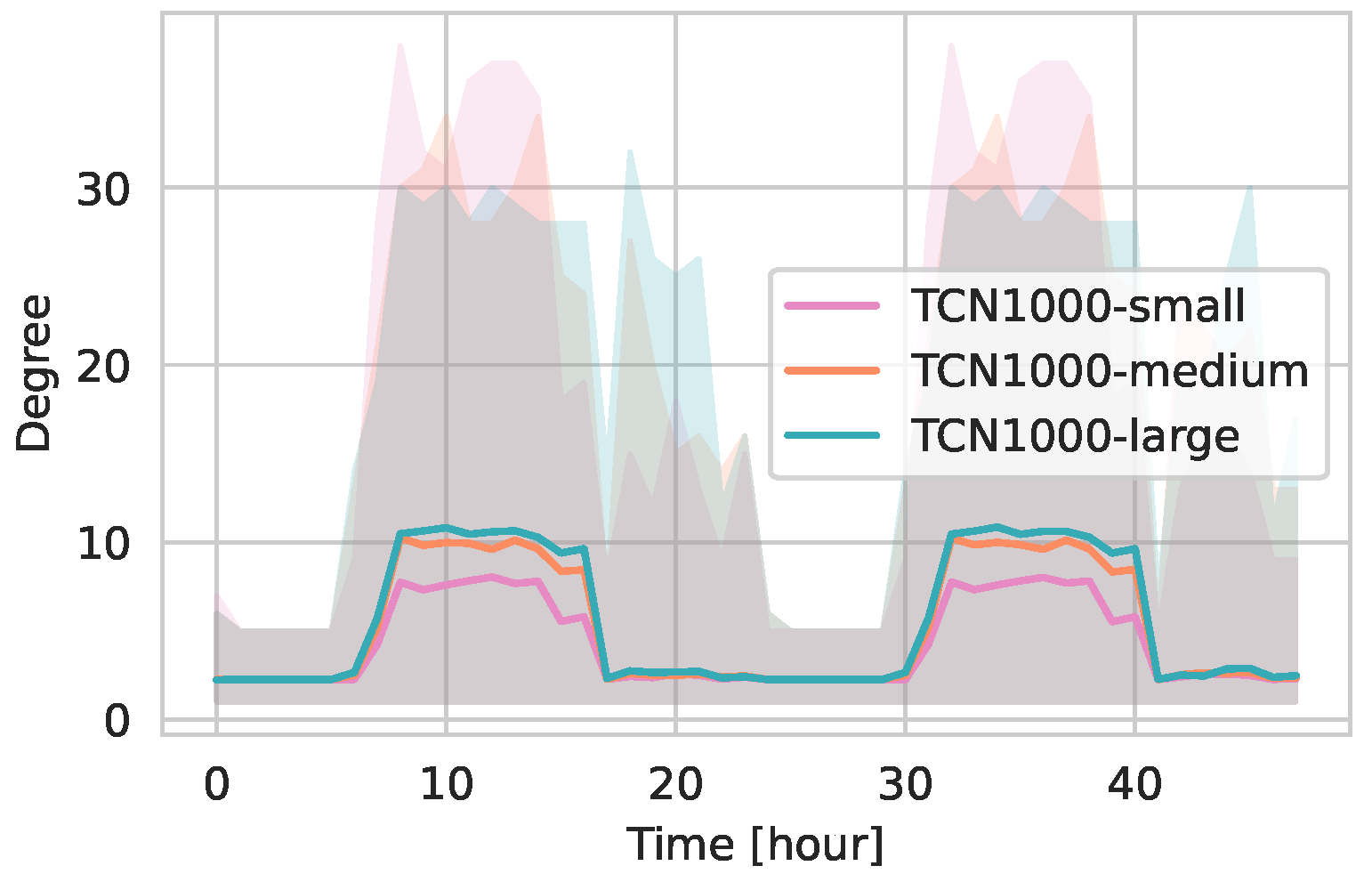
5.2.2. Daily Contact Patterns
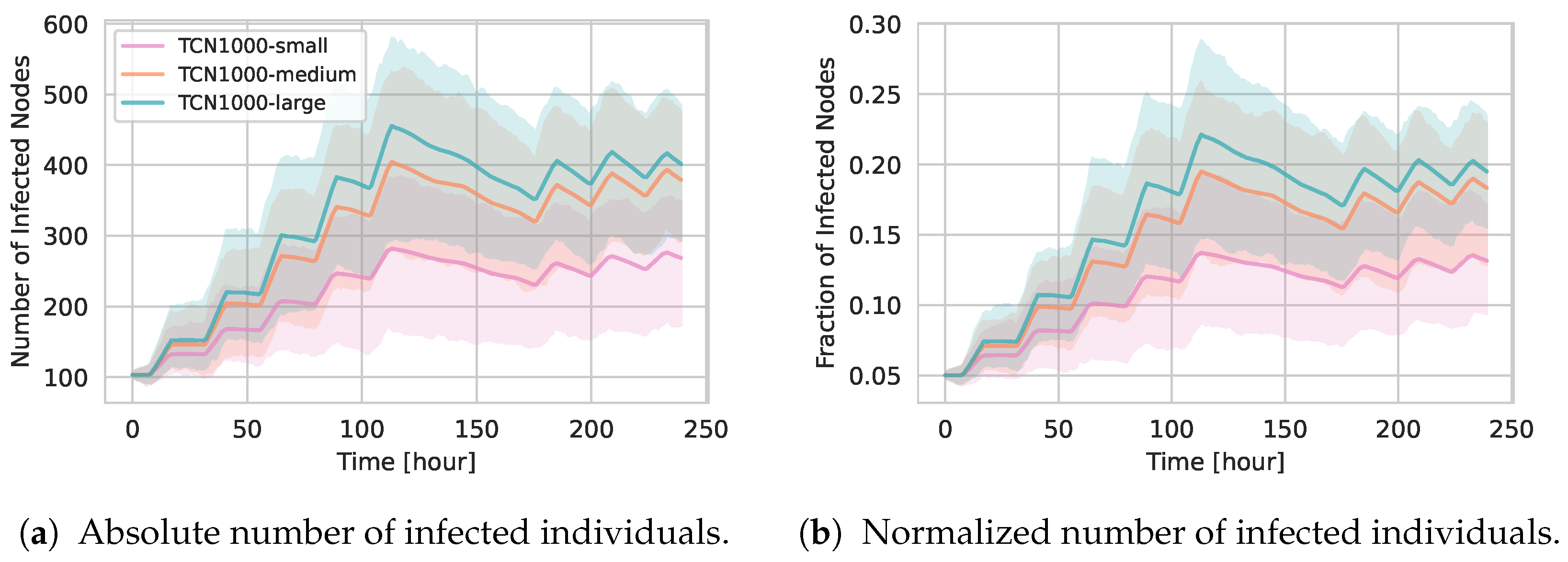
5.2.3. Epidemic Spreading
5.3. Location Sub-Graphs
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Zunker, H.; Schmieding, R.; Kerkmann, D.; Schengen, A.; Diexer, S.; Mikolajczyk, R.; Meyer-Hermann, M.; Kühn, M.J. Novel Travel Time Aware Metapopulation Models and Multi-Layer Waning Immunity for Late-Phase Epidemic and Endemic Scenarios. PLoS Comput. Biol. 2024, 20, e1012630. [Google Scholar] [CrossRef] [PubMed]
- Mueller, S.A.; Paltra, S.; Rehmann, J.; Ewert, R.; Nagel, K. Comparing GPS and Cell-Based Mobile Phone Data to Identify Activity Participation During the COVID-19 Pandemic. EPJ Data Sci. 2024, 13, 71. [Google Scholar] [CrossRef]
- Bansal, S.; Read, J.; Pourbohloul, B.; Meyers, L.A. The Dynamic Nature of Contact Networks in Infectious Disease Epidemiology. J. Biol. Dyn. 2010, 4, 478–489. [Google Scholar] [CrossRef] [PubMed]
- Macy, M.W. The Antecedents and Consequences of Network Mobility. Proc. Natl. Acad. Sci. USA 2023, 120, e2306897120. [Google Scholar] [CrossRef]
- Zhang, J.; Tan, S.; Peng, C.; Xu, X.; Wang, M.; Lu, W.; Wu, Y.; Sai, B.; Cai, M.; Kummer, A.G.; et al. Heterogeneous Changes in Mobility in Response to the SARS-CoV-2 Omicron BA.2 Outbreak in Shanghai. Proc. Natl. Acad. Sci. USA 2023, 120, e2306710120. [Google Scholar] [CrossRef]
- Tan, S.; Lai, S.; Fang, F.; Cao, Z.; Sai, B.; Song, B.; Dai, B.; Guo, S.; Liu, C.; Cai, M.; et al. Mobility in China, 2020: A Tale of Four Phases. Natl. Sci. Rev. 2021, 8, nwab148. [Google Scholar] [CrossRef]
- Buckee, C.O. Protect Privacy of Mobile Data. Nature 2014, 514, 35. [Google Scholar] [CrossRef]
- Anglemyer, A.; Moore, T.H.M.; Parker, L.; Chambers, T.; Grady, A.; Chiu, K.; Parry, M.; Wilczynska, M.; Flemyng, E.; Bero, L. Digital Contact Tracing Technologies in Epidemics: A Rapid Review. Cochrane Database Syst. Rev. 2020, 2020, CD013699. [Google Scholar] [CrossRef]
- Kleinman, R.A.; Merkel, C. Digital Contact Tracing for COVID-19. CMAJ 2020, 192, E653–E656. [Google Scholar] [CrossRef]
- Barrat, A.; Cattuto, C.; Kivelä, M.; Lehmann, S.; Saramäki, J. Effect of Manual and Digital Contact Tracing on COVID-19 Outbreaks: A Study on Empirical Contact Data. J. R. Soc. Interface 2021, 18, 20201000. [Google Scholar] [CrossRef]
- Stehlé, J.; Voirin, N.; Barrat, A.; Cattuto, C.; Isella, L.; Pinton, J.F.; Quaggiotto, M.; Van den Broeck, W.; Régis, C.; Lina, B.; et al. High-Resolution Measurements of Face-to-Face Contact Patterns in a Primary School. PLoS ONE 2011, 6, e23176. [Google Scholar] [CrossRef]
- Génois, M.; Barrat, A. Can Co-Location Be Used as a Proxy for Face-to-Face Contacts? EPJ Data Sci. 2018, 7, 1–18. [Google Scholar] [CrossRef]
- Tanis, C.C.; Nauta, F.H.; Boersma, M.J.; Van der Steenhoven, M.V.; Borsboom, D.; Blanken, T.F. Practical Behavioural Solutions to COVID-19: Changing the Role of Behavioural Science in Crises. PLoS ONE 2022, 17, e0272994. [Google Scholar] [CrossRef]
- Isella, L.; Stehlé, J.; Barrat, A.; Cattuto, C.; Pinton, J.F.; Van den Broeck, W. What’s in a Crowd? Analysis of Face-to-Face Behavioral Networks. J. Theor. Biol. 2011, 271, 166–180. [Google Scholar] [CrossRef]
- Mastrandrea, R.; Fournet, J.; Barrat, A. Contact Patterns in a High School: A Comparison Between Data Collected Using Wearable Sensors, Contact Diaries and Friendship Surveys. PLoS ONE 2015, 10, e0136497. [Google Scholar] [CrossRef] [PubMed]
- Kerr, C.C.; Stuart, R.M.; Mistry, D.; Abeysuriya, R.G.; Rosenfeld, K.; Hart, G.R.; Núñez, R.C.; Cohen, J.A.; Selvaraj, P.; Hagedorn, B.; et al. Covasim: An Agent-Based Model of COVID-19 Dynamics and Interventions. PLoS Comput. Biol. 2021, 17, e1009149. [Google Scholar] [CrossRef] [PubMed]
- Grefenstette, J.J.; Brown, S.T.; Rosenfeld, R.; DePasse, J.; Stone, N.T.B.; Cooley, P.C.; Wheaton, W.D.; Fyshe, A.; Galloway, D.D.; Sriram, A.; et al. FRED (A Framework for Reconstructing Epidemic Dynamics): An Open-Source Software System for Modeling Infectious Diseases and Control Strategies Using Census-Based Populations. BMC Public Health 2013, 13, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Shattock, A.J.; Le Rutte, E.A.; Dünner, R.P.; Sen, S.; Kelly, S.L.; Chitnis, N.; Penny, M.A. Impact of Vaccination and Non-Pharmaceutical Interventions on SARS-CoV-2 Dynamics in Switzerland. Epidemics 2022, 38, 100535. [Google Scholar] [CrossRef]
- Ponge, J.; Horstkemper, D.; Hellingrath, B.; Bayer, L.; Bock, W.; Karch, A. Evaluating Parallelization Strategies for Large-Scale Individual-Based Infectious Disease Simulations. In Proceedings of the 2023 Winter Simulation Conference (WSC), San Antonio, TX, USA, 10–13 December 2023; pp. 1088–1099. [Google Scholar] [CrossRef]
- Collier, N.; North, M. Parallel Agent-Based Simulation with Repast for High Performance Computing. Simulation 2013, 89, 1215–1235. [Google Scholar] [CrossRef]
- Collier, N.; Ozik, J. Distributed Agent-Based Simulation with Repast4Py. In Proceedings of the 2022 Winter Simulation Conference (WSC), Singapore, 11–14 December 2022; pp. 192–206. [Google Scholar] [CrossRef]
- Kühn, M.J.; Abele, D.; Kerkmann, D.; Korf, S.A.; Zunker, H.; Wendler, A.C.; Bicker, J.; Nguyen, K.; Schmieding, R.; Plötzke, L.; et al. MEmilio v1.3.0—A High Performance Modular Epidemics Simulation Software. Zenodo 2024. Available online: https://elib.dlr.de/209739/ (accessed on 3 April 2025).
- Diallo, D.; Schönfeld, J.; Hecking, T. Travel Demand Models for Micro-Level Contact Network Modeling. In Complex Networks & Their Applications XII; Cherifi, H., Rocha, L.M., Cherifi, C., Donduran, M., Eds.; Springer Nature: Basel, Switzerland, 2024; pp. 338–349. [Google Scholar] [CrossRef]
- Diallo, D.; Schönfeld, J.; Blanken, T.F.; Hecking, T. Dynamic Contact Networks in Confined Spaces: Synthesizing Micro-Level Encounter Patterns Through Human Mobility Models from Real-World Data. Entropy 2024, 26, 703. [Google Scholar] [CrossRef] [PubMed]
- Kerkmann, D.; Korf, S.; Nguyen, K.; Abele, D.; Schengen, A.; Gerstein, C.; Göbbert, J.H.; Basermann, A.; Kühn, M.J.; Meyer-Hermann, M. Agent-Based Modeling for Realistic Reproduction of Human Mobility and Contact Behavior to Evaluate Test and Isolation Strategies in Epidemic Infectious Disease Spread. arXiv 2024, arXiv:2410.08050. (Accepted for publication in Computers in Biology and Medicine). [Google Scholar] [CrossRef]
- González, M.C.; Hidalgo, C.A.; Barabási, A.L. Understanding Individual Human Mobility Patterns. Nature 2008, 453, 779–782. [Google Scholar] [CrossRef]
- Song, C.; Koren, T.; Wang, P.; Barabási, A.L. Modelling the Scaling Properties of Human Mobility. Nat. Phys. 2010, 6, 818–823. [Google Scholar] [CrossRef]
- Niedzielewski, K.; Bartczuk, R.P.; Bielczyk, N.; Bogucki, D.; Dreger, F.; Dudziuk, G.; Górski, Ł.; Gruziel-Słomka, M.; Haman, J.; Kaczorek, A.; et al. Forecasting SARS-CoV-2 epidemic dynamic in Poland with the pDyn agent-based model. Epidemics 2024, 49, 100801. [Google Scholar] [CrossRef]
- Adamik, B.; Bawiec, M.; Bezborodov, V.; Bock, W.; Bodych, M.; Burgard, J.P.; Götz, T.; Krueger, T.; Migalska, A.; Pabjan, B.; et al. Mitigation and Herd Immunity Strategy for COVID-19 is Likely to Fail. medRxiv 2020. [Google Scholar] [CrossRef]
- Bicher, M.; Rippinger, C.; Urach, C.; Brunmeir, D.; Siebert, U.; Popper, N. Evaluation of Contact-Tracing Policies against the Spread of SARS-CoV-2 in Austria: An Agent-Based Simulation. Med Decis. Mak. 2021, 41, 1017–1032. [Google Scholar] [CrossRef]
- Müller, S.A.; Balmer, M.; Charlton, W.; Ewert, R.; Neumann, A.; Rakow, C.; Schlenther, T.; Nagel, K. Predicting the Effects of COVID-19 Related Interventions in Urban Settings by Combining Activity-Based Modelling, Agent-Based Simulation, and Mobile Phone Data. PLoS ONE 2021, 16, e0259037. [Google Scholar] [CrossRef]
- Djurdjevac Conrad, N.; Helfmann, L.; Zonker, J.; Winkelmann, S.; Schütte, C. Human Mobility and Innovation Spreading in Ancient Times: A Stochastic Agent-Based Simulation Approach. EPJ Data Sci. 2018, 7, 24. [Google Scholar] [CrossRef]
- Ozik, J.; Wozniak, J.M.; Collier, N.; Macal, C.M.; Binois, M. A population data-driven workflow for COVID-19 modeling and learning. Int. J. High Perform. Comput. Appl. 2021, 35, 483–499. [Google Scholar] [CrossRef]
- Macal, C.M.; Collier, N.T.; Ozik, J.; Tatara, E.R.; Murphy, J.T. chiSIM: An agent-based simulation model of social interactions in a large urban area. In Proceedings of the 2018 Winter Simulation Conference (WSC), Gothenburg, Sweden, 9–12 December 2018; pp. 810–820. [Google Scholar] [CrossRef]
- Gaudou, B.; Huynh, N.Q.; Philippon, D.; Brugière, A.; Chapuis, K.; Taillandier, P.; Larmande, P.; Drogoul, A. Comokit: A modeling kit to understand, analyze, and compare the impacts of mitigation policies against the COVID-19 epidemic at the scale of a city. Front. Public Health 2020, 8, 563247. [Google Scholar] [CrossRef] [PubMed]
- Taillandier, P.; Gaudou, B.; Grignard, A.; Huynh, Q.N.; Marilleau, N.; Caillou, P.; Philippon, D.; Drogoul, A. Building, composing and experimenting complex spatial models with the GAMA platform. GeoInformatica 2019, 23, 299–322. [Google Scholar] [CrossRef]
- Wendler, A.C.; Plötzke, L.; Tritzschak, H.; Kühn, M.J. A Nonstandard Numerical Scheme for a Novel SECIR Integro Differential Equation-Based Model with Nonexponentially Distributed Stay Times. arXiv 2024, arXiv:2408.12228. [Google Scholar] [CrossRef]
- Bicker, J.; Schmieding, R.; Meyer-Hermann, M.; Kühn, M.J. Hybrid Metapopulation Agent-Based Epidemiological Models for Efficient Insight on the Individual Scale: A Contribution to Green Computing. Infect. Dis. Model. 2025, 10, 571–590. [Google Scholar] [CrossRef] [PubMed]
- Kühn, M.J.; Abele, D.; Binder, S.; Rack, K.; Klitz, M.; Kleinert, J.; Gilg, J.; Spataro, L.; Koslow, W.; Siggel, M.; et al. Regional opening strategies with commuter testing and containment of new SARS-CoV-2 variants in Germany. BMC Infect. Dis. 2022, 22, 333. [Google Scholar] [CrossRef]
- Schmidt, A.; Zunker, H.; Heinlein, A.; Kühn, M.J. Graph Neural Network Surrogates to leverage Mechanistic Expert Knowledge towards Reliable and Immediate Pandemic Response. arXiv 2024, arXiv:2411.06500. [Google Scholar] [CrossRef]
- Shin, R.; Hong, S.; Lee, K.; Chong, S. On the Levy-Walk Nature of Human Mobility: Do Humans Walk Like Monkeys? In Proceedings of the IEEE INFOCOM, Phoenix, AZ, USA, 13–18 April 2008; pp. 924–932. [Google Scholar] [CrossRef]
- Nguyen, A.D.; Sénac, P.; Ramiro, V.; Diaz, M. STEPS: An Approach for Human Mobility Modeling. In Proceedings of the 10th International IFIP TC 6 Networking Conference (NETWORKING 2011), Valencia, Spain, 9–13 May 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 254–265. [Google Scholar] [CrossRef]
- Vestergaard, C.L.; Génois, M. Temporal Gillespie Algorithm: Fast Simulation of Contagion Processes on Time-Varying Networks. PLoS Comput. Biol. 2015, 11, e1004579. [Google Scholar] [CrossRef]
- Statistisches Bundesamt (Destatis). Privathaushalte Nach Haushaltsgröße 2023. Available online: https://www.destatis.de/DE/Themen/Gesellschaft-Umwelt/Bevoelkerung/Haushalte-Familien/Tabellen/1-1-privathaushalte-haushaltsmitglieder.html (accessed on 3 April 2025).
- Statistisches Bundesamt (Destatis). Bevölkerung Nach Altersgruppen 2011 bis 2023. Available online: https://www.destatis.de/DE/Themen/Gesellschaft-Umwelt/Bevoelkerung/Bevoelkerungsstand/Tabellen/bevoelkerung-altersgruppen-deutschland.html (accessed on 3 April 2025).
- Pastor-Satorras, R.; Vespignani, A. Epidemic Spreading in Scale-Free Networks. Phys. Rev. Lett. 2001, 86, 3200. [Google Scholar] [CrossRef]
- Goh, K.I.; Barabási, A.L. Burstiness and Memory in Complex Systems. Europhys. Lett. 2008, 81, 48002. [Google Scholar] [CrossRef]
- Hiraoka, T.; Masuda, N.; Li, A.; Jo, H.H. Modeling Temporal Networks with Bursty Activity Patterns of Nodes and Links. Phys. Rev. Res. 2020, 2, 023073. [Google Scholar] [CrossRef]



| Household Type | Distribution |
|---|---|
| 1-person (41%) | 70%: 1 adult, 30%: 1 senior |
| 2-person (33.5%) | 70%: adult or senior couples, |
| 30%: 1 adult, 1 child | |
| 3-person (12%) | 100%: 2 adults, 1 child |
| 4-person (9.5%) | 100%: 2 adults, 2 children |
| 5+-person (4%) | 100%: 2 adults, 2 children, 1 senior |
| Scenario | Supermarkets | Social Events | ||
|---|---|---|---|---|
| TCN1000-small | 100 | 20 | 3 × 35 | 3 × 60 |
| TCN1000-medium | 200 | 50 | 2 × 50 | 2 × 90 |
| TCN1000-large | 400 | 100 | 1 × 100 | 1 × 180 |
| Network | # Nodes | Avg # Active Nodes | # Edges | Avg Degree (Overall/Active) | Diameter (Max/Median) |
|---|---|---|---|---|---|
| TCN1000 | 2058 | 1690.15 (82.13%) | 987,777 | 4.00/4.71 | 9/5 |
| TCN2000 | 4118 | 3379.36 (82.04%) | 2,001,219 | 4.05/4.78 | 11/5 |
| TCN5000 | 10,284 | 8456.24 (82.22%) | 4,997,222 | 4.05/4.76 | 10/5 |
| Network | # Nodes | Avg # Active Nodes | # Edges | Avg Degree (Overall/Active) | Diameter (Max/Median) |
|---|---|---|---|---|---|
| TCN1000-small | 2057 | 1688 | 818,351 | 3.32/3.93 | 9/4 |
| TCN1000-medium | 2058 | 1690 | 987,777 | 4.00/4.71 | 9/5 |
| TCN1000-large | 2057 | 1690 | 1,042,295 | 4.22/4.97 | 13/7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diallo, D.; Schoenfeld, J.; Schmieding, R.; Korf, S.; Kühn, M.J.; Hecking, T. Integrating Human Mobility Models with Epidemic Modeling: A Framework for Generating Synthetic Temporal Contact Networks. Entropy 2025, 27, 507. https://doi.org/10.3390/e27050507
Diallo D, Schoenfeld J, Schmieding R, Korf S, Kühn MJ, Hecking T. Integrating Human Mobility Models with Epidemic Modeling: A Framework for Generating Synthetic Temporal Contact Networks. Entropy. 2025; 27(5):507. https://doi.org/10.3390/e27050507
Chicago/Turabian StyleDiallo, Diaoulé, Jurij Schoenfeld, René Schmieding, Sascha Korf, Martin J. Kühn, and Tobias Hecking. 2025. "Integrating Human Mobility Models with Epidemic Modeling: A Framework for Generating Synthetic Temporal Contact Networks" Entropy 27, no. 5: 507. https://doi.org/10.3390/e27050507
APA StyleDiallo, D., Schoenfeld, J., Schmieding, R., Korf, S., Kühn, M. J., & Hecking, T. (2025). Integrating Human Mobility Models with Epidemic Modeling: A Framework for Generating Synthetic Temporal Contact Networks. Entropy, 27(5), 507. https://doi.org/10.3390/e27050507







