Quantum Phase Transition in the Coupled-Top Model: From Z2 to U(1) Symmetry Breaking
Abstract
1. Introduction
2. The Model and Symmetries
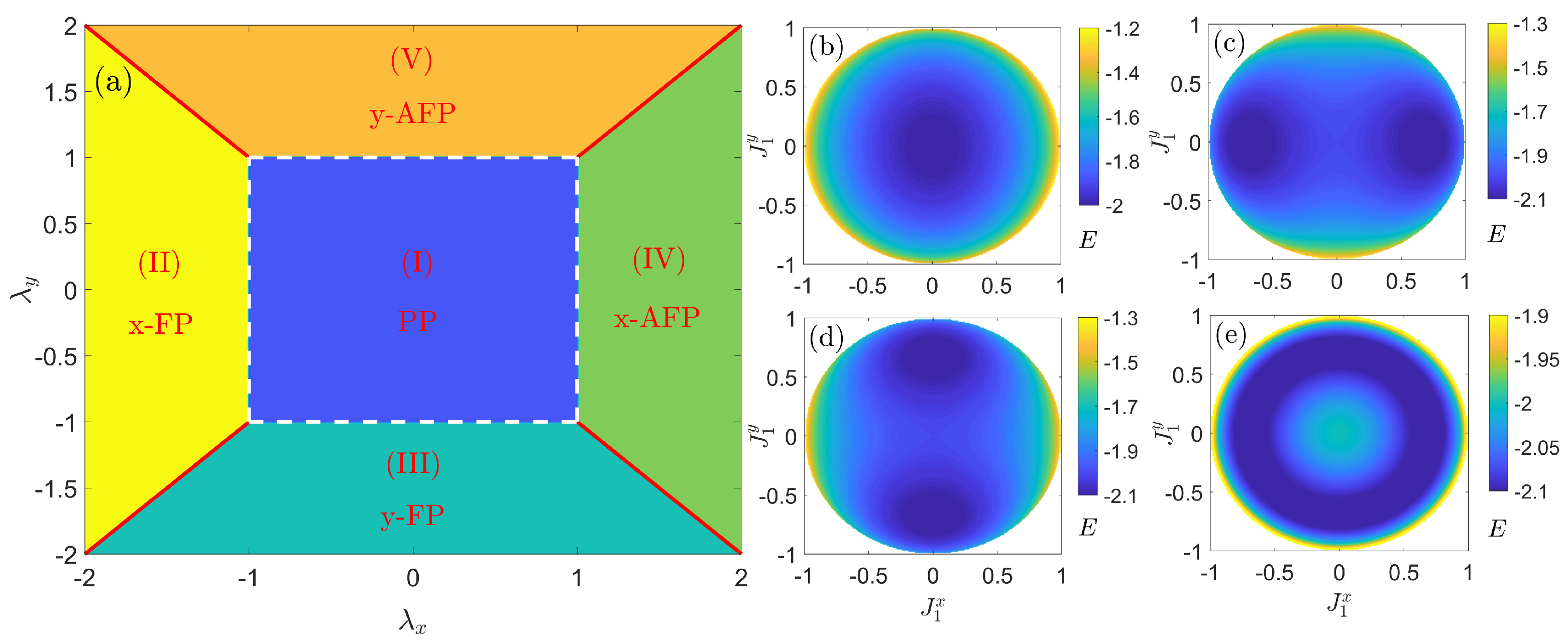
3. Phase Diagram
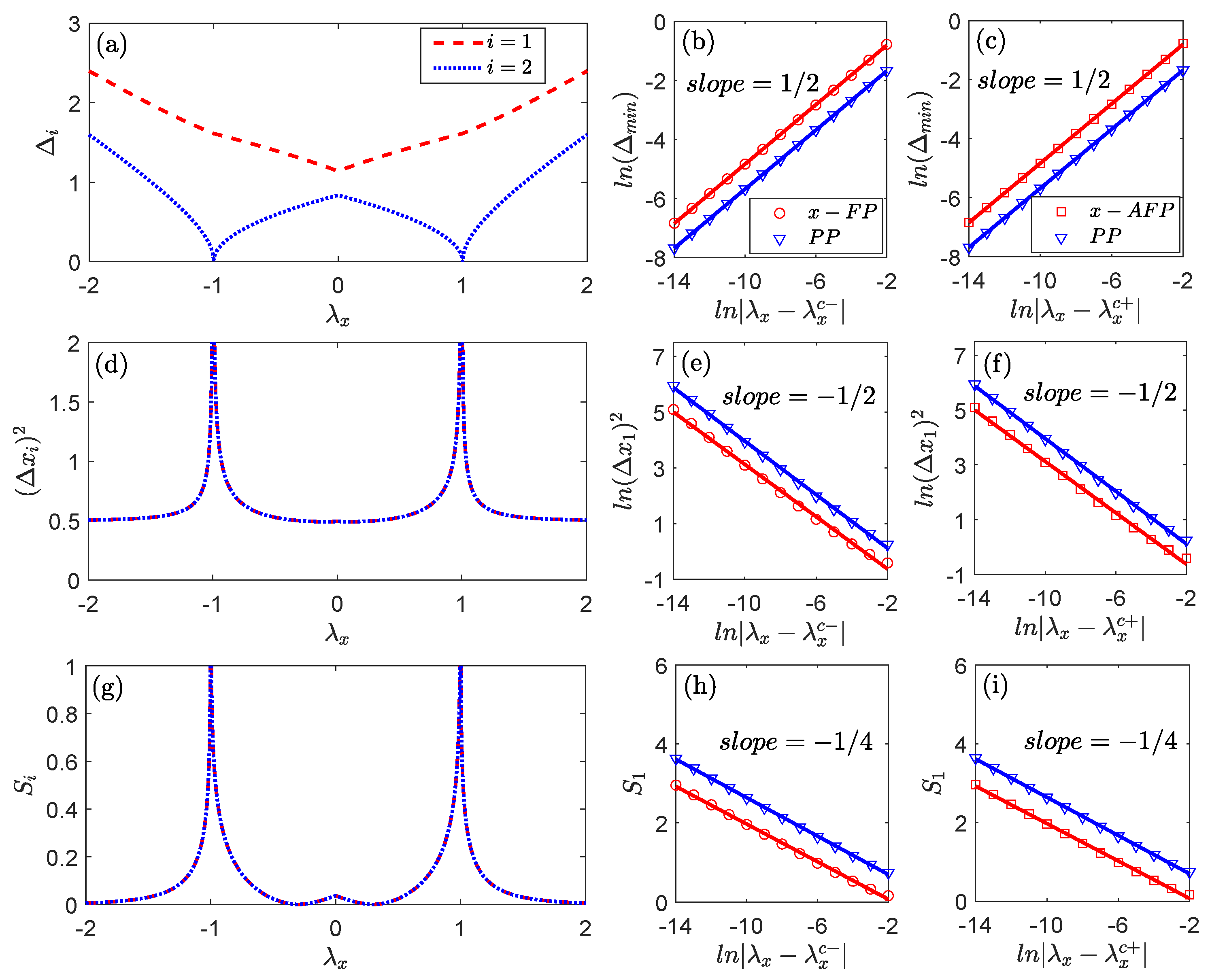
4. Quantum Criticality
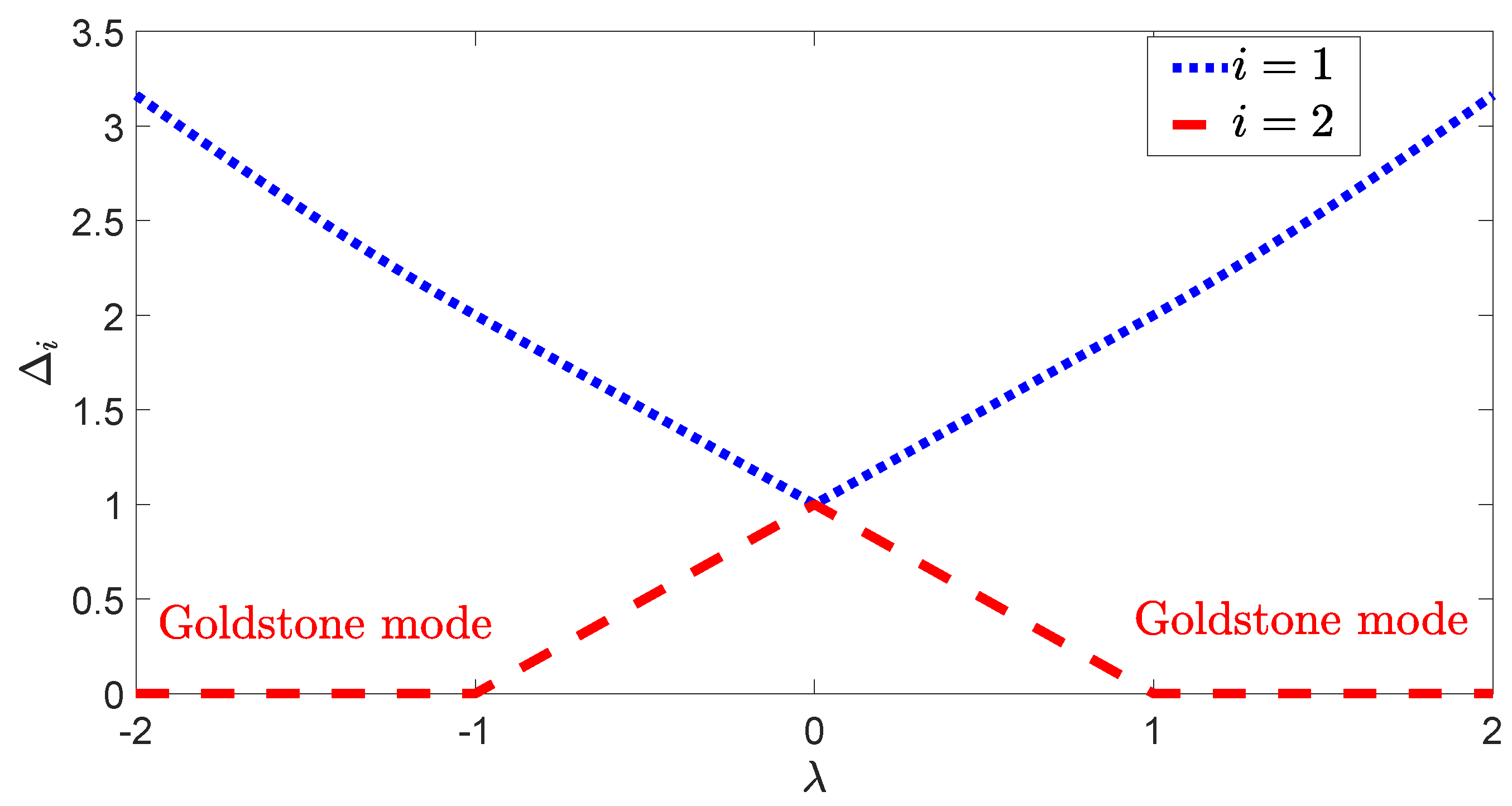
5. Excitation Spectra for U(1) Symmetry
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CTM | coupled-top model |
| TFIM | transverse-field Ising mode |
| PP | paramagnetic phase |
| FP | ferromagnetic phase |
| AFP | antiferromagnetic phase |
Appendix A. Expansion of the Hamiltonian with HP Transformation
Appendix B. The Excitation Energy Δi and Quantum Fluctuations (Δxi)2, (Δpi)2 Obtained from Symplectic Transformation S
References
- Solyom, J. The Fermi gas model of one-dimensional conductors. Adv. Phys. 1979, 28, 201. [Google Scholar] [CrossRef]
- Greiner, M.; Mandel, O.; Esslinger, T.; HaEnsch, T.W.; Bloch, I. Quantum phase transition from a superfluid to a Mott insulator in a gas of ultracold atoms. Nature 2002, 415, 39. [Google Scholar] [CrossRef]
- Sachdev, S. Quantum Phase Transitions, 2nd ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Frérot, I.; Roscilde, T. Quantum Critical Metrology. Phys. Rev. Lett. 2018, 121, 020402. [Google Scholar] [CrossRef]
- Garbe, L.; Bina, M.; Keller, A.; Paris, M.G.A.; Felicetti, S. Critical Quantum Metrology with a Finite-Component Quantum Phase Transition. Phys. Rev. Lett. 2020, 124, 120504. [Google Scholar] [CrossRef]
- Du, M.-M.; Zhang, D.-J.; Zhou, Z.-Y.; Tong, D.M. Visualizing quantum phase transitions in the XXZ model via the quantum steering ellipsoid. Phys. Rev. A 2021, 104, 012418. [Google Scholar] [CrossRef]
- Ying, Z.-J.; Felicetti, S.; Liu, G.; Braak, D. Critical Quantum Metrology in the Non-Linear Quantum Rabi Model. Entropy 2022, 24, 1015. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L. Entanglement Phase Transitions Non-Hermitian Floquet Systems. Phys. Rev. Res. 2024, 6, 023081. [Google Scholar] [CrossRef]
- Beaulieu, G.; Minganti, F.; Frasca, S.; Scigliuzzo, M.; Felicetti, S.; Candia, R.D.; Scarlino, P. Criticality-Enhanced Quantum Sensing with a Parametric Superconducting Resonator. Phys. Rev. X Quantum 2025, 6, 020301. [Google Scholar] [CrossRef]
- de Gennes, P.G. Collective motions of hydrogen bonds. Solid State Commun. 1963, 1, 132. [Google Scholar] [CrossRef]
- Brout, R.; Müller, K.; Thomas, H. Tunnelling and collective excitations in a microscopic model of ferroelectricity. Solid State Commun. 1966, 4, 507. [Google Scholar] [CrossRef]
- Pfeuty, P. The one-dimensional Ising model with a transverse field. Ann. Phys. 1970, 57, 79. [Google Scholar] [CrossRef]
- Stinchcombe, R.B. Ising model in a transverse field. I. Basic theory. J. Phys. C Solid State Phys. 1973, 6, 2459. [Google Scholar] [CrossRef]
- Suzuki, S.; Inoue, J.-I.; Chakrabarti, B.K. Quantum Ising Phases and Transitions in Transverse Ising Models, 2nd ed.; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Dziarmaga, J. Dynamics of a Quantum Phase Transition: Exact Solution of the Quantum Ising Model. Phys. Rev. Lett. 2005, 95, 245701. [Google Scholar] [CrossRef]
- Heyl, M.; Polkovnikov, A.; Kehrein, S. Dynamical Quantum Phase Transitions in the Transverse-Field Ising Model. Phys. Rev. Lett. 2013, 110, 135704. [Google Scholar] [CrossRef]
- Rohn, J.; Hörmann, M.; Genes, C.; Schmidt, K.P. Ising model in a light-induced quantized transverse field. Phys. Rev. Res. 2020, 2, 023131. [Google Scholar] [CrossRef]
- Pal, M.; Baez, W.D.; Majumdar, P.; Sen, A.; Datta, T. Dynamical phase transitions in the XY model: A Monte Carlo and mean-field-theory study. Phys. Rev. E 2024, 110, 054109. [Google Scholar] [CrossRef] [PubMed]
- Tu, C.P.; Ma, Z.; Wang, H.R.; Jiao, Y.H.; Dai, D.Z.; Li, S.Y. Gapped quantum spin liquid in a triangular-lattice Ising-type antiferromagnet PrMgAl11O19. Phys. Rev. Res. 2024, 6, 043147. [Google Scholar] [CrossRef]
- Kischel, F.; Wessel, S. Quantifying nonuniversal corner free-energy contributions in weakly anisotropic two-dimensional critical systems. Phys. Rev. E 2024, 110, 024106. [Google Scholar] [CrossRef] [PubMed]
- Pexe, G.E.L.; Rattighieri, L.A.M.; Malvezzi, A.L.; Fanchini, F.F. Using a feedback-based quantum algorithm to analyze the critical properties of the ANNNI model without classical optimization. Phys. Rev. B 2024, 110, 224422. [Google Scholar] [CrossRef]
- Hines, A.P.; McKenzie, R.H.; Milburn, G.J. Quantum entanglement and fixed-point bifurcations. Phys. Rev. A 2005, 71, 042303. [Google Scholar] [CrossRef]
- Mondal, D.; Sinha, S.; Sinha, S. Chaos and quantum scars in a coupled top model. Phys. Rev. E 2020, 102, 020101. [Google Scholar] [CrossRef]
- Mondal, D.; Sinha, S.; Sinha, S. Dynamical route to ergodicity and quantum scarring in kicked coupled top. Phys. Rev. E 2021, 104, 024217. [Google Scholar] [CrossRef] [PubMed]
- Mondal, D.; Sinha, S.; Sinha, S. Quantum transitions, ergodicity, and quantum scars in the coupled top model. Phys. Rev. E 2022, 105, 014130. [Google Scholar] [CrossRef]
- Prakash, R.; Lakshminarayan, A. Scrambling in strongly chaotic weakly coupled bipartite systems: Universality beyond the ehrenfest timescale. Phys. Rev. B 2020, 101, 121108. [Google Scholar] [CrossRef]
- Abbarchi, M.; Amo, A.; Sala, V.G.; Solnyshkov, D.D.; Flayac, H.; Ferrier, L.; Sagnes, I.; Galopin, E.; Lemaître, A.; Malpuech, G.; et al. Macroscopic quantum self-trapping and Josephson oscillations of exciton polaritons. Nat. Phys. 2013, 9, 275–279. [Google Scholar] [CrossRef]
- Albiez, M.; Gati, R.; Fölling, J.; Hunsmann, S.; Cristiani, M.; Oberthaler, M.K. Direct Observation of Tunneling and Nonlinear Self-Trapping in a Single Bosonic Josephson Junction. Phys. Rev. Lett. 2005, 95, 010402. [Google Scholar] [CrossRef]
- Raghavan, S.; Smerzi, A.; Fantoni, S.; Shenoy, S.R. Coherent oscillations between two weakly coupled Bose-Einstein condensates: Josephson effects, π oscillations, and macroscopic quantum self-trapping. Phys. Rev. Lett. 1999, 59, 620. [Google Scholar] [CrossRef]
- Wang, Q.; Pérez-Bernal, F. Signatures of excited-state quantum phase transitions in quantum many-body systems: Phase space analysis. Phys. Rev. E 2021, 104, 034119. [Google Scholar] [CrossRef]
- Varikuti, N.D.; Madhok, V. Out-of-time ordered correlators in kicked coupled tops: Information scrambling in mixed phase space and the role of conserved quantities. Chaos: Interdiscip. J. Nonlinear Sci. 2024, 34, 063124. [Google Scholar] [CrossRef]
- Ray, S.; Sinha, S.; Sengupta, K. Signature of chaos and delocalization in a periodically driven many-body system: An out-of-time-order-correlation study. Phys. Rev. B 2018, 98, 053631. [Google Scholar] [CrossRef]
- Li, J.; Fan, R.; Wang, H.; Ye, B.; Zeng, B.; Zhai, H.; Peng, X.; Du, J. Measuring Out-of-Time-Order Correlators on a Nuclear Magnetic Resonance Quantum Simulator. Phys. Rev. X 2017, 7, 031011. [Google Scholar] [CrossRef]
- Gärttner, M.; Bohnet, J.G.; Safavi-Naini, A.; Wall, M.L.; Bollinger, J.J.; Rey, A.M. Measuring out-of-time-order correlations and multiple quantum spectra in a trapped-ion quantum magnet. Nat. Phys. 2017, 13, 781–786. [Google Scholar] [CrossRef]
- Duan, L.; Wang, Y.-Z.; Chen, Q.-H. Quantum phase transitions in the triangular coupled-top model. Phys. Rev. B 2023, 107, 094415. [Google Scholar] [CrossRef]
- Braak, D. Integrability of the Rabi Model. Phys. Rev. Lett. 2011, 107, 100401. [Google Scholar] [CrossRef]
- Chen, Q.-H.; Wang, C.; He, S.; Liu, T.; Wang, K.L. Exact solvability of the quantum Rabi model using Bogoliubov operators. Phys. Rev. A 2012, 86, 023822. [Google Scholar] [CrossRef]
- Emary, C.; Brandes, T. Quantum Chaos Triggered by Precursors of a Quantum Phase Transition: The Dicke Model. Phys. Rev. Lett. 2003, 90, 044101. [Google Scholar] [CrossRef]
- Cong, L.; Sun, X.-M.; Liu, M.; Ying, Z.-J.; Luo, H.-G. Frequency-renormalized multipolaron expansion for the quantum Rabi model. Phys. Rev. A 2017, 95, 063803. [Google Scholar] [CrossRef]
- Ying, Z.-J.; Cong, L.; Sun, X.-M. Quantum phase transition and spontaneous symmetry breaking in a nonlinear quantum Rabi model. J. Phys. A Math. Theor. 2020, 53, 345301. [Google Scholar] [CrossRef]
- Hwang, M.-J.; Puebla, R.; Plenio, M.B. Quantum Phase Transition and Universal Dynamics in the Rabi Model. Phys. Rev. Lett. 2015, 115, 180404. [Google Scholar] [CrossRef]
- Emary, C.; Brandes, T. Chaos and the quantum phase transition in the Dicke model. Phys. Rev. E 2003, 67, 066203. [Google Scholar] [CrossRef]
- Leggett, A.J.; Chakravarty, S.; Dorsey, A.T.; Fisher, M.P.A.; Garg, A.; Zwerger, W. Dynamics of the dissipative two-state system. Rev. Mod. Phys. 1987, 59, 1. [Google Scholar] [CrossRef]
- Guo, C.; Weichselbaum, A.; von Delft, J.; Vojta, M. Critical and Strong-Coupling Phases in One- and Two-Bath Spin-Boson Models. Phys. Rev. Lett. 2012, 108, 160401. [Google Scholar] [CrossRef]
- Xie, Q.-T.; Cui, S.; Cao, J.-P.; Amico, L.; Fan, H. Anisotropic Rabi model. Phys. Rev. X 2014, 4, 021046. [Google Scholar] [CrossRef]
- Shen, L.-T.; Yang, Z.-B.; Wu, H.-Z.; Zheng, S.-B. Quantum phase transition and quench dynamics in the anisotropic Rabi model. Phys. Rev. A 2017, 95, 013819. [Google Scholar] [CrossRef]
- Liu, M.; Chesi, S.; Ying, Z.-J.; Chen, X.; Luo, H.-G.; Lin, H.-Q. Universal Scaling and Critical Exponents of the Anisotropic Quantum Rabi Model. Phys. Rev. Lett. 2017, 119, 220601. [Google Scholar] [CrossRef] [PubMed]
- Baksic, A.; Ciuti, C. Controlling Discrete and Continuous Symmetries in “Superradiant” Phase Transitions with Circuit QED Systems. Phys. Rev. Lett. 2014, 112, 173601. [Google Scholar] [CrossRef]
- Wang, Y.-Z.; He, S.; Duan, L.; Chen, Q.-H. Rich phase diagram of quantum phases in the anisotropic subohmic spin-boson model. Phys. Rev. B 2020, 101, 155147. [Google Scholar] [CrossRef]
- Hwang, M.-J.; Plenio, M.B. Quantum Phase Transition in the Finite Jaynes-Cummings Lattice Systems. Phys. Rev. Lett. 2016, 117, 123602. [Google Scholar] [CrossRef]
- Zou, J.H.; Liu, T.; Feng, M.; Yang, W.L.; Chen, C.Y.; Twamley, J. Quantum phase transition in a driven Tavis–Cummings model. New J. Phys. 2013, 15, 123032. [Google Scholar] [CrossRef]
- Wang, Y.-Z.; He, S.; Duan, L.; Chen, Q.-H. Quantum phase transitions in the spin-boson model without the counterrotating terms. Phys. Rev. B 2019, 100, 115106. [Google Scholar] [CrossRef]
- Anderson, P.W. Plasmons, Gauge Invariance, and Mass. Phys. Rev. 1963, 130, 439. [Google Scholar] [CrossRef]
- Higgs, P.W. Broken Symmetries and the Masses of Gauge Bosons. Phys. Rev. Lett. 1964, 13, 508. [Google Scholar] [CrossRef]
- Peng, J.; Rico, E.; Zhong, J.; Solano, E.; Egusquiza, I.L. Unified superradiant phase transitions. Phys. Rev. A 2019, 100, 063820. [Google Scholar] [CrossRef]
- Lieb, E.H. The classical limit of quantum spin systems. Commun. Math. Phys. 1973, 31, 327. [Google Scholar] [CrossRef]
- Dusuel, S.; Vidal, J. Continuous unitary transformations and finite-size scaling exponents in the Lipkin-Meshkov-Glick model. Phys. Rev. B 2005, 71, 224420. [Google Scholar] [CrossRef]
- Bakemeier, L.; Alvermann, A.; Fehske, H. Quantum phase transition in the Dicke model with critical and noncritical entanglement. Phys. Rev. A 2012, 85, 043821. [Google Scholar] [CrossRef]
- Duan, L. Quantum walk on the Bloch sphere. Phys. Rev. A 2022, 105, 042215. [Google Scholar] [CrossRef]
- Liu, W.; Duan, L. Quantum Phase Transitions in a Generalized Dicke Model. Entropy 2023, 25, 1492. [Google Scholar] [CrossRef]
- Zhao, J.; Hwang, M.J. Frustrated Superradiant Phase Transition. Phys. Rev. Lett. 2022, 128, 163601. [Google Scholar] [CrossRef]
- Soldati, R.R.; Mitchison, M.T.; Landi, G.T. Multipartite quantum correlations in a two-mode Dicke model. Phys. Rev. A 2021, 104, 052423. [Google Scholar] [CrossRef]
- Holstein, T.; Primakoff, H. Field Dependence of the Intrinsic Domain Magnetization of a Ferromagnet. Phys. Rev. 1940, 58, 1098. [Google Scholar] [CrossRef]
- Serafini, A. Quantum Continuous Variables; CRC Press: London, UK, 2017. [Google Scholar]
- Adesso, G.; Illuminati, F. Entanglement in continuous-variable systems: Recent advances and current perspectives. J. Phys. A Math. Theor. 2007, 40, 7821–7880. [Google Scholar] [CrossRef]
- Shi, Y.-Q.; Cong, L.; Eckle, H.-P. Entanglement resonance in the asymmetric quantum Rabi model. Phys. Rev. A 2022, 105, 062450. [Google Scholar] [CrossRef]
- Xu, Y.; Pu, H. Emergent Universality in a Quantum Tricritical Dicke Model. Phys. Rev. Lett. 2019, 122, 193201. [Google Scholar] [CrossRef]
- Larson, J.; Irish, E.K. Some remarks on ’superradiant’ phase transitions in light-matter systems. J. Phys. A Math. Theor. 2017, 50, 174002. [Google Scholar] [CrossRef]
| Ferromagnetic Phase () | Paramagnetic Phase () | Antiferromagnetic Phase () | |
|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, W.-J.; Ye, T.; Duan, L.; Wang, Y.-Z. Quantum Phase Transition in the Coupled-Top Model: From Z2 to U(1) Symmetry Breaking. Entropy 2025, 27, 474. https://doi.org/10.3390/e27050474
Mao W-J, Ye T, Duan L, Wang Y-Z. Quantum Phase Transition in the Coupled-Top Model: From Z2 to U(1) Symmetry Breaking. Entropy. 2025; 27(5):474. https://doi.org/10.3390/e27050474
Chicago/Turabian StyleMao, Wen-Jian, Tian Ye, Liwei Duan, and Yan-Zhi Wang. 2025. "Quantum Phase Transition in the Coupled-Top Model: From Z2 to U(1) Symmetry Breaking" Entropy 27, no. 5: 474. https://doi.org/10.3390/e27050474
APA StyleMao, W.-J., Ye, T., Duan, L., & Wang, Y.-Z. (2025). Quantum Phase Transition in the Coupled-Top Model: From Z2 to U(1) Symmetry Breaking. Entropy, 27(5), 474. https://doi.org/10.3390/e27050474






