Finite-Size Corrections from the Subleading Magnetic Scaling Field for the Ising and Potts Models in Two Dimensions
Abstract
1. Introduction
2. The Potts Model
3. Finite-Size Scaling
4. Monte Carlo Simulations
5. Results
5.1. O Loop Model on the Dense Branch
5.1.1.
5.1.2.
5.1.3.
5.2. O Loop Model
5.3. O Loop Model on the Dilute Branch
5.3.1.
5.3.2.
5.3.3.
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MC | Monte Carlo |
| FSS | Finite size scaling |
| RG | Renormalization group |
| 2D | Two dimensional |
| CFT | Conformal field theory |
| FK | Fortuin Kasteleyn |
| CG | Coulomb gas |
| CSD | Critical slowing down |
| DF | Degrees of freedom |
References
- Madras, N. Lectures on Monte Carlo Methods; AMS: Providence, RI, USA, 2002. [CrossRef]
- Landau, D.P.; Binder, K. A Guide to Monte-Carlo Simulations in Statistical Physics, 4th ed.; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Sokal, A.D. Monte Carlo methods in statistical mechanics: Foundations and new algorithms. In Functional Integration: Basics and Applications; DeWitt-Morette, C., Cartier, P., Folacci, A., Eds.; Plenum: New York, NY, USA, 1997; pp. 131–192. [Google Scholar] [CrossRef]
- Cardy, J. (Ed.) Finite-Size Scaling. In Current Physics–Sources and Comments; North Holland: Amsterdam, The Netherlands, 1988; Volume 2. [Google Scholar]
- Privman, V. Finite-size scaling theory. In Finite Size Scaling and Numerical Simulation of Statistical Physics; Privman, V., Ed.; World Scientific: Singapore, 1990; pp. 1–98. [Google Scholar] [CrossRef]
- Cardy, J. Scaling and Renormalization in Statistical Physics; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar] [CrossRef]
- Privman, V.; Fisher, M.E. Universal critical amplitudes in finite-size scaling. Phys. Rev. B 1984, 30, 322. [Google Scholar] [CrossRef]
- Salas, J.; Sokal, A.D. Universal amplitude ratios in the critical two-dimensional Ising model on a torus. J. Stat. Phys. 2000, 98, 551–588. [Google Scholar] [CrossRef]
- Pelissetto, A.; Vicari, E. Critical phenomena and renormalization-group theory. Phys. Rep. 2002, 368, 549–727. [Google Scholar] [CrossRef]
- Guo, H.; Jasnow, D. Hyperuniversality and the renormalization group for finite systems. Phys. Rev. B 1987, 35, 1846, Erratum in Phys. Rev. B 1989, 39, 753. [Google Scholar] [CrossRef] [PubMed]
- Privman, V.; Hohenberg, P.C.; Aharony, A. Universal critical point amplitude relations. In Phase Transitions and Critical Phenomena; Domb, C., Lebowitz, J.L., Eds.; Academic Press: London, UK, 1991; Volume 14, pp. 4–134. [Google Scholar]
- Li, M.; Fang, S.; Fan, J.; Deng, Y. Crossover finite-size scaling theory and its applications in percolation. arXiv 2024, arXiv:2412.06228. [Google Scholar]
- Nauenberg, M.; Scalapino, D.J. Singularities and scaling functions at the Potts-model multicritical point. Phys. Rev. Lett. 1980, 44, 837. [Google Scholar] [CrossRef]
- Cardy, J.L.; Nauenberg, M.; Scalapino, D.J. Scaling theory of the Potts-model multicritical point. Phys. Rev. B 1980, 22, 2560. [Google Scholar] [CrossRef]
- Salas, J.; Sokal, A.D. Logarithmic corrections and finite-size scaling in the two-dimensional 4-state Potts model. J. Stat. Phys. 1997, 88, 567–615. [Google Scholar] [CrossRef]
- Wegner, F.J. The critical state, general aspects. In Phase Transitions and Critical Phenomena; Domb, C., Green, M.S., Eds.; Academic Press: London, UK, 1976; Volume 6, p. 7. [Google Scholar]
- Di Francesco, P.; Mathieu, P.; Sénéchal, M. Conformal Field Theory; Springer: New York, NY, USA, 1997. [Google Scholar] [CrossRef]
- Ferdinand, A.E.; Fisher, M.E. Bounded and inhomogeneous Ising models. I. Specific-heat anomaly of a finite lattice. Phys. Rev. 1969, 185, 832–846. [Google Scholar] [CrossRef]
- Salas, J. Exact finite-size-scaling corrections to the critical two-dimensional Ising model on a torus. J. Phys. A Math. Gen. 2001, 34, 1311. [Google Scholar] [CrossRef]
- Salas, J. Exact finite-size-scaling corrections to the critical two-dimensional Ising model on a torus. II. Triangular and hexagonal lattices. J. Phys. A Math. Gen. 2002, 35, 1833. [Google Scholar] [CrossRef]
- Nienhuis, B. Analytical calculation of two leading exponents of the dilute Potts model. J. Phys. A Math. Gen. 1982, 15, 199–213. [Google Scholar] [CrossRef]
- Potts, R.B. Some generalized order-disorder transformations. Proc. Camb. Philos. Soc. 1952, 48, 106–109. [Google Scholar] [CrossRef]
- Wu, F.Y. The Potts model. Rev. Mod. Phys. 1982, 54, 235, Erratum in Rev. Mod. Phys. 1983, 55, 315.. [Google Scholar] [CrossRef]
- Wu, F.Y. Potts model of magnetism (invited). J. Appl. Phys. 1984, 55, 2421–2425. [Google Scholar] [CrossRef]
- Baxter, R.J. Exactly Solved Models in Statistical Mechanics; World Scientific: Singapore, 1985. [Google Scholar] [CrossRef]
- Nienhuis, B. Coulomb gas formulations of two-dimensional phase transitions. In Phase Transitions and Critical Phenomena; Domb, C., Lebowitz, J.L., Eds.; Academic Press: London, UK, 1987; Volume 11, pp. 1–53. [Google Scholar]
- Welsh, D.J.A. Complexity: Knots, Colourings and Counting; London Mathematical Society Lecture Notes Series; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Kasteleyn, P.W.; Fortuin, C.M. Phase transitions in lattice systems with random local properties. J. Phys. Soc. Jpn. 1969, 26, 11. [Google Scholar]
- Fortuin, C.M.; Kasteleyn, P.W. On the random-cluster model: I. Introduction and relation to other models. Physica 1972, 57, 536–564. [Google Scholar] [CrossRef]
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory, 2nd ed.; Taylor and Francis: London, UK, 1994. [Google Scholar] [CrossRef]
- Grimmett, G. Percolation; Springer: Heidelberg, Germany, 1999. [Google Scholar] [CrossRef]
- Bollobás, B.; Riordan, O. Percolation; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar] [CrossRef]
- Ziff, R.M. Correction-to-scaling exponent for two-dimensional percolation. Phys. Rev. E 2011, 83, 020107. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, T.; Zhou, Z.; Salas, J.; Deng, Y. Correction-to-scaling exponent for percolation and the Fortuin–Kasteleyn Potts model in two dimensions. Phys. Rev. E 2025, 111, 034108. [Google Scholar] [CrossRef]
- Nienhuis, B. Exact critical point and critical exponents of O(n) models in two dimensions. Phys. Rev. Lett. 1982, 49, 1062–1065. [Google Scholar] [CrossRef]
- Batchelor, M.; Blöte, H.W.J. Conformal invariance and critical behavior of the O(n) model on the honeycomb lattice. Phys. Rev. B 1989, 39, 2391–2402. [Google Scholar] [CrossRef]
- Peled, R.; Spinka, Y. Lectures on the Spin and Loop O(n) Models. In Sojourns in Probability Theory and Statistical Physics—I. Spin Glasses and Statistical Mechanics, A Festschrift for Charles M. Newman; Springer Proceedings in Mathematics & Statistics; Sidoravicius, V., Ed.; Springer Nature: Singapore, 2019; Volume 298, pp. 246–320. [Google Scholar] [CrossRef]
- Duminil-Copin, H.; Glazman, A.; Peled, R.; Spinka, Y. Macroscopic loops in the loop O(n) model at Nienhuis’ critical point. J. Eur. Math. Soc. 2021, 23, 315–347. [Google Scholar] [CrossRef]
- Baxter, R.J. q colourings of the triangular lattice. J. Phys. A Math. Gen. 1986, 19, 2821–2839. [Google Scholar] [CrossRef]
- Baxter, R.J. Chromatic polynomials of large triangular lattices. J. Phys. A Math. Gen. 1987, 20, 5241–5261. [Google Scholar] [CrossRef]
- Nienhuis, B. Critical behavior of two-dimensional spin models and charge asymmetry in the Coulomb gas. J. Stat. Phys. 1984, 34, 731. [Google Scholar] [CrossRef]
- Fang, S.; Ke, D.; Zhong, W.; Deng, Y. Backbone and shortest-path exponents of the two-dimensional Q-state Potts model. Phys. Rev. E 2022, 105, 044122. [Google Scholar] [CrossRef]
- Aharony, A.; Asikainen, J. Fractal dimensions and corrections to scaling for critical Potts clusters. Fractals 2003, 11, 3–7. [Google Scholar] [CrossRef]
- Asikainen, J.; Aharony, A.; Mandelbrot, B.B.; Rauch, E.M.; Hovi, J.P. Fractal geometry of critical Potts clusters. Eur. Phys. J. B 2003, 34, 479–487. [Google Scholar] [CrossRef]
- Rebbi, C.; Swendsen, R.H. Monte Carlo renormalization-group studies of q-state Potts models in two dimensions. Phys. Rev. B 1980, 21, 4094–4107. [Google Scholar] [CrossRef]
- Swendsen, R.H.; Andelman, D.; Nihat Berker, A. Critical exponents and marginality of the four-state Potts model: Monte Carlo renormalization group. Phys. Rev. B 1981, 24, 6732–6735. [Google Scholar] [CrossRef]
- Swendsen, R.H.; Nihat Berker, A. Critical behavior of the three-state Potts model: Monte Carlo renormalization group. Phys. Rev. B 1983, 28, 3897–3903. [Google Scholar] [CrossRef]
- Shankar, R.; Gupta, R. Clear evidence of redundant operators in Monte Carlo studies of the Ising model. Phys. Rev. B 1985, 32, 6084–6086. [Google Scholar] [CrossRef]
- Pawley, G.S.; Swendsen, R.H.; Wallace, D.J.; Wilson, K.G. Monte Carlo renormalization-group calculations of critical behavior in the simple-cubic Ising model. Phys. Rev. B 1984, 29, 4030–4040. [Google Scholar] [CrossRef]
- Baillie, C.F.; Gupta, R.; Hawick, K.A.; Pawley, G.S. Monte Carlo renormalization-group study of the three-dimensional Ising model. Phys. Rev. B 1992, 45, 10438–10453. [Google Scholar] [CrossRef]
- Baxter, R.J. Potts model at the critical temperature. J. Phys. C Solid State Phys. 1983, 6, L445–L448. [Google Scholar] [CrossRef]
- Nienhuis, B.; Berker, A.N.; Riedel, E.K.; Schick, M. First- and second-order phase transitions in Potts models: Renormalization-group solution. Phys. Rev. Lett. 1979, 43, 737–740. [Google Scholar] [CrossRef]
- Nienhuis, B.; Riedel, E.K.; Schick, M. Variational renormalisation-group approach to the q-state Potts model in two dimensions. J. Phys. A Math. Gen. 1980, 13, L31. [Google Scholar] [CrossRef]
- Murata, K.K. Hamiltonian formulation of site percolation in a lattice gas. J. Phys. A Math. Gen. 1979, 12, 81. [Google Scholar] [CrossRef]
- Janke, W.; Schakel, M.J. Geometrical vs. Fortuin–Kasteleyn clusters in the two-dimensional q-state Potts model. Nucl. Phys. B 2004, 700, 385–406. [Google Scholar] [CrossRef][Green Version]
- Deng, Y.; Heringa, J.R.; Blöte, H.W.J. Constrained tricritical phenomena in two dimensions. Phys. Rev. E 2005, 71, 036115. [Google Scholar] [CrossRef]
- Qian, X.; Deng, Y.; Blöte, H.W.J. Dilute Potts model in two dimensions. Phys. Rev. E 2005, 72, 056132. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Nienhuis, B.; Nauenberg, M. First-order phase transitions in renormalization-group theory. Phys. Rev. Lett. 1975, 45, 777–779. [Google Scholar] [CrossRef]
- Klein, W.; Wallace, D.J.; Zia, R.K.P. Essential singularities at first-order phase transitions. Phys. Rev. Lett. 1976, 37, 639–642. [Google Scholar] [CrossRef]
- Fisher, M.E.; Berker, N.H. Scaling for first-order transitions in thermodynamic and finite systems. Phys. Rev. B 1978, 26, 2507–2513. [Google Scholar] [CrossRef]
- Caselle, M.; Grinza, P.; Magnoli, N. Correction induced by irrelevant operators in the correlators of the two-dimensional Ising model in a magnetic field. J. Phys. A Math. Gen. 2001, 34, 8733. [Google Scholar] [CrossRef]
- Caselle, M.; Hasenbusch, M.; Pelissetto, A.; Vicari, E. Irrelevant operators in the two-dimensional Ising model. J. Phys. A Math. Gen. 2002, 35, 4861. [Google Scholar] [CrossRef]

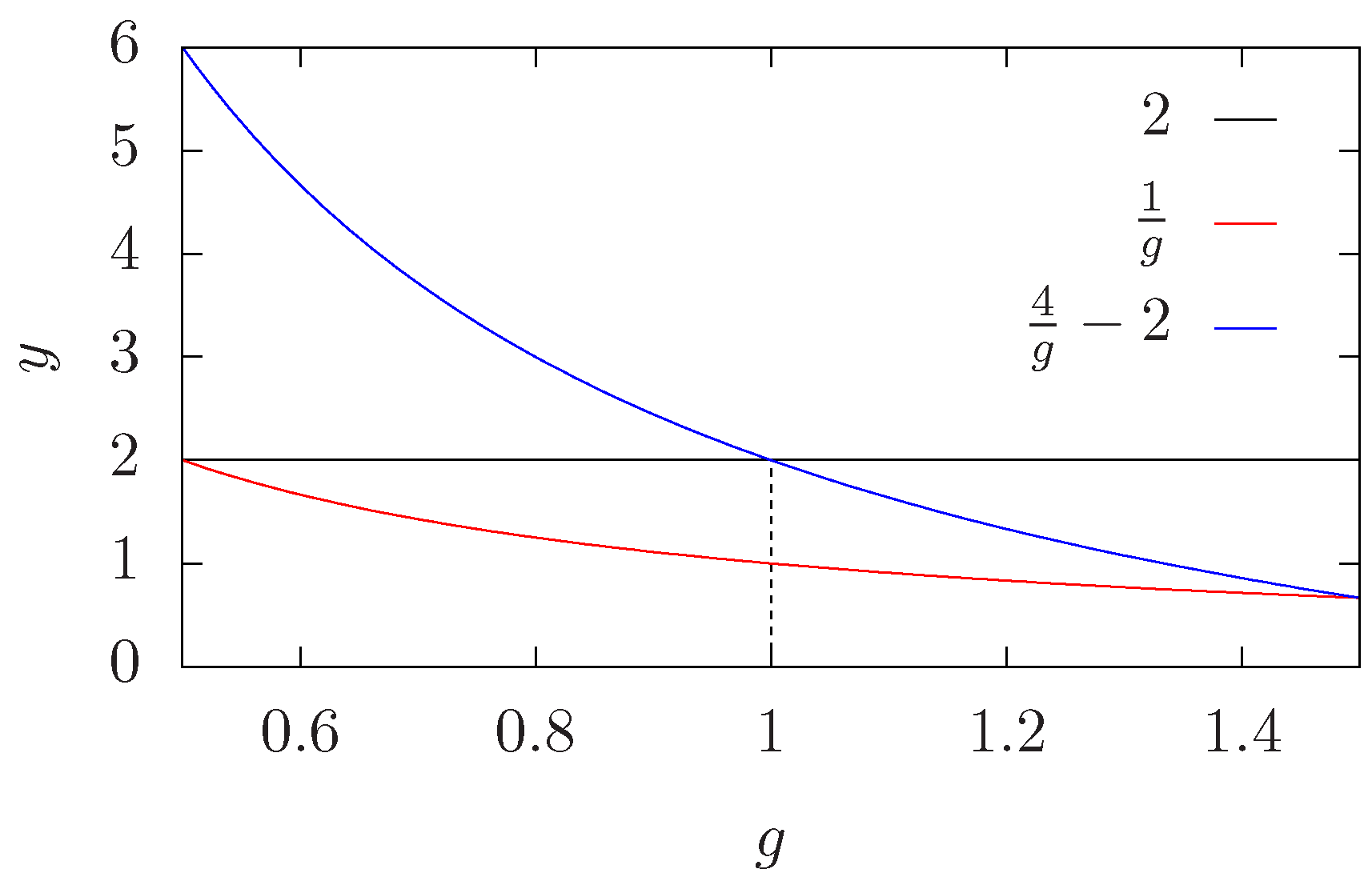




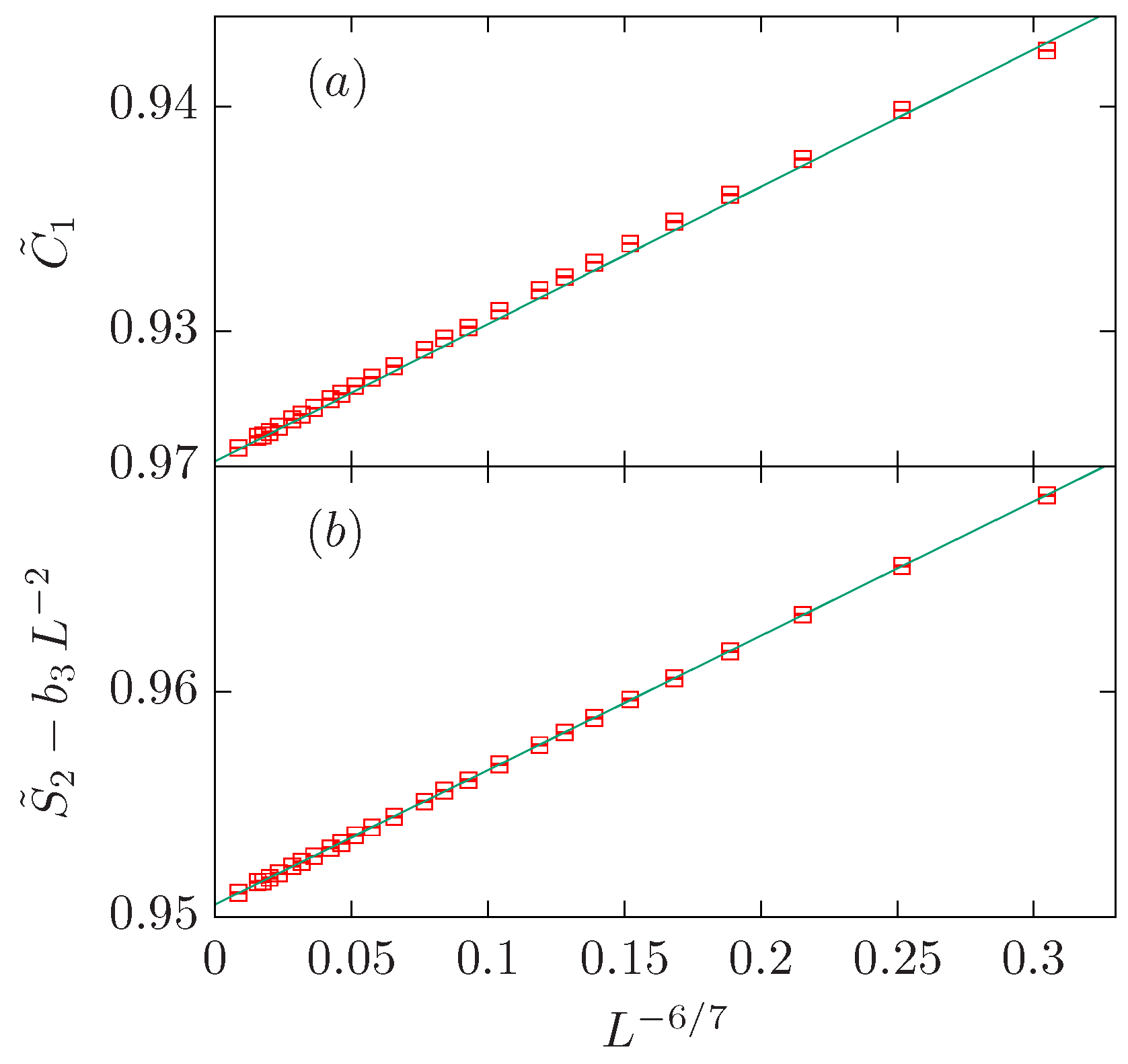
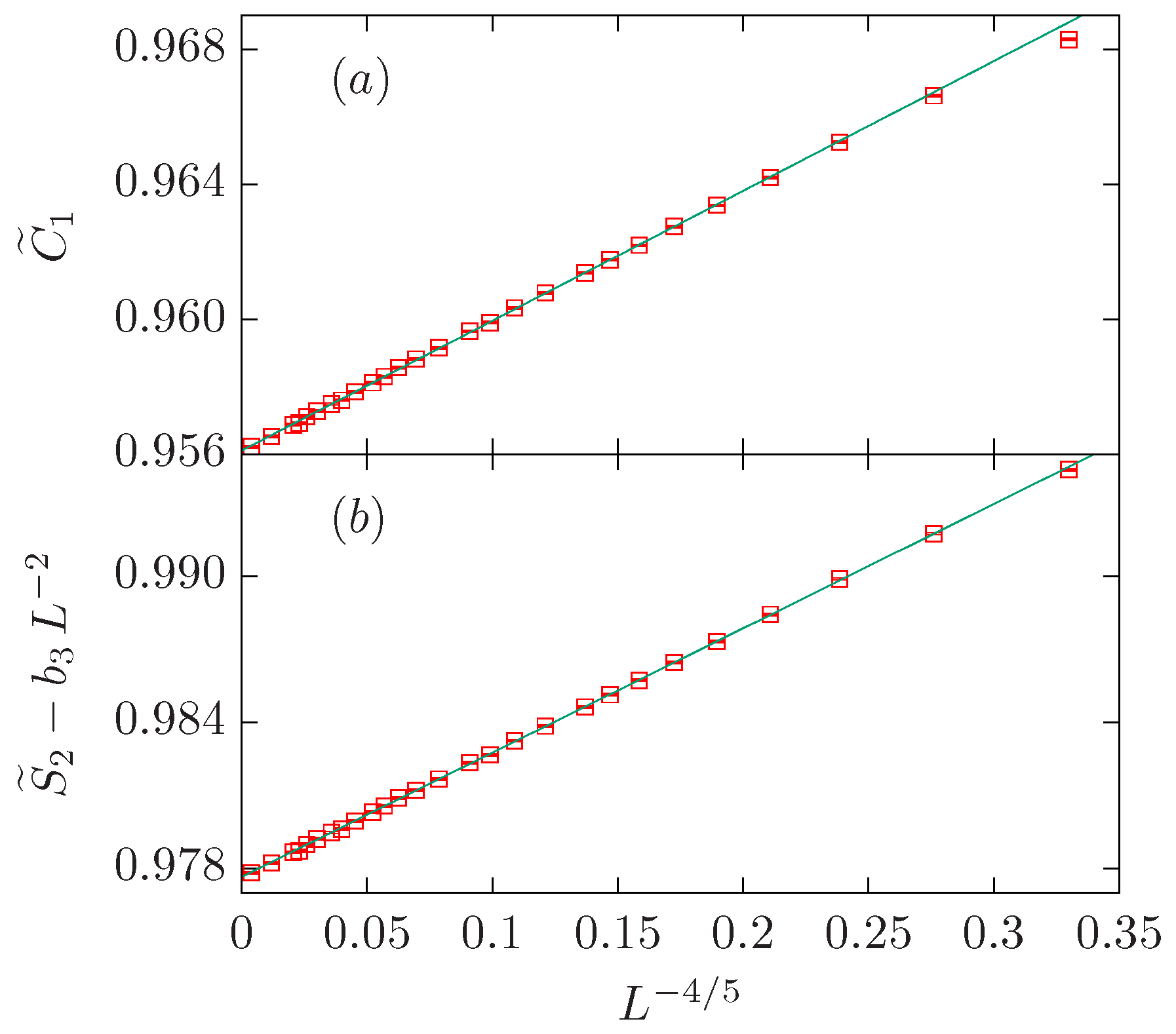
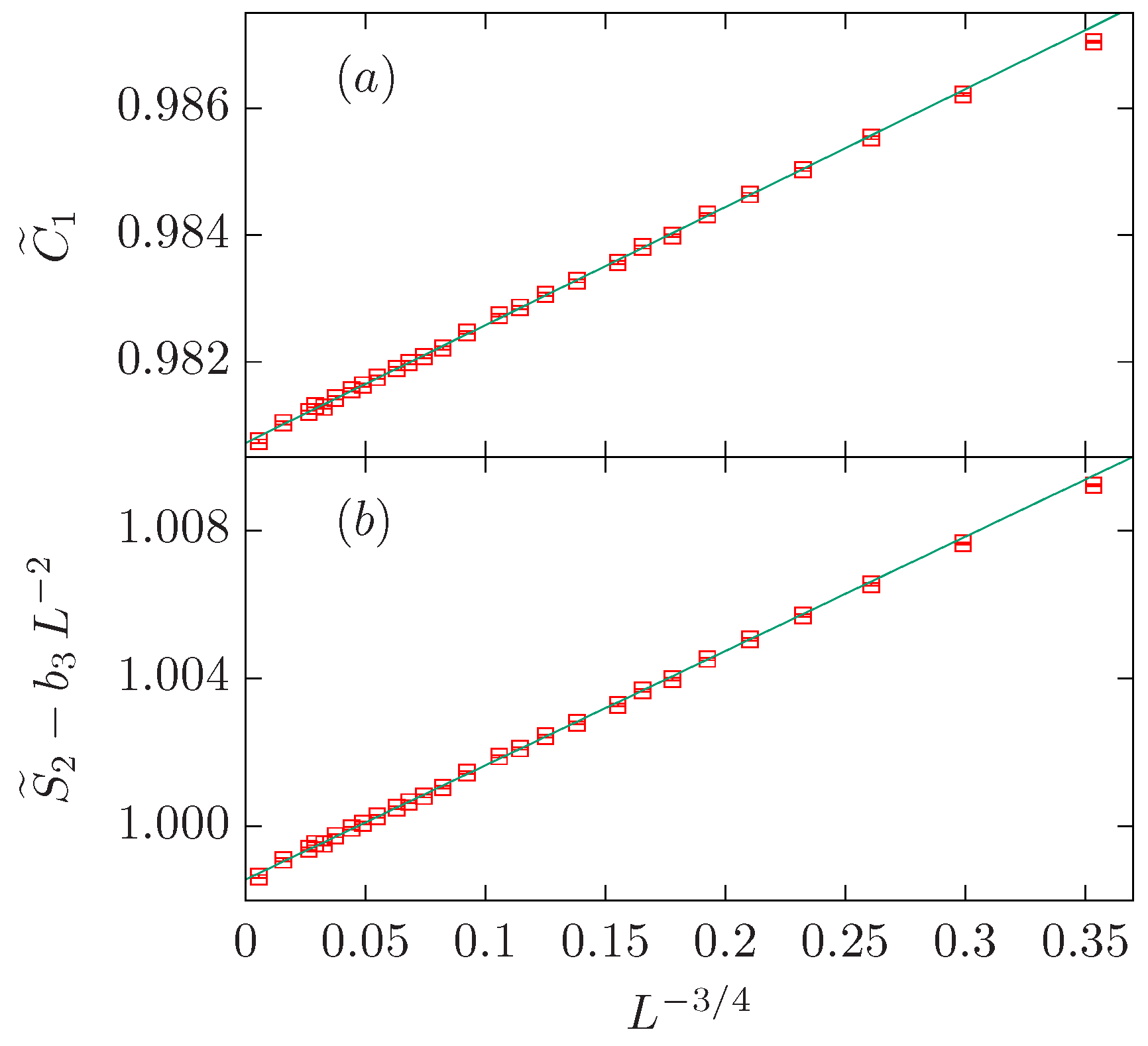

| Critical | Tricritical | |||||||
|---|---|---|---|---|---|---|---|---|
| g | 1 | |||||||
| 1 | ||||||||
| 0 | 1 | |||||||
| 1 | ||||||||
| Fits for on the Dense Branch | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 28 | 0.655033(7) | 0.304(9) | 1.383(9) | 0 | 0 | 6.9/9 | |||
| 12 | 0.655045(6) | 0.60(4) | 1.50(1) | −0.57(6) | 91/48 | 0 | 10.0/14 | ||
| 16 | 0.655052(8) | 0.58(7) | 1.50(2) | 0 | −0.7(1) | 2 | 7.1/12 | ||
| 12 | 0.655045(6) | 0.61(2) | 3/2 | −0.6(3) | 91/48 | 0.1(3) | 2 | 10.0/14 | |
| 12 | 0.655046(3) | 0.602(2) | 3/2 | −0.582(6) | 91/48 | 0 | 10.0/15 | ||
| 24 | 0.70729(1) | −0.175(10) | 1.31(2) | 0 | 0 | 7.5/10 | |||
| 7 | 0.707245(9) | −0.67(4) | 1.55(1) | 0.87(5) | 43/24 | 0 | 12.0/19 | ||
| 7 | 0.707251(9) | −0.46(2) | 1.50(1) | 0 | 0.68(3) | 2 | 11.4/19 | ||
| 7 | 0.707250(8) | −0.46(2) | 3/2 | 0.00(8) | 43/24 | 0.68(7) | 2 | 11.4/19 | |
| 7 | 0.707250(5) | −0.458(1) | 3/2 | 0 | 0.679(3) | 2 | 11.4/20 | ||
| Fits for the Dense Branch | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 40 | 0.709702(6) | 0.258(8) | 1.269(8) | 0 | 0 | 0.56/7 | ||||
| 9 | 0.709702(5) | 0.346(8) | 1.317(5) | −0.30(1) | 15/8 | 0 | 10.3/18 | |||
| 10 | 0.709701(5) | 0.316(7) | 1.304(5) | 0 | −0.31(2) | 2 | 6.9/17 | |||
| 9 | 0.709703(4) | 0.383(4) | 4/3 | −0.59(7) | 15/8 | 0.27(8) | 2 | 8.3/18 | ||
| 10 | 0.709711(3) | 0.3724(7) | 4/3 | −0.348(3) | 15/8 | 0 | 9.5/18 | |||
| 28 | 0.774568(9) | −0.179(6) | 1.22(1) | 0 | 0 | 6.3/10 | ||||
| 12 | 0.774550(9) | −0.47(5) | 1.39(2) | 0.55(6) | 7/4 | 0 | 7.0/15 | |||
| 6 | 0.774550(6) | −0.309(4) | 1.332(4) | 0 | 0.494(7) | 2 | 15.2/21 | |||
| 5 | 0.774552(5) | −0.313(3) | 4/3 | 0.02(1) | 7/4 | 0.47(1) | 2 | 16.7/22 | ||
| 6 | 0.774548(3) | −0.3098(3) | 4/3 | 0 | 0.496(1) | 2 | 15.3/22 | |||
| 24 | 0.758498(9) | 0.192(3) | 1.141(6) | 0 | 0 | 12.6/11 | ||||
| 10 | 0.758516(9) | 0.258(9) | 1.201(9) | −0.23(3) | 28/15 | 0 | 14.8/17 | |||
| 10 | 0.758512(9) | 0.237(7) | 1.186(8) | 0 | −0.23(2) | 2 | 15.4/17 | |||
| 10 | 0.758515(8) | 0.257(4) | 6/5 | −0.2(1) | 28/15 | 0.0(1) | 2 | 14.9/17 | ||
| 10 | 0.758515(5) | 0.2569(7) | 6/5 | −0.226(3) | 28/15 | 0 | 14.9/18 | |||
| 24 | 0.82358(1) | −0.110(3) | 1.084(9) | 0 | 0 | 12.9/11 | ||||
| 7 | 0.823531(9) | −0.265(9) | 1.257(8) | 0.35(1) | 26/15 | 0 | 16.5/20 | |||
| 9 | 0.82354(1) | −0.177(6) | 1.191(9) | 0 | 0.32(2) | 2 | 12.9/18 | |||
| 9 | 0.82354(8) | −0.187(4) | 6/5 | 0.04(4) | 26/15 | 0.29(5) | 2 | 13.1/18 | ||
| 9 | 0.823532(5) | −0.1831(5) | 6/5 | 0 | 0.338(3) | 2 | 13.9/19 | |||
| a | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Fits for the O loop model | |||||||||
| 24 | 0.84673(3) | 0.120(4) | 0.97(1) | 0 | 0 | 10.4/10 | |||
| 7 | 0.84673(2) | 0.127(4) | 0.98(1) | −0.06(1) | 15/8 | 0 | 18.4/19 | ||
| 7 | 0.84673(2) | 0.124(3) | 0.979(9) | 0 | −0.06(1) | 2 | 18.5/19 | ||
| 8 | 0.84674(2) | 0.137(2) | 1 | −0.3(1) | 15/8 | 0.3(1) | 2 | 16.2/18 | |
| 10 | 0.84676(1) | 0.1345(6) | 1 | −0.082(5) | 15/8 | 0 | 15.5/17 | ||
| 9 | 0.891851(4) | 0.079(9) | 2.01(5) | 0 | 0 | 16.1/18 | |||
| 8 | 0.89183(1) | 0.003(1) | 1 | −0.09(3) | 7/4 | 0.20(5) | 2 | 13.5/18 | |
| 9 | 0.891850(4) | 0 | 0.000(8) | 7/4 | 0.08(1) | 2 | 16.1/18 | ||
| 9 | 0.891850(3) | 0 | 0 | 0.0775(9) | 2 | 16.1/19 | |||
| Fits for the O loop model on the dilute branch | |||||||||
| 8 | 0.92423(3) | 0.0610(6) | 0.838(5) | 0 | 0 | 14.6/19 | |||
| 6 | 0.92431(4) | 0.069(3) | 0.88(1) | −0.029(6) | 40/21 | 0 | 11.6/20 | ||
| 6 | 0.92430(4) | 0.068(2) | 0.87(1) | 0 | −0.031(8) | 2 | 11.6/20 | ||
| 6 | 0.92428(2) | 0.064(1) | 6/7 | 0.1(1) | 40/21 | −0.2(1) | 2 | 14.7/20 | |
| 20 | 0.92428(1) | 0.0639(4) | 6/7 | 0 | 0 | 5.52/12 | |||
| 8 | 0.95050(3) | 0.0542(7) | 0.827(7) | 0 | 0 | 13.2/19 | |||
| 4 | 0.95059(3) | 0.064(2) | 0.88(1) | −0.031(4) | 38/21 | 0 | 10.6/22 | ||
| 4 | 0.95063(4) | 0.080(5) | 0.93(2) | −0.043(7) | 10/7 | 0 | 11.1/22 | ||
| 4 | 0.95058(3) | 0.061(2) | 0.87(1) | 0 | −0.031(4) | 2 | 10.6/22 | ||
| 4 | 0.95056(2) | 0.0590(8) | 6/7 | 0.02(2) | 38/21 | −0.05(3) | 2 | 10.7/22 | |
| 4 | 0.95057(2) | 0.059(1) | 6/7 | 0.006(7) | 10/7 | −0.036(9) | 2 | 10.6/22 | |
| 4 | 0.95055(1) | 0.0597(2) | 6/7 | 0 | −0.028(1) | 2 | 11.4/23 | ||
| Fits for the Dilute Branch | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 0.95603(2) | 0.0372(3) | 0.779(4) | 0 | 0 | 15.4/23 | ||||
| 5 | 0.95604(3) | 0.037(1) | 0.78(1) | 0.00(4) | 77/40 | 0 | 15.4/22 | |||
| 5 | 0.95604(3) | 0.037(1) | 0.78(1) | 0 | 0.00(4) | 2 | 15.4/22 | |||
| 5 | 0.95606(2) | 0.0401(6) | 4/5 | −0.13(8) | 77/40 | 0.13(9) | 2 | 15.4/22 | ||
| 20 | 0.95606(2) | 0.0396(4) | 4/5 | 0 | 0 | 9.60/13 | ||||
| 20 | 0.97761(5) | 0.050(3) | 0.79(2) | 0 | 0 | 10.4/12 | ||||
| 5 | 0.97760(4) | 0.051(2) | 0.79(1) | −0.027(5) | 37/20 | 0 | 16.8/22 | |||
| 8 | 0.97763(6) | 0.08(2) | 0.86(5) | −0.04(2) | 6/5 | 0 | 13.7/19 | |||
| 5 | 0.97759(4) | 0.049(2) | 0.79(1) | 0 | −0.029(6) | 2 | 16.9/22 | |||
| 6 | 0.97759(3) | 0.053(1) | 4/5 | −0.14(7) | 37/20 | 0.14(9) | 2 | 14.3/21 | ||
| 6 | 0.97758(3) | 0.055(2) | 4/5 | −0.013(8) | 6/5 | −0.01(1) | 2 | 15.0/21 | ||
| 7 | 0.97762(2) | 0.0516(4) | 4/5 | 0 | −0.039(4) | 2 | 15.6/21 | |||
| 1 | 10 | 0.98067(3) | 0.0174(6) | 0.72(2) | 0 | 0 | 16.4/18 | |||
| 5 | 0.98069(4) | 0.018(1) | 0.73(2) | 0.000(4) | 187/96 | 0 | 21.2/22 | |||
| 5 | 0.98069(3) | 0.018(1) | 0.73(2) | 0 | 0.000(4) | 2 | 21.2/22 | |||
| 8 | 0.98068(3) | 0.0200(9) | 3/4 | −0.5(3) | 187/96 | 0.5(3) | 2 | 18.8/19 | ||
| 14 | 0.98071(1) | 0.0187(2) | 3/4 | 0 | 0 | 15.7/16 | ||||
| 14 | 0.99850(6) | 0.027(1) | 0.70(2) | 0 | 0 | 13.6/15 | ||||
| 6 | 0.99854(6) | 0.030(2) | 0.73(3) | −0.021(7) | 91/48 | 0 | 21.1/21 | |||
| 4 | 0.99857(5) | 0.032(1) | 0.75(2) | 0 | −0.033(4) | 2 | 22.8/22 | |||
| 4 | 0.99858(3) | 0.0307(6) | 3/4 | 0.04(5) | 91/48 | −0.07(6) | 2 | 22.3/23 | ||
| 4 | 0.99858(4) | 0.030(2) | 3/4 | 0.001(4) | 1 | −0.034(5) | 2 | 22.7/23 | ||
| 4 | 0.99856(2) | 0.0312(2) | 3/4 | 0 | −0.032(1) | 2 | 22.8/24 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Salas, J.; Deng, Y. Finite-Size Corrections from the Subleading Magnetic Scaling Field for the Ising and Potts Models in Two Dimensions. Entropy 2025, 27, 418. https://doi.org/10.3390/e27040418
Xu Y, Salas J, Deng Y. Finite-Size Corrections from the Subleading Magnetic Scaling Field for the Ising and Potts Models in Two Dimensions. Entropy. 2025; 27(4):418. https://doi.org/10.3390/e27040418
Chicago/Turabian StyleXu, Yihao, Jesús Salas, and Youjin Deng. 2025. "Finite-Size Corrections from the Subleading Magnetic Scaling Field for the Ising and Potts Models in Two Dimensions" Entropy 27, no. 4: 418. https://doi.org/10.3390/e27040418
APA StyleXu, Y., Salas, J., & Deng, Y. (2025). Finite-Size Corrections from the Subleading Magnetic Scaling Field for the Ising and Potts Models in Two Dimensions. Entropy, 27(4), 418. https://doi.org/10.3390/e27040418






