Applications of Percolation Theory to Prevent the Propagation of Phytopathogens and Pests on Plantations
Abstract
1. Introduction
2. Monoculture Plantations
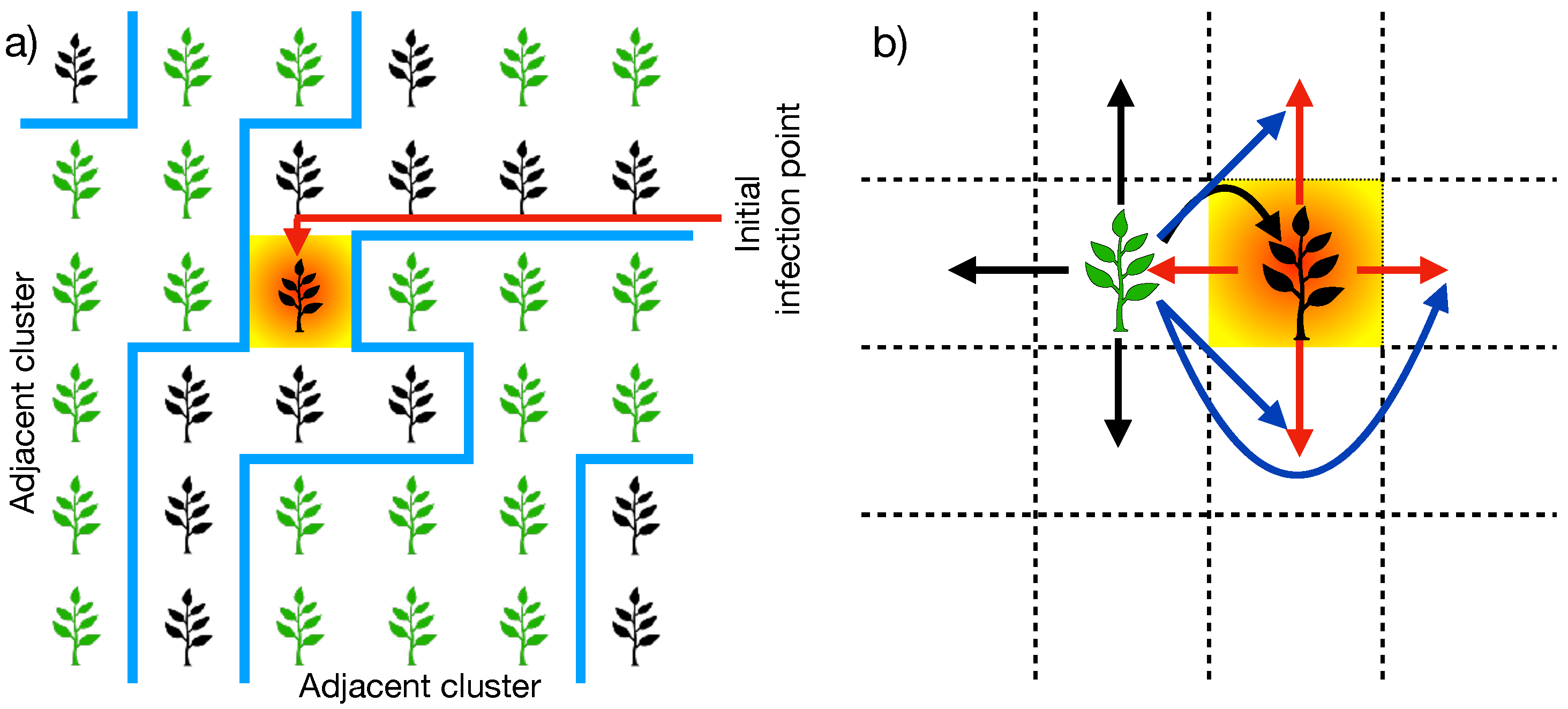
3. Zoospores’ Mobility Affects the Plantation Connectivity
4. Agroecological Strategies, Simulation, and Data Analysis
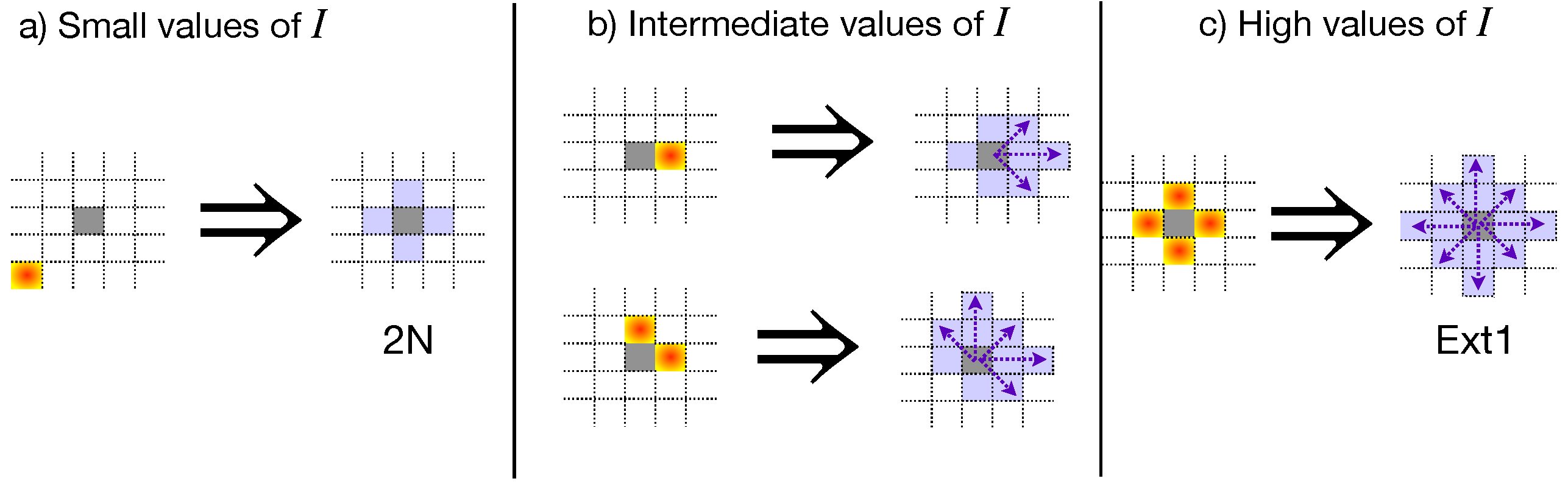
4.1. Agroecological Strategies
4.2. Simulation and Data Analysis
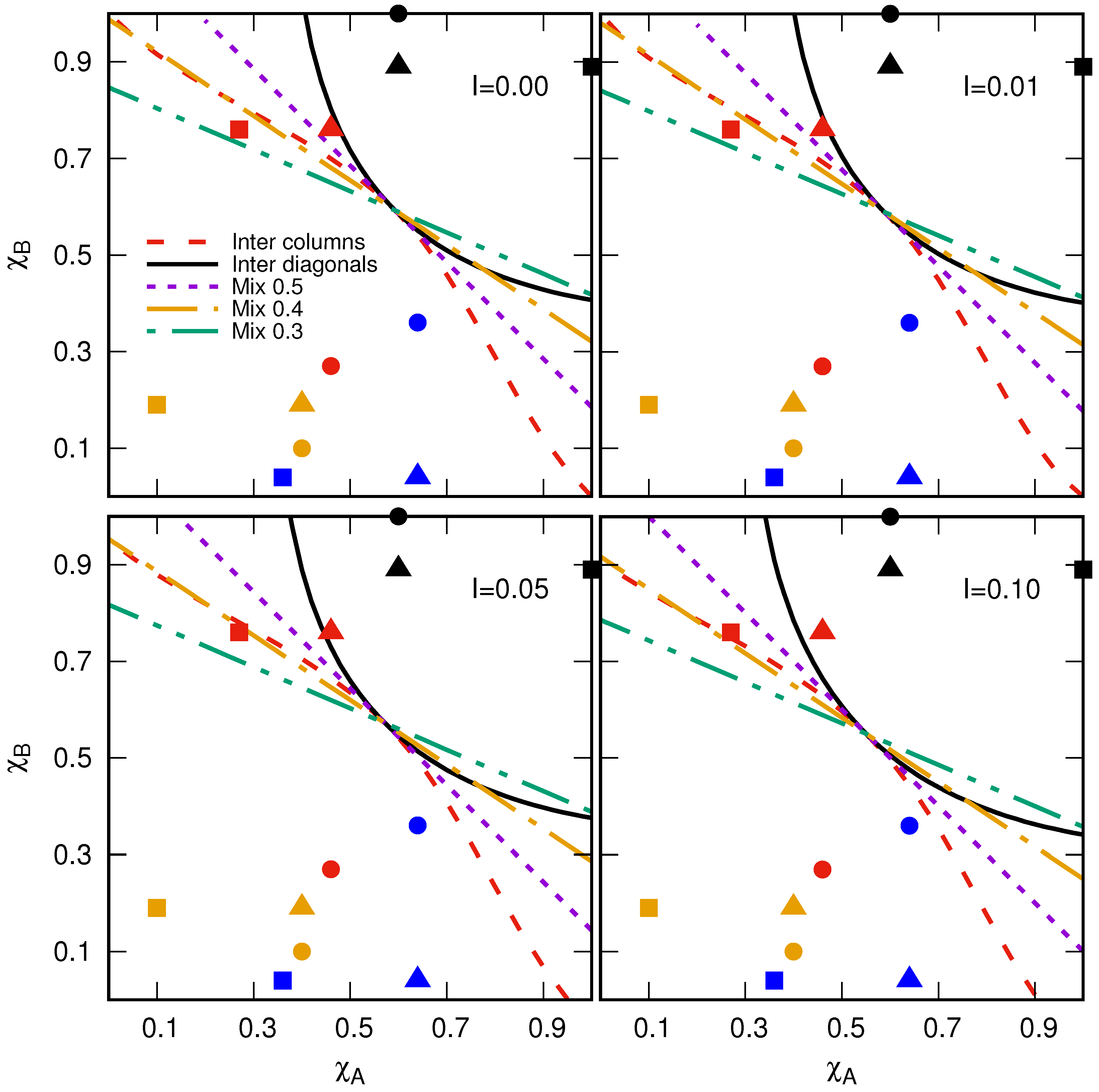
5. Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory; Taylor & Francis: Abingdon, UK, 2014. [Google Scholar] [CrossRef]
- Hammersley, J.M. Percolation. In Proceedings of the Biological Growth and Spread; Jäger, W., Rost, H., Tautu, P., Eds.; Springer: Berlin/Heidelberg, Germany, 1980; pp. 484–494. [Google Scholar] [CrossRef]
- Essam, J.W. Percolation theory. Rep. Prog. Phys. 1980, 43, 833. [Google Scholar] [CrossRef]
- Grimmett, G. Percolation; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar] [CrossRef]
- Binder, K. Theory of first-order phase transitions. Rep. Prog. Phys. 1987, 50, 783. [Google Scholar] [CrossRef]
- Sahimi, M. Applications of Percolation Theory; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar] [CrossRef]
- Ėfros, A.L. Physics and Geometry of Disorder: Percolation Theory; Science for Everyone; Mir Publishers: Moscow, Russia, 1986. [Google Scholar]
- Saberi, A.A. Recent advances in percolation theory and its applications. Phys. Rep. 2015, 578, 1–32. [Google Scholar] [CrossRef]
- D’Souza, R.M.; Gómez-Gardeñes, J.; Nagler, J.; Arenas, A. Explosive phenomena in complex networks. Adv. Phys. 2019, 68, 123–223. [Google Scholar] [CrossRef]
- Braun, M.A.; Dias de Deus, J.; Hirsch, A.S.; Pajares, C.; Scharenberg, R.P.; Srivastava, B.K. De-Confinement and Clustering of Color Sources in Nuclear Collisions. Phys. Rep. 2015, 599, 1–50. [Google Scholar] [CrossRef]
- Waheed, A.; Furlan, G. Aspects of quark-gluon plasma. Riv. Nuovo Cim. 1996, 19, 1–34. [Google Scholar] [CrossRef]
- Ramírez, J.E.; Díaz, B.; Pajares, C. Interacting color strings as the origin of the liquid behavior of the quark-gluon plasma. Phys. Rev. D 2021, 103, 094029. [Google Scholar] [CrossRef]
- Texca García, J.C.; Rosales Herrera, D.; Ramírez, J.E.; Fernández Téllez, A.; Pajares, C. Percolation leads to finite-size effects on the transition temperature and center-of-mass energy required for quark-gluon plasma formation. Phys. Rev. D 2022, 106, L031503. [Google Scholar] [CrossRef]
- Satz, H. Deconfinement and percolation. Nucl. Phys. A 1998, 642, c130–c142. [Google Scholar] [CrossRef]
- Satz, H. Cluster percolation and thermal critical behavior. Comput. Phys. Commun. 2002, 147, 46–51. [Google Scholar] [CrossRef]
- Rosales Herrera, D.; Ramírez, J.E.; Velázquez-Castro, J.; Díaz, B.; Martínez, M.I.; Vázquez Juárez, P.; Fernández Téllez, A. Estrategias de movilidad basadas en la teoría de percolación para evitar la diseminación de enfermedades: COVID-19. Rev. Mex. Fis. 2022, 68, 011701. [Google Scholar]
- Erwin, D. Phytophthora Diseases Worldwide; American Phytopathological Society: St Paul, MN, USA, 1996. [Google Scholar] [CrossRef]
- Bernhardt, E.; Grogan, R. Effect of soil matric potential on the formation and indirect germination of sporangia of Phytophthora parasitica, P. capsici and P. cryptogea. Phytopathology 1982, 72, 507–511. [Google Scholar] [CrossRef]
- Ownley, B.H.; Trigiano, R.N. Plant Pathology Concepts and Laboratory Exercises; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar] [CrossRef]
- Ploetz, R.C.; Haynes, J.L. How does Phytophthora capsici survive in squash fields in southeastern Florida during the off-season. Proc. Fla. State Hortic. Soc. 2000, 113, 211–215. [Google Scholar]
- Hardham, A.R. Phytophthora cinnamomi. Mol. Plant Path. 2005, 6, 589–604. [Google Scholar] [CrossRef]
- Roy, S.; Muraleedharan, N.; Mukhopadhyay, A. The red spider mite, Oligonychus coffeae (Acari: Tetranychidae): Its status, biology, ecology and management in tea plantations. Exp. Appl. Acarol. 2014, 63, 431–463. [Google Scholar] [CrossRef] [PubMed]
- Fry, W.E.; Goodwin, S.B. Re-emergence of potato and tomato late blight in the United States. Plant Dis. 1997, 81, 1349–1357. [Google Scholar] [CrossRef]
- Gevens, A.; Donahoo, R.; Lamour, K.; Hausbeck, M. Characterization of Phytophthora capsici from Michigan surface irrigation water. Phytopathology 2007, 97, 421–428. [Google Scholar] [CrossRef]
- Lamour, K. Phytophthora: A Global Perspective; Cabi: Wallingford, UK, 2013. [Google Scholar] [CrossRef]
- Power, J.; Follett, R. Monoculture. Sci. Am. 1987, 256, 78–87. [Google Scholar] [CrossRef]
- Ramírez, J.E.; Molina-Gayosso, E.; Lozada-Lechuga, J.; Flores-Rojas, L.M.; Martínez, M.I.; Fernández Téllez, A. Percolation strategy to improve the production of plants with high pathogen susceptibility. Phys. Rev. E 2018, 98, 062409. [Google Scholar] [CrossRef]
- Gilardi, G.; Baudino, M.; Moizio, M.; Pugliese, M.; Garibaldi, A.; Gullino, M. Integrated management of Phytophthora capsici on bell pepper by combining grafting and compost treatment. Crop Prot. 2013, 53, 13–19. [Google Scholar] [CrossRef]
- Newman, M.E.J.; Ziff, R.M. Efficient Monte Carlo Algorithm and High-Precision Results for Percolation. Phys. Rev. Lett. 2000, 85, 4104–4107. [Google Scholar] [CrossRef]
- Jacobsen, J.L. Critical points of Potts and O(N) models from eigenvalue identities in periodic Temperley–Lieb algebras. J. Phys. A-Math. Theor. 2015, 48, 454003. [Google Scholar] [CrossRef]
- Rosales Herrera, D.; Ramírez, J.E.; Martínez, M.I.; Cruz-Suárez, H.; Fernández Téllez, A.; López-Olguín, J.F.; Aragón García, A. Percolation-intercropping strategies to prevent dissemination of phytopathogens on plantations. Chaos 2021, 31, 063105. [Google Scholar] [CrossRef]
- Ramírez, J.E.; Pajares, C.; Martínez, M.I.; Rodriguez Fernandez, R.; Molina-Gayosso, E.; Lozada-Lechuga, J.; Fernandez Tellez, A. Site-bond percolation solution to preventing the propagation of P hytophthora zoospores on plantations. Phys. Rev. E 2020, 101, 032301. [Google Scholar] [CrossRef] [PubMed]
- Rosales Herrera, D.; Velázquez-Castro, J.; Fernández Téllez, A.; López-Olguín, J.F.; Ramírez, J.E. Site percolation threshold of composite square lattices and its agroecology applications. Phys. Rev. E 2024, 109, 014304. [Google Scholar] [CrossRef] [PubMed]
- Bermeo, A.; Couturier, S.; Galeana Pizaña, M. Conservation of traditional smallholder cultivation systems in indigenous territories: Mapping land availability for milpa cultivation in the Huasteca Poblana, Mexico. Appl. Geogr. 2014, 53, 299–310. [Google Scholar] [CrossRef]
- Newman, M.E.J.; Ziff, R.M. Fast Monte Carlo algorithm for site or bond percolation. Phys. Rev. E 2001, 64, 016706. [Google Scholar] [CrossRef]
- Rintoul, M.D.; Torquato, S. Precise determination of the critical threshold and exponents in a three-dimensional continuum percolation model. J. Phys. A-Math. Gen. 1997, 30, L585–L592. [Google Scholar] [CrossRef]
- Stauffer, D. Scaling theory of percolation clusters. Phys. Rep. 1979, 54, 1–74. [Google Scholar] [CrossRef]
- Sahimi, M. On the relationship between the critical exponents of percolation conductivity and static exponents of percolation. J. Phys. A-Math. Gen. 1984, 17, L601. [Google Scholar] [CrossRef]
- Scholl, F.; Binder, K. Selective sublattice dilution in ordered magnetic compounds: A new kind of percolation problem. Z. Phys. B Con. Mat. 1980, 39, 239–247. [Google Scholar] [CrossRef]
- Wattendorff, J.; Wessel, S. Sublattice-selective percolation on bipartite planar lattices. Phys. Rev. E 2024, 109, 044108. [Google Scholar] [CrossRef] [PubMed]



| Oomycete | |||
|---|---|---|---|
| PcV01 | 0.60 | 1.0 | 0.89 |
| PcV51 | 0.46 | 0.27 | 0.76 |
| PcV77 | 0.64 | 0.36 | 0.04 |
| PcV90 | 0.40 | 0.10 | 0.19 |
| Blank test | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alonso Tlali, J.; Alvarado García, J.R.; Cardenas Castro, B.; Fernández Téllez, A.; García Prieto, E.G.; López-Olguín, J.F.; Martínez Laguna, Y.; Ramírez, J.E.; Rosales Herrera, D.; Silva Montiel, J.D. Applications of Percolation Theory to Prevent the Propagation of Phytopathogens and Pests on Plantations. Entropy 2025, 27, 386. https://doi.org/10.3390/e27040386
Alonso Tlali J, Alvarado García JR, Cardenas Castro B, Fernández Téllez A, García Prieto EG, López-Olguín JF, Martínez Laguna Y, Ramírez JE, Rosales Herrera D, Silva Montiel JD. Applications of Percolation Theory to Prevent the Propagation of Phytopathogens and Pests on Plantations. Entropy. 2025; 27(4):386. https://doi.org/10.3390/e27040386
Chicago/Turabian StyleAlonso Tlali, J., J. R. Alvarado García, B. Cardenas Castro, A. Fernández Téllez, E. G. García Prieto, J. F. López-Olguín, Y. Martínez Laguna, J. E. Ramírez, D. Rosales Herrera, and J. D. Silva Montiel. 2025. "Applications of Percolation Theory to Prevent the Propagation of Phytopathogens and Pests on Plantations" Entropy 27, no. 4: 386. https://doi.org/10.3390/e27040386
APA StyleAlonso Tlali, J., Alvarado García, J. R., Cardenas Castro, B., Fernández Téllez, A., García Prieto, E. G., López-Olguín, J. F., Martínez Laguna, Y., Ramírez, J. E., Rosales Herrera, D., & Silva Montiel, J. D. (2025). Applications of Percolation Theory to Prevent the Propagation of Phytopathogens and Pests on Plantations. Entropy, 27(4), 386. https://doi.org/10.3390/e27040386








