Minimizing System Entropy: A Dual-Phase Optimization Approach for EV Charging Scheduling
Abstract
1. Introduction
- A novel entropy-driven objective function that explicitly links voltage deviations, line overloads, and user dissatisfaction to system disorder, providing a unified metric for optimization.
- A hybrid PSO-Q-learning architecture that combines global scheduling (via PSO) with real-time adjustments (via Q-learning), tailored to rural grids’ high-resistance lines and variable loads.
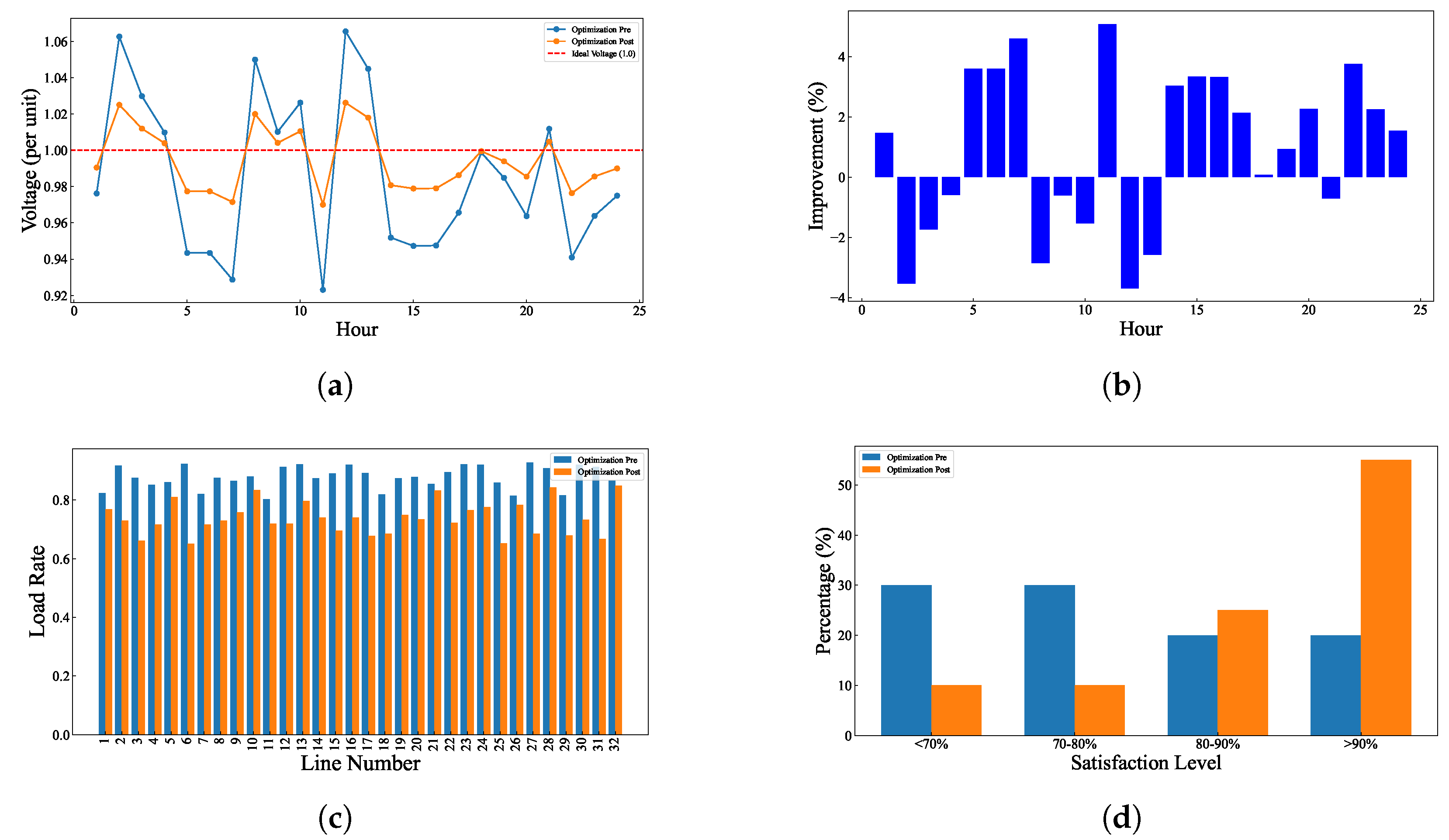
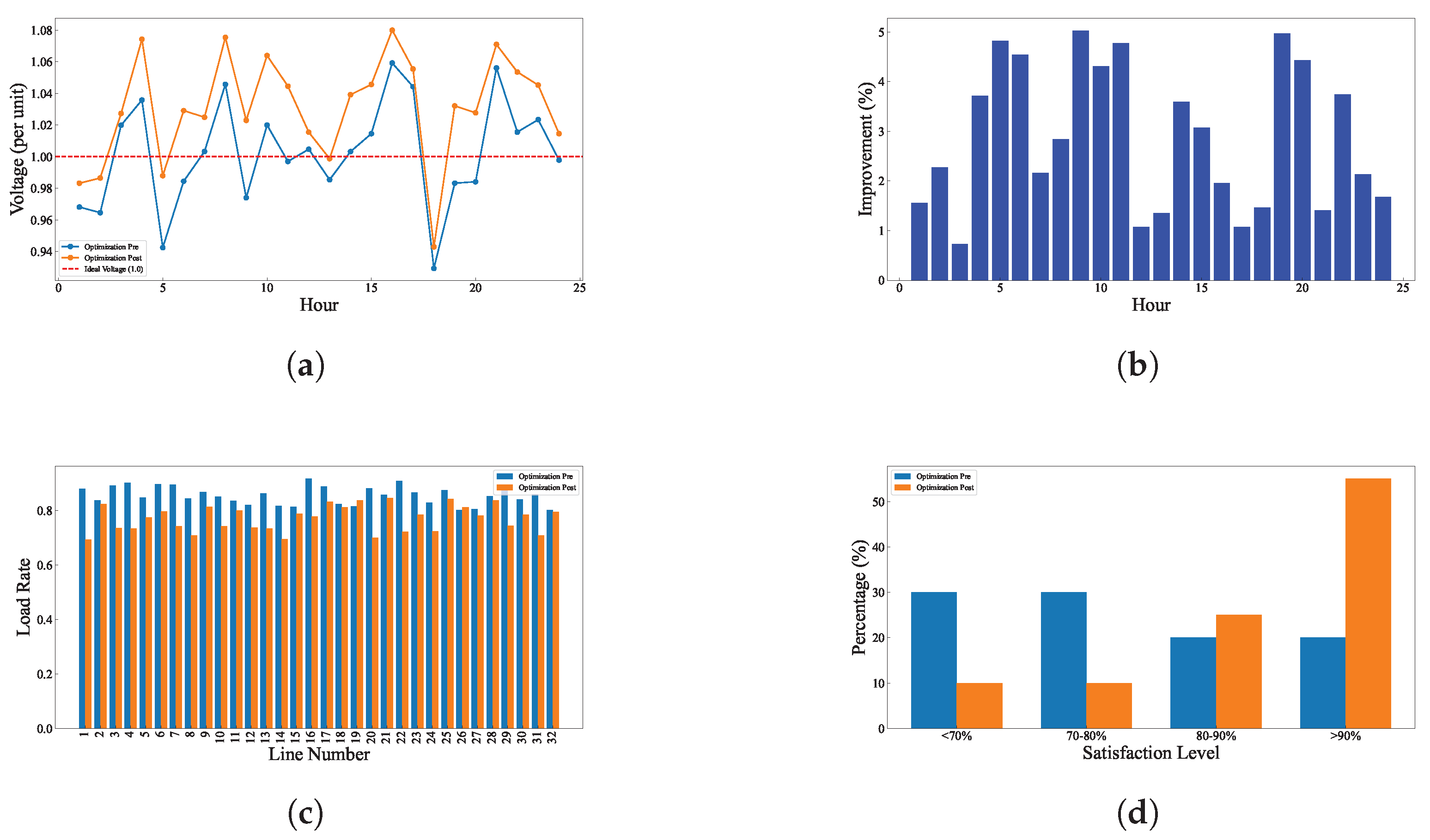
- Comprehensive validation under both baseline and high-stress scenarios, demonstrating significant improvements in voltage stability (65.5% reduction in deviation), load balancing, and user satisfaction compared to state-of-the-art methods.
2. Related Work
2.1. Electric Vehicle Charging Scheduling
2.2. Smart Grid and Multi-Objective Optimization
2.3. Challenges and Future Directions
3. Entropy-Guided Optimization Method
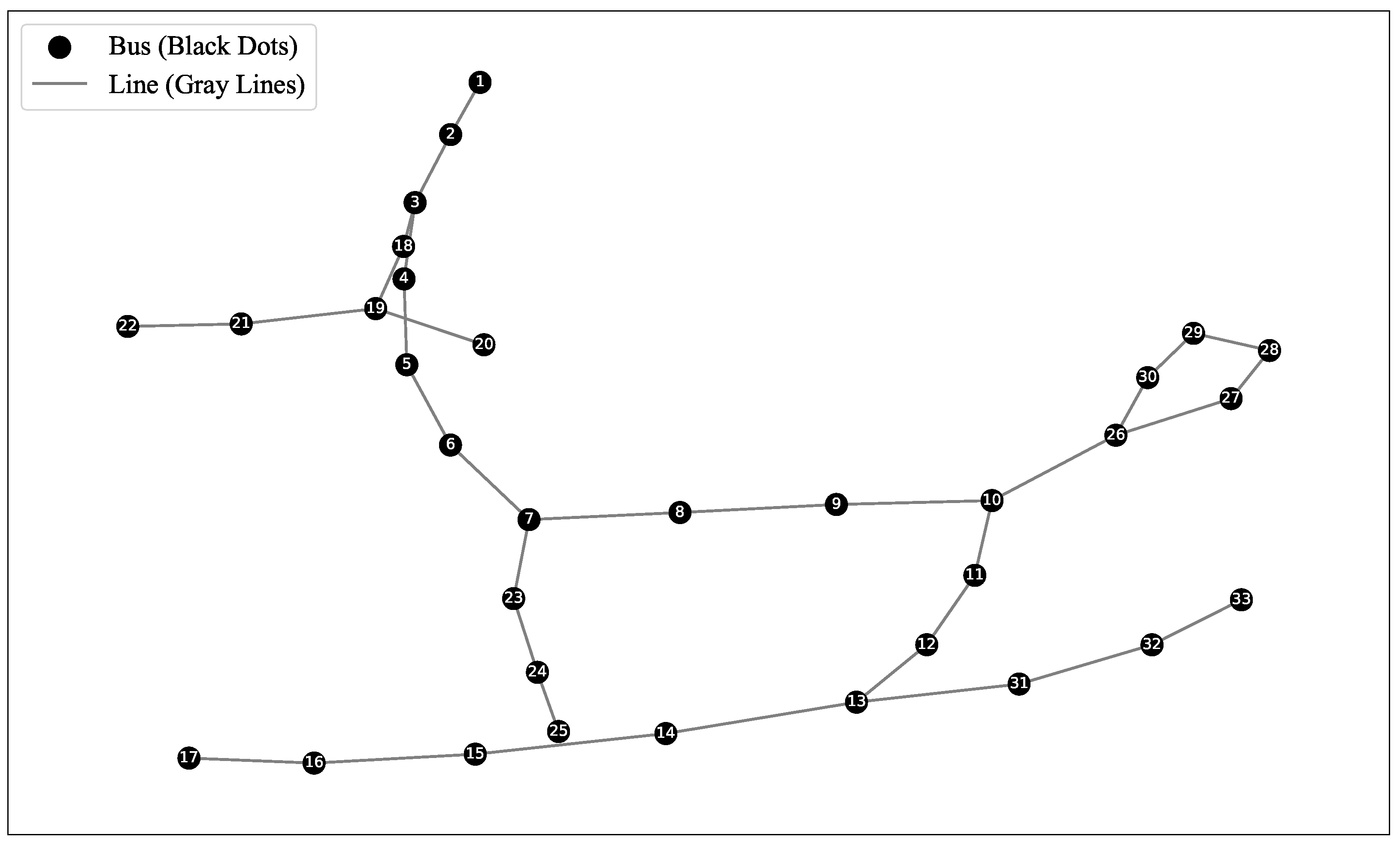
3.1. Data Description
3.2. Distribution Network Voltage and Overload Models
3.3. Optimization Objective and Constraints
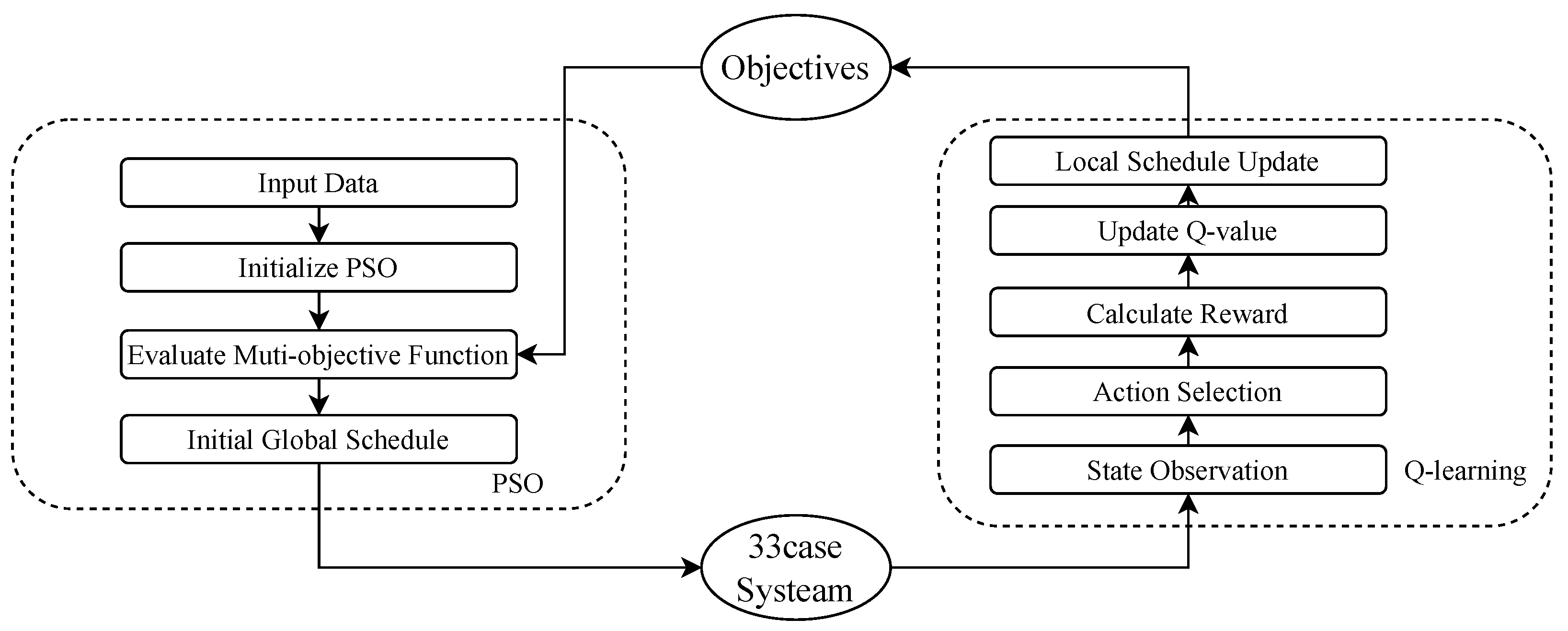
3.4. Dual-Phase Entropy Optimization Strategy
| Algorithm 1 Particle swarm optimization (PSO) for EV charging scheduling |
|
- Q-learning for Real-Time Adjustment
| Algorithm 2 Q-learning for real-time charging scheduling |
|
4. Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Description |
| Base load data at time t | |
| Historical load data at time t | |
| Regression function for modeling load variations | |
| N | Number of nodes in the distribution network (33 nodes in this study) |
| T | Time series length (24 h) |
| M | Number of electric vehicles in the region |
| Charging time window for EV i | |
| Charging demand for EV i | |
| Charging power of EV i at time t | |
| Maximum charging power of charging pile | |
| Voltage at node i at time t | |
| Reference voltage (standard value, e.g., 220 V or 110 V) | |
| Active power between nodes i and j at time t | |
| Reactive power between nodes i and j at time t | |
| Resistance of transmission line between nodes i and j | |
| Reactance of transmission line between nodes i and j | |
| Set of nodes electrically connected to node i | |
| Minimum allowable voltage | |
| Maximum allowable voltage | |
| Objective function for voltage deviation minimization | |
| Current between nodes i and j at time t | |
| Maximum current capacity for transmission line between nodes i and j | |
| Collection of all transmission lines in the network | |
| Objective function for overload minimization | |
| User satisfaction for EV i | |
| Battery level of EV i at the end of charging | |
| Target charging capacity of EV i | |
| Charging time for EV i | |
| Waiting time for EV i before charging begins | |
| Weight factors for charging time and waiting time in user satisfaction | |
| J | Overall objective function |
| User satisfaction objective function | |
| Weighting factors for voltage, overload, and user satisfaction terms | |
| Velocity of particle i at iteration t in PSO algorithm | |
| Position of particle i at iteration t in PSO algorithm | |
| w | Inertia weight in PSO algorithm |
| Cognitive and social learning factors in PSO algorithm | |
| Random numbers sampled from [0, 1] in PSO algorithm | |
| Personal best position for particle i in PSO algorithm | |
| Global best position in PSO algorithm | |
| Swarm size in PSO algorithm | |
| Maximum iterations in PSO algorithm | |
| Q-value function for state s and action a in Q-learning | |
| Learning rate in Q-learning algorithm | |
| Discount factor in Q-learning algorithm | |
| Immediate reward at time step t in Q-learning | |
| Exploration rate in Q-learning algorithm | |
| Maximum episodes in Q-learning algorithm | |
| Optimal policy derived from Q-learning |
References
- de Hoog, J.; Muenzel, V.; Jayasuriya, D.C.; Alpcan, T.; Brazil, M.; Thomas, D.A.; Mareels, I.; Dahlenburg, G.; Jegatheesan, R. The importance of spatial distribution when analysing the impact of electric vehicles on voltage stability in distribution networks. Energy Syst. 2015, 6, 63–84. [Google Scholar] [CrossRef]
- Bayindir, R.; Colak, I.; Fulli, G.; Demirtas, K. Smart grid technologies and applications. Renew. Sustain. Energy Rev. 2016, 66, 499–516. [Google Scholar] [CrossRef]
- Li, K.; Shao, C.; Hu, Z.; Shahidehpour, M. An MILP method for optimal planning of electric vehicle charging stations in coordinated urban power and transportation networks. IEEE Trans. Power Syst. 2022, 38, 5406–5419. [Google Scholar] [CrossRef]
- Dukpa, A.; Butrylo, B. MILP-based profit maximization of electric vehicle charging station based on solar and EV arrival forecasts. Energies 2022, 15, 5760. [Google Scholar] [CrossRef]
- Torkan, R.; Ilinca, A.; Ghorbanzadeh, M. A genetic algorithm optimization approach for smart energy management of microgrids. Renew. Energy 2022, 197, 852–863. [Google Scholar] [CrossRef]
- Jeyaranjani, J.; Devaraj, D. Improved genetic algorithm for optimal demand response in smart grid. Sustain. Comput. Inform. Syst. 2022, 35, 100710. [Google Scholar] [CrossRef]
- Chifu, V.R.; Cioara, T.; Pop, C.B.; Rusu, H.G.; Anghel, I. Deep Q-Learning-Based Smart Scheduling of EVs for Demand Response in Smart Grids. Appl. Sci. 2024, 14, 1421. [Google Scholar] [CrossRef]
- Park, K.; Moon, I. Multi-agent deep reinforcement learning approach for EV charging scheduling in a smart grid. Appl. Energy 2022, 328, 120111. [Google Scholar] [CrossRef]
- Zhang, L.; Li, Y. Optimal management for parking-lot electric vehicle charging by two-stage approximate dynamic programming. IEEE Trans. Smart Grid 2015, 8, 1722–1730. [Google Scholar] [CrossRef]
- Kumar, A.; Rizwan, M.; Nangia, U. A hybrid optimization technique for proficient energy management in smart grid environment. Int. J. Hydrogen Energy 2022, 47, 5564–5576. [Google Scholar] [CrossRef]
- Chen, Z. Graph Adaptive Attention Network with Cross-Entropy. Entropy 2024, 26, 576. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z. (HTBNet) Arbitrary Shape Scene Text Detection with Binarization of Hyperbolic Tangent and Cross-Entropy. Entropy 2024, 26, 560. [Google Scholar] [CrossRef]
- O’Connell, A.; Flynn, D.; Keane, A. Rolling multi-period optimization to control electric vehicle charging in distribution networks. IEEE Trans. Power Syst. 2013, 29, 340–348. [Google Scholar] [CrossRef]
- Hua, L.; Wang, J.; Zhou, C. Adaptive electric vehicle charging coordination on distribution network. IEEE Trans. Smart Grid 2014, 5, 2666–2675. [Google Scholar]
- Rassaei, F.; Soh, W.S.; Chua, K.C. Demand response for residential electric vehicles with random usage patterns in smart grids. IEEE Trans. Sustain. Energy 2015, 6, 1367–1376. [Google Scholar] [CrossRef]
- Shao, S.; Pipattanasomporn, M.; Rahman, S. Grid integration of electric vehicles and demand response with customer choice. IEEE Trans. Smart Grid 2012, 3, 543–550. [Google Scholar] [CrossRef]
- Fang, Z.; Hu, S.; Wang, J.; Deng, Y.; Chen, X.; Fang, Y. Prioritized Information Bottleneck Theoretic Framework with Distributed Online Learning for Edge Video Analytics. IEEE Trans. Netw. 2025, 1–17. [Google Scholar] [CrossRef]
- Huang, J.; Wu, B.; Duan, Q.; Dong, L.; Yu, S. A Fast UAV Trajectory Planning Framework in RIS-assisted Communication Systems with Accelerated Learning via Multithreading and Federating. IEEE Trans. Mob. Comput. 2025; early access. [Google Scholar] [CrossRef]
- Gao, J.; Chen, M.; Xu, C. Learning Probabilistic Presence-Absence Evidence for Weakly-Supervised Audio-Visual Event Perception. IEEE Trans. Pattern Anal. Mach. Intell. 2025; early access. [Google Scholar] [CrossRef]
- Chen, Z. Arbitrary Shape Text Detection with Discrete Cosine Transform and CLIP for Urban Scene Perception in ITS. IEEE Trans. Intell. Transp. Syst. 2025; early access. [Google Scholar] [CrossRef]
- Sheikhi, A.; Bahrami, S.; Ranjbar, A.; Oraee, H. Strategic charging method for plugged in hybrid electric vehicles in smart grids; a game theoretic approach. Int. J. Electr. Power Energy Syst. 2013, 53, 499–506. [Google Scholar] [CrossRef]
- Chen, N.; Tan, C.; Quek, T.Q.S. Electric Vehicle Charging in Smart Grid: Optimality and Valley-Filling Algorithms. IEEE J. Sel. Top. Signal Process. 2014, 8, 1073–1083. [Google Scholar] [CrossRef]
- Lee, Z.J.; Lee, G.S.; Lee, T.; Jin, C.; Lee, R.; Low, Z.; Chang, D.; Ortega, C.; Low, S. Adaptive Charging Networks: A Framework for Smart Electric Vehicle Charging. IEEE Trans. Smart Grid 2020, 12, 4339–4350. [Google Scholar] [CrossRef]
- Coelho, V.N.; Coelho, I.M.; Coelho, B.N.; Cohen, M.W.; Reis, A.J.; Silva, S.M.; Souza, M.J.; Fleming, P.J.; Guimaraes, F.G. Multi-objective energy storage power dispatching using plug-in vehicles in a smart-microgrid. Renew. Energy 2016, 89, 730–742. [Google Scholar] [CrossRef]
- Ullah, K.; Hafeez, G.; Khan, I.; Jan, S.; Javaid, N. A multi-objective energy optimization in smart grid with high penetration of renewable energy sources. Appl. Energy 2021, 299, 117104. [Google Scholar] [CrossRef]
- Mallaki, M.; Najibi, S.; Najafi, M.; Shirazi, N.C. Smart grid resiliency improvement using a multi-objective optimization approach. Sustain. Energy Grids Netw. 2022, 32, 100886. [Google Scholar] [CrossRef]
- Ali, A.; David, R.; Mahmoud, K. Adaptive multi-objective optimization for power loss minimization and voltage regulation in distribution systems. In Proceedings of the 2016 Eighteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 27–29 December 2016; pp. 573–578. [Google Scholar]
- Zakariazadeh, A.; Jadid, S.; Siano, P. Multi-objective scheduling of electric vehicles in smart distribution system. Energy Convers. Manag. 2014, 79, 43–53. [Google Scholar] [CrossRef]
- García-Villalobos, J.; Zamora, I.; Knezović, K.; Marinelli, M. Multi-objective optimization control of plug-in electric vehicles in low voltage distribution networks. Appl. Energy 2016, 180, 155–168. [Google Scholar] [CrossRef]
- Khan, H.W.; Usman, M.; Hafeez, G.; Albogamy, F.R.; Khan, I.; Shafiq, Z.; Khan, M.U.A.; Alkhammash, H.I. Intelligent optimization framework for efficient demand-side management in renewable energy integrated smart grid. IEEE Access 2021, 9, 124235–124252. [Google Scholar] [CrossRef]
- Wu, B.; Wu, W. Model-Free Cooperative Optimal Output Regulation for Linear Discrete-Time Multi-Agent Systems Using Reinforcement Learning. Math. Probl. Eng. 2023, 2023, 6350647. [Google Scholar] [CrossRef]
- Wu, B.; Cai, Z.; Wu, W.; Yin, X. AoI-aware resource management for smart health via deep reinforcement learning. IEEE Access 2023, 11, 81180–81195. [Google Scholar] [CrossRef]
- Deming, C.; Pasam, P.; Allam, A.R.; Mohammed, R.; Venkata, S.G.N.; Kothapalli, K.R.V. Real-Time Scheduling for Energy Optimization: Smart Grid Integration with Renewable Energy. Asia Pac. J. Energy Environ. 2021, 8, 77–88. [Google Scholar] [CrossRef]
- Moreno Escobar, J.J.; Morales Matamoros, O.; Tejeida Padilla, R.; Lina Reyes, I.; Quintana Espinosa, H. A comprehensive review on smart grids: Challenges and opportunities. Sensors 2021, 21, 6978. [Google Scholar] [CrossRef]
- Tan, C.; Cai, D.W.H.; Lou, X. Resistive Network Optimal Power Flow: Uniqueness and Algorithms. IEEE Trans. Power Syst. 2015, 30, 263–273. [Google Scholar] [CrossRef]

| Algorithm | Parameter | Value |
|---|---|---|
| PSO | Number of particles | 50 |
| Maximum iterations | 100 | |
| Inertia weight (w) | 0.7 | |
| Cognitive factor () | 1.5 | |
| Social factor () | 1.5 | |
| Q-learning | Learning rate () | 0.1 |
| Discount factor () | 0.89 | |
| Exploration rate () | 0.0001 | |
| Maximum episodes | 300 | |
| Multi-objective weights | Voltage deviation () | 0.51 |
| Line overload () | 0.36 | |
| User satisfaction () | 0.29 |
| Metric | Traditional FCFS | Standalone PSO | Two-Stages |
|---|---|---|---|
| Voltage Deviation (%) | 5.8 | 3.2 | 1.9 |
| Max Load Rate (%) | 95 | 88 | 82 |
| Avg. Satisfaction (%) | 75 | 82 | 88 |
| Computation Time (min) | - | 34 | 66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, W.; Guan, L. Minimizing System Entropy: A Dual-Phase Optimization Approach for EV Charging Scheduling. Entropy 2025, 27, 303. https://doi.org/10.3390/e27030303
Yuan W, Guan L. Minimizing System Entropy: A Dual-Phase Optimization Approach for EV Charging Scheduling. Entropy. 2025; 27(3):303. https://doi.org/10.3390/e27030303
Chicago/Turabian StyleYuan, Wenpeng, and Lin Guan. 2025. "Minimizing System Entropy: A Dual-Phase Optimization Approach for EV Charging Scheduling" Entropy 27, no. 3: 303. https://doi.org/10.3390/e27030303
APA StyleYuan, W., & Guan, L. (2025). Minimizing System Entropy: A Dual-Phase Optimization Approach for EV Charging Scheduling. Entropy, 27(3), 303. https://doi.org/10.3390/e27030303





