High-Accuracy Parallel Neural Networks with Hard Constraints for a Mixed Stokes/Darcy Model
Abstract
1. Introduction
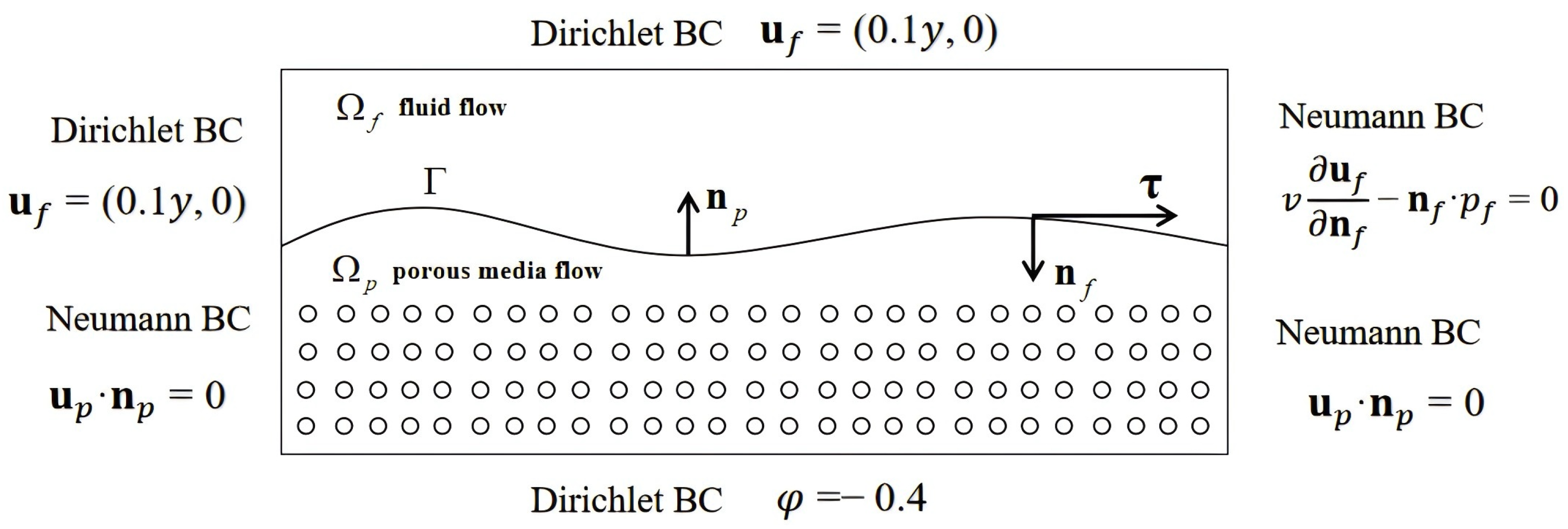
2. Problem Formulation
3. Methodology
3.1. Parallel Physics-Informed Neural Networks
| Algorithm 1 PPINNs for the mixed Stokes/Darcy model |
|
3.2. Hard Constrained PPINNs
| Algorithm 2 HC-PPINNs for the mixed Stokes/Darcy model |
|
4. Computational Results and Discussion
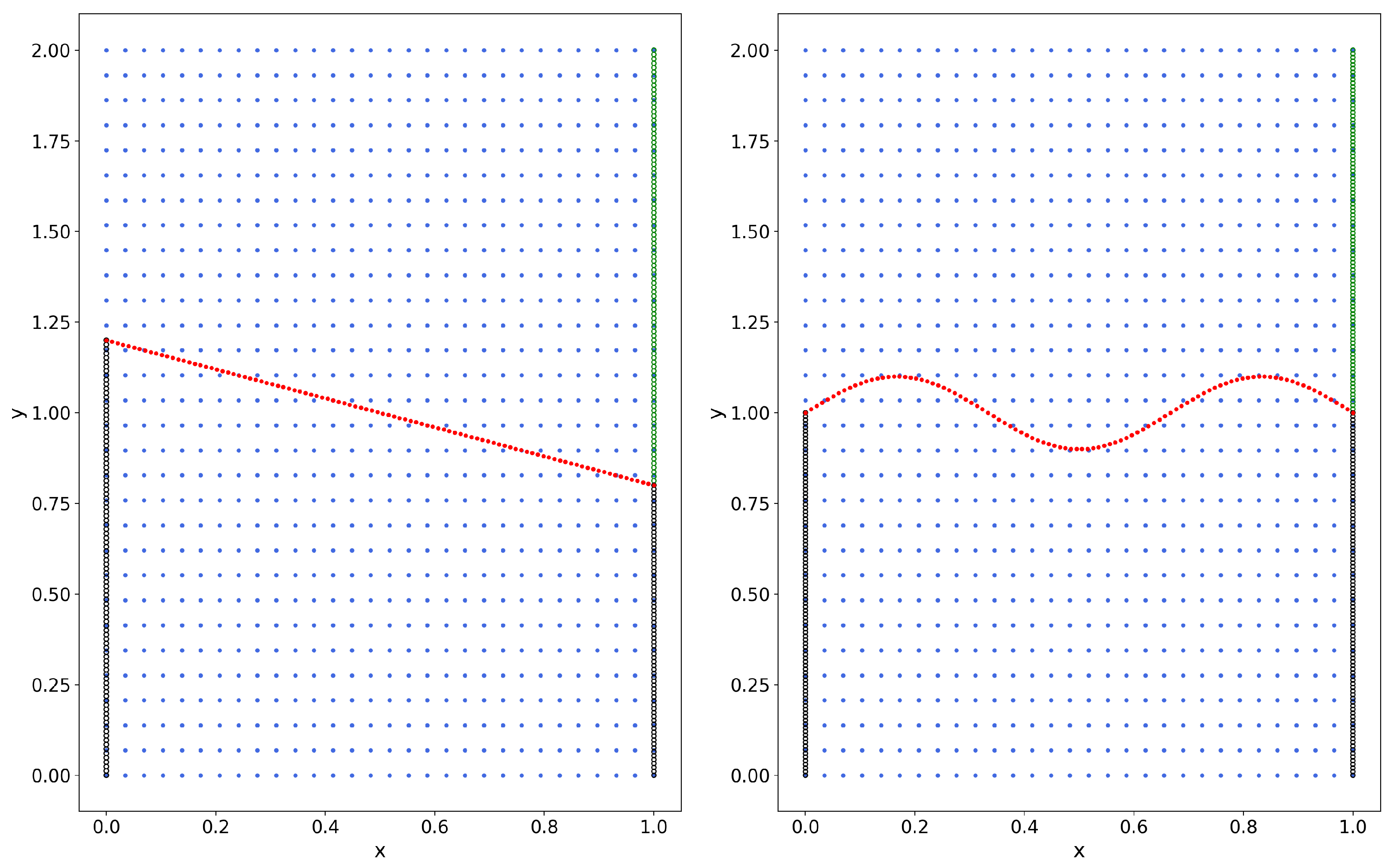
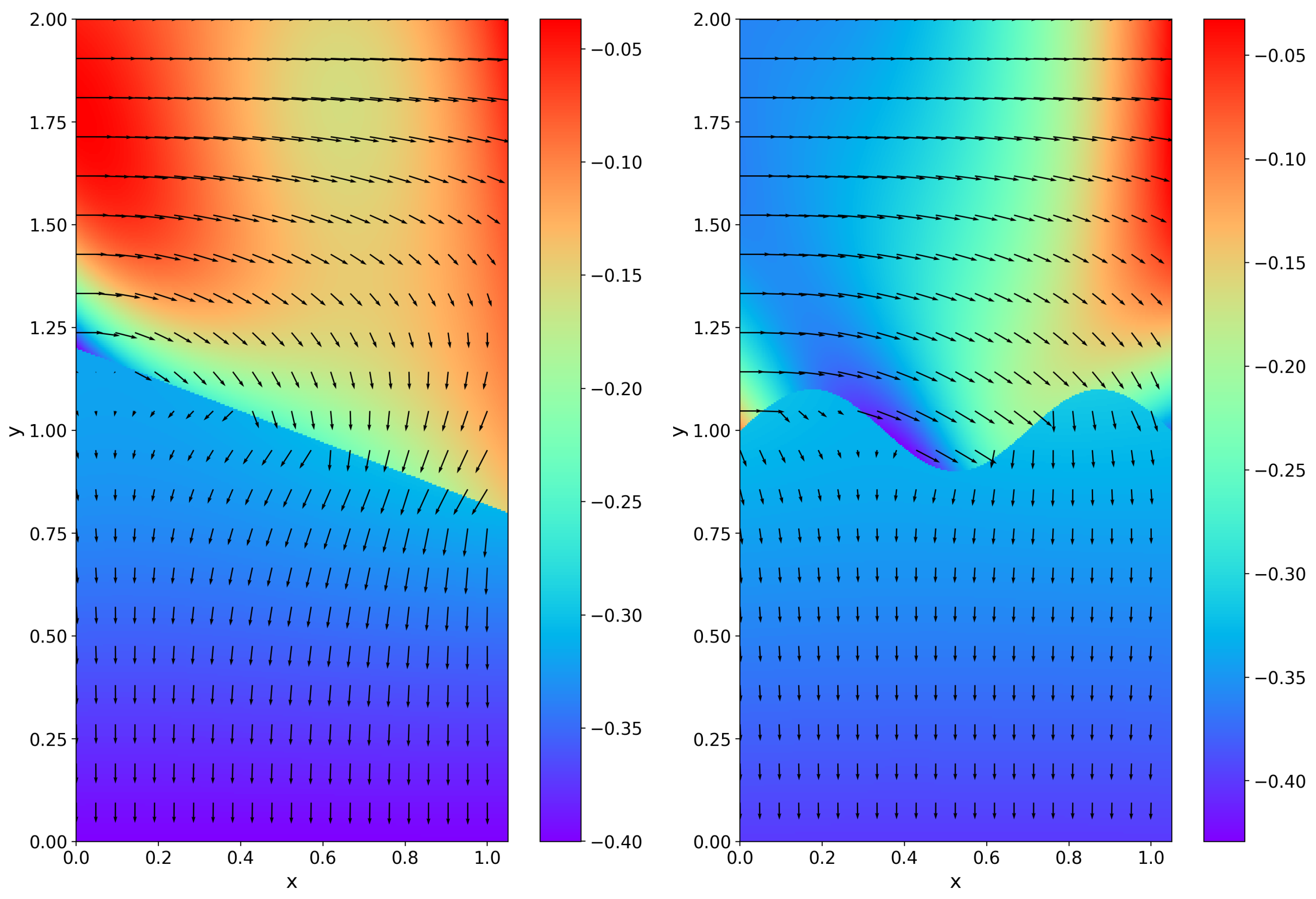
4.1. Example 1
4.2. Example 2
4.3. Example 3
4.4. Example 4
4.5. Example 5
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Bear, J. Hydraulics of Groundwater, 1st ed.; McGraw-Hill: New York, NY, USA, 1979. [Google Scholar]
- Discacciati, M. Domain Decomposition Methods for the Coupling of Surface and Groundwater Flows. Ph.D. Thesis, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 2008. [Google Scholar]
- Discacciati, M.; Miglio, E.; Quarteroni, A. Mathematical and numerical models for coupling surface and groundwater flows. Appl. Numer. Math. 2002, 43, 57–74. [Google Scholar] [CrossRef]
- Wood, W.L. Introduction to Numerical Methods for Water Resources, 1st ed.; Clarendon Press: Oxford, MS, USA, 1993. [Google Scholar]
- Beavers, G.S.; Joseph, D.D. Boundary conditions at a naturally permeable wall. J. Fluid. Mech. 1967, 30, 197–207. [Google Scholar] [CrossRef]
- Jones, I.P. Low reynolds number flow past a porous spherical shell. Proc. Camb. Phil. Soc. 1973, 73, 231–238. [Google Scholar] [CrossRef]
- Saffman, P.G. On the boundary condition at the interface of a porous medium. Stud. Appl. Math. 1971, 50, 93–101. [Google Scholar] [CrossRef]
- Arbogast, T.; Brunson, D.S. A computational method for approximating a Darcy-Stokes system governing a vuggy porous medium. Comput. Geosci. 2007, 11, 207–218. [Google Scholar] [CrossRef]
- Cao, Y.; Gunzburger, M.; Hu, X.; Hua, F.; Wang, X.; Zhao, W. Finite element approximations for Stokes-Darcy flow with Beavers-Joseph interface conditions. Siam. J. Numer. Anal. 2010, 47, 4239–4256. [Google Scholar] [CrossRef]
- Cao, Y.; Gunzburger, M.; Hu, X.; Hua, F.; Wang, X. Coupled Stokes-Darcy model with Beavers-Joseph interface boundary condition. Commun. Math. Sci. 2010, 8, 1–25. [Google Scholar] [CrossRef]
- Chidyagwai, P.; Riviére, B. Numerical modelling of coupled surface and subsurface flow systems. Adv. Water. Resour. 2010, 8, 92–105. [Google Scholar] [CrossRef]
- Hanspal, N.S.; Waghode, A.N.; Nassehi, V.; Wakeman, R.J. Numerical analysis of coupled Stokes/Darcy flows in industrial filtrations. Transport. Porous. Med. 2006, 64, 73–101. [Google Scholar] [CrossRef]
- Nassehi, V. Modelling of combined Navier-Stokes and Darcy flows in crossflow membrane filtration. Chem. Eng. Sci. 1998, 53, 1253–1265. [Google Scholar] [CrossRef]
- Pozrikidis, C.; Farrow, D.A. A model of fluid flow in solid tumors. Ann. Biomed. Eng. 2003, 31, 181–194. [Google Scholar] [CrossRef] [PubMed]
- Hanspal, N.S.; Waghode, A.N.; Nassehi, V.; Wakeman, R.J. Development of a predictive mathematical model for coupled Stokes/Darcy flows in cross-flow membrane filtration. Chem. Eng. J. 2009, 149, 132–142. [Google Scholar] [CrossRef]
- Disc, M.; Quarteroni, A. Convergence analysis of a subdomain iterative method for the finite element approximation of the coupling of Stokes and Darcy equations. Comput. Vis. Sci. 2004, 6, 93–103. [Google Scholar]
- Mikelic, A.; Jäger, W. On the interface boundary condition of Beavers, Joseph, and Saffman. Siam. J. Appl. Math. 2000, 60, 1111–1127. [Google Scholar] [CrossRef]
- Jäger, W.; Mikelic, A.; Neuss, N. Asymptotic analysis of the laminar viscous flow over a porous bed. Siam. J. Sci. Comput. 2001, 22, 2006–2028. [Google Scholar] [CrossRef]
- Layton, W.J.; Schieweck, F.; Yotov, I. Coupling fluid flow with porous media flow. Siam. J. Numer. Anal. 2002, 40, 2195–2218. [Google Scholar] [CrossRef]
- Miglio, E.; Quarteroni, A.; Saleri, F. Coupling of free surface and groundwater flows. Comput. Fluids 2003, 32, 73–83. [Google Scholar] [CrossRef]
- Riviére, B.; Yotov, I. Locally conservative coupling of Stokes and Darcy flows. Siam. J. Numer. Anal. 2005, 40, 1959–1977. [Google Scholar] [CrossRef]
- Lee, H.; Rife, K. Least squares approach for the time-dependent nonlinear Stokes-Darcy flow. Comput. Math. Appl. 2014, 67, 1806–1815. [Google Scholar] [CrossRef]
- Rybak, I.; Magiera, J. A multiple-time-step technique for coupled free flow and porous medium systems. J. Comput. Phys. 2014, 272, 327–342. [Google Scholar] [CrossRef]
- Mu, M.; Xu, J. A Two-Grid Method of a Mixed Stokes-Darcy Model for Coupling Fluid Flow with Porous Media Flow. Siam. J. Numer. Anal. 2007, 45, 1801–1813. [Google Scholar] [CrossRef]
- Mu, M.; Zhu, X. Decoupled schemes for a non-stationary mixed Stokes-Darcy model. Math. Comput. 2010, 79, 707–731. [Google Scholar] [CrossRef]
- Shan, L.; Zheng, H.; Layton, W.J. A decoupling method with different subdomain time steps for the nonstationary Stokes-Darcy model. Numer. Meth. Part. Differ. Equ. 2012, 29, 549–583. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Baker, N.; Alexander, F.; Bremer, T.; Hagberg, A.; Kevrekidis, Y.; Najm, H.; Parashar, M.; Patra, A.; Sethian, J.; Wild, S.; et al. Workshop Report on Basic Research Needs for Scientific Machine Learning: Core Technologies for Artificial Intelligence; Technical Report; USDOE Office of Science (SC): Washington, DC, USA, 2019.
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Raissi, M.; Yazdani, A.; Karniadakis, G.E. Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations. Science 2020, 367, 1026–1030. [Google Scholar] [CrossRef]
- Sirignano, J.; Spiliopoulos, K. DGM: A deep learning algorithm for solving partial differential equations. J. Comput. Phys. 2018, 375, 1339–1364. [Google Scholar] [CrossRef]
- Yu, B. The Deep Ritz Method: A Deep Learning-Based Numerical Algorithm for Solving Variational Problems. Commun. Math. Stat. 2018, 6, 1–12. [Google Scholar]
- Zang, Y.; Bao, G.; Ye, X.; Zhou, H. Weak adversarial networks for high-dimensional partial differential equations. J. Comput. Phys. 2020, 411, 109409. [Google Scholar] [CrossRef]
- Dong, S.; Li, Z. Local extreme learning machines and domain decomposition for solving linear and nonlinear partial differential equations. Comput. Methods Appl. Mech. Eng. 2021, 387, 114129. [Google Scholar] [CrossRef]
- Barron, A. Universal approximation bounds for superpositions of a sigmoidal function. IEEE Trans. Inform. Theory 1993, 39, 930–945. [Google Scholar] [CrossRef]
- Chen, T.; Chen, H. Universal approximation to nonlinear operators by neural networks with arbitrary activation functions and its application to dynamical systems. IEEE Trans. Neural Netw. 1995, 6, 911–917. [Google Scholar] [CrossRef] [PubMed]
- Poggio, T.; Mhaskar, H.; Rosasco, L.; Miranda, B.; Liao, Q. Why and when can deep but not shallow-networks avoid the curse of dimensionality: A review. Int. J. Autom. Comput. 2017, 14, 503–519. [Google Scholar] [CrossRef]
- Grohs, P.; Hornung, F.; Jentzen, A.; Wurstemberger, P. A proof that artificial neural networks overcome the curse of dimensionality in the numerical approximation of black-scholes partial differential equations. arXiv 2018, arXiv:1809.02362. [Google Scholar] [CrossRef]
- Kharazmi, E.; Zhang, Z.; Karniadakis, G.E.M. hp-VPINNs: Variational physics-informed neural networks with domain decomposition. Comput. Methods Appl. Mech. Eng. 2021, 374, 113547. [Google Scholar] [CrossRef]
- Jagtapa, A.D.; Kharazmia, E.; Karniadakis, G.E. Conservative physics-informed neural networks on discrete domains for conservation laws: Applications to forward and inverse problems. Comput. Methods Appl. Mech. Eng. 2020, 365, 113028. [Google Scholar] [CrossRef]
- Jagtapa, A.D.; Karniadakis, G.E. Extended Physics-Informed Neural Networks (XPINNs):A Generalized Space-Time Domain Decomposition Based Deep Learning Framework for Nonlinear Partial Differential Equations. Commun. Comput. Phys. 2020, 28, 2002–2041. [Google Scholar] [CrossRef]
- Sun, L.; Gao, H.; Panc, S.; Wang, J. Surrogate modeling for fluid flows based on physics-constrained deep learning without simulation data. Commun. Comput. Phys. 2020, 361, 112732. [Google Scholar] [CrossRef]
- Lu, L.; Pestourie, R.; Yao, W.; Wang, Z.; Verdugo, F.; Johnson, S.G. Physics-Informed Neural Networks with Hard Constraints for Inverse Design. Siam. J. Sci. Comput. 2020, 43, 1105–1132. [Google Scholar] [CrossRef]
- Cai, S.; Mao, Z.; Wang, Z.; Wang, Z.; Yin, M.; Karniadakis, G.E. Physics-informed neural networks (PINNs) for fluid mechanics: A review. Acta Mech. Sin. 2021, 37, 1727–1738. [Google Scholar] [CrossRef]
- Pu, R.; Feng, X. Physics-Informed Neural Networks for Solving Coupled Stokes-Darcy Equation. Entropy 2022, 24, 1106. [Google Scholar] [CrossRef]
- Yue, J.; Li, J. Efficient coupled deep neural networks for the time-dependent coupled Stokes-Darcy problems. Appl. Math. Comput. 2023, 437, 127514. [Google Scholar] [CrossRef]
- Zhang, Z. Neural Network Method for Solving Forward and Inverse Problems of Navier-Stokes/Darcy Coupling Model. Master’s Thesis, East China Normal University, Shanghai, China, 2023. [Google Scholar]
- McClenny, L.D.; Braga-Neto, U.M. Self-adaptive physics-informed neural networks. J. Comput. Phys. 2023, 474, 111722. [Google Scholar] [CrossRef]
- Berardi, M.; Difonzo, F.V.; Icardi, M. Inverse Physics-Informed Neural Networks for transport models in porous materials, Computer Methods in Applied Mechanics and Engineering. Comput. Methods Appl. Mech. Eng. 2025, 435, 117628. [Google Scholar] [CrossRef]
- Farkane, A.; Ghogho, M.; Oudani, M.; Boutayeb, M. Enhancing physics informed neural networks for solving Navier-Stokes equations. Int. J. Numer. Meth. Fluids 2024, 96, 381–396. [Google Scholar] [CrossRef]
- Berg, J.; Nyström, K. A unified deep artificial neural network approach to partial differential equations in complex geometries. Neurocomputing 2018, 317, 28–41. [Google Scholar] [CrossRef]
- Ren, P.; Rao, C.; Liu, Y.; Wang, J.; Sun, H. PhyCRNet: Physics-informed convolutional-recurrent network for solving spatiotemporal PDEs. Comput. Methods Appl. Mech. Eng. 2022, 389, 114399. [Google Scholar] [CrossRef]
- Arda, M.; Ali, C.B.; Ehsan, H.; Erdogan, M. An unsupervised latent/output physics-informed convolutional-LSTM network for solving partial differential equations using peridynamic differential operator. Comput. Methods Appl. Mech. Eng. 2023, 407, 115944. [Google Scholar]



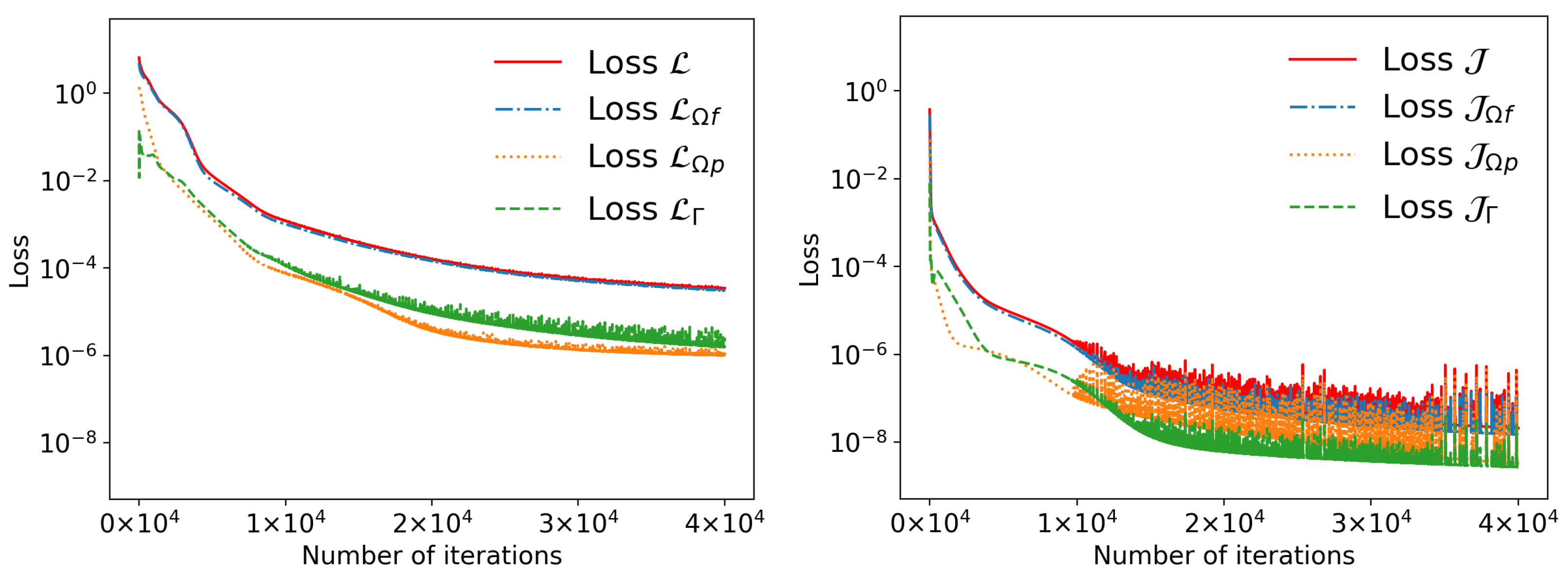
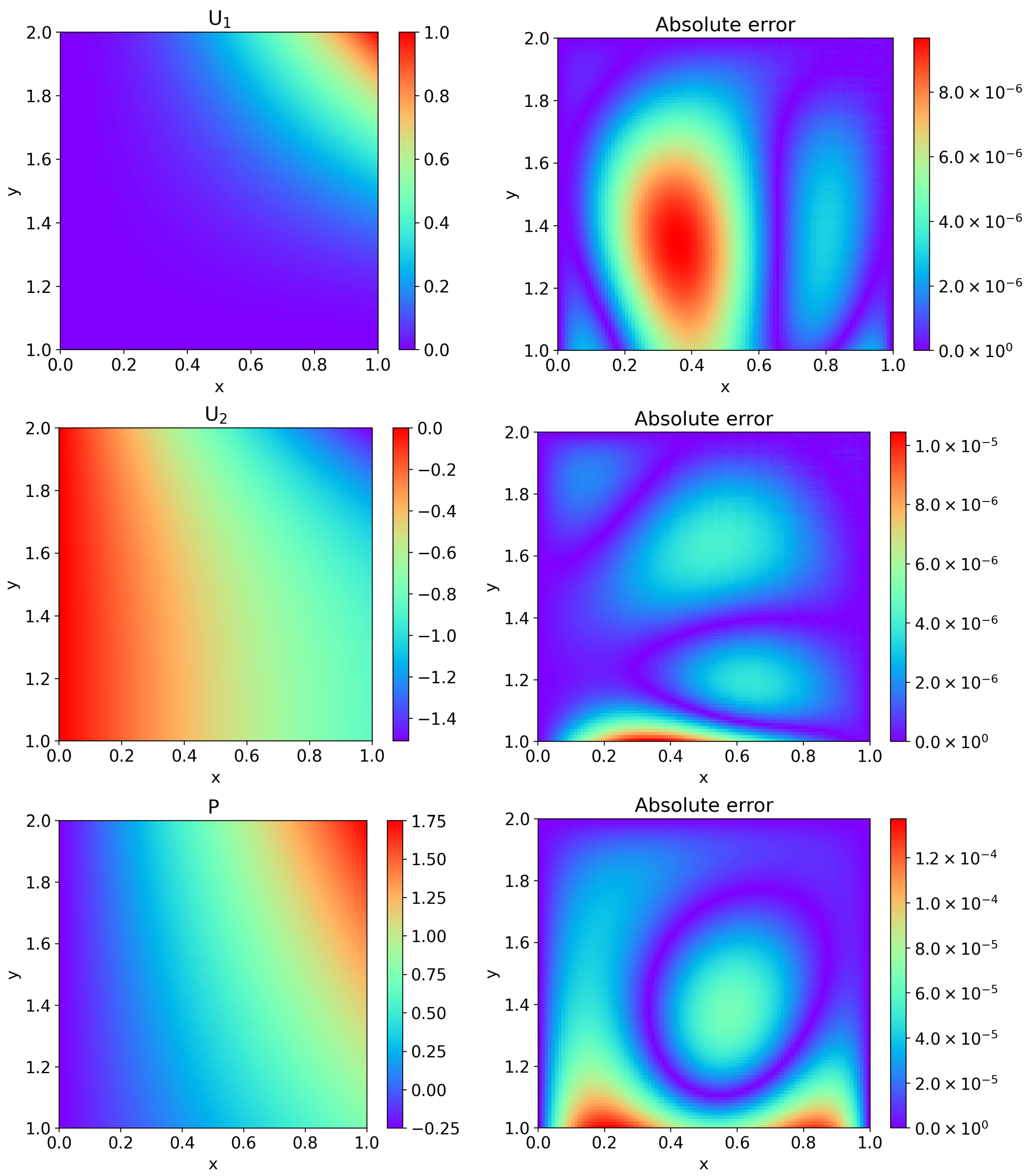
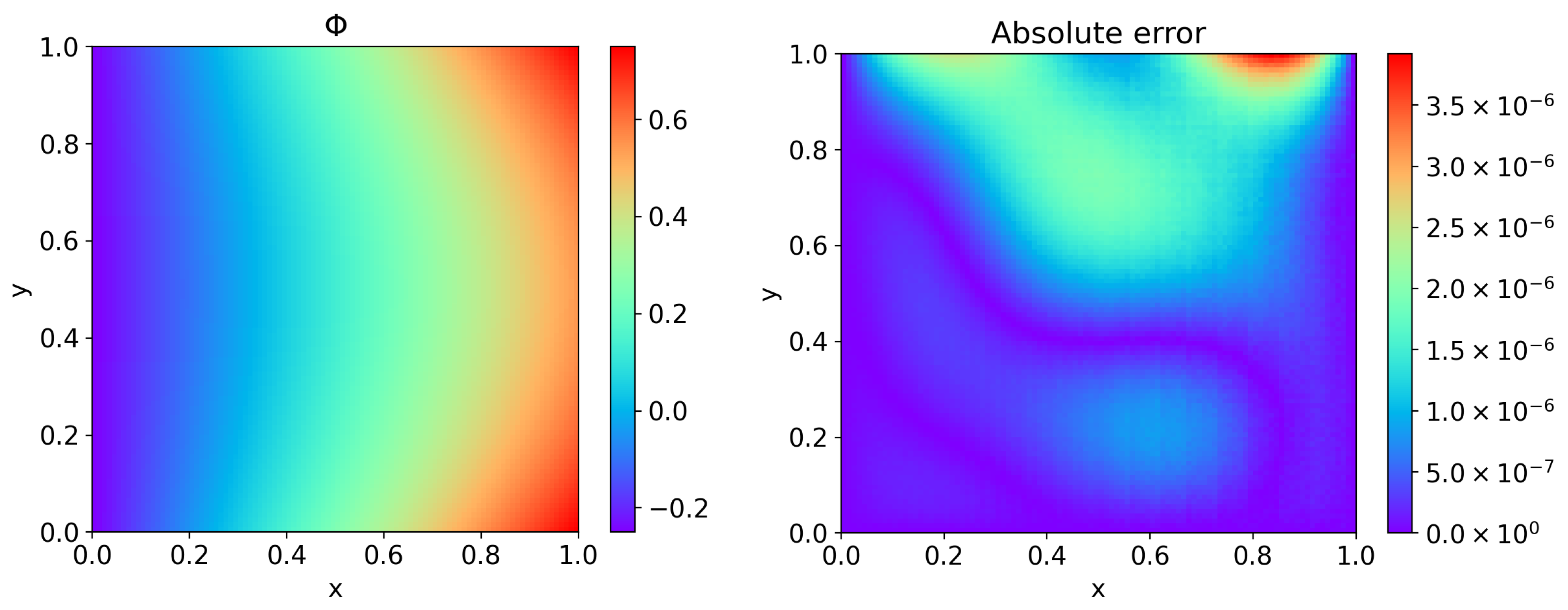
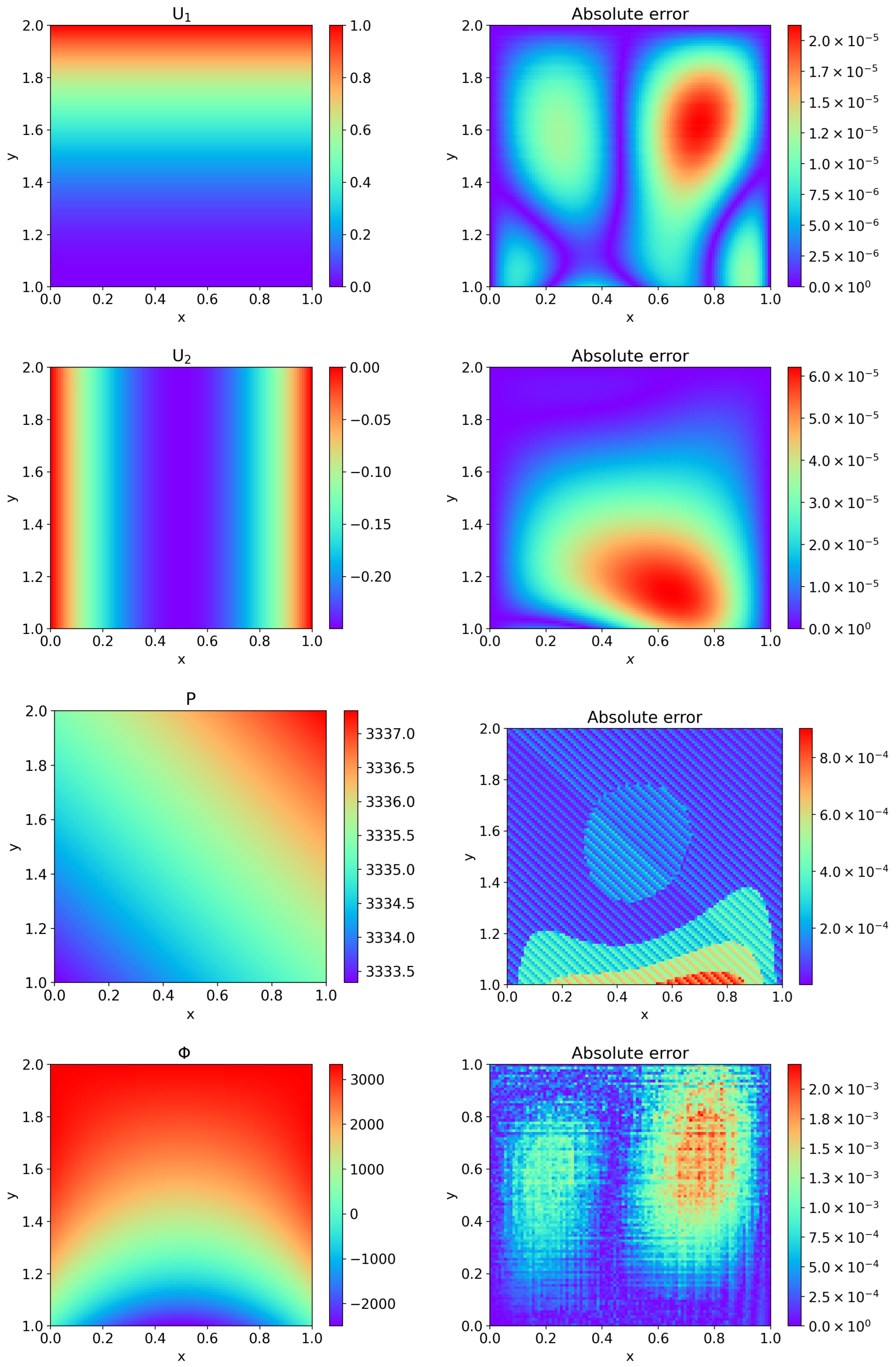


| Algorithm | ||||
|---|---|---|---|---|
| 8 | PPINNs | 4.97 × 10−3 | 6.52 × 10−3 | 2.71 × 10−3 |
| HC-PPINNs | 4.15 × 10−5 | 7.01 × 10−4 | 1.02 × 10−4 | |
| 16 | PPINNs | 1.84 × 10−3 | 2.63 × 10−3 | 1.51 × 10−3 |
| HC-PPINNs | 2.64 × 10−5 | 2.12 × 10−4 | 1.60 × 10−5 | |
| 32 | PPINNs | 1.71 × 10−3 | 3.17 × 10−3 | 1.65 × 10−3 |
| HC-PPINNs | 6.68 × 10−6 | 9.23 × 10−5 | 5.62 × 10−6 |
| Algorithm | K | |||
|---|---|---|---|---|
| HC-PPINNs | 1 | 1.69 × 10−5 | 1.93 × 10−5 | 2.50 × 10−6 |
| 3.48 × 10−5 | 1.75 × 10−5 | 2.60 × 10−6 | ||
| 4.86 × 10−5 | 6.87 × 10−6 | 4.65 × 10−6 | ||
| 6.56 × 10−5 | 6.39 × 10−7 | 1.12 × 10−6 | ||
| 6.17 × 10−5 | 6.06 × 10−8 | 4.59 × 10−7 | ||
| PPINNs | 4.66 × 10−2 | 1.22 × 10−3 | 4.73 × 10−3 |
| 8 | 1.23 × 10−5 | 9.58 × 10−5 | 2.12 × 10−6 |
| 16 | 8.51 × 10−6 | 6.94 × 10−5 | 1.08 × 10−6 |
| 32 | 5.67 × 10−6 | 3.98 × 10−5 | 3.79 × 10−6 |
| Number of Hidden Layers | Algorithm | |||
|---|---|---|---|---|
| HC-PPINNs | 2.24 × 10−5 | 1.63 × 10−4 | 1.90 × 10−5 | |
| 1 | PPINNs | 3.93 × 10−2 | 1.63 × 10−1 | 2.44 × 10−1 |
| CDNNs | 1.25 × 10−2 | 1.87 × 10−1 | 8.02 × 10−2 | |
| HC-PPINNs | 2.34 × 10−5 | 1.68 × 10−4 | 1.64 × 10−5 | |
| 2 | PPINNs | 1.71 × 10−2 | 6.32 × 10−2 | 7.40 × 10−2 |
| CDNNs | 5.00 × 10−4 | 1.64 × 10−2 | 1.09 × 10−3 | |
| HC-PPINNs | 1.21 × 10−5 | 1.28 × 10−4 | 8.46 × 10−6 | |
| 3 | PPINNs | 1.50 × 10−2 | 5.18 × 10−2 | 6.24 × 10−2 |
| CDNNs | 1.15 × 10−4 | 3.14 × 10−3 | 2.28 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Z.; Zhang, J.; Zhu, X. High-Accuracy Parallel Neural Networks with Hard Constraints for a Mixed Stokes/Darcy Model. Entropy 2025, 27, 275. https://doi.org/10.3390/e27030275
Lu Z, Zhang J, Zhu X. High-Accuracy Parallel Neural Networks with Hard Constraints for a Mixed Stokes/Darcy Model. Entropy. 2025; 27(3):275. https://doi.org/10.3390/e27030275
Chicago/Turabian StyleLu, Zhulian, Junyang Zhang, and Xiaohong Zhu. 2025. "High-Accuracy Parallel Neural Networks with Hard Constraints for a Mixed Stokes/Darcy Model" Entropy 27, no. 3: 275. https://doi.org/10.3390/e27030275
APA StyleLu, Z., Zhang, J., & Zhu, X. (2025). High-Accuracy Parallel Neural Networks with Hard Constraints for a Mixed Stokes/Darcy Model. Entropy, 27(3), 275. https://doi.org/10.3390/e27030275







