The Quantum Relative Entropy of the Schwarzschild Black Hole and the Area Law
Abstract
1. Introduction
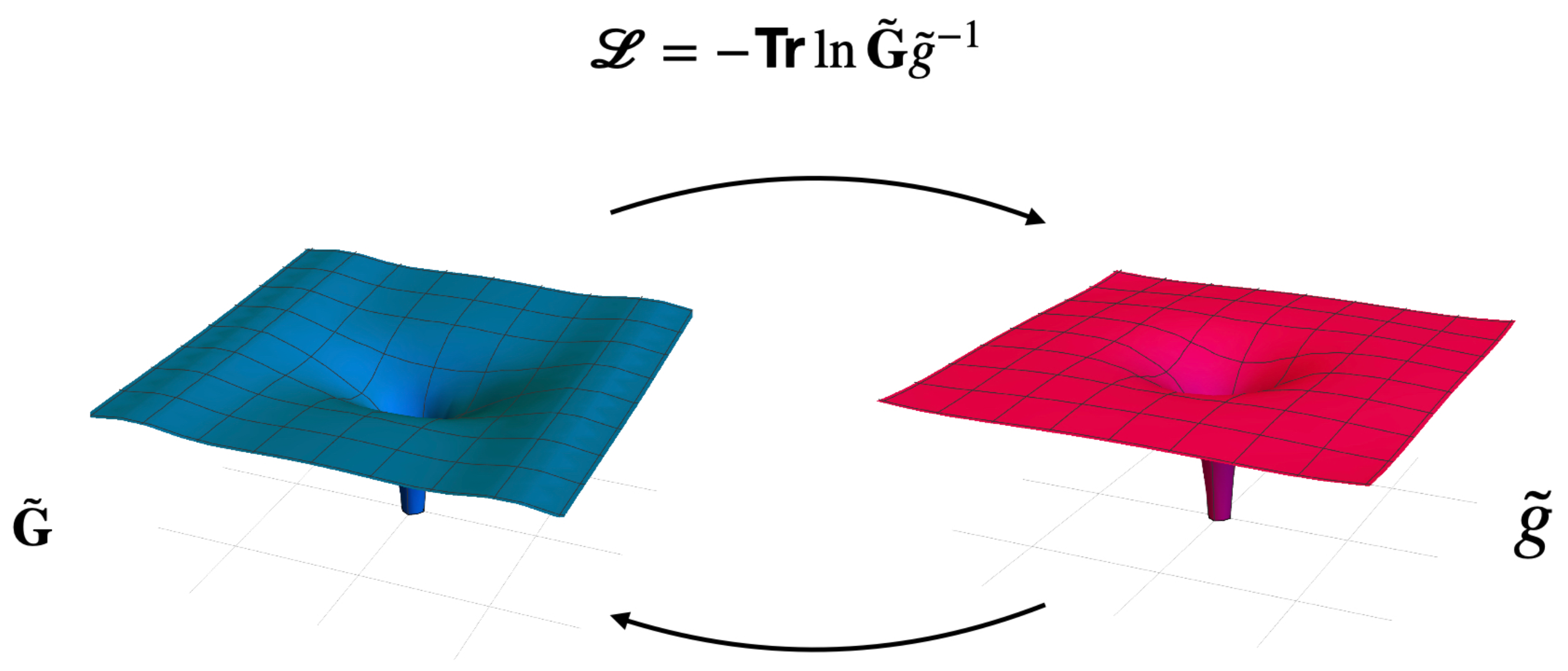
2. Boltzmann Legacy and the Quantum Relative Entropy for Gravity
3. Modified Einstein Equations in Vacuum
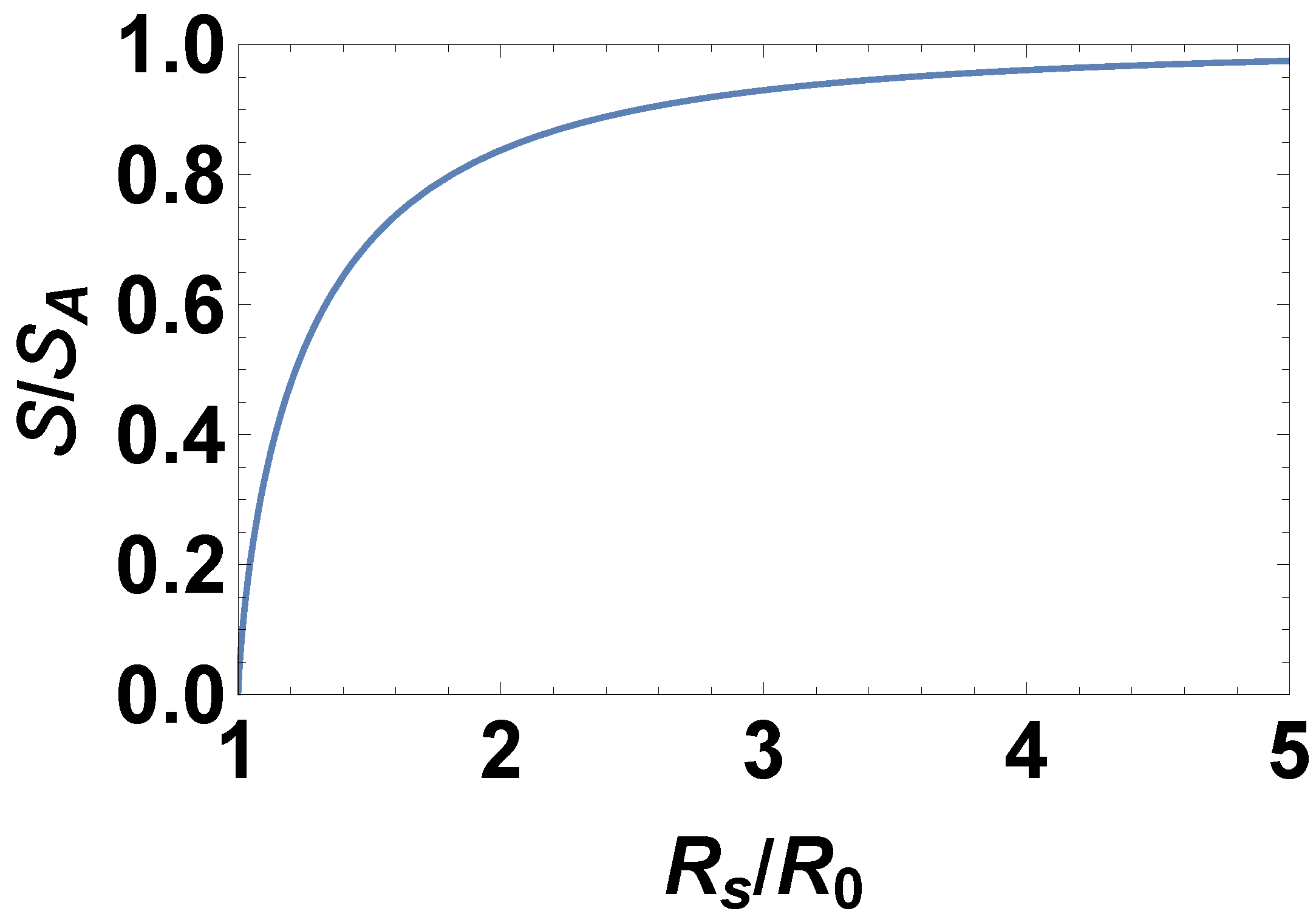
4. Quantum Relative Entropy of the Schwarzschild Black Hole
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Witten, E. Introduction to Black Hole Thermodynamics. arXiv 2024, arXiv:2412.16795. [Google Scholar]
- Mukhanov, V.; Winitzki, S. Introduction to Quantum Effects in Gravity; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Wald, R.M. Quantum Field Theory in Curved Spacetime and Black Hole Thermodynamics; University of Chicago Press: Chicago, IL, USA, 1994. [Google Scholar]
- Bekenstein, J.D. Black holes and entropy. Phys. Rev. D 1973, 7, 2333. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Generalized second law of thermodynamics in black-hole physics. Phys. Rev. D 1974, 9, 3292. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle creation by black holes. Commun. Math. Phys. 1975, 43, 199–220. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Hawking, S.W. Action integrals and partition functions in quantum gravity. Phys. Rev. D 1977, 15, 2752. [Google Scholar] [CrossRef]
- Wald, R.M. Black hole entropy is the Noether charge. Phys. Rev. D 1993, 48, R3427. [Google Scholar] [CrossRef] [PubMed]
- Calmet, X.; Kuipers, F. Quantum gravitational corrections to the entropy of a Schwarzschild black hole. Phys. Rev. D 2021, 104, 066012. [Google Scholar] [CrossRef]
- Strominger, A.; Vafa, C. Microscopic origin of the Bekenstein-Hawking entropy. Phys. Lett. B 1996, 379, 99–104. [Google Scholar] [CrossRef]
- Hooft, G. Dimensional reduction in quantum gravity. arXiv 1993, arXiv:gr-qc/9310026. [Google Scholar]
- Susskind, L. The world as a hologram. J. Math. Phys. 1995, 36, 6377–6396. [Google Scholar] [CrossRef]
- Maldacena, J. The large-N limit of superconformal field theories and supergravity. Int. J. Theor. Phys. 1999, 38, 1113–1133. [Google Scholar] [CrossRef]
- Ryu, S.; Takayanagi, T. Aspects of holographic entanglement entropy. J. High Energy Phys. 2006, 2006, 045. [Google Scholar] [CrossRef]
- Rovelli, C. Black hole entropy from loop quantum gravity. Phys. Rev. Lett. 1996, 77, 3288. [Google Scholar] [CrossRef] [PubMed]
- Amico, L.; Fazio, R.; Osterloh, A.; Vedral, V. Entanglement in many-body systems. Rev. Mod. Phys. 2008, 80, 517–576. [Google Scholar] [CrossRef]
- Eisert, J.; Cramer, M.; Plenio, M.B. Colloquium: Area laws for the entanglement entropy. Rev. Mod. Phys. 2010, 82, 277–306. [Google Scholar] [CrossRef]
- Belfiglio, A.; Chandran, S.M.; Luongo, O.; Mancini, S. Horizon entanglement area law from regular black hole thermodynamics. Phys. Rev. D 2025, 111, 024013. [Google Scholar] [CrossRef]
- Belfiglio, A.; Luongo, O.; Mancini, S. Entanglement area law violation from field-curvature coupling. Phys. Lett. B 2024, 848, 138398. [Google Scholar] [CrossRef]
- Vedral, V. The role of relative entropy in quantum information theory. Rev. Mod. Phys. 2002, 74, 197. [Google Scholar] [CrossRef]
- Araki, H. Relative entropy of states of von Neumann algebras. Publ. Res. Inst. Math. Sci. 1975, 11, 809–833. [Google Scholar] [CrossRef]
- Araki, H. Mathematical Theory of Quantum Fields; Oxford University Press: Cary, NC, USA, 1999. [Google Scholar]
- Witten, E. APS Medal for Exceptional Achievement in Research: Invited article on entanglement properties of quantum field theory. Rev. Mod. Phys. 2018, 90, 045003. [Google Scholar] [CrossRef]
- Ohya, M.; Petz, D. Quantum Entropy and Its Use; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Bianconi, G. Gravity from entropy. Phys. Rev. D. 2025, 111, 066001. [Google Scholar] [CrossRef]
- Rosen, N. A bi-metric theory of gravitation. Gen. Relativ. Gravit. 1973, 4, 435–447. [Google Scholar] [CrossRef]
- Hossenfelder, S. Bimetric theory with exchange symmetry. Phys. Rev. Part. Fields Gravit. Cosmol. 2008, 78, 044015. [Google Scholar] [CrossRef]
- Schuller, F.P.; Wohlfarth, M.N. Geometry of manifolds with area metric: Multi-metric backgrounds. Nucl. Phys. B 2006, 747, 398–422. [Google Scholar] [CrossRef]
- Borissova, J.N.; Dittrich, B.; Krasnov, K. Area-metric gravity revisited. Phys. Rev. D 2024, 109, 124035. [Google Scholar] [CrossRef]
- Kuipers, F. Quantum Theory, Gravity and Second Order Geometry. arXiv 2024, arXiv:2410.06799. [Google Scholar]
- Dittrich, B.; Kogios, A. From spin foams to area metric dynamics to gravitons. Class. Quantum Gravity 2023, 40, 095011. [Google Scholar] [CrossRef]
- Berti, E.; Barausse, E.; Cardoso, V.; Gualtieri, L.; Pani, P.; Sperhake, U.; Stein, L.C.; Wex, N.; Yagi, K.; Baker, T.; et al. Testing general relativity with present and future astrophysical observations. Class. Quantum Gravity 2015, 32, 243001. [Google Scholar] [CrossRef]
- Isi, M.; Farr, W.M.; Giesler, M.; Scheel, M.A.; Teukolsky, S.A. Testing the black-hole area law with GW150914. Phys. Rev. Lett. 2021, 127, 011103. [Google Scholar] [CrossRef]
- Barcelo, C.; Liberati, S.; Visser, M. Analogue gravity from Bose-Einstein condensates. Class. Quantum Gravity 2001, 18, 1137. [Google Scholar] [CrossRef]
- Weinfurtner, S.; Tedford, E.W.; Penrice, M.C.; Unruh, W.G.; Lawrence, G.A. Measurement of stimulated Hawking emission in an analogue system. Phys. Rev. Lett. 2011, 106, 021302. [Google Scholar] [CrossRef]
- Gooding, C.; Biermann, S.; Erne, S.; Louko, J.; Unruh, W.G.; Schmiedmayer, J.; Weinfurtner, S. Interferometric unruh detectors for Bose-Einstein condensates. Phys. Rev. Lett. 2020, 125, 213603. [Google Scholar] [CrossRef]
- Bose, S.; Mazumdar, A.; Morley, G.W.; Ulbricht, H.; Toroš, M.; Paternostro, M.; Geraci, A.A.; Barker, P.F.; Kim, M.; Milburn, G. Spin entanglement witness for quantum gravity. Phys. Rev. Lett. 2017, 119, 240401. [Google Scholar] [CrossRef]
- Marletto, C.; Vedral, V. Gravitationally induced entanglement between two massive particles is sufficient evidence of quantum effects in gravity. Phys. Rev. Lett. 2017, 119, 240402. [Google Scholar] [CrossRef]
- Marletto, C.; Vedral, V. Quantum-information methods for quantum gravity laboratory-based tests. arXiv 2024, arXiv:2410.07262. [Google Scholar]
- Howl, R.; Vedral, V.; Naik, D.; Christodoulou, M.; Rovelli, C.; Iyer, A. Non-gaussianity as a signature of a quantum theory of gravity. PRX Quantum 2021, 2, 010325. [Google Scholar] [CrossRef]
- Huang, K. Introduction to Statistical Physics; Chapman and Hall: London, UK; CRC: Boca Raton, FL, USA, 1987. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bianconi, G. The Quantum Relative Entropy of the Schwarzschild Black Hole and the Area Law. Entropy 2025, 27, 266. https://doi.org/10.3390/e27030266
Bianconi G. The Quantum Relative Entropy of the Schwarzschild Black Hole and the Area Law. Entropy. 2025; 27(3):266. https://doi.org/10.3390/e27030266
Chicago/Turabian StyleBianconi, Ginestra. 2025. "The Quantum Relative Entropy of the Schwarzschild Black Hole and the Area Law" Entropy 27, no. 3: 266. https://doi.org/10.3390/e27030266
APA StyleBianconi, G. (2025). The Quantum Relative Entropy of the Schwarzschild Black Hole and the Area Law. Entropy, 27(3), 266. https://doi.org/10.3390/e27030266





