Evaluating Methods for Detrending Time Series Using Ordinal Patterns, with an Application to Air Transport Delays
Abstract
1. Introduction
2. Materials and Methods
2.1. Detrending Methods
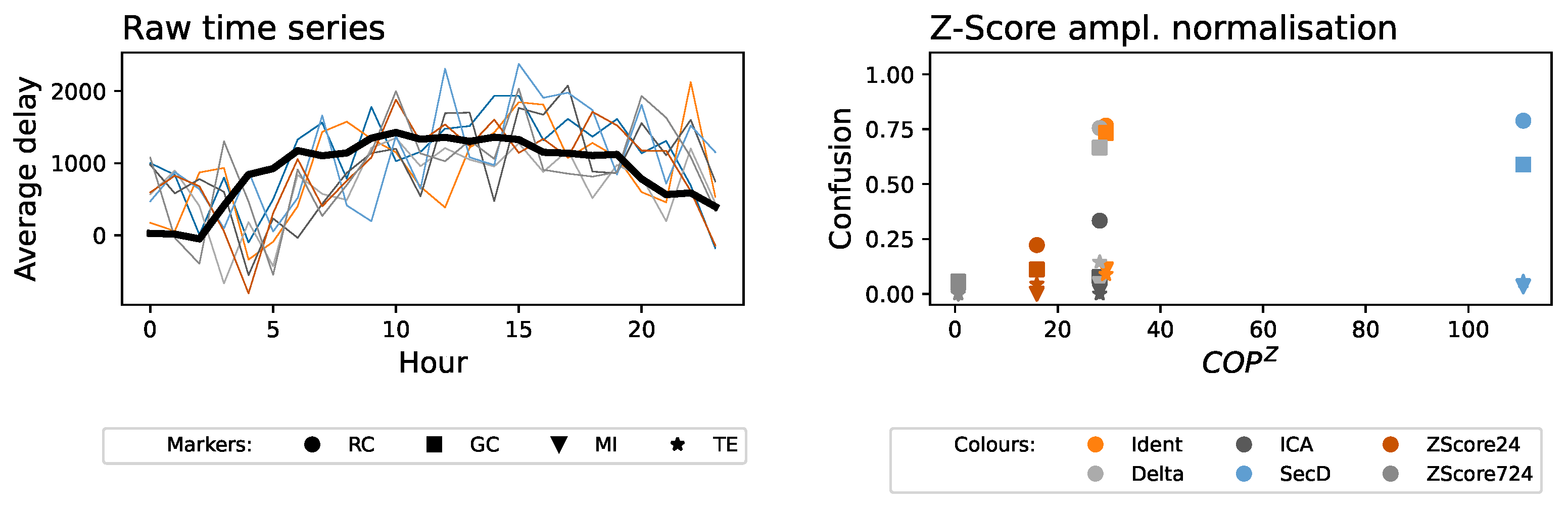
- Identity (Ident). As a reference, in the following analyses, we include the results corresponding to not performing any detrending on the time series.
- Delta (Delta). Simple detrending process based on evaluating the distance between the value at a given hour and the expected value observed for the same weekday and at the same hour: , with and representing the average.
- Independent Component Analysis (ICA). The time series are detrended by subtracting the three main components detected throughout all the airports by an Independent Component Analysis [26]. While computationally more costly than other solutions, it presents the advantage of being able to detect trends with variable periods, provided they are shared by multiple airports.
- Second Derivative (SecD). The second difference of the time series, i.e., . This approach is customary in the literature when no information about the nature of the underlying periodic trends is available.
- Z-Score by day (ZScore24). Detrending based on a Z-Score, defined as: . represents the set of values observed on different days at the same hour, i.e., with . In turn, and represent, respectively, the average and the standard deviation operators. The Z-Score encodes how much the observed value deviates from the expectation, in this case from the delay observed at the same hour on other days; but, as a difference with respect to the Delta approach, it takes into account the variability of the data.
- Z-Score by week (ZScore724). Same as the ZScore24, but taking as reference the delays observed at the same hour on the same day of the week. is thus here defined as with . ZScore724 should, therefore, also detrend with respect to weekly patterns, e.g., weekdays vs. weekends.
2.2. Evaluating the Detrending Process
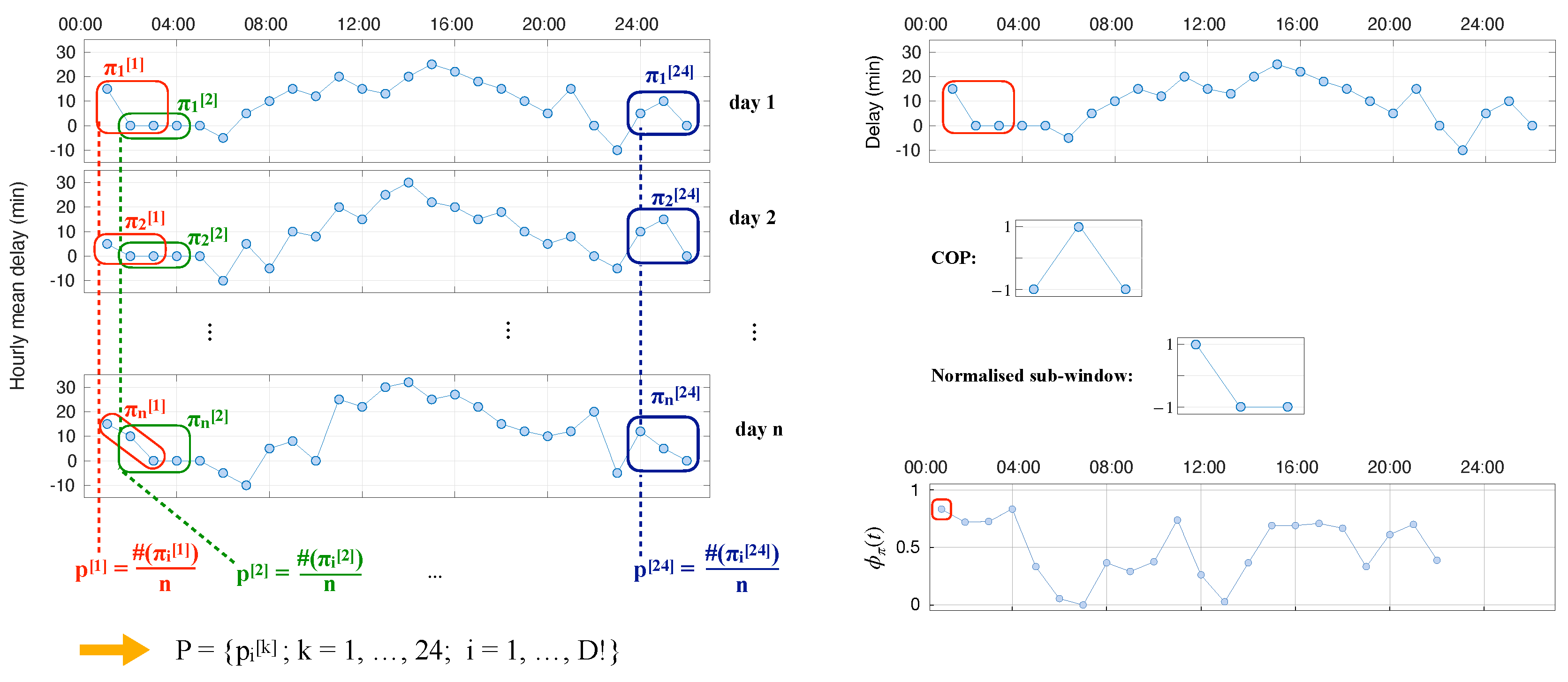
2.2.1. Ordinal Patterns in Time Series
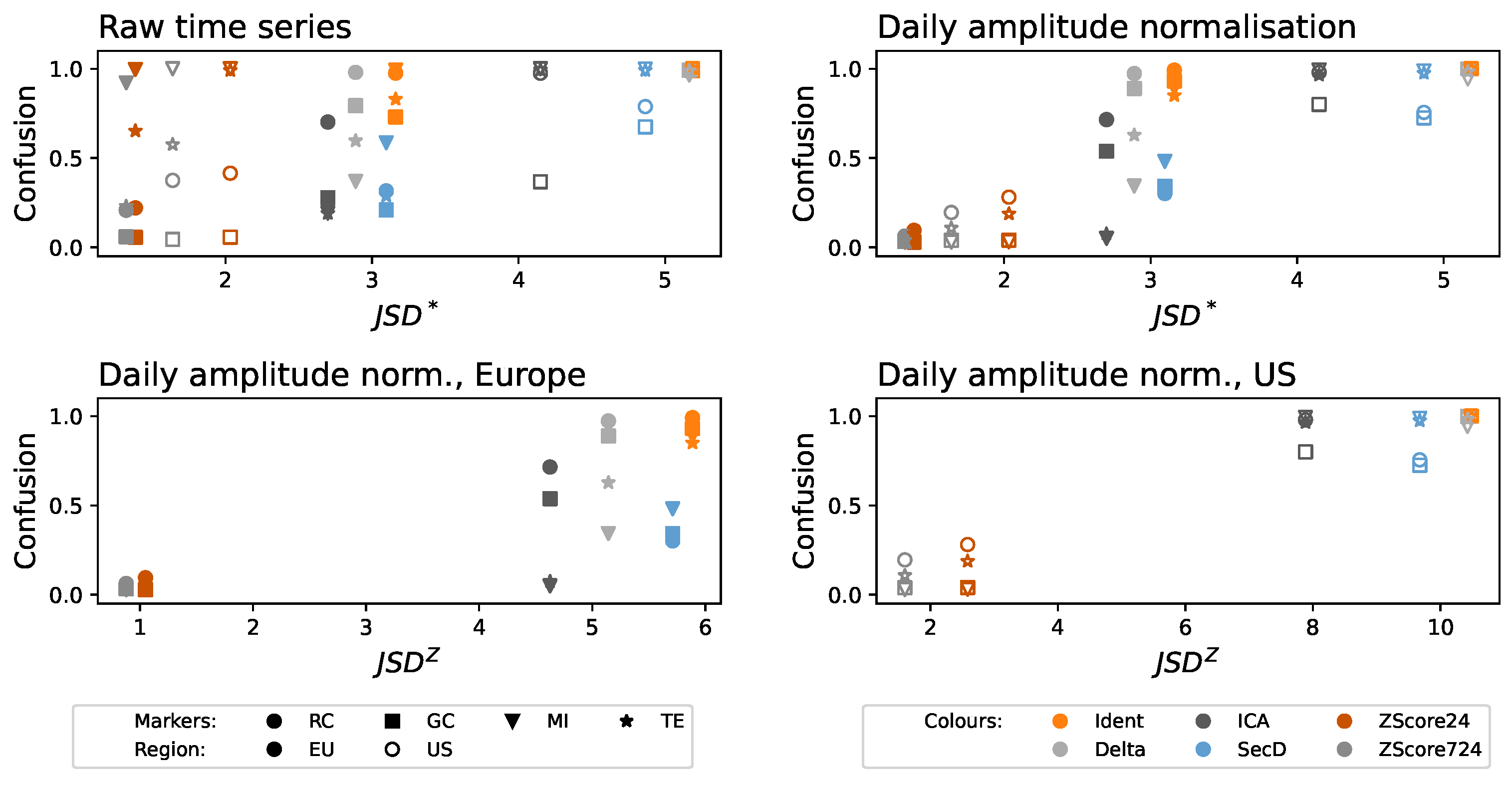
2.2.2. Jensen–Shannon Divergence of Ordinal Patterns
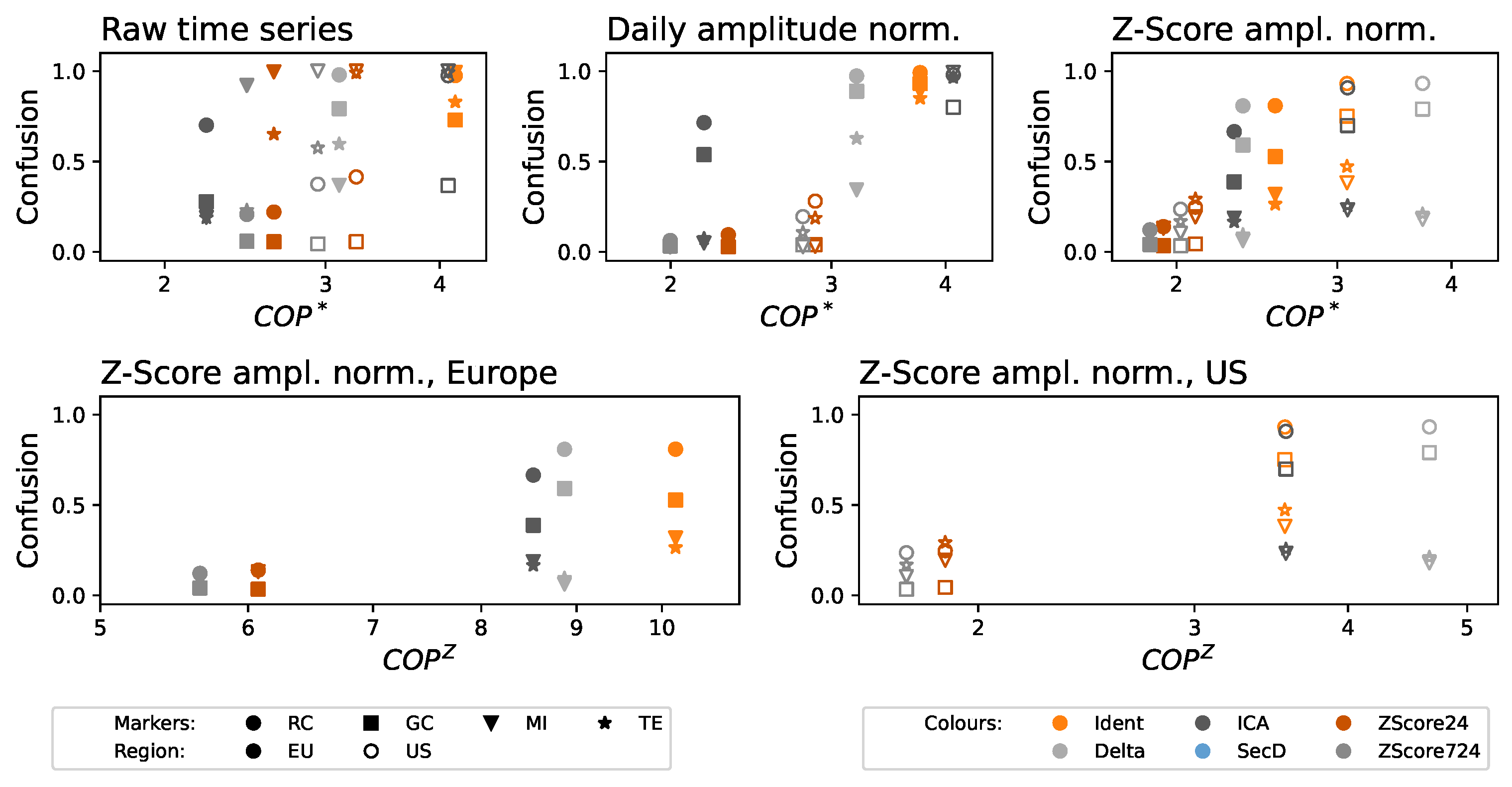
2.2.3. Continuous Ordinal Patterns
2.2.4. Metric Normalization
2.3. Assessing Functional Connectivity
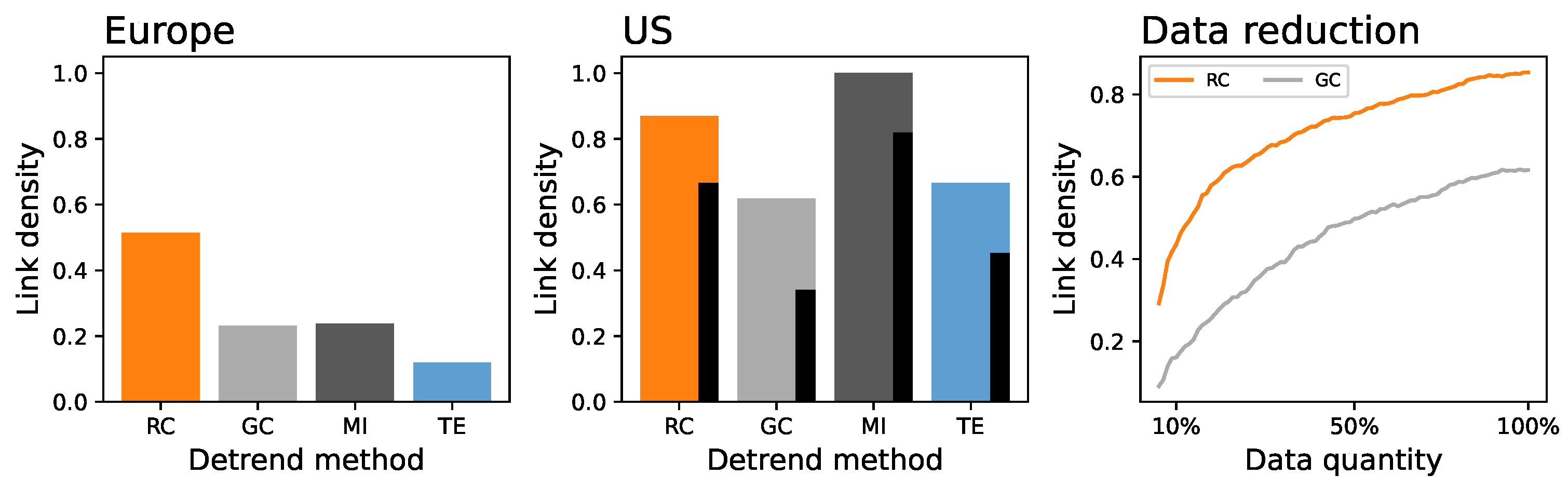
- Rank Correlation (RC). Spearman’s Rank Correlation between the two analyzed time series, calculated over shifted time series , with , to account for the time required by delays to propagate. The yielding the lower p-value is the one selected.
- Granger Causality (GC). The GC [47] is one of the best-known exponents of predictive causality [48] and assesses whether the inclusion of information about the driving element X helps predict the future dynamics of the driven element Y. As originally proposed, an autoregressive-moving-average (ARMA) model is used for the prediction. Two variants are constructed, forecasting Y by, respectively, introducing or not data about X’s past. Finally, the two models’ residuals are compared through an F-test, yielding a p-value indicating whether the presence of information about X is relevant—and, hence, whether a causality relationship is present.
- Mutual Information (MI). MI is an information-theoretic measure that captures the shared amount of information between any two random variables. The Shannon information for X and Y, respectively denoted as and , represent the corresponding amount of potential information or the degree of uncertainty [49]. MI quantifies how much of the uncertainty in Y is reduced or explained after knowing the full information of X, i.e.,where represents the joint probability distribution, while and denote the marginal probability distributions. MI is particularly interesting for investigating the relationship between two variables because, in contrast to cross-correlation, it is sensitive to non-linear dependencies. In this work, MI is estimated using the Kozachenko–Stögbauer–Grassberger (KSG) method [50], which is well suited for continuous random variables following non-parametric (or unknown) distributions.
- Transfer Entropy (TE). TE is also an information-theoretic measure that captures the amount of directional information flow from a source variable (e.g., X) to a target variable (e.g., Y) [51]. It is the measure of the amount of information contained in the past states of a source process (i.e., ) about the future state of the target process (i.e., Y) given that the past states of the target (i.e., ) are known:
2.4. Data on Airport Dynamics
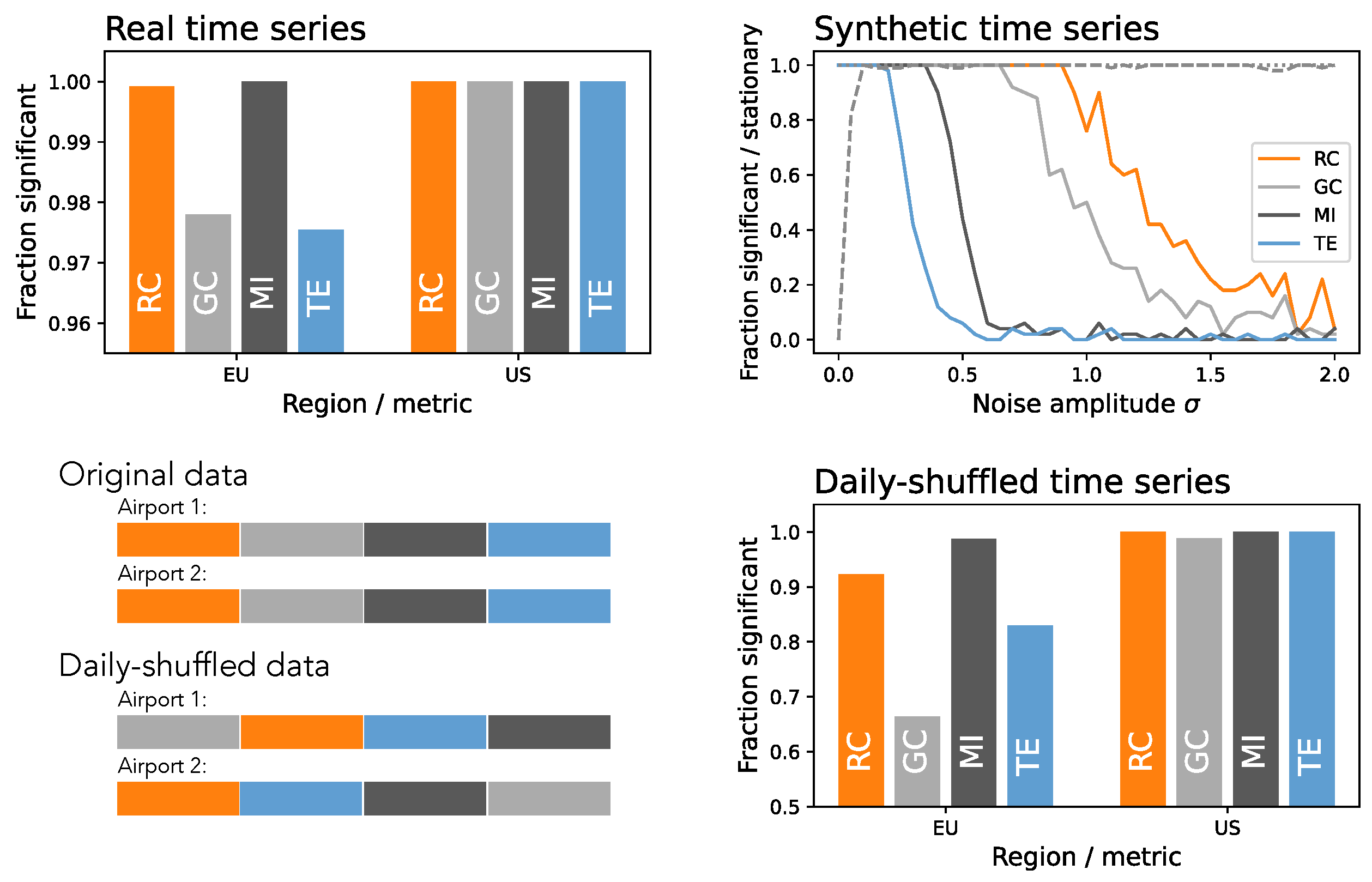
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Rank | Code | Name | Departures | Arrivals |
|---|---|---|---|---|
| 1 | EGLL | Heathrow Airport | 26.39 | 26.41 |
| 2 | LFPG | Charles de Gaulle Airport | 26.97 | 26.91 |
| 3 | EHAM | Amsterdam Airport Schiphol | 27.37 | 27.31 |
| 4 | EDDF | Frankfurt am Main Airport | 26.92 | 26.89 |
| 5 | LEMD | Adolfo Suárez Madrid-Barajas Airport | 21.93 | 21.90 |
| 6 | LEBL | Josep Tarradellas Barcelona-El Prat Airport | 17.77 | 17.76 |
| 7 | EDDM | Munich Airport | 22.13 | 22.14 |
| 8 | EGKK | Gatwick Airport | 15.83 | 15.79 |
| 9 | LIRF | Leonardo da Vinci-Fiumicino Airport | 17.17 | 17.17 |
| 10 | LFPO | Orly Airport | 12.96 | 12.94 |
| 11 | EIDW | Dublin Airport | 12.24 | 12.22 |
| 12 | LSZH | Zurich Airport | 14.15 | 14.11 |
| 13 | EKCH | Copenhagen Airport | 14.62 | 14.64 |
| 14 | LEPA | Palma de Mallorca Airport | 10.97 | 10.99 |
| 15 | LPPT | Lisbon Airport | 11.00 | 11.01 |
| 16 | ENGM | Oslo Airport, Gardermoen | 13.75 | 13.75 |
| 17 | EGCC | Manchester Airport | 10.84 | 10.82 |
| 18 | EGSS | London Stansted Airport | 10.01 | 10.00 |
| 19 | LOWW | Vienna International Airport | 13.91 | 13.89 |
| 20 | ESSA | Stockholm Arlanda Airport | 13.31 | 13.31 |
| 21 | EBBR | Brussels Airport | 12.54 | 12.51 |
| 22 | LIMC | Malpensa Airport | 10.49 | 10.49 |
| 23 | EDDL | Düsseldorf Airport | 11.96 | 11.94 |
| 24 | LGAV | Athens International Airport | 10.62 | 10.63 |
| 25 | EDDT | Berlin Tegel Airport | 10.18 | 10.17 |
| 26 | LEMG | Málaga Airport | 6.82 | 6.82 |
| 27 | EPWA | Warsaw Chopin Airport | 9.21 | 9.21 |
| 28 | LSGG | Geneva Airport | 9.63 | 9.63 |
| 29 | EDDH | Hamburg Airport | 8.16 | 8.16 |
| 30 | LKPR | Václav Havel Airport Prague | 7.80 | 7.81 |
| 31 | EGGW | Luton Airport | 6.84 | 6.85 |
| 32 | LHBP | Budapest Ferenc Liszt International Airport | 5.78 | 5.77 |
| 33 | EGPH | Edinburgh Airport | 6.87 | 6.86 |
| 34 | LEAL | Alicante-Elche Airport | 4.94 | 4.94 |
| 35 | LFMN | Nice Côte d’Azur Airport | 7.22 | 7.23 |
| 36 | LROP | Henri Coanda International Airport | 6.20 | 6.19 |
| 37 | EDDK | Cologne Bonn Airport | 7.27 | 7.26 |
| 38 | LIME | Orio al Serio International Airport | 4.69 | 4.68 |
| 39 | UKBB | Boryspil International Airport | 4.88 | 4.89 |
| 40 | EGBB | Birmingham Airport | 6.01 | 6.00 |
| 41 | LPPR | Porto Airport | 4.73 | 4.73 |
| 42 | EDDS | Stuttgart Airport | 6.45 | 6.45 |
| 43 | LIPZ | Venice Marco Polo Airport | 4.99 | 4.99 |
| 44 | LFLL | Lyon-Saint-Exupéry Airport | 6.30 | 6.30 |
| 45 | LICC | Catania-Fontanarossa Airport | 3.66 | 3.66 |
| 46 | LIRN | Naples Airport | 3.85 | 3.85 |
| 47 | EGPF | Glasgow Airport | 4.86 | 4.84 |
| 48 | LFBO | Toulouse-Blagnac Airport | 5.14 | 5.11 |
| 49 | LFML | Marseille Provence Airport | 5.21 | 5.20 |
| 50 | LIML | Linate Airport | 5.88 | 5.88 |
| Rank | Code | Name | Title 3 | Rank |
|---|---|---|---|---|
| 1 | ATL | Hartsfield-Jackson Atlanta International Airport | 41.63 | 41.61 |
| 2 | DEN | Denver International Airport | 25.41 | 25.38 |
| 3 | DFW | Dallas Fort Worth International Airport | 25.42 | 25.35 |
| 4 | LAX | Los Angeles International Airport | 23.76 | 23.77 |
| 5 | ORD | Chicago O’Hare International Airport | 31.42 | 31.37 |
| 6 | PHX | Phoenix Sky Harbor International Airport | 17.81 | 17.79 |
| 7 | MSP | Minneapolis-Saint Paul International Airport | 14.95 | 14.95 |
| 8 | CLT | Charlotte Douglas International Airport | 16.17 | 16.14 |
| 9 | SEA | Seattle-Tacoma International Airport | 14.88 | 14.88 |
| 10 | SFO | San Francisco International Airport | 18.77 | 18.77 |
| 11 | JFK | John F. Kennedy International Airport | 11.69 | 11.68 |
| 12 | IAH | George Bush Intercontinental Airport | 17.04 | 17.00 |
| 13 | MCO | Orlando International Airport | 14.51 | 14.51 |
| 14 | EWR | Newark Liberty International Airport | 13.48 | 13.46 |
| 15 | LAS | Harry Reid International Airport | 17.10 | 17.12 |
| 16 | FLL | Fort Lauderdale-Hollywood International Airport | 9.87 | 9.87 |
| 17 | BOS | General Edward Lawrence Logan International Airport | 14.34 | 14.36 |
| 18 | DTW | Detroit Metropolitan Wayne County Airport | 14.45 | 14.47 |
| 19 | MIA | Miami International Airport | 8.31 | 8.31 |
| 20 | LGA | LaGuardia Airport | 12.84 | 12.80 |
| 21 | IAD | Washington Dulles International Airport | 5.37 | 5.37 |
| 22 | BWI | Baltimore/Washington International Thurgood Marshall Airport | 10.96 | 10.96 |
| 23 | PHL | Philadelphia International Airport | 9.53 | 9.53 |
| 24 | SAN | San Diego International Airport | 9.28 | 9.28 |
| 25 | MDW | Chicago Midway International Airport | 9.45 | 9.43 |
| 26 | SLC | Salt Lake City International Airport | 11.91 | 11.93 |
| 27 | DCA | Ronald Reagan Washington National Airport | 10.32 | 10.32 |
| 28 | TPA | Tampa International Airport | 7.89 | 7.90 |
| 29 | PDX | Portland International Airport | 6.58 | 6.59 |
| 30 | STL | St. Louis Lambert International Airport | 6.47 | 6.48 |
| 31 | BNA | Nashville International Airport | 6.78 | 6.79 |
| 32 | AUS | Austin-Bergstrom International Airport | 6.04 | 6.05 |
| 33 | HNL | Daniel K. Inouye International Airport | 5.44 | 5.44 |
| 34 | SJC | San José International Airport | 5.50 | 5.50 |
| 35 | MCI | Kansas City International Airport | 5.24 | 5.25 |
| 36 | DAL | Dallas Love Field | 7.65 | 7.63 |
| 37 | SMF | Sacramento International Airport | 4.97 | 4.98 |
| 38 | MSY | Louis Armstrong New Orleans International Airport | 5.40 | 5.40 |
| 39 | SNA | John Wayne Airport | 4.56 | 4.57 |
| 40 | RDU | Raleigh-Durham International Airport | 4.88 | 4.89 |
| 41 | RSW | Southwest Florida International Airport | 3.42 | 3.42 |
| 42 | PIT | Pittsburgh International Airport | 3.78 | 3.79 |
| 43 | HOU | William P. Hobby Airport | 6.17 | 6.16 |
| 44 | IND | Indianapolis International Airport | 3.75 | 3.76 |
| 45 | SAT | San Antonio International Airport | 3.87 | 3.88 |
| 46 | SJU | Luis Mu noz Marín International Airport | 2.84 | 2.85 |
| 47 | CLE | Cleveland Hopkins International Airport | 4.36 | 4.37 |
| 48 | OAK | Oakland International Airport | 5.54 | 5.53 |
| 49 | CVG | Cincinnati/Northern Kentucky International Airport | 3.10 | 3.11 |
| 50 | CMH | John Glenn Columbus International Airport | 3.44 | 3.45 |
References
- Anderson, P.W. More Is Different: Broken symmetry and the nature of the hierarchical structure of science. Science 1972, 177, 393–396. [Google Scholar] [CrossRef] [PubMed]
- Strogatz, S.H. Exploring complex networks. Nature 2001, 410, 268–276. [Google Scholar] [CrossRef] [PubMed]
- Bullmore, E.; Sporns, O. Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 2009, 10, 186–198. [Google Scholar] [CrossRef] [PubMed]
- Sporns, O. Structure and function of complex brain networks. Dialogues Clin. Neurosci. 2013, 15, 247–262. [Google Scholar] [CrossRef]
- Park, H.J.; Friston, K. Structural and functional brain networks: From connections to cognition. Science 2013, 342, 1238411. [Google Scholar] [CrossRef]
- Lee, I.; Date, S.V.; Adai, A.T.; Marcotte, E.M. A probabilistic functional network of yeast genes. Science 2004, 306, 1555–1558. [Google Scholar] [CrossRef]
- Lezon, T.R.; Banavar, J.R.; Cieplak, M.; Maritan, A.; Fedoroff, N.V. Using the principle of entropy maximization to infer genetic interaction networks from gene expression patterns. Proc. Natl. Acad. Sci. USA 2006, 103, 19033–19038. [Google Scholar] [CrossRef]
- Boone, C.; Bussey, H.; Andrews, B.J. Exploring genetic interactions and networks with yeast. Nat. Rev. Genet. 2007, 8, 437–449. [Google Scholar] [CrossRef]
- Tsonis, A.A.; Roebber, P.J. The architecture of the climate network. Phys. A Stat. Mech. Its Appl. 2004, 333, 497–504. [Google Scholar] [CrossRef]
- Donges, J.F.; Zou, Y.; Marwan, N.; Kurths, J. The backbone of the climate network. Europhys. Lett. 2009, 87, 48007. [Google Scholar] [CrossRef]
- Zanin, M.; Belkoura, S.; Zhu, Y. Network analysis of Chinese air transport delay propagation. Chin. J. Aeronaut. 2017, 30, 491–499. [Google Scholar] [CrossRef]
- Pastorino, L.; Zanin, M. Air delay propagation patterns in Europe from 2015 to 2018: An information processing perspective. J. Phys. Complex. 2021, 3, 015001. [Google Scholar] [CrossRef]
- Guo, Z.; Hao, M.; Yu, B.; Yao, B. Detecting delay propagation in regional air transport systems using convergent cross mapping and complex network theory. Transp. Res. Part E Logist. Transp. Rev. 2022, 157, 102585. [Google Scholar] [CrossRef]
- Carlier, S.; De Lépinay, I.; Hustache, J.C.; Jelinek, F. Environmental impact of air traffic flow management delays. In Proceedings of the 7th USA/Europe air traffic management research and development seminar (ATM2007), Barcelona, Spain, 2–5 July 2007; Volume 2, p. 16. [Google Scholar]
- Peterson, E.B.; Neels, K.; Barczi, N.; Graham, T. The economic cost of airline flight delay. J. Transp. Econ. Policy (JTEP) 2013, 47, 107–121. [Google Scholar]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Costa, L.d.F.; Rodrigues, F.A.; Travieso, G.; Villas Boas, P.R. Characterization of complex networks: A survey of measurements. Adv. Phys. 2007, 56, 167–242. [Google Scholar] [CrossRef]
- Kwiatkowski, D.; Phillips, P.C.; Schmidt, P.; Shin, Y. Testing the null hypothesis of stationarity against the alternative of a unit root: How sure are we that economic time series have a unit root? J. Econom. 1992, 54, 159–178. [Google Scholar] [CrossRef]
- Dickey, D.A.; Fuller, W.A. Distribution of the estimators for autoregressive time series with a unit root. J. Am. Stat. Assoc. 1979, 74, 427–431. [Google Scholar]
- Zanin, M.; Olivares, F. Ordinal patterns-based methodologies for distinguishing chaos from noise in discrete time series. Commun. Phys. 2021, 4, 190. [Google Scholar] [CrossRef]
- Leyva, I.; Martínez, J.H.; Masoller, C.; Rosso, O.A.; Zanin, M. 20 years of ordinal patterns: Perspectives and challenges. Europhys. Lett. 2022, 138, 31001. [Google Scholar] [CrossRef]
- Bandt, C.; Shiha, F. Order patterns in time series. J. Time Ser. Anal. 2007, 28, 646–665. [Google Scholar] [CrossRef]
- Weiß, C.H. Non-parametric tests for serial dependence in time series based on asymptotic implementations of ordinal-pattern statistics. Chaos Interdiscip. J. Nonlinear Sci. 2022, 32, 093107. [Google Scholar] [CrossRef] [PubMed]
- Zanin, M. Continuous ordinal patterns: Creating a bridge between ordinal analysis and deep learning. Chaos Interdiscip. J. Nonlinear Sci. 2023, 33, 033114. [Google Scholar] [CrossRef] [PubMed]
- Acharya, K.; Olivares, F.; Zanin, M. How representative are air transport functional complex networks? A quantitative validation. Chaos Interdiscip. J. Nonlinear Sci. 2024, 34, 043133. [Google Scholar] [CrossRef]
- Lee, T.W.; Lee, T.W. Independent Component Analysis; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Amigó, J.M.; Zambrano, S.; Sanjuán, M.A. True and false forbidden patterns in deterministic and random dynamics. Europhys. Lett. 2007, 79, 50001. [Google Scholar] [CrossRef]
- Zunino, L.; Soriano, M.C.; Fischer, I.; Rosso, O.A.; Mirasso, C.R. Permutation-information-theory approach to unveil delay dynamics from time-series analysis. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2010, 82, 046212. [Google Scholar] [CrossRef]
- Rosso, O.A.; Carpi, L.C.; Saco, P.M.; Ravetti, M.G.; Plastino, A.; Larrondo, H.A. Causality and the entropy–complexity plane: Robustness and missing ordinal patterns. Phys. A Stat. Mech. Its Appl. 2012, 391, 42–55. [Google Scholar] [CrossRef]
- Rosso, O.A.; Larrondo, H.; Martin, M.T.; Plastino, A.; Fuentes, M.A. Distinguishing noise from chaos. Phys. Rev. Lett. 2007, 99, 154102. [Google Scholar] [CrossRef]
- Zunino, L.; Soriano, M.C.; Rosso, O.A. Distinguishing chaotic and stochastic dynamics from time series by using a multiscale symbolic approach. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2012, 86, 046210. [Google Scholar] [CrossRef]
- Amigó, J.M.; Rosso, O.A. Ordinal methods: Concepts, applications, new developments, and challenges-In memory of Karsten Keller (1961–2022). Chaos Interdiscip. J. Nonlinear Sci. 2023, 33, 080401. [Google Scholar] [CrossRef] [PubMed]
- Amigó, J.M.; Kocarev, L.; Szczepanski, J. Order patterns and chaos. Phys. Lett. A 2006, 355, 27–31. [Google Scholar] [CrossRef]
- Carpi, L.C.; Saco, P.M.; Rosso, O.A. Missing ordinal patterns in correlated noises. Phys. A Stat. Mech. Its Appl. 2010, 389, 2020–2029. [Google Scholar] [CrossRef]
- Olivares, F.; Zunino, L.; Pérez, D.G. Revisiting the decay of missing ordinal patterns in long-term correlated time series. Phys. A Stat. Mech. Its Appl. 2019, 534, 122100. [Google Scholar] [CrossRef]
- Zunino, L.; Zanin, M.; Tabak, B.M.; Pérez, D.G.; Rosso, O.A. Forbidden patterns, permutation entropy and stock market inefficiency. Phys. A Stat. Mech. Its Appl. 2009, 388, 2854–2864. [Google Scholar] [CrossRef]
- Tiana-Alsina, J.; Buldu, J.M.; Torrent, M.; García-Ojalvo, J. Quantifying stochasticity in the dynamics of delay-coupled semiconductor lasers via forbidden patterns. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2010, 368, 367–377. [Google Scholar] [CrossRef]
- Olivares, F.; Zunino, L.; Soriano, M.C.; Pérez, D.G. Unraveling the decay of the number of unobserved ordinal patterns in noisy chaotic dynamics. Phys. Rev. E 2019, 100, 042215. [Google Scholar] [CrossRef]
- Bandt, C. Statistics and contrasts of order patterns in univariate time series. Chaos Interdiscip. J. Nonlinear Sci. 2023, 33, 033124. [Google Scholar] [CrossRef]
- Martínez, J.H.; Herrera-Diestra, J.L.; Chavez, M. Detection of time reversibility in time series by ordinal patterns analysis. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 123111. [Google Scholar] [CrossRef]
- Zanin, M.; Rodríguez-González, A.; Menasalvas Ruiz, E.; Papo, D. Assessing time series reversibility through permutation patterns. Entropy 2018, 20, 665. [Google Scholar] [CrossRef]
- Zunino, L.; Olivares, F.; Ribeiro, H.V.; Rosso, O.A. Permutation Jensen-Shannon distance: A versatile and fast symbolic tool for complex time-series analysis. Phys. Rev. E 2022, 105, 045310. [Google Scholar] [CrossRef] [PubMed]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Olivares, F.; Zunino, L.; Zanin, M. Markov-modulated model for landing flow dynamics: An ordinal analysis validation. Chaos Interdiscip. J. Nonlinear Sci. 2023, 33, 033142. [Google Scholar] [CrossRef] [PubMed]
- Zanin, M. Augmenting granger causality through continuous ordinal patterns. Commun. Nonlinear Sci. Numer. Simul. 2024, 128, 107606. [Google Scholar] [CrossRef]
- Granger, C.W. Investigating causal relations by econometric models and cross-spectral methods. Econom. J. Econom. Soc. 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Diebold, F.X. Independent Component Analysis; Elements of Forecasting; Cengage Learning: Mason, OH, USA, 1998. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69, 066138. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring Information Transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef]
- Wiener, N. The theory of prediction. In Modern Mathematics for the Engineer; Beckenbach, E.F., Ed.; McGraw-Hill: New York, NY, USA, 1956; pp. 125–139. [Google Scholar]
- Gomez-Herrero, G.; Wu, W.; Rutanen, K.; Soriano, M.; Pipa, G.; Vicente, R. Assessing Coupling Dynamics from an Ensemble of Time Series. Entropy 2010, 17, 1958–1970. [Google Scholar] [CrossRef]
- Cook, A.; Belkoura, S.; Zanin, M. ATM performance measurement in Europe, the US and China. Chin. J. Aeronaut. 2017, 30, 479–490. [Google Scholar] [CrossRef]
- Raffalovich, L.E. Detrending time series: A cautionary note. Sociol. Methods Res. 1994, 22, 492–519. [Google Scholar] [CrossRef]
- Azami, H.; Escudero, J. Amplitude-aware permutation entropy: Illustration in spike detection and signal segmentation. Comput. Methods Programs Biomed. 2016, 128, 40–51. [Google Scholar] [CrossRef] [PubMed]
- Cuesta Frau, D. Permutation entropy: Influence of amplitude information on time series classification performance. Math. Biosci. Eng. 2019, 16, 6842–6857. [Google Scholar] [CrossRef] [PubMed]
- Fadlallah, B.; Chen, B.; Keil, A.; Príncipe, J. Weighted-permutation entropy: A complexity measure for time series incorporating amplitude information. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2013, 87, 022911. [Google Scholar] [CrossRef]
- Stosic, D.; Stosic, D.; Stosic, T.; Stosic, B. Generalized weighted permutation entropy. Chaos Interdiscip. J. Nonlinear Sci. 2022, 32. [Google Scholar] [CrossRef]
- Cuesta-Frau, D. Slope entropy: A new time series complexity estimator based on both symbolic patterns and amplitude information. Entropy 2019, 21, 1167. [Google Scholar] [CrossRef]
- Knight, M.I.; Nunes, M.; Nason, G. Modelling, detrending and decorrelation of network time series. arXiv 2016, arXiv:1603.03221. [Google Scholar]
- Eurocontrol; FAA. Comparison of Air Traffic Management Related Operational and Economic Performance U.S.—Europe; Technical Report; 2024. Available online: https://www.eurocontrol.int/publication/comparison-air-traffic-management-related-operational-and-economic-performance (accessed on 25 December 2024).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olivares, F.; Marín-Rodríguez, F.J.; Acharya, K.; Zanin, M. Evaluating Methods for Detrending Time Series Using Ordinal Patterns, with an Application to Air Transport Delays. Entropy 2025, 27, 230. https://doi.org/10.3390/e27030230
Olivares F, Marín-Rodríguez FJ, Acharya K, Zanin M. Evaluating Methods for Detrending Time Series Using Ordinal Patterns, with an Application to Air Transport Delays. Entropy. 2025; 27(3):230. https://doi.org/10.3390/e27030230
Chicago/Turabian StyleOlivares, Felipe, F. Javier Marín-Rodríguez, Kishor Acharya, and Massimiliano Zanin. 2025. "Evaluating Methods for Detrending Time Series Using Ordinal Patterns, with an Application to Air Transport Delays" Entropy 27, no. 3: 230. https://doi.org/10.3390/e27030230
APA StyleOlivares, F., Marín-Rodríguez, F. J., Acharya, K., & Zanin, M. (2025). Evaluating Methods for Detrending Time Series Using Ordinal Patterns, with an Application to Air Transport Delays. Entropy, 27(3), 230. https://doi.org/10.3390/e27030230









