Adsorption Kinetics Model of Hydrogen on Graphite
Abstract
1. Introduction
2. Theoretical Considerations
2.1. Isothermal Adsorption Kinetics
2.1.1. Net Rate—Non-Langmuir Kinetics
2.1.2. Net Rate—Langmuir Kinetics
2.1.3. Net Rate—Henry’s Regime
2.2. The Transport Equation
2.2.1. Isothermal Conditions
2.2.2. Non-Isothermal Conditions
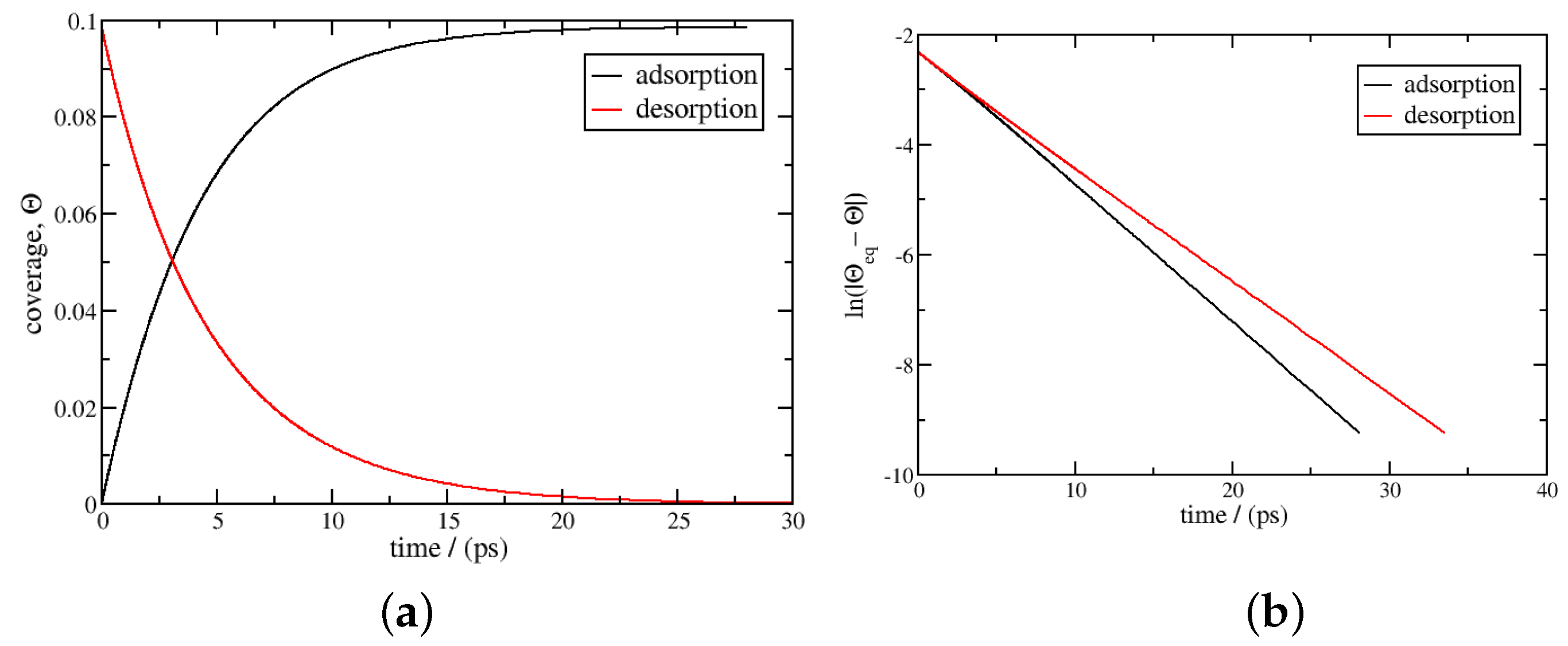
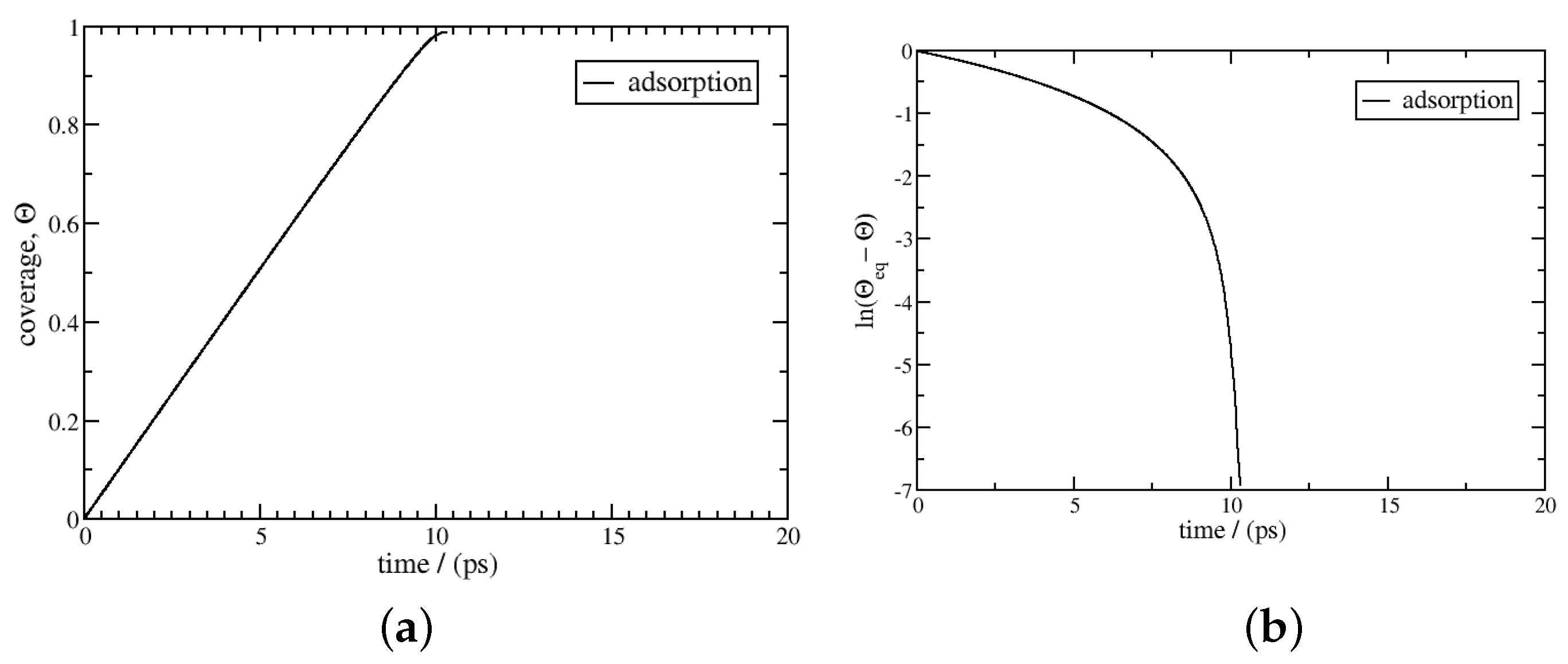
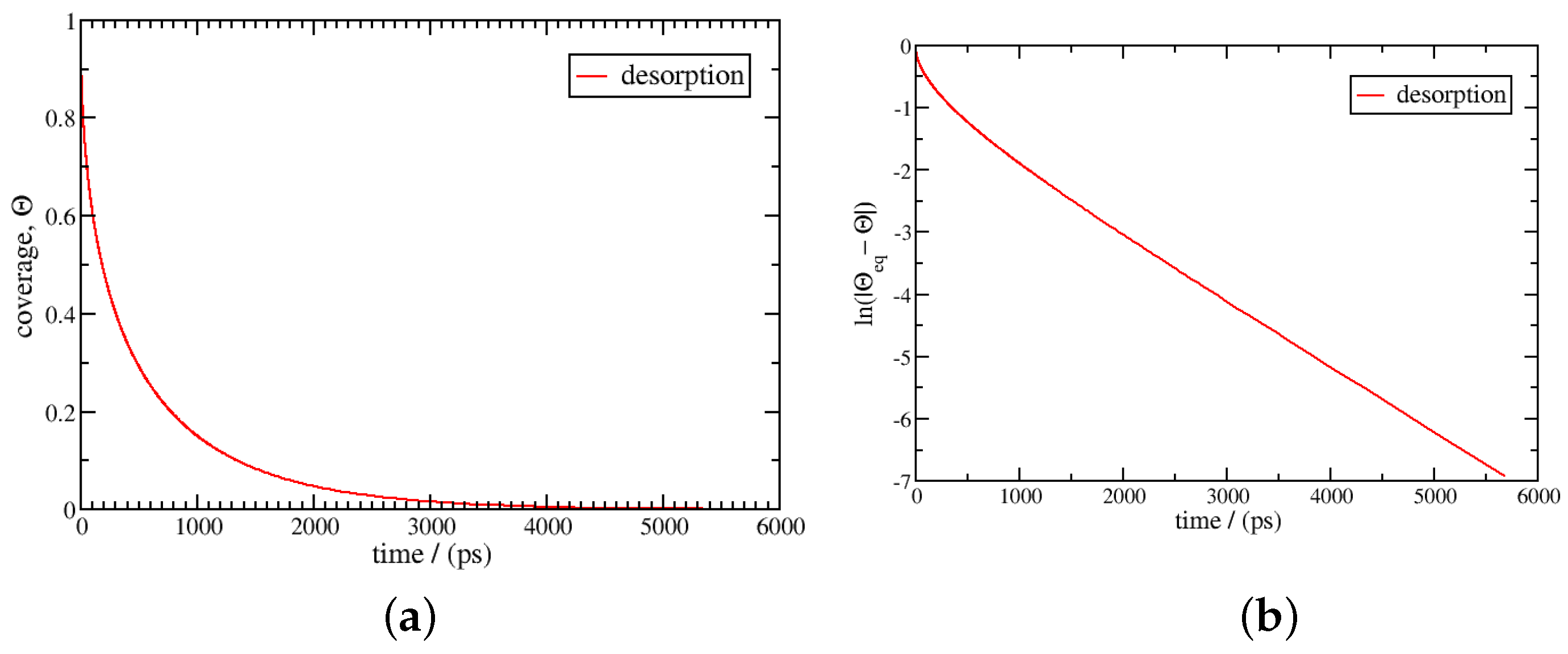
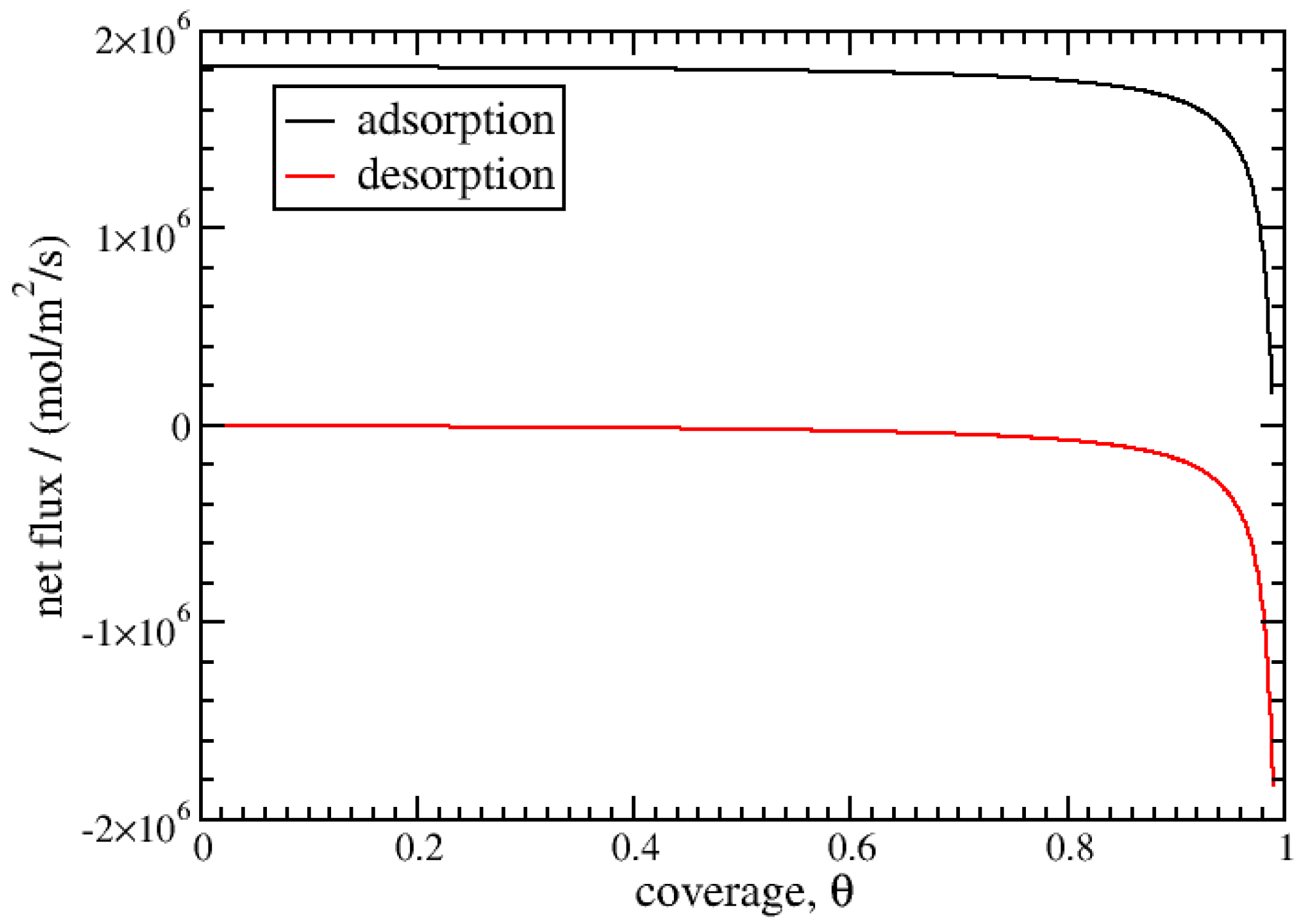
3. Results and Discussion
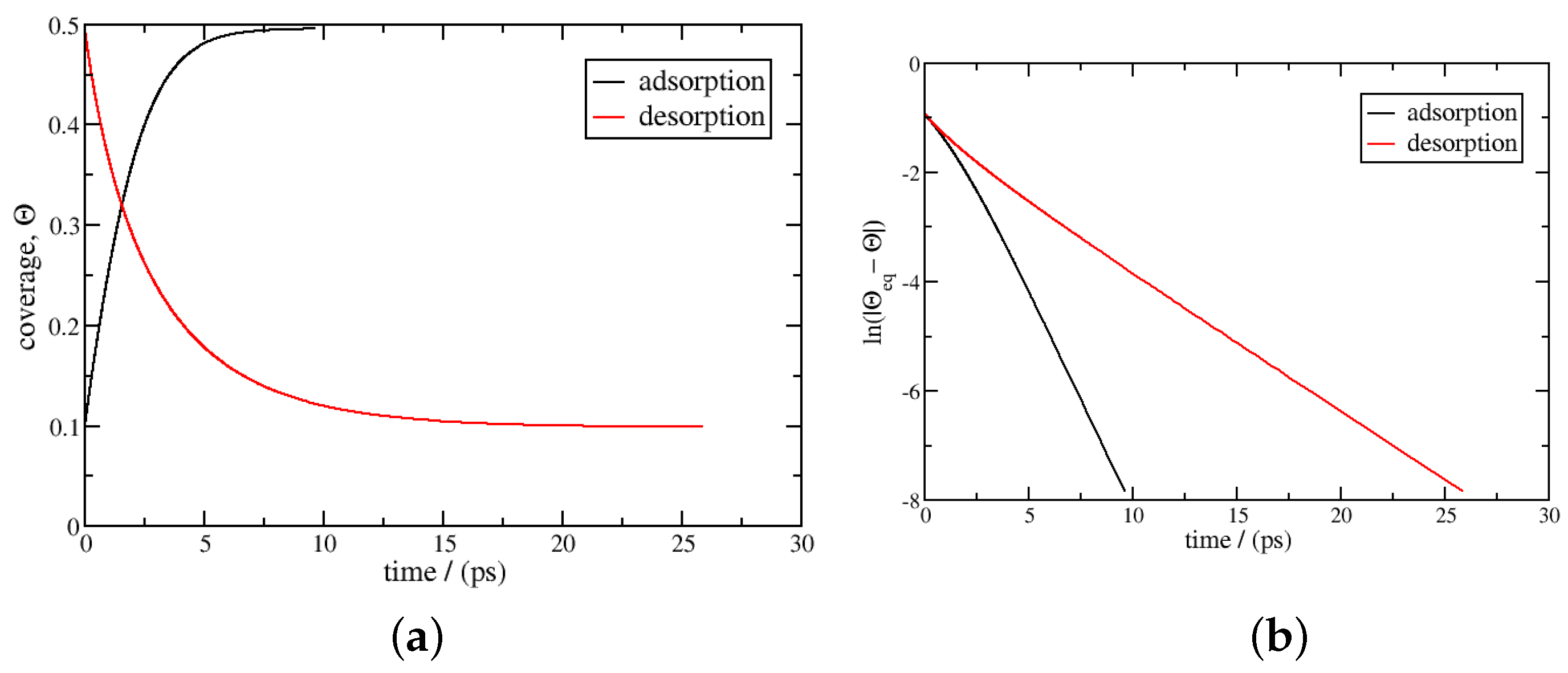
3.1. Isothermal Kinetics of Adsorption and Desorption
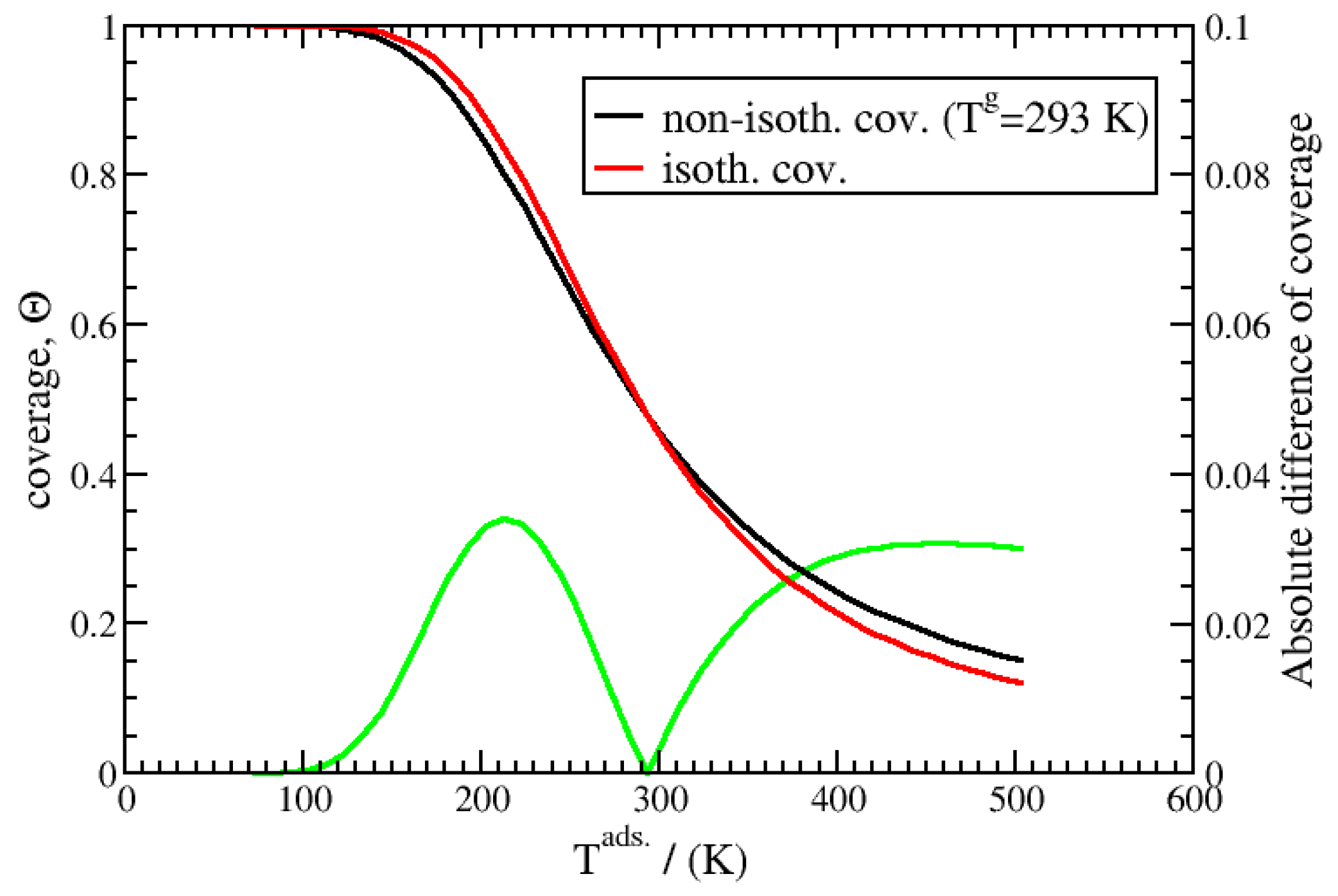
3.2. Non-Isothermal Kinetics of Adsorption
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of Symbols
| Greek symbols | |
| the activity factor of the adsorbed phase; | |
| , | the chemical potential of the gas phase and the standard phase (J/mol), where the subscript indicates the properties under equilibrium; |
| , | the chemical potential of the adsorbed phase and the reference phase (J/mol), where the subscript indicates the properties under equilibrium; |
| the characteristic times for adsorption/desorption under non-Langmuir kinetics (s); | |
| , , | coverage (), the equilibrium value and the initial value; |
| this is used as a superscript for and to indicate that the properties take the value in equilibrium with the actual adsorbed phase and given by the Langmuir equation. | |
| Latin symbols | |
| gas activity; | |
| activity of the adsorbed phase; | |
| , | monolayer surface concentration and saturated equivalent (mol/m2); |
| the subscript indicates the properties under equilibrium; | |
| this superscript on and indicates the properties extending beyond close equilibrium; | |
| , | unidirectional adsorption/desorption flux (mol/s/m2); |
| net flux at the limit of the adsorbed phase (mol/s/m2); | |
| net flux at the limit of the gas phase (mol/s/m2); | |
| net flux (mol/s/m2) (); | |
| , | the unidirectional adsorption/desorption rate constant (mol/s/m2), where the superscript L refers to the Langmuir kinetics; |
| K | the Langmuir constant; |
| the non-isothermal Langmuir constant; | |
| the surface cross-coupling heat and mass transport coefficient (K.mol/s/m2), where the superscripts and g refer to the limit of the adsorbed and gas phases, respectively; | |
| the surface mass transport coefficient (K.mol2/(J.m2.s), where the superscripts and g refer to the limit of the adsorbed and gas phases, respectively; | |
| p | gas pressure (Pa); |
| standard pressure (105 Pa); | |
| J/K/mol | a perfect gas constant; |
| the subscript on , , or a refers to the properties in the stationary state under non-isothermal conditions; | |
| t | time (s); |
| , | adsorption/desorption characteristic time based on the exponential part of the kinetics (s), where the superscript L refers to the Langmuir kinetics; |
| T | temperature (K); |
| , | temperatures at the limit of the gas/adsorbed phase (K). |
References
- Pareek, A.; Dom, R.; Gupta, J.; Chandran, J.; Adepu, V.; Borse, P.H. Insights into renewable hydrogen energy: Recent advances and prospects. Mater. Sci. Energy Technol. 2020, 3, 319–327. [Google Scholar] [CrossRef]
- Le, T.T.; Sharma, P.; Bora, B.J.; Tran, V.D.; Truong, T.H.; Le, H.C.; Nguyen, P.Q.P. Fueling the future: A comprehensive review of hydrogen energy systems and their challenges. Int. J. Hydrogen Energy 2024, 54, 791–816. [Google Scholar] [CrossRef]
- Hassan, I.; Ramadan, H.S.; Saleh, M.A.; Hissel, D. Hydrogen storage technologies for stationary and mobile applications: Review, analysis and perspectives. Renew. Sustain. Energy Rev. 2021, 149, 111311. [Google Scholar] [CrossRef]
- Zgonnik, V. The occurrence and geoscience of natural hydrogen: A comprehensive review. Earth-Sci. Rev. 2020, 203, 103140. [Google Scholar] [CrossRef]
- Al-Shafi, M.; Massarweh, O.; Abushaikha, A.S.; Bicer, Y. A review on underground gas storage systems: Natural gas, hydrogen and carbon sequestration. Energy Rep. 2023, 9, 6251–6266. [Google Scholar] [CrossRef]
- Epelle, E.I.; Obande, W.; Udourioh, G.A.; Afolabi, I.C.; Desongu, K.S.; Orivri, U.; Gunes, B.; Okolie, J.A. Perspectives and prospects of underground hydrogen storage and natural hydrogen. Sustain. Energy Fuels 2022, 6, 3324–3343. [Google Scholar] [CrossRef]
- Simon, J.M.; Haas, O.E.; Kjelstrup, S. Adsorption and desorption of H2 on graphite by molecular dynamics simulations. J. Phys. Chem. C 2010, 114, 10212–10220. [Google Scholar] [CrossRef]
- van Erp, T.S.; Trinh, T.; Kjelstrup, S.; Glavatskiy, K.S. On the relation between the Langmuir and thermodynamic flux equations. Front. Phys. 2014, 1, 36. [Google Scholar] [CrossRef][Green Version]
- de Groot, S.R.; Mazur, P. Non-Equilibrium Thermodynamics; Dover Publications, Dover: New York, NY, USA, 1984. [Google Scholar]
- Kjelstrup, S.; Bedeaux, D. Non-Equilibrium Thermodynamics of Heterogeneous Systems; Series on Advances in Statistical Mechanics; World Scientific Publishing Co. Pte, Ltd.: Singapore, 2008; Volume 16. [Google Scholar]
- Inzoli, I.; Kjelstrup, S.; Bedeaux, D.; Simon, J.M. Transport coefficients of n-butane into and through the surface of silicalite-1 from non-equilibrium molecular dynamics study. Microporous Mesoporous Mater. 2009, 125, 112–125. [Google Scholar] [CrossRef]
- Burress, J.W.; Kraus, M.; Beckner, M.; Cepel, R.; Suppes, G.; Wexler, C.; Pfeifer, P. Hydrogen storage in engineered carbon nanospaces. Nanotechnology 2009, 20, 204026. [Google Scholar] [CrossRef] [PubMed]
- Inzoli, I.; Kjelstrup, S.; Bedeaux, D.; Simon, J. Transfer coefficients for the liquid–vapor interface of a two-component mixture. Chem. Eng. Sci. 2011, 66, 4533–4548. [Google Scholar] [CrossRef]
- Xu, J.; Kjelstrup, S.; Bedeaux, D.; Røsjorde, A.; Rekvig, L. Verification of Onsager’s reciprocal relations for evaporation and condensation using non-equilibrium molecular dynamics. J. Colloid Interface Sci. 2006, 299, 452–463. [Google Scholar] [CrossRef]
- Røsjorde, A.; Kjelstrup, S.; Bedeaux, D.; Hafskjold, B. Nonequilibrium molecular dynamics simulations of steady-state heat and mass transport in condensation. II. Transfer coefficients. J. Colloid Interface Sci. 2001, 240, 355–364. [Google Scholar] [CrossRef] [PubMed]
- Johannessen, E.; Bedeaux, D. Integral relations for the heat and mass transfer resistivities of the liquid–vapor interface. Phys. A Stat. Mech. Its Appl. 2006, 370, 258–274. [Google Scholar] [CrossRef]
- Glavatskiy, K. Resistances for heat and mass transfer through a liquid—Vapor interface in a binary mixture. J. Chem. Phys. 2010, 133, 234501. [Google Scholar] [CrossRef] [PubMed]
- Inzoli, I.; Simon, J.M.; Kjelstrup, S.; Bedeaux, D. Thermal effects during adsorption of n-butane on a silicalite-1 membrane: A non-equilibrium molecular dynamics study. J. Colloid Interface Sci. 2007, 313, 563–573. [Google Scholar] [CrossRef] [PubMed]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simon, J.-M.; Carneiro Queiroz da Silva, G. Adsorption Kinetics Model of Hydrogen on Graphite. Entropy 2025, 27, 229. https://doi.org/10.3390/e27030229
Simon J-M, Carneiro Queiroz da Silva G. Adsorption Kinetics Model of Hydrogen on Graphite. Entropy. 2025; 27(3):229. https://doi.org/10.3390/e27030229
Chicago/Turabian StyleSimon, Jean-Marc, and Guilherme Carneiro Queiroz da Silva. 2025. "Adsorption Kinetics Model of Hydrogen on Graphite" Entropy 27, no. 3: 229. https://doi.org/10.3390/e27030229
APA StyleSimon, J.-M., & Carneiro Queiroz da Silva, G. (2025). Adsorption Kinetics Model of Hydrogen on Graphite. Entropy, 27(3), 229. https://doi.org/10.3390/e27030229






