An Open Quantum System Interacting with an Interference Engineering Environment
Abstract
1. Introduction
2. Model and Dynamics
2.1. Indefinite Environments for the Two-Qubit System as an Illustration
2.2. Central Spin Model and Its Dynamics
3. Results
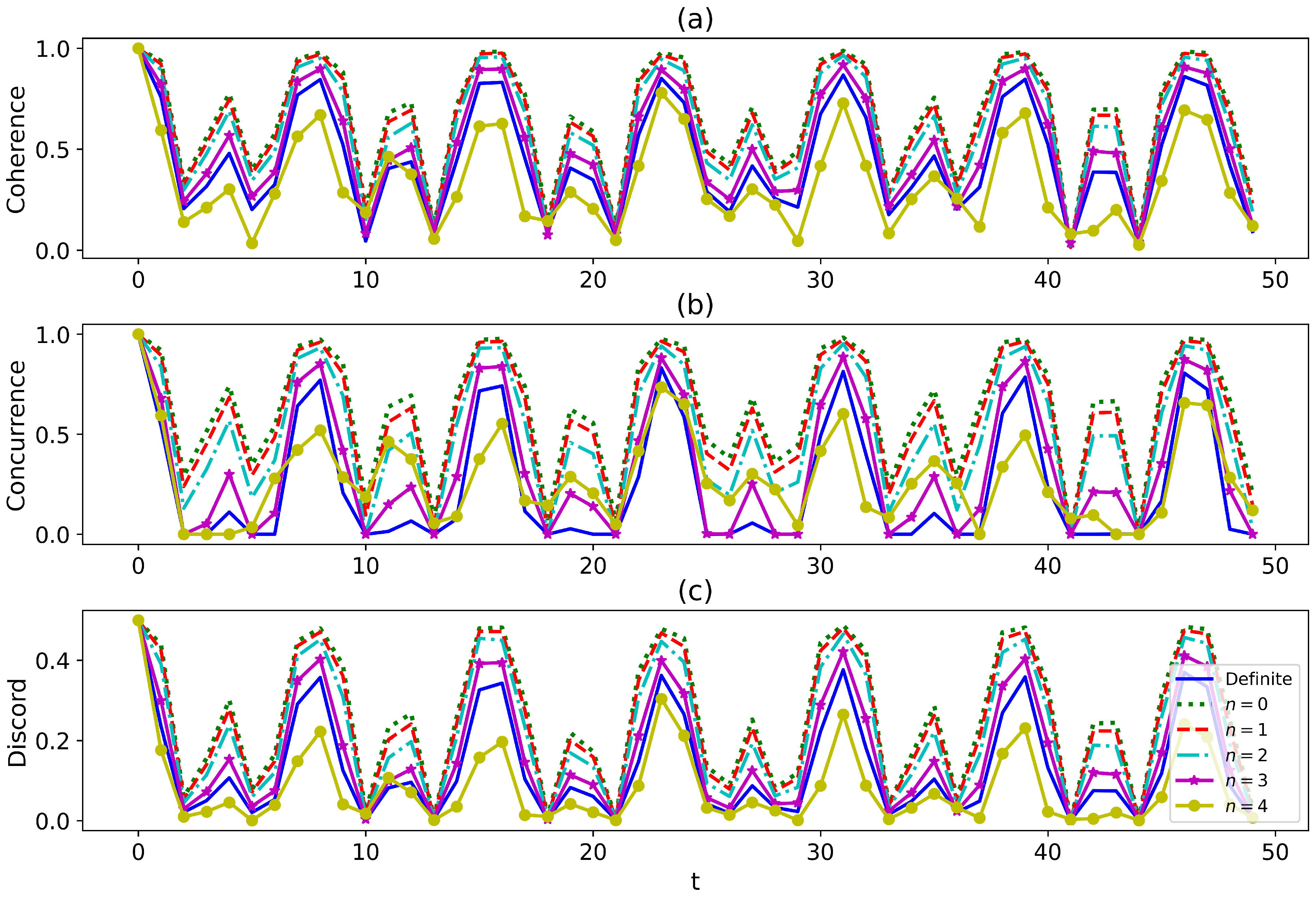
3.1. Boosting the Quantum Correlations with the Indefiniteness
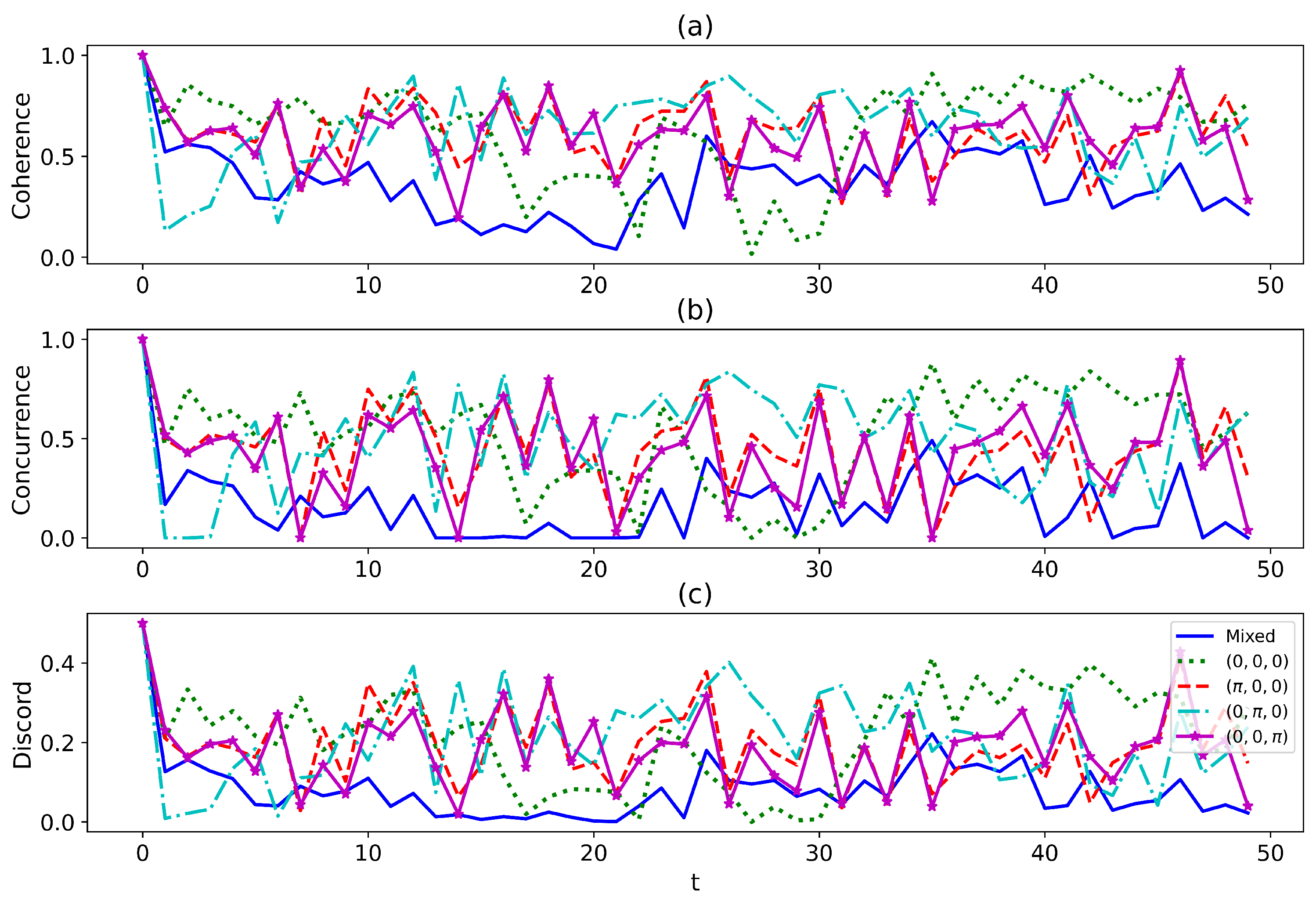
3.2. Indefinite System in the Indefinite Environment
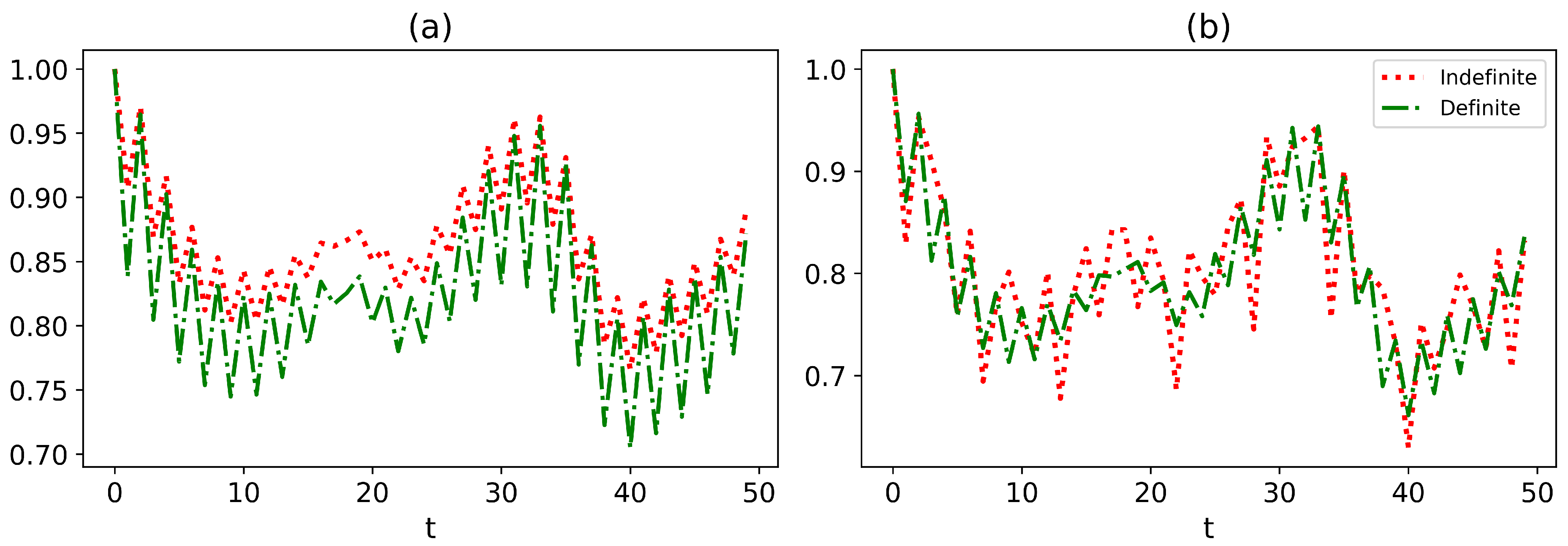
3.3. Teleportation in the Indefinite Environment
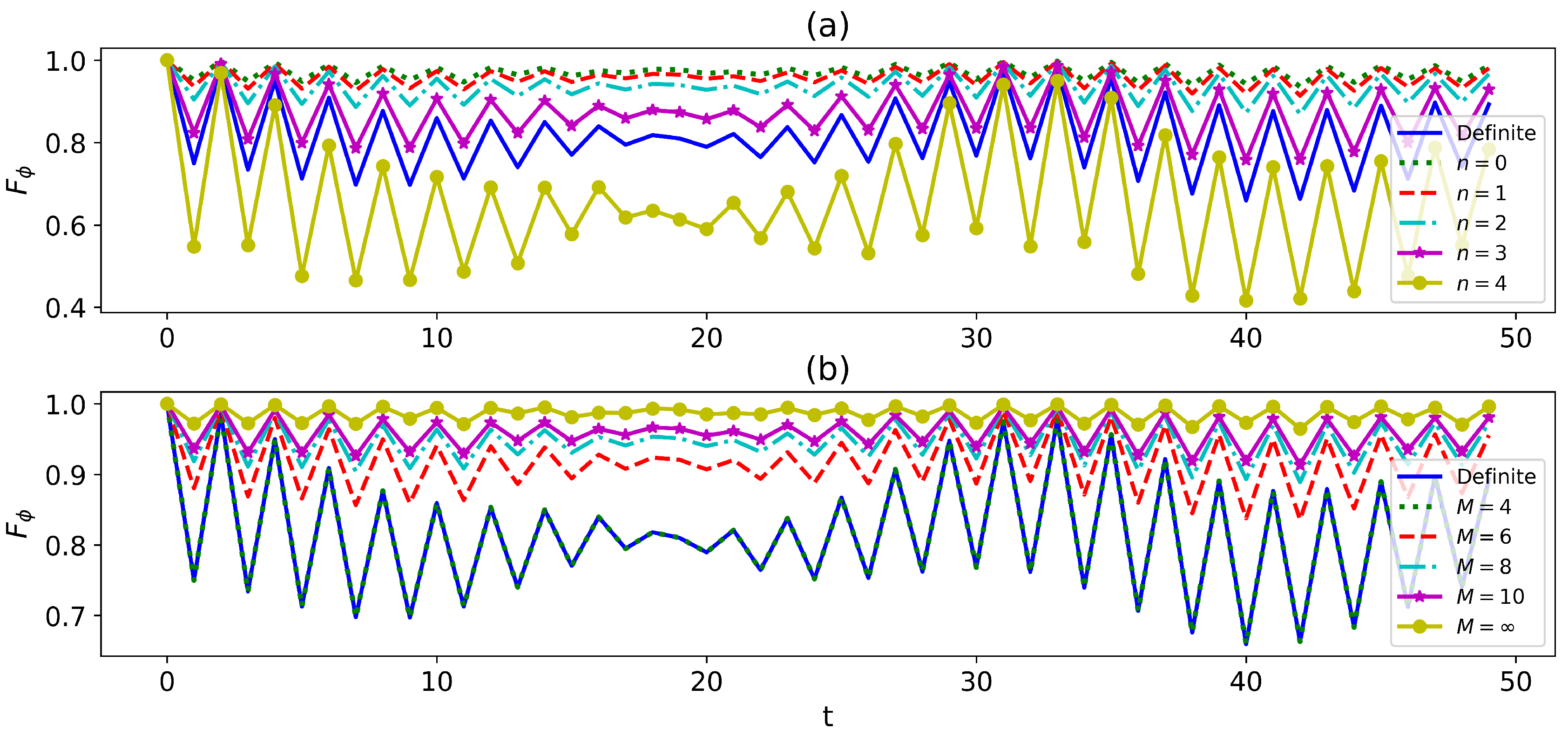
3.4. Enhancing the Quantum Parameter Estimation with the Indefiniteness
4. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. The Evolution of the Two-Qubit System in Indefinite Environments
Appendix B. The Evolution of the System Density Matrix for the Teleportation Process
Appendix C. The Maximum Fidelity of Teleporting Certain States
References
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Roffe, J. Quantum error correction: An introductory guide. Contemp. Phys. 2019, 60, 226–245. [Google Scholar] [CrossRef]
- Zanardi, P.; Rasetti, M. Noiseless Quantum Codes. Phys. Rev. Lett. 1997, 79, 3306. [Google Scholar] [CrossRef]
- Lidar, D.A.; Chuang, I.L.; Whaley, K.B. Decoherence-Free Subspaces for Quantum Computation. Phys. Rev. Lett. 1998, 81, 2594. [Google Scholar] [CrossRef]
- Lidar, D.A. Review of decoherence free subspaces, noiseless subsystems, and dynamical decoupling. Adv. Chem. Phys. 2014, 154, 295. [Google Scholar]
- Viola, L.; Knill, E.; Lloyd, S. Dynamical Generation of Noiseless Quantum Subsystems. Phys. Rev. Lett. 2000, 85, 3520. [Google Scholar] [CrossRef]
- Choi, M.-D.; Kribs, D.W. Method to Find Quantum Noiseless Subsystems. Phys. Rev. Lett. 2006, 96, 050501. [Google Scholar] [CrossRef]
- Wiseman, H.M. Quantum theory of continuous feedback. Phys. Rev. A 1994, 49, 2133. [Google Scholar] [CrossRef] [PubMed]
- Doherty, A.C.; Habib, S.; Jacobs, K.; Mabuchi, H.; Tan, S.M. Quantum feedback control and classical control theory. Phys. Rev. A 2000, 62, 012105. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Y.-X.; Wu, R.-B.; Jacobs, K.; Nori, F. Quantum feedback: Theory, experiments, and applications. Phys. Rep. 2017, 679, 1. [Google Scholar] [CrossRef]
- Viola, L.; Knill, E.; Lloyd, S. Dynamical Decoupling of Open Quantum Systems. Phys. Rev. Lett. 1999, 82, 2417. [Google Scholar] [CrossRef]
- Itano, W.M.; Heinzen, D.J.; Bollinger, J.J.; Wineland, D.J. Quantum Zeno effect. Phys. Rev. A 1990, 41, 2295. [Google Scholar] [CrossRef] [PubMed]
- Facchi, P.; Pascazio, S. Quantum Zeno Subspaces. Phys. Rev. Lett. 2002, 89, 080401. [Google Scholar] [CrossRef] [PubMed]
- Koshino, K.; Shimizu, A. Quantum Zeno effect by general measurements. Phys. Rep. 2005, 412, 191. [Google Scholar] [CrossRef]
- Chaudhry, A.Z.; Gong, J. Zeno and anti-Zeno effects on dephasing. Phys. Rev. A 2014, 90, 012101. [Google Scholar] [CrossRef]
- Chaudhry, A.Z. A general framework for the quantum Zeno and anti-Zeno effects. Sci. Rep. 2016, 6, 29497. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; An, J.-H.; Luo, H.-G.; Sun, C.P.; Oh, C.H. Floquet control of quantum dissipation in spin chains. Phys. Rev. A 2015, 91, 052122. [Google Scholar] [CrossRef]
- Yang, W.L.; Song, W.L.; An, J.-H.; Feng, M.; Suter, D.; Du, J. Floquet engineering to entanglement protection of distant nitrogen vacancy centers. New J. Phys. 2019, 21, 013007. [Google Scholar] [CrossRef]
- Bai, S.-Y.; An, J.-H. Floquet engineering to reactivate a dissipative quantum battery. Phys. Rev. A 2020, 102, 060201. [Google Scholar] [CrossRef]
- Wang, H.; Wang, J. Entanglement and work statistics in the driven open system. arXiv 2023, arXiv:2301.00915. [Google Scholar] [CrossRef]
- Lin, J.-D.; Kuo, P.-C.; Lambert, N.; Miranowicz, A.; Nori, F.; Chen, Y.-N. Non-Markovian quantum exceptional points. Nat. Commun. 2025, 16, 1289. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wang, J. The effect of nonequilibrium entropy production on the quantum Fisher information and correlations. Quantum Inf. Process. 2022, 21, 16. [Google Scholar] [CrossRef]
- Wang, H.; Xu, L.; Wang, J. Quantum correlations of a two-qubit system and the Aubry-André chain in bosonic environments. Phys. Rev. A 2022, 106, 052404. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, J. Entanglement versus Bell nonlocality of quantum nonequilibrium steady states. Quantum Inf. Process. 2021, 20, 147. [Google Scholar] [CrossRef]
- Wang, X.; Wang, J. Nonequilibrium effects on quantum correlations: Discord, mutual information, and entanglement of a two-fermionic system in bosonic and fermionic environments. Phys. Rev. A 2019, 100, 052331. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, W.; Wang, J. Steady-state entanglement and coherence of two coupled qubits in equilibrium and nonequilibrium environments. Phys. Rev. A 2019, 99, 042320. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, J. Shape, orientation and magnitude of the curl quantum flux, the coherence and the statistical correlations in energy transport at nonequilibrium steady state. New J. Phys. 2015, 17, 093021. [Google Scholar] [CrossRef]
- Plenio, M.B.; Huelga, S.F.; Beige, A.; Knight, P.L. Cavity Loss Induced Generation of Entangled Atoms. Phys. Rev. A 1999, 59, 2468–2475. [Google Scholar] [CrossRef]
- Kraus, B.; Büchler, H.P.; Diehl, S.; Kantian, A.; Micheli, A.; Zoller, P. Preparation of entangled states by quantum Markov processes. Phys. Rev. A 2008, 78, 042307. [Google Scholar] [CrossRef]
- Verstraete, F.; Wolf, M.M.; Cirac, J.I. Quantum computation and quantum-state engineering driven by dissipation. Nat. Phys. 2009, 5, 633–636. [Google Scholar] [CrossRef]
- Chiribella, G. Perfect discrimination of no-signalling channels via quantum superposition of causal structures. Phys. Rev. A 2012, 86, 040301. [Google Scholar] [CrossRef]
- Ibnouhsein, I.; Grinbaum, A. Information-theoretic constraints on correlations with indefinite causal order. Phys. Rev. A 2015, 92, 042124. [Google Scholar] [CrossRef]
- Ebler, D.; Salek, S.; Chiribella, G. Enhanced communication with the assistance of indefinite causal order. Phys. Rev. Lett. 2018, 120, 120502. [Google Scholar] [CrossRef]
- Goswami, K.; Giarmatzi, C.; Kewming, M.; Costa, F.; Branciard, C.; Romero, J.; White, A.G. Indefinite causal order in a quantum switch. Phys. Rev. Lett. 2018, 121, 090503. [Google Scholar] [CrossRef]
- Loizeau, N.; Grinbaum, A. Channel capacity enhancement with indefinite causal order. Phys. Rev. A 2020, 101, 012340. [Google Scholar] [CrossRef]
- Mukhopadhyay, C.; Pati, A.K. Superposition of causal order enables perfect quantum teleportation with very noisy singlets. J. Phys. Commun. 2020, 4, 105003. [Google Scholar] [CrossRef]
- Cardoso-Isidoro, C.; Delgado, F. Featuring causal order in teleportation of two quantum teleportation channels. J. Phys. Conf. Ser. 2020, 1540, 012024. [Google Scholar] [CrossRef]
- Mukhopadhyay, C.; Gupta, M.K.; Pati, A.K. Superposition of causal order as a metrological resource for quantum thermometry. arXiv 2018, arXiv:1812.07508. [Google Scholar]
- Chapeau-Blondeau, F. Noisy quantum metrology with the assistance of indefinite causal order. Phys. Rev. A 2021, 103, 032615. [Google Scholar] [CrossRef]
- Chapeau-Blondeau, F. Quantum parameter estimation on coherently superposed noisy channel. Phys. Rev. A 2021, 104, 032214. [Google Scholar] [CrossRef]
- Chapeau-Blondeau, F. Indefinite causal order for quantum metrology with quantum thermal noise. Phys. Lett. A 2021, 447, 128300. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, Y.; Chiribella, G. Quantum metrology with indefinite causal order. Phys. Rev. Lett. 2022, 124, 190503. [Google Scholar] [CrossRef] [PubMed]
- Ban, M. Quantum Fisher information of phase estimation in the presence of indefinite causal order. Phys. Lett. A 2023, 468, 128749. [Google Scholar] [CrossRef]
- Felce, D.; Vedral, V. Quantum Refrigeration with Indefinite Causal Order. Phys. Rev. Lett. 2020, 125, 070603. [Google Scholar] [CrossRef] [PubMed]
- Nie, X.; Zhu, X.; Huang, K.; Tang, K.; Long, X.; Lin, Z.; Tian, Y.; Qiu, C.; Xi, C.; Yang, X.; et al. Experimental Realization of a Quantum Refrigerator Driven by Indefinite Causal Orders. Phys. Rev. Lett. 2022, 129, 100603. [Google Scholar] [CrossRef] [PubMed]
- Siltanen, O.; Kuusela, T.; Piilo, J. Interferometric approach to open quantum systems and non-Markovian dynamics. Phys. Rev. A 2021, 103, 032223. [Google Scholar] [CrossRef]
- Lin, J.-D.; Huang, C.-Y.; Lambert, N.; Chen, G.-Y.; Nori, F.; Chen, Y.-N. Space-time dual quantum Zeno effect: Interferometric engineering of open quantum system dynamics. Phys. Rev. Res. 2022, 4, 033143. [Google Scholar] [CrossRef]
- Lin, J.-D.; Chen, Y.-N. Boosting entanglement growth of many-body localization by superpositions of disorder. arXiv 2023, arXiv:2304.08849. [Google Scholar] [CrossRef]
- Ban, M. Relaxation process of a two-level system in a coherent superposition of two environments. Quantum Inf. Process. 2020, 19, 351. [Google Scholar] [CrossRef]
- Ban, M. Decoherence of a two-level system in a coherent superposition of two dephasing environments. Quantum Inf. Process. 2020, 19, 409. [Google Scholar] [CrossRef]
- Ban, M. Two-qubit correlation in two independent environments with indefiniteness. Phys. Lett. A 2021, 385, 126936. [Google Scholar] [CrossRef]
- Ban, M. Temporal steering of a two-level system interacting with a coherent superposition of two environments. Quantum Inf. Process. 2022, 21, 13. [Google Scholar] [CrossRef]
- Ban, M. Quantum correlations of two qubits indefinitely interacting with dephasing environments. Quantum Inf. Process. 2022, 21, 231. [Google Scholar] [CrossRef]
- Wood, C.E.; Verma, H.; Costa, F.; Zych, M. Operational models of temperature superpositions. arXiv 2021, arXiv:2112.07860. [Google Scholar]
- Breuer, H.P.; Amato, G.; Vacchini, B. Mixing-induced quantum non-Markovianity and information flow. New J. Phys. 2018, 20, 043007. [Google Scholar] [CrossRef]
- Yuan, X.-Z.; Goan, H.-S.; Zhu, K.-D. Non-Markovian reduced dynamics and entanglement evolution of two coupled spins in a quantum spin environment. Phys. Rev. B 2007, 75, 045331. [Google Scholar] [CrossRef]
- Wu, W.; Wang, J. Wave–Particle–Entanglement–Ignorance Complementarity for General Bipartite Systems. Entropy 2020, 22, 813. [Google Scholar] [CrossRef] [PubMed]
- Venegas-Andraca, S.E. Quantum walks: A comprehensive review. Quantum Inf. Process. 2012, 11, 1015–1106. [Google Scholar] [CrossRef]
- Urbaszek, B.; Marie, X.; Amand, T.; Krebs, O.; Voisin, P.; Maletinsky, P.; Högele, A.; Imamoglu, A. Nuclear spin physics in quantum dots: An optical investigation. Rev. Mod. Phys. 2013, 85, 79. [Google Scholar] [CrossRef]
- Zhang, Z.; Fu, H.; Wang, J. Nonequilibrium-induced enhancement of dynamical quantum coherence and entanglement of spin arrays. Phys. Rev. B 2017, 95, 144306. [Google Scholar] [CrossRef]
- Koh, C.Y.; Kwek, L.C. Entanglement and quantum phase transition of spin glass: A renormalization group approach. Phys. lett. A 2014, 378, 2743–2749. [Google Scholar] [CrossRef]
- Tsomokos, D.I.; Ashhab, S.; Nori, F. Fully connected network of superconducting qubits in a cavity. New J. Phys. 2008, 10, 113020. [Google Scholar] [CrossRef]
- Casta nos, O.; López-Pexnxa, R.; Nahmad-Achar, E.; Hirsch, J.G. Quantum phase transitions in the LMG model by means of quantum information concepts. J. Phys. Conf. Ser. 2012, 387, 012021. [Google Scholar] [CrossRef]
- Xu, K.; Sun, Z.-H.; Liu, W.; Zhang, Y.-R.; Li, H.; Dong, H.; Ren, W.; Zhang, P.; Nori, F.; Zheng, D.; et al. Probing dynamical phase transitions with a superconducting quantum simulator. Sci. Adv. 2020, 6, eaba4935. [Google Scholar] [CrossRef] [PubMed]
- Grossi, M.; Kiss, O.; Luca, F.D.; Zollo, C.; Gremese, I.; Mandarino, A. Finite-size criticality in fully connected spin models on superconducting quantum hardware. Phys. Rev. E 2023, 107, 024113. [Google Scholar] [CrossRef]
- Diamantini, M.C.; Trugenberger, C.A. Quantum Pattern Retrieval by Qubit Networks with Hebb Interactions. Phys. Rev. Lett. 2006, 77, 130503. [Google Scholar] [CrossRef] [PubMed]
- Rotondo, P.; Marcuzzi, M.; Garrahan, J.P.; Lesanovsky, I.; Müller, M. Open quantum generalisation of Hopfield neural networks. J. Phys. A Math. Theor. 2018, 51, 115301. [Google Scholar] [CrossRef]
- Russomanno, A.; Iemini, F.; Dalmonte, M.; Fazio, R. Floquet time crystal in the Lipkin-Meshkov-Glick model. Phys. Rev. B 2017, 95, 214307. [Google Scholar] [CrossRef]
- Piccitto, G.; Wauters, M.; Nori, F.; Shammah, N. Symmetries and conserved quantities of boundary time crystals in generalized spin models. Phys. Rev. B 2021, 104, 014307. [Google Scholar] [CrossRef]
- Wang, H.; Wang, J. The time crystal phase emerges from the qubit network under unitary random operations. arXiv 2023, arXiv:2304.02884. [Google Scholar]
- Xiao, X.; Fang, M.F.; Li, Y.L.; Kang, G.D.; Wu, C. Non-Markovian entanglement dynamics of two spin-1/2 particles embedded in two separate spin star baths with tunable external magnetic fields. Eur. Phys. J. D 2010, 57, 447–453. [Google Scholar] [CrossRef]
- Mukhopadhyay, C.; Bhattacharya, S.; Misra, A.; Pati, A.K. Dynamics and thermodynamics of a central spin immersed in a spin bath. Phys. Rev. A 2017, 96, 052125. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Banerjee, S. Revisiting the Quantum Open System Dynamics of Central Spin Model. Quanta 2021, 10, 55–64. [Google Scholar] [CrossRef]
- Tiwari, D.; Datta, S.; Bhattacharya, S.; Banerjee, S. Dynamics of two central spins immersed in spin baths. Phys. Rev. A 2022, 106, 032435. [Google Scholar] [CrossRef]
- Tiwari, D.; Paulson, K.G.; Banerjee, S. Quantum Correlations and Speed Limit of Central Spin Systems. Ann. Phys. 2023, 535, 2200452. [Google Scholar] [CrossRef]
- Korenblit, S.; Kafri, D.; Campbell, W.C.; Islam, R.; Edwards, E.E.; Gong, Z.-X.; Lin, G.-D.; Duan, L.-M.; Kim, J.; Kim, K. Quantum simulation of spin models on an arbitrary lattice with trapped ions. New J. Phys. 2012, 14, 095024. [Google Scholar] [CrossRef]
- Monroe, C.; Campbell, W.C.; Duan, L.-M.; Gong, Z.-X.; Gorshkov, A.V.; Hess, P.W.; Islam, R.; Kim, K.; Linke, N.M.; Pagano, G.; et al. Programmable quantum simulations of spin systems with trapped ions. Rev. Mod. Phys. 2021, 93, 025001. [Google Scholar] [CrossRef]
- Holstein, T.; Primakoff, H. Field Dependence of the Intrinsic Domain Magnetization of a Ferromagnet. Phys. Rev. 1940, 58, 1098. [Google Scholar] [CrossRef]
- Cramer, B.T.M.; Plenio, M.B. Quantifying Coherence. Phys. Rev. Lett. 2014, 113, 140401. [Google Scholar]
- Bennett, C.H.; Brassard, G.; Crepeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895–1899. [Google Scholar] [CrossRef]
- Ekert, A.K. Quantum Cryptography Based on Bell’s Theorem. Phys. Rev. Lett. 1991, 67, 661–663. [Google Scholar] [CrossRef] [PubMed]
- Schaetz, T.; Barrett, M.D.; Leibfried, D.; Chiaverini, J.; Britton, J.; Itano, W.M.; Jost, J.D.; Langer, C.; Wineland, D.J. Quantum Dense Coding with Atomic Qubits. Phys. Rev. Lett. 2004, 93, 040505. [Google Scholar] [CrossRef] [PubMed]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865. [Google Scholar] [CrossRef]
- Hill, S.; Wootters, W.K. Entanglement of a Pair of Quantum Bits. Phys. Rev. Lett. 1997, 78, 5022. [Google Scholar] [CrossRef]
- Ollivier, H.; Zurek, W.H. Quantum Discord: A Measure of the Quantumness of Correlations. Phys. Rev. Lett. 2001, 88, 017901. [Google Scholar] [CrossRef] [PubMed]
- Dakic, B.; Vedral, V.; Brukner, C. Necessary and Sufficient Condition for Nonzero Quantum Discord. Phys. Rev. Lett. 2010, 105, 4649. [Google Scholar] [CrossRef]
- Horodecki, R.; Horodecki, M.; Horodecki, P. Teleportation, Bell’s inequalities and inseparability. Phys. Lett. A 1996, 222, 21–25. [Google Scholar] [CrossRef]
- Popescu, S. Bell’s inequalities versus teleportation: What is nonlocality? Phys. Rev. A 1994, 72, 797. [Google Scholar] [CrossRef] [PubMed]
- Braun, D.; Adesso, G.; Benatti, F.; Floreanini, R.; Marzolino, U.; Mitchell, M.W.; Pirandola, S. Quantum-enhanced measurements without entanglement. Rev. Mod. Phys. 2018, 90, 035006. [Google Scholar] [CrossRef]
- Pezzè, L.; Smerzi, A.; Oberthaler, M.K.; Schmied, R.; Treutlein, P. Quantum metrology with nonclassical states of atomic ensembles. Rev. Mod. Phys. 2018, 90, 035005. [Google Scholar] [CrossRef]
- Hyllus, P.; Laskowski, W.; Krischek, R.; Schwemmer, C.; Wieczorek, W.; Weinfurter, H.; Pezzé, L.; Smerzi, A. Fisher information and multiparticle entanglement. Phys. Rev. A 2012, 85, 022321. [Google Scholar] [CrossRef]
- Wootters, W.K.; Zurek, W.H. Complementarity in the double-slit experiment: Quantum nonseparability and a quantitive statement of Bohr’s principle. Phys. Rev. D 1979, 19, 473–484. [Google Scholar] [CrossRef]
- Jakob, M.; Bergou, J.A. Quantitative complementarity relations in bipartite systems: Entanglement as a physical reality. Opt. Commun. 2010, 283, 827–830. [Google Scholar] [CrossRef]
- Tessier, T.E. Complementarity relations for multi-qubit systems. Found. Phys. Lett. 2005, 18, 107–121. [Google Scholar] [CrossRef][Green Version]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Wang, J. An Open Quantum System Interacting with an Interference Engineering Environment. Entropy 2025, 27, 228. https://doi.org/10.3390/e27030228
Wang H, Wang J. An Open Quantum System Interacting with an Interference Engineering Environment. Entropy. 2025; 27(3):228. https://doi.org/10.3390/e27030228
Chicago/Turabian StyleWang, He, and Jin Wang. 2025. "An Open Quantum System Interacting with an Interference Engineering Environment" Entropy 27, no. 3: 228. https://doi.org/10.3390/e27030228
APA StyleWang, H., & Wang, J. (2025). An Open Quantum System Interacting with an Interference Engineering Environment. Entropy, 27(3), 228. https://doi.org/10.3390/e27030228






