Sensing-Assisted Secure Communications over Correlated Rayleigh Fading Channels
Abstract
1. Introduction
1.1. Main Contributions
- We establish an inner bound on the rate region for stochastically degraded secure ISAC channels under bivariate Rayleigh fading by employing a Gaussian input. Our formulation shows how channel-output feedback can be leveraged to significantly improve the secrecy rate, enabling the system to surpass classical secrecy capacity results.
- We derive integral expressions stemming from the involved differential entropies in the achievable rate region. These expressions are amenable to numerically stable and simplified evaluations, facilitating practical performance analysis.
- For some integral expressions in the achievable rate region, we provide closed form solutions in special cases, such as high SNR regime and uncorrelated fading, which significantly simplifies the numerical evaluations.
- We provide fundamental insights into sensing-assisted secure communication systems, including parameter regimes where the achievable secure-ISAC rates can exceed the secrecy capacity and where approaching the channel capacity (i.e., the maximum possible rate without a secrecy constraint) can be possible. We further present accurate approximations that enable straightforward numerical evaluations and guide system design.
1.2. Paper Organization
1.3. Notation
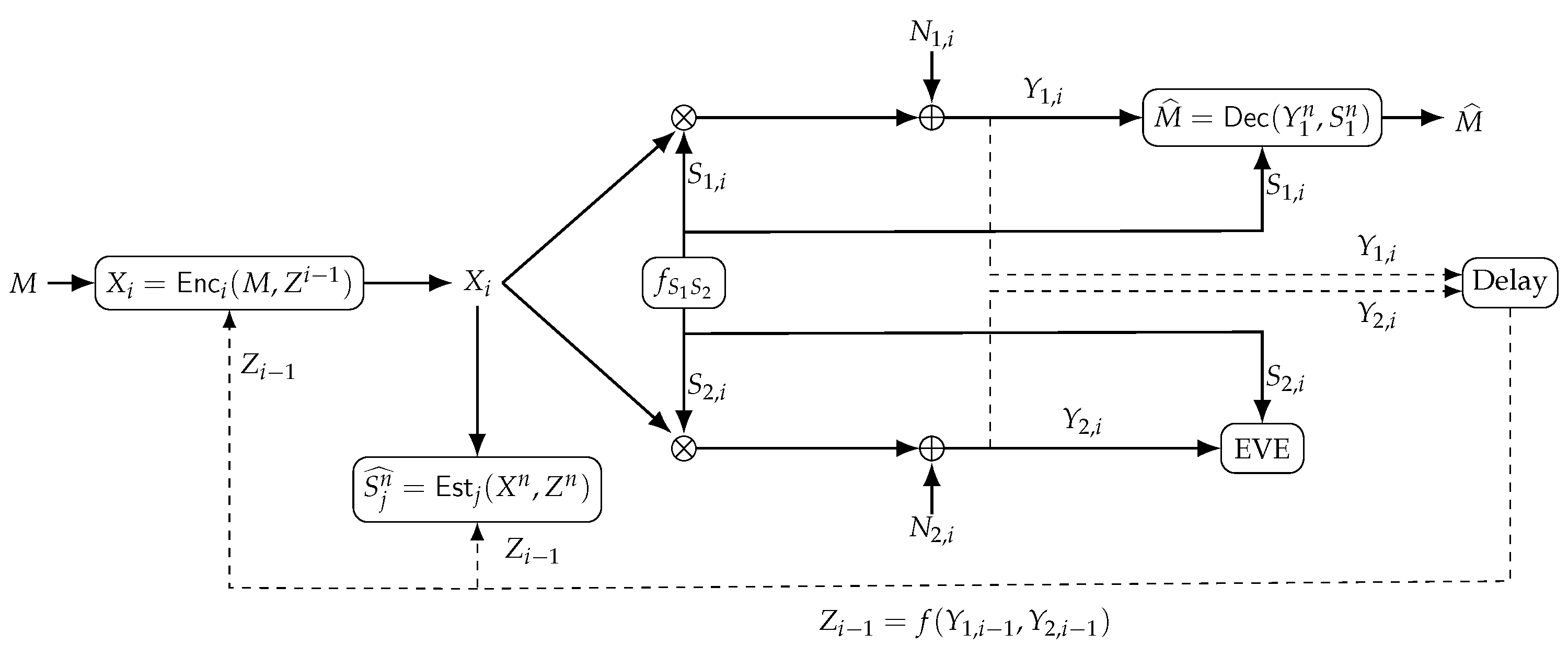
2. System Model and Problem Definition
3. Correlated Fading AGN ISAC Channel Secrecy-Distortion Regions
3.1. Secrecy-Distortion Region
- (i)
- the outer bound applies to arbitrary random variables and does not assume any degradedness;
- (ii)
- there is a discretization procedure to generalize the achievability proof to well-behaved continuous-alphabet random variables, such as the considered fading and noise distributions ([24] Remark 3.8); and
- (iii)
- one can show that changing the estimator form does not change the entropy terms in the rate region, although achieved distortion levels might change since the estimators given in ([14], Theorem 1) should also be adapted.
3.2. Bivariate Rayleigh Fading
4. Achievable Rates for Gaussian Input
4.1. Evaluation of Equation (8a)
4.2. Evaluation of Equation (8b)
4.3. Evaluation of Equation (8c)
5. Numerical Results and Discussions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wild, T.; Braun, V.; Viswanathan, H. Joint Design of Communication and Sensing for Beyond 5G and 6G Systems. IEEE Access 2021, 9, 30845–30857. [Google Scholar] [CrossRef]
- Wei, Z.; Liu, F.; Masouros, C.; Su, N.; Petropulu, A.P. Towards Multi-Functional 6G Wireless Networks: Integrating Sensing, Communication and Security. IEEE Commun. Mag. 2022, 60, 65–71. [Google Scholar] [CrossRef]
- Fettweis, G.; Schlüter, M.; Thomä, R.; Boche, H.; Schotten, H.; Barreto, A.; Mueller, A.; Bilgic, A.; Hildebrand, C.; Schupke, D.; et al. Joint Communications & Sensing—Common Radio-Communications and Sensor Technology. VDE Positionspapier 2021. [Google Scholar]
- Zhang, W.; Vedantam, S.; Mitra, U. Joint Transmission and State Estimation: A Constrained Channel Coding Approach. IEEE Trans. Inf. Theory 2011, 57, 7084–7095. [Google Scholar] [CrossRef]
- Wymeersch, H.; Shrestha, D.; de Lima, C.M.; Yajnanarayana, V.; Richerzhagen, B.; Keskin, M.F.; Schindhelm, K.; Ramirez, A.; Wolfgang, A.; de Guzman, M.F.; et al. Integration of Communication and Sensing in 6G: A Joint Industrial and Academic Perspective. In Proceedings of the IEEE Annual International Symposium on Personal, Indoor and Mobile Radio Communications, Helsinki, Finland, 13–16 September 2021; pp. 1–7. [Google Scholar]
- Ahmadipour, M.; Kobayashi, M.; Wigger, M.; Caire, G. An Information-Theoretic Approach to Joint Sensing and Communication. IEEE Trans. Inf. Theory 2024, 70, 1124–1146. [Google Scholar] [CrossRef]
- Kobayashi, M.; Hamad, H.; Kramer, G.; Caire, G. Joint State Sensing and Communication over Memoryless Multiple Access Channels. In Proceedings of the IEEE International Symposium on Information Theory, Paris, France, 7–12 July 2019; pp. 270–274. [Google Scholar]
- Welling, T.; Günlü, O.; Yener, A. Transmitter Actions for Secure Integrated Sensing and Communication. In Proceedings of the IEEE International Symposium on Information Theory, Athens, Greece, 7–12 July 2024; pp. 2580–2585. [Google Scholar]
- Wang, S.Y.; Chang, M.C.; Bloch, M.R. Covert Joint Communication and Sensing under Variational Distance Constraint. In Proceedings of the Annual Conference on Information Sciences and Systems, Princeton, NJ, USA, 13–15 March 2024; pp. 1–6. [Google Scholar]
- Wang, X.; Fei, Z.; Liu, P.; Zhang, J.A.; Wu, Q.; Wu, N. Sensing-Aided Covert Communications: Turning Interference Into Allies. IEEE Trans. Wirel. Commun. 2024, 23, 10726–10739. [Google Scholar] [CrossRef]
- Welling, T.; Günlü, O.; Yener, A. Low-latency Secure Integrated Sensing and Communication with Transmitter Actions. In Proceedings of the IEEE International Workshop on Signal Processing Advances in Wireless Communications, Lucca, Italy, 10–13 September 2024; pp. 351–355. [Google Scholar]
- Günlü, O.; Bloch, M.; Schaefer, R.F.; Yener, A. Nonasymptotic Performance Limits of Low-Latency Secure Integrated Sensing and Communication Systems. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Seoul, Republic of Korea, 14–19 April 2024; pp. 12971–12975. [Google Scholar]
- Nikbakht, H.; Wigger, M.; Shamai, S.; Poor, H.V. Integrated Sensing and Communication in the Finite Blocklength Regime. In Proceedings of the IEEE International Symposium on Information Theory, Athens, Greece, 7–12 July 2024; pp. 2790–2795. [Google Scholar]
- Günlü, O.; Bloch, M.; Schaefer, R.F.; Yener, A. Secure Integrated Sensing and Communication. IEEE J. Sel. Inf. Theory 2023, 4, 40–53. [Google Scholar] [CrossRef]
- Günlü, O.; Bloch, M.; Schaefer, R.F.; Yener, A. Secure Integrated Sensing and Communication for Binary Input Additive White Gaussian Noise Channels. In Proceedings of the IEEE International Symposium on Joint Communications & Sensing, Seefeld, Austria, 5–7 March 2023; pp. 1–6. [Google Scholar]
- Ahmadipour, M.; Wigger, M.; Shamai, S. Integrated Communication and Receiver Sensing with Security Constraints on Message and State. In Proceedings of the IEEE International Symposium on Information Theory, Taipei, Taiwan, 25–30 June 2023; pp. 2738–2743. [Google Scholar]
- Dong, F.; Liu, F.; Lu, S.; Xiong, Y. Secure ISAC Transmission With Random Signaling. In Proceedings of the IEEE GLOBECOM Workshops, Kuala Lumpur, Malaysia, 4–8 December 2023; pp. 407–412. [Google Scholar]
- Su, N.; Liu, F.; Masouros, C. Sensing-Assisted Eavesdropper Estimation: An ISAC Breakthrough in Physical Layer Security. IEEE Trans. Wirel. Commun. 2024, 23, 3162–3174. [Google Scholar] [CrossRef]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. (Eds.) NIST Handbook of Mathematical Functions; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Tse, D.; Yates, R. Fading Broadcast Channels with State Information at the Receivers. IEEE Trans. Inf. Theory 2012, 58, 3453–3471. [Google Scholar] [CrossRef]
- Bassi, G.; Piantanida, P.; Shamai, S. The Wiretap Channel With Generalized Feedback: Secure Communication and Key Generation. IEEE Trans. Inf. Theory 2019, 65, 2213–2233. [Google Scholar] [CrossRef]
- Günlü, O.; Schaefer, R.F. An Optimality Summary: Secret Key Agreement With Physical Unclonable Functions. Entropy 2021, 23, 16. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Li, M.; Liu, A.; Ong, L.; Yener, A. Fundamental Limits of Multiple-Access Integrated Sensing and Communication Systems. arXiv 2023, arXiv:2205.05328. [Google Scholar]
- Gamal, A.E.; Kim, Y.H. Network Information Theory; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Lin, P.H.; Jorswieck, E. On the Fast Fading Gaussian Wiretap Channel with Statistical Channel State Information at the Transmitter. IEEE Trans. Inf. Forensics Secur. 2016, 11, 46–58. [Google Scholar] [CrossRef]
- Papoulis, A.; Pillai, S.U. Probability, Random Variables, and Stochastic Processes, 4th ed.; McGraw-Hill: Boston, MA, USA, 2002. [Google Scholar]
- Prudnikov, A.P.; Brychov, Y.A.; Marichev, O.I. Integrals and Series, Volume 2: Special Functions; Gordon and Breach Science: New York, NY, USA, 1986. [Google Scholar]
- Prudnikov, A.P.; Brychov, Y.A.; Marichev, O.I. Integrals and Series, Volume 1: Elementary Functions; Gordon and Breach: New York, NY, USA, 1986. [Google Scholar]
- Ge, Y.; Ching, P.C. Energy Efficiency for Proactive Eavesdropping in Cooperative Cognitive Radio Networks. IEEE Int. Things J. 2022, 9, 13443–13457. [Google Scholar] [CrossRef]
- Xiong, B.; Zhang, Z.; Ge, Y.; Wang, H.; Jiang, H.; Wu, L.; Zhang, Z. Channel Modeling for Heterogeneous Vehicular ISAC System with Shared Clusters. In Proceedings of the IEEE Vehicular Technology Conference, Hong Kong, 10–13 October 2023; pp. 1–6. [Google Scholar]

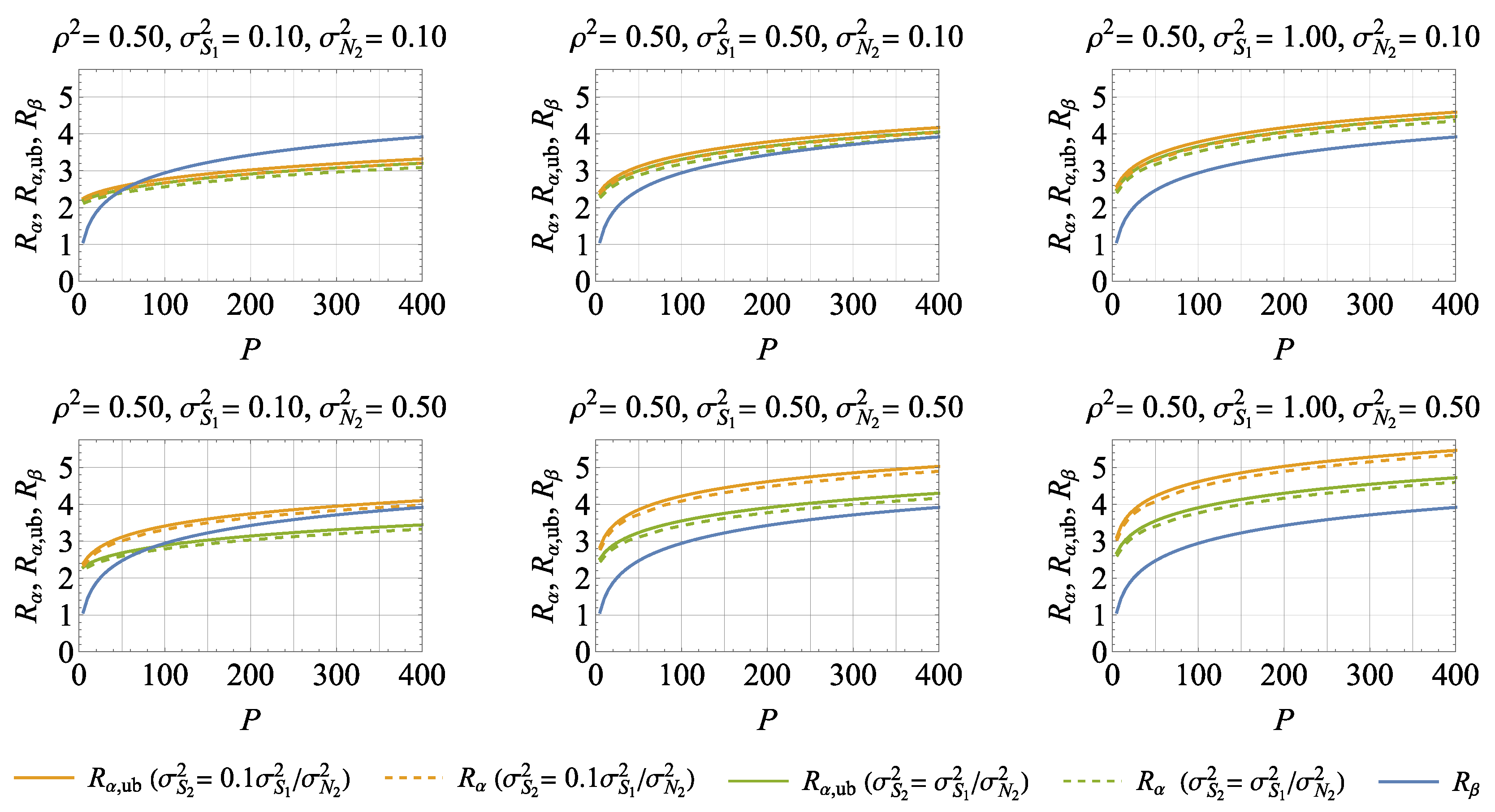
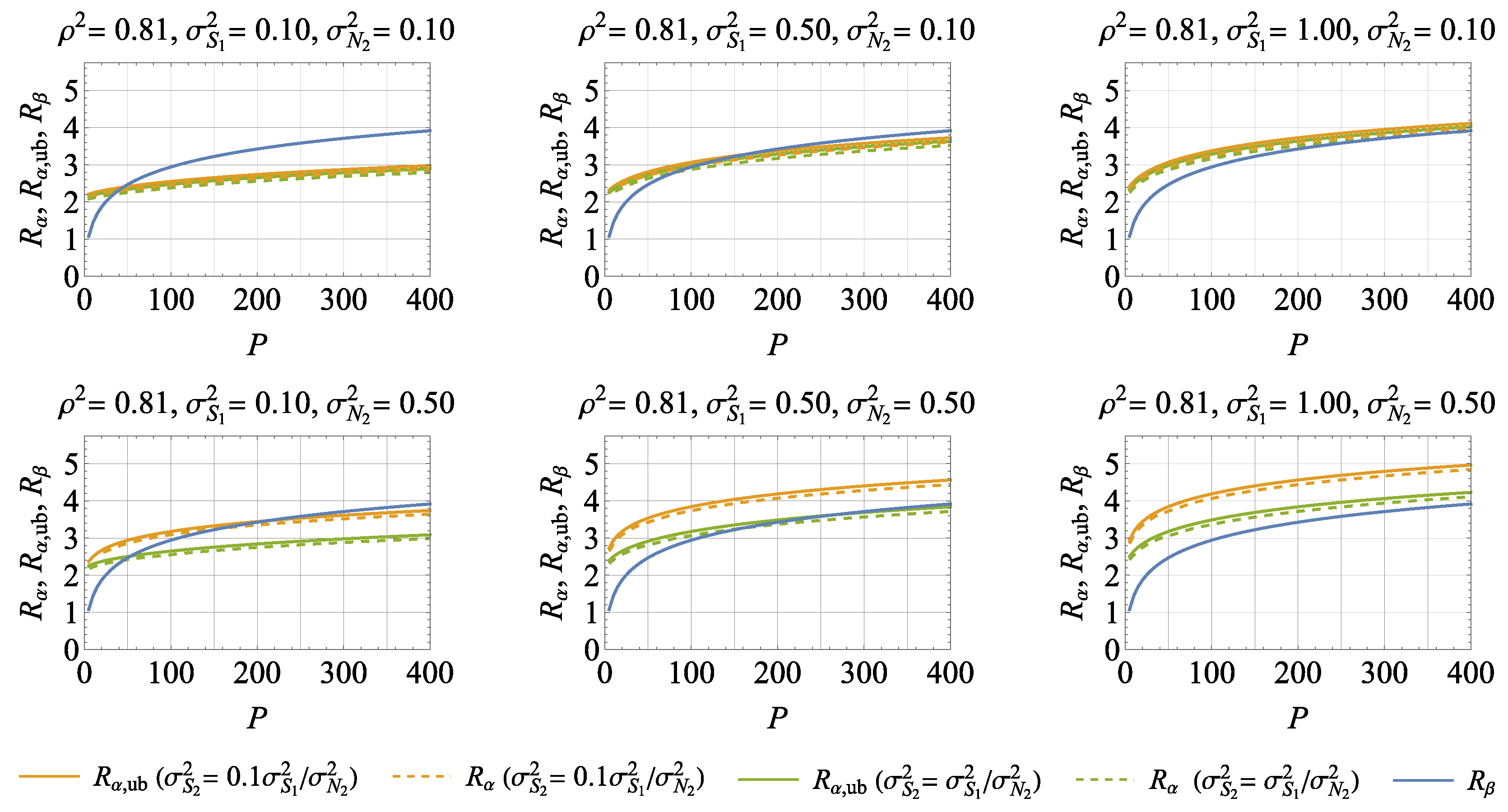

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mittelbach, M.; Schaefer, R.F.; Bloch, M.; Yener, A.; Günlü, O. Sensing-Assisted Secure Communications over Correlated Rayleigh Fading Channels. Entropy 2025, 27, 225. https://doi.org/10.3390/e27030225
Mittelbach M, Schaefer RF, Bloch M, Yener A, Günlü O. Sensing-Assisted Secure Communications over Correlated Rayleigh Fading Channels. Entropy. 2025; 27(3):225. https://doi.org/10.3390/e27030225
Chicago/Turabian StyleMittelbach, Martin, Rafael F. Schaefer, Matthieu Bloch, Aylin Yener, and Onur Günlü. 2025. "Sensing-Assisted Secure Communications over Correlated Rayleigh Fading Channels" Entropy 27, no. 3: 225. https://doi.org/10.3390/e27030225
APA StyleMittelbach, M., Schaefer, R. F., Bloch, M., Yener, A., & Günlü, O. (2025). Sensing-Assisted Secure Communications over Correlated Rayleigh Fading Channels. Entropy, 27(3), 225. https://doi.org/10.3390/e27030225







