Exploring ISAC: Information-Theoretic Insights
Abstract
1. Introduction
Notation
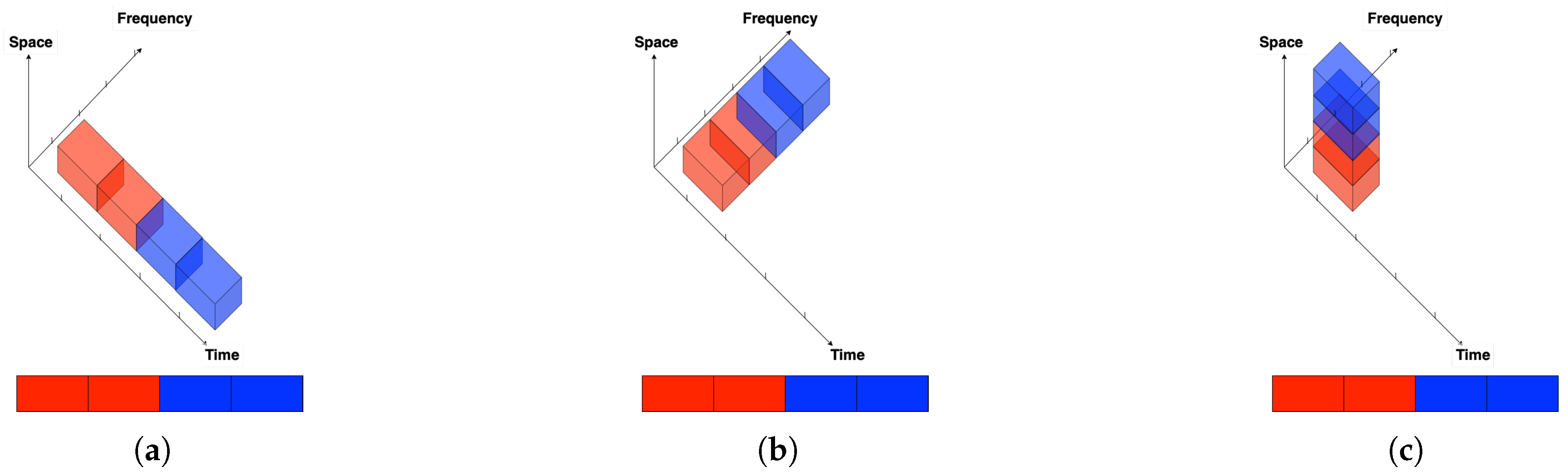
2. Pre-ISAC: Sensing (Radar) vs. Communication
2.1. Radar Systems
2.2. Wireless Communication Systems
2.3. Coexisting Communication and Radar Systems
- Sensing modeThe system aims to design a suitable waveform to attain the minimum possible distortion. In this model, the waveform is translated into an input distribution; thus, the input probability mass function (pmf) is chosen to minimize the distortion, and hence, the minimum distortion is achieved. The communication rate is zero.
- Communication modeThe system is designed to transfer as much reliable data as possible. Therefore, the input distribution is chosen to maximize the rate and communicates rate equals channel capacity. The estimator is set to a constant value regardless of the feedback and the input signals. The mode thus suffers from a large distortion.
- Sensing mode with communication The input pmf is chosen to achieve minimum distortion. At the same time, the transmitter is also equipped with a communication encoder. It uses this input pmf to simultaneously transmit data at the rate given by the input-output mutual information of the system.
- Communication mode with sensing The input distribution is chosen to maximize the communication rate, i.e., achieve the capacity of the channel. The transmitter is, however, also equipped with a radar estimation device that optimally guesses the state sequence based on the transmitted and backscattered signals.
2.4. Integrated Sensing and Communication (ISAC)
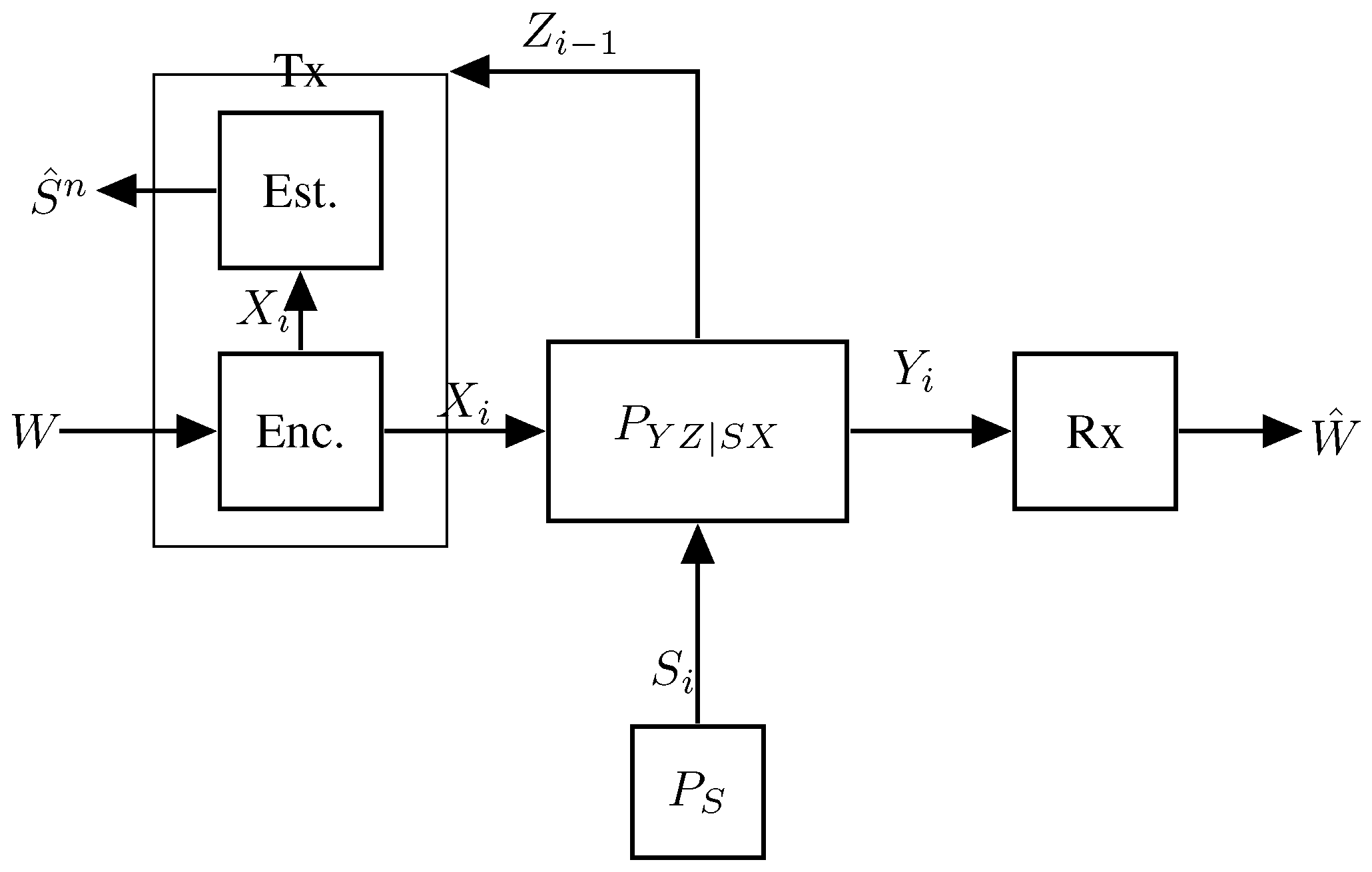
3. Mono-Static ISAC with Sensing Distortion
3.1. The Memoryless Model
3.2. The Capacity–Distortion–Cost Tradeoff
3.3. Log-Loss Distortion
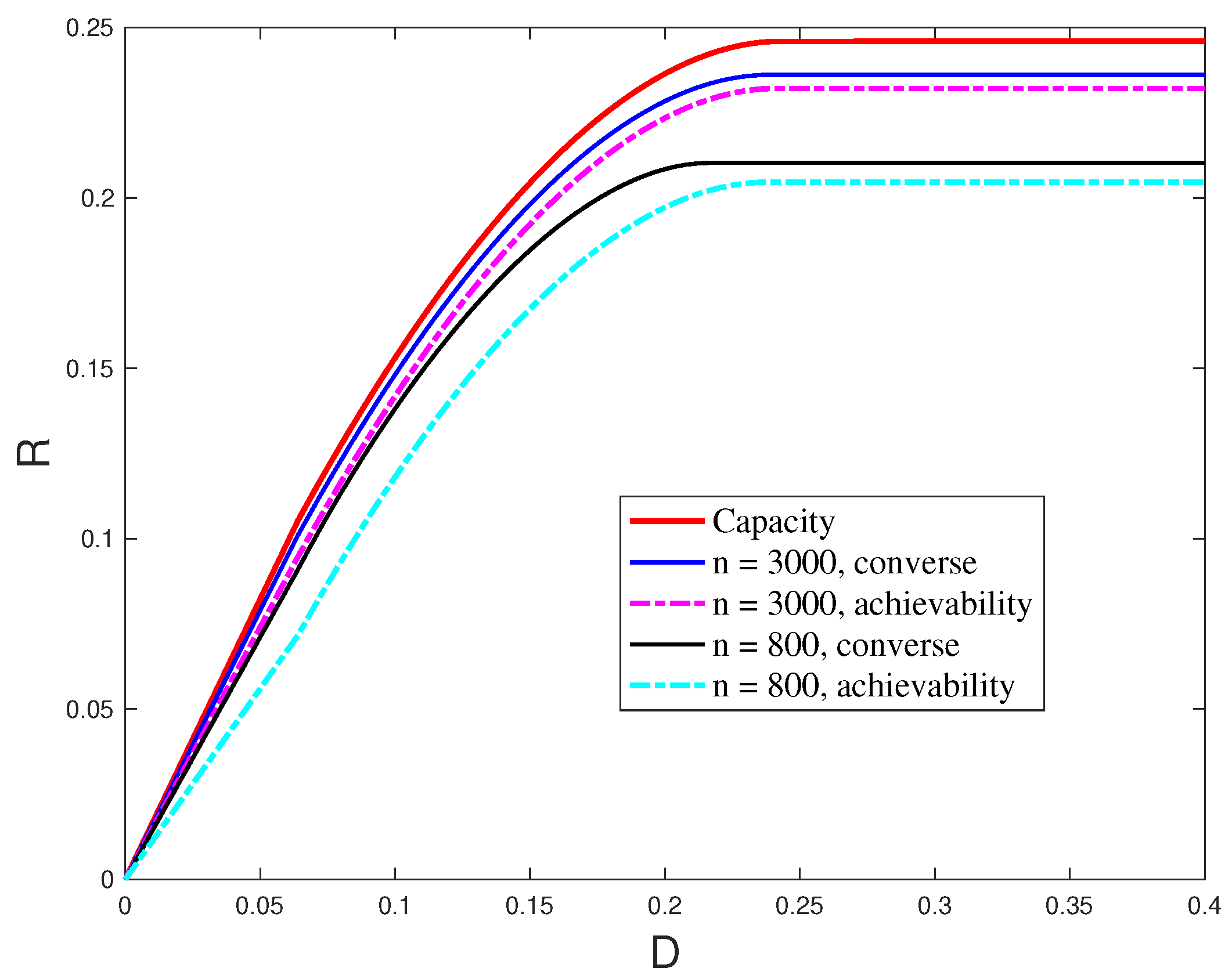
3.4. Finite Blocklength Results
3.5. Channels with Memory
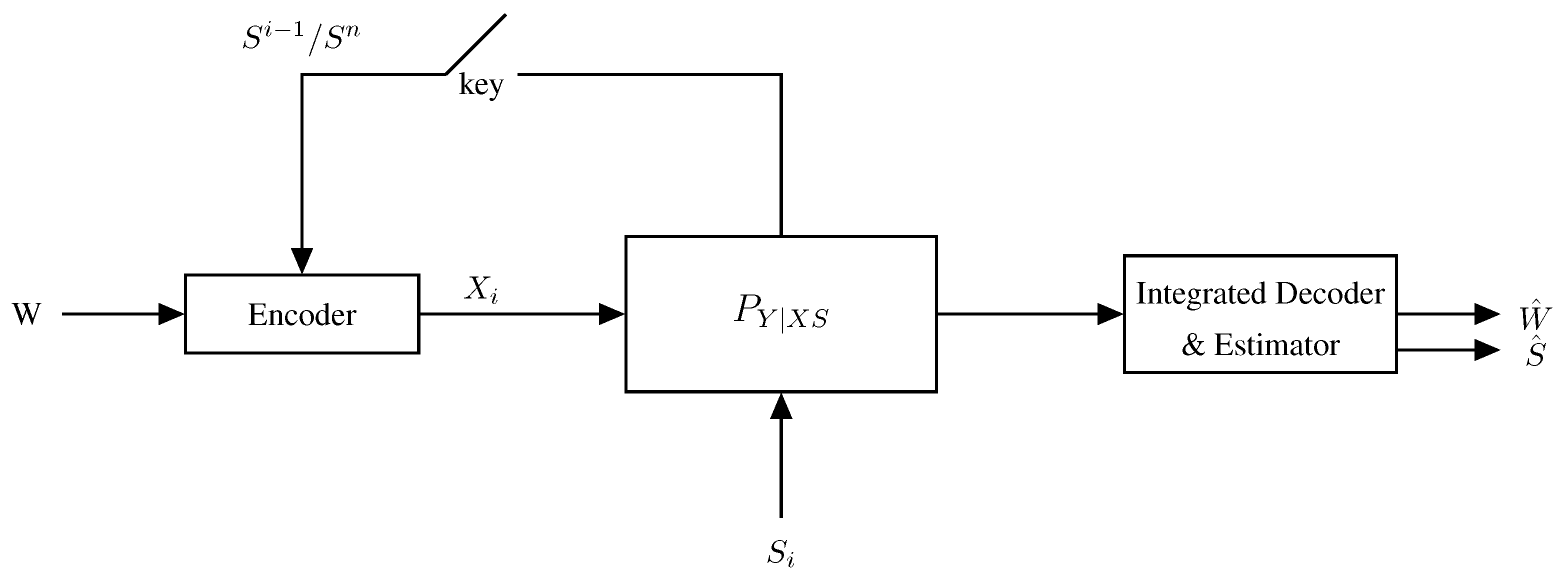
4. Sensing at the Rx (Rx-ISAC) with Sensing Distortion
4.1. A Memoryless Model
- The Tx has no information about ;
- The Tx knows the entire sequence non-causally, i.e., before the entire transmission starts;
- The Tx knows in a strictly causal way, i.e., it learns only after channel use i and prior to channel use ;
- The Tx knows in a causal way, i.e., it learns just before channel use i.
4.2. Capacity–Distortion Tradeoffs
5. Network ISAC with Sensing Distortion
5.1. One-to-Many Communication (Broadcast Channels) with Tx Sensing
5.1.1. The Memoryless Model
5.1.2. Results
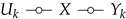 .
.5.1.3. Example
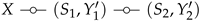 and the physically degradedness of the BC. For physically degraded BCs, the presented inner and outer bounds coincide [64] and thus, we can obtain the exact characterization of the capacity–distortion tradeoff of this example, which is shown numerically in Figure 9.
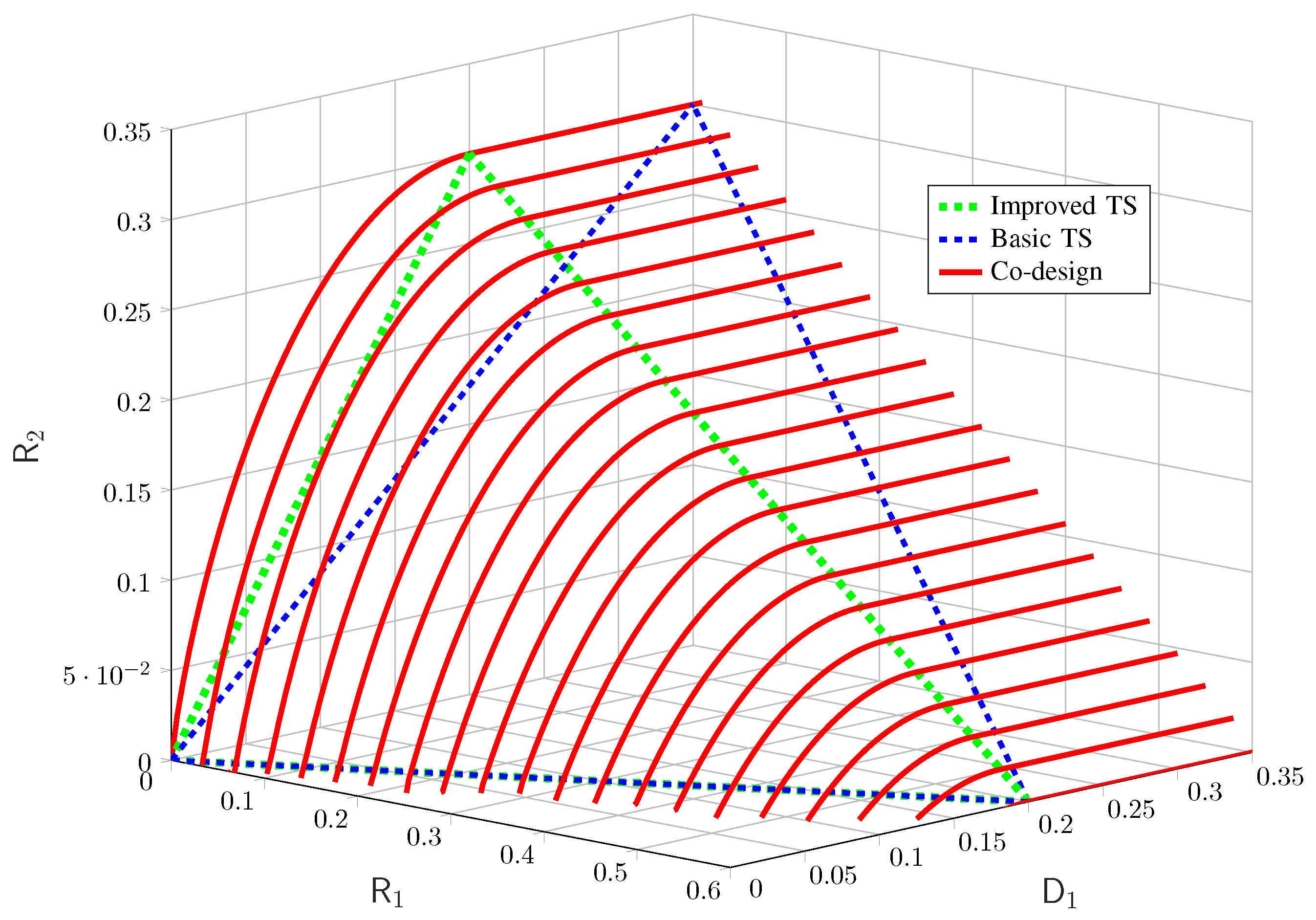
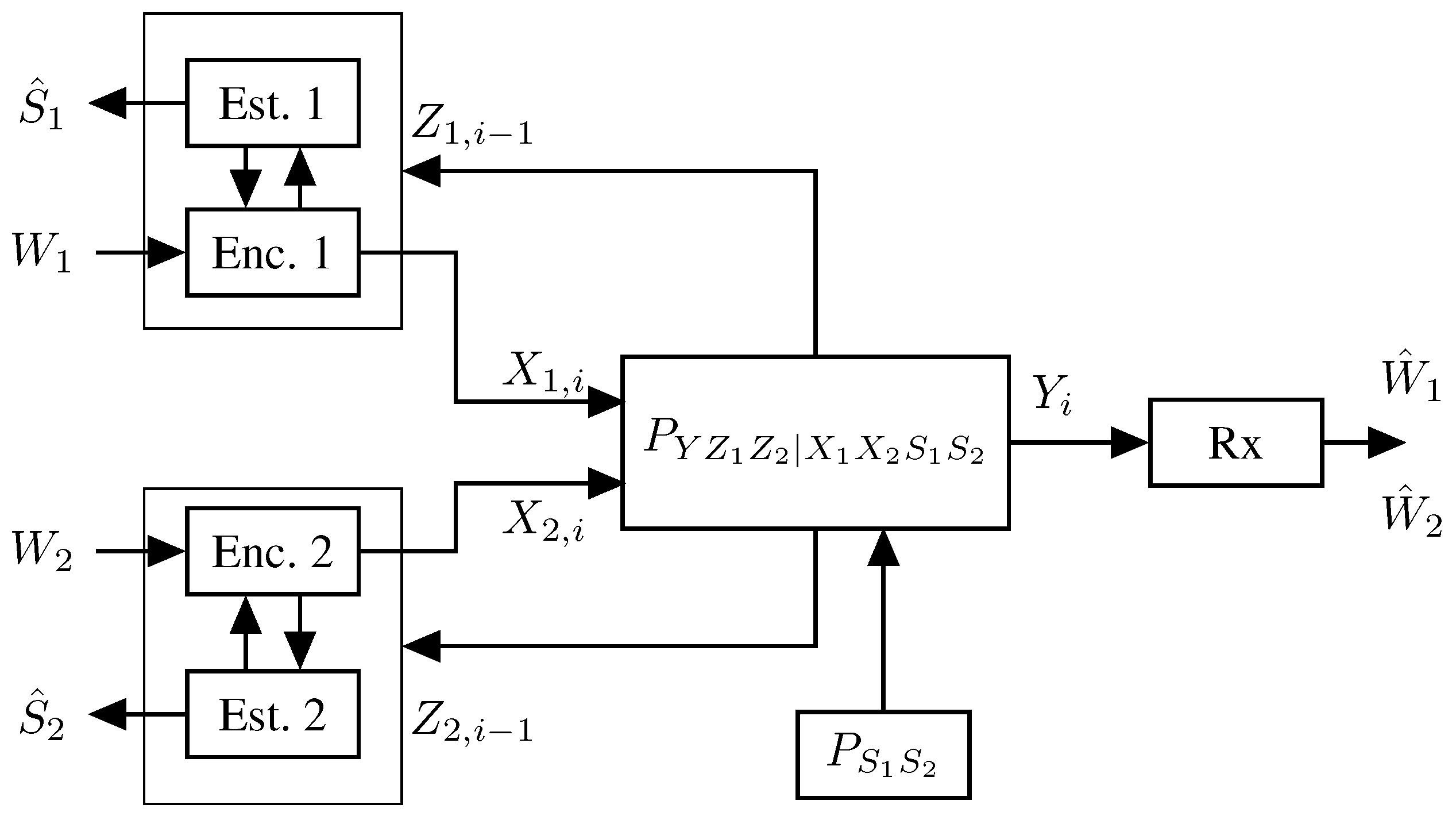
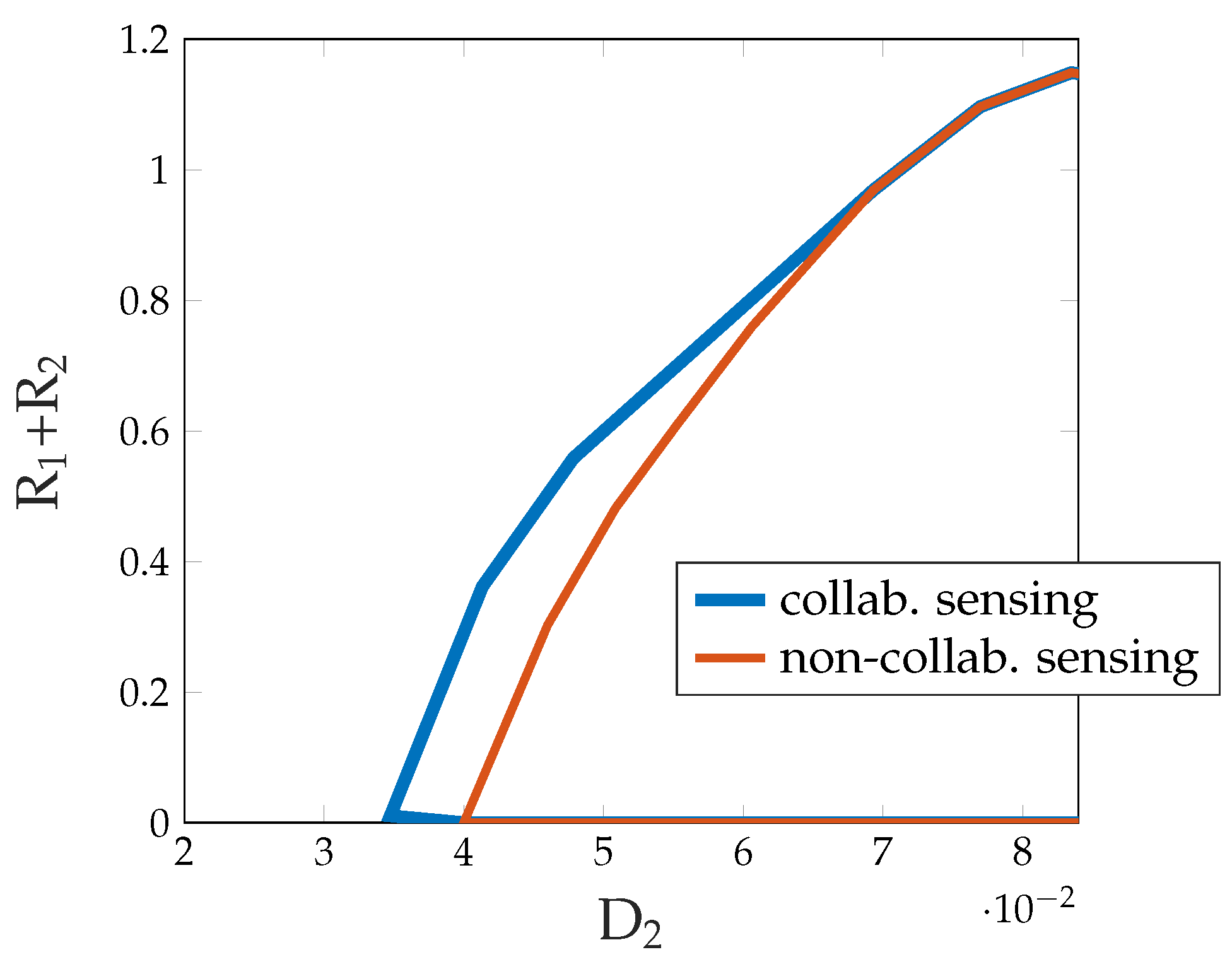
and the physically degradedness of the BC. For physically degraded BCs, the presented inner and outer bounds coincide [64] and thus, we can obtain the exact characterization of the capacity–distortion tradeoff of this example, which is shown numerically in Figure 9.5.2. Multi-Access ISAC: Collaborative Sensing and Suboptimality of Symbolwise Estimators
5.2.1. The Memoryless Model
5.2.2. Results
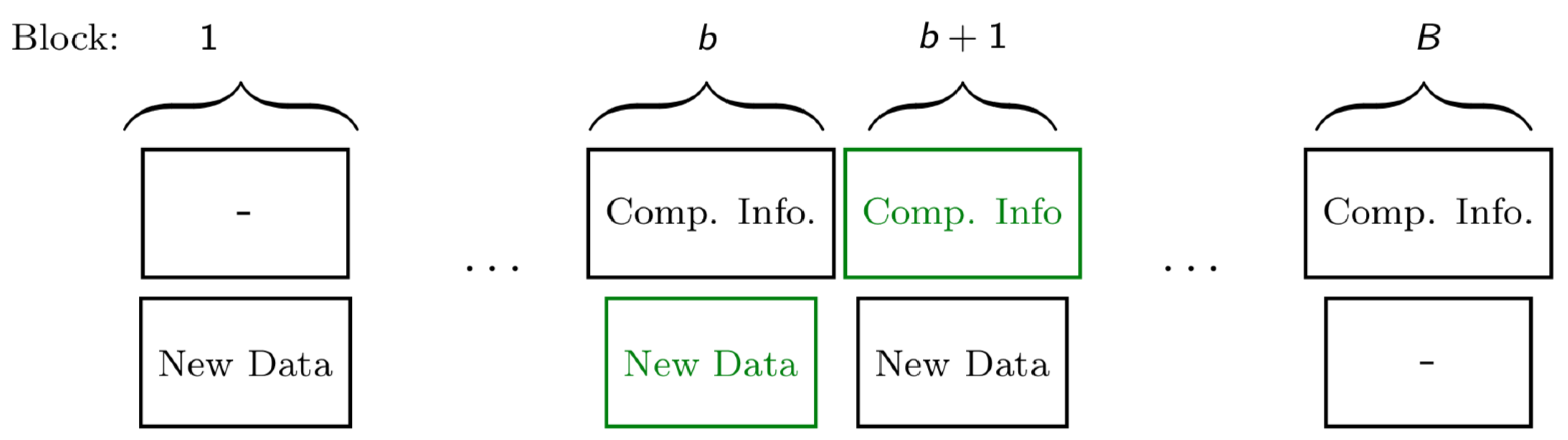
- In the top layer, each Tx independently sends new data in each block. These data are decoded at the Rx only, following the backward decoding algorithm described later.
- In the middle layer, each Tx independently sends new data in each block. These data are decoded at the other Tx at the end of the block and at the Rx following the backward decoding algorithm described later.
- In the lowest layer, the two Txs cooperate and jointly resend the data sent by the two Txs in the middle layer of the previous block (recall that the medium layer data of the previous block has been decoded by the other Tx at the end of the previous block). These data are decoded at the Rx following the backward decoding algorithm described next.
- The receiver decodes all transmitted data using a backward decoding procedure, starting from the last block. Specifically, for each block it decodes the data in the top and lowest layer, while it already is informed of the data sent in the middle layer, because it has decoded it in the previous step.
5.2.3. Example
5.3. Device-to-Device (D2D) Communication (Two-Way Channel)
6. Secrecy of ISAC Systems
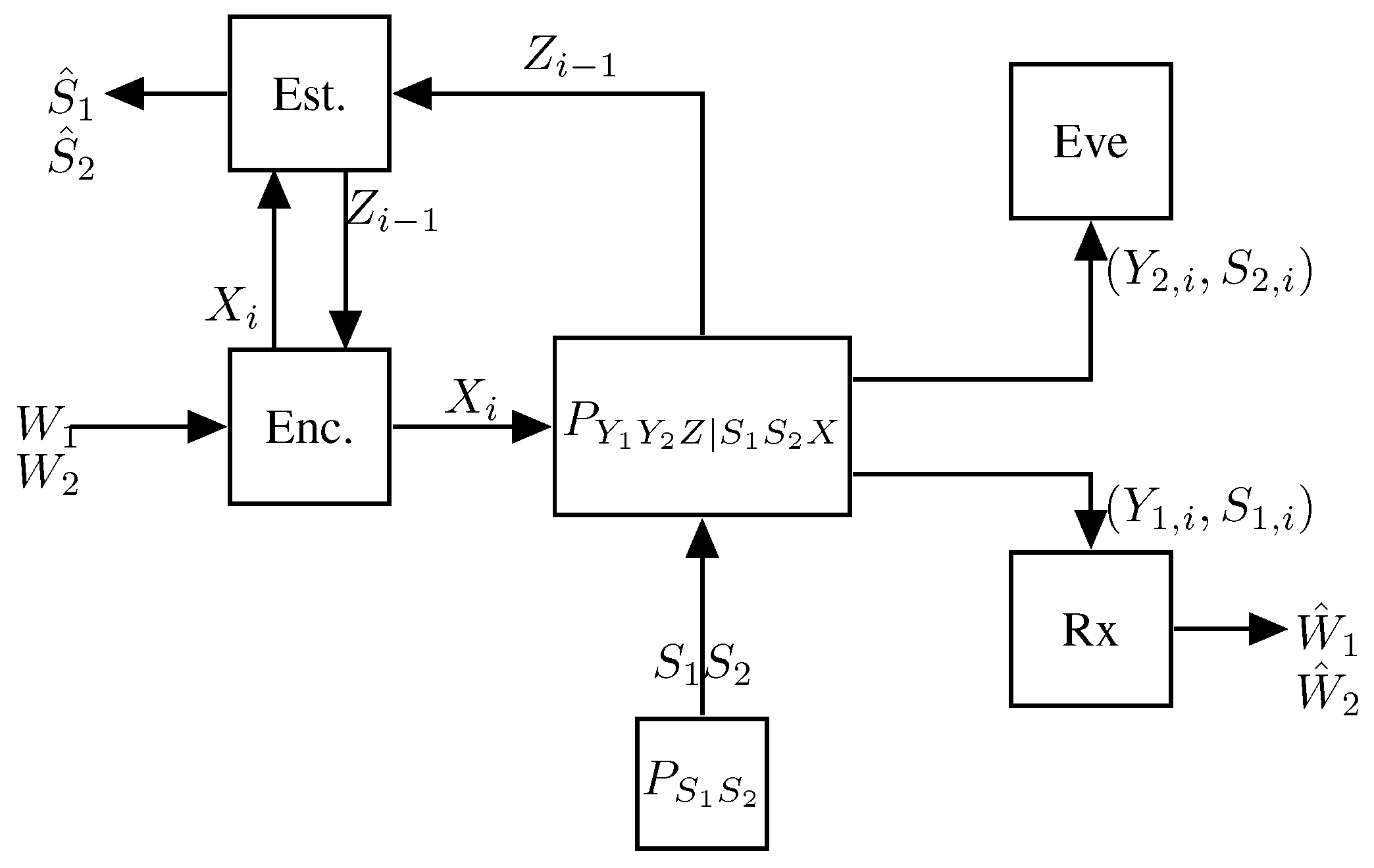
6.1. Secrecy of the Message: The Memoryless Model
6.2. Secrecy of Messages: Results
6.3. Secrecy of Data and Sensing Information
7. ISAC with Detection-Error Exponents
7.1. The Memoryless Block Model
7.2. Results on the Block Model
- In the Stein setup, a non-negative rate–detection-error pair is achievable if, and only if,
- In the exponent-region sense, a non-negative rate–detection-error pair is achievable if, and only if, for some input distribution :
- In the symmetric setup, a non-negative rate–detection-exponent pair is achievable if, and only if, for some input distribution :
7.3. Sequential (Variable-Length) ISAC with Detection-Exponents
- At each time , the Tx forms the channel input as , for an appropriate encoding function ;
- At the end of the transmission, the Tx guesses the state as , for an appropriate guessing function h;
- At the end of transmission, the Rx decodes the transmitted message bits as for an appropriate decoding function g.
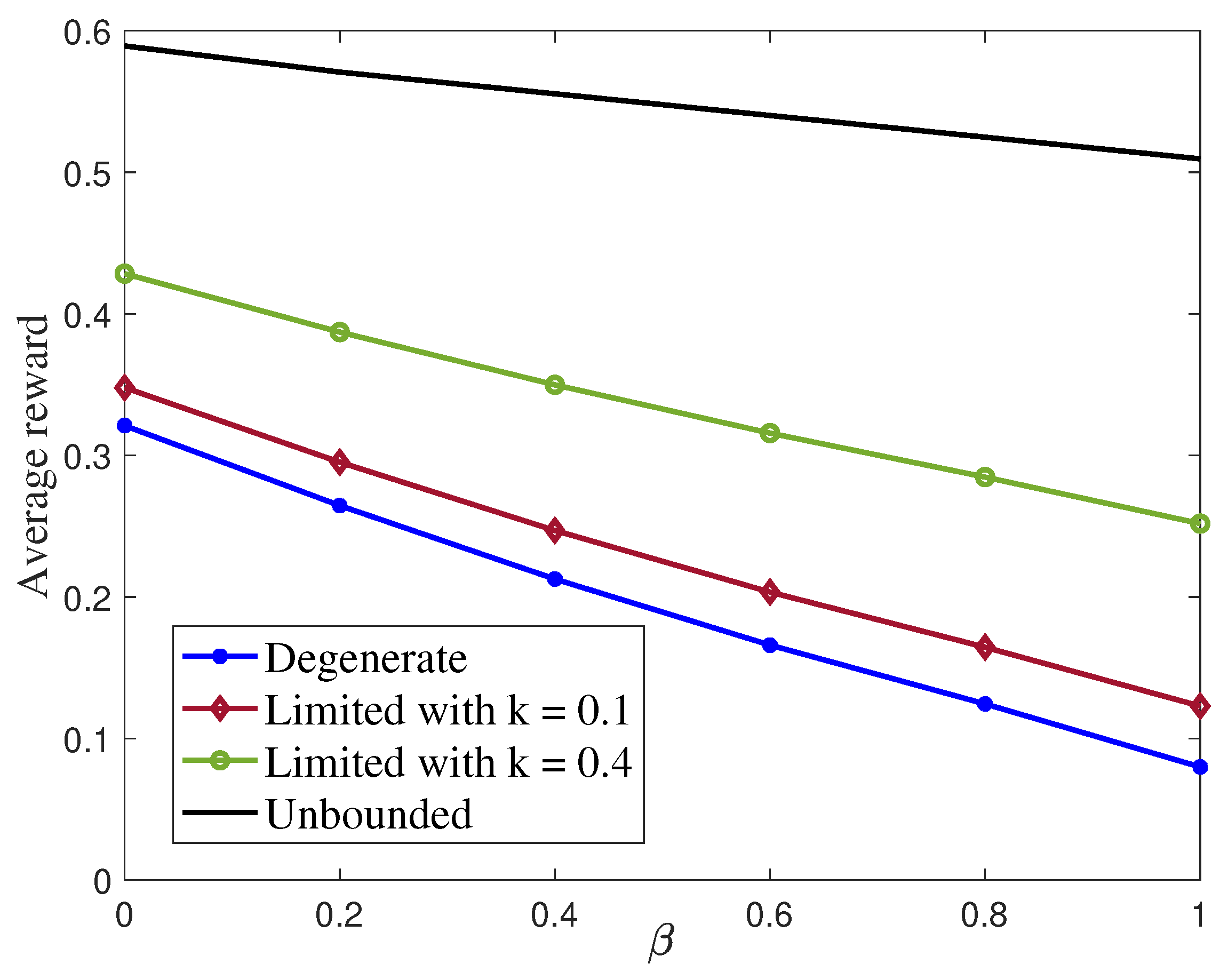
7.4. Sequential (Variable-Length) ISAC with Change-Point Detection
8. Conclusions and Future Research Direction
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Du, R.; Hua, H.; Xie, H.; Song, X.; Lyu, Z.; Hu, M.; Narengerile; Xin, Y.; McCann, S.; Montemurro, M.; et al. An Overview on IEEE 802.11bf: WLAN Sensing. IEEE Commun. Surv. Tutor. 2025, 27, 184–217. [Google Scholar] [CrossRef]
- Wu, Y.; Wigger, M. Coding schemes with rate-limited feedback that improve over the nofeedback capacity for a large class of broadcast channels. IEEE Trans. Inf. Theory 2016, 62, 2009–2033. [Google Scholar] [CrossRef]
- Steinberg, Y. Instances of the relay-broadcast channel and cooperation strategies. In Proceedings of the IEEE International Symposium on Information Theory (ISIT), Hong Kong, China, 14–19 June 2015; pp. 2653–2657. [Google Scholar]
- Venkataramanan, R.; Pradhan, S.S. An achievable rate region for the broadcast channel with feedback. IEEE Trans. Inf. Theory 2013, 59, 6175–6191. [Google Scholar]
- Shayevitz, O.; Wigger, M. On the Capacity of the Discrete Memoryless Broadcast Channel With Feedback. IEEE Trans. Inf. Theory 2013, 59, 1329–1345. [Google Scholar]
- Gatzianas, M.; Georgiadis, L.; Tassiulas, L. Multiuser broadcast erasure channel with feedback: Capacity and algorithms. IEEE Trans. Inf. Theory 2013, 59, 5779–5804. [Google Scholar]
- Kim, H.; Chia, Y.K.; Gamal, A.E. A Note on the Broadcast Channel With Stale State Information at the Transmitter. IEEE Trans. Inf. Theory 2015, 61, 3622–3631. [Google Scholar]
- Watanabe, S. Neyman–Pearson Test for Zero-Rate Multiterminal Hypothesis Testing. IEEE Trans. Inf. Theory 2018, 64, 4923–4939. [Google Scholar] [CrossRef]
- Tian, C.; Chen, J. Successive refinement for hypothesis testing and lossless one-helper problem. IEEE Trans. Inf. Theory 2008, 54, 4666–4681. [Google Scholar]
- Shimokawa, H.; Han, T.; Amari, S.I. Error bound for hypothesis testing with data compression. In Proceedings of the 1994 IEEE International Symposium on Information Theory, Trondheim, Norway, 27 June–1 July 1994; p. 114. [Google Scholar]
- Escamilla, P.; Wigger, M.; Zaidi, A. Distributed hypothesis testing: Cooperation and concurrent detection. IEEE Trans. Inf. Theory 2020, 66, 7550–7564. [Google Scholar]
- Weinberger, N.; Kochman, Y.; Wigger, M. Exponent Trade-off for Hypothesis Testing Over Noisy Channels. In Proceedings of the 2019 IEEE International Symposium on Information Theory (ISIT), Paris, France, 7–12 July 2019; pp. 1852–1856. [Google Scholar] [CrossRef]
- Haim, E.; Kochman, Y. Binary distributed hypothesis testing via Korner-Marton coding. In Proceedings of the 2016 IEEE Information Theory Workshop (ITW), Cambridge, UK, 11–14 September 2016. [Google Scholar]
- Zhao, W.; Lai, L. Distributed testing with cascaded encoders. IEEE Trans. Inf. Theory 2018, 64, 7339–7348. [Google Scholar]
- Salehkalaibar, S.; Tan, V.Y. Distributed Sequential Hypothesis Testing with Zero-Rate Compression. In Proceedings of the 2021 IEEE Information Theory Workshop (ITW), Kanazawa, Japan, 17–21 October 2021; pp. 1–5. [Google Scholar]
- Katz, G.; Piantanida, P.; Debbah, M. Distributed binary detection with lossy data compression. IEEE Trans. Inf. Theory 2017, 63, 5207–5227. [Google Scholar] [CrossRef]
- Han, T.; Kobayashi, K. Exponential-type error probabilities for multiterminal hypothesis testing. IEEE Trans. Inf. Theory 1989, 35, 2–14. [Google Scholar] [CrossRef]
- Han, T.S. Hypothesis testing with multiterminal data compression. IEEE Trans. Inf. Theory 1987, 33, 759–772. [Google Scholar]
- Rahman, M.S.; Wagner, A.B. On the optimality of binning for distributed hypothesis testing. IEEE Trans. Inf. Theory 2012, 58, 6282–6303. [Google Scholar] [CrossRef]
- Ahlswede, R. Certain results in coding theory for compound channels. In Proceedings of the Colloquium on Information Theory; Rényi, A., Ed.; Colloquia mathematica Societatis János Bolyai/Bolyai Janos Matematikai Tarsulat; 1, Budapest; Bolyai Mathematical Society: Debrecen, Hungary, 1967; pp. 35–60. [Google Scholar]
- Zhang, W.; Vedantam, S.; Mitra, U. Joint Transmission and State Estimation: A Constrained Channel Coding Approach. IEEE Trans. Inf. Theory 2011, 57, 7084–7095. [Google Scholar] [CrossRef]
- Isik, B.; Chen, W.N.; Ozgur, A.; Weissman, T.; No, A. Exact Optimality of Communication-Privacy-Utility Tradeoffs in Distributed Mean Estimation. In Proceedings of the NIPS’23: 37th International Conference on Neural Information Processing Systems, New Orleans, LA, USA, 10–16 December 2023. [Google Scholar]
- Hadar, U.; Shayevitz, O. Distributed Estimation of Gaussian Correlations. IEEE Trans. Inf. Theory 2019, 65, 5323–5338. [Google Scholar] [CrossRef]
- Berg, T.; Ordentlich, O.; Shayevitz, O. Statistical Inference With Limited Memory: A Survey. IEEE J. Sel. Areas Inf. Theory 2024, 5, 623–644. [Google Scholar] [CrossRef]
- Wyner, A. On source coding with side information at the decoder. IEEE Trans. Inf. Theory 1975, 21, 294–300. [Google Scholar] [CrossRef]
- Slepian, D.; Wolf, J. Noiseless coding of correlated information sources. IEEE Trans. Inf. Theory 1973, 19, 471–480. [Google Scholar] [CrossRef]
- Tuncel, E. Slepian-Wolf coding over broadcast channels. IEEE Trans. Inf. Theory 2006, 52, 1469–1482. [Google Scholar] [CrossRef]
- Minero, P.; Lim, S.H.; Kim, Y.H. A Unified Approach to Hybrid Coding. IEEE Trans. Inf. Theory 2015, 61, 1509–1523. [Google Scholar] [CrossRef]
- Gray, R.M.; Wyner, A.D. Source coding for a simple network. Bell Syst. Tech. J. 1974, 53, 1681–1721. [Google Scholar]
- Merhav, N. Universal decoding for source-channel coding with side information. In Proceedings of the 2016 IEEE International Symposium on Information Theory (ISIT), Barcelona, Spain, 10–15 July 2016; pp. 1093–1097. [Google Scholar] [CrossRef]
- Heegard, C.; Berger, T. Rate distortion when side information may be absent. IEEE Trans. Inf. Theory 1985, 31, 727–734. [Google Scholar] [CrossRef]
- Liu, F.; Masouros, C.; Petropulu, A.P.; Griffiths, H.; Hanzo, L. Joint radar and communication design: Applications, state-of-the-art, and the road ahead. IEEE Trans. Commun. 2020, 68, 3834–3862. [Google Scholar]
- Liu, A.; Huang, Z.; Li, M.; Wan, Y.; Li, W.; Han, T.X.; Liu, C.; Du, R.; Tan, D.K.P.; Lu, J.; et al. A Survey on Fundamental Limits of Integrated Sensing and Communication. IEEE Commun. Surv. Tutor. 2022, 24, 994–1034. [Google Scholar] [CrossRef]
- Heath, R.W. Communications and Sensing: An Opportunity for Automotive Systems. IEEE Signal Process. Mag. 2020, 37, 3–13. [Google Scholar]
- Flagship, G. 6G White Paper on Localization and Sensing; University of Oulu: Oulu, Finland, 2020. [Google Scholar]
- Ma, D.; Shlezinger, N.; Huang, T.; Liu, Y.; Eldar, Y.C. Joint Radar-Communication Strategies for Autonomous Vehicles: Combining Two Key Automotive Technologies. IEEE Signal Process. Mag. 2020, 37, 85–97. [Google Scholar] [CrossRef]
- Mishra, K.V.; Shankar, M.B.; Koivunen, V.; Ottersten, B.; Vorobyov, S.A. Towards millimeter wave joint radar-communications: A signal processing perspective. IEEE Signal Process. Mag. 2019, 36, 100–114. [Google Scholar]
- Zheng, L.; Lops, M.; Eldar, Y.C.; Wang, X. Radar and Communication Co-existence: An Overview: A Review of Recent Methods. IEEE Signal Process. Mag. 2019, 36, 85–99. [Google Scholar]
- Lu, S.; Liu, F.; Li, Y.; Zhang, K.; Huang, H.; Zou, J.; Li, X.; Dong, Y.; Dong, F.; Zhu, J.; et al. Integrated Sensing and Communications: Recent Advances and Ten Open Challenges. IEEE Internet Things J. 2024, 11, 19094–19120. [Google Scholar] [CrossRef]
- Wei, Z.; Jia, J.; Niu, Y.; Wang, L.; Wu, H.; Yang, H.; Feng, Z. Integrated Sensing and Communication Channel Modeling: A Survey. IEEE Internet Things J. 2024, 1. [Google Scholar] [CrossRef]
- Temiz, M.; Zhang, Y.; Fu, Y.; Zhang, C.; Meng, C.; Kaplan, O.; Masouros, C. Deep Learning-based Techniques for Integrated Sensing and Communication Systems: State-of-the-Art, Challenges, and Opportunities. TechRxiv 2024. [Google Scholar] [CrossRef]
- Kobayashi, M.; Caire, G. Information Theoretic Aspects of Joint Sensing and Communications; Wiley: Hoboken, NJ, USA, 2024. [Google Scholar]
- Liu, A.; Li, M.; Kobayashi, M.; Caire, G. Fundamental Limits for ISAC: Information and Communication Theoretic Perspective. In Integrated Sensing and Communications; Liu, F., Masouros, C., Eldar, Y.C., Eds.; Springer Nature: Singapore, 2023; pp. 23–52. [Google Scholar] [CrossRef]
- Liu, F.; Masouros, C.; Li, A.; Sun, H.; Hanzo, L. MU-MIMO communications with MIMO radar: From co-existence to joint transmission. IEEE Trans. Wirel. Commun. 2018, 17, 2755–2770. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P. MIMO Radar with Colocated Antennas. IEEE Signal Process. Mag. 2007, 24, 106–114. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, S. MIMO Integrated Sensing and Communication Exploiting Prior Information. IEEE J. Sel. Areas Commun. 2024, 42, 2306–2321. [Google Scholar] [CrossRef]
- Zhang, R.; Cheng, L.; Wang, S.; Lou, Y.; Gao, Y.; Wu, W. Integrated Sensing and Communication with Massive MIMO: A Unified Tensor Approach for Channel and Target Parameter Estimation. IEEE Trans. Wirel. Commun. 2024, 23, 8571–8587. [Google Scholar] [CrossRef]
- Gaudio, L.; Kobayashi, M.; Caire, G.; Colavolpe, G. Joint Radar Target Detection and Parameter Estimation with MIMO OTFS. arXiv 2020, arXiv:2004.11035. [Google Scholar]
- Liu, Y.; Liu, X.; Chen, Y. Cell-Free ISAC MIMO Systems: Joint Sensing and Communication Design. arXiv 2023, arXiv:2301.11328. [Google Scholar]
- Zhang, J.; Dai, L.; Wang, Z. Interference Management in MIMO-ISAC Systems. arXiv 2024, arXiv:2407.05391. [Google Scholar]
- Zhang, H.; Di, B.; Song, L. Sensing-Efficient Transmit Beamforming for ISAC with MIMO Radar. Remote Sens. 2023, 16, 3028. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y.; Tao, M. Information and Sensing Beamforming Optimization for Multi-User MIMO-ISAC Systems. EURASIP J. Adv. Signal Process. 2023, 2023, 15. [Google Scholar] [CrossRef]
- Xiong, Y.; Liu, F.; Cui, Y.; Yuan, W.; Han, T.X.; Caire, G. On the Fundamental Tradeoff of Integrated Sensing and Communications Under Gaussian Channels. IEEE Trans. Inf. Theory 2023, 69, 5723–5751. [Google Scholar] [CrossRef]
- Li, X.; Min, H.; Zeng, Y.; Jin, S.; Dai, L.; Yuan, Y.; Zhang, R. Sparse MIMO for ISAC: New Opportunities and Challenges. arXiv 2024, arXiv:2406.12270. [Google Scholar] [CrossRef]
- Ouyang, C.; Liu, Y.; Yang, H. MIMO-ISAC: Performance Analysis and Rate Region Characterization. IEEE Wirel. Commun. Lett. 2022, 12, 669–673. [Google Scholar]
- Kobayashi, M.; Caire, G.; Kramer, G. Joint State Sensing and Communication: Optimal Tradeoff for a Memoryless Case. In Proceedings of the 2018 IEEE International Symposium on Information Theory (ISIT), Vail, CO, USA, 17–22 June 201; pp. 111–115.
- Ahmadipour, M.; Wigger, M.; Shamai, S. Strong Converses for Memoryless Bi-Static ISAC. In Proceedings of the 2023 IEEE International Symposium on Information Theory (ISIT), Taipei, Taiwan, 25–30 June 2023; pp. 1818–1823. [Google Scholar] [CrossRef]
- Joudeh, H.; Caire, G. Joint communication and state sensing under logarithmic loss. In Proceedings of the 4th IEEE International Symposium on Joint Communications & Sensing (JC&S), Leuven, Belgium, 19–21 March 2024. [Google Scholar]
- Nikbakht, H.; Wigger, M.; Shamai, S.; Poor, H. Integrated Sensing and Communication in the Finite Blocklength Regime. In Proceedings of the 2024 IEEE International Symposium on Information Theory (ISIT), Athens, Greece, 7–12 July 2024. [Google Scholar]
- Chen, Y.; Oechtering, T.; Skoglund, M.; Luo, Y. On General Capacity-Distortion Formulas of Integrated Sensing and Communication. arXiv 2023, arXiv:2310.11080. [Google Scholar]
- Choudhuri, C.; Kim, Y.H.; Mitra, U. Causal State Communication. IEEE Trans. Inf. Theory 2013, 59, 3709–3719. [Google Scholar] [CrossRef]
- Sutivong, A.; Chiang, M.; Cover, T.M.; Kim, Y.H. Channel capacity and state estimation for state-dependent Gaussian channels. IEEE Trans. Inf. Theory 2005, 51, 1486–1495. [Google Scholar] [CrossRef]
- Ahmadipour, M. An Information-Theoretic Approach to Integrated Sensing and Communication. Ph.D. Thesis, Institut Polytechnique de Paris, Paris, France, November 2022. [Google Scholar]
- Ahmadipour, M.; Kobayashi, M.; Wigger, M.; Caire, G. An Information-Theoretic Approach to Joint Sensing and Communication. IEEE Trans. Inf. Theory 2022, 70, 1124–1146. [Google Scholar] [CrossRef]
- Kobayashi, M.; Hamad, H.; Kramer, G.; Caire, G. Joint state sensing and communication over memoryless multiple access channels. In Proceedings of the 2019 IEEE International Symposium on Information Theory (ISIT), Paris, France, 7–12 July 2019; pp. 270–274. [Google Scholar]
- Liu, Y.; Li, M.; Liu, A.; Ong, L.; Yener, A. Fundamental Limits of Multiple-Access Integrated Sensing and Communication Systems. arXiv 2023, arXiv:2205.05328v3. [Google Scholar] [CrossRef]
- Ahmadipour, M.; Wigger, M.; Kobayashi, M. Coding for Sensing: An Improved Scheme for Integrated Sensing and Communication over MACs. In Proceedings of the 2022 IEEE International Symposium on Information Theory (ISIT), Espoo, Finland, 26 June–1 July 2022; pp. 3025–3030. [Google Scholar] [CrossRef]
- Ahmadipour, M.; Wigger, M. An Information-Theoretic Approach to Collaborative Integrated Sensing and Communication for Two-Transmitter Systems. IEEE J. Sel. Areas Inf. Theory 2023, 4, 112–127. [Google Scholar] [CrossRef]
- Günlü, O.; Bloch, M.R.; Schaefer, R.F.; Yener, A. Secure Integrated Sensing and Communication. IEEE J. Sel. Areas Inf. Theory 2023, 4, 40–53. [Google Scholar] [CrossRef]
- Ahmadipour, M.; Wigger, M.; Shamai, S. Integrated Communication and Receiver Sensing with Security Constraints on Message and State. In Proceedings of the 2023 IEEE International Symposium on Information Theory (ISIT), Taipei, Taiwan, 25–30 June 2023; pp. 2738–2743. [Google Scholar] [CrossRef]
- Joudeh, H.; Willems, F.M.J. Joint Communication and Binary State Detection. IEEE J. Sel. Areas Inf. Theory 2022, 3, 113–124. [Google Scholar] [CrossRef]
- Wu, H.; Joudeh, H. On Joint Communication and Channel Discrimination. In Proceedings of the 2022 IEEE International Symposium on Information Theory (ISIT), Espoo, Finland, 26 June–1 July 2022; pp. 3321–3326. [Google Scholar] [CrossRef]
- Chang, M.C.; Erdogan.; Wang, S.Y.; Bloch, M.R. Rate and Detection Error-Exponent Tradeoffs of Joint Communication and Sensing. In Proceedings of the 2nd IEEE International Symposium on Joint Communications and Sensing (JCS), Seefeld, Austria, 9–10 March 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Ahmadipour, M.; Wigger, M.; Shamai, S. Strong Converse for Bi-Static ISAC with Two Detection-Error Exponents. In Proceedings of the International Zurich Seminar on Information and Communication (IZS 2024), Zurich, Switzerland, 6–8 March 2024; p. 45. [Google Scholar]
- Seo, D.; Lim, S.H. On the Fundamental Tradeoff of Joint Communication and Quickest Change Detection. arXiv 2024, arXiv:2401.12499. [Google Scholar]
- Mealey, R.M. A Method for Calculating Error Probabilities in a Radar Communication System. IEEE Trans. Space Electron. Telem. 1963, 9, 37–42. [Google Scholar] [CrossRef]
- Winkler, M.R. Chirp signals for communications. In Proceedings of the IEEE WESCON Convention Record, Los Angeles, CA, USA, 21–24 August 1962. Paper 14.2. [Google Scholar]
- Bemi, A.I.; Grcgg, W. On the utility of chirp modulation for digital signaling. IEEE Trans. Cnmmun. 1973, 21, 748–751. [Google Scholar]
- Zhang, Q.; Sun, H.; Gao, X.; Wang, X.; Feng, Z. Time-Division ISAC Enabled Connected Automated Vehicles Cooperation Algorithm Design and Performance Evaluation. IEEE J. Sel. Areas Commun. 2022, 40, 2206–2218. [Google Scholar] [CrossRef]
- Shi, C.; Wang, F.; Sellathurai, M.; Zhou, J.; Salous, S. Power Minimization-Based Robust OFDM Radar Waveform Design for Radar and Communication Systems in Coexistence. IEEE Trans. Signal Process. 2018, 66, 1316–1330. [Google Scholar] [CrossRef]
- Mohammed, S.K.; Hadani, R.; Chockalingam, A.; Calderbank, R. OTFS—A mathematical foundation for communication and radar sensing in the delay-Doppler domain. IEEE BITS Inf. Theory Mag. 2022, 2, 36–55. [Google Scholar]
- Wu, J.; Yuan, W.; Wei, Z.; Zhang, K.; Liu, F.; Wing Kwan Ng, D. Low-Complexity Minimum BER Precoder Design for ISAC Systems: A Delay-Doppler Perspective. IEEE Trans. Wirel. Commun. 2025, 24, 1526–1540. [Google Scholar] [CrossRef]
- Lin, X. 3GPP Evolution from 5G to 6G: A 10-Year Retrospective. arXiv 2024, arXiv:2412.21077. [Google Scholar]
- Sodagari, S.; Khawar, A.; Clancy, T.C.; McGwier, R. A projection based approach for radar and telecommunication systems coexistence. In Proceedings of the 2012 IEEE Global Communications Conference (GLOBECOM), Anaheim, CA, USA, 3–7 December 2012; pp. 5010–5014. [Google Scholar] [CrossRef]
- Günlü, O.; Bloch, M.; Schaefer, R.F.; Yener, A. Nonasymptotic Performance Limits of Low-Latency Secure Integrated Sensing and Communication Systems. In Proceedings of the ICASSP 2024—IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024; pp. 12971–12975. [Google Scholar] [CrossRef]
- Nikbakht, H.; Wigger, M.; Shamai, S.; Poor, H.V. A Memory-Based Reinforcement Learning Approach to Integrated Sensing and Communication. arXiv 2024, arXiv:2412.01077. [Google Scholar]
- Aharoni, Z.; Sabag, O.; Permuter, H.H. Computing the Feedback Capacity of Finite State Channels using Reinforcement Learning. In Proceedings of the 2019 IEEE International Symposium on Information Theory (ISIT), Paris, France, 7–12 July 2019; pp. 837–841. [Google Scholar] [CrossRef]
- Zhang, W.; Vedantam, S.; Mitra, U. A constrained channel coding approach to joint communication and channel estimation. In Proceedings of the 2008 IEEE International Symposium on Information Theory, Paris, France, 7–12 July 2008; pp. 930–934. [Google Scholar] [CrossRef]
- Choudhuri, C.; Ming, U.M. On non-causal side information at the encoder. In Proceedings of the 50th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 1–5 October 2012; pp. 648–655. [Google Scholar] [CrossRef]
- Salimi, A.; Zhang, W.; Vedantam, S.; Mitra, U. The capacity-distortion function for multihop channels with state. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 2228–2232. [Google Scholar] [CrossRef]
- Gelfand, S.I.; Pinsker, M.S. Coding for channels with random parameters. Probl. Control. Inf. Theory 1980, 9, 19–31. [Google Scholar]
- Gamal, A.E.; Kim, Y.H. Network Information Theory; Cambridge University Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Koivunen, V.; Keskin, M.F.; Wymeersch, H.; Valkama, M.; González-Prelcic, N. Multicarrier ISAC: Advances in waveform design, signal processing, and learning under nonidealities [Special Issue on Signal Processing for the Integrated Sensing and Communications Revolution]. IEEE Signal Process. Mag. 2024, 41, 17–30. [Google Scholar]
- Gamal, A. The feedback capacity of degraded broadcast channels (Corresp.). IEEE Trans. Inf. Theory 1978, 24, 379–381. [Google Scholar] [CrossRef]
- Willems, F.; van der Meulen, E.; Schalkwijk, J. Achievable rate region for the multiple access channel with generalized feedback. In Proceedings of the Annual Allerton Conference on Communication, Control and Computing, 1 December 1983; pp. 284–292. Available online: https://experts.boisestate.edu/en/publications/coefficient-assignment-for-siso-time-delay-systems (accessed on 19 January 2025).
- Kramer, G. Capacity results for the discrete memoryless network. IEEE Trans. Inf. Theory 2003, 49, 4–21. [Google Scholar] [CrossRef]
- Ozarow, L. The capacity of the white Gaussian multiple access channel with feedback. IEEE Trans. Inf. Theory 1984, 30, 623–629. [Google Scholar] [CrossRef]
- Willems, F. The feedback capacity region of a class of discrete memoryless multiple access channels (Corresp.). IEEE Trans. Inf. Theory 1982, 28, 93–95. [Google Scholar] [CrossRef]
- Gaarder, N.; Wolf, J. The capacity region of a multiple-access discrete memoryless channel can increase with feedback. IEEE Trans. Inf. Theory 1975, 21, 100–102. [Google Scholar] [CrossRef]
- Cover, T.; Leung, C. An achievable rate region for the multiple-access channel with feedback. IEEE Trans. Inf. Theory 1981, 27, 292–298. [Google Scholar] [CrossRef]
- Carleial, A. Multiple-access channels with different generalized feedback signals. IEEE Trans. Inf. Theory 1982, 28, 841–850. [Google Scholar] [CrossRef]
- Hekstra, A.; Willems, F. Dependence balance bounds for single-output two-way channels. IEEE Trans. Inf. Theory 1989, 35, 44–53. [Google Scholar] [CrossRef]
- Lapidoth, A.; Steinberg, Y. The Multiple-Access Channel with Causal Side Information: Double State. IEEE Trans. Inf. Theory 2013, 59, 1379–1393. [Google Scholar] [CrossRef]
- Lapidoth, A.; Steinberg, Y. The Multiple-Access Channel with Causal Side Information: Common State. IEEE Trans. Inf. Theory 2013, 59, 32–50. [Google Scholar] [CrossRef]
- Somekh-Baruch, A.; Shamai, S.; Verdu, S. Cooperative Multiple-Access Encoding with States Available at One Transmitter. IEEE Trans. Inf. Theory 2008, 54, 4448–4469. [Google Scholar] [CrossRef]
- Kotagiri, S.; Laneman, J.N. Multiaccess Channels with State Known to One Encoder: A Case of Degraded Message Sets. In Proceedings of the 2007 IEEE International Symposium on Information Theory, Nice, France, 24–29 June 2007; pp. 1566–1570. [Google Scholar] [CrossRef]
- Li, M.; Simeone, O.; Yener, A. Multiple Access Channels With States Causally Known at Transmitters. IEEE Trans. Inf. Theory 2013, 59, 1394–1404. [Google Scholar] [CrossRef]
- Liu, Y.; Li, M.; Han, Y.; Ong, L. Information- Theoretic Limits of Integrated Sensing and Communication over Interference Channels. In Proceedings of the ICC 2024—IEEE International Conference on Communications, Denver, CO, USA, 9–13 June 2024; pp. 3561–3566. [Google Scholar] [CrossRef]
- Han, T. A general coding scheme for the two-way channel. IEEE Trans. Inf. Theory 1984, 30, 35–44. [Google Scholar] [CrossRef]
- Kramer, G. Directed Information for Channels with Feedback. Ph.D. Thesis, Swiss Federal Institute of Technology, Zurich, Switzerland, 1998. [Google Scholar]
- Gunlu, O.; Bloch, M.; Schaefer, R.F.; Yener, A. Secure Integrated Sensing and Communication for Binary Input Additive White Gaussian Noise Channels. In Proceedings of the 2023 IEEE 3rd International Symposium on Joint Communications & Sensing (JC & S), Seefeld, Austria, 5–7 March 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Mittelbach, M.; Schaefer, R.F.; Bloch, M.; Yener, A.; Gunlu, O. Secure Integrated Sensing and Communication Under Correlated Rayleigh Fading. arXiv 2024, arXiv:2408.17050v1. [Google Scholar]
- Yassaee, M.H.; Aref, M.R.; Gohari, A. Achievability Proof via Output Statistics of Random Binning. IEEE Trans. Inf. Theory 2014, 60, 6760–6786. [Google Scholar] [CrossRef]
- Chang, M.C.; Wang, S.Y.; Erdoğan, T.; Bloch, M.R. Rate and Detection-Error Exponent Tradeoff for Joint Communication and Sensing of Fixed Channel States. IEEE J. Sel. Areas Inf. Theory 2023, 4, 245–259. [Google Scholar] [CrossRef]
- Lapidoth, A.; Narayan, P. Reliable communication under channel uncertainty. IEEE Trans. Inf. Theory 1998, 44, 2148–2177. [Google Scholar] [CrossRef]
- Chang, M.C.; Wang, S.Y.; Bloch, M.R. Sequential Joint Communication and Sensing of Fixed Channel States. In Proceedings of the 2023 IEEE Information Theory Workshop (ITW), Saint-Malo, France, 23–28 April 2023; pp. 462–467. [Google Scholar] [CrossRef]
- Tandon, A.; Motani, M.; Varshney, L.R. Subblock-Constrained Codes for Real-Time Simultaneous Energy and Information Transfer. IEEE Trans. Inf. Theory 2016, 62, 4212–4227. [Google Scholar] [CrossRef]
- Wen, D.; Zhou, Y.; Li, X.; Shi, Y.; Huang, K.; Letaief, K.B. A Survey on Integrated Sensing, Communication, and Computation. IEEE Commun. Surv. Tutor 2024. epub ahead of printing. [Google Scholar] [CrossRef]
- Cong, J.; You, C.; Li, J.; Chen, L.; Zheng, B.; Liu, Y. Near-Field Integrated Sensing and Communication: Opportunities and Challenges. IEEE Wirel. Commun. 2024, 31, 162–169. [Google Scholar]
- Jiang, W.; Zhou, Q.; He, J.; Habibi, M.A.; Melnyk, S.; El-Absi, M. Terahertz Communications and Sensing for 6G and Beyond: A Comprehensive Review. IEEE Commun. Surv. Tutor. 2024, 26, 2326–2381. [Google Scholar]
- Elbir, A.M.; Mishra, K.V.; Chatzinotas, S.; Bennis, M. Terahertz-Band Integrated Sensing and Communications: Challenges and Opportunities. IEEE Aerosp. Electron. Syst. Mag. 2024, 39, 38–49. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, H.; Di, B.; Renzo, M.D.; Han, Z.; Poor, H.V. Holographic Integrated Sensing and Communication. IEEE J. Sel. Areas Commun. 2022, 40, 2114–2130. [Google Scholar]
- Liu, R.; Li, M.; Luo, H.; Liu, Q.; Swindlehurst, A.L. Integrated Sensing and Communication with Reconfigurable Intelligent Surfaces: Opportunities, Applications, and Future Directions. IEEE Wirel. Commun. 2023, 30, 50–57. [Google Scholar] [CrossRef]
- Ye, Q.; Huang, Y.; Luo, Q.; Hu, Z.; Zhang, Z.; Zhao, Q.; Su, Y.; Hu, S.; Yang, G. A General Integrated Sensing and Communication Channel Model Combined with Scattering Clusters. IEEE Trans. Veh. Technol. 2024, 1–14. [Google Scholar] [CrossRef]
- Wu, N.; Jiang, R.; Wang, X.; Yang, L.; Zhang, K.; Yi, W.; Nallanathan, A. AI-Enhanced Integrated Sensing and Communications: Advancements, Challenges, and Prospects. IEEE Commun. Mag. 2024, 62, 144–150. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, H.; Sun, K.; Long, K.; Karagiannidis, G.K. AI-Driven Integration of Sensing and Communication in the 6G Era. IEEE Netw. 2024, 38, 210–217. [Google Scholar] [CrossRef]









| Category | Result Description | Reference(s) |
|---|---|---|
| Sensing as Monostatic Radar | Lemma 1: Optimal estimator for P2P and BC | [56] |
| Theorem 1: Exact Capacity–Distortion for Memoryless P2P, asymptotic analysis | [56] | |
| Strong converse Remark 1 | [57] | |
| Log-Loss Distortion Theorem 2 | [58] | |
| Nonasymptotic P2P, Theorem 3 | [59] | |
| Channel with memory, RL approach Theorem 3 | [60] | |
| Sensing as Bi-Static Radar (P2P) | C-D with No CSI at Tx Theorem 4 | [21] |
| C-D with Strictly Causal CSI at Tx Theorem 5 | [61] | |
| C-D Non-Causal CSI, Gaussian Channel at Tx Theorem 6 | [62] | |
| Network-ISAC | General BC Outer Theorem 7 and inner Proposition 1 bounds | [63,64] |
| Optimal symbolwise estimator | – | |
| Outerbounds for MAC Theorem 8 | [65,66] | |
| Innerbound MAC Theorem 9 | [65,66,67,68] | |
| Innerbound D2D Theorem 10 | [68] | |
| Secrecy-ISAC | Secrecy–Capacity–Distortion Inner Theorem 11 and Outer Theorem 12 Bounds | [69] |
| Secrecy of the Message and the State Theorem 13 | [70] | |
| ISAC with Detection-Error Exponents | Non-adaptive Rate–Detection-Exponent Theorem 14 | [57,71,72,73,74] |
| Adaptive Rate–Detection-Exponent Theorem 15 | [73] | |
| Sequential (Variable Length) Rate–Detection-Exponent Theorem 16 | [73] | |
| Sequential (Variable Length) ISAC with Change Point Detection Theorem 17 | [75] |
| Communication | Sensing |
|---|---|
| 2.4 GHz | 24–79 GHz |
| Data/Source Transmission | Estimation/Detection |
| Bit/Signal/Frame Error Rate | Minimum Mean Squared Error (MMSE), Cramer–Rao Bound (CRB) |
| Distortion | Detection/False Alarm Probability |
| All Propagation Paths | Line of Sight (LoS) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmadipour, M.; Wigger, M.; Shamai, S. Exploring ISAC: Information-Theoretic Insights. Entropy 2025, 27, 378. https://doi.org/10.3390/e27040378
Ahmadipour M, Wigger M, Shamai S. Exploring ISAC: Information-Theoretic Insights. Entropy. 2025; 27(4):378. https://doi.org/10.3390/e27040378
Chicago/Turabian StyleAhmadipour, Mehrasa, Michèle Wigger, and Shlomo Shamai. 2025. "Exploring ISAC: Information-Theoretic Insights" Entropy 27, no. 4: 378. https://doi.org/10.3390/e27040378
APA StyleAhmadipour, M., Wigger, M., & Shamai, S. (2025). Exploring ISAC: Information-Theoretic Insights. Entropy, 27(4), 378. https://doi.org/10.3390/e27040378




.png)


