Critical Relaxation in the Quantum Yang–Lee Edge Singularity
Abstract
1. Introduction
2. Model and Its Static Scaling
3. Relaxation Scaling
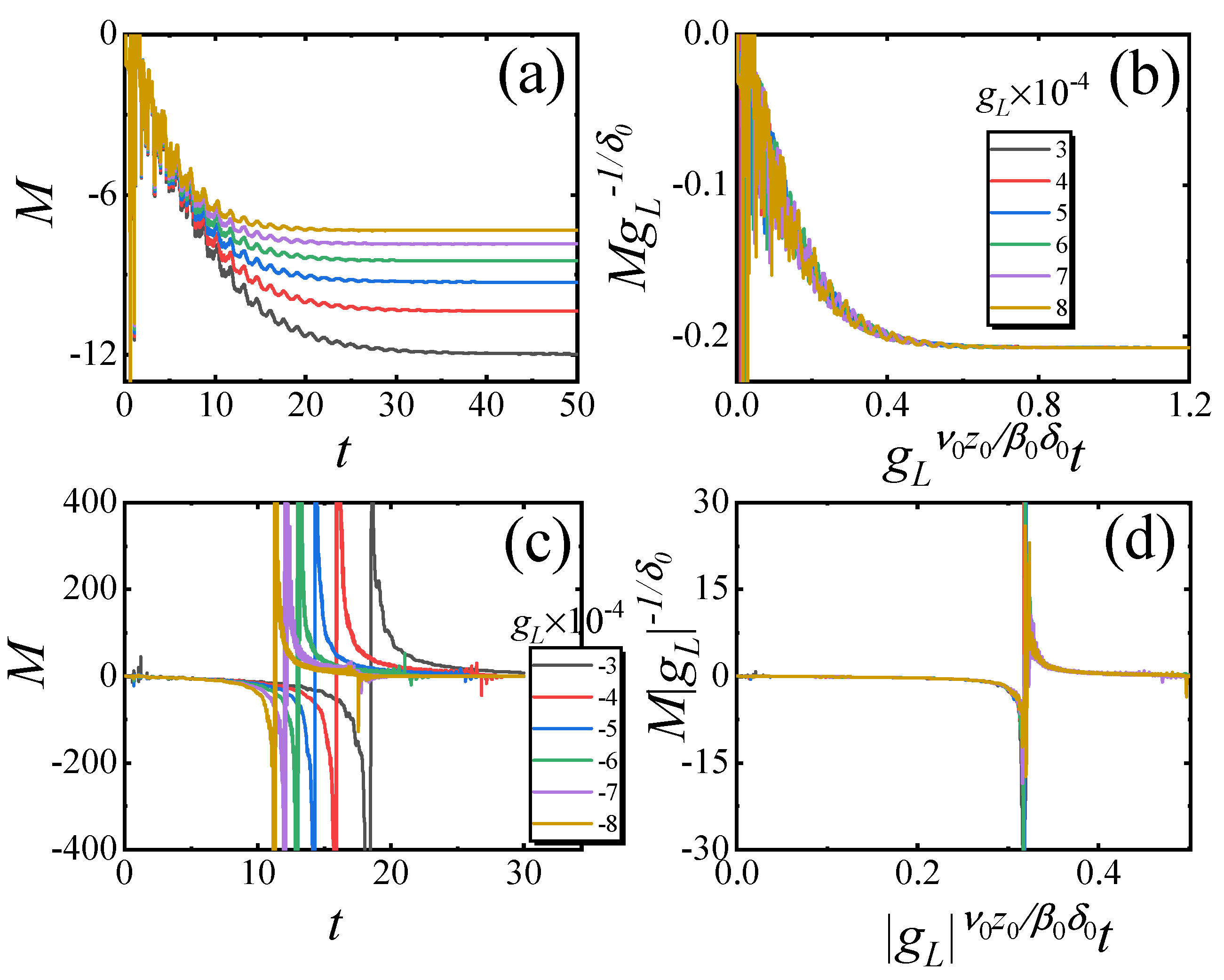
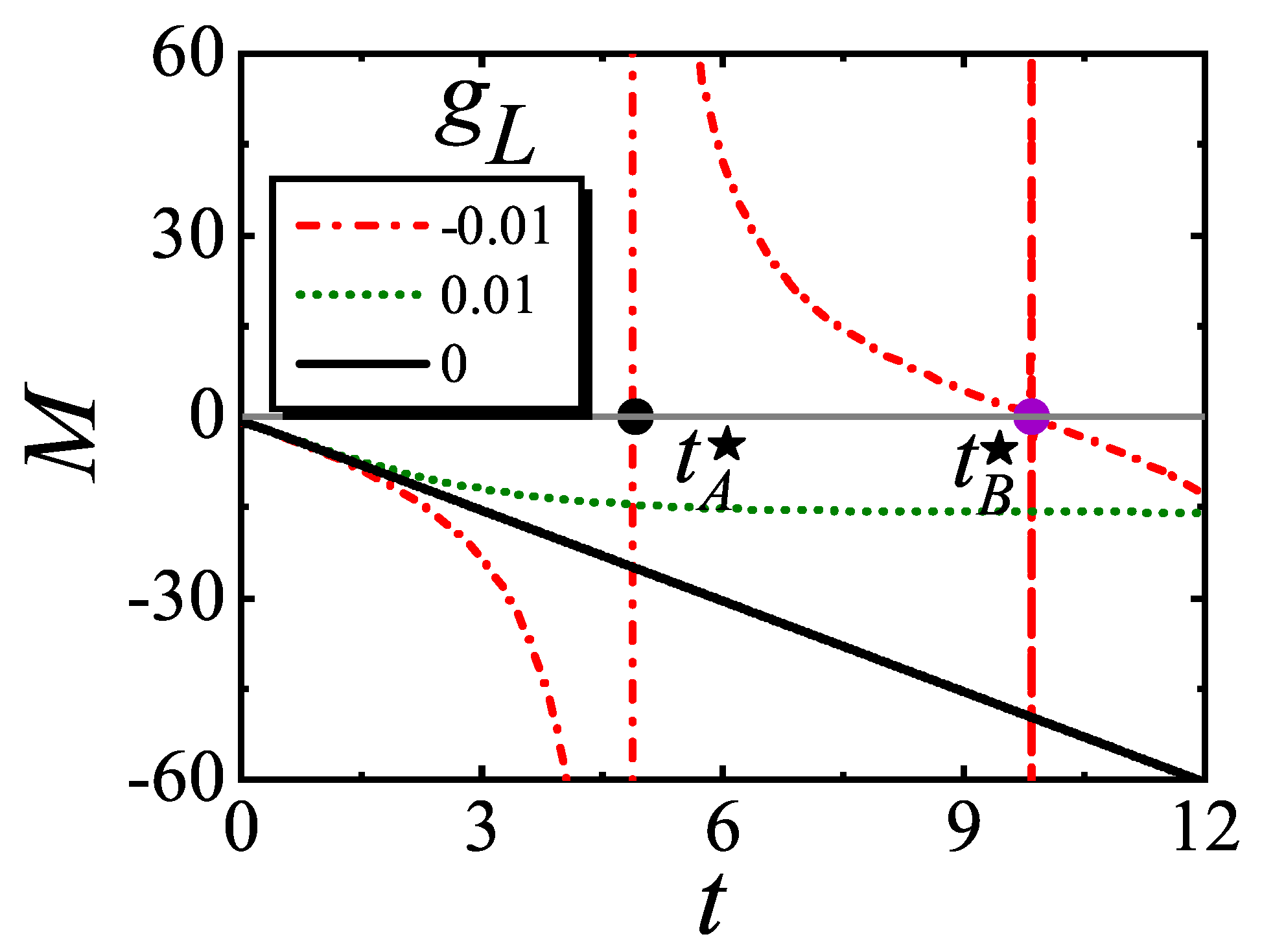
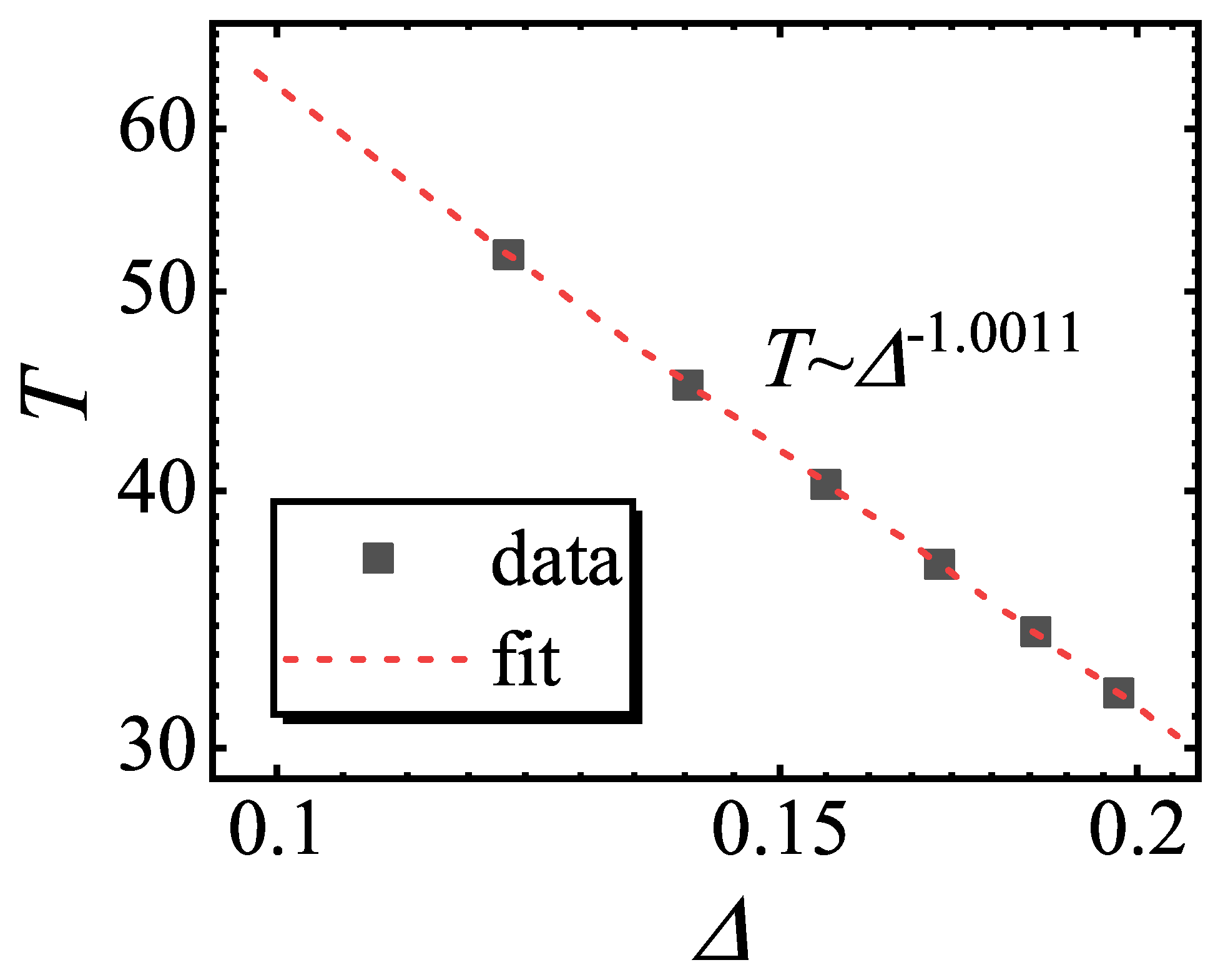
4. Relaxation for Single-Spin YLES
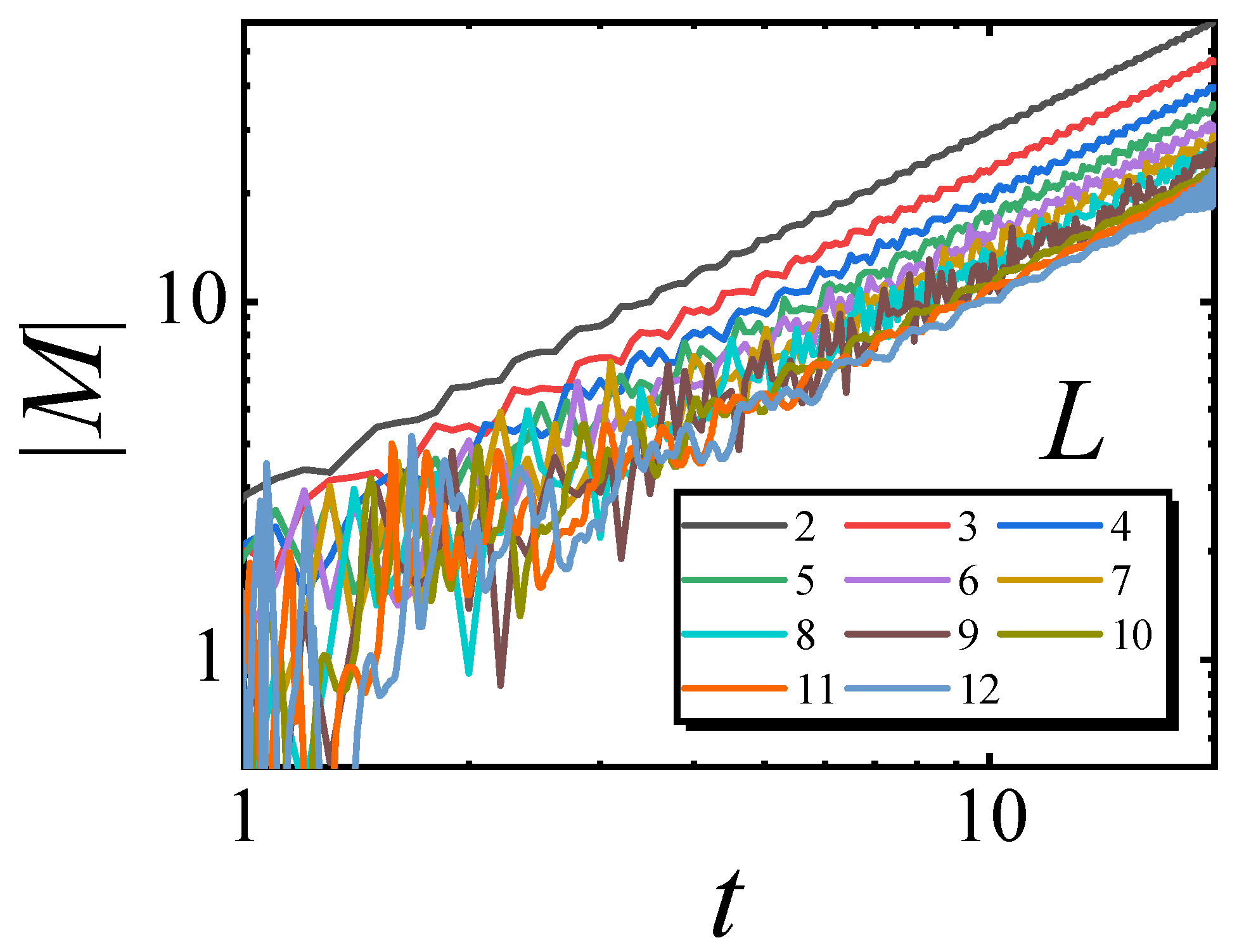
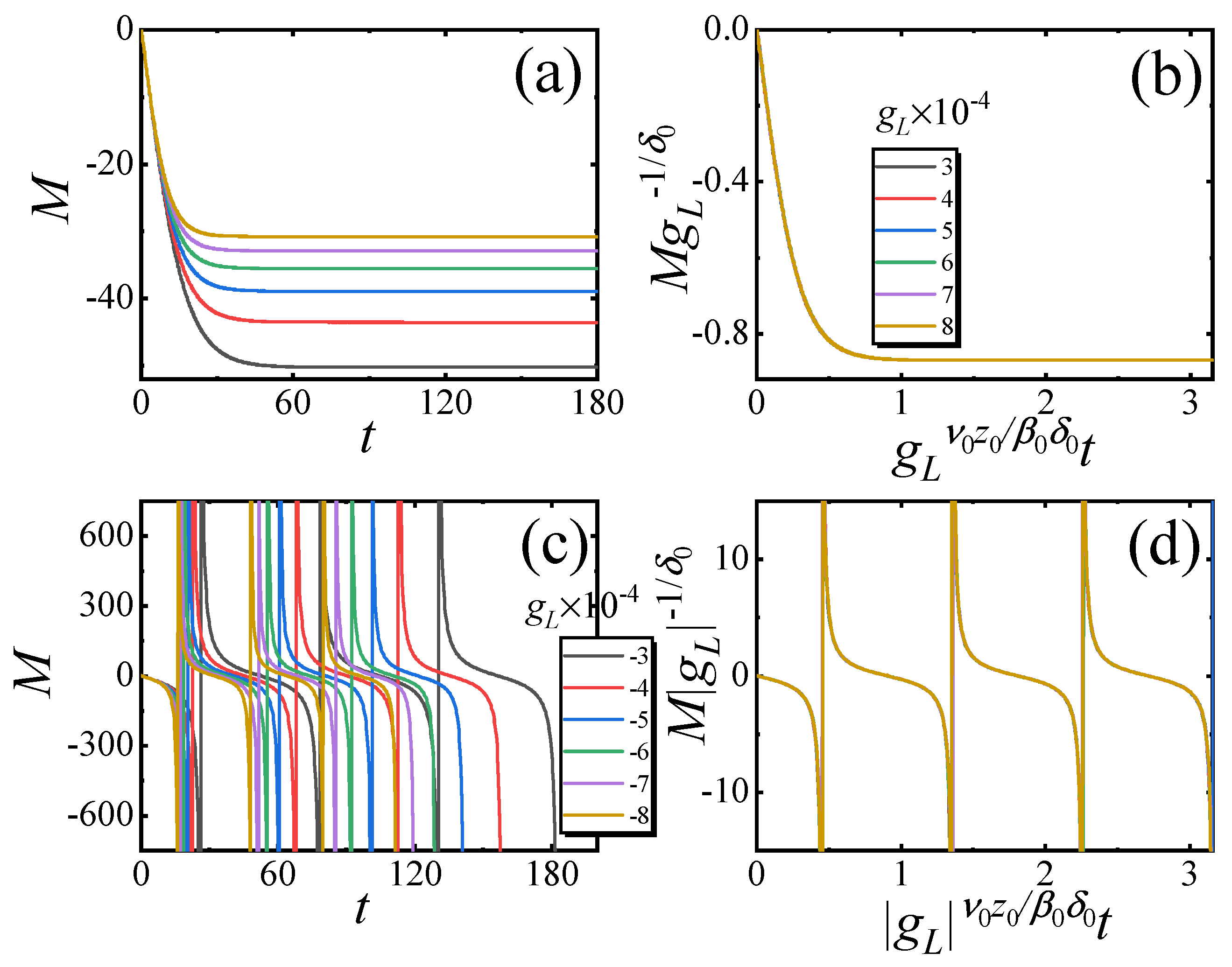
5. Relaxation for Finite-Size YLES
6. Summary
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| YLES | Yang–Lee edge singularity |
| PT | parity-time |
| DQPTs | dynamical quantum phase transitions |
References
- Yang, C.; Lee, T. Statistical Theory of Equations of State and Phase Transitions I. Theory of Condensation. Phys. Rev. 1952, 87, 404. [Google Scholar] [CrossRef]
- Lee, T.; Yang, C. Statistical Theory of Equations of State and Phase Transitions II. Lattice Gas and Ising Model. Phys. Rev. 1952, 87, 410. [Google Scholar] [CrossRef]
- Kortman, P.; Griffiths, R. Density of Zeros on the Lee-Yang Circle for Two Ising Ferromagnets. Phys. Rev. Lett. 1971, 27, 1439. [Google Scholar] [CrossRef]
- Fisher, M. Yang-Lee Edge Singularity and ϕ3 Field Theory. Phys. Rev. Lett. 1978, 40, 1610. [Google Scholar] [CrossRef]
- Gao, H.; Wang, K.; Xiao, L.; Nakagawa, M.; Matsumoto, N.; Qu, D.; Lin, H.; Ueda, M.; Xue, P. Experimental observation of the Yang-Lee quantum criticality in open systems. Phys. Rev. Lett. 2024, 132, 176601. [Google Scholar] [CrossRef]
- Lan, Z.; Liu, W.; Wu, Y.; Ye, X.; Yang, Z.; Duan, C.-K.; Wang, Y.; Rong, X. Experimental Investigation of Lee-Yang Criticality Using Non-Hermitian Quantum System. Chin. Phys. Lett. 2024, 41, 050301. [Google Scholar] [CrossRef]
- Binek, C. Density of Zeros on the Lee-Yang Circle Obtained from Magnetization Data of a Two-Dimensional Ising Ferromagnet. Phys. Rev. Lett. 1998, 81, 5644. [Google Scholar] [CrossRef]
- Binek, C.; Kleemann, W.; Aruga Katori, H. Yang-Lee edge singularities determined from experimental high-field magnetization data. J. Phys. Condens. Matter 2001, 13, L811. [Google Scholar] [CrossRef]
- Peng, X.; Zhou, H.; Wei, B.; Cui, J.; Du, J.; Liu, R. Experimental Observation of Lee-Yang Zeros. Phys. Rev. Lett. 2015, 114, 010601. [Google Scholar] [CrossRef]
- Brandner, K.; Maisi, V.F.; Pekola, J.P.; Garrahan, J.P.; Flindt, C. Experimental Determination of Dynamical Lee-Yang Zeros. Phys. Rev. Lett. 2017, 118, 180601. [Google Scholar] [CrossRef]
- Wei, B.; Liu, R. Lee-Yang Zeros and Critical Times in Decoherence of a Probe Spin Coupled to a Bath. Phys. Rev. Lett. 2012, 109, 185701. [Google Scholar]
- Matsumoto, N.; Nakagawa, M.; Ueda, M. Embedding the Yang-Lee quantum criticality in open quantum systems. Phys. Rev. Res. 2022, 4, 033250. [Google Scholar] [CrossRef]
- Shen, R.; Chen, T.; Aliyu, M.M.; Qin, F.; Zhong, Y.; Loh, H.; Lee, C.H. Proposal for Observing Yang-Lee Criticality in Rydberg Atomic Arrays. Phys. Rev. Lett. 2023, 131, 080403. [Google Scholar] [CrossRef] [PubMed]
- Wei, B.-B. Probing Yang-Lee edge singularity by central spin decoherence. New J. Phys. 2017, 19, 083009. [Google Scholar] [CrossRef]
- Liu, B.; Li, Y.; Yang, B.; Shen, X.; Yang, Y.; Hang, Z.H.; Ezawa, M. Experimental observation of non-Hermitian higher-order skin interface states in topological electric circuits. Phys. Rev. Res. 2023, 5, 043034. [Google Scholar] [CrossRef]
- Wang, W.; Hu, M.; Wang, X.; Ma, G.; Ding, K. Experimental Realization of Geometry-Dependent Skin Effect in a Reciprocal Two-Dimensional Lattice. Phys. Rev. Lett. 2023, 131, 207201. [Google Scholar] [CrossRef] [PubMed]
- Xiao, L.; Qu, D.; Wang, K.; Li, H.-W.; Dai, J.-Y.; D’ora, B.; Heyl, M.; Moessner, R.; Yi, W.; Xue, P. Non-Hermitian Kibble-Zurek Mechanism with Tunable Complexity in Single-Photon Interferometry. PRX Quantum 2021, 2, 020313. [Google Scholar]
- Ding, K.; Fang, C.; Ma, G. Non-Hermitian topology and exceptional-point geometries. Nat. Rev. Phys. 2022, 4, 745. [Google Scholar] [CrossRef]
- Peng, B.; Özdemir, Ṣ.K.; Lei, F.; Monifi, F.; Gianfreda, M.; Long, G.L.; Fan, S.; Nori, F.; Bender, C.M.; Yang, L. Parity-time-symmetric whispering-gallery microcavities. Nat. Phys. 2014, 10, 394. [Google Scholar] [CrossRef]
- Feng, L.; Wong, Z.J.; Ma, R.M.; Wang, Y.; Zhang, X. Single-mode laser by parity-time symmetry breaking. Science 2014, 346, 972. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Zhang, Y.; Sheng, J.; Yang, L.; Ali Miri, M.; Christodoulides, D.N.; He, B.; Zhang, Y.; Xiao, M. Observation of Parity-Time Symmetry in Optically Induced Atomic Lattices. Phys. Rev. Lett. 2016, 117, 123601. [Google Scholar] [CrossRef] [PubMed]
- Zhen, B.; Hsu, C.W.; Igarashi, Y.; Lu, L.; Kaminer, I.; Pick, A.; Chua, S.; Joannopoulos, J.D.; Soljači’c, M. Spawning rings of exceptional points out of Dirac cones. Nature 2015, 525, 354. [Google Scholar] [CrossRef] [PubMed]
- Yao, S.; Song, F.; Wang, Z. Non-hermitian chern bands. Phys. Rev. Lett. 2018, 121, 136802. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, Q.-h.; Wang, H.; Gong, J. Dynamical quantum phase transitions in non-Hermitian lattices. Phys. Rev. A 2018, 98, 022129. [Google Scholar] [CrossRef]
- Bender, C.M. Making sense of non-Hermitian Hamiltonians. Rep. Prog. Phys. 2007, 70, 947. [Google Scholar] [CrossRef]
- Zhai, L.-J.; Huang, G.-Y.; Yin, S. Nonequilibrium dynamics of the localization-delocalization transition in the non-Hermitian Aubry-Andr’e model. Phys. Rev. B 2022, 106, 014204. [Google Scholar] [CrossRef]
- Moiseyev, N. Non-Hermitian Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Weiss, U. Quantum Dissipative Systems, 3rd ed.; World Scientific: Singapore, 2008. [Google Scholar]
- Ashida, Y.; Gong, Z.; Ueda, M. Non-Hermitian physics. Adv. Phys. 2021, 69, 249. [Google Scholar]
- Okuma, N.; Kawabata, K.; Shiozaki, K.; Sato, M. Topological Origin of Non-Hermitian Skin Effects. Phys. Rev. Lett. 2020, 124, 086801. [Google Scholar] [CrossRef]
- Kawabata, K.; Sato, M.; Shiozaki, K. Higher-order non-Hermitian skin effect. Phys. Rev. B 2020, 102, 205118. [Google Scholar] [CrossRef]
- Borgnia, D.S.; Kruchkov, A.J.; Slager, R.-J. Non-Hermitian Boundary Modes and Topology. Phys. Rev. Lett. 2020, 124, 056802. [Google Scholar] [CrossRef] [PubMed]
- Longhi, S. Unraveling the non-Hermitian skin effect in dissipative systems. Phys. Rev. B 2020, 102, 201103. [Google Scholar] [CrossRef]
- Fu, Y.; Hu, J.; Wan, S. Non-Hermitian second-order skin and topological modes. Phys. Rev. B 2021, 103, 045420. [Google Scholar] [CrossRef]
- Liu, J.S.; Han, Y.Z.; Liu, C.S. A new way to construct topological invariants of non-Hermitian systems with the non-Hermitian skin effect. Chin. Phys. B 2020, 29, 010302. [Google Scholar] [CrossRef]
- Xue, W.-T.; Hu, Y.-M.; Song, F.; Wang, Z. Non-Hermitian Edge Burst. Phys. Rev. Lett. 2022, 128, 120401. [Google Scholar] [CrossRef]
- El-Ganainy, R.; Makris, K.G.; Khajavikhan, M.; Musslimani, Z.H.; Rotter, S.; Christodoulides, D.N. Non-Hermitian physics and PT symmetry. Nat. Phys. 2018, 14, 11. [Google Scholar] [CrossRef]
- Bender, C.M.; Boettcher, S. Real Spectra in Non-Hermitian Hamiltonians Having PT Symmetry. Phys. Rev. Lett. 1998, 80, 5243–5246. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Pseudo-Hermiticity versus PT symmetry: The necessary condition for the reality of the spectrum of a non-Hermitian Hamiltonian. J. Math. Phys. 2001, 43, 205–214. [Google Scholar] [CrossRef]
- Shen, R.; Lee, C.H. Non-Hermitian skin clusters from strong interactions. Commun. Phys. 2022, 5, 238. [Google Scholar] [CrossRef]
- Zhang, S.; Jin, L.; Song, Z. Topology of a parity-time symmetric non-Hermitian rhombic lattice. Chin. Phys. B 2022, 31, 010312. [Google Scholar] [CrossRef]
- Kunst, F.K.; Edvardsson, E.; Budich, J.C.; Bergholtz, E.J. Biorthogonal Bulk-Boundary Correspondence in Non-Hermitian Systems. Phys. Rev. Lett. 2018, 121, 026808. [Google Scholar] [CrossRef]
- Bergholtz, E.J.; Budich, J.C.; Kunst, F.K. Exceptional topology of non-Hermitian systems. Rev. Mod. Phys. 2021, 93, 015005. [Google Scholar] [CrossRef]
- Kawabata, K.; Ashida, Y.; Ueda, M. Information retrieval and criticality in parity-time-symmetric systems. Phys. Rev. Lett. 2017, 119, 190401. [Google Scholar] [CrossRef] [PubMed]
- Zhong, F. Renormalization-group theory of dynamics of first-order phase transitions in a field-driven scalar model. arXiv 2012, arXiv:1205.1400. [Google Scholar] [CrossRef]
- Viteau, M.; Bason, M.G.; Radogostowicz, J.; Malossi, N.; Ciampini, D.; Morsch, O.; Arimondo, E. Rydberg Excitations in Bose-Einstein Condensates in Quasi-One-Dimensional Potentials and Optical Lattices. Phys. Rev. Lett. 2011, 107, 060402. [Google Scholar] [CrossRef] [PubMed]
- Diehl, S.; Micheli, A.; Kantian, A.; Kraus, B.; Büchler, H.; Zoller, P. Quantum states and phases in driven open quantum systems with cold atoms. Nat. Phys. 2008, 4, 878. [Google Scholar] [CrossRef]
- Diehl, S.; Yi, W.; Daley, A.; Zoller, P. Dissipation-Induced d-Wave Pairing of Fermionic Atoms in an Optical Lattice. Phys. Rev. Lett. 2010, 105, 227001. [Google Scholar] [CrossRef]
- Li, J.; Harter, A.K.; Liu, J.; de Melo, L.; Joglekar, Y.N.; Luo, L. Observation of parity-time symmetry breaking transitions in a dissipative Floquet system of ultracold atoms. Nat. Commun. 2019, 10, 855. [Google Scholar] [CrossRef]
- Marcuzzi, M.; Levi, E.; Li, W.; Garrahan, J.P.; Olmos, B.; Lesanovsky, I. Non-equilibrium universality in the dynamics of dissipative cold atomic gases. New J. Phys. 2015, 17, 072003. [Google Scholar] [CrossRef]
- Yin, S.; Huang, G.-Y.; Lo, C.-Y.; Chen, P. Kibble-Zurek Scaling in the Yang-Lee Edge Singularity. Phys. Rev. Lett. 2017, 118, 065701. [Google Scholar] [CrossRef] [PubMed]
- Zhai, L.-J.; Huang, G.-Y.; Yin, S. Hybridized Kibble-Zurek scaling in the driven critical dynamics across an overlapping critical region. Phys. Rev. B 2018, 97, 134108. [Google Scholar] [CrossRef]
- Dziarmaga, J. Dynamics of a quantum phase transition and relaxation to a steady state. Adv. Phys. 2010, 59, 1063. [Google Scholar] [CrossRef]
- Marino, J.; Eckstein, M.; Foster, M.S.; Rey, A.M. Dynamical phase transitions in the collisionless pre-thermal states of isolated quantum systems: Theory and experiments. Rep. Prog. Phys. 2022, 85, 116001. [Google Scholar] [CrossRef]
- Uzelac, K.; Pfeuty, P.; Jullien, R. Yang-Lee Edge Singularity from a Real-Space Renormalization-Group Method. Phys. Rev. Lett. 1979, 43, 805. [Google Scholar] [CrossRef]
- Sachdev, S. Quantum Phase Transitions; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- von Gehlen, G. Critical and off-critical conformal analysis of the Ising quantum chain in an imaginary field. J. Phys. A Math. Gen. 1991, 24, 5371. [Google Scholar] [CrossRef]
- Breuer, N.; Janssen, H. Equation of State and Dynamical Properties Near the Yang-Lee Edge Singularity. Z. Physik. Condens. Matter 1981, 41, 55. [Google Scholar] [CrossRef]
- Yin, S.; Lo, C.-Y.; Chen, P. Scaling behavior of quantum critical relaxation dynamics of a system in a heat bath. Phys. Rev. B 2016, 93, 184301. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, S. Dynamical evolution in a one-dimensional incommensurate lattice with PT symmetry. Phys. Rev. A 2021, 103, 043325. [Google Scholar] [CrossRef]
- Tang, J.-C.; Kou, S.-P.; Sun, G. Dynamical scaling of Loschmidt echo in non-Hermitian systems. Europhys. Lett. 2022, 137, 40001. [Google Scholar] [CrossRef]
- Rossini, D.; Vicari, E. Dynamics after quenches in one-dimensional quantum Ising-like systems. Phys. Rev. B 2020, 102, 054444. [Google Scholar] [CrossRef]
- Cao, K.; Guo, H.; Yang, G.; Cao, K.; Guo, H.; Yang, G. Aperiodic dynamical quantum phase transition in multi-band Bloch Hamiltonian and its origin. J. Phys. Condens. Matter 2024, 36, 15. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.-M.; Wang, X.; Zhai, L.-J. Critical Relaxation in the Quantum Yang–Lee Edge Singularity. Entropy 2025, 27, 170. https://doi.org/10.3390/e27020170
Sun Y-M, Wang X, Zhai L-J. Critical Relaxation in the Quantum Yang–Lee Edge Singularity. Entropy. 2025; 27(2):170. https://doi.org/10.3390/e27020170
Chicago/Turabian StyleSun, Yue-Mei, Xinyu Wang, and Liang-Jun Zhai. 2025. "Critical Relaxation in the Quantum Yang–Lee Edge Singularity" Entropy 27, no. 2: 170. https://doi.org/10.3390/e27020170
APA StyleSun, Y.-M., Wang, X., & Zhai, L.-J. (2025). Critical Relaxation in the Quantum Yang–Lee Edge Singularity. Entropy, 27(2), 170. https://doi.org/10.3390/e27020170