Performance Improvement for Discretely Modulated Continuous-Variable Measurement-Device-Independent Quantum Key Distribution with Imbalanced Modulation
Abstract
1. Introduction
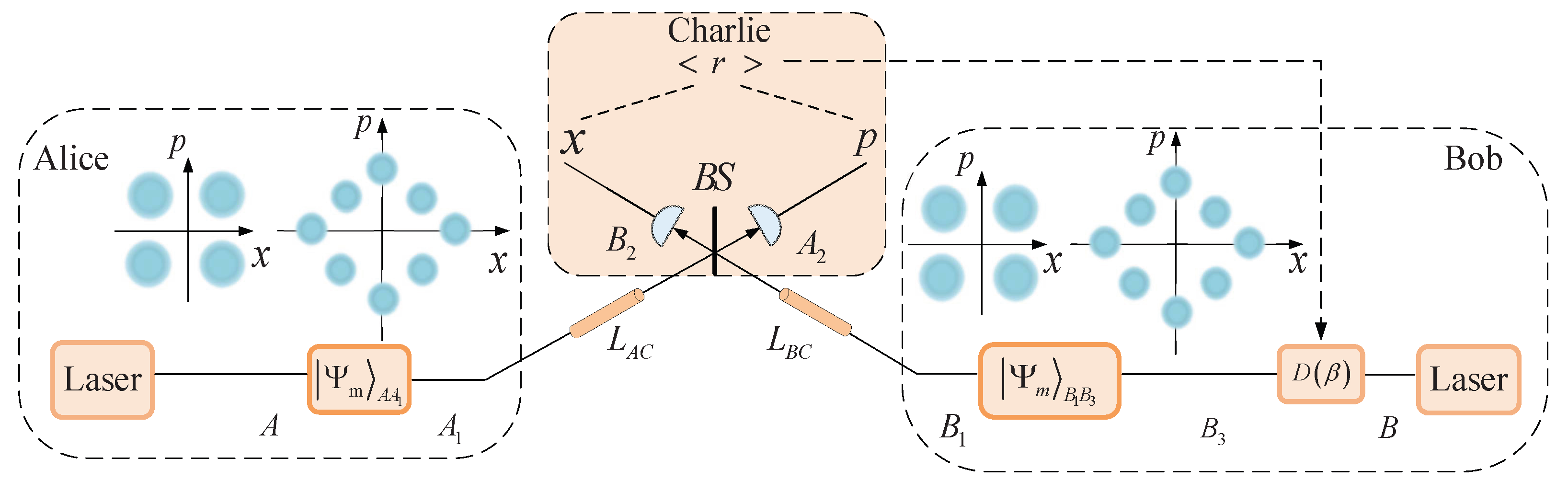
2. Discrete-State CV-QKD with Imbalanced Modulation
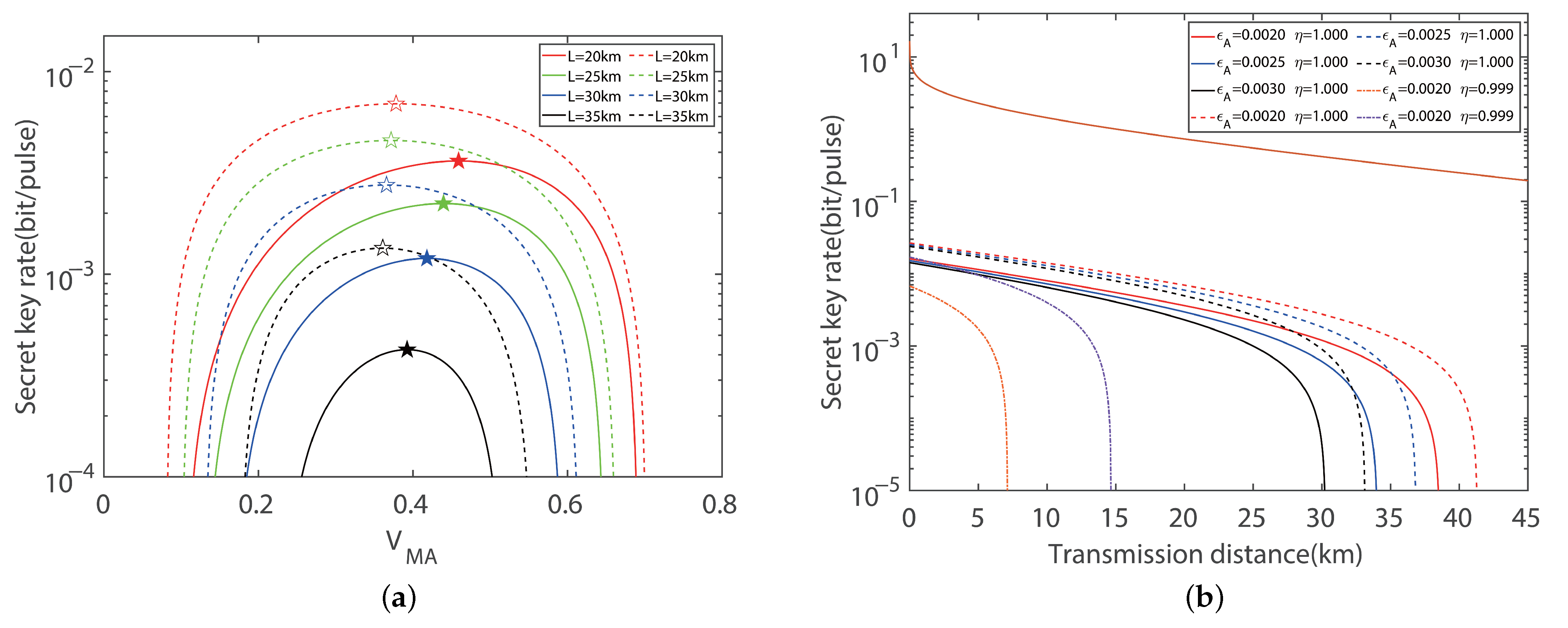
3. CV-MDI-QKD Protocol for Four-State and Eight-State Imbalanced Modulations Under Symmetric Distances
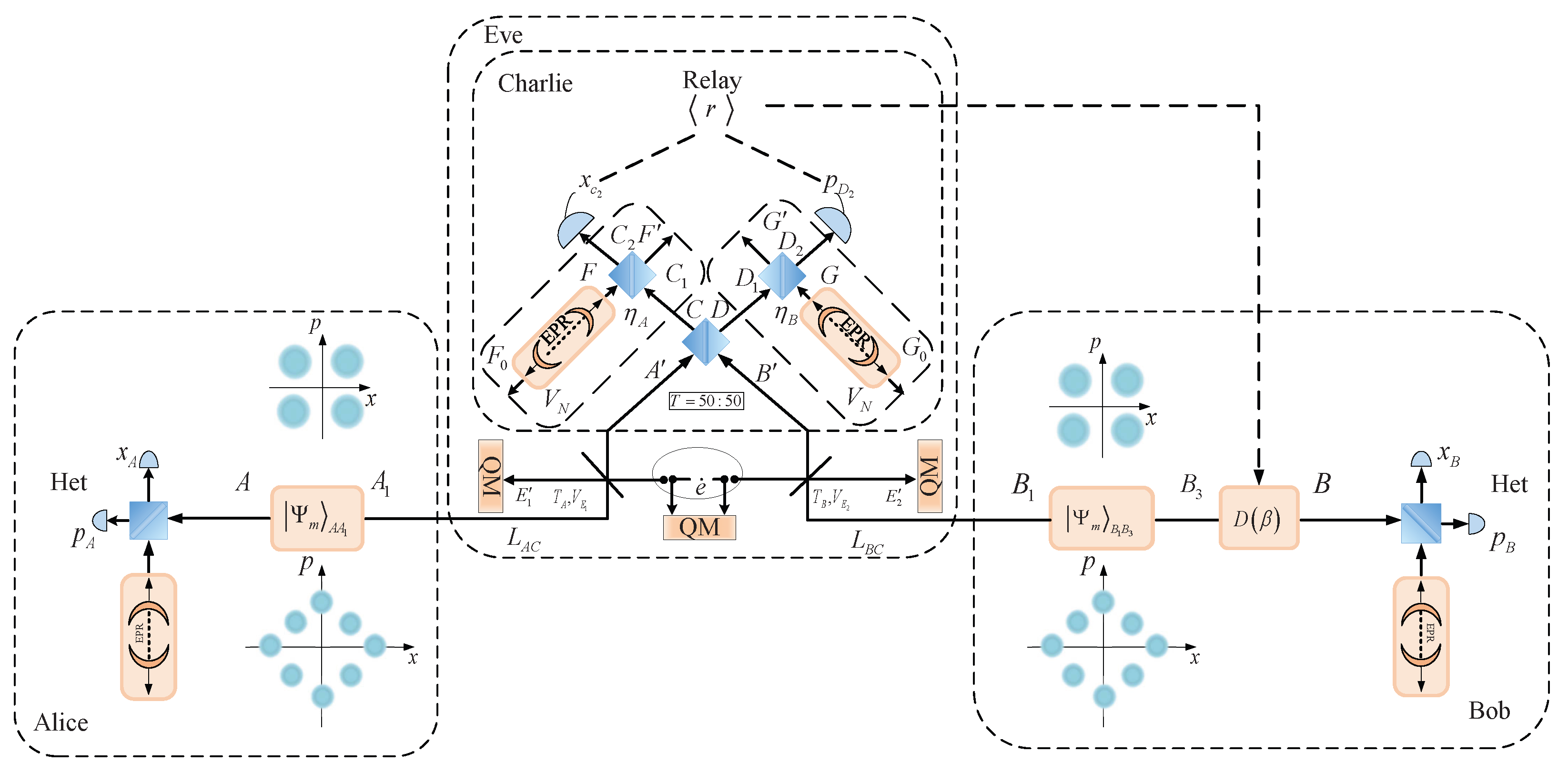
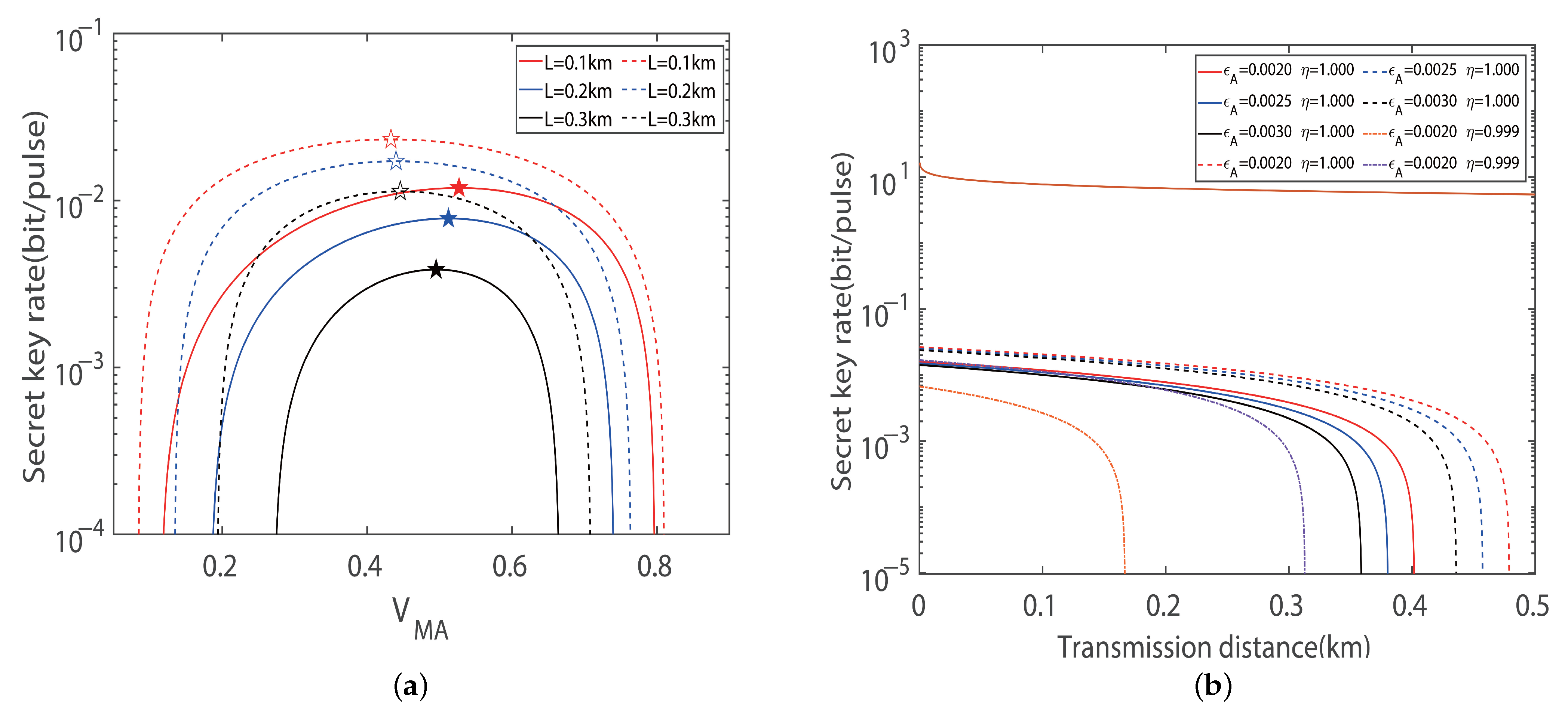
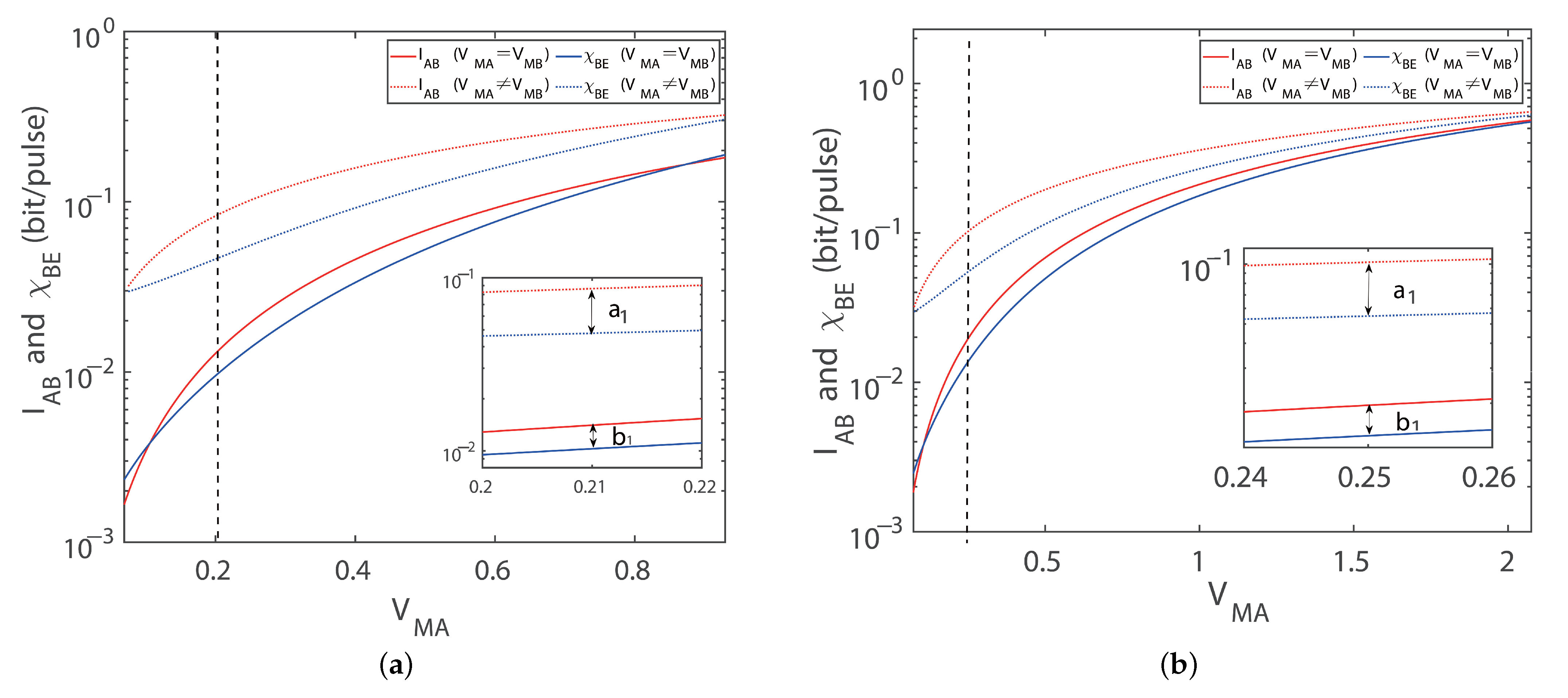
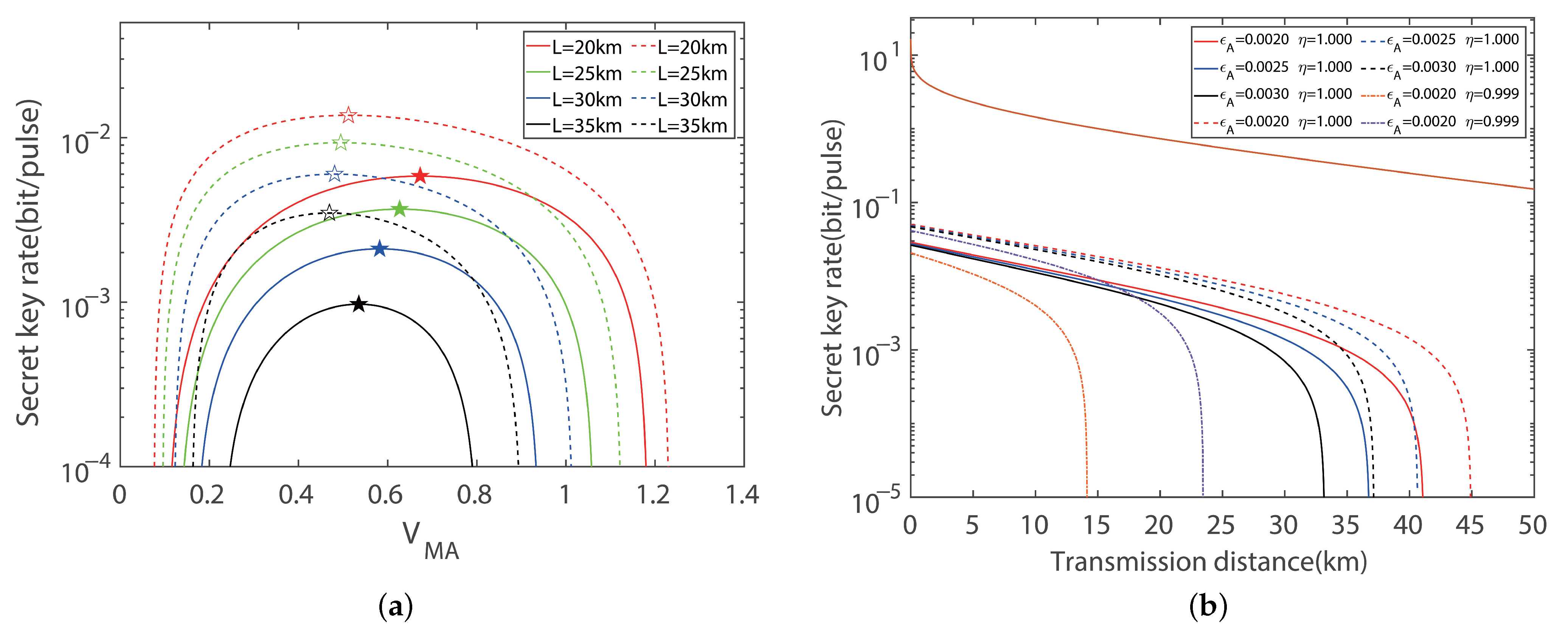
4. CV-MDI-QKD Protocol for Four-State and Eight-State Imbalanced Modulations Under Asymmetric Distances
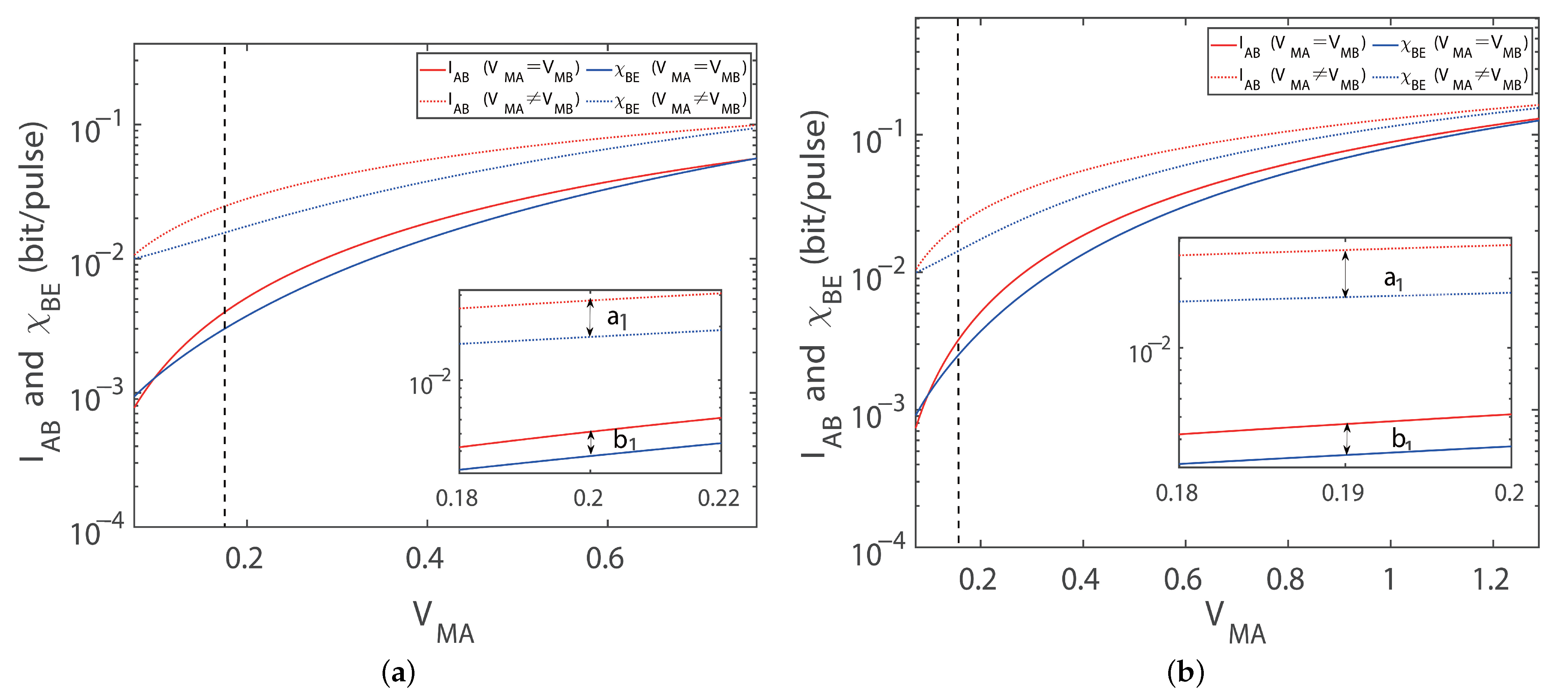
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 145–195. [Google Scholar] [CrossRef]
- Scarani, V.; Bechmann-Pasquinucci, H.; Cerf, N.J.; Dušek, M.; Lütkenhaus, N.; Peev, M. The security of practical quantum key distribution. Rev. Mod. Phys. 2009, 81, 1301–1350. [Google Scholar] [CrossRef]
- Weedbrook, C.; Pirandola, S.; García-Patrón, R.; Cerf, N.J.; Ralph, T.C.; Shapiro, J.H.; Lloyd, S. Gaussian quantum information. Rev. Mod. Phys. 2012, 84, 621–669. [Google Scholar] [CrossRef]
- Lo, H.K.; Curty, M.; Tamaki, K. Secure quantum key distribution. Nat. Photon. 2014, 8, 595–604. [Google Scholar] [CrossRef]
- Pirandola, S.; Andersen, U.L.; Banchi, L.; Berta, M.; Bunandar, D.; Colbeck, R.; Englund, D.; Gehring, T.; Lupo, C.; Ottaviani, C.; et al. Advances in quantum cryptography. Adv. Opt. Photon. 2020, 12, 1012–1236. [Google Scholar] [CrossRef]
- Xu, F.H.; Ma, X.F.; Zhang, Q.; Lo, H.K.; Pan, J.W. Secure quantum key distribution with realistic devices. Rev. Mod. Phys. 2020, 92, 025002. [Google Scholar] [CrossRef]
- Rozenman, G.G.; Kundu, N.K.; Liu, R.Q.; Zhang, L.Y.; Maslennikov, A.; Reches, Y.; Youm, H.Y. The quantum internet: A synergy of quantum information technologies and 6G networks. IET Quan. Commun. 2023, 4, 147–166. [Google Scholar] [CrossRef]
- Wei, S.H.; Jing, B.; Zhang, X.Y.; Liao, J.Y.; Yuan, C.Z.; Fan, B.Y.; Lyu, C.; Zhou, D.L.; Wang, Y.; Deng, G.W.; et al. Towards Real-World Quantum Networks: A Review. Laser Photonics Rev. 2022, 3, 2100219. [Google Scholar] [CrossRef]
- Zhang, C.M.; Wang, Z.; Wu, Y.D.; Zhu, J.R.; Wang, R.; Li, H.W. Discrete-phase-randomized twin-field quantum key distribution with advantage distillation. Phys. Rev. A 2024, 109, 052432. [Google Scholar] [CrossRef]
- Chen, J.P.; Zhang, C.; Liu, Y.; Jiang, C.; Zhang, W.J.; Hu, X.L.; Guan, J.Y.; Yu, Z.W.; Xu, H.; Lin, J.; et al. Sending-or-Not-Sending with Independent Lasers: Secure Twin-Field Quantum Key Distribution over 509 km. Phys. Rev. Lett. 2020, 124, 070501. [Google Scholar] [CrossRef]
- Leverrier, A.; Grangier, P. Unconditional Security Proof of Long-Distance Continuous-Variable Quantum Key Distribution with Discrete Modulation. Phys. Rev. Lett. 2012, 102, 14030–14041. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.Y.; Wang, T.Y. Security Analysis of Unidimensional Continuous-variable Quantum Key Distribution with Discretized Amplitude Modulation. J. Phys. B At. Mol. Opt. Phys. 2024, 57, 145502. [Google Scholar] [CrossRef]
- Ding, J.Z.; Li, Y.; Mao, Y.; Guo, Y. Discrete modulation continuous variable quantum secret sharing. Int. J. Theor. Phys. 2022, 61, 108. [Google Scholar] [CrossRef]
- Wu, L.X.; Feng, Y.Y.; Zhou, J.; Shi, R.H.; Shi, J.J. The effect of acceleration on continuous-variable quantum key distribution with discrete modulation. Eur. Phys. J. Plus 2023, 138, 963. [Google Scholar] [CrossRef]
- Li, M.; Cvijetic, M. Continuous-Variable Quantum Key Distribution With Self-Reference Detection and Discrete Modulation. IEEE J. Quantum Electron. 2018, 54, 8000408. [Google Scholar] [CrossRef]
- Bennett, C.H.; Bessette, F.; Brassard, G.; Salvail, L.; Smolin, J. Experimental quantum cryptography. J. Cryptology 1992, 5, 3–28. [Google Scholar] [CrossRef]
- Lo, H.K.; Chau, H.F. Unconditional security of quantum key distribution over arbitrarily long distances. Science 1999, 283, 2050–2056. [Google Scholar] [CrossRef]
- Deutsch, D.; Ekert, A.; Jozsa, R.; Macchiavello, C.; Popescu, S.; Sanpera, A. Quantum privacy amplification and the security of quantum cryptography over noisy channels. Phys. Rev. Lett. 1996, 77, 2818. [Google Scholar] [CrossRef]
- Renner, R. Security of quantum key distribution. Int. J. Quantum Inf. 2008, 6, 1–127. [Google Scholar] [CrossRef]
- Scarani, V.; Renner, R. Quantum cryptography with finite resources: Unconditional security bound for discrete-variable protocols with one-way postprocessing. Phys. Rev. Lett. 2008, 100, 200501. [Google Scholar] [CrossRef]
- Liao, Q.; Xiao, G.; Xu, C.G.; Xu, Y.; Guo, Y. Discretely modulated continuous-variable quantum key distribution with an untrusted entanglement source. Phys. Rev. A 2020, 102, 032604. [Google Scholar] [CrossRef]
- Yang, J.; Xu, B.J.; Peng, X.; Guo, H. Four-state continuous-variable quantum key distribution with long secure distance. Phys. Rev. A 2012, 85, 052302. [Google Scholar] [CrossRef]
- Becir, A.; El-Orany, F.; Wahiddin, M. Continuous-variable quantum key distribution protocols with eight-state discrete modulation. Int. J. Quantum Inf. 2012, 10, 1250004. [Google Scholar] [CrossRef]
- Grosshans, F.; Van Assche, G.; Wenger, J.; Brouri, R.; Cerf, N.J.; Grangier, P. Quantum key distribution using gaussian-modulated coherent states. Nature 2003, 421, 238–241. [Google Scholar] [CrossRef]
- Lance, A.M.; Symul, T.; Sharma, V.; Weedbrook, C.; Ralph, T.C.; Lam, P.K. No-switching quantum key distribution using broadband modulated coherent light. Phys. Rev. Lett. 2005, 95, 180503. [Google Scholar] [CrossRef]
- Qi, B.; Huang, L.L.; Qian, L.; Lo, H.K. Experimental study on the Gaussian-modulated coherent-state quantum key distribution over standard telecommunication fibers. Phys. Rev. A 2007, 76, 052323. [Google Scholar] [CrossRef]
- Lodewyck, J.; Bloch, M.; García-Patrón, R.; Fossier, S.; Karpov, E.; Diamanti, E.; Debuisschert, T.; Cerf, N.J.; McLaughlin, S.W.; Grangier, P.; et al. Quantum key distribution over 25 km with an all-fiber continuous-variable system. Phys. Rev. A 2007, 76, 042305. [Google Scholar] [CrossRef]
- Qi, B.; Zhu, W.; Qian, L.; Lo, H.K. Feasibility of quantum key distribution through a dense wavelength division multiplexing network. New J. Phys. 2010, 12, 103024. [Google Scholar] [CrossRef]
- Madsen, L.S.; Usenko, V.C.; Lassen, M.; Filip, R.; Andersen, U.L. Continuous variable quantum key distribution with modulated entangled states. Nat. Commun. 2012, 3, 1083. [Google Scholar] [CrossRef]
- Jouguet, P.; Kunz-Jacques, S.; Leverrier, A.; Grangier, P.; Diamanti, E. Experimental demonstration of long-distance continuous-variable quantum key distribution. Nat. Photon. 2013, 7, 378–381. [Google Scholar] [CrossRef]
- Kumar, R.; Hao, Q.; Alléaume, R. Coexistence of continuous variable QKD with intense DWDM classical channels. New J. Phys. 2015, 17, 043027. [Google Scholar] [CrossRef]
- Pirandola, S.; Ottaviani, C.; Spedalieri, G.; Weedbrook, C.; Braunstein, S.L.; Lloyd, S.; Gehring, T.; Jacobsen, C.S.; Andersen, U.L. High-rate measurement-device-independent quantum cryptography. Nat. Photon. 2015, 9, 397–403. [Google Scholar] [CrossRef]
- Walk, N.; Hosseini, S.; Geng, J.; Thearle, O.; Haw, J.Y.; Armstrong, S.J.; Assad, S.M.; Janousek, J.; Ralph, T.C.; Symul, T.; et al. Experimental demonstration of Gaussian protocols for one-sided device-independent quantum key distribution. Optica 2016, 3, 634–642. [Google Scholar] [CrossRef]
- Li, Y.M.; Wang, X.Y.; Bai, Z.L.; Liu, W.Y.; Yang, S.S.; Peng, K.C. Continuous variable quantum key distribution. Chin. Phys. B 2017, 26, 040303. [Google Scholar] [CrossRef]
- Liu, W.Y.; Wang, X.Y.; Wang, N.; Du, S.N.; Li, Y.M. Imperfect state preparation in continuous-variable quantum key distribution. Phys. Rev. A 2017, 96, 042312. [Google Scholar] [CrossRef]
- Liu, W.Y.; Cao, Y.X.; Wang, X.Y.; Li, Y.M. Continuous-variable quantum key distribution under strong channel polarization disturbance. Phys. Rev. A 2020, 102, 032625. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, P.; Liu, J.Q.; Du, S.; Liu, W.Y.; Lu, Z.G.; Wang, X.Y.; Li, Y.M. Experimental demonstration of continuous-variable measurement-device-independent quantum key distribution over optical fiber. Optica 2022, 9, 492–500. [Google Scholar] [CrossRef]
- Karinou, F.; Brunner, H.H.; Fung, C.H.F.; Comandar, L.C.; Bettelli, S.; Hillerkuss, D.; Kuschnerov, M.; Mikroulis, S.; Wang, D.; Xie, C.S.; et al. Toward the Integration of CV Quantum Key Distribution in Deployed Optical Networks. IEEE Photon. Technol. Lett. 2018, 30, 650–653. [Google Scholar] [CrossRef]
- Huang, D.; Lin, D.K.; Wang, C.; Liu, W.Q.; Fang, S.H.; Peng, J.Y.; Huang, P.; Zeng, G.H. Continuous-variable quantum key distribution with 1 Mbps secure key rate. Opt. Express 2015, 23, 17511–17519. [Google Scholar] [CrossRef]
- Kleis, S.; Steinmayer, J.; Derksen, R.H.; Schaeffer, C.G. Experimental investigation of heterodyne quantum key distribution in the S-band or L-band embedded in a commercial C-band DWDM system. Opt. Express 2019, 27, 16540–16549. [Google Scholar] [CrossRef]
- Eriksson, T.A.; Hirano, T.; Puttnam, B.J.; Rademacher, G.; Luis, R.S.; Fujiwara, M.; Namiki, R.; Awaji, Y.; Takeoka, M.; Wada, N.; et al. Wavelength division multiplexing of continuous variable quantum key distribution and 18.3 Tbit/s data channels. Commun. Phys. 2019, 2, 9. [Google Scholar] [CrossRef]
- Braunstein, S.L.; Pirandola, S. Side-channel-free quantum key distribution. Phys. Rev. Lett. 2012, 108, 130502. [Google Scholar] [CrossRef] [PubMed]
- Lo, H.K.; Curty, M.; Qi, B. Measurement-device-independent quantum key distribution. Phys. Rev. Lett. 2012, 108, 130503. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Wang, X.B. Efficient implementation of the decoy-state measurement-device-independent quantum key distribution with heralded single-photon sources. Phys. Rev. A 2013, 88, 052332. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, T.Y.; Wang, L.J.; Liang, H.; Shentu, G.L.; Wang, J.; Cui, K.; Yin, H.L.; Liu, N.L.; Li, L.; et al. Experimental Measurement-Device-Independent Quantum Key Distribution. Phys. Rev. Lett. 2013, 111, 130502. [Google Scholar] [CrossRef]
- Hu, X.L.; Cao, Y.; Yu, Z.W.; Wang, X.B. Measurement-device-independent quantum key distribution over asymmetric channel and unstable channel. Sci. Rep. 2018, 8, 17634. [Google Scholar] [CrossRef]
- Liu, H.; Wang, W.Y.; Wei, K.J.; Fang, X.T.; Li, L.; Liu, N.L.; Liang, H.; Zhang, S.J.; Zhang, W.J.; Li, H.; et al. Experimental demonstration of high-rate measurement-device-independent quantum key distribution over asymmetric channels. Phys. Rev. Lett. 2019, 122, 160501. [Google Scholar] [CrossRef]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661–663. [Google Scholar] [CrossRef]
- Ma, H.X.; Huang, P.; Bai, D.Y.; Wang, T.; Wang, S.Y.; Bao, W.S.; Zeng, G.H.Z. Long-distance continuous-variable measurement-device-independent quantum key distribution with discrete modulation. Phys. Rev. A 2019, 99, 022322. [Google Scholar] [CrossRef]
- Wei, Y.; Guo, Y.; Zhang, H.; Zhong, H.; Mao, Y.; Hu, L.Y. Enhancing discrete-modulated continuous-variable measurement-device-independent quantum key distribution via quantum catalysis. J. Phys. B Mol. Opt. 2021, 54, 045501. [Google Scholar]
- Zhao, W.; Shi, R.H.; Shi, J.J.; Ruan, X.C.; Guo, Y.; Huang, D. Phase-noise estimation using Bayesian inference for discretely modulated measurement-device-independent continuous-variable quantum key distribution. Phys. Rev. A 2020, 102, 022621. [Google Scholar] [CrossRef]
- Khan, M.B.; Waseem, M.; Irfan, M.; Mehmood, A.; Qamar, S. Zero-photon catalysis based eight-state discrete modulated measurement-device-independent continuous-variable quantum key distribution. J. Opt. Soc. Am. B 2023, 40, 763–772. [Google Scholar] [CrossRef]
- Wu, X.D.; Huang, D.; Huang, P.; Guo, Y. Discrete modulation continuous-variable measurement-device-independent quantum key distribution scheme based on realistic detector compensation. Acta Phys. Sin. 2022, 71, 240304. [Google Scholar] [CrossRef]
- Li, Z.Y.; Zhang, Y.C.; Xu, F.H.; Peng, X.; Guo, H. Continuous-variable measurement-device-independent quantum key distribution. Phys. Rev. A 2014, 89, 052301. [Google Scholar] [CrossRef]
- Ma, X.C.; Sun, S.H.; Jiang, M.S.; Gui, M.; Liang, L.M. Gaussian-modulated coherent-state measurement-device-independent quantum key distribution. Phys. Rev. A 2014, 89, 042335. [Google Scholar] [CrossRef]
- Wang, P.; Wang, X.Y.; Li, Y.M. Continuous-variable measurement-device-independent quantum key distribution using modulated squeezed states and optical amplifiers. Phys. Rev. A 2019, 99, 042309. [Google Scholar] [CrossRef]
- Zheng, Y.; Shi, H.B.; Pan, W.; Wang, Q.T.; Mao, J.H. Security Analysis of Continuous-Variable Measurement-Device-Independent Quantum Key Distribution Systems in Complex Communication Environments. Entropy 2022, 24, 127. [Google Scholar] [CrossRef]
- Song, T.T.; Wen, Q.Y.; Guo, F.Z.; Tan, X.Q. Finite-key analysis for measurement-device-independent quantum key distribution. Phys. Rev. A 2012, 86, 022332. [Google Scholar] [CrossRef]
- Curty, M.; Xu, F.H.; Gui, W.; Lim, C.C.W.; Tamaki, K.; Lo, H.K. Finite-key analysis for measurement-device-independent quantum key distribution. Nat. Commun. 2014, 5, 3732. [Google Scholar] [CrossRef]
- Papanastasiou, P.; Ottaviani, C.; Pirandola, S. Finite-size analysis of measurement-device-independent quantum cryptography with continuous variables. Phys. Rev. A 2017, 96, 042332. [Google Scholar] [CrossRef]
- Liu, W.Y.; Liu, Z.H.; Bai, J.D.; Jie, Q.; Zhang, G.W.; Tian, Y.; Jing, J.J. Impact of Imbalanced Modulation on Security of Continuous-Variable Measurement-Device-Independent Quantum Key Distribution. Photonics 2024, 11, 649. [Google Scholar] [CrossRef]
- Ma, X.F.; Fung, C.H.F.; Razavi, M. Statistical fluctuation analysis for measurement-device-independent quantum key distribution. Phys. Rev. A 2012, 86, 052305. [Google Scholar] [CrossRef]
- Yu, Z.W.; Zhou, Y.H.; Wang, X.B. Statistical fluctuation analysis for measurement-device-independent quantum key distribution with three-intensity decoy-state method. Phys. Rev. A 2015, 91, 032318. [Google Scholar] [CrossRef]
- Wang, C.; Yin, Z.Q.; Wang, S.; Chen, W.; Guo, G.C.; Han, Z.F. Measurement-device-independent quantum key distribution robust against environmental disturbances. Optica 2017, 4, 1016–1023. [Google Scholar] [CrossRef]
- Zang, Y.C.; Li, Z.Y.; Yu, S.; Gu, W.Y.; Peng, X.; Guo, H. Continuous-variable measurement-device-independent quantum key distribution using squeezed states. Phys. Rev. A 2014, 90, 052325. [Google Scholar] [CrossRef]
- Fossier, S.; Diamanti, E.; Debuisschert, T. Improvement of continuous-variable quantum key distribution systems by using optical preamplifiers. J. Phys. B-AT. Mol. Opt. 2009, 42, 114014. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Bai, J.; Li, F.; Li, Y.; Tian, Y.; Liu, W. Performance Improvement for Discretely Modulated Continuous-Variable Measurement-Device-Independent Quantum Key Distribution with Imbalanced Modulation. Entropy 2025, 27, 160. https://doi.org/10.3390/e27020160
Liu Z, Bai J, Li F, Li Y, Tian Y, Liu W. Performance Improvement for Discretely Modulated Continuous-Variable Measurement-Device-Independent Quantum Key Distribution with Imbalanced Modulation. Entropy. 2025; 27(2):160. https://doi.org/10.3390/e27020160
Chicago/Turabian StyleLiu, Zehui, Jiandong Bai, Fengchao Li, Yijun Li, Yan Tian, and Wenyuan Liu. 2025. "Performance Improvement for Discretely Modulated Continuous-Variable Measurement-Device-Independent Quantum Key Distribution with Imbalanced Modulation" Entropy 27, no. 2: 160. https://doi.org/10.3390/e27020160
APA StyleLiu, Z., Bai, J., Li, F., Li, Y., Tian, Y., & Liu, W. (2025). Performance Improvement for Discretely Modulated Continuous-Variable Measurement-Device-Independent Quantum Key Distribution with Imbalanced Modulation. Entropy, 27(2), 160. https://doi.org/10.3390/e27020160




