Levy Noise Affects Ornstein–Uhlenbeck Memory
Abstract
1. Introduction
- ▶
- The Levy approach yields memory effects that are markedly more profound than those of the OUP.
- ▶
- The Gauss approach yields memory effects that are qualitatively identical to those of the OUP.
2. Setting the Stage
2.1. Measuring Randomness
- G1.
- The standard deviation is non-negative, , and it vanishes if and only if the random variable is deterministic:where the equality on the right-hand side holds with probability one.
- G2.
- The standard-deviation’s response to an affine transformation of the random variable is:where a and b are, respectively, the slope and the intercept of the affine transformation.
2.2. Levy Distribution
- F1.
- The random variable X is symmetric about its center c, and hence: the median of X is its center, .
- F2.
- When the Levy exponent is in the range then the mean absolute deviation of X from its center diverges: .
- F3.
- When the Levy exponent is one, , then the statistical distribution of X is Cauchy.
- F4.
- When the Levy exponent is in the range then: the mean of X is its center, ; and the mean squared deviation of X from its center diverges, .
- F5.
- When the Levy exponent is two, , then the statistical distribution of X is Gauss, and hence: the parameters c and s are, respectively, the mean and the standard deviation of X.
2.3. Levy Noise
- L1.
- The integral of the noise over a time interval of duration is a Levy random variable with center zero and scale (where p is the Levy exponent).
- L2.
- The integrals of the noise over disjoint time intervals are independent random variables.
2.4. Langevin, Ornstein and Uhlenbeck
3. Increments of the Levy-Driven OUP
3.1. Increments’ Unconditional Statistics
3.2. Increments’ Conditional Statistics
4. Three Ratios
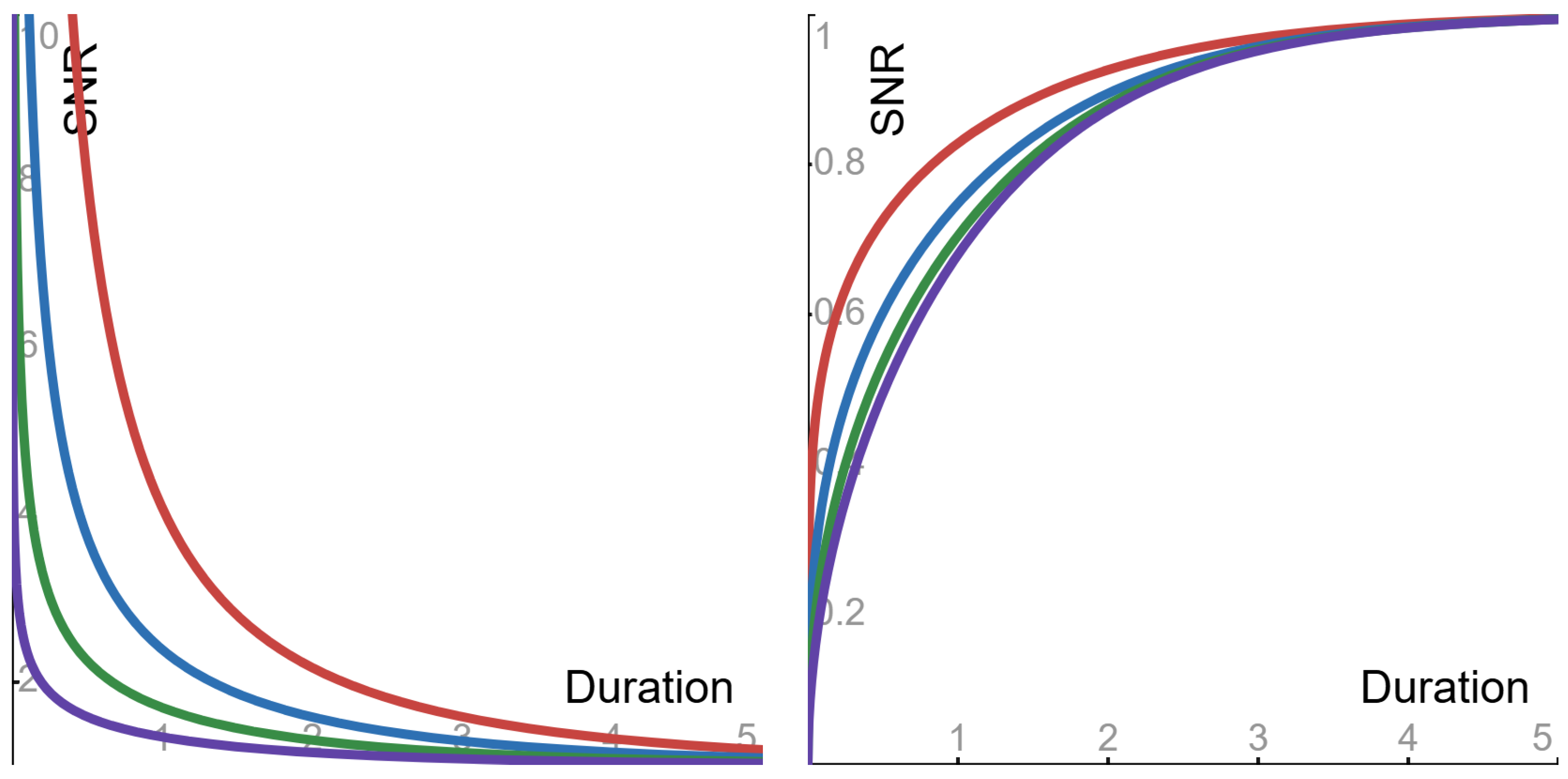
4.1. Signal-to-Noise Ratio
- ▶
- Sub-Cauchy () case: the ratio is monotone decreasing from ∞ to its asymptotic value.
- ▶
- Cauchy () case: the ratio is flat, and its constant value is its asymptotic value.
- ▶
- Super-Cauchy () and Gauss () cases: the ratio is monotone increasing from 0 to its asymptotic value.
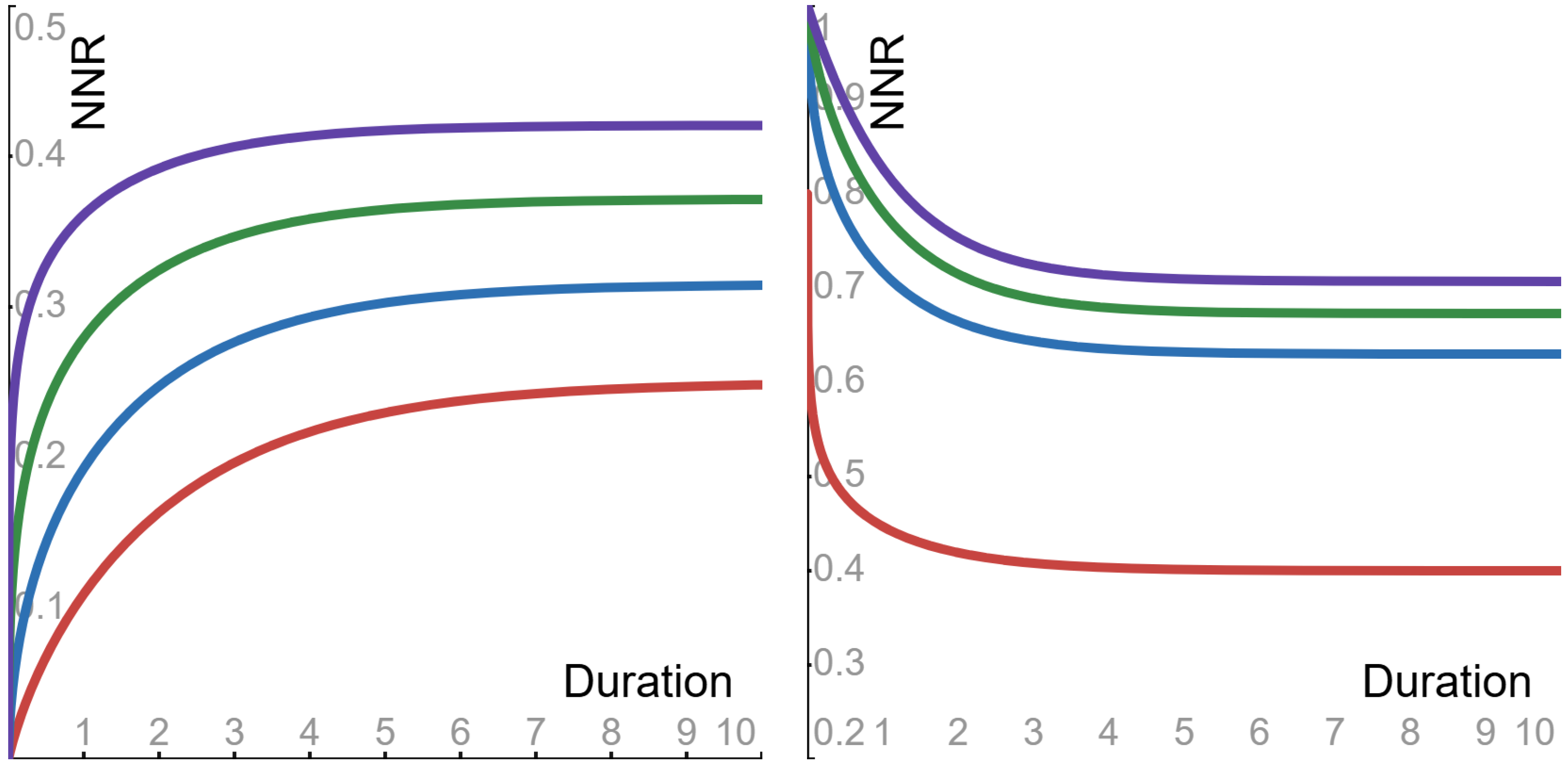
4.2. Noise-to-Noise Ratio
- ▶
- Sub-Cauchy () case: the ratio is monotone increasing from 0 to its asymptotic value.
- ▶
- Cauchy () case: the ratio is flat, and its constant value is its asymptotic value.
- ▶
- Super-Cauchy () and Gauss () cases: the ratio is monotone decreasing from 1 to its asymptotic value.
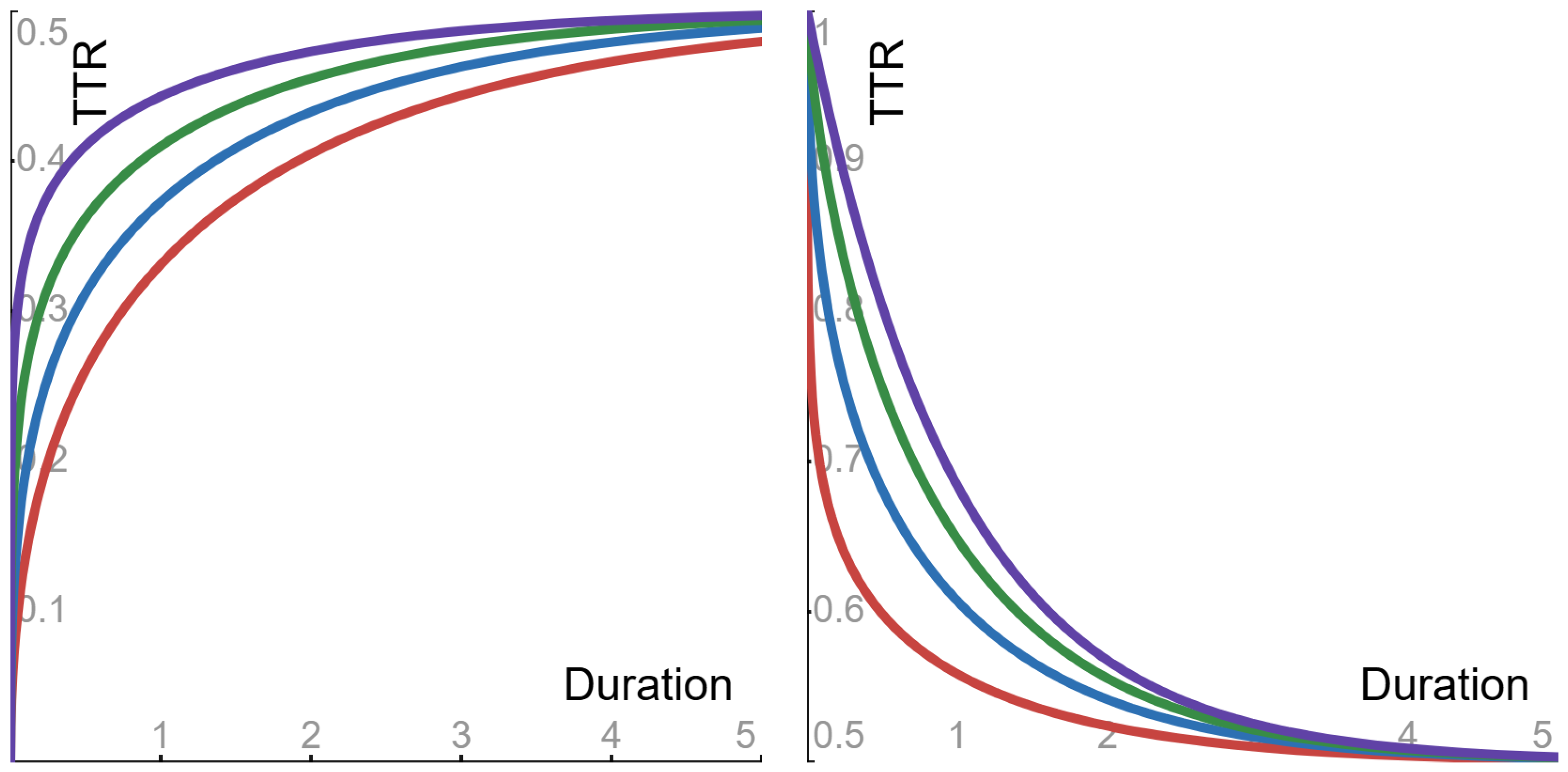
4.3. Tail-to-Tail Ratio
- ▶
- Sub-Cauchy () case: the ratio is monotone increasing from 0 to its asymptotic value.
- ▶
- Cauchy () case: the ratio is flat, and its constant value is its asymptotic value.
- ▶
- Super-Cauchy () case: the ratio is monotone decreasing from 1 to its asymptotic value.
5. Gauss Approach
6. Discussion
6.1. Levy vs. Gauss
6.2. Cauchy Threshold
6.3. Noah vs. Joseph
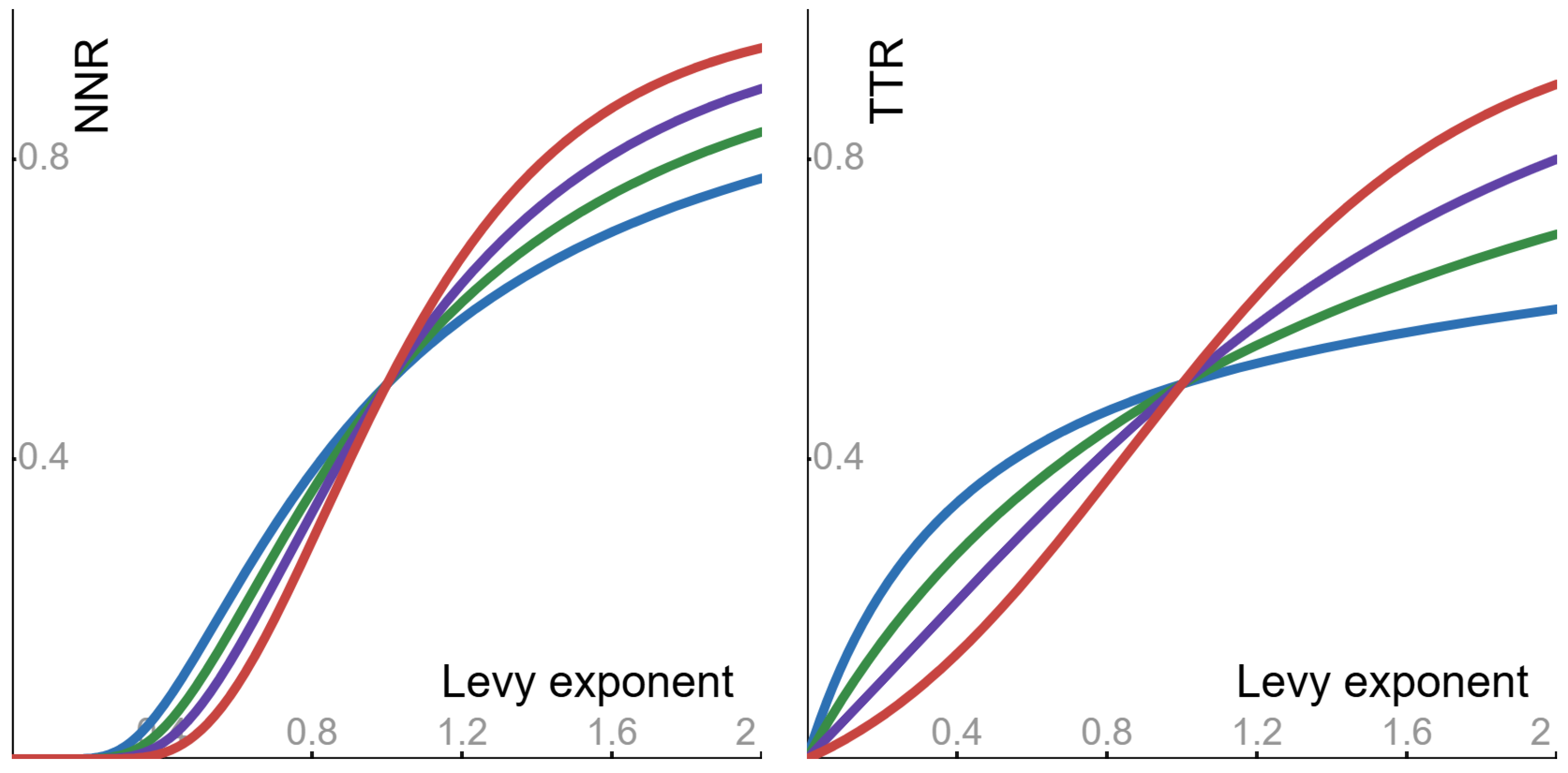
6.4. Levy Fluctuations
- ▶
- As a function of the Levy exponent p, the noise-to-noise ratio is monotone increasing from 0 to .
- ▶
- As a function of the Levy exponent p, the tail-to-tail ratio is monotone increasing from 0 to .
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. The Function of Equation (13)
Appendix A.1.1. The Function of Equation (13) with Respect to Its Variable
Appendix A.1.2. The Function of Equation (13) with Respect to Its Parameter
Appendix A.1.3. A Transformation of the Function of Equation (13)
Appendix A.2. Bivariate Normal Calculations
Appendix A.2.1. Signal-to-Noise Ratio
Appendix A.2.2. Noise-to-Noise Ratio
Appendix A.2.3. Tail-to-Tail Ratio
Appendix A.2.4. Gaussian Stationary Processes
References
- Uhlenbeck, G.E.; Ornstein, L.S. On the theory of the Brownian motion. Phys. Rev. 1930, 36, 823. [Google Scholar] [CrossRef]
- Caceres, M.O.; Budini, A.A. The generalized Ornstein-Uhlenbeck process. J. Phys. A Math. Gen. 1997, 30, 8427. [Google Scholar] [CrossRef]
- Bezuglyy, V.; Mehlig, B.; Wilkinson, M.; Nakamura, K.; Arvedson, E. Generalized ornstein-uhlenbeck processes. J. Math. Phys. 2006, 47, 073301. [Google Scholar] [CrossRef]
- Maller, R.A.; Muller, G.; Szimayer, A. Ornstein-Uhlenbeck Processes and Extensions; Handbook of Financial Time Series; Springer: Berlin/Heidelberg, Germany, 2009; pp. 421–437. [Google Scholar]
- Doob, J.L. The Brownian movement and stochastic equations. Ann. Math. 1942, 43, 351–369. [Google Scholar] [CrossRef]
- MacKay, D.J.C. Introduction to Gaussian processes. NATO ASI Ser. F Comput. Syst. Sci. 1998, 168, 133–166. [Google Scholar]
- Ibragimov, I.; Rozanov, Y. Gaussian Random Processes; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Lifshits, M. Lectures on Gaussian Processes; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Lindgren, G. Stationary Stochastic Processes: Theory and Applications; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Lindgren, G.; Rootzen, H.; Sandsten, M. Stationary Stochastic Processes for Scientists and Engineers; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Hida, T. Stationary Stochastic Processes; MN-8; Princeton University Press: Princeton, NJ, USA, 2015; Volume 8. [Google Scholar]
- Gillespie, D.T. Markov Processes: An Introduction for Physical Scientists; Elsevier: Amsterdam, The Netherlands, 1991. [Google Scholar]
- Liggett, T.M. Continuous Time Markov Processes: An Introduction; American Mathematical Society: Providence, RI, USA, 2010; Volume 113. [Google Scholar]
- Dynkin, E.B. Theory of Markov Processes; Dover: Mineola, NY, USA, 2012. [Google Scholar]
- Langevin, P. Sur la theorie du mouvement Brownien. Compt. Rendus 1908, 146, 530–533. [Google Scholar]
- Coffey, W.; Kalmykov, Y.P. The Langevin Equation: With Applications to Stochastic Problems in Physics, Chemistry and Electrical Engineering; World Scientific: Singapore, 2012. [Google Scholar]
- Pavliotis, G.A. Stochastic Processes and Applications: Diffusion Processes, the Fokker-Planck and Langevin Equations; Springer: Berlin/Heidelberg, Germany, 2014; Volume 60. [Google Scholar]
- Borodin, A.N.; Salminen, P. Handbook of Brownian Motion: Facts and Formulae; Birkhauser: Basel, Switzerland, 2015. [Google Scholar]
- Debbasch, F.; Mallick, K.; Rivet, J.-P. Relativistic Ornstein-Uhlenbeck process. J. Stat. Phys. 1997, 88, 945–966. [Google Scholar] [CrossRef]
- Graversen, S.; Peskir, G. Maximal inequalities for the Ornstein-Uhlenbeck process. Proc. Am. Math. Soc. 2000, 128, 3035–3041. [Google Scholar] [CrossRef]
- Aalen, O.O.; Gjessing, H.K. Survival models based on the Ornstein-Uhlenbeck process. Lifetime Data Anal. 2004, 10, 407–423. [Google Scholar] [CrossRef]
- Larralde, H. A first passage time distribution for a discrete version of the Ornstein-Uhlenbeck process. J. Phys. A Math. Gen. 2004, 37, 3759. [Google Scholar] [CrossRef]
- Eliazar, I.; Klafter, J. Markov-breaking and the emergence of long memory in Ornstein-Uhlenbeck systems. J. Phys. A Math. Theor. 2008, 41, 122001. [Google Scholar] [CrossRef]
- Eliazar, I.; Klafter, J. From Ornstein-Uhlenbeck dynamics to long-memory processes and fractional Brownian motion. Phys. Rev. E 2009, 79, 021115. [Google Scholar] [CrossRef]
- Wilkinson, M.; Pumir, A. Spherical Ornstein-Uhlenbeck processes. J. Stat. Phys. 2011, 145, 113. [Google Scholar] [CrossRef]
- Gajda, J.; Wylomańska, A. Time-changed Ornstein-Uhlenbeck process. J. Phys. A Math. Theor. 2015, 48, 135004. [Google Scholar] [CrossRef]
- Bonilla, L.L. Active Ornstein-Uhlenbeck particles. Phys. Rev. E 2019, 100, 022601. [Google Scholar] [CrossRef]
- Sevilla, F.J.; Rodriguez, R.F.; Ruben Gomez-Solano, J. Generalized Ornstein-Uhlenbeck model for active motion. Phys. Rev. E 2019, 100, 032123. [Google Scholar] [CrossRef]
- Martin, D.; O’Byrne, J.; Cates, M.E.; Fodor, E.; Nardini, C.; Tailleur, J.; Wijland, F.V. Statistical mechanics of active Ornstein-Uhlenbeck particles. Phys. Rev. E 2021, 103, 032607. [Google Scholar] [CrossRef]
- Nguyen, G.H.P.; Wittmann, R.; Lowen, H. Active Ornstein–Uhlenbeck model for self-propelled particles with inertia. J. Phys. Condens. Matter 2021, 34, 035101. [Google Scholar] [CrossRef]
- Dabelow, L.; Eichhorn, R. Irreversibility in active matter: General framework for active Ornstein-Uhlenbeck particles. Front. Phys. 2021, 8, 582992. [Google Scholar] [CrossRef]
- Trajanovski, P.; Jolakoski, P.; Zelenkovski, K.; Iomin, A.; Kocarev, L.; Sandev, T. Ornstein-Uhlenbeck process and generalizations: Particle dynamics under comb constraints and stochastic resetting. Phys. Rev. E 2023, 107, 054129. [Google Scholar] [CrossRef]
- Trajanovski, P.; Jolakoski, P.; Kocarev, L.; Sandev, T. Ornstein-Uhlenbeck Process on Three-Dimensional Comb under Stochastic Resetting. Mathematics 2023, 11, 3576. [Google Scholar] [CrossRef]
- Dubey, A.; Pal, A. First-passage functionals for Ornstein Uhlenbeck process with stochastic resetting. arXiv 2023, arXiv:2304.05226. [Google Scholar] [CrossRef]
- Strey, H.H. Estimation of parameters from time traces originating from an Ornstein-Uhlenbeck process. Phys. Rev. E 2019, 100, 062142. [Google Scholar] [CrossRef] [PubMed]
- Janczura, J.; Magdziarz, M.; Metzler, R. Parameter estimation of the fractional Ornstein-Uhlenbeck process based on quadratic variation. Chaos Interdiscip. J. Nonlinear Sci. 2023, 33, 103125. [Google Scholar] [CrossRef] [PubMed]
- Cherstvy, A.G.; Thapa, S.; Mardoukhi, Y.; Chechkin, A.V.; Metzler, R. Time averages and their statistical variation for the Ornstein-Uhlenbeck process: Role of initial particle distributions and relaxation to stationarity. Phys. Rev. E 2018, 98, 022134. [Google Scholar] [CrossRef]
- Thomas, P.J.; Lindner, B. Phase descriptions of a multidimensional Ornstein-Uhlenbeck process. Phys. Rev. E 2019, 99, 062221. [Google Scholar] [CrossRef] [PubMed]
- Mardoukhi, Y.; Chechkin, A.; Metzler, R. Spurious ergodicity breaking in normal and fractional Ornstein-Uhlenbeck process. New J. Phys. 2020, 22, 073012. [Google Scholar] [CrossRef]
- Giorgini, L.T.; Moon, W.; Wettlaufer, J.S. Analytical Survival Analysis of the Ornstein-Uhlenbeck Process. J. Stat. Phys. 2020, 181, 2404–2414. [Google Scholar] [CrossRef]
- Kearney, M.J.; Martin, R.J. Statistics of the first passage area functional for an Ornstein-Uhlenbeck process. J. Phys. A Math. Theor. 2021, 54, 055002. [Google Scholar] [CrossRef]
- Goerlich, R.; Li, M.; Albert, S.; Manfredi, G.; Hervieux, P.; Genet, C. Noise and ergodic properties of Brownian motion in an optical tweezer: Looking at regime crossovers in an Ornstein-Uhlenbeck process. Phys. Rev. E 2021, 103, 032132. [Google Scholar] [CrossRef]
- Smith, N.R. Anomalous scaling and first-order dynamical phase transition in large deviations of the Ornstein-Uhlenbeck process. Phys. Rev. E 2022, 105, 014120. [Google Scholar] [CrossRef]
- Kersting, H.; Orvieto, A.; Proske, F.; Lucchi, A. Mean first exit times of Ornstein-Uhlenbeck processes in high-dimensional spaces. J. Phys. A Math. Theor. 2023, 56, 215003. [Google Scholar] [CrossRef]
- Trajanovski, P.; Jolakoski, P.; Kocarev, L.; Metzler, R.; Sandev, T. Generalised Ornstein-Uhlenbeck process: Memory effects and resetting. J. Phys. Math. Theor. 2025, 58, 045001. [Google Scholar] [CrossRef]
- Adler, R.; Feldman, R.; Taqqu, M. A Practical Guide to Heavy Tails: Statistical Techniques and Applications; Springer: New York, NY, USA, 1998. [Google Scholar]
- Nair, J.; Wierman, A.; Zwart, B. The Fundamentals of Heavy-Tails: Properties, Emergence, and Identification; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar]
- Mandelbrot, B.B.; Wallis, J.R. Noah, Joseph, and operational hydrology. Water Resour. Res. 1968, 4, 909–918. [Google Scholar] [CrossRef]
- Bertoin, J. Levy Processes; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Ken-Iti, S. Levy Processes and Infinitely Divisible Distributions; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Barndorff-Nielsen, O.E.; Mikosch, T.; Resnick, S.I. (Eds.) Levy Processes: Theory and Applications; Springer Science & Business Media: New York, NY, USA, 2001. [Google Scholar]
- Garbaczewski, P.; Olkiewicz, R. Ornstein-Uhlenbeck-Cauchy process. J. Math. Phys. 2000, 41, 6843–6860. [Google Scholar] [CrossRef]
- Eliazar, I.; Klafter, J. A growth-collapse model: Levy inflow, geometric crashes, and generalized Ornstein-Uhlenbeck dynamics. Phys. A Stat. Mech. Its Appl. 2004, 334, 1–21. [Google Scholar] [CrossRef]
- Jongbloed, G.; Meulen, F.H.V.D.; Vaart, A.W.V.D. Nonparametric inference for Levy-driven Ornstein-Uhlenbeck processes. Bernoulli 2005, 11, 759–791. [Google Scholar] [CrossRef]
- Eliazar, I.; Klafter, J. Levy, Ornstein-Uhlenbeck, and subordination: Spectral vs. jump description. J. Stat. Phys. 2004, 119, 165–196. [Google Scholar] [CrossRef]
- Eliazar, I.; Klafter, J. Stochastic Ornstein-Uhlenbeck Capacitors. J. Stat. Phys. 2005, 118, 177–198. [Google Scholar] [CrossRef]
- Brockwell, P.J.; Davis, R.A.; Yang, Y. Estimation for non-negative Levy-driven Ornstein-Uhlenbeck processes. J. Appl. Probab. 2007, 44, 977–989. [Google Scholar] [CrossRef]
- Magdziarz, M. Short and long memory fractional Ornstein-Uhlenbeck alpha-stable processes. Stoch. Model. 2007, 23, 451–473. [Google Scholar] [CrossRef]
- Magdziarz, M. Fractional Ornstein-Uhlenbeck processes. Joseph effect in models with infinite variance. Phys. A Stat. Mech. Its Appl. 2008, 387, 123–133. [Google Scholar] [CrossRef]
- Brockwell, P.J.; Lindner, A. Ornstein-Uhlenbeck related models driven by Levy processes. Stat. Methods Stoch. Differ. Equ. 2012, 124, 383–427. [Google Scholar]
- Toenjes, R.; Sokolov, I.M.; Postnikov, E.B. Nonspectral relaxation in one dimensional Ornstein-Uhlenbeck processes. Phys. Rev. Lett. 2013, 110, 150602. [Google Scholar] [CrossRef] [PubMed]
- Riedle, M. Ornstein-Uhlenbeck processes driven by cylindrical Levy processes. Potential Anal. 2015, 42, 809–838. [Google Scholar] [CrossRef]
- Thiel, F.; Sokolov, I.M.; Postnikov, E.B. Nonspectral modes and how to find them in the Ornstein-Uhlenbeck process with white μ-stable noise. Phys. Rev. E 2016, 93, 052104. [Google Scholar] [CrossRef]
- Fogedby, H.C. Langevin equations for continuous time Levy flights. Phys. Rev. E 1994, 50, 1657. [Google Scholar] [CrossRef]
- Jespersen, S.; Metzler, R.; Fogedby, H.C. Levy flights in external force fields: Langevin and fractional Fokker-Planck equations and their solutions. Phys. Rev. E 1999, 59, 2736. [Google Scholar] [CrossRef]
- Chechkin, A.; Gonchar, V.; Klafter, J.; Metzler, R.; Tanatarov, L. Stationary states of non-linear oscillators driven by Levy noise. Chem. Phys. 2002, 284, 233–251. [Google Scholar] [CrossRef]
- Brockmann, D.; Sokolov, I.M. Levy flights in external force fields: From models to equations. Chem. Phys. 2002, 284, 409–421. [Google Scholar] [CrossRef]
- Eliazar, I.; Klafter, J. Levy-driven Langevin systems: Targeted stochasticity. J. Stat. Phys. 2003, 111, 739–768. [Google Scholar] [CrossRef]
- Chechkin, A.V.; Gonchar, V.Y.; Klafter, J.; Metzler, R.; Tanatarov, L.V. Levy flights in a steep potential well. J. Stat. Phys. 2004, 115, 1505–1535. [Google Scholar] [CrossRef]
- Dybiec, B.; Gudowska-Nowak, E.; Sokolov, I.M. Stationary states in Langevin dynamics under asymmetric Levy noises. Phys. Rev. E Nonlinear Soft Matter Phys. 2007, 76, 041122. [Google Scholar] [CrossRef] [PubMed]
- Dybiec, B.; Sokolov, I.M.; Chechkin, A.V. Stationary states in single-well potentials under symmetric Levy noises. J. Stat. Mech. Theory Exp. 2010, 2010, P07008. [Google Scholar] [CrossRef]
- Eliazar, I.I.; Shlesinger, M.F. Langevin unification of fractional motions. J. Phys. A Math. Theor. 2012, 45, 162002. [Google Scholar] [CrossRef]
- Magdziarz, M.; Szczotka, W.; Zebrowski, P. Langevin picture of Levy walks and their extensions. J. Stat. Phys. 2012, 147, 74–96. [Google Scholar] [CrossRef]
- Sandev, T.; Metzler, R.; Tomovski, Z. Velocity and displacement correlation functions for fractional generalized Langevin equations. Fract. Calc. Appl. Anal. 2012, 15, 426–450. [Google Scholar] [CrossRef]
- Liemert, A.; Sandev, T.; Kantz, H. Generalized Langevin equation with tempered memory kernel. Phys. A Stat. Mech. Its Appl. 2017, 466, 356–369. [Google Scholar] [CrossRef]
- Wolpert, R.L.; Taqqu, M.S. Fractional Ornstein-Uhlenbeck Levy processes and the Telecom process: Upstairs and downstairs. Signal Process. 2005, 85, 1523–1545. [Google Scholar] [CrossRef]
- Shu, Y.; Feng, Q.; Kao, E.P.C.; Liu, H. Levy-driven non-Gaussian Ornstein-Uhlenbeck processes for degradation-based reliability analysis. IIE Trans. 2016, 48, 993–1003. [Google Scholar] [CrossRef]
- Chevallier, J.; Goutte, S. Estimation of Levy-driven Ornstein-Uhlenbeck processes: Application to modeling of CO2 and fuel-switching. Ann. Oper. Res. 2017, 255, 169–197. [Google Scholar] [CrossRef]
- Kabanov, Y.; Pergamenshchikov, S. Ruin probabilities for a Levy-driven generalised Ornstein–Uhlenbeck process. Financ. Stochastics 2020, 24, 39–69. [Google Scholar] [CrossRef]
- Onalan, O. Financial modelling with Ornstein-Uhlenbeck processes driven by Levy process. In Proceedings of the World Congress on Engineering, London, UK, 1–3 July 2009; Volume 2, pp. 1–3. [Google Scholar]
- Onalan, O. Fractional Ornstein-Uhlenbeck processes driven by stable Levy motion in finance. Int. Res. J. Financ. Econ. 2010, 42, 129–139. [Google Scholar]
- Endres, S.; Stubinger, J. Optimal trading strategies for Levy-driven Ornstein–Uhlenbeck processes. Appl. Econ. 2019, 51, 3153–3169. [Google Scholar] [CrossRef]
- Shlesinger, M.F.; Klafter, J. Levy walks versus Levy flights. In On Growth and Form: Fractal and Non-Fractal Patterns in Physics; Springer: Dordrecht, The Netherlands, 1986; pp. 279–283. [Google Scholar]
- Shlesinger, M.F.; Klafter, J.; West, B.J. Levy walks with applications to turbulence and chaos. Phys. A Stat. Mech. Its Appl. 1986, 140, 212–218. [Google Scholar] [CrossRef]
- Allegrini, P.; Grigolini, P.; West, B.J. Dynamical approach to Levy processes. Phys. Rev. E 1996, 54, 4760. [Google Scholar] [CrossRef]
- Shlesinger, M.F.; West, B.J.; Klafter, J. Levy dynamics of enhanced diffusion: Application to turbulence. Phys. Rev. Lett. 1987, 58, 1100. [Google Scholar] [CrossRef]
- Uchaikin, V.V. Self-similar anomalous diffusion and Levy-stable laws. Phys.-Uspekhi 2003, 46, 821. [Google Scholar] [CrossRef]
- Chechkin, A.V.; Gonchar, V.Y.; Klafter, J.; Metzler, R. Fundamentals of Levy flight processes. In Fractals, Diffusion, and Relaxation in Disordered Complex Systems: Advances in Chemical Physics, Part B; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006; pp. 439–496. [Google Scholar]
- Metzler, R.; Chechkin, A.V.; Gonchar, V.Y.; Klafter, J. Some fundamental aspects of Levy flights. Chaos Solitons Fractals 2007, 34, 129–142. [Google Scholar] [CrossRef]
- Chechkin, A.V.; Metzler, R.; Klafter, J.; Gonchar, V.Y. Introduction to the theory of Levy flights. In Anomalous Transport: Foundations and Applications; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2008; pp. 129–162. [Google Scholar]
- Dubkov, A.A.; Spagnolo, B.; Uchaikin, V.V. Levy flight superdiffusion: An introduction. Int. J. Bifurc. Chaos 2008, 18, 2649–2672. [Google Scholar] [CrossRef]
- Schinckus, C. How physicists made stable Levy processes physically plausible. Braz. J. Phys. 2013, 43, 281–293. [Google Scholar] [CrossRef]
- Zaburdaev, V.; Denisov, S.; Klafter, J. Levy walks. Rev. Mod. Phys. 2015, 87, 483–530. [Google Scholar] [CrossRef]
- Reynolds, A.M. Current status and future directions of Levy walk research. Biol. Open 2018, 7, bio030106. [Google Scholar] [CrossRef]
- Abe, M.S. Functional advantages of Levy walks emerging near a critical point. Proc. Natl. Acad. Sci. USA 2013, 117, 24336–24344. [Google Scholar] [CrossRef]
- Garg, K.; Kello, C.T. Efficient Levy walks in virtual human foraging. Sci. Rep. 2021, 11, 5242. [Google Scholar] [CrossRef]
- Mukherjee, S.; Singh, R.K.; James, M.; Ray, S.S. Anomalous diffusion and Levy walks distinguish active from inertial turbulence. Phys. Rev. Lett. 2021, 127, 118001. [Google Scholar] [CrossRef]
- Gunji, Y.-P.; Kawai, T.; Murakami, H.; Tomaru, T.; Minoura, M.; Shinohara, S. Levy walk in swarm models based on Bayesian and inverse Bayesian inference. Comput. Struct. Biotechnol. J. 2021, 19, 247–260. [Google Scholar] [CrossRef]
- Park, S.; Thapa, S.; Kim, Y.; Lomholt, M.A.; Jeon, J.-H. Bayesian inference of Levy walks via hidden Markov models. J. Phys. A Math. Theor. 2021, 54, 484001. [Google Scholar] [CrossRef]
- Romero-Ruiz, A.; Rivero, M.J.; Milne, A.; Morgan, S.; Filho, P.M.; Pulley, S.; Segura, C.; Harris, P.; Lee, M.R.; Coleman, K.; et al. Grazing livestock move by Levy walks: Implications for soil health and environment. J. Environ. Manag. 2023, 345, 118835. [Google Scholar] [CrossRef] [PubMed]
- Sakiyama, T.; Okawara, M. A short memory can induce an optimal Levy walk. In World Conference on Information Systems and Technologies; Springer Nature Switzerland: Cham, Switzerland, 2023; pp. 421–428. [Google Scholar]
- Levernier, N.; Textor, J.; Benichou, O.; Voituriez, R. Inverse square Levy walks are not optimal search strategies for d ≥ 2. Phys. Rev. Lett. 2020, 124, 080601. [Google Scholar] [CrossRef]
- Guinard, B.; Korman, A. Intermittent inverse-square Levy walks are optimal for finding targets of all sizes. Sci. Adv. 2021, 7, eabe8211. [Google Scholar] [CrossRef] [PubMed]
- Clementi, A.; d’Amore, F.; Giakkoupis, G.; Natale, E. Search via parallel Levy walks on Z2. In Proceedings of the 2021 ACM Symposium on Principles of Distributed Computing, Virtual, 26–30 July 2021; pp. 81–91. [Google Scholar]
- Padash, A.; Sandev, T.; Kantz, H.; Metzler, R.; Chechkin, A.V. Asymmetric Levy flights are more efficient in random search. Fractal Fract. 2022, 6, 260. [Google Scholar] [CrossRef]
- Majumdar, S.N.; Mounaix, P.; Sabhapandit, S.; Schehr, G. Record statistics for random walks and Levy flights with resetting. J. Phys. A Math. Theor. 2021, 55, 034002. [Google Scholar] [CrossRef]
- Zbik, B.; Dybiec, B. Levy flights and Levy walks under stochastic resetting. Phys. Rev. E 2024, 109, 044147. [Google Scholar] [CrossRef]
- Radice, M.; Cristadoro, G. Optimizing leapover lengths of Levy flights with resetting. Phys. Rev. 2024, 110, L022103. [Google Scholar] [CrossRef] [PubMed]
- Xu, P.; Zhou, T.; Metzler, R.; Deng, W. Levy walk dynamics in an external harmonic potential. Phys. Rev. E 2020, 101, 062127. [Google Scholar] [CrossRef] [PubMed]
- Aghion, E.; Meyer, P.G.; Adlakha, V.; Kantz, H.; Bassler, K.E. Moses, Noah and Joseph effects in Levy walks. New J. Phys. 2021, 23, 023002. [Google Scholar] [CrossRef]
- Cleland, J.D.; Williams, M.A.K. Analytical Investigations into Anomalous Diffusion Driven by Stress Redistribution Events: Consequences of Levy Flights. Mathematics 2022, 10, 3235. [Google Scholar] [CrossRef]
- Mba, J.C.; Mwambi, S.M.; Pindza, E. A Monte Carlo Approach to Bitcoin Price Prediction with Fractional Ornstein–Uhlenbeck Levy Process. Forecasting 2022, 4, 409–419. [Google Scholar] [CrossRef]
- Mariani, M.C.; Asante, P.K.; Kubin, W.; Tweneboah, O.K. Data Analysis Using a Coupled System of Ornstein–Uhlenbeck Equations Driven by Levy Processes. Axioms 2022, 11, 160. [Google Scholar] [CrossRef]
- Barrera, G.; Hogele, M.A.; Pardo, J.C. Cutoff thermalization for Ornstein–Uhlenbeck systems with small Levy noise in the Wasserstein distance. J. Stat. Phys. 2021, 184, 27. [Google Scholar] [CrossRef]
- Zhang, X.; Shu, H.; Yi, H. Parameter Estimation for Ornstein–Uhlenbeck Driven by Ornstein–Uhlenbeck Processes with Small Levy Noises. J. Theor. Probab. 2023, 36, 78–98. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, X.; Deng, W. Langevin dynamics for a Levy walk with memory. Phys. Rev. E 2019, 99, 012135. [Google Scholar] [CrossRef] [PubMed]
- Barrera, G.; Hogele, M.A.; Pardo, J.C. The cutoff phenomenon in Wasserstein distance for nonlinear stable Langevin systems with small Levy noise. J. Dyn. Differ. Equ. 2024, 36, 251–278. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, J.; Zhang, M.-g. Exponential Contractivity and Propagation of Chaos for Langevin Dynamics of McKean-Vlasov Type with Levy Noises. Potential Anal. 2024, 1–34. [Google Scholar] [CrossRef]
- Bao, J.; Fang, R.; Wang, J. Exponential ergodicity of Levy driven Langevin dynamics with singular potentials. Stoch. Process. Their Appl. 2024, 172, 104341. [Google Scholar] [CrossRef]
- Wang, X.; Chen, Y.; Deng, W. Levy-walk-like Langevin dynamics. New J. Phys. 2019, 21, 013024. [Google Scholar] [CrossRef]
- Chen, Y.; Deng, W. Levy-walk-like Langevin dynamics affected by a time-dependent force. Phys. Rev. E 2021, 103, 012136. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, X.; Ge, M. Levy-walk-like Langevin dynamics with random parameters. Chaos Interdiscip. J. Nonlinear Sci. 2024, 34, 013109. [Google Scholar] [CrossRef]
- Cox, B.; Laufer, J.G.; Arridge, S.R.; Beard, P.C.; Laufer, A.J.G.; Arridge, A.S.R. Long Range Dependence: A Review; In Iowa State University: Ames, IA, USA, 1984. [Google Scholar]
- Doukhan, P.; Oppenheim, G.; Taqqu, M. (Eds.) Theory and Applications of Long-Range Dependence; Springer Science & Business Media: New York, NY, USA, 2002. [Google Scholar]
- Rangarajan, G.; Ding, M. (Eds.) Processes with Long-Range Correlations: Theory and Applications; Springer Science & Business Media: New York, NY, USA, 2003. [Google Scholar]
- Eliazar, I. How random is a random vector? Ann. Phys. 2015, 363, 164–184. [Google Scholar] [CrossRef]
- Eliazar, I. Five degrees of randomness. Phys. A Stat. Mech. Its Appl. 2021, 568, 125662. [Google Scholar] [CrossRef]
- Jelinek, F.; Mercer, R.L.; Bahl, L.R.; Baker, J.K. Perplexity: A measure of the difficulty of speech recognition tasks. J. Acoust. Soc. Am. 1977, 62, S63. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Bell, R.J.; Dean, P.; Hibbins-Butler, D.C. Localization of normal modes in vitreous silica, germania and beryllium fluoride. J. Phys. C Solid State Phys. 1970, 3, 2111. [Google Scholar] [CrossRef]
- Bell, R.J.; Dean, P. The structure of vitreous silica: Validity of the random network theory. Philos. Mag. 1972, 25, 1381–1398. [Google Scholar] [CrossRef]
- Bosyk, G.M.; Portesi, M.; Plastino, A. Collision entropy and optimal uncertainty. Phys. Rev. A 2012, 85, 012108. [Google Scholar] [CrossRef]
- Skorski, M. Shannon entropy versus renyi entropy from a cryptographic viewpoint. In Proceedings of the IMA International Conference on Cryptography and Coding, Oxford, UK, 15–17 December 2015; pp. 257–274. [Google Scholar]
- Simpson, E.H. Measurement of diversity. Nature 1949, 163, 688. [Google Scholar] [CrossRef]
- Hirschman, A.O. National Power and the Structure of Foreign Trade; University of Califorina Press: Berkeley, CA, USA, 1945. [Google Scholar]
- Hill, M.O. Diversity and evenness: A unifying notation and its consequences. Ecology 1973, 54, 427–432. [Google Scholar] [CrossRef]
- Peet, R.K. The measurement of species diversity. Annu. Rev. Ecol. Syst. 1974, 5, 285–307. [Google Scholar] [CrossRef]
- Magurran, A.E. Ecological Diversity and Its Measurement; Princeton University Press: Princeton, NJ, USA, 1988. [Google Scholar]
- Jost, L. Entropy and diversity. Oikos 2006, 113, 363–375. [Google Scholar] [CrossRef]
- Legendre, P.; Legendre, L. Numerical Ecology; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Renyi, A. On measures of information and entropy. In Proceedings of the 4th Berkeley Symposium on Mathematics, Statistics and Probability, Berkeley, CA, USA, 20–30 July 1960; Volume 1, pp. 547–561. [Google Scholar]
- Zolotarev, V.M. One-Dimensional Stable Distributions; American Mathematical Society: Providence, RI, USA, 1986; Volume 65. [Google Scholar]
- Borak, S.; Hardle, W.; Weron, R. Stable Distributions; Humboldt-Universitat zu Berlin: Berlin, Germany, 2005. [Google Scholar]
- Nolan, J.P. Univariate Stable Distributions; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Brownrigg, D.R.K. The weighted median filter. Commun. ACM 1984, 27, 807–818. [Google Scholar] [CrossRef]
- Yin, L.; Yang, R.; Gabbouj, M.; Neuvo, Y. Weighted median filters: A tutorial. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 1996, 43, 157–192. [Google Scholar] [CrossRef]
- Justusson, B.I. Median filtering: Statistical properties. In Two-Dimensional Digital Signal Prcessing II: Transforms and Median Filters; Springer: Berlin/Heidelberg, Germany, 2006; pp. 161–196. [Google Scholar]
- Bentes, S.R.; Menezes, R. Entropy: A new measure of stock market volatility? J. Phys. Conf. Ser. 2012, 394, 012033. [Google Scholar] [CrossRef]
- Bose, R.; Hamacher, K. Alternate entropy measure for assessing volatility in financial markets. Phys. Rev. E- Nonlinear Soft Matter Phys. 2012, 86, 056112. [Google Scholar] [CrossRef]
- Ruiz, M.d.C.; Guillamon, A.; Gabaldon, A. A new approach to measure volatility in energy markets. Entropy 2012, 14, 74–91. [Google Scholar] [CrossRef]
| Ratio | Levy Approach | Gauss Approach |
|---|---|---|
| Signal-to-noise | increasing | |
| Noise-to-noise | decreasing | |
| Tail-to-tail | zero |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eliazar, I. Levy Noise Affects Ornstein–Uhlenbeck Memory. Entropy 2025, 27, 157. https://doi.org/10.3390/e27020157
Eliazar I. Levy Noise Affects Ornstein–Uhlenbeck Memory. Entropy. 2025; 27(2):157. https://doi.org/10.3390/e27020157
Chicago/Turabian StyleEliazar, Iddo. 2025. "Levy Noise Affects Ornstein–Uhlenbeck Memory" Entropy 27, no. 2: 157. https://doi.org/10.3390/e27020157
APA StyleEliazar, I. (2025). Levy Noise Affects Ornstein–Uhlenbeck Memory. Entropy, 27(2), 157. https://doi.org/10.3390/e27020157





