Probability via Expectation Measures
Abstract
1. Introduction
1.1. Organization of the Paper
1.2. Terminology
2. Probability Theory Since Kolmogorov
2.1. Kolmogorov’s Contribution
2.2. Probabilities or Expectations?
2.3. Probability Theory and Category Theory
- For any fixed the mappingis measurable.
- For every fixed , the mappingis a measure on .

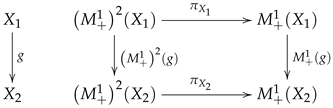
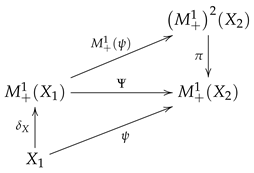

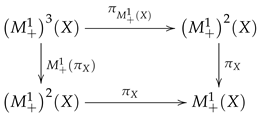
2.4. Preliminaries on Point Processes
- For all the measure is locally finite.
- For all bounded sets the random variable is a count variable.
2.5. Poisson Distributions and Poisson Point Processes
- For all , the random variable is Poisson distributed with mean value .
- If are disjoint, then the random variables and are independent.
2.6. Valuations
- Strictness .
- Monotonicity For all subsets , implies .
- Modularity For all subsets ,
- Continuity for any directed net .
3. Observations
3.1. Observations as Multiset Classifications
3.2. Observations as Empirical Measures
- Addition.
- Restriction.
- Inducing.
3.3. Categorical Properties of the Empirical Measures and Some Generalizations
3.4. Lossless Compression of Data
3.5. Lossy Compression of Data
4. Expectations
4.1. Simple Expectation Measures
- There are many ways of writing t as a product where and n is an integer.
- There are many different sampling schemes that will lead to a multiplication be .
- There are many ways of generating the randomness that is needed to perform the sampling.
4.2. Categorical Properties of the Expectation Measures and Some Generalizations
4.3. The Poisson Interpretation
- is Poisson distributed for any open set B.
- For any open sets the random variable is independent of the random variable given the random variable if and only if .
4.4. Normalization, Conditioning, and Other Operations on Expectation Measures
4.5. Independence
4.6. Information Divergence for Expectation Measures
- with equality when
- is minimal when
- for all
5. Applications
5.1. Goodness-of-Fit Tests
5.2. Improper Prior Distributions
5.3. Markov Chains
5.4. Inequalities for Information Projections
6. Discussion and Conclusions
| Probability theory | Expectation theory |
| Probability | Expected value |
| Outcome | Instance |
| Outcome space | Multiset monad |
| P-value | E-Value |
| Probability measure | Expectation measure |
| Binomial distribution | Poisson distribution |
| Density | Intensity |
| Bernoulli random variable | Count variable |
| Empirical distribution | Empirical measure |
| KL-divergence | Information divergence |
| Uniform distribution | Poisson point process |
| State space | State cone |
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| bin | Binomial distribution |
| DCC | Descending chain condition |
| E-statistic | Evidence statistic |
| E-value | Observed value of an E-statistic |
| hyp | Hypergeometric distribution |
| IID | Independent identically distributed |
| KL-divergence | Information divergence restricted to probability measures |
| MDL | Minimum description length |
| Mset | Multiset |
| N | Gaussian distribution |
| PM | Probability measure |
| Po | Poisson distribution |
| mset | Multiset |
| Poset | Partially ordered set |
| Pr | Probability |
References
- Kolmogorov, A.N. Grundbegriffe der Wahrscheinlichkeitsrechnung; Springer: Berlin, Germany, 1933. [Google Scholar]
- Lardy, T.; Grünwald, P.; Harremoës, P. Reverse Information Projections and Optimal E-statistics. IEEE Trans. Inf. Theory 2024, 70, 7616–7631. [Google Scholar] [CrossRef]
- Perrone, P. Categorical Probability and Stochastic Dominance in Metric Spaces. Ph.D. Thesis, Max Planck, Institute for Mathematics in the Sciences, Leipzig, Germany, 2018. [Google Scholar]
- nLab Authors. Monads of Probability, Measures, and Valuations. Available online: https://ncatlab.org/nlab/show/monads+of+probability%2C+measures%2C+and+valuations (accessed on 20 October 2024).
- Shiryaev, A.N. Probability; Springer: New York, NY, USA, 1996. [Google Scholar]
- Whittle, P. Probability via Expectation, 3rd ed.; Springer Texts in Statistics; Springer: New York, NY, USA, 1992. [Google Scholar]
- Kallenberg, O. Random Measures; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Lawvere. The Category of Probabilistic Mappings, 1962. Lecture Notes. Available online: https://github.com/mattearnshaw/lawvere/blob/master/pdfs/1962-the-category-of-probabilistic-mappings.pdf (accessed on 20 October 2024).
- Scibior, A.; Ghahramani, Z.; Gordon, A.D. Practical probabilistic programming with monads. In Proceedings of the 2015 ACM SIGPLAN Symposium on Haskell, Vancouver, BC, Canada, 3–4 September 2015; pp. 165–176. [Google Scholar]
- Giry, M. A categorical approach to probability theory. In Categorical Aspects of Topology and Analysis; Banaschewski, B., Ed.; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1982; Volume 915, pp. 68–85. [Google Scholar]
- Lieshout, M.V. Spatial Point Process Theory. In Handbook of Spatial Statistics; Handbooks of Modern Statistical Methods; Chapman and Hall: London, UK, 2010; Chapter 16. [Google Scholar]
- Dash, S.; Staton, S. A Monad for Probabilistic Point Processes. Available online: https://arxiv.org/abs/2101.10479 (accessed on 20 October 2024).
- Jacobs, B. From Multisets over Distributions to Distributions over Multisets. In Proceedings of the 36th Annual ACM/IEEE Symposium on Logic in Computer Science, Rome, Italy, 29 June–2 July 2021; pp. 1–13. [Google Scholar]
- Last, G.; Penrose, M. Lectures on the Poisson Process; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Rényi, A. A characterization of Poisson processes. Magy. Tud. Akad. Mat. Kutaló Int. Közl. 1956, 1, 519–527. [Google Scholar]
- Kallenberg, O. Limits of Compound and Thinned Point Processes. J. Appl. Probab. 2016, 12, 269–278. [Google Scholar] [CrossRef]
- nLab Authors. Valuation (Measure Theory). Available online: https://ncatlab.org/nlab/show/valuation+%28measure+theory%29 (accessed on 20 October 2024).
- Heckmann, R. Spaces of valuations. In Papers on General Topology and Applications; Academy of Sciences: New York, NY, USA, 1996. [Google Scholar]
- Blizard, W.D. The development of multiset theory. Mod. Log. 1991, 1, 319–352. [Google Scholar]
- Monro, G.P. The Concept of Multiset. Math. Log. Q. 1987, 33, 171–178. [Google Scholar] [CrossRef]
- Isah, A.; Teella, Y. The Concept of Multiset Category. Br. J. Math. Comput. Sci. 2015, 9, 427–437. [Google Scholar] [CrossRef]
- Grätzer, G. Lattice Theory; Dover: Downers Grove, IL, USA, 1971. [Google Scholar]
- Wille, R. Formal Concept Analysis as Mathematical Theory. In Formal Concept Analysis; Ganter, B., Stumme, G., Wille, R., Eds.; Number 3626 in Lecture Notes in Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2005; pp. 1–33. [Google Scholar]
- Topsøe, F. Compactness in Space of Measures. Stud. Math. 1970, 36, 195–212. [Google Scholar] [CrossRef]
- Alvarez-Manilla, M. Extension of valuations on locally compact sober spaces. Topol. Appl. 2002, 124, 397–433. [Google Scholar] [CrossRef]
- Harremoës, P. Extendable MDL. In Proceedings of the 2013 IEEE International Symposium on Information Theory, Istanbul, Turkey, 7–12 July 2013; pp. 1516–1520. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: Hoboken, NJ, USA, 1991. [Google Scholar]
- Csiszár, I. The Method of Types. IEEE Trans. Inform. Theory 1998, 44, 2505–2523. [Google Scholar] [CrossRef]
- Harremoës, P. Rate Distortion Theory for Descriptive Statistics. Entropy 2023, 25, 456. [Google Scholar] [CrossRef] [PubMed]
- Rényi, A. On an Extremal Property of the Poisson Process. Ann. Inst. Stat. Math. 1964, 16, 129–133. [Google Scholar] [CrossRef]
- McFadden, J.A. The Entropy of a Point Process. J. Soc. Indst. Appl. Math. 1965, 13, 988–994. [Google Scholar] [CrossRef]
- Harremoës, P. Binomial and Poisson Distributions as Maximum Entropy Distributions. IEEE Trans. Inform. Theory 2001, 47, 2039–2041. [Google Scholar] [CrossRef]
- Harremoës, P.; Johnson, O.; Kontoyiannis, I. Thinning, Entropy and the Law of Thin Numbers. IEEE Trans. Inf. Theory 2010, 56, 4228–4244. [Google Scholar] [CrossRef]
- Hillion, E.; Johnson, O. A proof of the Shepp-Olkin entropy concavity conjecture. Bernoulli 2017, 23, 3638–3649. [Google Scholar] [CrossRef]
- Dawid, A.P. Separoids: A mathematical framework for conditional independence and irrelevance. Ann. Math. Artif. Intell. 2001, 32, 335–372. [Google Scholar] [CrossRef]
- Harremoës, P. Entropy inequalities for Lattices. Entropy 2018, 20, 748. [Google Scholar] [CrossRef] [PubMed]
- Leskelä, L. Information Divergences and Likelihood Ratios of Poisson Processes and Point Patterns. IEEE Trans. Inform. Theory 2024, 70, 9084–9101. [Google Scholar] [CrossRef]
- Harremoës, P. Divergence and Sufficiency for Convex Optimization. Entropy 2017, 19, 206. [Google Scholar] [CrossRef]
- Csiszár, I. I-Divergence Geometry of Probability Distributions and Minimization Problems. Ann. Probab. 1975, 3, 146–158. [Google Scholar] [CrossRef]
- Pfaffelhuber, E. Minimax Information Gain and Minimum Discrimination Principle. In Colloquia Mathematica Societatis János Bolyai; Proceedings of the Topics in Information Theory; Csiszár, I., Elias, P., Eds.; János Bolyai Mathematical Society: Budapest, Hungary; North-Holland: Amsterdam, The Netherlands, 1977; Volume 16, pp. 493–519. [Google Scholar]
- Topsøe, F. Information Theoretical Optimization Techniques. Kybernetika 1979, 15, 8–27. [Google Scholar]
- Csiszár, I.; Tusnády, G. Information Geometry and Alternating Minimization Procedures. Stat. Decis. 1984, 1, 205–237. [Google Scholar]
- Li, J.Q. Estimation of Mixture Models. Ph.D. Dissertation, Department of Statistics, Yale University, New Haven, CT, USA, 1999. [Google Scholar]
- Li, J.Q.; Barron, A.R. Mixture Density Estimation. In Proceedings of the Conference on Neural Information Processing Systems: Natural and Synthetic, Cenver, CO, USA, 29 November–4 December 1999. [Google Scholar]
- Harremoës, P. Bounds on tail probabilities for negative binomial distributions. Kybernetika 2016, 52, 943–966. [Google Scholar] [CrossRef][Green Version]
- Harremoës, P.; Tusnády, G. Information Divergence is more χ2-distributed than the χ2-statistic. In Proceedings of the 2012 IEEE International Symposium on Information Theory, IEEE, Cambridge, MA, USA, 1–6 July 2012; pp. 538–543. [Google Scholar]
- Kass, R.E.; Wasserman, L.A. The Selection of Prior Distributions by Formal Rules. J. Am. Stat. Assoc. 1996, 91, 1343–1370. [Google Scholar] [CrossRef]
- Grünwald, P. The Minimum Description Length Principle; MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Harremoës, P. Entropy on Spin Factors. In Springer Proceedings in Mathematics & Statistics; Proceedings of the Information Geometry and Its Applications; Ay, N., Gibilisco, P., Matúš, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; Volume 252, pp. 247–278. [Google Scholar]
- Harremoës, P.; Matúš, F. Bounds on the Information Divergence for Hypergeometric Distributions. Kybernetika 2020, 56, 1111–1132. [Google Scholar] [CrossRef]
- Harremoës, P.; Ruzankin, P. Rate of Convergence to Poisson Law in Terms of Information Divergence. IEEE Trans. Inf. Theory 2004, 50, 2145–2149. [Google Scholar] [CrossRef]
- Kontoyiannis, I.; Harremoës, P.; Johnson, O. Entropy and the Law of Small Numbers. IEEE Trans. Inform. Theory 2005, 51, 466–472. [Google Scholar] [CrossRef]
- Harremoës, P. Lower Bounds for Divergence in the Central Limit Theorem. In General Theory of Information Transfer and Combinatorics; Springer: Berlin/Heidelberg, Germany, 2006; pp. 578–594. [Google Scholar]
- Harremoës, P. Maximum Entropy on Compact groups. Entropy 2009, 11, 222–237. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harremoës, P. Probability via Expectation Measures. Entropy 2025, 27, 102. https://doi.org/10.3390/e27020102
Harremoës P. Probability via Expectation Measures. Entropy. 2025; 27(2):102. https://doi.org/10.3390/e27020102
Chicago/Turabian StyleHarremoës, Peter. 2025. "Probability via Expectation Measures" Entropy 27, no. 2: 102. https://doi.org/10.3390/e27020102
APA StyleHarremoës, P. (2025). Probability via Expectation Measures. Entropy, 27(2), 102. https://doi.org/10.3390/e27020102





