An Intelligent Bearing Fault Transfer Diagnosis Method Based on Improved Domain Adaption
Abstract
1. Introduction
- (1)
- At present, in the field of cross-domain fault diagnosis, the adversarial-based diagnosis method classifies the target domain samples by adding a domain classifier after the feature extraction network. Ganin et al. proposed a domain adversarial neural network (DANN) and trained the network through a gradient reversal layer [26]. Wang et al. introduced DANN into the bearing fault diagnosis to achieve the purpose of completing the diagnosis under the transfer task of different loads [27]. It was also verified that DANN can provide competitive results in the limited available training time [27]. Li et al. constructed a new deep convolutional residual feature network to extract features and used the source domain labeled samples and the target domain unlabeled samples for domain adversarial training to improve the transmission performance of the diagnostic model [28]. The above methods can effectively reduce the training time by using domain classifiers to train on samples in the source domain and target domain, but this method lacks the representation of the feature information of the input domain and will have the defect of single network feature extraction.
- (2)
- In cross-domain fault diagnosis, the diagnostic method based on distribution discrepancy metrics uses MMD to reduce the difference in feature distribution between samples in the source domain and the target domain. For example, by employing a single kernel MMD as a domain distance loss, Tzeng et al. proposed the deep domain confusion model (DDC) to obtain the discrepancy of the features which are, respectively, learned from the source domain and target-domain at the highest layer of the feature extraction networks [29]. To reduce distribution discrepancy and inter-class distance of transferable features learned by the network, Lei et al. construct FTNN to minimize multi-layer and multi-kernel MMD (ML-MK MMD) between source domain and target domain, leading to learning transferable features more efficiently [30]. Although it achieves some degree of transfer learning ability, the DDC suffers the drawback of merely learning single layer feature related to fault data. ML-MK MMD with better domain adaptive ability may be an option for handling this problem.
- (3)
- To solve the problems of domain shift and single extracted features, related researchers combined MMD with domain classifier loss. Guo et al. proposed a Deep Convolutional Transfer Learning Network (DCTLN)-based approach that combines a single-kernel MMD with domain classifier loss to construct a new loss function that maximizes domain-invariant features across domains by training the network [31]. Yao et al. constructed a pair of pseudo-Siamese feature extractors by constructing two network-based feature extractors with the same structure but unshared parameters, and combined MMD and unbalanced adversarial training algorithms to train a domain adaptive network to accomplish cross-domain fault diagnosis [32]. However, the above methods only use the combination of single-layer MMD and domain classifier loss to construct a new loss function to train the network. This method only calculates the MMD of the highest layer of the network but ignores the discrepancy in the feature distribution of other layers in the network, which leads to the problem that the extracted high-level features in the network are insufficient. In conclusion, the first problem in the above methods is the insufficient extraction of features by the feature transfer network. The second problem is that there is a discrepancy in the cross-domain sample distribution. To address the aforementioned challenges, Fast Fourier Transform (FFT) is initially employed to preprocess the input signal and extract its frequency-domain features. Subsequently, the multi-layer multi-kernel maximum mean discrepancy (ML-MK MMD) is utilized to quantify the distributional differences in features between the source and target domain samples. This approach enables the feature extraction network to thoroughly extract maximal domain-invariant features. To further reduce the feature distribution discrepancy between the source and target domains, the ML-MK MMD is integrated with a domain classifier loss during training to construct a novel loss function. This new loss function is used to train the network, effectively minimizing the discrepancy in feature distributions between the source and target domains.
2. Theoretical Background
2.1. Transfer Learning
- (1)
- The source and target domains are related but exhibit distinct data distributions.
- (2)
- The fault diagnosis tasks remain consistent across domains, with shared class labels.
- (3)
- Labeled data from the source domain are utilized to train the network model.
- (4)
- Unlabeled data from the target domain are employed for both training and testing of the network model.
2.2. Question Description
- An unavoidable domain shift exists between the source and target domains, resulting in a distribution discrepancy that must be addressed, and most of the existing methods choose to add a domain classifier to reduce the domain distribution discrepancy; however, this method lacks an adequate feature representation of the input signals, which will lead to poor cross-domain diagnosis ability and poor generalization performance of the trained diagnostic model.
- In terms of feature extraction, most of the existing methods use a single-layer, single-kernel MMD, and the use of this method to train the network will lead to the network having the defect of insufficiently extracting features and not being able to adequately extract cross-domain maximized domain-invariant features. To address the aforementioned challenges, an enhanced domain adaptation method for cross-domain fault diagnosis is introduced. To overcome the limitation of single feature extraction, ML-MK MMD is utilized to measure the distribution discrepancy between the source and target domains. Furthermore, a feature extraction network is designed to extract comprehensive domain-invariant features. To mitigate the domain shift issue, a novel loss function is formulated by integrating ML-MK MMD with the domain classifier loss. This strategy effectively optimizes the objective function, reducing the distribution discrepancy between the source and target domain samples, and ultimately enabling accurate cross-domain fault diagnosis.
2.3. Maximum Mean Discrepancy (MMD)
- (1)
- Universal approximation property: Gaussian kernels are universal kernels [26], meaning that the RKHS they induce is dense in the space of continuous functions. This ensures that MMD with Gaussian kernels can distinguish between any two different probability distributions, making it a powerful metric for detecting distribution discrepancies.
- (2)
- Smoothness and differentiability: Gaussian kernels are infinitely differentiable, which is crucial for gradient-based optimization during neural network training.
- (3)
- Interpretable bandwidth parameter: The bandwidth σ controls the scale at which distribution differences are measured. Small bandwidths capture local differences, while large bandwidths capture global distributional shifts. Since some MMDs with different kernels are employed to act on RHKS, Gaussian kernels with distinct bandwidth parameters are selected as the feature kernels for MMD.
3. Proposed Method
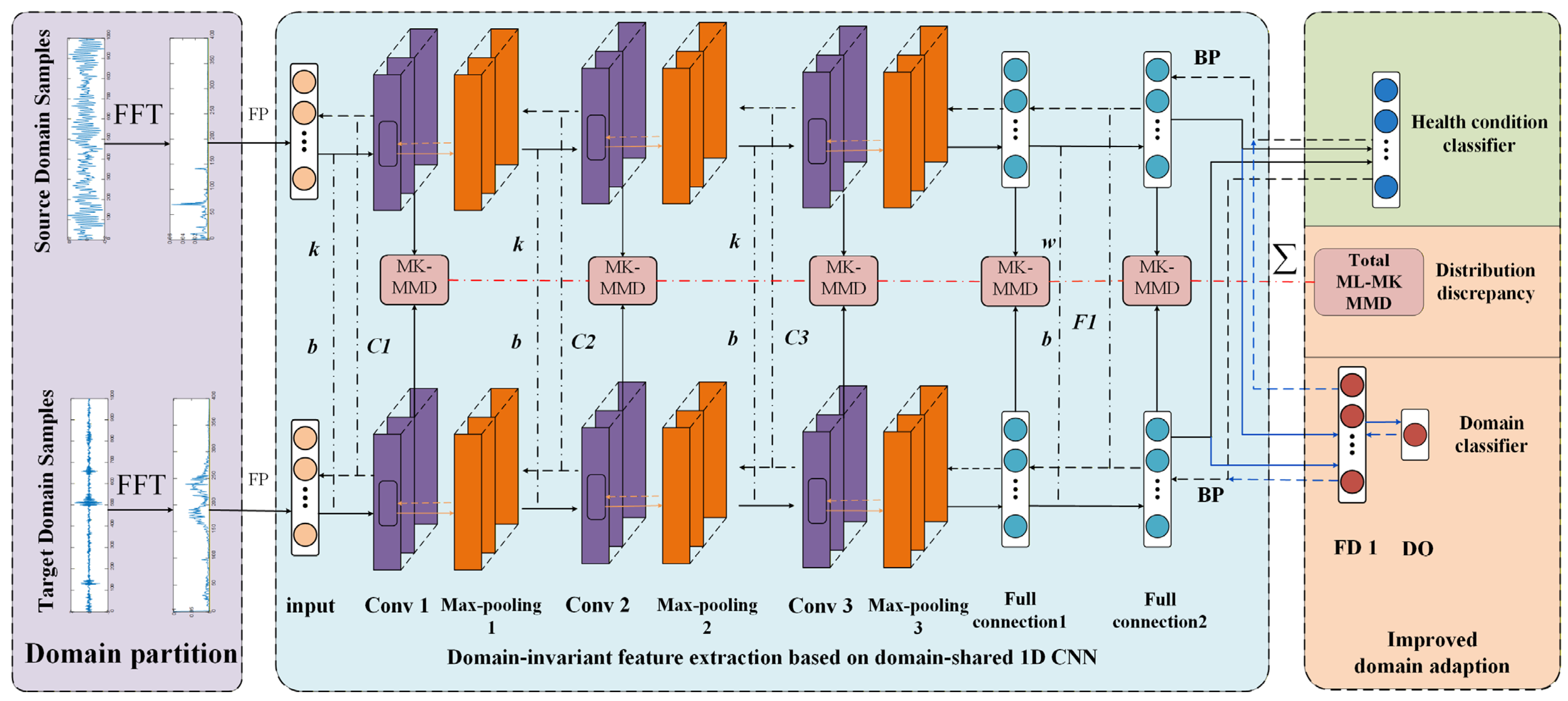
3.1. Framework
3.1.1. Domain Partition Module
3.1.2. Feature Extraction Module
3.1.3. Domain Classification Module
- (1)
- Domain discrimination: The classifier attempts to distinguish whether an input sample originates from the source domain (label = 0) or the target domain (label = 1) based on the learned features.
- (2)
- Adversarial feature learning: Through the Gradient Reversal Layer (GRL) mechanism, the domain classifier engages in adversarial training with the feature extractor. Specifically, the domain classifier tries to correctly classify domain labels (minimize its classification error). The feature extractor tries to fool the domain classifier (produce features that make domain classification difficult). When the domain classifier cannot accurately distinguish between source and target domain samples, this indicates that the feature extractor has successfully learned domain-invariant features. These domain-invariant features contain information relevant to fault types while being insensitive to domain shifts caused by different operating conditions.
3.1.4. Improvement of the Domain Adaptive Module
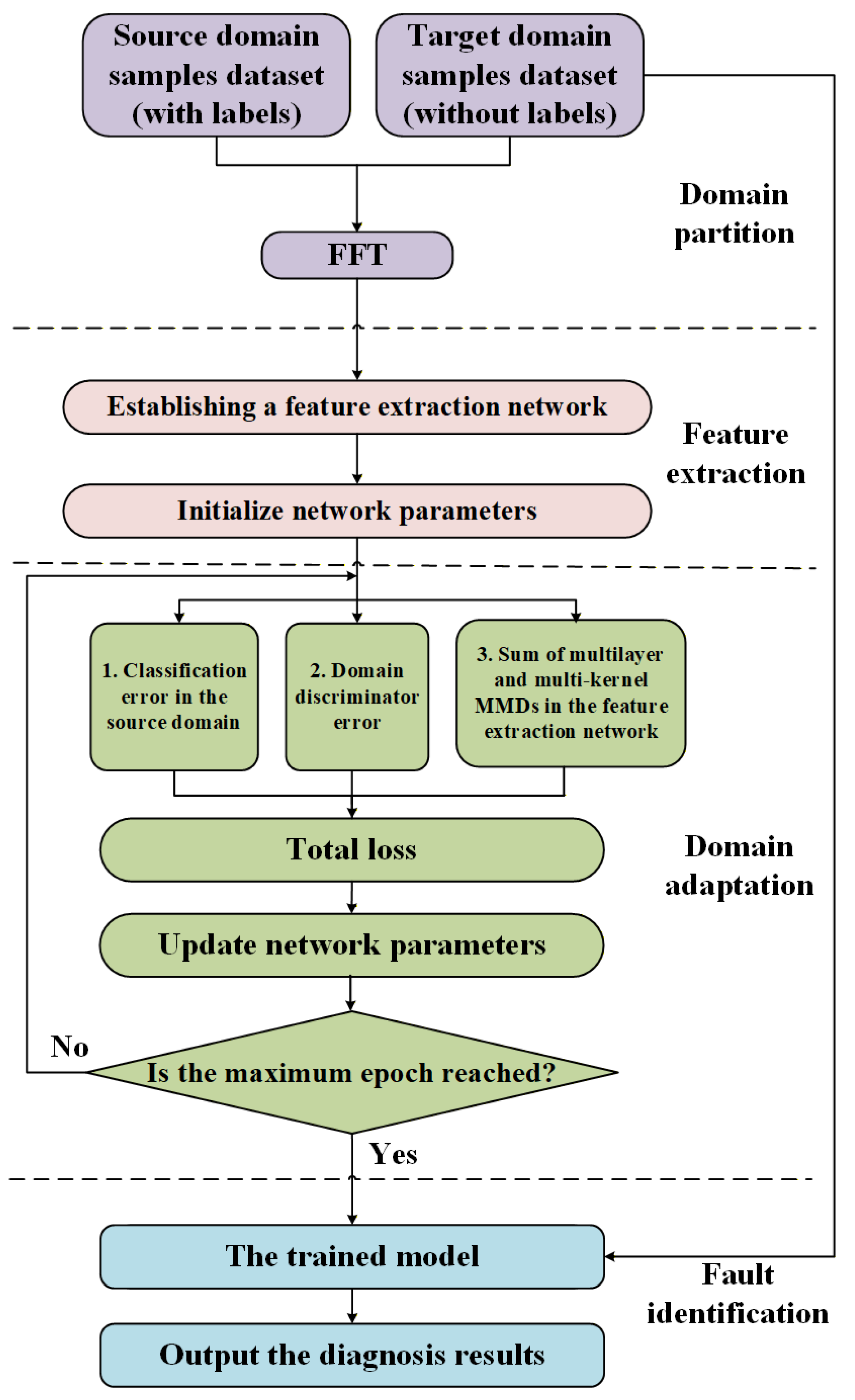
3.2. Optimization Objective
- (1)
- Minimize the fault classification loss Lc for labeled samples in the source domain (Equation (11)). This loss is only computed on source domain samples because only they have fault labels.
- (2)
- Maximize the domain classification loss Ld for samples from both source and target domains (Equations (12) and (13)). This loss uses domain labels (source/target) rather than fault labels and can be computed for both domains.
- (3)
- Minimize multilayer MMD for transferable features learned from both source and target domain datasets (Equation (10)). This is a distribution-based metric that does not require labels.
3.2.1. Classification Loss
3.2.2. Domain Classification Loss
3.2.3. ML-MK MMD Loss and Total Loss Function
3.3. Training Process
4. Experiment
4.1. Dataset Introduction
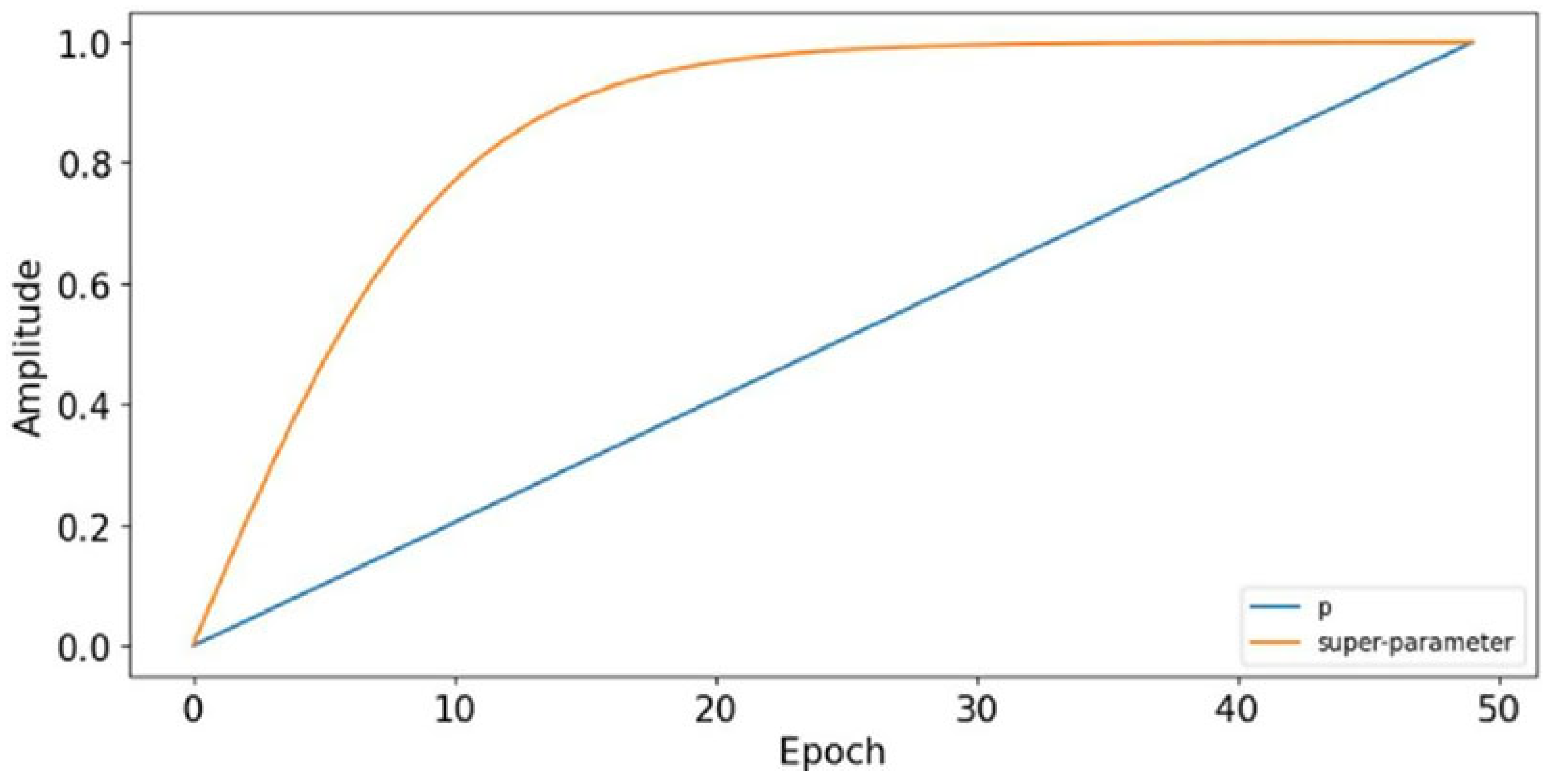
4.2. Parameters Selection
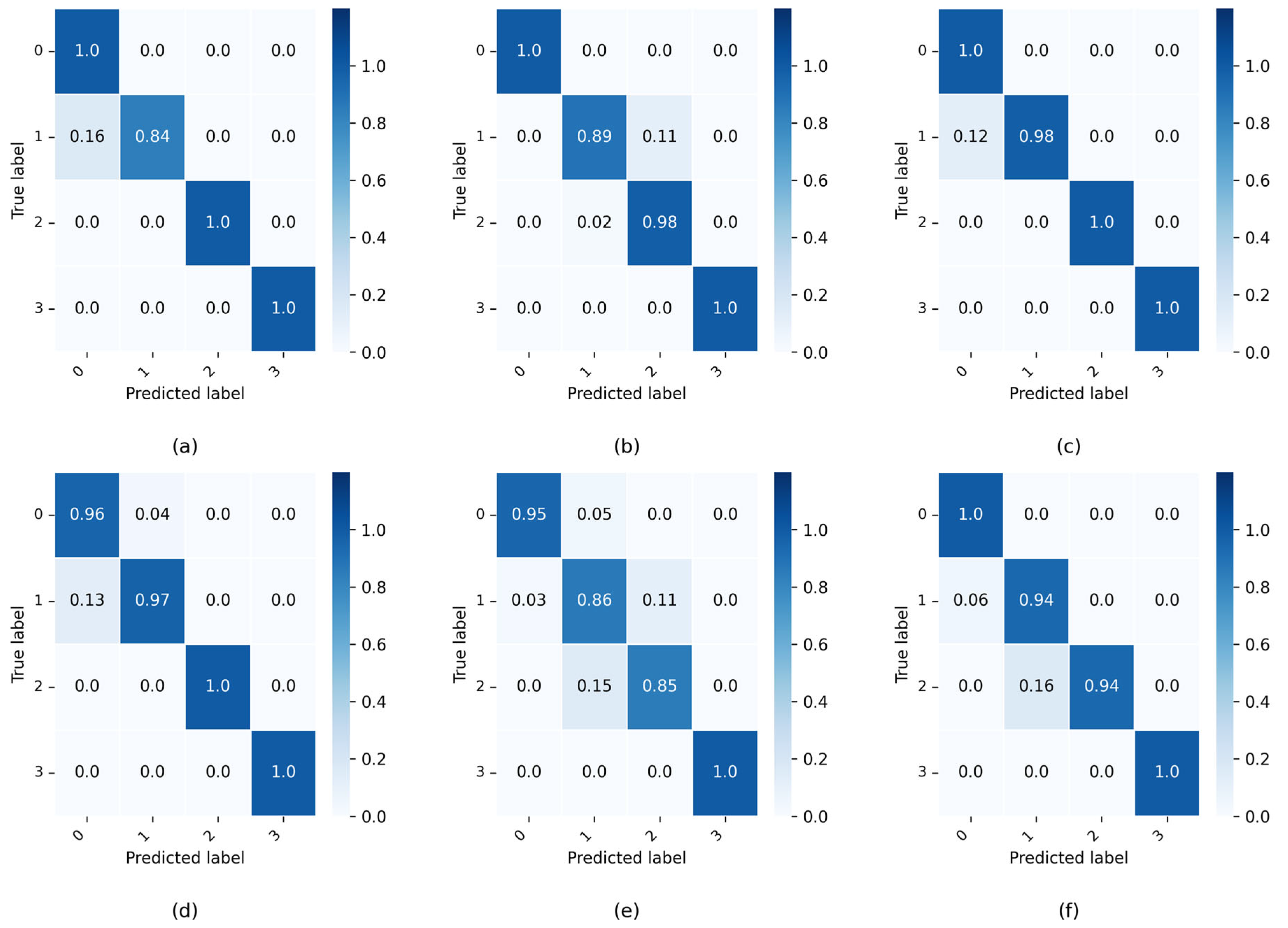
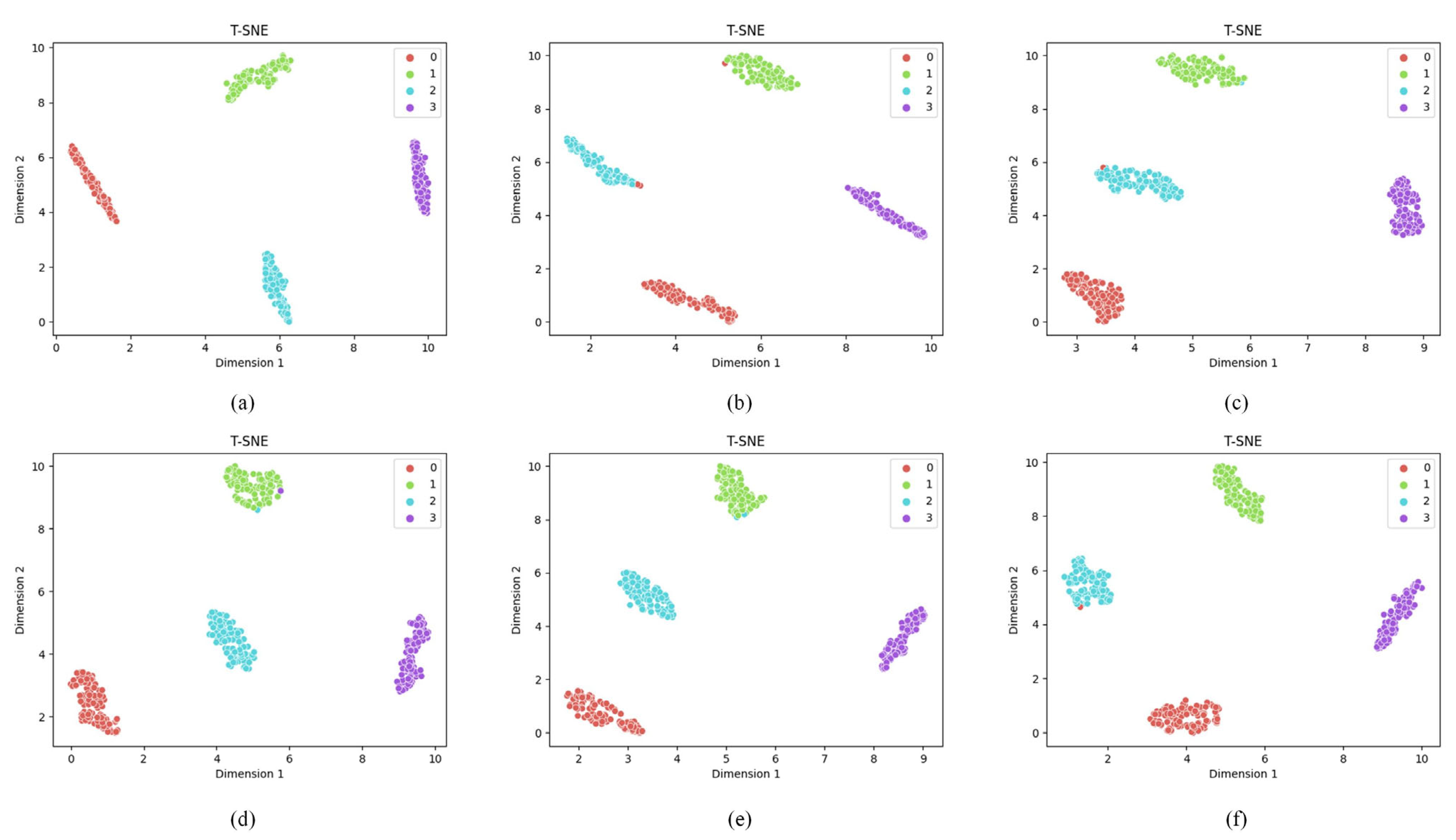
4.3. Results
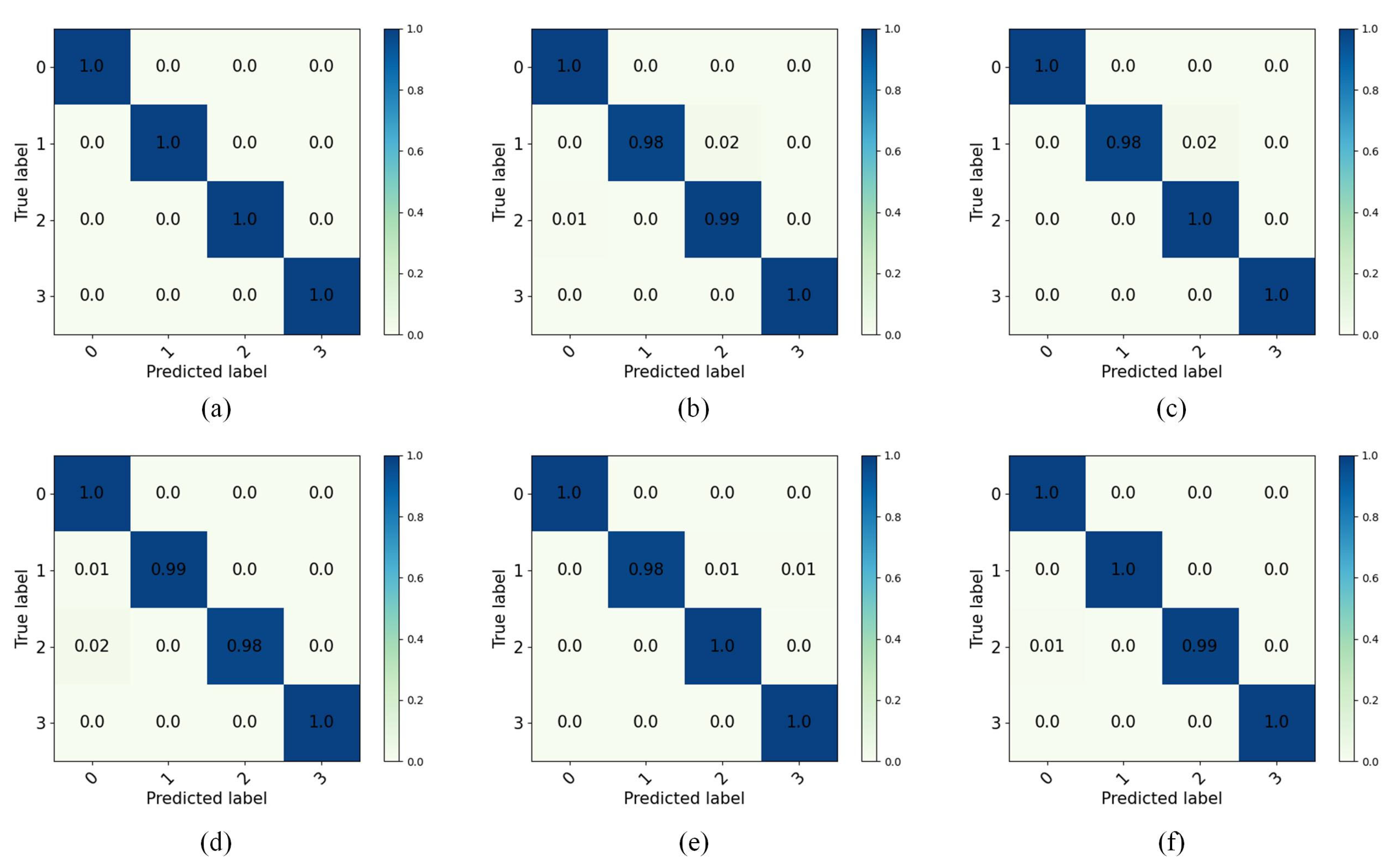
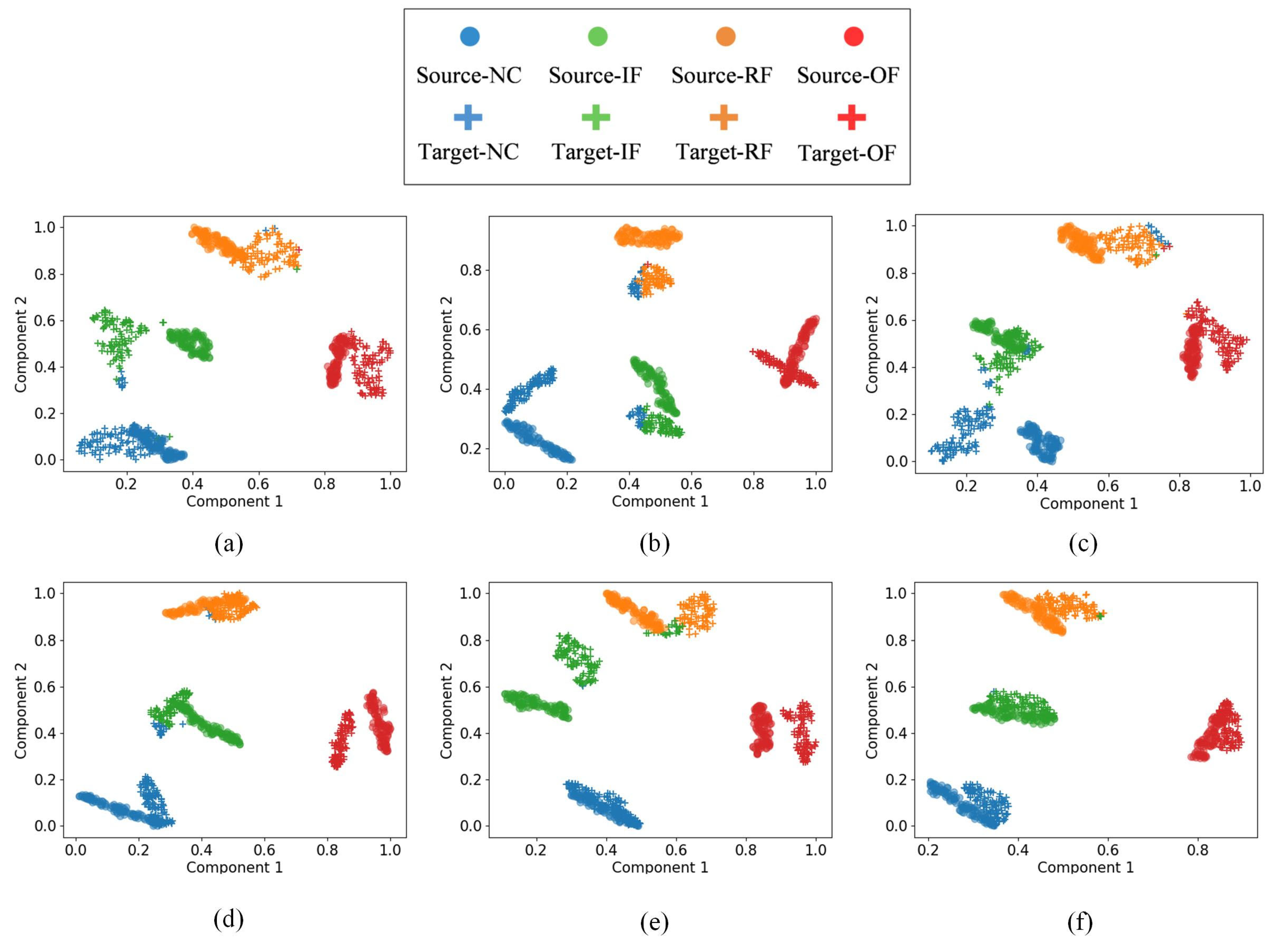
- (a)
- Task A→B: The feature distributions show excellent clustering with clear separation between all four fault classes (NC, IF, BF, OF). The clusters are compact and well-separated, indicating perfect domain adaptation, which is consistent with the 100% accuracy shown in Figure 5a. This task demonstrates the best transfer performance among all scenarios.
- (b)
- Task A→C: The visualization reveals good overall clustering, with NC and BF forming distinct, well-separated clusters. However, slight overlap is observed between IF (class 1, red points) and OF (class 3, purple points) in the feature space, explaining the minor misclassifications observed in the confusion matrix. Despite this, the majority of samples remain correctly clustered.
- (c)
- Task B→C: Similar to Task A→C, this scenario shows clear separation for NC and BF, while a small number of IF and OF samples exhibit proximity in the feature space, leading to occasional misclassifications. The overall clustering structure remains intact, indicating effective but not perfect domain adaptation.
- (d)
- Task B→A: The t-SNE plot demonstrates good clustering quality for NC and OF, with both classes forming tight, well-separated clusters. However, some IF and BF samples show partial overlap, resulting in minor misclassifications. The majority of samples from each class remain correctly grouped.
- (e)
- Task C→A: This task shows moderate clustering performance. While NC maintains clear separation from other classes, there is noticeable overlap between IF, BF, and OF in certain regions of the feature space. This explains the slightly lower accuracy compared to Task A→B, though the model still achieves acceptable classification performance.
- (f)
- Task C→B: The visualization indicates good separation for NC and reasonable clustering for other fault types. Some IF and OF samples appear close in the feature space, consistent with the minor misclassifications observed in the confusion matrix.
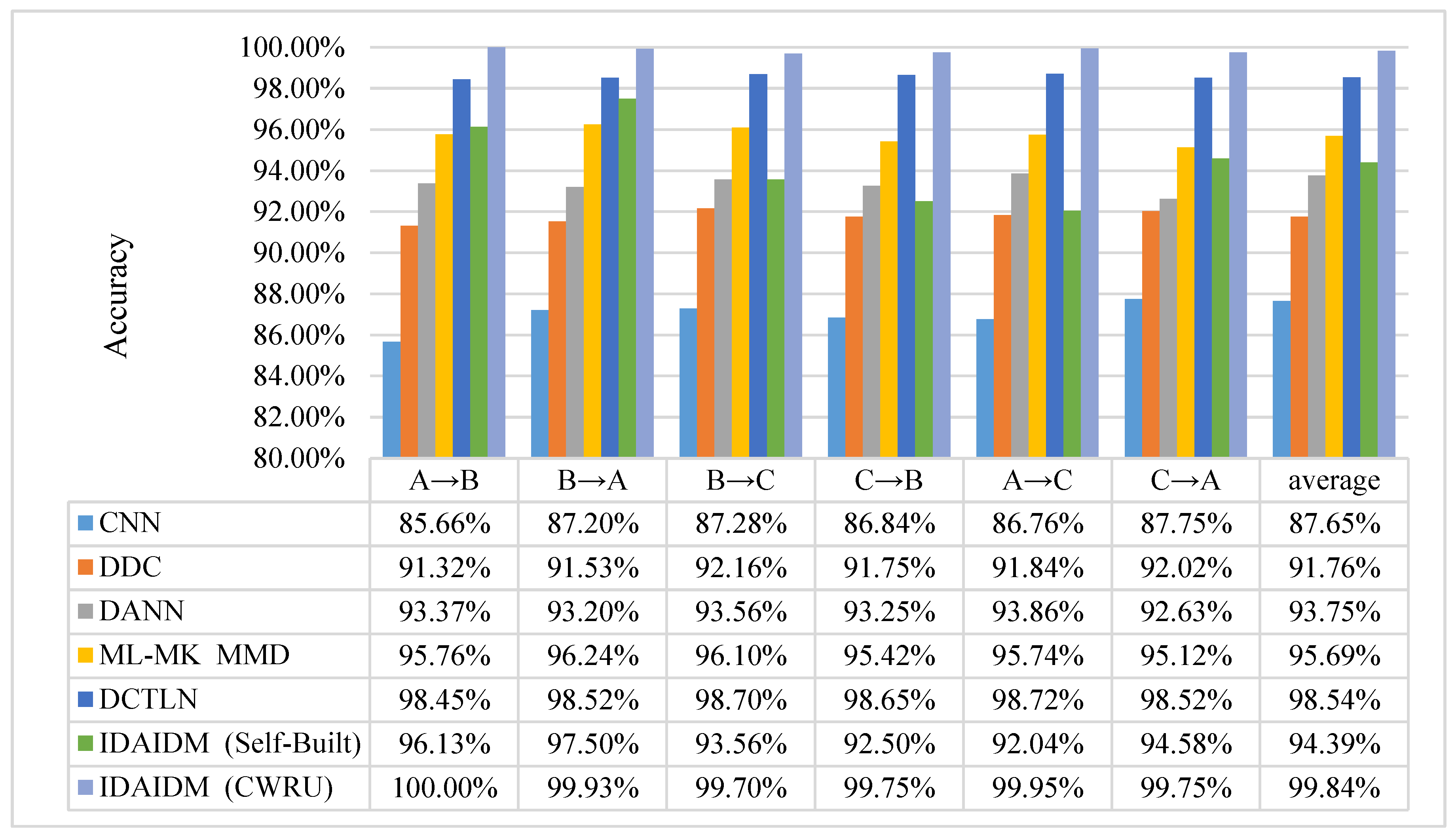
4.4. Comparisons with Other Methods
5. Conclusions
- (1)
- IDAIDM achieved an average diagnostic accuracy of 99.84% across six different cross-domain transfer tasks (A→B, A→C, B→A, B→C, C→A, C→B), significantly outperforming five baseline methods including CNN (87.65%), DDC (91.76%), DANN (93.75%), ML-MK MMD (95.69%), and DCTLN (98.54%).
- (2)
- The t-SNE visualizations confirm that IDAIDM successfully learns features with smaller intra-class distances and larger inter-class distances, indicating effective extraction of domain-invariant and discriminative features.
- (3)
- The combination of ML-MK MMD with adversarial training through the domain classifier provides complementary benefits: MMD explicitly minimizes distribution discrepancy through feature statistics, while the domain classifier implicitly learns domain-invariant representations through adversarial training.
- (1)
- validating the method on more complex industrial datasets with greater variability in operating conditions and noise levels.
- (2)
- investigating the integration of more advanced signal processing techniques, such as envelope analysis, with the domain adaptation framework.
- (3)
- extending the method to handle scenarios with different fault types between source and target domains (partial domain adaptation).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Glowacz, A.; Glowacz, W.; Glowacz, Z.; Kozik, J. Early fault diagnosis of bearing and stator faults of the single-phase induction motor using acoustic signals. Measurement 2018, 113, 1–9. [Google Scholar] [CrossRef]
- Sun, R.B.; Yang, Z.B.; Gryllias, K.; Chen, X.F. Sparse representation based on parametric impulsive dictionary design for bearing fault diagnosis. J. Sound Vib. 2020, 471, 115175. [Google Scholar] [CrossRef]
- Yan, X.; She, D.; Xu, Y.; Jia, M. Deep regularized variational autoencoder for intelligent fault diagnosis of rotor–bearing system within entire life-cycle process. Entropy 2021, 23, 1372. [Google Scholar] [CrossRef]
- Li, Z.; Jiang, Y.; Hu, C.; Peng, Z. Recent progress on decoupling diagnosis of hybrid failures in gear transmission systems using vibration sensor signal: A review. Measurement 2016, 90, 4–19. [Google Scholar] [CrossRef]
- Sun, J.; Wen, J.; Yuan, C.; Liu, Z.; Xiao, Q. Bearing fault diagnosis based on multiple transformation domain fusion and improved residual dense networks. IEEE Sens. J. 2021, 22, 1541–1551. [Google Scholar] [CrossRef]
- Kumar, A.; Gandhi, C.; Zhou, Y.; Kumar, R.; Xiang, J. Latest developments in gear defect diagnosis and prognosis: A review. Measurement 2020, 158, 107735. [Google Scholar] [CrossRef]
- Xiao, Q.; Li, S.; Zhou, L.; Shi, W. Improved variational mode decomposition and CNN for intelligent rotating machinery fault diagnosis. Entropy 2022, 24, 908. [Google Scholar] [CrossRef]
- Zhang, W.; Peng, G.; Li, C.; Chen, Y.; Zhang, Z. A new deep learning model for fault diagnosis with good anti-noise and domain adaptation ability on raw vibration signals. Sensors 2017, 17, 425. [Google Scholar] [CrossRef] [PubMed]
- Vos, K.; Peng, Z.; Jenkins, C.; Shahriar, M.R.; Borghesani, P.; Wang, W. Vibration-based anomaly detection using LSTM/SVM approaches. Mech. Syst. Signal Process. 2022, 169, 108752. [Google Scholar] [CrossRef]
- Mao, X.; Zhang, F.; Wang, G.; Chu, Y.; Yuan, K. Bearing fault diagnosis based on a multi-head graph convolutional weighting network. Measurement 2021, 173, 108603. [Google Scholar] [CrossRef]
- Xu, Z.; Jia, Z.; Wei, Y.; Zhang, S.; Jin, Z.; Dong, W. A strong anti-noise and easily deployable bearing fault diagnosis model based on time-frequency dual-channel Transformer. Measurement 2024, 236, 115054. [Google Scholar] [CrossRef]
- Mirzaeibonehkhater, M.; Labbaf-Khaniki, M.A.; Manthouri, M. Transformer-Based Bearing Fault Detection using Temporal Decomposition Attention Mechanism. arXiv 2024, arXiv:2412.11245. [Google Scholar] [CrossRef]
- Xiang, L.; Bing, H.; Li, X.; Hu, A. A frequency channel-attention based vision Transformer method for bearing fault identification across different working conditions. Expert Syst. Appl. 2025, 262, 125686. [Google Scholar] [CrossRef]
- Mu, S.; Yao, D.; Yang, J.; Zhu, B. A Dual-Branch Dynamic Attention and Sparse Transformer Network for Noise-Robust Bearing Fault Diagnosis. Signal Image Video Process. 2025, 19, 982. [Google Scholar] [CrossRef]
- Cen, J.; Si, W.; Liu, X.; Zhao, B.; Huang, H.; Liu, J. Intelligent fault diagnosis method based on data generation and long-patch vision transformer under small samples. Appl. Intell. 2025, 55, 650. [Google Scholar] [CrossRef]
- Wang, C.; Cheng, Y.; Liu, W.; Wang, Y. A Novel Unbalanced Fault Diagnosis Method with Diffusion Model in Rotating Machinery. In Proceedings of the 6th International Conference on Structural Health Monitoring and Integrity Management, Zhengzhou, China, 8–10 November 2024. [Google Scholar]
- Lei, Y.; Yang, B.; Jiang, X.; Jia, F.; Li, N.; Nandi, A.K. Applications of machine learning to machine fault diagnosis: A review and roadmap. Mech. Syst. Signal Process. 2020, 138, 106587. [Google Scholar] [CrossRef]
- Weiss, K.; Khoshgoftaar, T.M.; Wang, D. A survey of transfer learning. J. Big Data 2016, 3, 9. [Google Scholar] [CrossRef]
- Shao, H.; Li, W.; Cai, B.; Wan, J.; Xiao, Y.; Yan, S. Dual-threshold attention-guided GAN and limited infrared thermal images for rotating machinery fault diagnosis under speed fluctuation. IEEE Trans. Ind. Inform. 2023, 19, 9933–9942. [Google Scholar] [CrossRef]
- Cai, W.; Zhao, D.; Wang, T. Multi-scale Dynamic Graph Mutual Information Network for planetary bearing health monitoring under imbalanced data. Adv. Eng. Inform. 2025, 64, 103096. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J. Long short term memory recurrent neural network based bearing fault diagnosis. Appl. Soft Comput. 2022, 123, 108934. [Google Scholar] [CrossRef]
- Zhong, H.; Yu, S.; Trinh, H.; Lv, Y.; Yuan, R.; Wang, Y. A review on synchronous micro-phasor measurement units and their applications. Measurement 2023, 210, 112421. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W. Deep learning-based partial domain adaptation method on intelligent machinery fault diagnostics. IEEE Trans. Ind. Electron. 2021, 68, 4351–4361. [Google Scholar] [CrossRef]
- Yao, Q.; Qin, Y.; Wang, X.; Qian, Q. Adaptive residual convolutional neural network for fault diagnosis of rotating machinery. Eng. Appl. Artif. Intell. 2021, 104, 104383. [Google Scholar] [CrossRef]
- Schwendemann, S.; Amjad, Z.; Sikora, A. A survey of machine-learning techniques for condition monitoring and predictive maintenance of bearings in grinding machines. Eng. Appl. Artif. Intell. 2021, 105, 104415. [Google Scholar] [CrossRef]
- Ganin, Y.; Ustinova, E.; Ajakan, H.; Germain, P.; Larochelle, H.; Laviolette, F.; March, M.; Lempitsky, V. Domain-adversarial training of neural networks. J. Mach. Learn. Res. 2016, 17, 1–35. [Google Scholar]
- Wang, Q.; Michau, G.; Fink, O. Domain adaptive transfer learning for fault diagnosis. In Proceedings of the 2019 Prognostics and System Health Management Conference (PHM-Paris), Paris, France, 2–5 May 2019; pp. 279–285. [Google Scholar]
- Li, F.; Tang, T.; Tang, B.; He, Q. Deep convolution domain-adversarial transfer learning for fault diagnosis of rolling bearings. Measurement 2021, 169, 108339. [Google Scholar] [CrossRef]
- Tzeng, E.; Hoffman, J.; Zhang, N.; Saenko, K.; Darrell, T. Deep domain confusion: Maximizing for domain invariance. arXiv 2014, arXiv:1412.3474. [Google Scholar] [CrossRef]
- Yang, B.; Lei, Y.; Jia, F.; Xing, S. An intelligent fault diagnosis approach based on transfer learning from laboratory bearings to locomotive bearings. Mech. Syst. Signal Process. 2019, 122, 692–706. [Google Scholar] [CrossRef]
- Guo, L.; Lei, Y.; Xing, S.; Yan, T.; Li, N. Deep convolutional transfer learning network: A new method for intelligent fault diagnosis of machines with unlabeled data. IEEE Trans. Ind. Electron. 2019, 66, 7316–7325. [Google Scholar] [CrossRef]
- Yao, Q.; Qian, Q.; Qin, Y.; Guo, L.; Wu, F. Multiscale domain adaptive transfer learning via pseudo-siamese network for intelligent fault diagnosis. Eng. Appl. Artif. Intell. 2022, 113, 104932. [Google Scholar] [CrossRef]
- Gretton, A.; Borgwardt, K.M.; Rasch, M.J.; Schölkopf, B.; Smola, A. A kernel two-sample test. J. Mach. Learn. Res. 2012, 13, 723–773. [Google Scholar]
- Long, M.; Zhu, H.; Wang, J.; Jordan, M.I. Deep transfer learning with joint adaptation networks. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 2208–2217. [Google Scholar]
- Long, M.; Cao, Z.; Wang, J.; Jordan, M.I. Conditional adversarial domain adaptation. In Advances in Neural Information Processing Systems; Curran Associates Inc.: Red Hook, NY, USA, 2018; Volume 31. [Google Scholar]
- Li, X.; Zhang, W.; Ding, Q.; Sun, J.Q. Intelligent rotating machinery fault diagnosis based on deep learning using data augmentation. Signal Process. 2019, 157, 180–197. [Google Scholar] [CrossRef]
- Randall, R.B.; Antoni, J. Rolling element bearing diagnostics—A tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Smith, W.A.; Randall, R.B. Rolling element bearing diagnostics using the Case Western Reserve University data: A benchmark study. Mech. Syst. Signal Process. 2015, 64–65, 100–131. [Google Scholar] [CrossRef]

| Layers | Parameters | Stride | Padding | Activation Function | Input Size | Output Size |
|---|---|---|---|---|---|---|
| Input | / | / | / | / | / | (1 × 1024) |
| Conv1 | (1,16,64) | 1 | 32 | ReLU | (1 × 1024) | (16 × 1024) |
| Max pooling1 | 2 × 1 | 2 | 0 | / | (16 × 1024) | (16 × 512) |
| Conv2 | (16,32,5) | 1 | 2 | ReLU | (16 × 512) | (32 × 512) |
| Max pooling2 | 2 × 1 | 2 | 0 | / | (32 × 512) | (32 × 256) |
| Conv3 | (32,64,5) | 1 | 2 | ReLU | (32 × 256) | (64 × 256) |
| Max pooling3 | 2 × 1 | 2 | 0 | / | (64 × 256) | (64 × 128) |
| Flatten | 0 | / | / | ReLU | (64 × 128) | 8192 |
| FC1 | (128 × 64,1024) | / | / | / | 8192 | 1024 |
| FC2 | (1024,512) | / | / | / | 1024 | 512 |
| FC3 | (512,Class) | / | / | Softmax | 512 | Class |
| Layers Categories | Parameters | Output Size |
|---|---|---|
| FD1 | (512,256) | 256 |
| D0 | (256,1) | 1 |
| Datasets | Fault Categories | Labels | Number of Samples | Operation Conditions |
|---|---|---|---|---|
| A | NC | 0 | 1000 | (0HP) 1797 r/min |
| IF | 1 | |||
| BF | 2 | |||
| OF | 3 | |||
| B | NC | 0 | 1000 | (2HP) 1750 r/min |
| IF | 1 | |||
| BF | 2 | |||
| OF | 3 | |||
| C | NC | 0 | 1000 | (3HP) 1730 r/min |
| IF | 1 | |||
| BF | 2 | |||
| OF | 3 | |||
| D | NC | 0 | 1000 | (0HP) 1800 r/min |
| IF | 1 | |||
| BF | 2 | |||
| OF | 3 | |||
| E | NC | 0 | 1000 | (1HP) 1800r/min |
| IF | 1 | |||
| BF | 2 | |||
| OF | 3 | |||
| F | NC | 0 | 1000 | (0HP) 2400 r/min |
| IF | 1 | |||
| BF | 2 | |||
| OF | 3 | |||
| G | NC | 0 | 1000 | (1HP) 2400 r/min |
| IF | 1 | |||
| BF | 2 | |||
| OF | 3 |
| Methods | FFT | Domain Classifier | Single-Kernel MMD | ML-MK MMD | Accuracy |
|---|---|---|---|---|---|
| CNN | √ | 87.65% | |||
| DDC | √ | √ | 91.76% | ||
| DANN | √ | √ | 93.75% | ||
| ML-MKMMD | √ | √ | 95.69% | ||
| DCTLN | √ | √ | √ | 98.54% | |
| IDAIDM (Self-Built) | √ | √ | √ | 94.39% | |
| IDAIDM (CWRU) | √ | √ | √ | 99.84% |
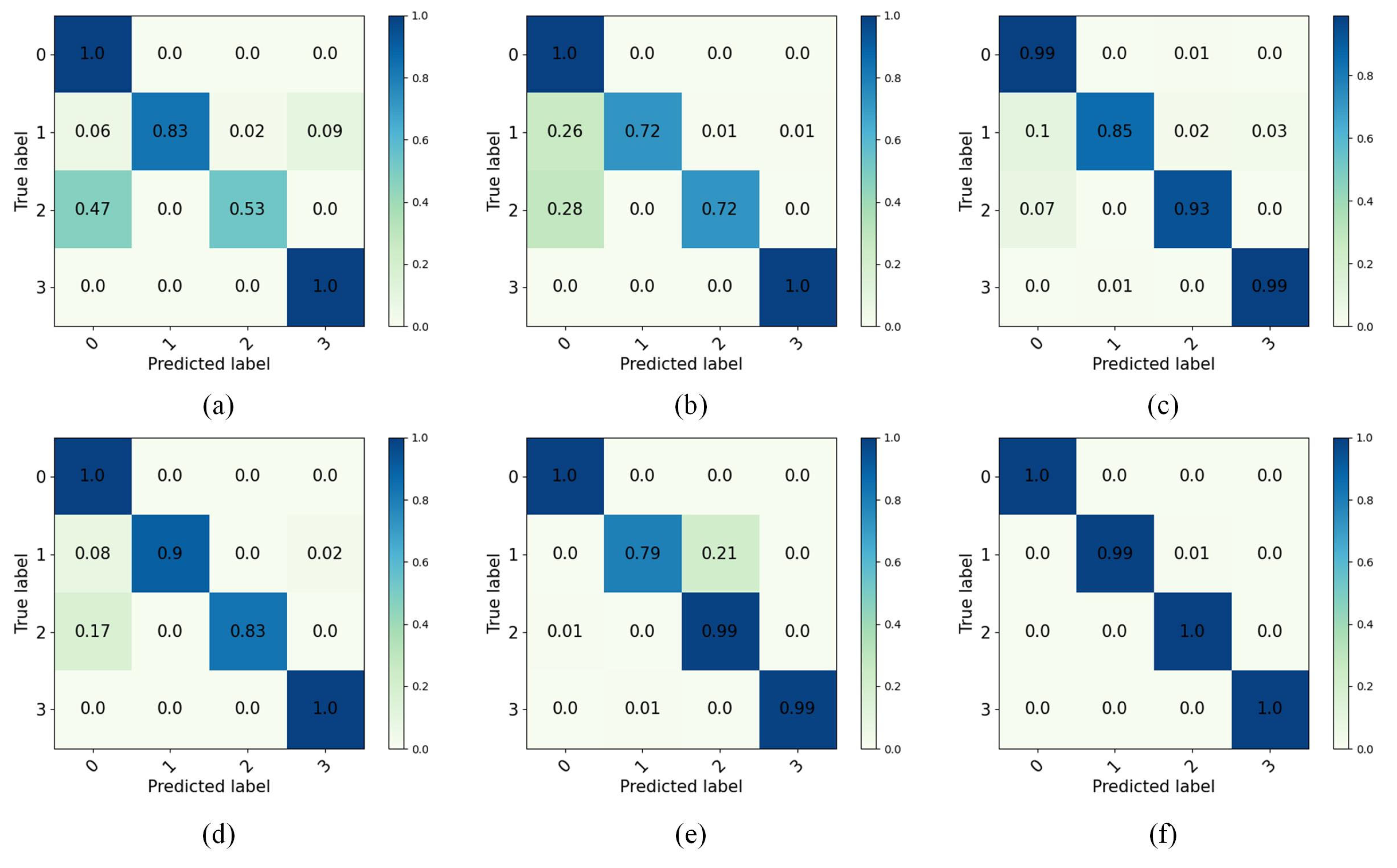
| Methods | NC | IF | BF | OF |
|---|---|---|---|---|
| CNN | 1.00 | 0.83 | 0.53 | 1.00 |
| DDC | 1.00 | 0.72 | 0.28 | 1.00 |
| DANN | 0.99 | 0.85 | 0.93 | 0.99 |
| ML-MK MMD | 1.00 | 0.90 | 0.83 | 1.00 |
| DCTLN | 1.00 | 0.79 | 0.99 | 0.99 |
| IDAIDM | 1.00 | 0.99 | 1.00 | 1.00 |
| Transfer Task | Complete Method | w/o Discriminator | w/o ML-MK MMD |
|---|---|---|---|
| A→B | 1.00 | 0.94 | 0.92 |
| A→C | 0.99 | 0.95 | 0.88 |
| B→C | 0.99 | 0.94 | 0.92 |
| B→A | 0.99 | 0.96 | 0.91 |
| C→A | 0.99 | 0.96 | 0.93 |
| C→B | 0.99 | 0.96 | 0.92 |
| Average | 0.99 | 0.95 | 0.91 |
| Performance Drop | / | −0.04 | −0.08 |
| Acronyms and Abbreviations | Complete Semantics |
|---|---|
| BF | Ball Fault |
| CDAN | Conditional Domain Adversarial Network |
| CNN | Convolutional Neural Network |
| CWRU | Case Western Reserve University |
| DANN | Domain Adversarial Neural Network |
| DCTLN | Deep Convolutional Transfer Learning Network |
| EMD | Empirical Mode Decomposition |
| FC | Fully Connected Layer |
| FD | Fully Connected Layer in Domain Classifier |
| FFT | Fast Fourier Transform |
| FTNN | Feature Transfer Neural Network |
| GAN | Generative Adversarial Network |
| GRL | Gradient Reversal Layer |
| HP | Horsepower |
| IDAIDM | Improved Domain Adaptive Intelligent Diagnosis Method |
| IF | Inner Ring Fault |
| JAN | Joint Adaptation Network |
| JMMD | Joint Maximum Mean Discrepancy |
| LSTM | Long Short-Term Memory |
| ML-MK MMD | Multi-Layer Multi-Kernel Maximum Mean Discrepancy |
| NC | Normal Condition |
| OF | Outer Ring Fault |
| RKHS | Reproducing Kernel Hilbert Space |
| RMS | Root Mean Square |
| RNN | Recurrent Neural Network |
| SGD | Stochastic Gradient Descent |
| STFT | Short-Time Fourier Transform |
| t-SNE | t-Distributed Stochastic Neighbor Embedding |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Che, J.; Fang, L.; Ma, Q.; Yu, G.; Sun, X.; Zhu, X. An Intelligent Bearing Fault Transfer Diagnosis Method Based on Improved Domain Adaption. Entropy 2025, 27, 1178. https://doi.org/10.3390/e27111178
Che J, Fang L, Ma Q, Yu G, Sun X, Zhu X. An Intelligent Bearing Fault Transfer Diagnosis Method Based on Improved Domain Adaption. Entropy. 2025; 27(11):1178. https://doi.org/10.3390/e27111178
Chicago/Turabian StyleChe, Jinli, Liqing Fang, Qiao Ma, Guibo Yu, Xiaoting Sun, and Xiujie Zhu. 2025. "An Intelligent Bearing Fault Transfer Diagnosis Method Based on Improved Domain Adaption" Entropy 27, no. 11: 1178. https://doi.org/10.3390/e27111178
APA StyleChe, J., Fang, L., Ma, Q., Yu, G., Sun, X., & Zhu, X. (2025). An Intelligent Bearing Fault Transfer Diagnosis Method Based on Improved Domain Adaption. Entropy, 27(11), 1178. https://doi.org/10.3390/e27111178








