Quantum Digital Signature Using Entangled States for Network
Abstract
1. Introduction
- Alice–Bob and Alice–Charlie are connected by imperfect quantum channels.
- Alice–Bob and Alice–Charlie are connected by authenticated classical channels.
- Bob–Charlie link is confidential and authenticated, and its content (indices, test positions) is never revealed to Alice. (In our symmetrization-free QDS this assumption is unnecessary, and the reasons will become clear as the protocol is presented.)
- In the key generation step within the distribution phase, participating users all act honestly.
2. Quantum Digital Signature Using Entangled States
2.1. The Distribution Phase
2.1.1. Key Generation Step
- Alice sends to Bob and to Charlie. She measures her states on a randomly chosen basis, thereby forming a sequence of outcomes ( and ).
- Bob and Charlie make a measurement on each state of received sequence ( and , respectively) by randomly selecting from the measurement bases, - or -basis. They announce all the click (measured) events through an authenticated channel to Alice. Only part of quantum states can be detected due to channel loss and imperfect detection [26,27,28,29,30,31]. Alice and Bob throw away all the events that have not clicked on either side. It means that they keep the left data of length l (), denoted as , kept by Alice and kept by Bob. Alice and Charlie also repeat the same process to form kept by Alice and kept by Charlie. Of course, there is no correlation between the states of sequences of Bob and Charlie at this stage because Alice randomly and independently generated and distributed entangled states.
- Alice announces the intensity information of all qubits. According to the intensity data, the legitimate three users divide each of their sequence into three strings. For example, Bob divides into , , and . In a similar manner, Charlie partitions the sequence. We describe these three intensities as (.
2.1.2. Reordering Step
- 1.
- Alice, using the sequence as a reference, reorders the positions of each bit within the sequence to match the bit sequence of the sequence . This rearranged sequence is denoted as . Alice shares the repositioning information with Charlie, allowing Charlie to transform the sequence to the sequence accordingly. We use parentheses and prime (′) to indicate that a sequence has been reordered. This procedure effectively eliminates the canonical symmetrization step in standard QS-L [21].
- 2.
- They generate new bit strings through the BAP; specifically, Alice obtains , Bob obtains , and Charlie obtains . Note that Bob and Charlie do not reveal which bits are conclusive results.
2.2. Estimation Phase
- The signer Alice chooses the authenticator from among Bob and Charlie; the remaining user naturally becomes the verifier of the signature. In this protocol, the authenticator serves as a kind of intermediary for non-repudiation services. The verifier plays the role of validator, verifying Alice’s signature. For the description of the protocol, we suppose that Bob is the authenticator and Charlie is the verifier.
- Alice, Bob, and Charlie publicly announce all data about -, and 0-sequences: Alice’s candidate pair announcements and the measurement outcomes of Bob and Charlie.
- They estimate the bit error rate of entangled pairs in sequences (between and , and and ) using the all data of sequence (between and , and and ) and 0 sequence (between and , and and ). In other words, the bit error rate for the central sequence (μ sequence) is calculated by the decoy method commonly used in QKD.
- Charlie randomly selects a proportion of in the sequence to use as test bits, then requests Alice to announce the bit values at those locations. We describe test bit sequences as , , and . Also, let us denote and as the mismatch rate of conclusive results between and , and and , respectively. In QKD, just as in the method used to determine post-processing based on the bit error rate, if and are too high, the subsequent steps are not performed.
- Bob and Charlie estimate the conclusive event rates on and . These are denoted as and , respectively. Under ideal statistics, and are expected to approach 1/4. If they deviate substantially from this nominal value, the protocol is aborted.
- Based on , , , and , Alice, Bob, and Charlie set the authentication security threshold and verification security thresholds . Set where are one-sided finite-size margins derived from the conclusive sample sizes [32,33]. The thresholds are required to satisfy . In other words, by excluding the post-processing procedures that are essential, in general, QKD when setting up and , the comprehensive effects of losses and errors included in the shared key are reflected.
- The three legitimate users discard the test bits and keep the remaining bits in strings with length . We denote these remaining bit sequences as , , and .
2.3. Message Phase
- Alice sends the message and the corresponding signature to the authenticator Bob to sign message .
- Bob receives and estimates the error rate between and . If , Bob accepts the signature and transmits to the verifier Charlie; otherwise, he aborts the signature and announces the failure result.
- In a similar way to Bob, Charlie calculates the error rate between and . Charlie accepts the signature if . As a result, Charlie accepts as Alice’s signature for message with signature verification using and .
3. Security Analysis
3.1. Robustness
3.2. Unforgeability
- (1)
- Estimate the lower bound of the secure single-photon pair events between Alice and Charlie by decoy-state analysis:The meaning of each variable is specified below.
- : Observed number of conclusive detection events on the Alice–Charlie link when the source intensity is .
- , , : Shorthand for the above counts at the signal (μ), weak decoy (ν), and vacuum (0) settings, respectively.
- , : Poisson weight factors appearing in the decoy linear relations for pair sources when isolating the single-photon contribution from .
- (2)
- Compute the maximum number of single-photon error events :
- (3)
- Calculate minimum expected mismatch rate :
- (4)
- Bound the forgery success probability using Chernoff bound [10]:
3.3. Repudiation Resistance
- First, we compute the relative Hamming distance between the bit sequences held by the authenticator Bob and verifier Charlie after the reordering step:
- Finally, with fixed, the repudiation probability can be evaluated as follows:
3.4. Overall Security Discussion
3.5. Conclusion of Security Analysis
4. Realization Discussion
5. Integration with Quantum Networks and Deployment Considerations
5.1. Network Native Rationale
5.2. Topologies and Relay Placement
5.3. Interoperability with Control/Management Planes
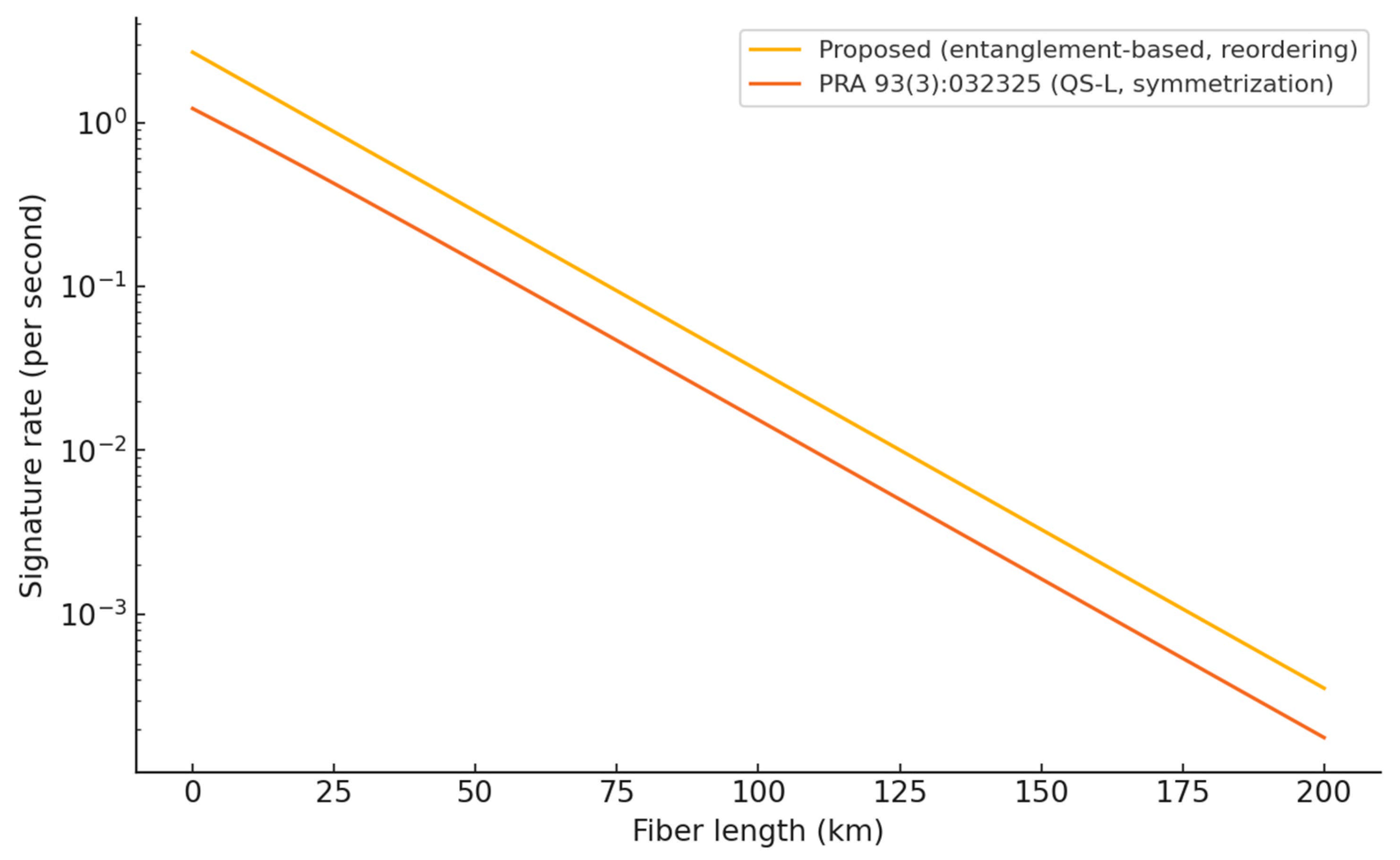
5.4. Empirical Evidence from Network Trials
5.5. Scalability via Integrated Photonics
5.6. Extending Reach with Repeaters and Swapping
5.7. Operational Mapping of Protocol Steps
5.8. Summary
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
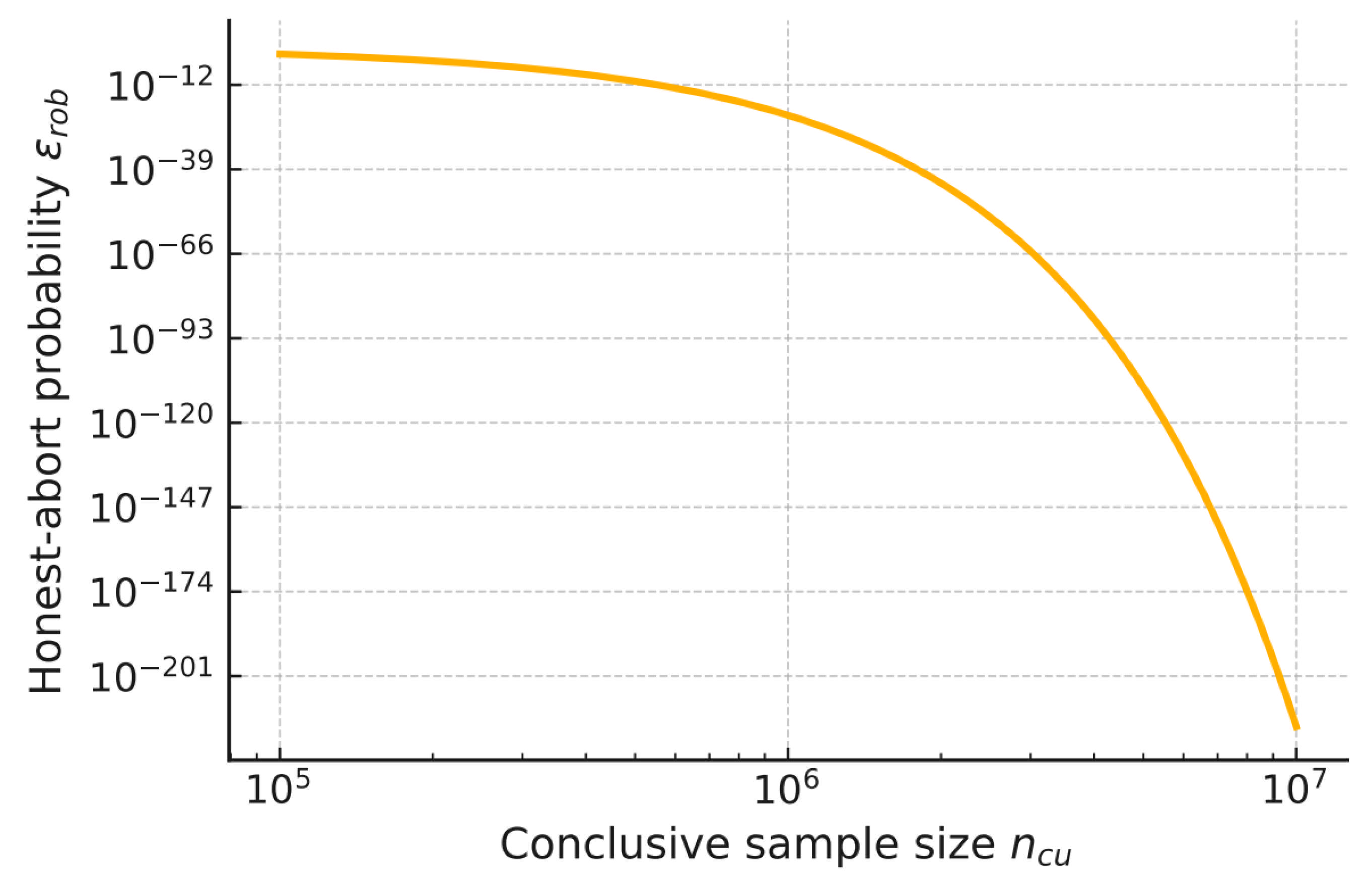
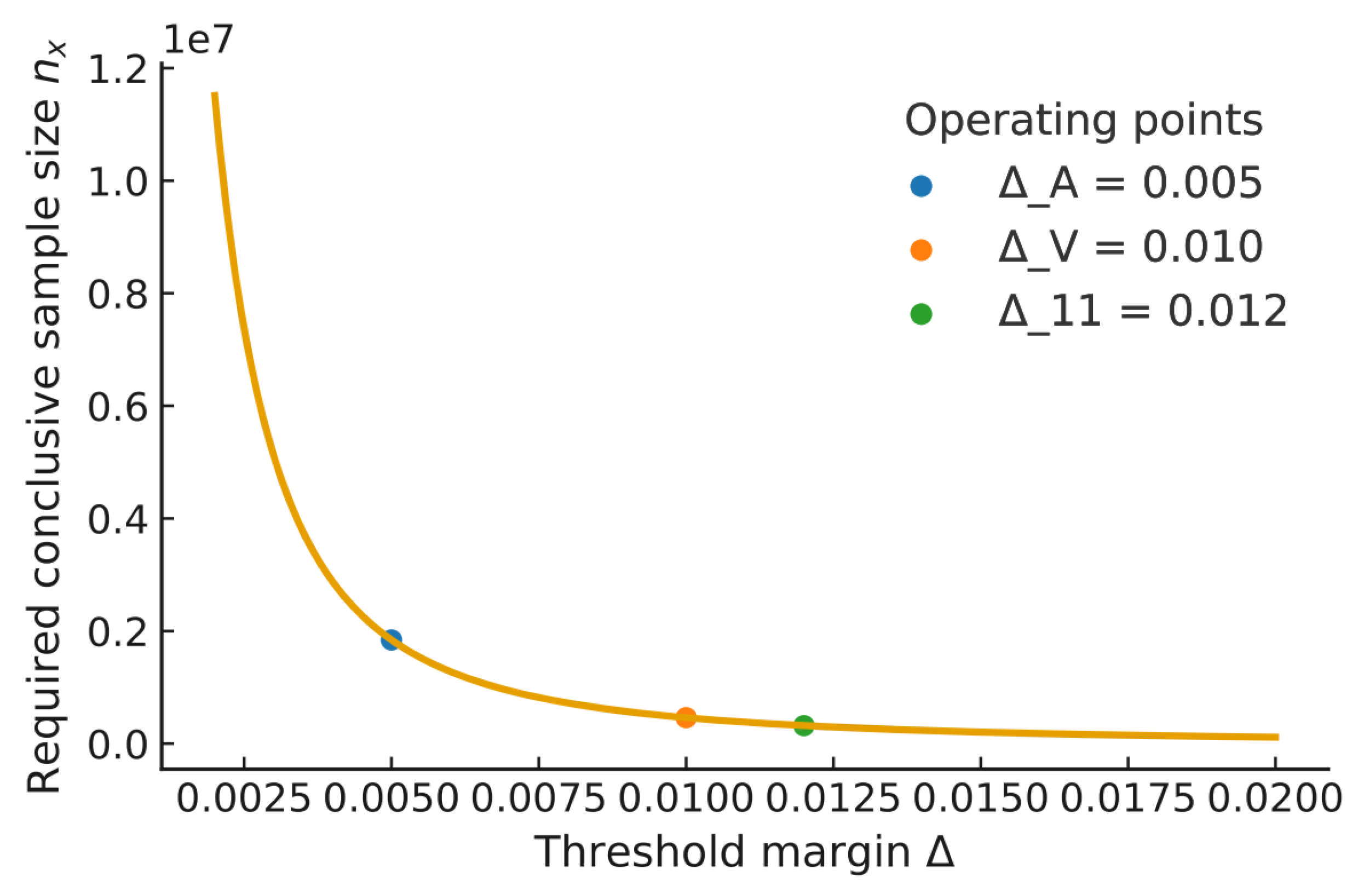
Appendix A. Finite-Size Calibration Examples
- Next, adopting the tail-calibration rule used in Section 4, the required conclusive sample size for a target failure budget and margin is as follows:
References
- NIST. Status Report on the Fourth Round of the NIST Post-Quantum Cryptography Standardization Process; NIST IR 8545; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2025. [Google Scholar]
- Gottesman, D.; Chuang, I. Quantum Digital Signatures. arXiv 2001, arXiv:quant-ph/0105032. [Google Scholar] [CrossRef]
- Lamport, L. Constructing Digital Signatures from a One-Way Function; Technical Report SRI-CSL-98; SRI International: Menlo Park, CA, USA, 1979. [Google Scholar]
- Dunjko, V.; Wallden, P.; Andersson, E. Quantum Digital Signatures without Quantum Memory. Phys. Rev. Lett. 2014, 112, 040502. [Google Scholar] [CrossRef]
- Li, B.-H.; Xie, Y.-M.; Cao, X.-Y.; Li, C.-L.; Fu, Y.; Yin, H.-L.; Chen, Z.-B. One-Time Universal Hashing Quantum Digital Signatures without Perfect Keys. Phys. Rev. Appl. 2023, 20, 044011. [Google Scholar] [CrossRef]
- Puthoor, I.V.; Amiri, R.; Wallden, P.; Lucamarini, M.; Andersson, E. Measurement-Device-Independent Quantum Digital Signatures. Phys. Rev. A 2016, 94, 022328. [Google Scholar] [CrossRef]
- Du, Y.; Li, B.-H.; Hua, X.; Cao, X.-Y.; Zhao, Z.; Xie, F.; Zhang, Z.; Yin, H.-L.; Xiao, X.; Wei, K. Chip-Integrated Quantum Signature Network over 200 km. Light Sci. Appl. 2025, 14, 108. [Google Scholar] [CrossRef]
- Bian, J.-W.; Li, B.-H.; Xie, Y.-M.; Yin, H.-L.; Chen, Z.-B. Asynchronous Measurement-Device-Independent Quantum Digital Signatures. Phys. Rev. A 2024, 110, 012609. [Google Scholar] [CrossRef]
- Zhu, J.-L.; Zhang, C.-H.; Wang, Q. Improved Finite-Size Analysis for Measurement-Device-Independent Quantum Digital Signatures. Opt. Lett. 2025, 50, 6245–6248. [Google Scholar] [CrossRef]
- Yin, H.-L.; Wang, W.-L.; Tang, Y.-L.; Zhao, Q.; Liu, H.; Sun, X.-X.; Zhang, W.-J.; Li, H.; Puthoor, I.V.; You, L.-X.; et al. Experimental Measurement-Device-Independent Quantum Digital Signatures over a Metropolitan Network. Phys. Rev. A 2017, 95, 042338. [Google Scholar] [CrossRef]
- Yin, H.-L.; Fu, Y.; Liu, H.; Tang, Q.-J.; Wang, J.; You, L.-X.; Zhang, W.-J.; Chen, S.-J.; Wang, Z.; Zhang, Q.; et al. Experimental Quantum Digital Signature over 102 km. Phys. Rev. A 2017, 95, 032334. [Google Scholar] [CrossRef]
- Clarke, P.J.; Donaldson, W.; Collins, R.J.; Amiri, R.; Fujiwara, M.; Honjo, T.; Shimizu, K.; Takeoka, M.; Andersson, E.; Sasaki, M. Quantum Digital Signatures over 134 km Equivalent Installed Fiber. Sci. Rep. 2017, 7, 4635. [Google Scholar]
- Chapman, J.C.; Alshowkan, M.; Qi, B.; Peters, N.A. Entanglement-Based Quantum Digital Signatures over a Deployed Campus Network. Opt. Express 2024, 32, 7521–7539. [Google Scholar] [CrossRef]
- Yin, H.-L.; Fu, Y.; Li, C.-L.; Weng, C.-X.; Li, B.-H.; Gu, J.; Lu, Y.-S.; Huang, S.; Chen, Z.-B. Experimental Quantum Secure Network with Digital Signatures and Encryption. Natl. Sci. Rev. 2023, 10, nwac228. [Google Scholar] [CrossRef] [PubMed]
- Pirandola, S.; Andersen, U.L.; Banchi, L.; Berta, M.; Bunandar, D.; Colbeck, R.; Englund, D.; Gehring, T.; Lupo, C.; Ottaviani, C.; et al. Advances in quantum cryptography. Adv. Opt. Photonics 2020, 12, 1012–1236. [Google Scholar] [CrossRef]
- Pan, D.; Liu, Y.-C.; Niu, P.; Zhang, H.; Zhang, F.; Wang, M.; Song, X.-T.; Chen, X.; Zheng, C.; Long, G.-L. Simultaneous Transmission of Information and Key Exchange Using the Same Photonic Quantum States. Sci. Adv. 2025, 11, eadt4627. [Google Scholar] [CrossRef]
- Wang, M.; Long, G.-L. Quantum Secure Direct Communication: Whispering with Photons. Natl. Sci. Rev. 2025, 12, nwaf096. [Google Scholar] [CrossRef]
- Zhou, L.; Sheng, Y.-B.; Long, G.L. Device-Independent Quantum Secure Direct Communication against Collective Attacks. Sci. Bull. 2020, 65, 12–20. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Zhang, C.; Gu, S.-P.; Wang, X.-F.; Zhou, L.; Sheng, Y.-B. Receiver-Device-Independent Quantum Secure Direct Communication. Sci. China Phys. Mech. Astron. 2025, 68, 250311. [Google Scholar] [CrossRef]
- Ding, C.-W.; Wang, W.-Y.; Zhang, W.-D.; Zhou, L.; Sheng, Y.-B. Quantum Secure Direct Communication Based on Quantum Error Correction Code. Appl. Phys. Lett. 2025, 126, 024002. [Google Scholar] [CrossRef]
- Lu, Y.-S.; Cao, X.-Y.; Weng, C.-X.; Gu, J.; Xie, Y.-M.; Zhou, M.-G.; Yin, H.-L.; Chen, Z.-B. Efficient Quantum Digital Signature without Symmetrization Step. Opt. Express 2021, 29, 10162–10171. [Google Scholar] [CrossRef]
- Scarani, V.; Acín, A.; Ribordy, G.; Gisin, N. Quantum Cryptography Protocols Robust against Photon Number Splitting Attacks for Weak Laser Pulse Implementations. Phys. Rev. Lett. 2004, 92, 057901. [Google Scholar] [CrossRef]
- Wei, Z.; Wang, W.; Zhang, Z.; Gao, M.; Ma, Z.; Ma, X. Decoy-State Quantum Key Distribution with Biased Basis Choice. Sci. Rep. 2013, 3, 2453. [Google Scholar] [CrossRef]
- Grasselli, F.; Curty, M. Practical Decoy-State Method for Twin-Field Quantum Key Distribution. New J. Phys. 2019, 21, 073001. [Google Scholar] [CrossRef]
- Tsurumaru, T.; Tamaki, K. Security Proof for Quantum-Key-Distribution System with Threshold Detectors. Phys. Rev. A 2008, 78, 032302. [Google Scholar] [CrossRef]
- Ekert, A.K. Quantum Cryptography Based on Bell’s Theorem. Phys. Rev. Lett. 1991, 67, 661–663. [Google Scholar] [CrossRef] [PubMed]
- Gerhardt, I.; Liu, Q.; Lamas-Linares, A.; Skaar, J.; Kurtsiefer, C.; Makarov, V. Full-Field Implementation of a Perfect Eavesdropper on a Quantum Cryptography System. Nat. Commun. 2011, 2, 349. [Google Scholar] [CrossRef]
- Sajeed, S.; Huang, A.; Sun, S.; Xu, F.; Makarov, V.; Curty, M. Insecurity of Detector-Device-Independent Quantum Key Distribution. Phys. Rev. Lett. 2016, 117, 250505. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, T.-Y.; Wang, L.-J.; Liang, H.; Shentu, G.-L.; Wang, J.; Cui, K.; Yin, H.; Liu, N.-L.; Li, L.; et al. Experimental Measurement-Device-Independent Quantum Key Distribution. Phys. Rev. Lett. 2013, 111, 130502. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Zhou, Y.; Zhang, C.; Wang, X.; Xu, F.; Lo, H.-K. Security of Quantum Key Distribution with Source and Detector Imperfections through Combined Analysis. arXiv 2025, arXiv:2507.03549. [Google Scholar]
- Chen, X.; Li, Z.; Liu, Y.; Zhang, Q.; Pan, J.-W. Automatically Identifying Imperfections and Attacks in Practical Quantum Key Distribution Using Machine Learning. Sci. China Inf. Sci. 2023, 66, 180503. [Google Scholar] [CrossRef]
- Scarani, V.; Renner, R. Quantum Cryptography with Finite Resources. Phys. Rev. Lett. 2008, 100, 200501. [Google Scholar] [CrossRef]
- Li, M.-Y.; Cao, X.-Y.; Xie, Y.-M.; Yin, H.-L.; Chen, Z.-B. Finite-Key Analysis for Coherent One-Way Quantum Key Distribution. Phys. Rev. Res. 2024, 6, 013022. [Google Scholar] [CrossRef]
- Amiri, R.; Wallden, P.; Kent, A.; Andersson, E. Secure Quantum Signatures Using Insecure Quantum Channels. Phys. Rev. A 2016, 93, 032325. [Google Scholar] [CrossRef]
- Wehner, S.; Elkouss, D.; Hanson, R. Quantum Internet: A Vision for the Road Ahead. Science 2018, 362, eaam9288. [Google Scholar] [CrossRef]
- Recommendation Y.3800 (10/2019); Overview on Networks Supporting Quantum Key Distribution (QKD). ITU-T: Geneva, Switzerland, 2019. Available online: https://www.itu.int/rec/T-REC-Y.3800 (accessed on 17 November 2025).
- Kržič, A.; Sharma, S.; Spiess, C.; Chandrashekara, U.; Töpfer, S.; Sauer, G.; del Campo, L.J.G.-M.; Kopf, T.; Petscharnig, S.; Grafenauer, T.; et al. Towards Metropolitan Free-Space Quantum Networks. npj Quantum Inf. 2023, 9, 59. [Google Scholar] [CrossRef]
- ETSI GS QKD 014 V1.1.1 (2019-02); Quantum Key Distribution (QKD); Protocol and Data Format of REST-Based Key Delivery API. ETSI: Sophia Antipolis, France, 2019. Available online: https://www.etsi.org/deliver/etsi_gs/QKD/001_099/014/01.01.01_60/gs_qkd014v010101p.pdf (accessed on 17 November 2025).
- ETSI GS QKD 015 (2022-04); Quantum Key Distribution (QKD); Control Interface for Software-Defined Networks. ETSI: Sophia Antipolis, France, 2022. Available online: https://www.etsi.org/deliver/etsi_gs/QKD/001_099/015/02.01.01_60/gs_qkd015v020101p.pdf (accessed on 17 November 2025).
- Sasaki, M.; Fujiwara, M.; Ishizuka, H.; Klaus, W.; Wakui, K.; Takeoka, M.; Miki, S.; Yamashita, T.; Wang, Z.; Tanaka, A.; et al. Field Test of Quantum Key Distribution in the Tokyo QKD Network. Opt. Express 2011, 19, 10387–10409. [Google Scholar] [CrossRef] [PubMed]
- Poppe, A.; Peev, M.; Maurhart, O. Outline of the SECOQC Quantum-Key-Distribution Network in Vienna. Int. J. Quantum Inf. 2008, 6, 209–218. [Google Scholar] [CrossRef]
- Bunandar, D.; Lentine, A.; Lee, C.; Cai, H.; Long, C.M.; Boynton, N.; Martinez, N.; DeRose, C.; Chen, C.; Grein, M.; et al. Metropolitan Quantum Key Distribution with Silicon Photonics. Phys. Rev. X 2018, 8, 021009. [Google Scholar] [CrossRef]
- Ng, S.Q.; Kanitschar, F.; Zhang, G.; Wang, C. Gigabit-Rate Quantum Key Distribution on Integrated Photonic Chips. arXiv 2025, arXiv:2504.08298. [Google Scholar] [CrossRef]
- Bian, Y.; Pan, Y.; Xu, X.; Zhao, L.; Li, Y.; Huang, W.; Zhang, L.; Yu, S.; Zhang, Y.; Xu, B. Continuous-Variable Quantum Key Distribution over 28.6 km Fiber with an Integrated Silicon Photonic Receiver Chip. Appl. Phys. Lett. 2024, 124, 174001. [Google Scholar] [CrossRef]
- Briegel, H.-J.; Dür, W.; Cirac, J.I.; Zoller, P. Quantum Repeaters: The Role of Imperfect Local Operations in Quantum Communication. Phys. Rev. Lett. 1998, 81, 5932–5935. [Google Scholar] [CrossRef]
- Żukowski, M.; Zeilinger, A.; Horne, M.A.; Ekert, A.K. “Event-Ready-Detectors” Bell Experiment via Entanglement Swapping. Phys. Rev. Lett. 1993, 71, 4287–4290. [Google Scholar] [CrossRef] [PubMed]
- CN-QCN Consortium. Implementation of Carrier-Grade Quantum Communication Networks over 10,000 km. npj Quantum Inf. 2025, 11, 89. [Google Scholar] [CrossRef]
- Li, Y.; Cai, W.-Q.; Ren, J.-G.; Wang, C.-Z.; Yang, M.; Zhang, L.; Wu, H.-Y.; Chang, L.; Wu, J.-C.; Jin, B.; et al. Microsatellite-Based Real-Time Quantum Key Distribution. Nature 2025, 640, 47–54. [Google Scholar] [CrossRef] [PubMed]
| User/Source | Sequence | |
|---|---|---|
| Source | ||
| Alice | ) | |
| Bob | ||
| Charlie | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, C.; Jeong, Y.-C.; Kwon, O.; Ji, S.-W. Quantum Digital Signature Using Entangled States for Network. Entropy 2025, 27, 1179. https://doi.org/10.3390/e27111179
Hong C, Jeong Y-C, Kwon O, Ji S-W. Quantum Digital Signature Using Entangled States for Network. Entropy. 2025; 27(11):1179. https://doi.org/10.3390/e27111179
Chicago/Turabian StyleHong, Changho, Youn-Chang Jeong, Osung Kwon, and Se-Wan Ji. 2025. "Quantum Digital Signature Using Entangled States for Network" Entropy 27, no. 11: 1179. https://doi.org/10.3390/e27111179
APA StyleHong, C., Jeong, Y.-C., Kwon, O., & Ji, S.-W. (2025). Quantum Digital Signature Using Entangled States for Network. Entropy, 27(11), 1179. https://doi.org/10.3390/e27111179






