Effect of Running Speed on Gait Variability in Individuals with Functional Ankle Instability
Abstract
1. Introduction
2. Materials and Methods
2.1. Participant Recruitment
2.2. Experiment Procedure
2.3. Data Processing
2.4. Statistical Analyses
3. Results
3.1. Participants
3.2. Coefficient of Variation
3.3. Sample Entropy
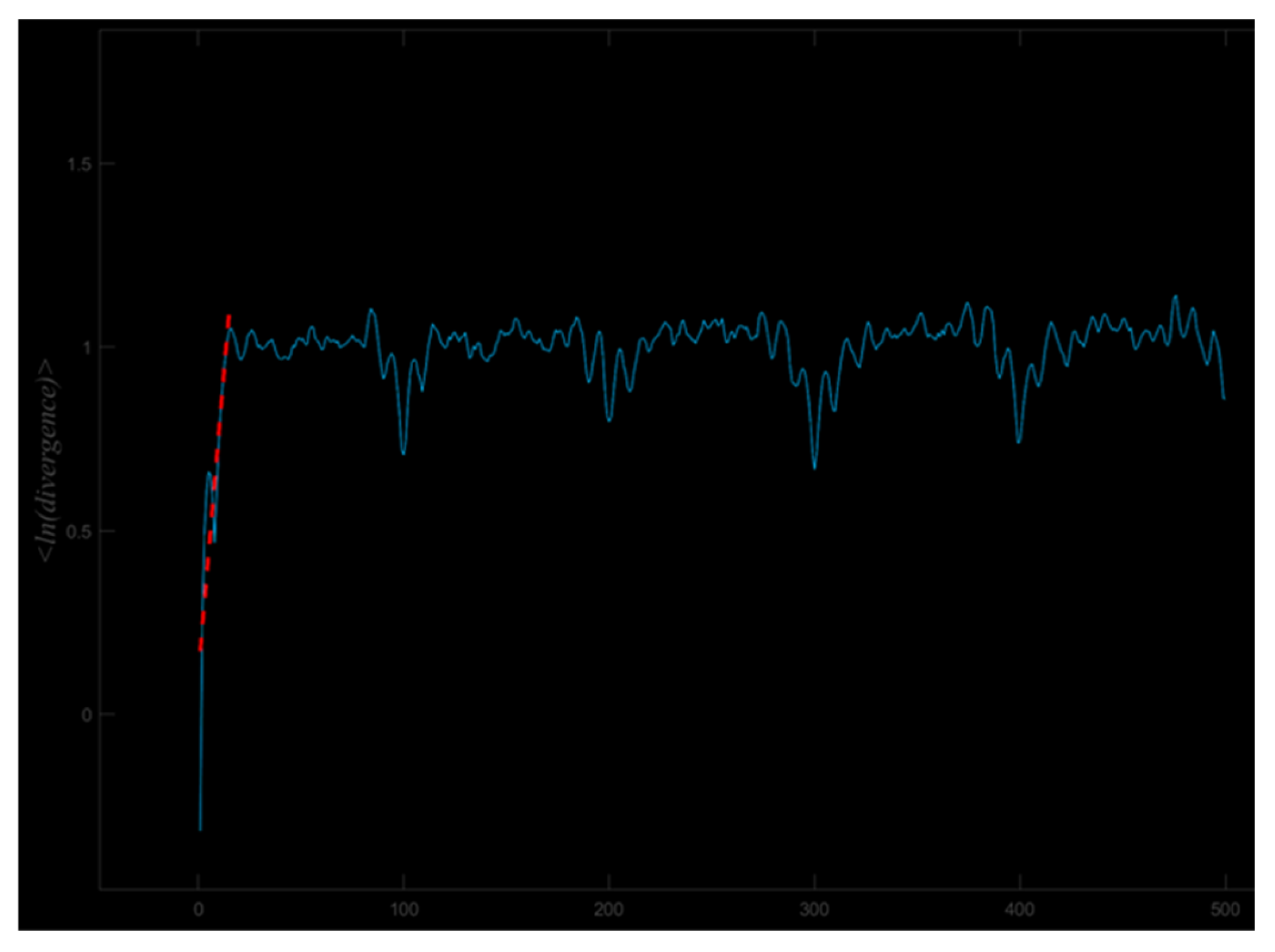
3.4. Largest Lyapunov Exponent
4. Discussion
4.1. Comparison of Variability Between Fai and Con
4.2. Comparison of Variability Across Speeds
4.3. Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Koshino, Y.; Samukawa, M.; Murata, H.; Osuka, S.; Kasahara, S.; Yamanaka, M.; Tohyama, H. Prevalence and characteristics of chronic ankle instability and copers identified by the criteria for research and clinical practice in collegiate athletes. Phys. Ther. Sport. 2020, 45, 23–29. [Google Scholar] [CrossRef]
- Kim, H.; Palmieri-Smith, R.; Kipp, K. Muscle Synergies in People With Chronic Ankle Instability During Anticipated and Unanticipated Landing-Cutting Tasks. J. Athl. Train. 2023, 58, 143–152. [Google Scholar] [CrossRef]
- Brunner, R.; Frigo, C.A. Control of Tibial Advancement by the Plantar Flexors during the Stance Phase of Gait Depends on Knee Flexion with Respect to the Ground Reaction Force. Bioengineering 2023, 11, 41. [Google Scholar] [CrossRef] [PubMed]
- Michels, F.; Pereira, H.; Calder, J.; Matricali, G.; Glazebrook, M.; Guillo, S.; Karlsson, J.; Acevedo, J.; Batista, J.; Bauer, T.; et al. Searching for consensus in the approach to patients with chronic lateral ankle instability: Ask the expert. Knee Surg. Sports Traumatol. Arthrosc. Off. J. ESSKA 2018, 26, 2095–2102. [Google Scholar] [CrossRef] [PubMed]
- Duysens, J.; Hoogkamer, W.; Levin, O. Is there “arthrogenic inhibition” of cutaneous reflexes in subjects with functional ankle instability? Clin. Neurophysiol. Off. J. Int. Fed. Clin. Neurophysiol. 2013, 124, 1264–1266. [Google Scholar] [CrossRef]
- Hertel, J. Functional Anatomy, Pathomechanics, and Pathophysiology of Lateral Ankle Instability. J. Athl. Train. 2002, 37, 364–375. [Google Scholar]
- Xu, X.; Bowtell, J.; Fong, D.T.P.; Young, W.R.; Williams, G.K.R. Kinematics of balance controls in people with chronic ankle instability during unilateral stance on a moving platform. Sci. Rep. 2025, 15, 1126. [Google Scholar] [CrossRef]
- Carbone, A.; Rodeo, S. Review of current understanding of post-traumatic osteoarthritis resulting from sports injuries. J. Orthop. Res. Off. Publ. Orthop. Res. Soc. 2017, 35, 397–405. [Google Scholar] [CrossRef]
- Houston, M.N.; Hoch, J.M.; Gabriner, M.L.; Kirby, J.L.; Hoch, M.C. Clinical and laboratory measures associated with health-related quality of life in individuals with chronic ankle instability. Phys. Ther. Sport 2015, 16, 169–175. [Google Scholar] [CrossRef]
- Moisan, G.; Mainville, C.; Descarreaux, M.; Cantin, V. Lower limb biomechanics in individuals with chronic ankle instability during gait: A case-control study. J. Foot Ankle Res. 2021, 14, 36. [Google Scholar] [CrossRef]
- Luan, L.; Orth, D.; Newman, P.; Adams, R.; El-Ansary, D.; Han, J. Do individuals with ankle instability show altered lower extremity kinematics and kinetics during walking? A systematic review and meta-analysis. Physiotherapy 2024, 125, 101420. [Google Scholar] [CrossRef]
- Son, S.J.; Kim, H.; Seeley, M.K.; Hopkins, J.T. Altered Walking Neuromechanics in Patients With Chronic Ankle Instability. J. Athl. Train. 2019, 54, 684–697. [Google Scholar] [CrossRef]
- Zhao, J.; Shao, E.; Song, Y.; Baker, J.S.; Liang, M.; Gu, Y. The Effect of Chronic Ankle Instability on Lower Limb Biomechanics During Medial Landings in Badminton Players. Adv. Biomed. Eng. 2025, 14, 134–145. [Google Scholar] [CrossRef]
- Caballero, C.; Davids, K.; Heller, B.; Wheat, J.; Moreno, F.J. Movement variability emerges in gait as adaptation to task constraints in dynamic environments. Gait Posture 2019, 70, 1–5. [Google Scholar] [CrossRef]
- Kwon, Y.U.; Harrison, K.; Kweon, S.J.; Williams, D.S.B., 3rd. Ankle Coordination in Chronic Ankle Instability, Coper, and Control Groups in Running. Med. Sci. Sports Exerc. 2020, 52, 663–672. [Google Scholar] [CrossRef] [PubMed]
- Wanner, P.; Schmautz, T.; Kluge, F.; Eskofier, B.; Pfeifer, K.; Steib, S. Ankle angle variability during running in athletes with chronic ankle instability and copers. Gait Posture 2019, 68, 329–334. [Google Scholar] [CrossRef] [PubMed]
- Lilley, T.; Herb, C.C.; Hart, J.; Hertel, J. Lower extremity joint coupling variability during gait in young adults with and without chronic ankle instability. Sports Biomech. 2018, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Springer, S.; Gottlieb, U. Effects of dual-task and walking speed on gait variability in people with chronic ankle instability: A cross-sectional study. BMC Musculoskelet. Disord. 2017, 18, 316. [Google Scholar] [CrossRef]
- Hamacher, D.; Hollander, K.; Zech, A. Effects of ankle instability on running gait ankle angles and its variability in young adults. Clin. Biomech. 2016, 33, 73–78. [Google Scholar] [CrossRef]
- Terada, M.; Bowker, S.; Thomas, A.C.; Pietrosimone, B.; Hiller, C.E.; Rice, M.S.; Gribble, P.A. Alterations in stride-to-stride variability during walking in individuals with chronic ankle instability. Hum. Mov. Sci. 2015, 40, 154–162. [Google Scholar] [CrossRef]
- Terada, M.; Morgan, K.D.; Gribble, P.A. Altered movement strategy of chronic ankle instability individuals with postural instability classified based on Nyquist and Bode analyses. Clin. Biomech. 2019, 69, 39–43. [Google Scholar] [CrossRef] [PubMed]
- Nohelova, D.; Bizovska, L.; Vuillerme, N.; Svoboda, Z. Gait Variability and Complexity during Single and Dual-Task Walking on Different Surfaces in Outdoor Environment. Sensors 2021, 21, 4792. [Google Scholar] [CrossRef] [PubMed]
- Stergiou, N.; Harbourne, R.; Cavanaugh, J. Optimal movement variability: A new theoretical perspective for neurologic physical therapy. J. Neurol. Phys. Ther. JNPT 2006, 30, 120–129. [Google Scholar] [CrossRef] [PubMed]
- Beauchet, O.; Annweiler, C.; Lecordroch, Y.; Allali, G.; Dubost, V.; Herrmann, F.R.; Kressig, R.W. Walking speed-related changes in stride time variability: Effects of decreased speed. J. Neuroeng. Rehabil. 2009, 6, 32. [Google Scholar] [CrossRef]
- Winner, T.S.; Rosenberg, M.C.; Berman, G.J.; Kesar, T.M.; Ting, L.H. Gait signature changes with walking speed are similar among able-bodied young adults despite persistent individual-specific differences. Sci. Rep. 2024, 14, 19730. [Google Scholar] [CrossRef]
- Blair, S.; Lake, M.J.; Ding, R.; Sterzing, T. Magnitude and variability of gait characteristics when walking on an irregular surface at different speeds. Hum. Mov. Sci. 2018, 59, 112–120. [Google Scholar] [CrossRef]
- Padulo, J.; Rampichini, S.; Borrelli, M.; Buono, D.M.; Doria, C.; Esposito, F. Gait Variability at Different Walking Speeds. J. Funct. Morphol. Kinesiol. 2023, 8, 158. [Google Scholar] [CrossRef]
- Jordan, K.; Challis, J.H.; Newell, K.M. Walking speed influences on gait cycle variability. Gait Posture 2007, 26, 128–134. [Google Scholar] [CrossRef]
- Dingwell, J.B.; Marin, L.C. Kinematic variability and local dynamic stability of upper body motions when walking at different speeds. J. Biomech. 2006, 39, 444–452. [Google Scholar] [CrossRef]
- Banakheiri, T.; Naimi, S.S.; Ebrahimabadi, Z.; Yousefi, M.; Daryabor, A. Reliability of Nonlinear Kinematic Analysis in Patients with Functional Ankle Instability During Dual-Task Walking. Mltj Muscles Ligaments Tendons J. 2023, 13, 335–343. [Google Scholar] [CrossRef]
- Esteves, J.; Dinis, R.; Fernandes, O.; Castro, M.A.; Oliveira, R.; Pezarat-Correia, P. Differences in postural control between healthy and subjects with chronic ankle instability. Phys. Ther. Sport 2022, 56, 8–14. [Google Scholar] [CrossRef]
- Moisan, G.; Mainville, C.; Descarreaux, M.; Cantin, V. Kinematic, kinetic and electromyographic differences between young adults with and without chronic ankle instability during walking. J. Electromyogr. Kinesiol. 2020, 51, 102399. [Google Scholar] [CrossRef] [PubMed]
- Huang, P.Y.; Jankaew, A.; Lin, C.F. Effects of Plyometric and Balance Training on Neuromuscular Control of Recreational Athletes with Functional Ankle Instability: A Randomized Controlled Laboratory Study. Int. J. Environ. Res. Public Health 2021, 18, 5269. [Google Scholar] [CrossRef] [PubMed]
- Hiller, C.E.; Refshauge, K.M.; Bundy, A.C.; Herbert, R.D.; Kilbreath, S.L. The Cumberland ankle instability tool: A report of validity and reliability testing. Arch. Phys. Med. Rehabil. 2006, 87, 1235–1241. [Google Scholar] [CrossRef] [PubMed]
- Van Melick, N.; Meddeler, B.M.; Hoogeboom, T.J.; Nijhuis-van der Sanden, M.W.G.; van Cingel, R.E.H. How to determine leg dominance: The agreement between self-reported and observed performance in healthy adults. PLoS ONE 2017, 12, e0189876. [Google Scholar] [CrossRef]
- Abbasi, A.; Yazdanbakhsh, F.; Tazji, M.K.; Aghaie Ataabadi, P.; Svoboda, Z.; Nazarpour, K.; Vieira, M.F. A comparison of coordination and its variability in lower extremity segments during treadmill and overground running at different speeds. Gait Posture 2020, 79, 139–144. [Google Scholar] [CrossRef]
- Raffalt, P.C.; Kent, J.A.; Wurdeman, S.R.; Stergiou, N. Selection Procedures for the Largest Lyapunov Exponent in Gait Biomechanics. Ann. Biomed. Eng. 2019, 47, 913–923. [Google Scholar] [CrossRef]
- Gaßner, H.; Jensen, D.; Marxreiter, F.; Kletsch, A.; Bohlen, S.; Schubert, R.; Muratori, L.M.; Eskofier, B.; Klucken, J.; Winkler, J.; et al. Gait variability as digital biomarker of disease severity in Huntington’s disease. J. Neurol. 2020, 267, 1594–1601. [Google Scholar] [CrossRef]
- Raghavachari, M. Applied Multivariate Statistics in Geohydrology and Related Sciences. J. Technometrics 2001, 43, 110. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Krysko, A.V.; Erofeev, N.P.; Dobriyan, V.; Barulina, M.A.; Krysko, V.A. Quantifying Chaos by Various Computational Methods. Part 1: Simple Systems. Entropy 2018, 20, 175. [Google Scholar] [CrossRef]
- Riva, F.; Grimpampi, E.; Mazzà, C.; Stagni, R. Are gait variability and stability measures influenced by directional changes? Biomed. Eng. Online 2014, 13, 56. [Google Scholar] [CrossRef] [PubMed]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences; Academic Press: London, UK, 1969. [Google Scholar]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences; Routledge: London, UK, 2013. [Google Scholar]
- Hamill, J.; van Emmerik, R.E.; Heiderscheit, B.C.; Li, L. A dynamical systems approach to lower extremity running injuries. Clin. Biomech. 1999, 14, 297–308. [Google Scholar] [CrossRef] [PubMed]
- He, Z.; Zhu, H.; Ye, B.; Zheng, Z.; Liu, G.; Pan, H.; Liu, R. Does chronic ankle instability patients lead to changes in biomechanical parameters associated with anterior cruciate ligament injury during landing? A systematic review and meta-analysis. Front. Physiol. 2024, 15, 1428879. [Google Scholar] [CrossRef]
- Zhou, Z.; Xu, D.; Wang, M.; Jie, T.; Baker, J.S.; Zhou, H.; Gu, Y. Assessment of Muscle Synergies in Chronic Ankle Instability Patients During Unanticipated and Anticipated Landing. Bioengineering 2024, 11, 1237. [Google Scholar] [CrossRef]
- Akl, A.R.; Conceição, F.; Richards, J. An exploration of muscle co-activation during different walking speeds and the association with lower limb joint stiffness. J. Biomech. 2023, 157, 111715. [Google Scholar] [CrossRef]
- Almarwani, M.; VanSwearingen, J.M.; Perera, S.; Sparto, P.J.; Brach, J.S. Challenging the motor control of walking: Gait variability during slower and faster pace walking conditions in younger and older adults. Arch. Gerontol. Geriatr. 2016, 66, 54–61. [Google Scholar] [CrossRef]
- Bruijn, S.M.; van Dieën, J.H.; Meijer, O.G.; Beek, P.J. Is slow walking more stable? J. Biomech. 2009, 42, 1506–1512. [Google Scholar] [CrossRef]
- Lai, A.; Schache, A.G.; Lin, Y.-C.; Pandy, M.G. Tendon elastic strain energy in the human ankle plantar-flexors and its role with increased running speed. J. Exp. Biol. 2014, 217, 3159–3168. [Google Scholar] [CrossRef]
- Buurke, T.J.W.; den Otter, R. The relationship between the anteroposterior and mediolateral margins of stability in able-bodied human walking. Gait Posture 2021, 90, 80–85. [Google Scholar] [CrossRef]
- Jordan, K.; Challis, J.H.; Newell, K.M. Speed influences on the scaling behavior of gait cycle fluctuations during treadmill running. Hum. Mov. Sci. 2007, 26, 87–102. [Google Scholar] [CrossRef]
- Nakayama, Y.; Kudo, K.; Ohtsuki, T. Variability and fluctuation in running gait cycle of trained runners and non-runners. Gait Posture 2010, 31, 331–335. [Google Scholar] [CrossRef]
- Toro, I.S.; Weir, G.; Amado, A.; Emmerik, R.V.; Ervilha, U.; Hamill, J. Is coordination variability using vector coding different in overground and treadmill walking and running? Gait Posture 2022, 92, 413–420. [Google Scholar] [CrossRef]

| FAI Patients (n = 15) | Controls (n = 15) | p | |
|---|---|---|---|
| Age (years) | 22.00 ± 2.56 | 23.67 ± 1.05 | 0.537 |
| Height (cm) | 179.00 ± 4.63 | 176.73 ± 3.51 | 0.142 |
| Body mass (kg) | 72.70 ± 7.76 | 70.03 ± 4.95 | 0.271 |
| BMI (kg/m2) | 22.66 ± 1.88 | 22.41 ± 1.22 | 0.671 |
| CAIT (scores) | 18.00 ± 4.54 | 29.33 ± 0.98 | 0.006 * |
| IPAQ (MT-min/W) | 5796 ± 2361 | 6212 ± 1124 | 0.419 |
| Slower speed (km/h) | 5.41 ± 0.34 | 5.51 ± 0.41 | 0.473 |
| Preferred speed (km/h) | 6.77 ± 0.42 | 6.90 ± 0.51 | 0.452 |
| Faster speed (km/h) | 8.13 ± 0.50 | 8.29 ± 0.61 | 0.438 |
| Plane | Group | Faster Speed | Preferred Speed | Slower Speed |
|---|---|---|---|---|
| Hip Sagittal | FAI | 0.686 ± 0.363 | 0.661 ± 0.214 | 0.854 ± 0.504 |
| CON | 0.690 ± 0.146 | 0.664 ± 0.186 | 0.807 ± 0.463 | |
| Hip Coronal | FAI | 0.680 ± 0.462 | 0.463 ± 0.121 | 0.595 ± 0.229 |
| CON | 0.568 ± 0.123 | 0.536 ± 0.153 | 0.579 ± 0.140 | |
| Hip Horizontal | FAI | 1.014 ± 0.541 | 0.809 ± 0.227 | 1.091 ± 0.603 |
| CON | 0.805 ± 0.272 | 0.896 ± 0.340 | 0.809 ± 0.161 | |
| Knee Sagittal &,@ | FAI | 1.830 ± 0.604 | 1.925 ± 0.728 | 2.592 ± 1.432 |
| CON | 1.840 ± 0.608 | 1.782 ± 0.546 | 2.120 ± 0.942 | |
| Knee Coronal | FAI | 0.440 ± 0.180 | 0.384 ± 0.114 | 0.531 ± 0.328 |
| CON | 0.419 ± 0.082 | 0.422 ± 0.187 | 0.420 ± 0.133 | |
| Knee Horizontal | FAI | 0.709 ± 0.258 | 0.686 ± 0.210 | 0.948 ± 0.551 |
| CON | 0.741 ± 0.209 | 0.757 ± 0.261 | 0.695 ± 0.154 | |
| Ankle Sagittal | FAI | 0.940 ± 0.446 | 0.954 ± 0.411 | 1.179 ± 0.602 |
| CON | 1.087 ± 0.315 | 0.992 ± 0.319 | 1.068 ± 0.462 | |
| Ankle Coronal | FAI | 0.713 ± 0.325 | 0.695 ± 0.284 | 0.831 ± 0.305 |
| CON | 0.835 ± 0.433 | 0.733 ± 0.246 | 0.774 ± 0.321 | |
| Ankle Horizontal | FAI | 0.723 ± 0.238 | 0.763 ± 0.252 | 0.918 ± 0.356 |
| CON | 0.810 ± 0.243 | 0.785 ± 0.202 | 0.818 ± 0.285 |
| Plane | Group | Faster Speed | Preferred Speed | Slower Speed |
|---|---|---|---|---|
| Hip Sagittal *,& | FAI | 0.182 ± 0.024 | 0.191 ± 0.025 | 0.210 ± 0.041 |
| CON | 0.175 ± 0.027 | 0.180 ± 0.032 | 0.187 ± 0.035 | |
| Hip Coronal & | FAI | 0.324 ± 0.044 | 0.310 ± 0.045 | 0.304 ± 0.043 |
| CON | 0.349 ± 0.036 | 0.321 ± 0.046 | 0.306 ± 0.046 | |
| Hip Horizontal * | FAI | 0.558 ± 0.099 | 0.588 ± 0.086 | 0.548 ± 0.118 |
| CON | 0.631 ± 0.094 | 0.586 ± 0.108 | 0.604 ± 0.092 | |
| Knee Sagittal * | FAI | 0.308 ± 0.027 | 0.311 ± 0.027 | 0.315 ± 0.023 |
| CON | 0.319 ± 0.023 | 0.327 ± 0.025 | 0.334 ± 0.031 | |
| Knee Coronal * | FAI | 0.438 ± 0.091 | 0.456 ± 0.100 | 0.407 ± 0.098 |
| CON | 0.485 ± 0.126 | 0.497 ± 0.092 | 0.472 ± 0.124 | |
| Knee Horizontal | FAI | 0.432 ± 0.061 | 0.436 ± 0.074 | 0.437 ± 0.079 |
| CON | 0.440 ± 0.067 | 0.442 ± 0.068 | 0.456 ± 0.062 | |
| Ankle Sagittal & | FAI | 0.281 ± 0.042 | 0.292 ± 0.049 | 0.311 ± 0.053 |
| CON | 0.275 ± 0.033 | 0.297 ± 0.022 | 0.319 ± 0.025 | |
| Ankle Coronal * | FAI | 0.354 ± 0.077 | 0.345 ± 0.075 | 0.339 ± 0.089 |
| CON | 0.396 ± 0.069 | 0.386 ± 0.066 | 0.360 ± 0.064 | |
| Ankle Horizontal | FAI | 0.474 ± 0.056 | 0.443 ± 0.080 | 0.467 ± 0.077 |
| CON | 0.462 ± 0.093 | 0.452 ± 0.089 | 0.436 ± 0.083 |
| Plane | Group | Faster Speed | Preferred Speed | Slower Speed |
|---|---|---|---|---|
| Hip Sagittal * | FAI | 5.64 ± 0.81 | 5.66 ± 1.17 | 5.98 ± 1.18 |
| CON | 6.17 ± 0.66 | 6.08 ± 0.54 | 6.84 ± 0.66 | |
| Hip Coronal & | FAI | 5.64 ± 1.25 | 5.72 ± 1.15 | 4.86 ± 1.14 |
| CON | 6.23 ± 1.10 | 5.78 ± 0.92 | 5.30 ± 1.19 | |
| Hip Horizontal | FAI | 5.48 ± 2.31 | 5.56 ± 2.17 | 4.21 ± 1.67 |
| CON | 6.39 ± 1.87 | 6.07 ± 2.56 | 4.99 ± 2.09 | |
| Knee Sagittal *,& | FAI | 5.90 ± 0.44 | 6.34 ± 0.78 | 6.31 ± 0.80 |
| CON | 6.32 ± 0.63 | 6.63 ± 0.45 | 7.09 ± 0.69 | |
| Knee Coronal | FAI | 5.44 ± 2.38 | 6.04 ± 1.95 | 5.22 ± 1.83 |
| CON | 5.62 ± 1.73 | 5.58 ± 1.87 | 5.98 ± 1.45 | |
| Knee Horizontal | FAI | 4.82 ± 1.13 | 4.91 ± 1.11 | 4.57 ± 1.40 |
| CON | 5.76 ± 1.52 | 4.85 ± 1.68 | 4.65 ± 1.35 | |
| Ankle Sagittal * | FAI | 5.23 ± 0.56 | 5.57 ± 0.56 | 5.68 ± 0.68 |
| CON | 6.02 ± 0.96 | 5.92 ± 0.68 | 6.34 ± 0.59 | |
| Ankle Coronal | FAI | 5.14 ± 1.01 | 5.29 ± 1.19 | 5.20 ± 1.42 |
| CON | 4.87 ± 0.88 | 4.75 ± 1.03 | 5.47 ± 1.01 | |
| Ankle Horizontal | FAI | 4.68 ± 1.10 | 4.83 ± 1.03 | 4.25 ± 1.29 |
| CON | 5.37 ± 1.69 | 4.76 ± 1.04 | 4.67 ± 1.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, W.; Zhao, K.; Xu, X.; Sun, M.; Wang, K.; Xu, Y.; Li, L. Effect of Running Speed on Gait Variability in Individuals with Functional Ankle Instability. Entropy 2025, 27, 1131. https://doi.org/10.3390/e27111131
Mao W, Zhao K, Xu X, Sun M, Wang K, Xu Y, Li L. Effect of Running Speed on Gait Variability in Individuals with Functional Ankle Instability. Entropy. 2025; 27(11):1131. https://doi.org/10.3390/e27111131
Chicago/Turabian StyleMao, Wenhui, Kanglong Zhao, Xiangguo Xu, Mengzi Sun, Kai Wang, Yilin Xu, and Li Li. 2025. "Effect of Running Speed on Gait Variability in Individuals with Functional Ankle Instability" Entropy 27, no. 11: 1131. https://doi.org/10.3390/e27111131
APA StyleMao, W., Zhao, K., Xu, X., Sun, M., Wang, K., Xu, Y., & Li, L. (2025). Effect of Running Speed on Gait Variability in Individuals with Functional Ankle Instability. Entropy, 27(11), 1131. https://doi.org/10.3390/e27111131







