Self-Diffusion in Two-Dimensional Colloidal Systems: A Computer Simulation Study
Abstract
1. Introduction
2. Models and Methods
3. Results and Discussion
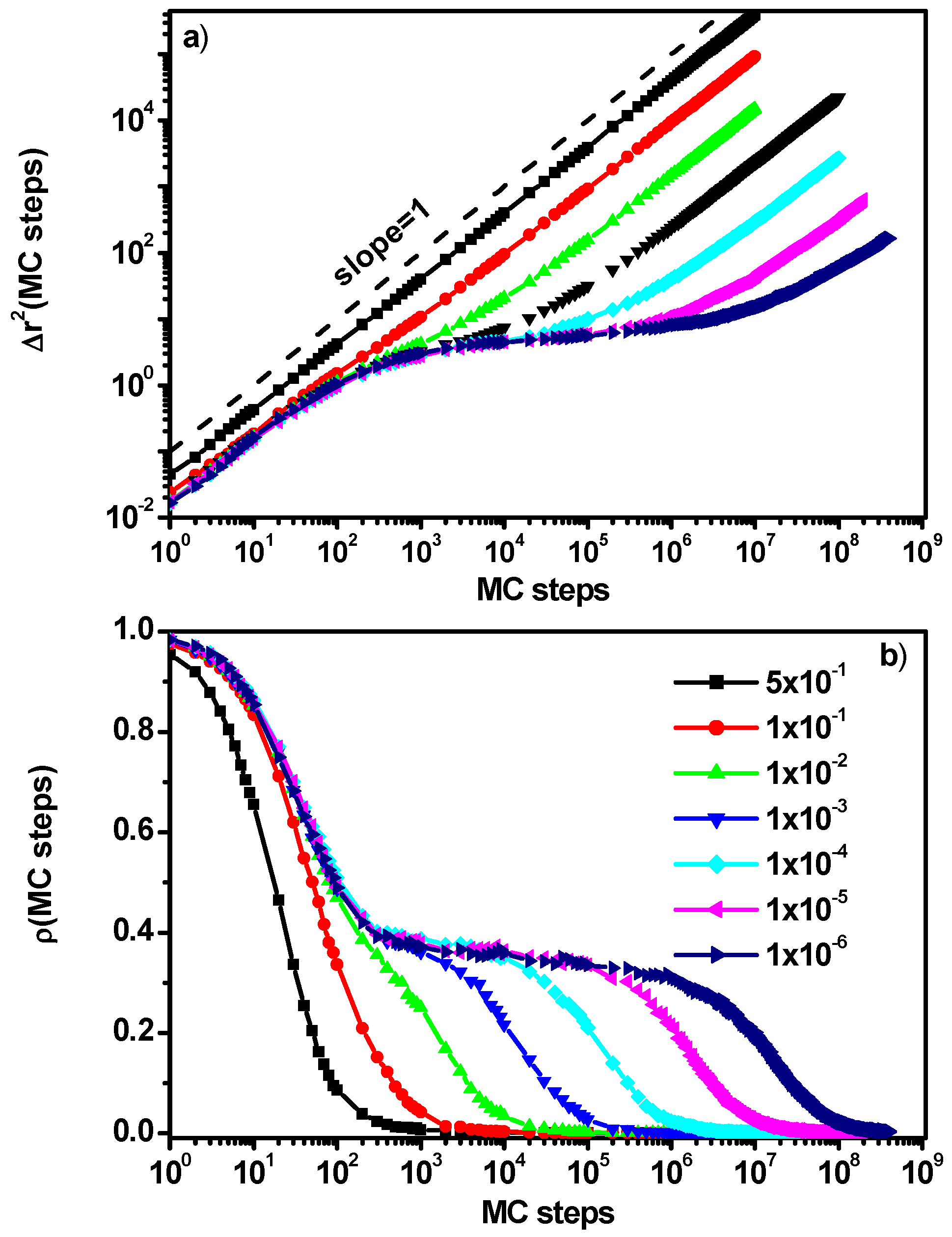
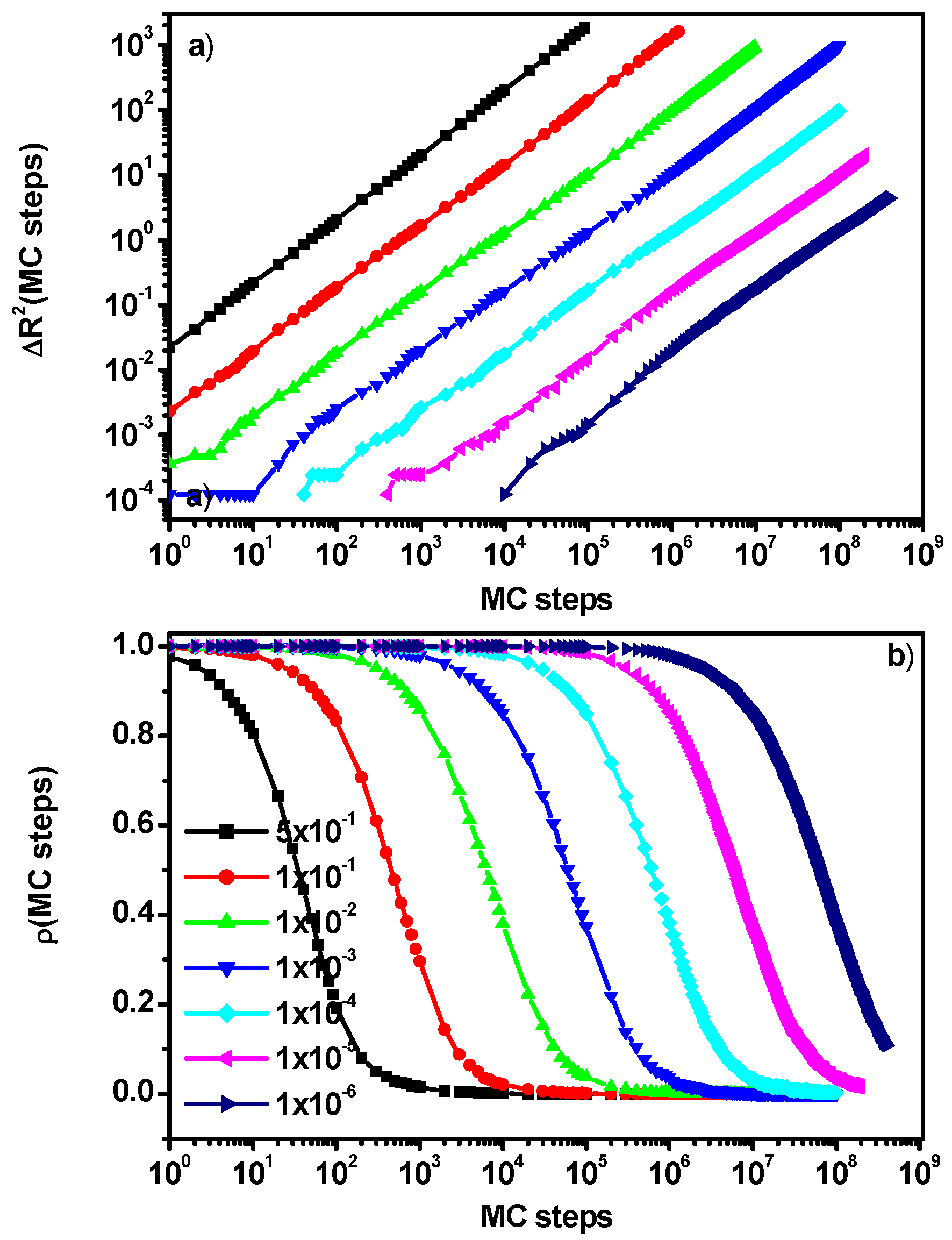
3.1. Mean-Squared Displacement
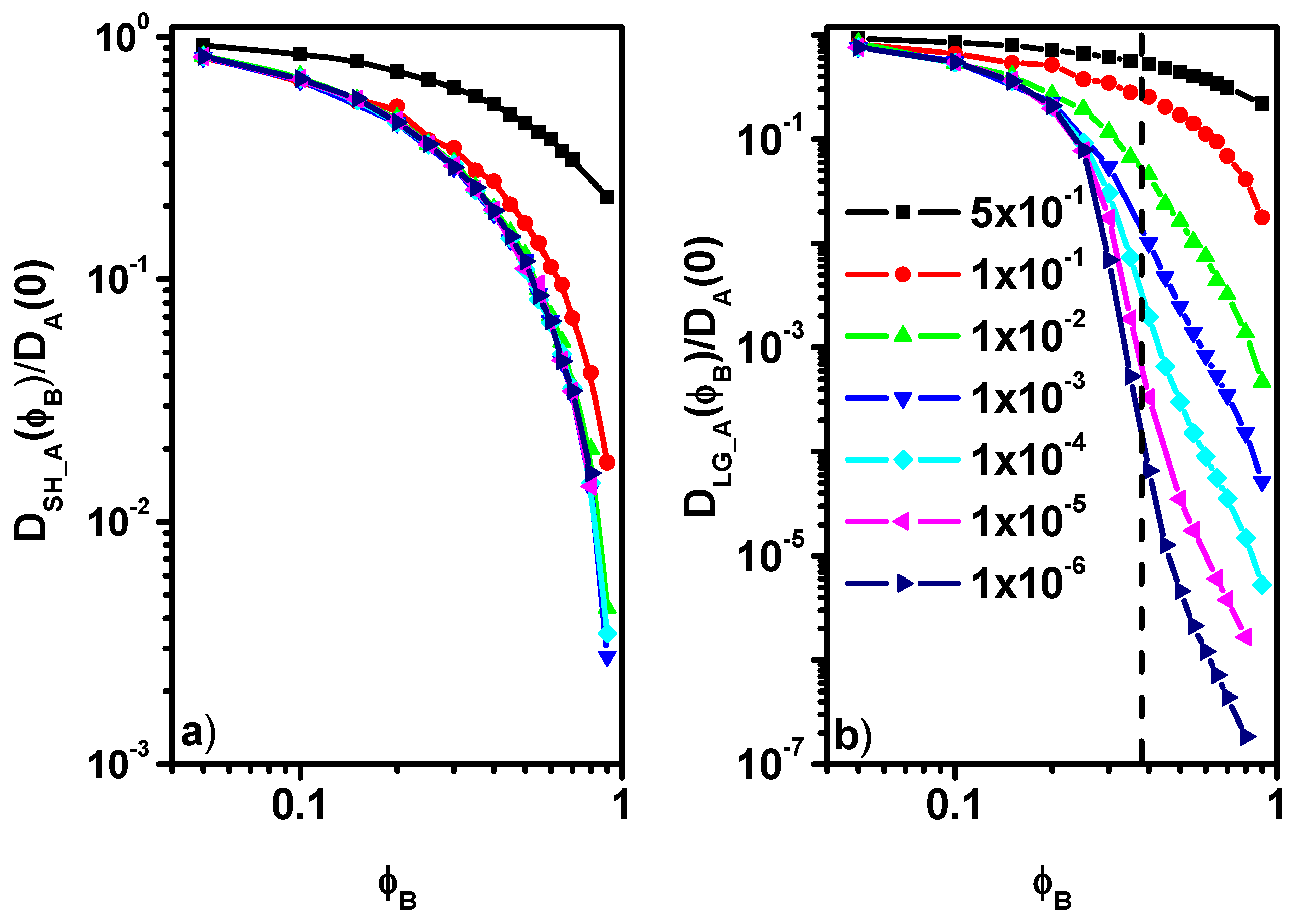
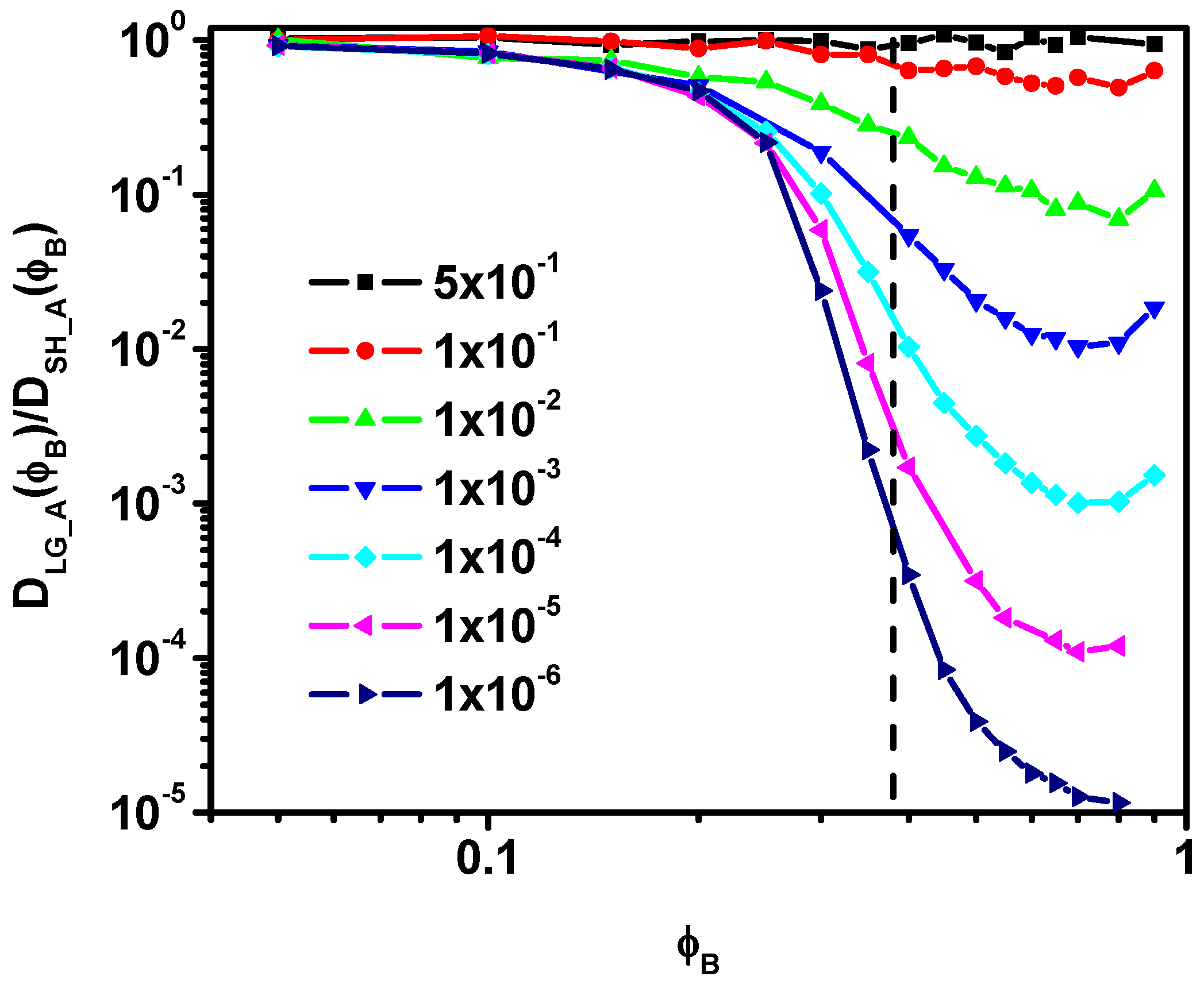
3.2. Diffusion Coefficient
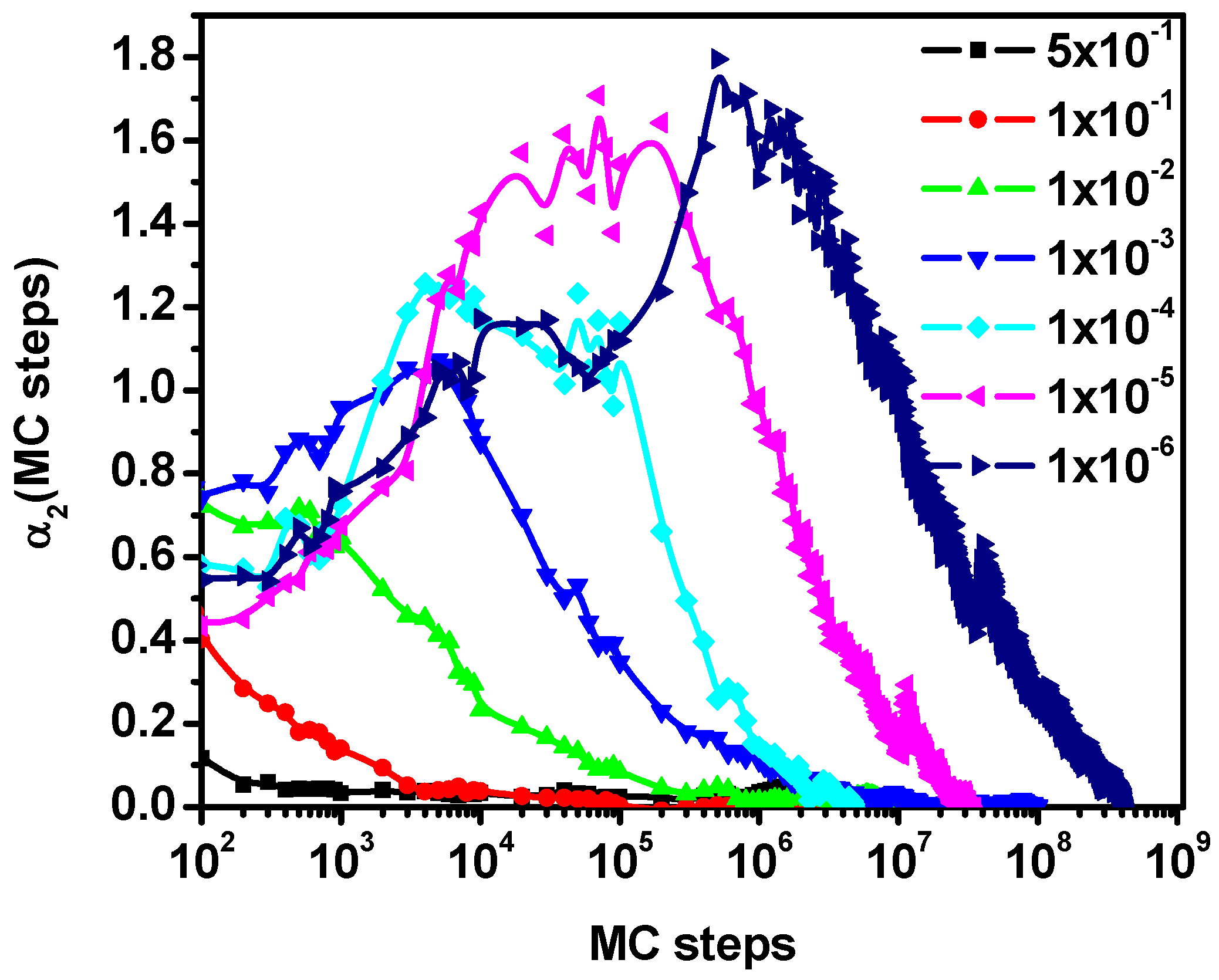
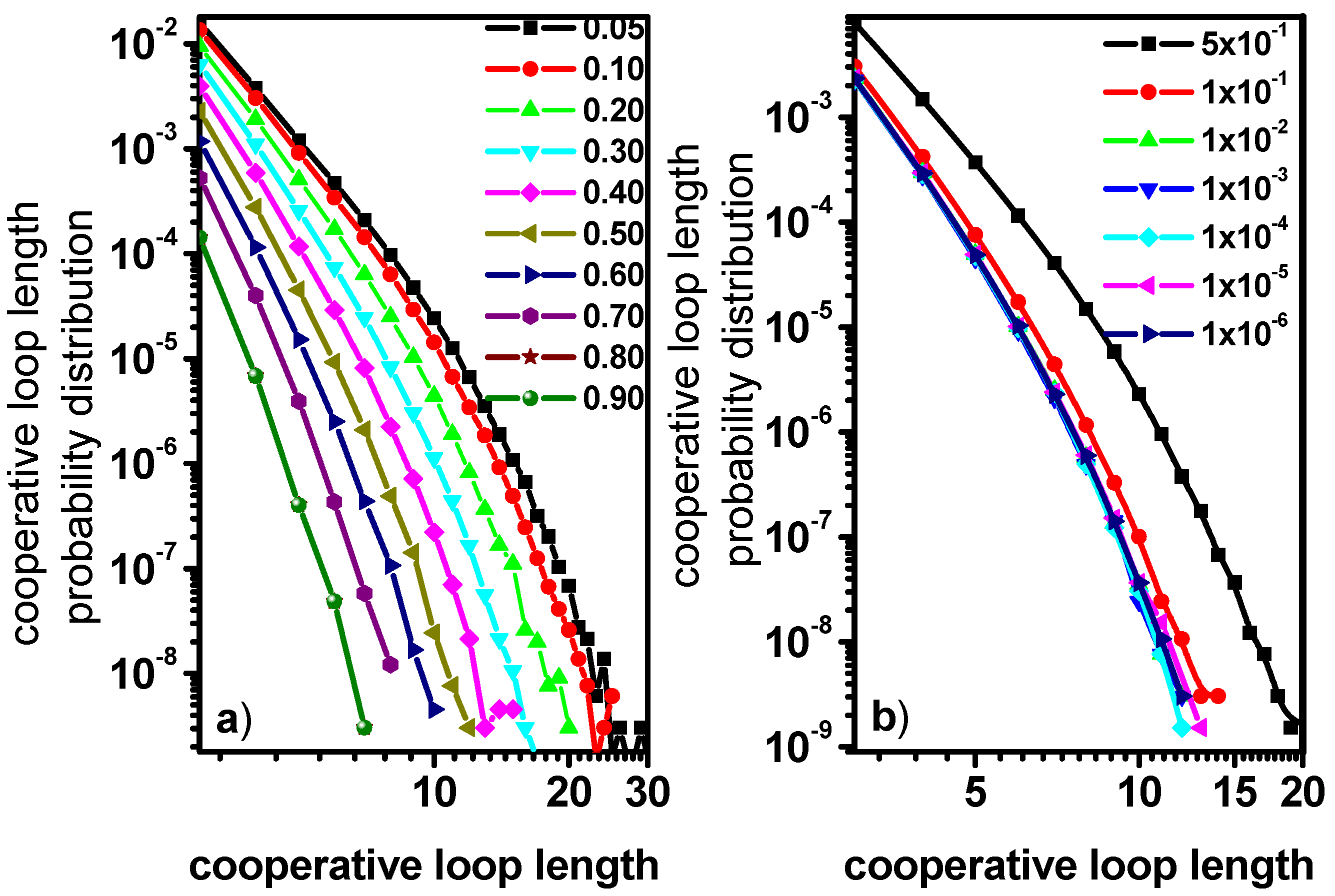
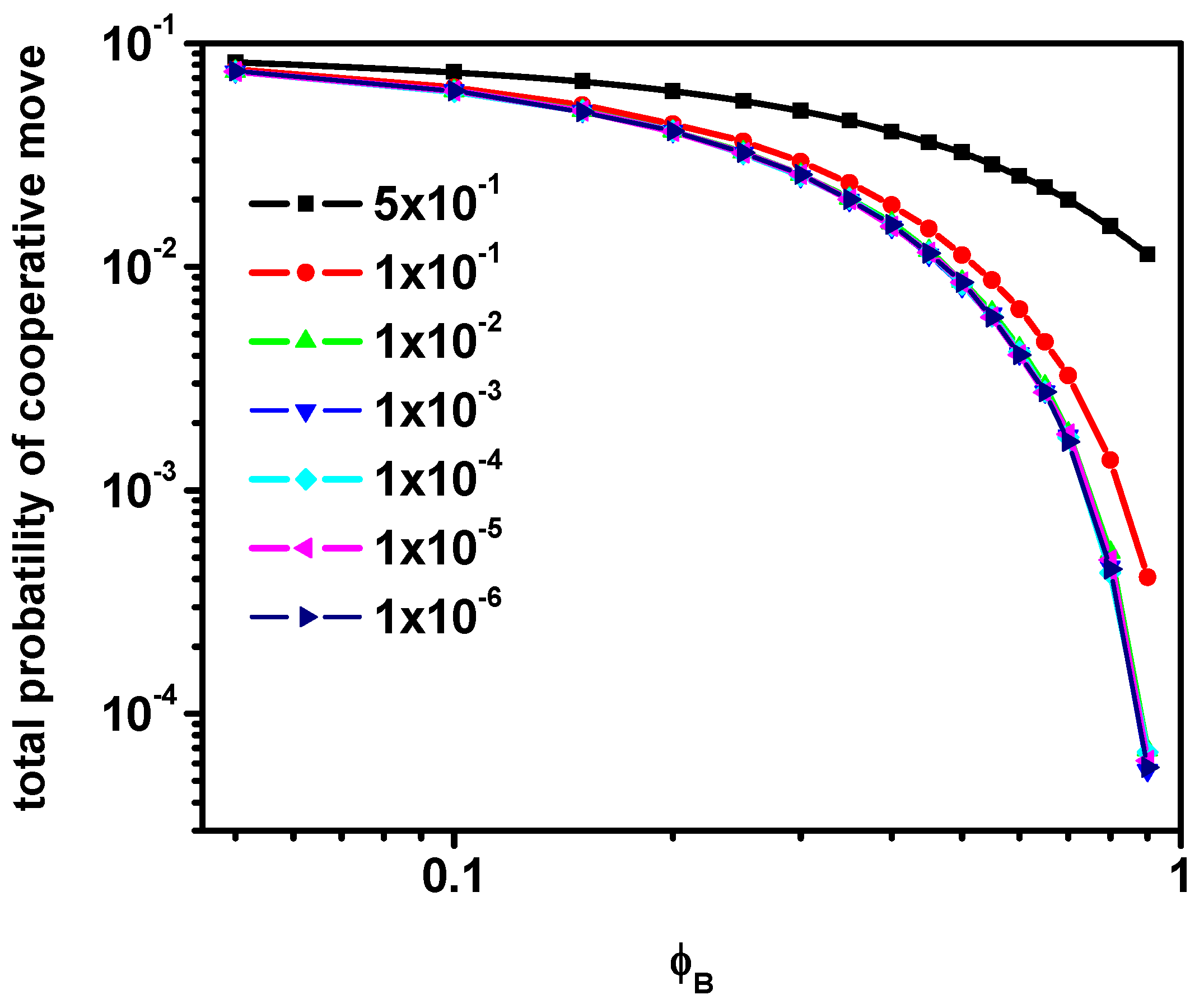
3.3. Motion in a Cooperative Loop
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Han, Y.; Alsayed, A.M.; Nobili, M.; Zhang, J.; Lubensky, T.C.; Yodh, A.G. Brownian motion of an ellipsoid. Science 2006, 314, 626–630. [Google Scholar] [CrossRef] [PubMed]
- Edmond, K.V.; Elsesser, M.T.; Hunter, G.L.; Weeks, G.R. Decoupling of rotational and translational diffusion in supercooled colloidal fluids. Proc. Natl. Acad. Sci. USA 2012, 109, 17891–17896. [Google Scholar] [CrossRef]
- Kraft, D.J.; Wittkowski, R.; ten Hagen, B.; Edmond, K.V.; Pine, D.J.; Löwen, H. Brownian motion and the hydrodynamic friction tensor for colloidal particles of complex shape. Phys. Rev. E 2013, 88, 050301. [Google Scholar] [CrossRef]
- García-Castillo, A.; Arauz-Lara, J.L. Static structure of confined dumbbell-sphere colloidal mixtures. Phys. Rev. E 2008, 78, 020401. [Google Scholar] [CrossRef]
- Neild, A.; Padding, J.T.; Yu, L.; Bhaduri, B.; Briels, W.J.; Ng, T.W. Translational and rotational coupling in Brownian rods near a solid surface. Phys. Rev. R 2010, 82, 041126. [Google Scholar] [CrossRef]
- Panczyk, M.N.; Wagner, N.J.; Furst, E.M. Short-time diffusivity of dicolloids. Phys. Rev. E 2014, 89, 062311. [Google Scholar] [CrossRef]
- Skinner, T.O.E.; Schnyder, S.K.; Aarts, D.G.A.L.; Horbach, J.; Dullens, R.P.A. Localization dynamics of fluids in random confinement. Phys. Rev. Lett. 2013, 111, 128301. [Google Scholar] [CrossRef]
- Peng, Y.; Chen, W.; Fischer, T.M.; Weitz, D.A.; Tong, P. Short-time self-diffusion of nearly hard spheres at an oil–water interface. J. Fluid Mech. 2009, 618, 243–261. [Google Scholar] [CrossRef]
- Santana-Solano, J.; Arauz-Lara, J.L. Hydrodynamic interactions in quasi-two-dimensional colloidal suspensions. Phys. Rev. Lett. 2001, 87, 038302. [Google Scholar] [CrossRef]
- Cui, B.; Diamant, H.; Lin, B.; Rice, S.A. Anomalous hydrodynamic interaction in a quasi-two-dimensional suspension. Phys. Rev. Lett. 2004, 92, 258301. [Google Scholar] [CrossRef]
- Santana-Solano, J.; Ramírez-Saito, A.; Arauz-Lara, J.L. Short-time dynamics in quasi-two-dimensional colloidal suspensions. Phys. Rev. Lett. 2005, 95, 198301. [Google Scholar] [CrossRef]
- Michailidou, V.N.; Petekidis, G.; Swan, J.W.; Brady, J.F. Dynamics of concentrated hard-sphere colloids near a wall. Phys. Rev. Lett. 2009, 102, 068302. [Google Scholar] [CrossRef] [PubMed]
- Skinner, T.O.E.; Aarts, D.G.A.L.; Dullens, R.P.A. Grain-boundary fluctuations in two-dimensional colloidal crystals. Phys. Rev. Lett. 2010, 105, 168301. [Google Scholar] [CrossRef] [PubMed]
- Bonilla-Capilla, B.; Ramírez-Saito, A.; Ojeda-López, M.A.; Arauz-Lara, J.L. Hydrodynamic interactions between colloidal particles in a planar pore. J. Phys. Condens. Matter 2012, 24, 464126. [Google Scholar] [CrossRef] [PubMed]
- Thorneywork, A.L.; Abbott, J.L.; Aarts, D.G.A.L.; Dullens, R.P.A. Two-dimensional melting of colloidal hard spheres. Phys. Rev. Lett. 2017, 118, 158001. [Google Scholar] [CrossRef]
- Sarmiento-Gómez, E.; Villanueva-Valencia, J.R.; Herrera-Velarde, S.; Ruiz-Santoyo, J.; Santana-Solano, J.; Arauz-Lara, J.L.; Castañeda-Priego, R. Short-time dynamics of monomers and dimers in quasi-two-dimensional colloidal mixtures. Phys. Rev. E 2016, 94, 012608. [Google Scholar] [CrossRef]
- Thorneywork, A.L.; Rozas, R.E.; Dullens, R.P.A.; Horbach, J. Effect of hydrodynamic interactions on self-diffusion of quasi-two-dimensional colloidal hard spheres. Phys. Rev. Lett. 2015, 115, 268301. [Google Scholar] [CrossRef]
- Royall, C.P.; Charbonneau, P.; Dijkstra, M.; Russo, J.; Smallenburg, F.; Speck, T.; Valeriani, C. Colloidal hard spheres: Triumphs, challenges, and mysteries. Rev. Mod. Phys. 2004, 96, 045003. [Google Scholar] [CrossRef]
- Alder, B.J.; Wainwright, T.E. Phase transition for a hard sphere system. J. Chem. Phys. 1957, 27, 1208–1209. [Google Scholar] [CrossRef]
- Lodge, J.F.M.; Heyes, D.M. Transient colloidal gels by Brownian dynamics computer simulation. Phys. Chem. Chem. Phys. 1999, 1, 2119–2130. [Google Scholar] [CrossRef]
- García Daza, F.A.; Cuetos, A.; Patti, A. Dynamic Monte Carlo simulations of inhomogeneous colloidal suspensions. Phys. Rev. E 2020, 102, 013302. [Google Scholar] [CrossRef] [PubMed]
- Patti, A.; Cuetos, A. Brownian dynamics and dynamic Monte Carlo simulations of isotropic and liquid crystal phases of anisotropic colloidal particles: A comparative study. Phys. Rev. E 2012, 86, 011403. [Google Scholar] [CrossRef] [PubMed]
- Sanz, E.; Marenduzzo, D. Dynamic Monte Carlo versus Brownian dynamics: A comparison for self-diffusion and crystallization in colloidal fluids. J. Chem. Phys. 2010, 32, 194102. [Google Scholar] [CrossRef] [PubMed]
- Jabbari-Farouji, S.; Trizac, E. Dynamic Monte Carlo simulations of anisotropic colloids. J. Chem. Phys. 2012, 137, 054107. [Google Scholar] [CrossRef]
- Pesché, R.; Kollmann, M.; Nägele, G. Brownian dynamics study of dynamic scaling and related freezing criteria in quasi-two-dimensional dispersions. J. Chem. Phys. 2001, 114, 8701–8707. [Google Scholar] [CrossRef]
- Falck, E.; Lahtinen, J.M.; Vattulainen, I.; Ala-Nissila, T. Influence of hydrodynamics on many-particle diffusion in 2D colloidal suspensions. Eur. Phys. J. B 2004, 13, 267–275. [Google Scholar] [CrossRef]
- Bleibel, J.; Dominguez, A.; Günther, F.; Harting, J.; Oettel, M. Hydrodynamic interactions induce anomalous diffusion under partial confinement. Soft Matter 2014, 10, 2945–2948. [Google Scholar] [CrossRef]
- Müller, P.; Pöschel, T. Event-driven molecular dynamics of soft particles. Phys. Rev. E 2013, 87, 033301. [Google Scholar] [CrossRef]
- Smallenburg, F. Efficient event-driven simulations of hard spheres. Eur. Phys. J. E 2022, 45, 22. [Google Scholar] [CrossRef]
- Castagnède, A.; Filion, L.; Smallenburg, F. Fast event-driven simulations for soft spheres: From dynamics to Laves phase nucleation. J. Chem. Phys. 2024, 161, 024116. [Google Scholar] [CrossRef]
- Ando, T.; Skolnick, J. Crowding and hydrodynamic interactions likely dominate in vivo macromolecular motion. Proc. Natl. Acad. Sci. 2010, 107, 18457–18462. [Google Scholar] [CrossRef] [PubMed]
- Fiore, A.M.; Swan, J.W. Fast Stokesian dynamics. J. Fluid Mech. 2019, 878, 544–597. [Google Scholar] [CrossRef]
- Ouaknin, G.Y.; Su, Y.; Zia, R.N. Parallel accelerated Stokesian dynamics with Brownian motion. J. Comput. Phys. 2021, 442, 110447. [Google Scholar] [CrossRef]
- Brown, F.L.H. Continuum simulations of biomembrane dynamics and the importance of hydrodynamic effects. Q. Rev. Biophys. 2011, 44, 391–432. [Google Scholar] [CrossRef]
- Lubachevsky, B.D. How to simulate billiards and similar systems. J. Comput. Phys. 1991, 94, 255–283. [Google Scholar] [CrossRef]
- Bannerman, M.N.; Sargant, R.; Lue, L. DynamO: A free o(N) general event-driven molecular dynamics simulator. J. Comput. Chem. 2011, 32, 3329–3338. [Google Scholar] [CrossRef]
- Banchio, A.J.; Nägele, G.; Bergenholtz, J. Collective diffusion, self-diffusion and freezing criteria of colloidal suspensions. J. Chem. Phys. 2000, 113, 3381–3396. [Google Scholar] [CrossRef]
- Doni, A. Hydrodynamic interactions between charged and uncharged Brownian colloids at a fluid-fluid interface. J. Colloid Interface Sci. 2022, 628 Pt B, 931–945. [Google Scholar] [CrossRef]
- Kundu, M.; Kritika, K.; Wani, Y.M.; Nikoubashman, A.; Howard, M.P. Exploring the role of hydrodynamic interactions in spherically confined drying colloidal suspensions. J. Chem. Phys. 2025, 162, 154904. [Google Scholar] [CrossRef]
- Varga, Z.; Swan, J. Hydrodynamic interactions enhance gelation in dispersions of colloids with short-ranged attraction and long-ranged repulsion. Soft Matter 2016, 12, 7670–7681. [Google Scholar] [CrossRef]
- Polanowski, P.; Sikorski, A. Simulation of diffusion in a crowded environment. Soft Matter 2014, 10, 3597–3607. [Google Scholar] [CrossRef]
- Polanowski, P.; Sikorski, A. Simulation studies of dynamical heterogeneity in a dense two-dimensional dimer-solvent system with obstacles. Entropy 2024, 26, 1086. [Google Scholar] [CrossRef] [PubMed]
- Santo, K.P.; Neimark, A.V. Dissipative particle dynamics simulations in colloid and interface science: A review. Adv. Colloid Interface Sci. 2021, 298, 102545. [Google Scholar] [CrossRef] [PubMed]
- Polanowski, P.; Sikorski, A. The concept of cooperative dynamics in simulations of soft matter. Front. Phys. 2020, 8, 607480. [Google Scholar] [CrossRef]
- Polanowski, P.; Pakula, T. Studies of mobility, interdiffusion, and self-diffusion in two-component mixtures using the dynamic lattice liquid model. J. Chem. Phys. 2003, 118, 11139–11146. [Google Scholar]
- Polanowski, P.; Sikorski, A. Liquid dynamics in a crowded environment: Bond percolation vs. site percolation. Chaos 2025, 35, 073101. [Google Scholar] [CrossRef]
- Kozanecki, M.; Hałagan, K.; Saramak, J.; Matyjaszewski, K. Diffusive properties of solvent molecules in the neighborhood of a polymer chain as seen by Monte-Carlo simulations. Soft Matter 2016, 12, 5519–5528. [Google Scholar] [CrossRef]
- Hałagan, K.; Duniec, P.; Kozanecki, M.; Sikorski, A. The influence of local constraints on the motion of solvent in polymer materials. Materials 2024, 17, 4711. [Google Scholar] [CrossRef]
- Polanowski, P.; Jeszka, J.K.; Sikorski, A. Dynamic properties of linear and cyclic chains in two dimensions. Computer simulation studies. Macromolecules 2014, 47, 4830–4839. [Google Scholar] [CrossRef]
- Polanowski, P.; Sikorski, A. The kinetics of polymer brush growth in the frame of the reaction diffusion front formalism. Polymers 2024, 16, 2963. [Google Scholar] [CrossRef]
- Polanowski, P.; Hałagan, K.; Pietrasik, J.; Jeszka, J.K.; Matyjaszewski, K. Growth of polymer brushes by “grafting from” via ATRP e Monte Carlo simulations. Polymer 2017, 130, 267–279. [Google Scholar] [CrossRef]
- Raj, W.; Hałagan, K.; Kadłubowski, S.; Maczugowska, P.; Szutkowski, K.; Jung, J.; Pietrasik, J.; Jurga, S.; Sikorski, A. The structure and dynamics of bottlebrushes: Simulation and experimental studies combined. Polymer 2022, 261, 125409. [Google Scholar] [CrossRef]
- Isvoran, A.; Vilaseca, E.; Unipan, L.; Garcés, J.L.; Mas, F. Computational study of diffusion in cellular two-dimensional crowed media modeled as mixtures of mobile and immobile obstacles. Rev. Roum. Chim. 2008, 53, 415–419. [Google Scholar]
- Vilaseca, E.; Isvoran, A.; Madurga, S.; Pastor, I.; Garcés, J.L.; Mas, F. New insights into diffusion in 3D crowded media by Monte Carlo simulations: Effect of size, mobility and spatial distribution of obstacles. Phys. Chem. Chem. Phys. 2011, 13, 7396–7407. [Google Scholar] [CrossRef]
- Berry, H.; Chaté, H. Anomalous diffusion due to hindering by mobile obstacles undergoing Brownian motion or Orstein-Ulhenbeck processes. Phys. Rev. E 2014, 89, 022708. [Google Scholar] [CrossRef]
- Wedemeier, A.; Merlitz, H.; Langowski, J. Anomalous diffusion in the presence of mobile obstacles. Europhys. Lett. 2009, 88, 38004. [Google Scholar] [CrossRef]
- Höfling, F.; Franosch, T. Anomalous transport in the crowded world of biological cells. Rep. Prog. Phys. 2013, 76, 046602. [Google Scholar] [CrossRef]
- Kompella, V.P.S.; Romano, M.C.; Stansfield, I.; Mancera1, R.L. What determines sub-diffusive behavior in crowded protein solutions? Biophys. J. 2024, 123, 134–146. [Google Scholar] [CrossRef]
- Cvitkovic, M.; Ghanti, D.; Raake, N.; Smith, A.-S. Crowding competes with trapping to enhance interfacial diffusion. Eur. Phys. J. Plus 2022, 137, 355. [Google Scholar] [CrossRef]
- Sokolov, I.M. Models of anomalous diffusion in crowded environments. Soft Matter 2012, 8, 9043–9052. [Google Scholar] [CrossRef]
- Hellmann, M.; Klafter, J.; Heermann, D.W.; Weiss, M. Challenges in determining anomalous diffusion in crowded fluids. J. Phys. Condens. Matter 2011, 23, 234113. [Google Scholar] [CrossRef]
- Ben-Avraham, D.; Havlin, S. Diffusion and Reactions in Fractals and Disordered Systems; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2010, 339, 1–77. [Google Scholar] [CrossRef]
- Metzler, R.; Jeon, J.-H.; Cherstvy, A.G.; Barkai, E. Anomalous diffusion models and their properties: Non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 2014, 16, 24128–24164. [Google Scholar] [CrossRef]
- Klett, K.; Cherstvy, A.G.; Shin, J.; Sokolov, I.M.; Metzler, R. Non-Gaussian, transiently anomalous, and ergodic self-diffusion of flexible dumbbells in crowded two-dimensional environments: Coupled translational and rotational motions. Phys. Rev. 2021, 104, 064603. [Google Scholar] [CrossRef]
- Zhang, X.; Dai, X.; Wei, W.; Chen, W.; Gao, L.; Yan, L.-T. Dynamic heterogeneities of rod rotation in macromolecular networks. Macromolecules 2023, 56, 8428–8437. [Google Scholar] [CrossRef]
- Zhang, X.; Dai, X.; Habib, M.; Gao, L.; Chen, W.; Wei, W.; Tang, Z.; Qi, X.; Gong, X.; Jiang, L.; et al. Unconventionally fast transport through sliding dynamics of rodlike particles in macromolecular networks. Nat. Commun. 2024, 15, 525. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polanowski, P.; Sikorski, A. Self-Diffusion in Two-Dimensional Colloidal Systems: A Computer Simulation Study. Entropy 2025, 27, 1091. https://doi.org/10.3390/e27111091
Polanowski P, Sikorski A. Self-Diffusion in Two-Dimensional Colloidal Systems: A Computer Simulation Study. Entropy. 2025; 27(11):1091. https://doi.org/10.3390/e27111091
Chicago/Turabian StylePolanowski, Piotr, and Andrzej Sikorski. 2025. "Self-Diffusion in Two-Dimensional Colloidal Systems: A Computer Simulation Study" Entropy 27, no. 11: 1091. https://doi.org/10.3390/e27111091
APA StylePolanowski, P., & Sikorski, A. (2025). Self-Diffusion in Two-Dimensional Colloidal Systems: A Computer Simulation Study. Entropy, 27(11), 1091. https://doi.org/10.3390/e27111091






