NetTopoBFT: Network Topology-Aware Byzantine Fault Tolerance for High-Coverage Consortium Blockchains
Abstract
1. Introduction
- Towards more efficient BFT consensus: Efficiency of replication is the highest priority for most BFT applications, including permissioned blockchain platforms such as HyperLedger and CCF [15]. After PBFT pioneered a practical solution for BFT consensus, numerous approaches have proposed extensions and optimizations to improve system performance. Among these, leader-based BFT algorithms have gained favor due to their efficient coordination in the consensus processes during normal operation.
- Towards more robust BFT consensus: While efficient BFT algorithms achieve high performance under normal operation, they may have sacrificed robustness and become vulnerable under a diverse attack vector. The second category comprises BFT algorithms that prioritize robustness and security against various attacks and malicious behavior. Key aspects under this category include defending against various attacks, penalizing misbehavior, and improving fairness in ordering transactions.
- Towards more available BFT consensus: These studies prioritize availability and system responsiveness under different network conditions. On the one hand, they have developed asynchronous BFT protocols that are capable of operating in scenarios with varying levels of synchrony. On the other hand, considering many leader-based algorithms are susceptible to single points of failure, particularly when targeting the primary server. In such cases, the system must first detect a primary failure and then invoke a view-change protocol to select a new primary, they have developed leaderless BFT protocols.
- By leveraging the node structure characteristics of a consortium blockchain, this study establishes a connection between weighted signed networks and consortium blockchains for the first time. Based on the weighted signed network, a communication model for the system is established, and then a two-layer Bayesian smoothing node evaluation model is designed. This model utilizes the node’s original reputation and the system’s global reputation as the two layers of smoothing to ultimately derive a unique global reputation for the node. This method not only can enhance the fault tolerance of the consortium blockchain but also provides a more comprehensive assessment of a node’s actual value through a dual-dimensional evaluation of ‘behavioral reputation + structural importance’.
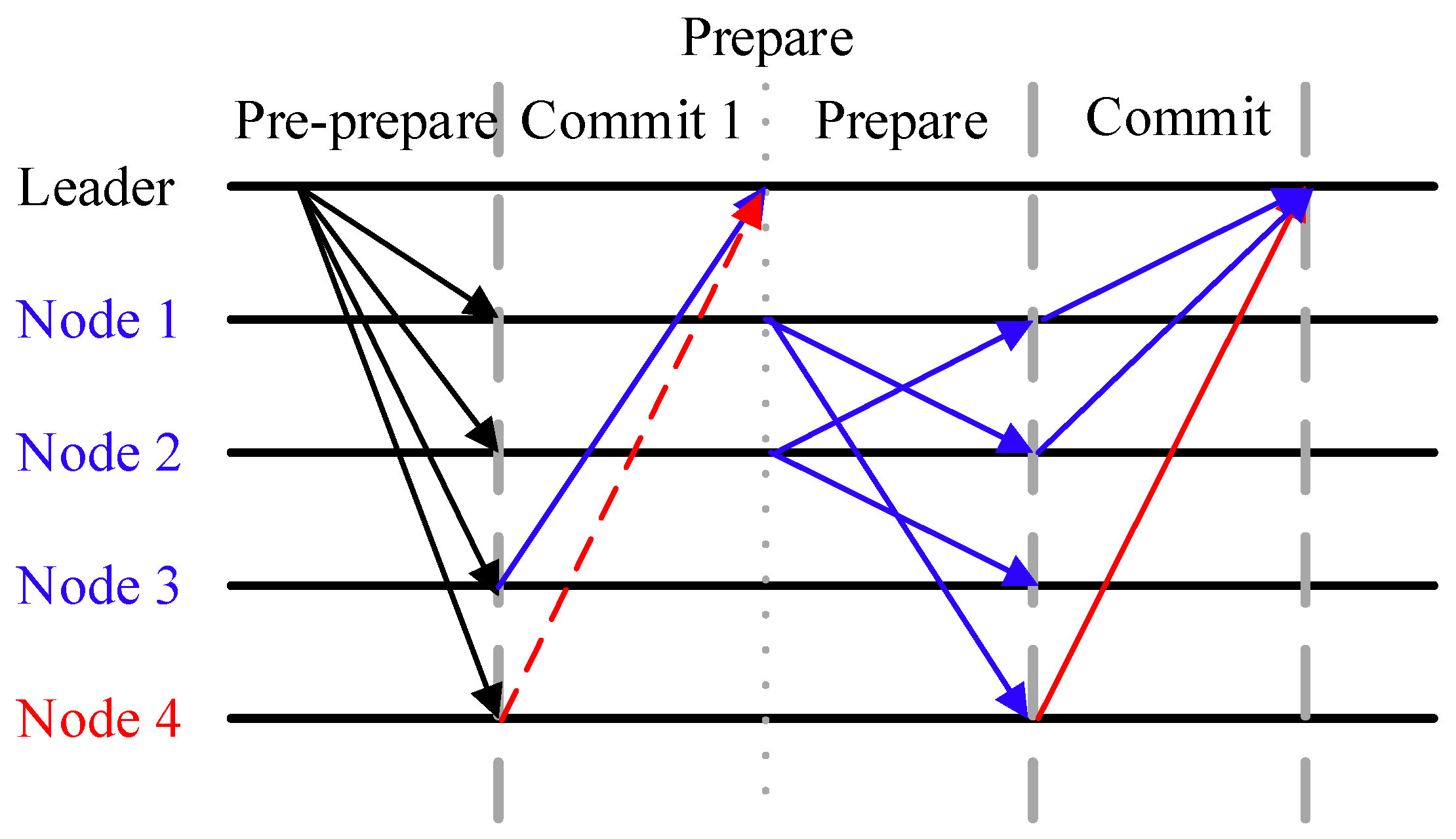
- A new consensus protocol and view-change protocol is designed. We first optimize the commit phase based on the PBFT three-phase consensus protocol and design an autonomous decision-making cross-verification mechanism based on neighbor node reputation to reduce the communication complexity of the consensus protocol, Meanwhile, we use a duplicate coverage-driven waitlisting mechanism to ensure network consistency before and after the view-change protocol.
- Theoretical analysis and experimental verification of the proposed algorithm from multiple aspects, including node selection, network communication overhead, network coverage, and network security are conducted. The results show that the algorithm can not only effectively select high-quality consensus nodes based on the structural characteristics of nodes in the consortium chain while ensuring a certain degree of decentralization, but also, to our knowledge, it is the first consortium chain BFT algorithm that achieves simultaneous optimization of communication overhead and security without affecting network coverage.
2. System Model
2.1. Network Model
2.2. Threat Model
3. The Design of NetTopoBFT
3.1. Framework Overview
- Node reputation value calculation: A two-dimensional evaluation of ‘behavioral reputation + structural importance’ is adopted, and a two-layer Bayesian smoothing is used to calculate the unique global reputation value of each node.
- Consensus Node Selection: Based on the calculated global reputation value, nodes are further screened according to their structural characteristics to select eligible nodes as consensus nodes.
- Leader Node and Its Backup Node Election: A verifiable random function is used to randomly select nodes from the consensus nodes as leader nodes, and corresponding backup nodes are selected based on the node coverage repetition rate metric.
- Blockchain consensus phase: After the leader node and its backup nodes are determined, the system enters a consensus process based on an improved PBFT. This phase introduces a dynamic weighting voting mechanism, using the node’s global reputation value as the voting weight. Concurrently, real-time coverage detection of backup nodes is integrated. If the leader node fails, the corresponding backup node can quickly assume proposal authority, ensuring communication efficiency optimization and topological structure stability for the consensus process.
3.2. Node Reputation Value Calculation
3.2.1. Node’s Original Smooth Reputation
3.2.2. Global Average Reputation
3.2.3. Node’s Global Reputation
3.3. Consensus Node Selection
3.4. Leader Node and Its Backup Node Election
3.4.1. VRF-Based Random Election Mechanism for Leader Nodes
3.4.2. Candidate Node Selection Strategy Based on Node Coverage Overlap Ratio
3.5. Blockchain Consensus Phase
4. Theoretical Analysis
4.1. Security Analysis
4.1.1. Edge Node Penetration Attacks
4.1.2. Targeted Attacks on Core Nodes
4.2. Liveness Analysis
5. Experimental Verification
5.1. Experimental Setup
5.2. Experimental Results
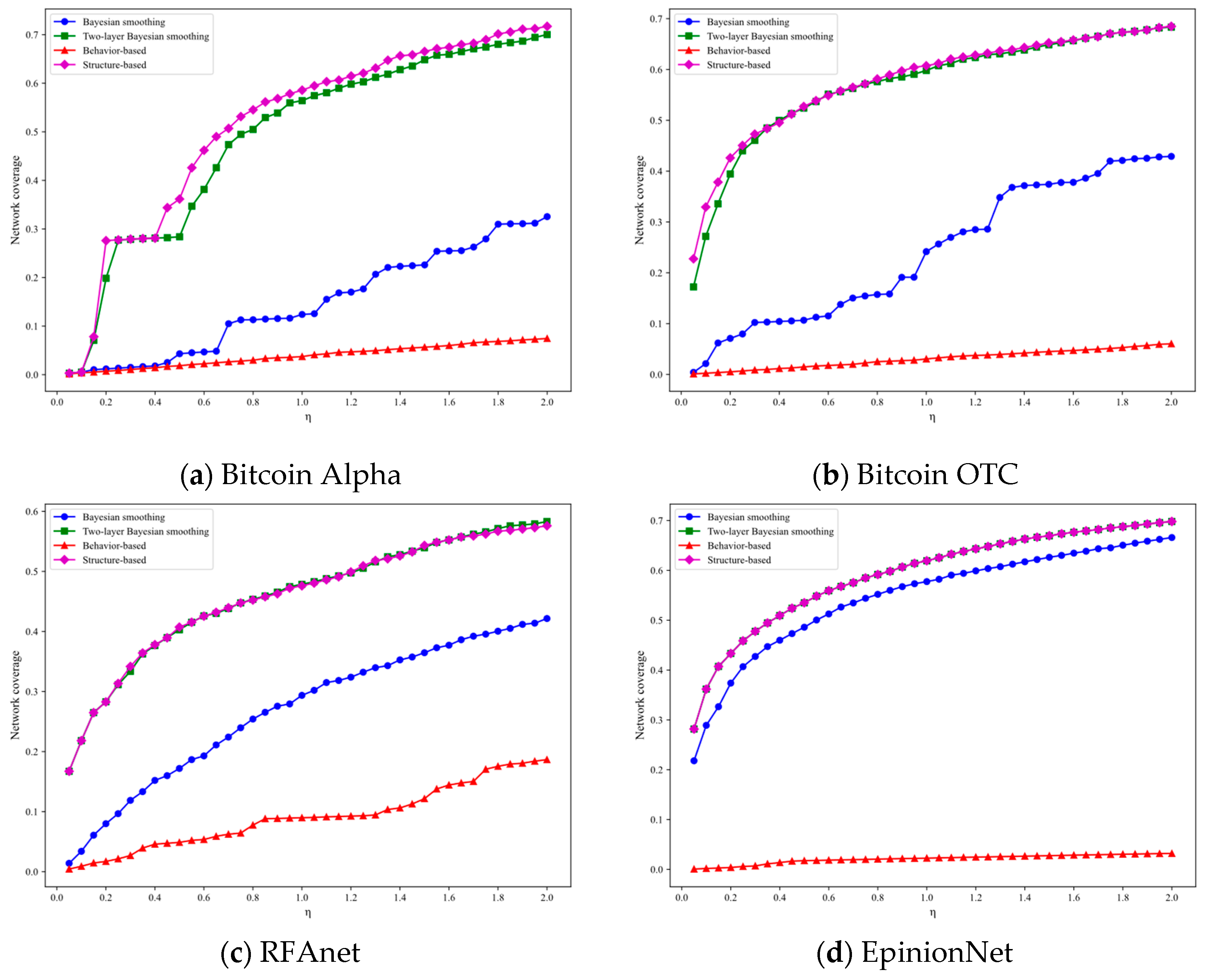
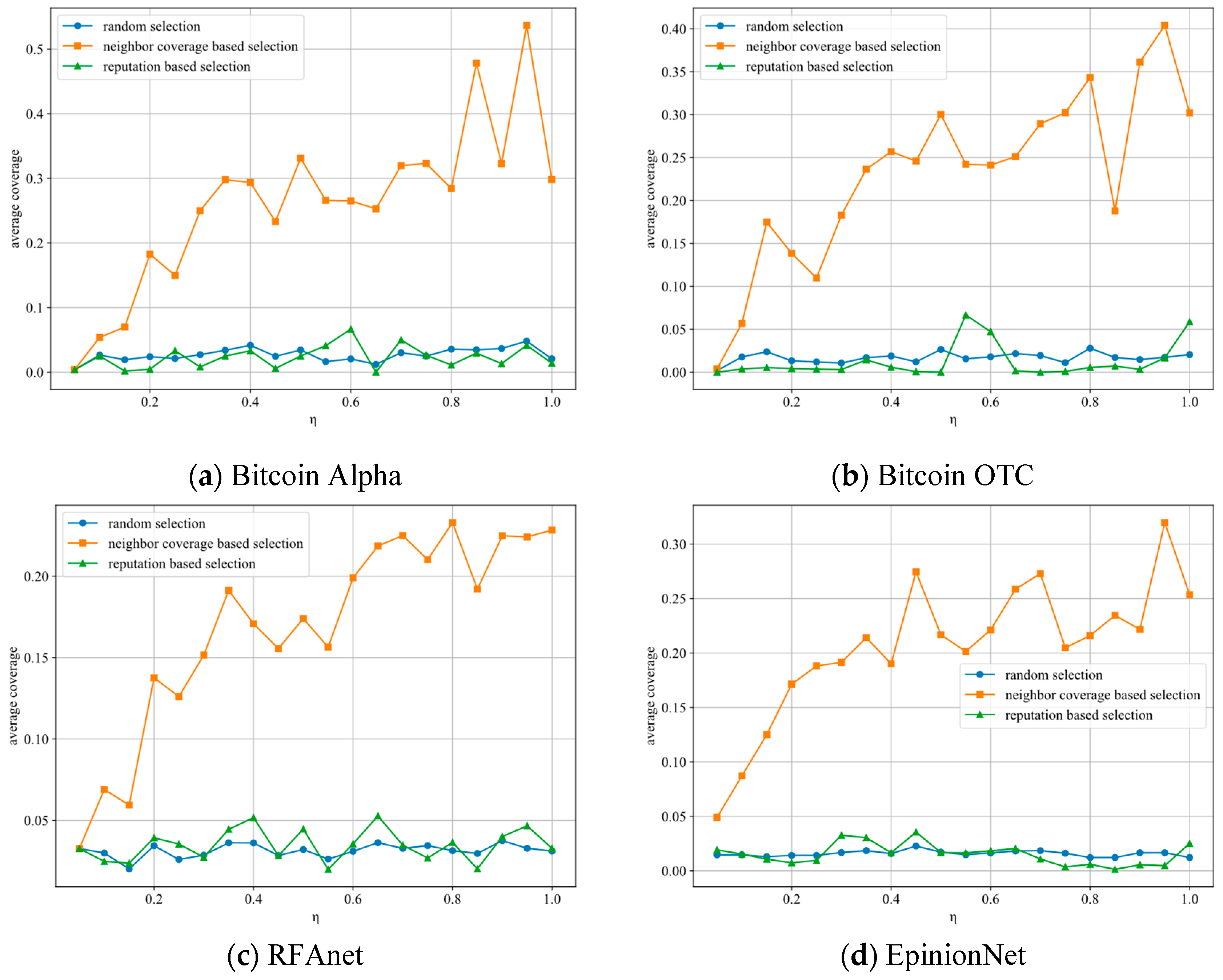
5.2.1. Evaluation of Node Selection Models
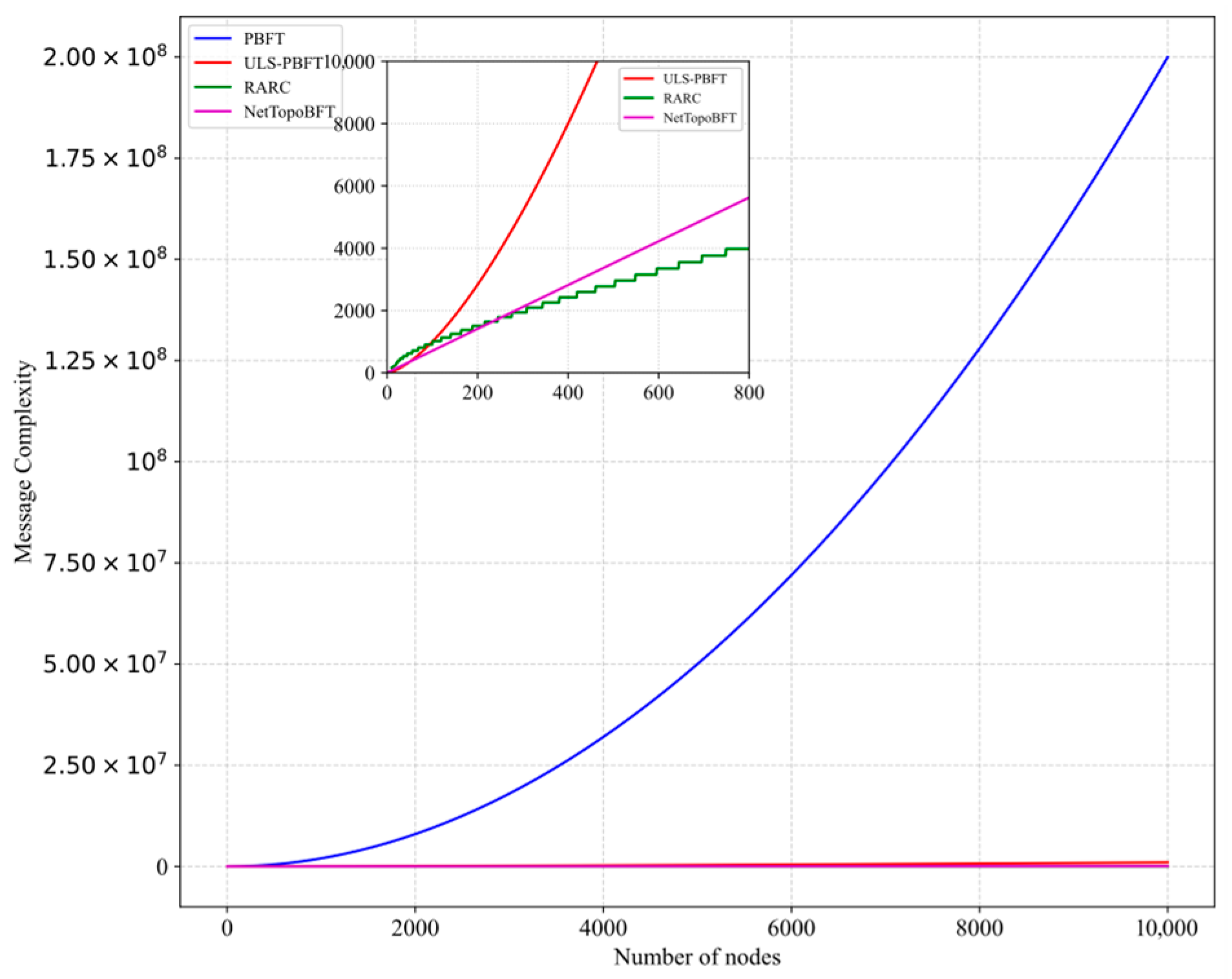
5.2.2. Communication Complexity
5.2.3. Security Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Della Monica, P.; Fedeli, M.; Salonico, C.; Vitaletti, A.; Zecchini, M. Enabling efficient verification in a DApp: The case of copyright management. Blockchain Res. Appl. 2025, 6, 100234. [Google Scholar] [CrossRef]
- Sun, W. Application of blockchain technology in the supply chain finance. In Proceedings of the 2022 7th International Conference on Cloud Computing and Big Data Analytics (ICCCBDA), Chengdu, China, 22–24 April 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 205–209. [Google Scholar]
- Rout, S.; Koul, B. Application of Blockchain Technology to facilitate security in Smart Grid. In Proceedings of the 2022 IEEE Delhi Section Conference (DELCON), New Delhi, India, 11–13 February 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–8. [Google Scholar]
- Xu, G.; Liu, Y.; Khan, P.W. Improvement of the DPoS consensus mechanism in blockchain based on vague sets. IEEE Trans. Ind. Inform. 2019, 16, 4252–4259. [Google Scholar] [CrossRef]
- Xiong, Y.; Hu, C. Comparative research on blockchain consensus algorithms. In Proceedings of the 2022 International Conference on Blockchain Technology and Information Security (ICBCTIS), Huaihua City, China, 15–17 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 160–164. [Google Scholar]
- Jo, M.; Kim, D.; Park, S. Analysis of Byzantine Fault Tolerant Consensus Algorithms. In Proceedings of the 2024 International Conference on Information Networking (ICOIN), Ho Chi Minh City, Vietnam, 17–19 January 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 205–207. [Google Scholar]
- Yang, J.; Jia, Z.; Su, R.; Wu, X.; Qin, J. Improved fault-tolerant consensus based on the PBFT algorithm. IEEE Access 2022, 10, 30274–30283. [Google Scholar] [CrossRef]
- Tang, S.; Wang, Z.; Jiang, J.; Ge, S.; Tan, G. Improved PBFT algorithm for high-frequency trading scenarios of alliance blockchain. Sci. Rep. 2022, 12, 4426. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Li, X.; Zhao, H.; Yu, B.; Zhou, T.; Cheng, H.; Sheng, N. MANDALA: A scalable blockchain model with mesh-and-spoke network and H-PBFT consensus algorithm. Peer-to-Peer Netw. Appl. 2023, 16, 226–244. [Google Scholar] [CrossRef]
- Liu, Y.; Xing, X.; Cheng, H.; Li, D.; Guan, Z.; Liu, J.; Wu, Q. A flexible sharding blockchain protocol based on cross-shard byzantine fault tolerance. IEEE Trans. Inf. Forensics Secur. 2023, 18, 2276–2291. [Google Scholar] [CrossRef]
- Wan, J.; Hu, K.; Li, J.; Su, H. AnonymousFox: An efficient and scalable blockchain consensus algorithm. IEEE Internet Things J. 2022, 9, 24236–24252. [Google Scholar] [CrossRef]
- Klianev, I. Different perspectives on FLP impossibility. arXiv 2022, arXiv:2210.02695. [Google Scholar]
- Gilbert, S.; Lynch, N. Brewer’s conjecture and the feasibility of consistent, available, partition-tolerant web services. ACM Sigact News 2002, 33, 51–59. [Google Scholar] [CrossRef]
- Zhang, G.; Pan, F.; Mao, Y.; Tijanic, S.; Dang’Ana, M.; Motepalli, S.; Zhang, S.; Jacobsen, H.A. Reaching consensus in the byzantine empire: A comprehensive review of bft consensus algorithms. ACM Comput. Surv. 2024, 56, 1–41. [Google Scholar] [CrossRef]
- Shamis, A.; Pietzuch, P.; Canakci, B.; Castro, M.; Fournet, C.; Ashton, E.; Chamayou, A.; Clebsch, S.; Delignat-Lavaud, A.; Kerner, M.; et al. IA-CCF: Individual accountability for permissioned ledgers. In Proceedings of the 19th USENIX Symposium on Networked Systems Design and Implementation (NSDI 22), Renton, WA, USA, 4–6 April 2022; pp. 467–491. [Google Scholar]
- Kotla, R.; Alvisi, L.; Dahlin, M.; Clement, A.; Wong, E. Zyzzyva: Speculative byzantine fault tolerance. In Proceedings of the Twenty-First ACM SIGOPS Symposium on Operating Systems Principles, Stevenson, WA, USA, 14–17 October 2007; pp. 45–58. [Google Scholar]
- Gueta, G.G.; Abraham, I.; Grossman, S.; Malkhi, D.; Pinkas, B.; Reiter, M.; Seredinschi, D.-A.; Tamir, O.; Tomescu, A. SBFT: A scalable and decentralized trust infrastructure. In Proceedings of the 2019 49th Annual IEEE/IFIP International Conference on Dependable Systems and Networks (DSN), Portland, OR, USA, 24–27 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 568–580. [Google Scholar]
- Yin, M.; Malkhi, D.; Reiter, M.K.; Gueta, G.G.; Abraham, I. HotStuff: BFT consensus with linearity and responsiveness. In Proceedings of the 2019 ACM Symposium on Principles of Distributed Computing, Toronto, ON, Canada, 29 July–2 August 2019; pp. 347–356. [Google Scholar]
- Zhang, Y.; Setty, S.; Chen, Q.; Zhou, L.; Alvisi, L. Byzantine ordered consensus without byzantine oligarchy. In Proceedings of the 14th USENIX Symposium on Operating Systems Design and Implementation (OSDI 20), Online, 4–6 November 2020; pp. 633–649. [Google Scholar]
- Stathakopoulou, C.; Rüsch, S.; Brandenburger, M.; Vukolić, M. Adding fairness to order: Preventing front-running attacks in bft protocols using tees. In Proceedings of the 2021 40th International Symposium on Reliable Distributed Systems (SRDS), Chicago, IL, USA, 20–23 September 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 34–45. [Google Scholar]
- Zhang, G.; Jacobsen, H.A. Prosecutor: An efficient BFT consensus algorithm with behavior-aware penalization against Byzantine attacks. In Proceedings of the 22nd International Middleware Conference, Québec City, QC, Canada, 6–10 December 2021; pp. 52–63. [Google Scholar]
- Zhang, G.; Pan, F.; Tijanic, S.; Jacobsen, H.A. Prestigebft: Revolutionizing view changes in bft consensus algorithms with reputation mechanisms. In Proceedings of the 2024 IEEE 40th International Conference on Data Engineering (ICDE), Utrecht, The Netherlands, 13–16 May 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1930–1943. [Google Scholar]
- Stathakopoulou, C.; David, T.; Pavlovic, M.; Vukolić, M. Mir-bft: High-throughput robust bft for decentralized networks. arXiv 2019, arXiv:1906.05552. [Google Scholar]
- Stathakopoulou, C.; Pavlovic, M.; Vukolić, M. State machine replication scalability made simple. In Proceedings of the Seventeenth European Conference on Computer Systems, Rennes, France, 5–8 April 2022; pp. 17–33. [Google Scholar]
- Keidar, I.; Kokoris-Kogias, E.; Naor, O.; Spiegelman, A. All you need is dag. In Proceedings of the 2021 ACM Symposium on Principles of Distributed Computing, Virtual Event, 26–30 July 2021; pp. 165–175. [Google Scholar]
- Danezis, G.; Kokoris-Kogias, L.; Sonnino, A.; Spiegelman, A. Narwhal and tusk: A dag-based mempool and efficient bft consensus. In Proceedings of the Seventeenth European Conference on Computer Systems, Rennes, France, 5–8 April 2022; pp. 34–50. [Google Scholar]
- Crain, T.; Gramoli, V.; Larrea, M.; Raynal, M. Dbft: Efficient leaderless byzantine consensus and its application to blockchains. In Proceedings of the 2018 IEEE 17th International Symposium on Network Computing and Applications (NCA), Cambridge, MA, USA, 1–3 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–8. [Google Scholar]
- Miller, A.; Xia, Y.; Croman, K.; Shi, E.; Song, D. The honey badger of BFT protocols. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; pp. 31–42. [Google Scholar]
- Amir, Y.; Coan, B.; Kirsch, J.; Lane, J. Prime: Byzantine replication under attack. IEEE Trans. Dependable Secur. Comput. 2010, 8, 564–577. [Google Scholar] [CrossRef]
- Veronese, G.S.; Correia, M.; Bessani, A.N.; Lung, L.C. Spin one’s wheels? Byzantine fault tolerance with a spinning primary. In Proceedings of the 2009 28th IEEE International Symposium on Reliable Distributed Systems, Niagara Falls, NY, USA, 27–30 September 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 135–144. [Google Scholar]
- Momose, A.; Cruz, J.P.; Kaji, Y. Hybrid-bft: Optimistically Responsive Synchronous Consensus with Optimal Latency or Resilience. Cryptology Eprint Archive. 2020. Available online: https://eprint.iacr.org/2020/406 (accessed on 19 October 2025).
- Androulaki, E.; Barger, A.; Bortnikov, V.; Cachin, C.; Christidis, K.; De Caro, A.; Enyeart, D.; Ferris, C.; Manevich, Y.; Muralidharan, S.; et al. Hyperledger fabric: A distributed operating system for permissioned blockchains. In Proceedings of the Thirteenth EuroSys Conference, Porto, Portugal, 23–26 April 2018; pp. 1–15. [Google Scholar]
- Wang, H.; Wang, T.; Shi, L.; Liu, N.; Zhang, S. A blockchain-empowered framework for decentralized trust management in internet of battlefield things. Comput. Netw. 2023, 237, 110048. [Google Scholar] [CrossRef]
- Chen, R.; Guan, Y. Hierarchical Reputation Consensus Model for VANET. IEEE Access 2025, 13, 3521–3531. [Google Scholar] [CrossRef]
- Aublin, P.L.; Mokhtar, S.B.; Quéma, V. Rbft: Redundant byzantine fault tolerance. In Proceedings of the 2013 IEEE 33rd International Conference on Distributed Computing Systems, Philadelphia, PA, USA, 8–11 July 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 297–306. [Google Scholar]
- Zhang, R.; Xue, R.; Liu, L. Security and privacy on blockchain. ACM Comput. Surv. (CSUR) 2019, 52, 1–34. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Z.; Sun, Y.; Liu, Y.; Zhang, L. Blockchain network analysis: A comparative study of decentralized banks. In Science and Information Conference; Springer Nature Switzerland: Cham, Switzerland, 2023; pp. 1022–1042. [Google Scholar]
- Feng, L.; Yu, B.; He, Z.; Yao, S. A Verifiable Transaction Selection Method for DAG Blockchain with VRF. IEEE Internet Things J. 2025, 12, 24185–24198. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, Y.; Guo, D.; Luo, L.; Li, L.; Nian, Q.; Zhu, S.; Yang, F. A reputation awareness randomization consensus mechanism in blockchain systems. IEEE Internet Things J. 2024, 11, 32745–32758. [Google Scholar] [CrossRef]
- Yang, W.; Dai, X.; Xiao, J.; Jin, H. LDV: A lightweight DAG-based blockchain for vehicular social networks. IEEE Trans. Veh. Technol. 2020, 69, 5749–5759. [Google Scholar] [CrossRef]
- Kumar, S.; Spezzano, F.; Subrahmanian, V.S.; Faloutsos, C. Edge weight prediction in weighted signed networks. In Proceedings of the 2016 IEEE 16th International Conference on Data Mining (ICDM), Barcelona, Spain, 12–15 December 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 221–230. [Google Scholar]
- Luo, H. ULS-PBFT: An ultra-low storage overhead PBFT consensus for blockchain. Blockchain Res. Appl. 2023, 4, 100155. [Google Scholar] [CrossRef]


| Categories | Subcategories | Algorithms | |
|---|---|---|---|
| PBFT | More efficient | Reducing message complexity | Zyzzyva [16], SBFT [17], Hotstuff [18] |
| Ordering fairness | Pompe [19], Fairy [20] | ||
| Reputation consensus | Prosecutor [21], PrestigeBFT [22] | ||
| Multi-leader | MirBFT [23], ISS [24] | ||
| DAG-based | DAG-Rider [25], Narwhal [26] | ||
| More robust | Asynchronous and leaderless | DBFT [27], Honeybadger [28] | |
| More available | Defending various attacks | Timing attack: Prime [29] | |
| Performance attack: Aardvark [30] |
| Symbol | Description |
|---|---|
| Node number | |
| The node’s original in-degree credibility and original out-degree credibility | |
| The nodes’ original smoothed in-degree credibility and out-degree credibility | |
| Number of directed edges to a node | |
| Number of directed edges from node | |
| The nodes’ original smoothed reputation | |
| Global average reputation | |
| The global reputation of node |
| Consensus Mechanism | Communication Complexity | Byzantine Fault Tolerance | Scalability |
|---|---|---|---|
| PBFT | Low | ||
| Tendermint | Medium | ||
| DPoS | - | High | |
| Hotstuff | High | ||
| Zyzzyva | Medium | ||
| NetTopoBFT | High |
| Network | Soc-Sign-Bitcoinalpha | Soc-Sign-Bitcoinotc | RFAnet | EpinionNet |
|---|---|---|---|---|
| Vertices | 3783 | 5881 | 9654 | 125,247 |
| Edges | 24,186 | 35,592 | 104,554 | 1,048,575 |
| Average node degree | 6.39 | 6.05 | 10.03 | 8.37 |
| Median node degree | 4 | 4 | 4 | 2 |
| Maximum node degree | 511 | 795 | 627 | 9734 |
| Minimum node degree | 1 | 1 | 1 | 1 |
| Positive Edges | 93% | 89% | 83.7% | 95.42% |
| Proportion | Dataset | Index | Two-Layer Bayesian Smoothing | Bayesian Smoothing | Behavior-Based | Structure-Based |
|---|---|---|---|---|---|---|
| 5% | Bitcoin Alpha | Q1 | 95.21 | 97.86 | 100 | 90.91 |
| 84.66 | 42.86 | 6.35 | 100 | |||
| Bitcoin OTC | Q1 | 89.00 | 97.55 | 98.16 | 84.54 | |
| 98.64 | 55.44 | 5.1 | 100 | |||
| RFAnet | Q1 | 98.23 | 99.12 | 99.37 | 97.96 | |
| 100 | 100 | 62.03 | 100 | |||
| EpinionNet | Q1 | 99.16 | 99.49 | 100 | 99.19 | |
| 100 | 100 | 67.65 | 100 | |||
| 10% | Bitcoin Alpha | Q1 | 94.40 | 98.34 | 100 | 92.80 |
| 88.89 | 44.44 | 11.90 | 92.06 | |||
| Bitcoin OTC | Q1 | 91.95 | 97.52 | 87.11 | 87.11 | |
| 98.3 | 54.59 | 11.39 | 91.84 | |||
| RFAnet | Q1 | 97.61 | 98.77 | 98.91 | 97.59 | |
| 100 | 99.69 | 65.28 | 100 | |||
| EpinionNet | Q1 | 97.55 | 98.50 | 100 | 97.89 | |
| 100 | 100 | 75.13 | 100 | |||
| 20% | Bitcoin Alpha | Q1 | 95.60 | 97.92 | 99.01 | 94.36 |
| 86.24 | 50.66 | 26.72 | 82.54 | |||
| Bitcoin OTC | Q1 | 92.01 | 97.42 | 89.44 | 89.44 | |
| 84.78 | 53.32 | 21.17 | 77.47 | |||
| RFAnet | Q1 | 96.32 | 97.45 | 98.74 | 96.09 | |
| 97.98 | 100 | 62.95 | 100 | |||
| EpinionNet | Q1 | 95.12 | 97.32 | 99.94 | 96.21 | |
| 99.99 | 92.67 | 73.25 | 99.81 |
| In-Degree Reputation | Out-Degree Reputation | Avg In-Degree Reputation | Avg Out-Degree Reputation | Degree Centrality | Total Reputation | |
|---|---|---|---|---|---|---|
| 1 | 50 | 50 | 10 | 10 | 5 | 2.39967 |
| 2 | 60 | 60 | 10 | 10 | 6 | 2.4421 |
| 3 | 70 | 70 | 10 | 10 | 7 | 2.46731 |
| 4 | 80 | 80 | 10 | 10 | 8 | 2.48170 |
| 5 | 90 | 90 | 10 | 10 | 9 | 2.48909 |
| 6 | 100 | 100 | 10 | 10 | 10 | 2.49190 |
| 7 | 200 | 200 | 10 | 10 | 20 | 2.44862 |
| 8 | 300 | 300 | 10 | 10 | 30 | 2.40087 |
| 9 | 500 | 500 | 10 | 10 | 50 | 2.34297 |
| 10 | 1000 | 1000 | 10 | 10 | 100 | 2.28443 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, R.; Zhu, R.; Wang, L. NetTopoBFT: Network Topology-Aware Byzantine Fault Tolerance for High-Coverage Consortium Blockchains. Entropy 2025, 27, 1088. https://doi.org/10.3390/e27111088
Chen R, Zhu R, Wang L. NetTopoBFT: Network Topology-Aware Byzantine Fault Tolerance for High-Coverage Consortium Blockchains. Entropy. 2025; 27(11):1088. https://doi.org/10.3390/e27111088
Chicago/Turabian StyleChen, Runyu, Rangang Zhu, and Lunwen Wang. 2025. "NetTopoBFT: Network Topology-Aware Byzantine Fault Tolerance for High-Coverage Consortium Blockchains" Entropy 27, no. 11: 1088. https://doi.org/10.3390/e27111088
APA StyleChen, R., Zhu, R., & Wang, L. (2025). NetTopoBFT: Network Topology-Aware Byzantine Fault Tolerance for High-Coverage Consortium Blockchains. Entropy, 27(11), 1088. https://doi.org/10.3390/e27111088





