Information Content and Maximum Entropy of Compartmental Systems in Equilibrium
Abstract
1. Introduction
2. Mathematical Background: Information Entropy and Compartmental Systems as Markov Chains
2.1. Short Summary of Shannon Information Entropy
2.2. Compartmental Systems in Equilibrium
2.3. The One-Particle Perspective
2.4. The Path of a Single Particle
3. Entropy Measures, MaxEnt, and Structural Model Identification
- (1)
- As a particle travels through a system of interconnected compartments, it jumps a certain number of times to the next compartment until it finally jumps out of the system. Between two jumps, the particle resides in some compartment. The path entropy measures the entire uncertainty about the particle’s travel through the system, including both the sequence of visited compartments and the respective times spent there.
- (2)
- The entire travel of the particle takes a certain time. In each unit time interval before the particle leaves the system, uncertainties exist as to whether the particle jumps, where it jumps, and even how often it jumps. The mean of these uncertainties over the mean length of the travel interval is measured by the entropy rate per unit time.
- (3)
- Each jump comes with uncertainties about which compartment will be next and how long will the particle stay there. The entropy rate per jump measures the average of these uncertainties with respect to the mean number of jumps until the particle’s exit from the system.
3.1. Path Entropy, Entropy Rate per Unit Time, and Entropy Rate per Jump
3.2. From Microscopic Particle Entropy to Macroscopic System Entropy
3.3. The Maximum Entropy Principle (MaxEnt)
3.4. Structural Model Identification Assisted by MaxEnt
4. Application to Particular Systems
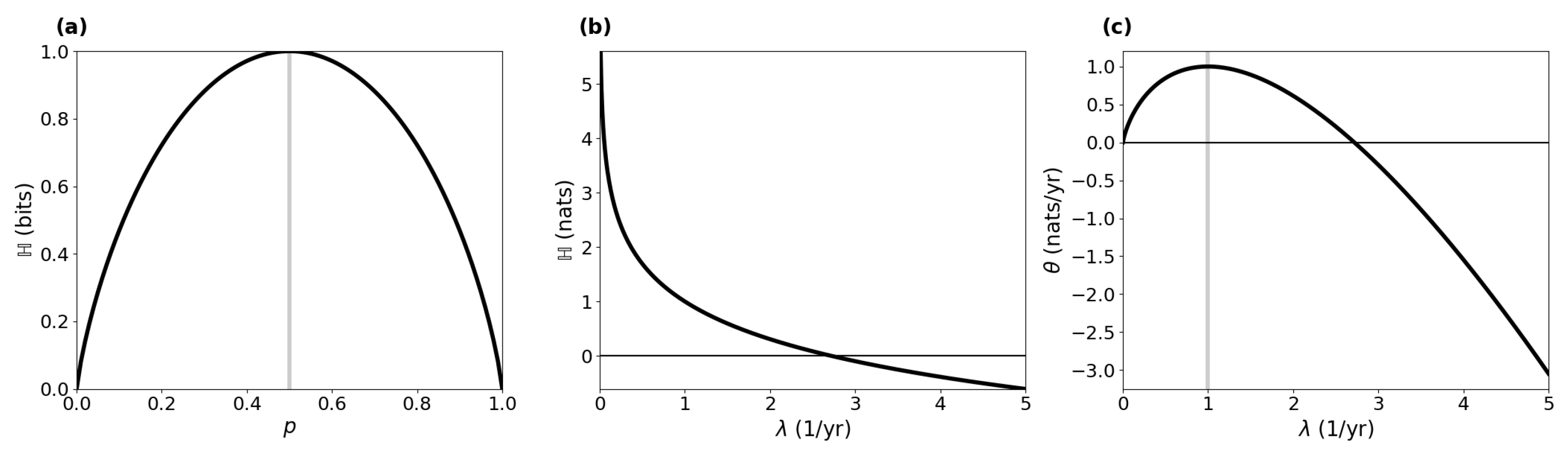
4.1. Simple Examples
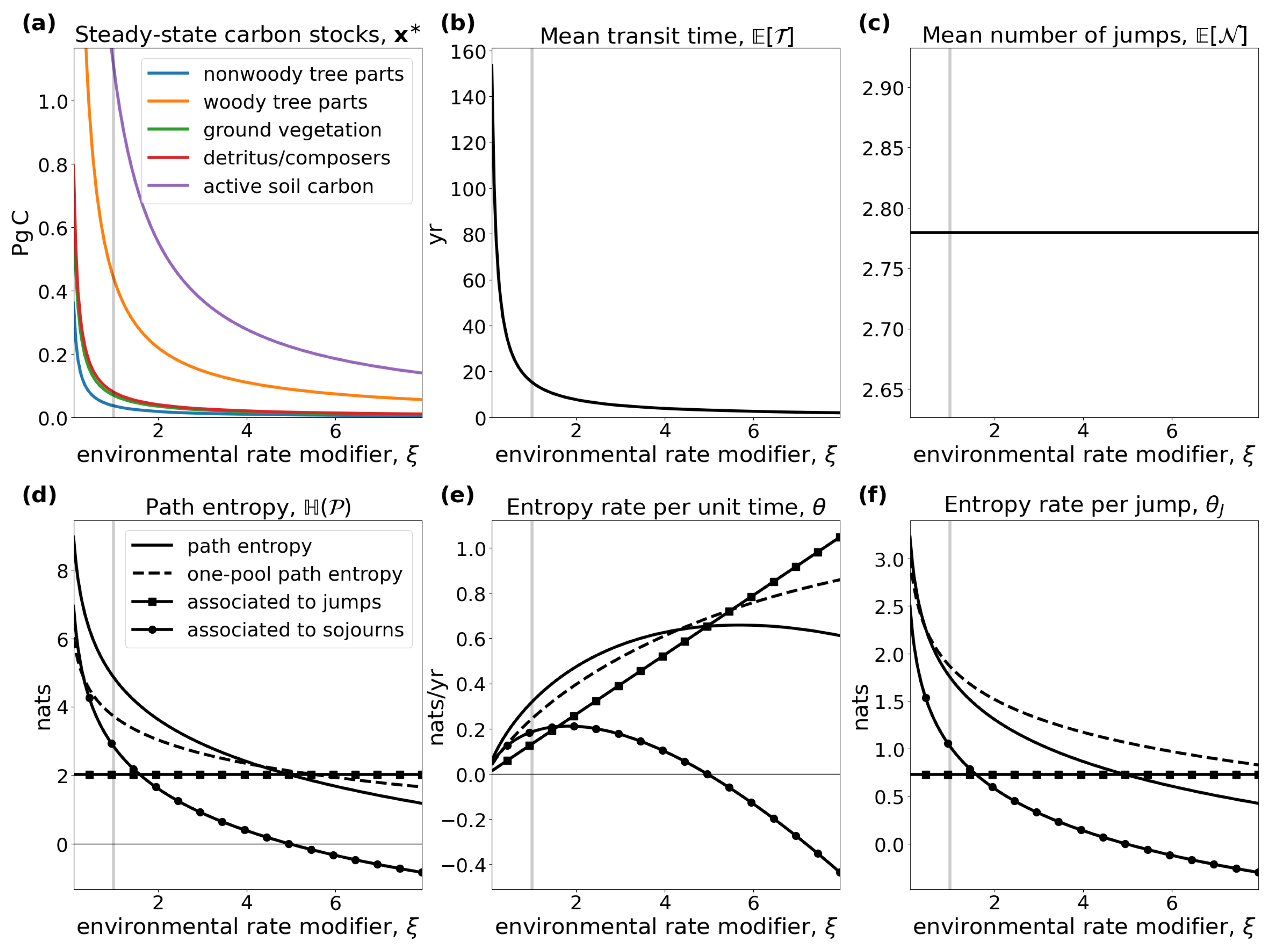
4.2. A Linear Autonomous Global Carbon-Cycle Model
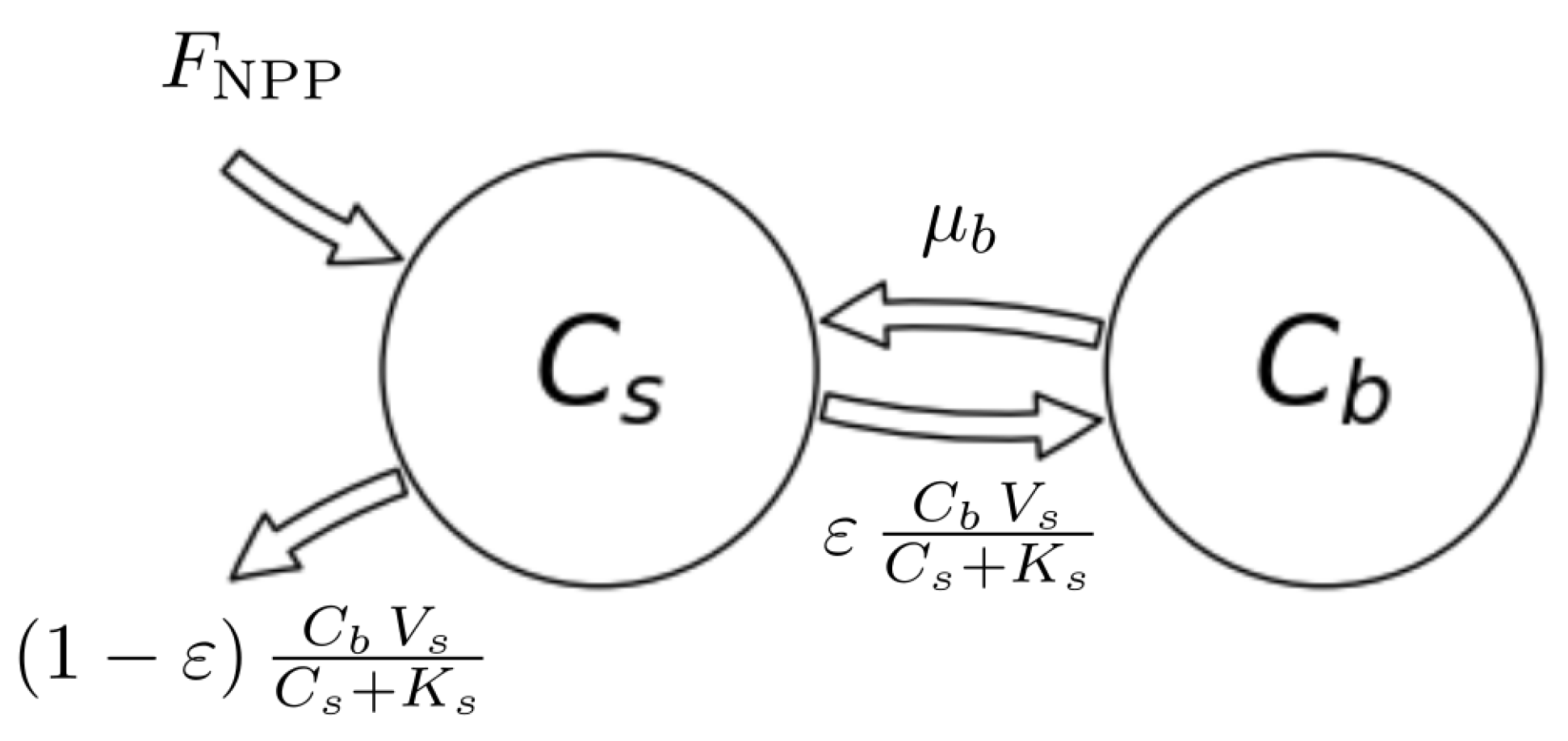
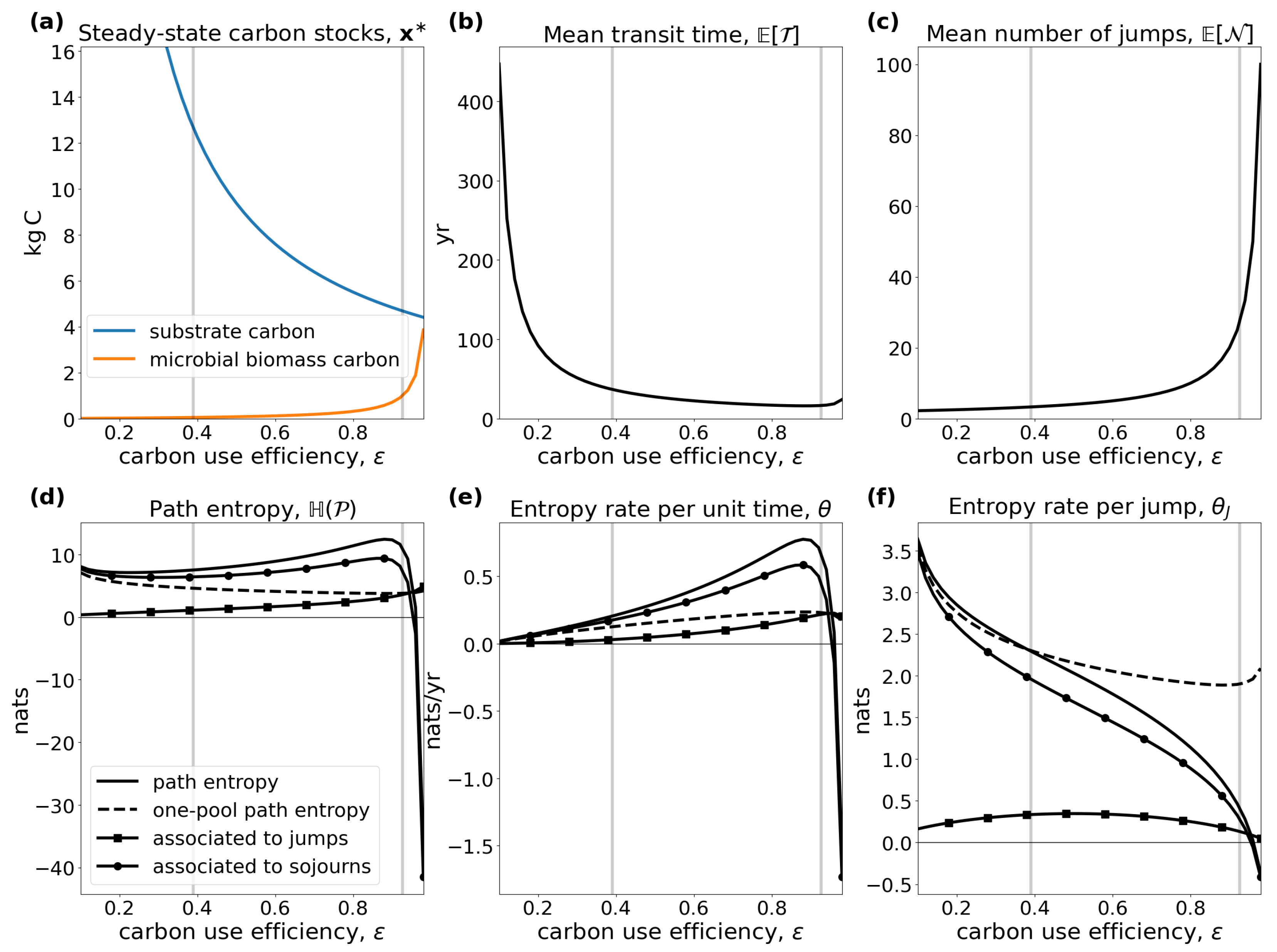
4.3. A Nonlinear Autonomous Soil Organic Matter Decomposition Model
4.4. Model Identification via Maxent
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Stationary Process Z
Appendix B. Proofs of the MaxEnt Examples
References
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach; Springer: New York, NY, USA; Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Höge, M.; Wöhling, T.; Nowak, W. A Primer for Model Selection: The Decisive Role of Model Complexity. Water Resour. Res. 2018, 54, 1688–1715. [Google Scholar] [CrossRef]
- Golan, A.; Harte, J. Information theory: A foundation for complexity science. Proc. Natl. Acad. Sci. USA 2022, 119, e2119089119. [Google Scholar] [CrossRef] [PubMed]
- Jost, J. Dynamical Systems: Examples of Complex Behaviour; Springer: Berlin, Germany; New York, NY, USA, 2005. [Google Scholar]
- Fan, J.; Meng, J.; Ludescher, J.; Chen, X.; Ashkenazy, Y.; Kurths, J.; Havlin, S.; Schellnhuber, H.J. Statistical physics approaches to the complex Earth system. Phys. Rep. 2021, 896, 1–84. [Google Scholar] [CrossRef] [PubMed]
- Anderson, D.H. Compartmental Modeling and Tracer Kinetics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1983; Volume 50. [Google Scholar]
- Walter, G.G.; Contreras, M. Compartmental Modeling with Networks; Birkhäuser: Basel, Switzerland, 1999. [Google Scholar]
- Haddad, W.M.; Chellaboina, V.; Hui, Q. Nonnegative and Compartmental Dynamical Systems; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Eriksson, E. Compartment Models and Reservoir Theory. Annu. Rev. Ecol. Syst. 1971, 2, 67–84. [Google Scholar] [CrossRef]
- Bolin, B.; Rodhe, H. A note on the concepts of age distribution and transit time in natural reservoirs. Tellus 1973, 25, 58–62. [Google Scholar] [CrossRef]
- Rasmussen, M.; Hastings, A.; Smith, M.J.; Agusto, F.B.; Chen-Charpentier, B.M.; Hoffman, F.M.; Jiang, J.; Todd-Brown, K.E.O.; Wang, Y.; Wang, Y.P.; et al. Transit times and mean ages for nonautonomous and autonomous compartmental systems. J. Math. Biol. 2016, 73, 1379–1398. [Google Scholar] [CrossRef]
- Sierra, C.A.; Müller, M.; Metzler, H.; Manzoni, S.; Trumbore, S.E. The muddle of ages, turnover, transit, and residence times in the carbon cycle. Glob. Chang. Biol. 2017, 23, 1763–1773. [Google Scholar] [CrossRef]
- Metzler, H.; Sierra, C.A. Linear Autonomous Compartmental Models as Continuous-Time Markov Chains: Transit-Time and Age Distributions. Math. Geosci. 2018, 50, 1–34. [Google Scholar] [CrossRef]
- Metzler, H.; Müller, M.; Sierra, C.A. Transit-time and age distributions for nonlinear time-dependent compartmental systems. Proc. Natl. Acad. Sci. USA 2018, 115, 1150–1155. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information Theory and Statistical Mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information Theory and Statistical Mechanics. II. Phys. Rev. 1957, 108, 171–190. [Google Scholar] [CrossRef]
- Pressé, S.; Ghosh, K.; Lee, J.; Dill, K.A. Principles of maximum entropy and maximum caliber in statistical physics. Rev. Mod. Phys. 2013, 85, 1115. [Google Scholar] [CrossRef]
- Pesin, Y.B. Characteristic Lyapunov exponents and smooth ergodic theory. Uspekhi Mat. Nauk 1977, 32, 55–112. [Google Scholar]
- Dehmer, M.; Mowshowitz, A. A history of graph entropy measures. Inf. Sci. 2011, 181, 57–78. [Google Scholar] [CrossRef]
- Trucco, E. A note on the information content of graphs. Bull. Math. Biol. 1956, 18, 129–135. [Google Scholar] [CrossRef]
- Morzy, M.; Kajdanowicz, T.; Kazienko, P. On Measuring the Complexity of Networks: Kolmogorov Complexity versus Entropy. Complexity 2017, 2017, 3250301. [Google Scholar] [CrossRef]
- Bonchev, D.; Buck, G.A. Quantitative Measures of Network Csomplexity. In Complexity in Chemistry, Biology, and Ecology; Springer: Berlin/Heidelberg, Germany, 2005; pp. 191–235. [Google Scholar]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; The University of Illinois Press: Urbana, IL, USA, 1949. [Google Scholar]
- Jaynes, E.T. Macroscopic prediction. In Complex Systems—Operational Approaches in Neurobiology, Physics, and Computers; Springer: Berlin/Heidelberg, Germany, 1985; pp. 254–269. [Google Scholar]
- Roach, T.N.F. Use and Abuse of Entropy in Biology: A Case for Caliber. Entropy 2020, 22, 1335. [Google Scholar] [CrossRef] [PubMed]
- Aoki, I. Entropy laws in ecological networks at steady state. Ecol. Model. 1988, 42, 289–303. [Google Scholar] [CrossRef]
- Haddad, W.M. A Unification between Dynamical System Theory and Thermodynamics Involving an Energy, Mass, and Entropy State Space Formalism. Entropy 2013, 15, 1821–1846. [Google Scholar] [CrossRef]
- Haddad, W.M. A Dynamical Systems Theory of Thermodynamics; Princeton University Press: Princeton, NJ, USA, 2019. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Bad Dumitrescu, M.E. Some informational properties of Markov pure-jump processes. Časopis Pro Pěstování Mat. 1988, 113, 429–434. [Google Scholar]
- Gaspard, P.; Wang, X.J. Noise, chaos, and (ε, τ)-entropy per unit time. Phys. Rep. 1993, 235, 291–343. [Google Scholar] [CrossRef]
- Jacquez, J.A.; Simon, C.P. Qualitative theory of compartmental systems. Siam Rev. 1993, 35, 43–79. [Google Scholar] [CrossRef]
- Norris, J.R. Markov Chains; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Neuts, M.F. Matrix-Geometric Solutions in Stochastic Models: An Algorithmic Approach; The Johns Hopkins University Press: Baltimore, MD, USA, 1981. [Google Scholar]
- Albert, A. Estimating the Infinitesimal Generator of a Continuous Time, Finite State Markov Process. Ann. Math. Stat. 1962, 33, 727–753. [Google Scholar] [CrossRef]
- Doob, J.L. Stochastic Processes; Wiley: New York, NY, USA, 1953; Volume 7. [Google Scholar]
- Walter, G.G. Size identifiability of compartmental models. Math. Biosci. 1986, 81, 165–176. [Google Scholar] [CrossRef]
- Bellman, R.; Åström, K.J. On structural identifiability. Math. Biosci. 1970, 7, 329–339. [Google Scholar] [CrossRef]
- Emanuel, W.R.; Killough, G.G.; Olson, J.S. Modelling the Circulation of Carbon in the World’s Terrestrial Ecosystems. In Carbon Cycle Modelling; SCOPE 16; John Wiley and Sons: Hoboken, NJ, USA, 1981; pp. 335–353. [Google Scholar]
- Sierra, C.A.; Quetin, G.R.; Metzler, H.; Müller, M. A decrease in the age of respired carbon from the terrestrial biosphere and increase in the asymmetry of its distribution. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2023. [Google Scholar] [CrossRef]
- Thompson, M.V.; Randerson, J.T. Impulse response functions of terrestrial carbon cycle models: Method and application. Glob. Chang. Biol. 1999, 5, 371–394. [Google Scholar] [CrossRef]
- Wang, Y.P.; Chen, B.C.; Wieder, W.R.; Leite, M.; Medlyn, B.E.; Rasmussen, M.; Smith, M.J.; Agusto, F.B.; Hoffman, F.; Luo, Y.Q. Oscillatory behavior of two nonlinear microbial models of soil carbon decomposition. Biogeosciences 2014, 11, 1817–1831. [Google Scholar] [CrossRef]
- Ågren, G.I. Investigating soil carbon diversity by combining the MAXimum ENTropy principle with the Q model. Biogeochemistry 2021, 153, 85–94. [Google Scholar] [CrossRef]
- García-Rodríguez, L.d.C.; Prado-Olivarez, J.; Guzmán-Cruz, R.; Rodríguez-Licea, M.A.; Barranco-Gutiérrez, A.I.; Perez-Pinal, F.J.; Espinosa-Calderon, A. Mathematical Modeling to Estimate Photosynthesis: A State of the Art. Appl. Sci. 2022, 12, 5537. [Google Scholar] [CrossRef]
- Manzoni, S.; Porporato, A. Soil carbon and nitrogen mineralization: Theory and models across scales. Soil Biol. Biochem. 2009, 41, 1355–1379. [Google Scholar] [CrossRef]
- Zaehle, S.; Medlyn, B.E.; De Kauwe, M.G.; Walker, A.P.; Dietze, M.C.; Hickler, T.; Luo, Y.; Wang, Y.P.; El-Masri, B.; Thornton, P.; et al. Evaluation of 11 terrestrial carbon–nitrogen cycle models against observations from two temperate Free-Air CO2 Enrichment studies. New Phytol. 2014, 202, 803–822. [Google Scholar] [CrossRef]
- Farquhar, G.D.; von Caemmerer, S.v.; Berry, J.A. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 1980, 149, 78–90. [Google Scholar] [CrossRef]
- Friedlingstein, P.; Cox, P.; Betts, R.; Bopp, L.; von Bloh, W.; Brovkin, V.; Cadule, P.; Doney, S.; Eby, M.; Fung, I.; et al. Climate–carbon cycle feedback analysis: Results from the C4MIP model intercomparison. J. Clim. 2006, 19, 3337–3353. [Google Scholar] [CrossRef]
- Friedlingstein, P.; Meinshausen, M.; Arora, V.K.; Jones, C.D.; Anav, A.; Liddicoat, S.K.; Knutti, R. Uncertainties in CMIP5 climate projections due to carbon cycle feedbacks. J. Clim. 2014, 27, 511–526. [Google Scholar] [CrossRef]
- Todd-Brown, K.E.; Randerson, J.T.; Post, W.M.; Hoffman, F.M.; Tarnocai, C.; Schuur, E.A.; Allison, S.D. Causes of variation in soil carbon simulations from CMIP5 Earth system models and comparison with observations. Biogeosciences 2013, 10, 1717–1736. [Google Scholar] [CrossRef]
- Ceballos-Núñez, V.; Müller, M.; Sierra, C.A. Towards better representations of carbon allocation in vegetation: A conceptual framework and mathematical tool. Theor. Ecol. 2020, 13, 317–332. [Google Scholar] [CrossRef]
- Sierra, C.A.; Harmon, M.E.; Perakis, S.S. Decomposition of heterogeneous organic matter and its long-term stabilization in soils. Ecol. Monogr. 2011, 81, 619–634. [Google Scholar] [CrossRef]
- Ge, H.; Pressé, S.; Ghosh, K.; Dill, K.A. Markov processes follow from the principle of maximum caliber. J. Chem. Phys. 2012, 136, 064108. [Google Scholar] [CrossRef]
- Girardin, V. Entropy Maximization for Markov and Semi-Markov Processes. Methodol. Comput. Appl. Probab. 2004, 6, 109–127. [Google Scholar] [CrossRef]


| Structure | ||||||
|---|---|---|---|---|---|---|
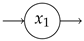 | 2.00 | |||||
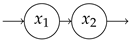 | 0.67 | 3.00 | 1.00 | 2.00 | 2.00 | |
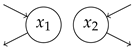 | 0.85 | 2.00 | 1.69 | 1.00 | 1.69 | |
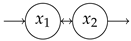 | 1.08 | 5.00 | 1.35 | 4.00 | 5.39 | |
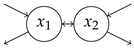 | 1.36 | 3.00 | 2.04 | 2.00 | 4.08 | |
 | 0.75 | 4.00 | 1.00 | 3.00 | 3.00 | |
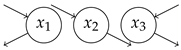 | 1.05 | 2.00 | 2.10 | 1.00 | 2.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Metzler, H.; Sierra, C.A. Information Content and Maximum Entropy of Compartmental Systems in Equilibrium. Entropy 2025, 27, 1085. https://doi.org/10.3390/e27101085
Metzler H, Sierra CA. Information Content and Maximum Entropy of Compartmental Systems in Equilibrium. Entropy. 2025; 27(10):1085. https://doi.org/10.3390/e27101085
Chicago/Turabian StyleMetzler, Holger, and Carlos A. Sierra. 2025. "Information Content and Maximum Entropy of Compartmental Systems in Equilibrium" Entropy 27, no. 10: 1085. https://doi.org/10.3390/e27101085
APA StyleMetzler, H., & Sierra, C. A. (2025). Information Content and Maximum Entropy of Compartmental Systems in Equilibrium. Entropy, 27(10), 1085. https://doi.org/10.3390/e27101085








