Noise Robustness of Transcript-Based Estimators for Properties of Interactions
Abstract
1. Introduction
2. Methods
2.1. Ordinal Patterns, Transcripts, and Order Classes
2.2. Transcript-Based Estimators for Direction, Strength, and Complexity of an Interaction
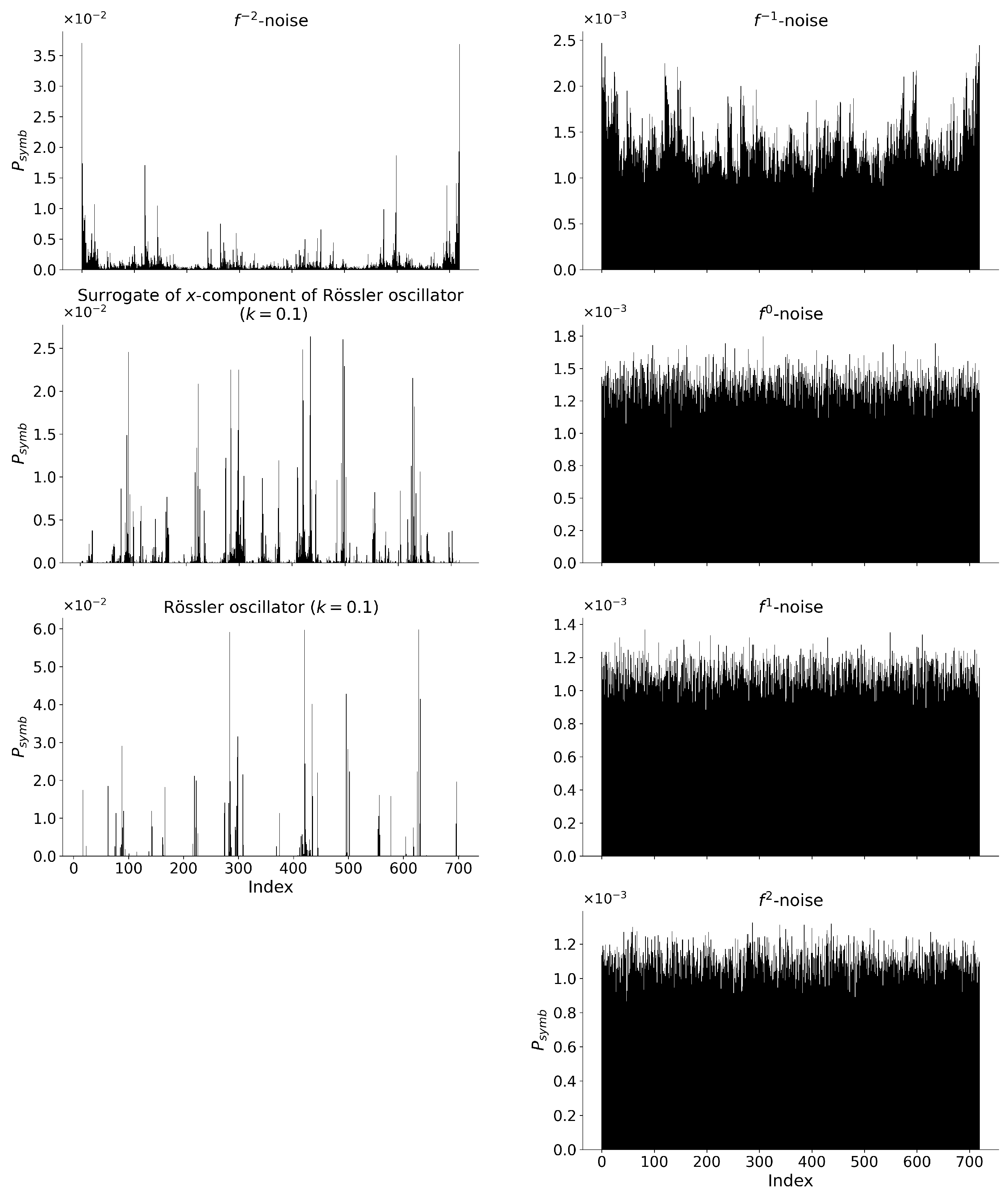
3. Model Systems
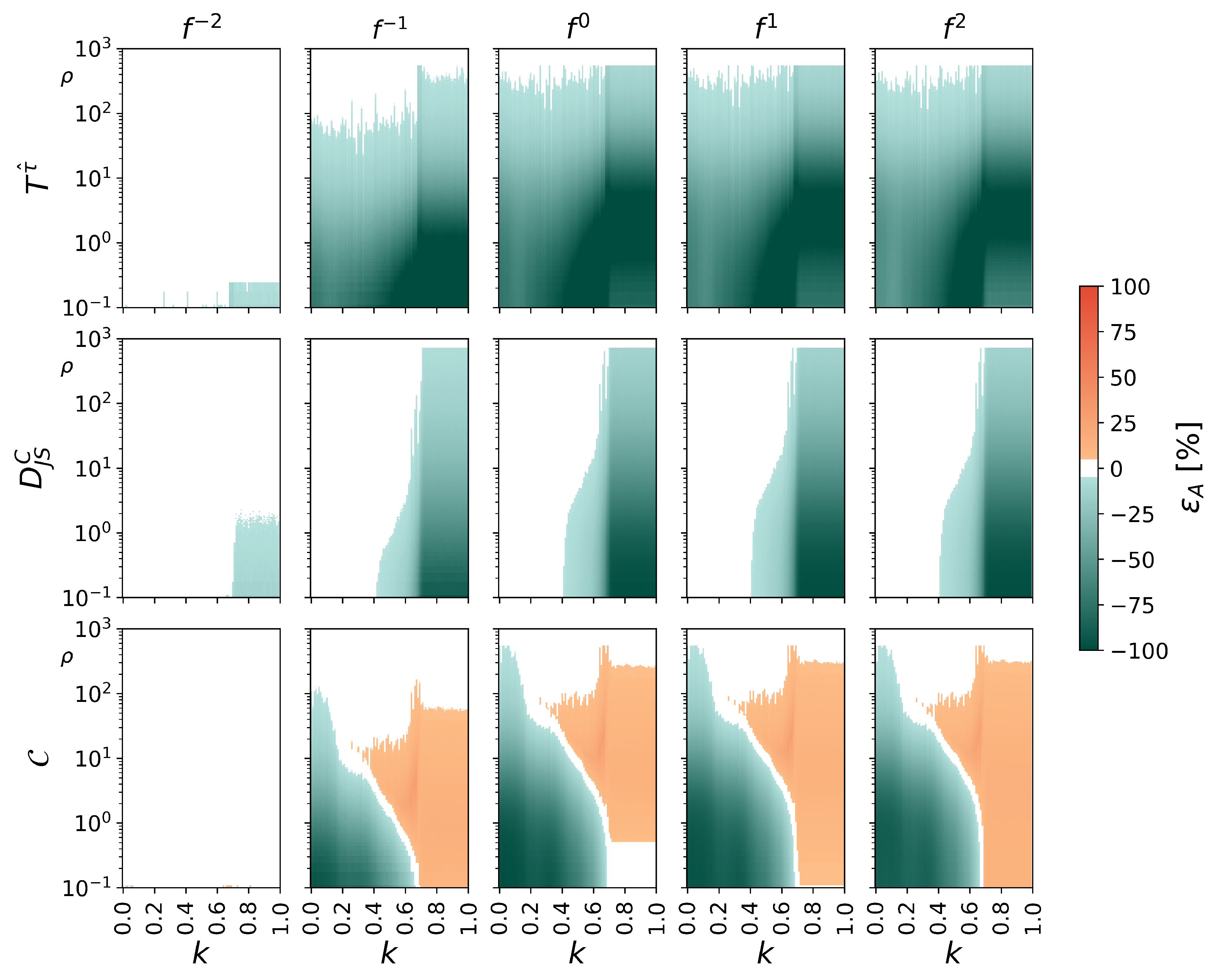
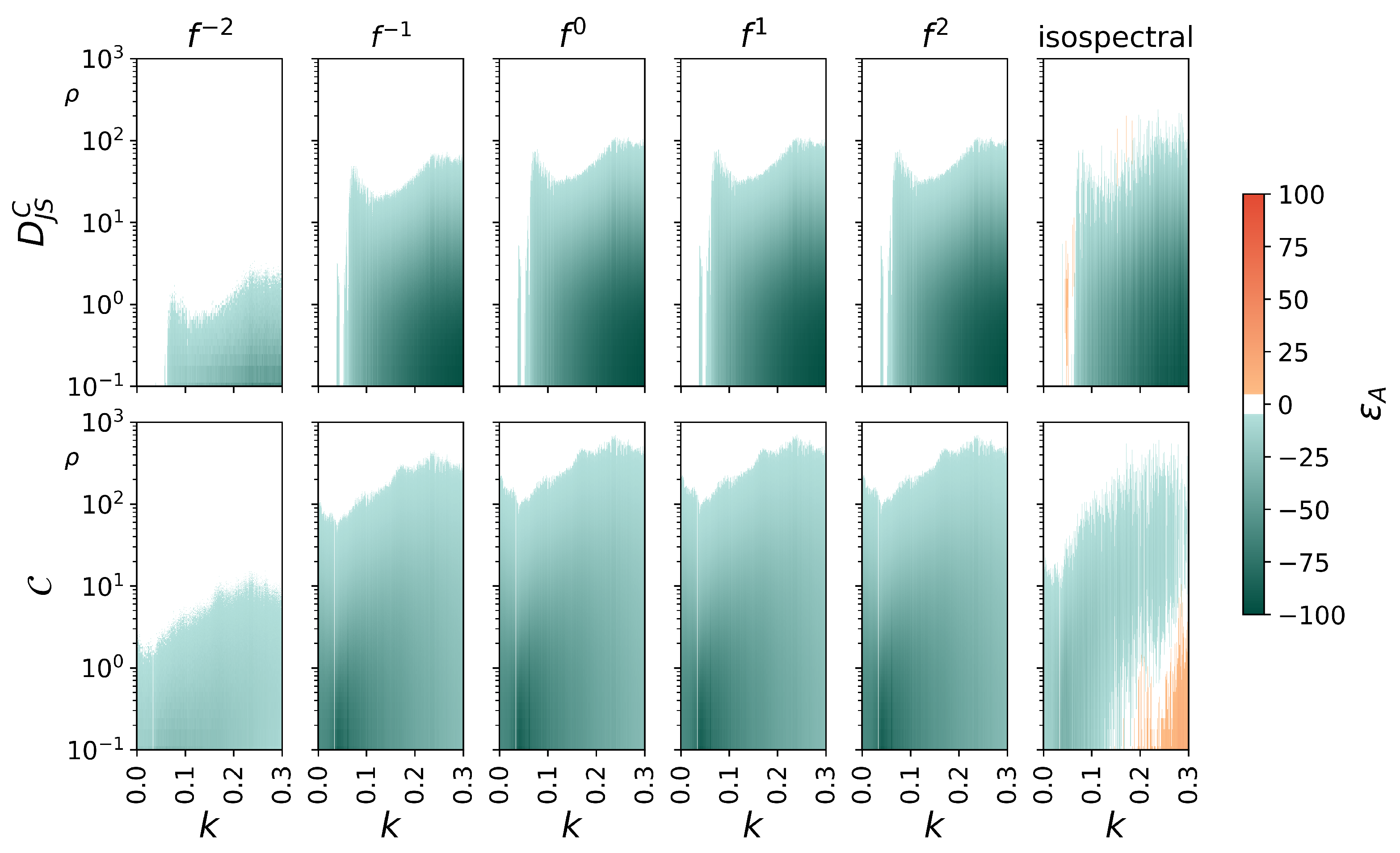
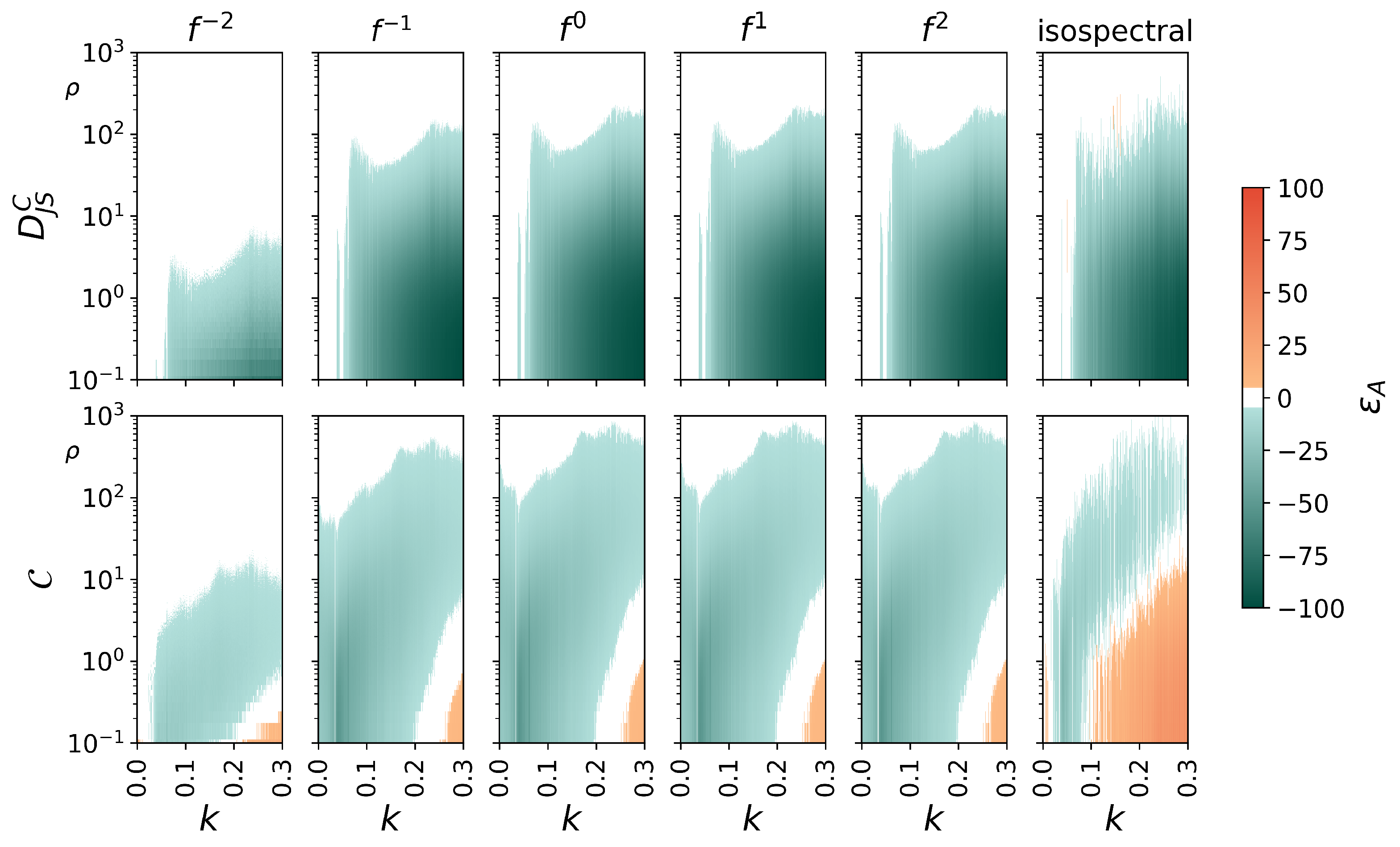
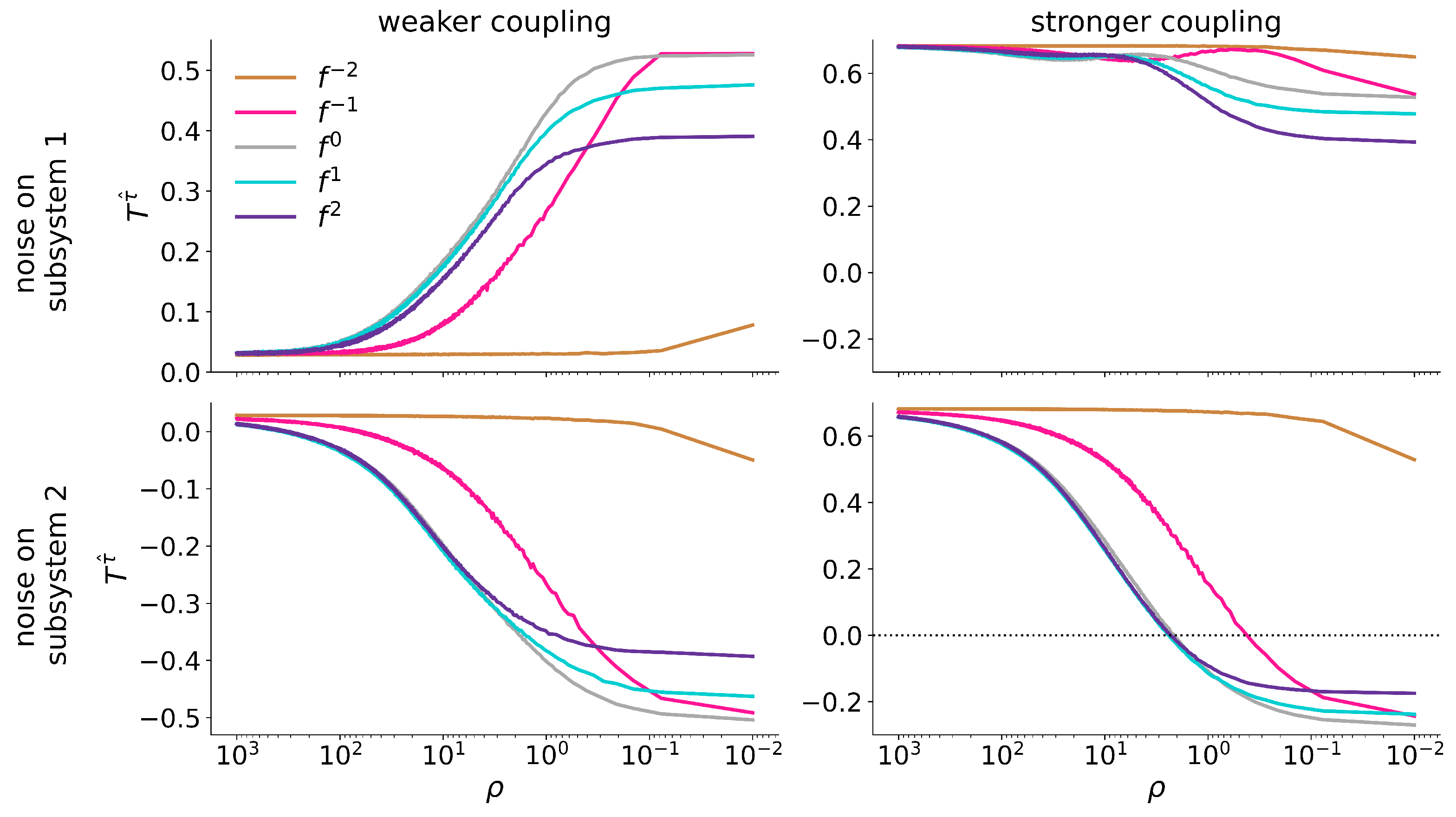
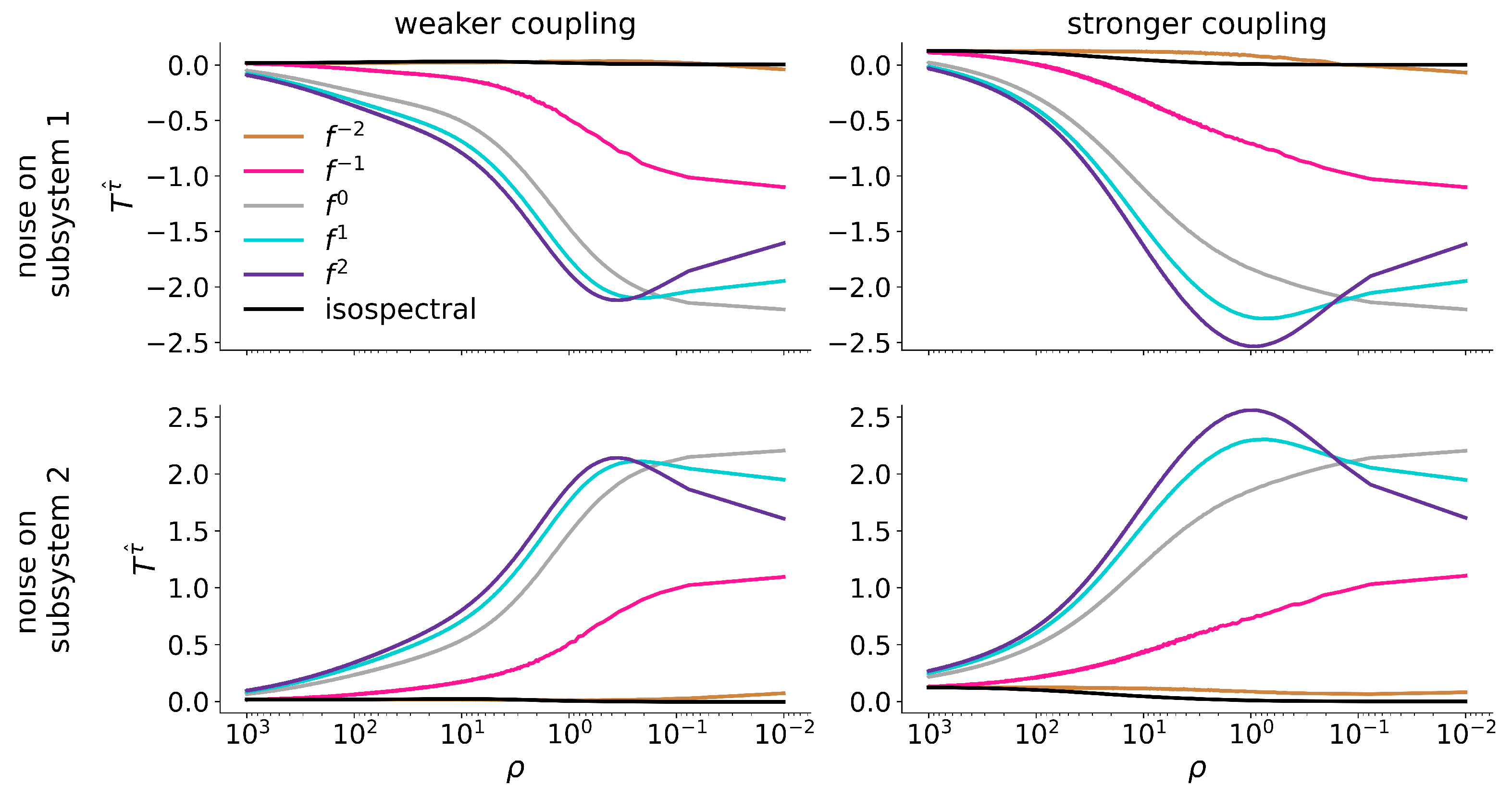
4. Results
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
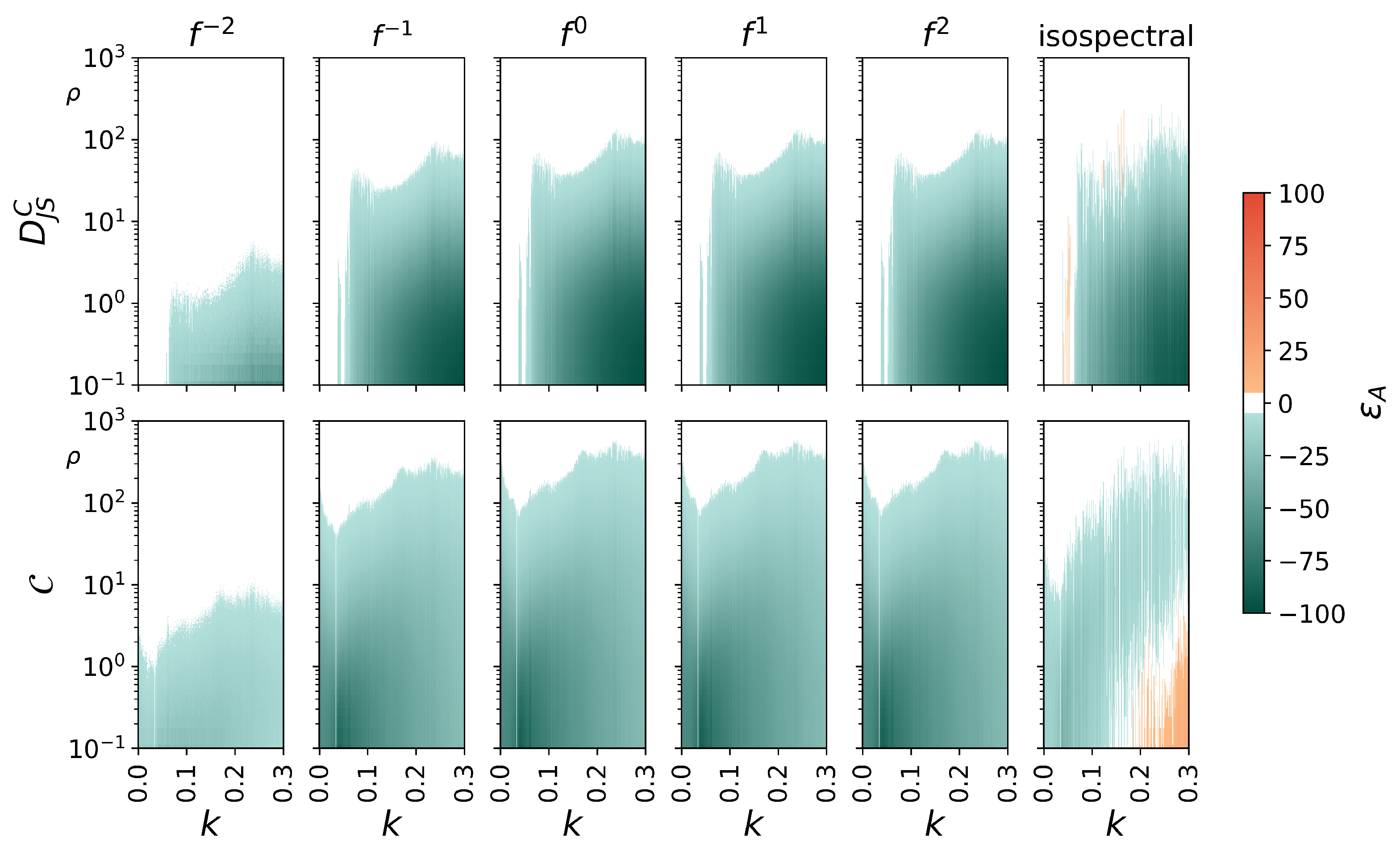
Appendix A. Asymmetric Noise Contamination

References
- Pikovsky, A.S.; Rosenblum, M.G.; Kurths, J. Synchronization: A Universal Concept in Nonlinear Sciences; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Varela, F.J.; Lachaux, J.P.; Rodriguez, E.; Martinerie, J. The brain web: Phase synchronization and large-scale integration. Nat. Rev. Neurosci. 2001, 2, 229–239. [Google Scholar] [PubMed]
- Boccaletti, S.; Kurths, J.; Osipov, G.; Valladares, D.L.; Zhou, C.S. The synchronization of chaotic systems. Phys. Rep. 2002, 366, 1–101. [Google Scholar] [CrossRef]
- Hlaváčková-Schindler, K.; Paluš, M.; Vejmelka, M.; Bhattacharya, J. Causality detection based on information-theoretic approaches in time series analysis. Phys. Rep. 2007, 441, 1–46. [Google Scholar] [CrossRef]
- Hegland, S.J.; Nielsen, A.; Lázaro, A.; Bjerknes, A.L.; Totland, Ø. How does climate warming affect plant-pollinator interactions? Ecol. Lett. 2009, 12, 184–195. [Google Scholar]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture–climate interactions in a changing climate: A review. Earth-Sci. Rev. 2010, 99, 125–161. [Google Scholar]
- Fell, J.; Axmacher, N. The role of phase synchronization in memory processes. Nat. Rev. Neurosci. 2011, 12, 105–118. [Google Scholar] [CrossRef]
- Stankovski, T.; Pereira, T.; McClintock, P.V.E.; Stefanovska, A. Coupling functions: Universal insights into dynamical interaction mechanisms. Rev. Mod. Phys. 2017, 89, 045001. [Google Scholar] [CrossRef]
- Kiss, I.Z. Synchronization engineering. Curr. Opin. Chem. Eng. 2018, 21, 1–9. [Google Scholar] [CrossRef]
- Hao, B.l. Symbolic dynamics and characterization of complexity. Phys. D Nonlinear Phenom. 1991, 51, 161–176. [Google Scholar]
- Amigó, J. Permutation Complexity in Dynamical Systems: Ordinal Patterns, Permutation Entropy and All That; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Lind, D.; Marcus, B. An Introduction to Symbolic Dynamics and Coding, 2nd ed.; Cambridge University Press: Cambrdige, UK, 2021. [Google Scholar]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Staniek, M.; Lehnertz, K. Symbolic Transfer Entropy. Phys. Rev. Lett. 2008, 100, 158101. [Google Scholar] [CrossRef] [PubMed]
- Zanin, M.; Zunino, L.; Rosso, O.A.; Papo, D. Permutation entropy and its main biomedical and econophysics applications: A review. Entropy 2012, 14, 1553–1577. [Google Scholar] [CrossRef]
- Amigo, J.M.; Monetti, R.; Aschenbrenner, T.; Bunk, W. Transcripts: An algebraic approach to coupled time series. Chaos Interdiscip. J. Nonlinear Sci. 2012, 22, 013105. [Google Scholar]
- Amigó, J.M.; Keller, K.; Kurths, J. Recent progress in Symbolic Dynamic and Permutation Complexity: Ten Years of Permutation Entropy. Eur. Phys. J. Spec. Top. 2013, 222, 241. [Google Scholar]
- Riedl, M.; Müller, A.; Wessel, N. Practical considerations of permutation entropy: A tutorial review. Eur. Phys. J. Spec. Top. 2013, 222, 249–262. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, J.; Tang, M.; Guo, H.; Small, M.; Zou, Y. Constructing ordinal partition transition networks from multivariate time series. Sci. Rep. 2017, 7, 7795. [Google Scholar] [CrossRef]
- Hirata, Y.; Amigó, J.M. A review of symbolic dynamics and symbolic reconstruction of dynamical systems. Chaos Interdiscip. J. Nonlinear Sci. 2023, 33, 052101. [Google Scholar]
- Amigó, J.M.; Rosso, O.A. Ordinal methods: Concepts, applications, new developments, and challenges—In memory of Karsten Keller (1961–2022). Chaos Interdiscip. J. Nonlinear Sci. 2023, 33, 080401. [Google Scholar]
- Lehnertz, K.; Dickten, H. Assessing directionality and strength of coupling through symbolic analysis: An application to epilepsy patients. Phil. Trans. R. Soc. A 2015, 373, 20140094. [Google Scholar]
- Guo, H.; Zhang, J.Y.; Zou, Y.; Guan, S.G. Cross and joint ordinal partition transition networks for multivariate time series analysis. Front. Phys. 2018, 13, 130508. [Google Scholar] [CrossRef]
- Ruan, Y.; Donner, R.V.; Guan, S.; Zou, Y. Ordinal partition transition network based complexity measures for inferring coupling direction and delay from time series. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 043111. [Google Scholar]
- Almendral, J.A.; Leyva, I.; Sendiña-Nadal, I. Unveiling the connectivity of complex networks using ordinal transition methods. Entropy 2023, 25, 1079. [Google Scholar] [CrossRef] [PubMed]
- Du, M.; Wei, J.; Li, M.Y.; Gao, Z.k.; Kurths, J. Interconnected ordinal pattern complex network for characterizing the spatial coupling behavior of gas–liquid two-phase flow. Chaos Interdiscip. J. Nonlinear Sci. 2023, 33, 063108. [Google Scholar] [CrossRef]
- Lehnertz, K. Ordinal methods for a characterization of evolving functional brain networks. Chaos Interdiscip. J. Nonlinear Sci. 2023, 33, 022101. [Google Scholar]
- Daw, C.; Finney, C.; Tracy, E. A review of symbolic analysis of experimental data. Rev. Sci. Instrum. 2003, 74, 915–930. [Google Scholar]
- Zanin, M.; Olivares, F. Ordinal patterns-based methodologies for distinguishing chaos from noise in discrete time series. Commun. Phys. 2021, 4, 190. [Google Scholar] [CrossRef]
- Moss, F.; McClintock, P.V.E. Noise in Nonlinear Dynamical Systems; Cambridge University Press: Cambridge, UK, 1989; Volume 3. [Google Scholar]
- Hänggi, P.; Jung, P. Colored noise in dynamical systems. Adv. Chem. Phys. 1994, 89, 239–326. [Google Scholar]
- Rosso, O.A.; Carpi, L.C.; Saco, P.M.; Ravetti, M.G.; Plastino, A.; Larrondo, H.A. Causality and the entropy–complexity plane: Robustness and missing ordinal patterns. Phys. A Stat. Mech. Appl. 2012, 391, 42–55. [Google Scholar]
- Boaretto, B.R.; Budzinski, R.C.; Rossi, K.L.; Prado, T.L.; Lopes, S.R.; Masoller, C. Evaluating temporal correlations in time series using permutation entropy, ordinal probabilities and machine learning. Entropy 2021, 23, 1025. [Google Scholar] [CrossRef]
- Theiler, J.; Eubank, S.; Longtin, A.; Galdrikian, B.; Farmer, J.D. Testing for nonlinearity in time series: The method of surrogate data. Physica D 1992, 58, 77. [Google Scholar]
- Monetti, R.; Bunk, W.; Aschenbrenner, T.; Jamitzky, F. Characterizing synchronization in time series using information measures extracted from symbolic representations. Phys. Rev. E 2009, 79, 046207. [Google Scholar] [CrossRef]
- Monetti, R.; Amigó, J.; Aschenbrenner, T.; Bunk, W. Permutation complexity of interacting dynamical systems. Eur. Phys. J. Spec. Top. 2013, 222, 421–436. [Google Scholar]
- Monetti, R.; Bunk, W.; Aschenbrenner, T.; Springer, S.; Amigó, J.M. Information directionality in coupled time series using transcripts. Phys. Rev. E 2013, 88, 022911. [Google Scholar] [CrossRef]
- Adams, M.; Amigó, J.M.; Lehnertz, K. Transcript-based estimators for characterizing interactions. 2025; submitted. [Google Scholar]
- Takens, F. Detecting Strange Attractors in Turbulence; Springer: Berlin/Heidelberg, Germany, 1981; pp. 366–381. [Google Scholar]
- Staniek, M.; Lehnertz, K. Parameter selection in permutation entropy measurements. Int. J. Bifurc. Chaos Appl. Sci. Eng. 2007, 17, 3729. [Google Scholar]
- Amigó, J.M.; Aschenbrenner, T.; Bunk, W.; Monetti, R. Dimensional reduction of conditional algebraic multi-information via transcripts. Inf. Sci. 2014, 278, 298–310. [Google Scholar] [CrossRef]
- Dickten, H.; Lehnertz, K. Identifying delayed directional couplings with symbolic transfer entropy. Phys. Rev. E 2014, 90, 062706. [Google Scholar] [CrossRef] [PubMed]
- Schiff, S.J.; So, P.; Chang, T.; Burke, R.E.; Sauer, T. Detecting dynamical interdependence and generalized synchrony through mutual prediction in a neural ensemble. Phys. Rev. E 1996, 54, 6708–6724. [Google Scholar] [CrossRef] [PubMed]
- Timmer, J.; König, M. On generating power law noise. Astron. Astrophys. 1995, 300, 707. [Google Scholar]
- Schreiber, T.; Schmitz, A. Improved surrogate data for nonlinearity tests. Phys. Rev. Lett. 1996, 77, 635–638. [Google Scholar] [CrossRef]
- Martini, M.; Kranz, T.A.; Wagner, T.; Lehnertz, K. Inferring directional interactions from transient signals with symbolic transfer entropy. Phys. Rev. E 2011, 83, 011919. [Google Scholar] [CrossRef]
- Boccaletti, S.; Valladares, D. Characterization of intermittent lag synchronization. Phys. Rev. E 2000, 62, 7497. [Google Scholar] [CrossRef]
- Gammaitoni, L.; Hänggi, P.; Jung, P.; Marchesoni, F. Stochastic resonance. Rev. Mod. Phys. 1998, 70, 223–287. [Google Scholar] [CrossRef]
- Lehnertz, K. Assessing directed interactions from neurophysiological signals—An overview. Physiol. Meas. 2011, 32, 1715. [Google Scholar] [CrossRef]
- Smirnov, D.A.; Bezruchko, B.P. Estimation of interaction strength and direction from short and noisy time series. Phys. Rev. E 2003, 68, 046209. [Google Scholar]
- Albo, Z.; Di Prisco, G.V.; Chen, Y.; Rangarajan, G.; Truccolo, W.; Feng, J.; Vertes, R.P.; Ding, M. Is partial coherence a viable technique for identifying generators of neural oscillations? Biol. Cybern. 2004, 90, 318–326. [Google Scholar] [CrossRef] [PubMed]
- Chicharro, D.; Andrzejak, R.G. Reliable detection of directional couplings using rank statistics. Phys. Rev. E 2009, 80, 026217. [Google Scholar] [CrossRef] [PubMed]
- Krakovská, A.; Jakubík, J.; Chvosteková, M.; Coufal, D.; Jajcay, N.; Paluš, M. Comparison of six methods for the detection of causality in a bivariate time series. Phys. Rev. E 2018, 97, 042207. [Google Scholar] [CrossRef]
- Edinburgh, T.; Eglen, S.J.; Ercole, A. Causality indices for bivariate time series data: A comparative review of performance. Chaos Interdiscip. J. Nonlinear Sci. 2021, 31, 083111. [Google Scholar]
- Porta, A.; de Abreu, R.M.; Bari, V.; Gelpi, F.; De Maria, B.; Catai, A.M.; Cairo, B. On the validity of the state space correspondence strategy based on k-nearest neighbor cross-predictability in assessing directionality in stochastic systems: Application to cardiorespiratory coupling estimation. Chaos Interdiscip. J. Nonlinear Sci. 2024, 34, 053115. [Google Scholar] [CrossRef] [PubMed]
- Hirata, Y.; Shiro, M.; Amigó, J.M. Surrogate data preserving all the properties of ordinal patterns up to a certain length. Entropy 2019, 21, 713. [Google Scholar] [CrossRef]
- Moore, J.M.; Yan, G.; Altmann, E.G. Nonparametric power-law surrogates. Phys. Rev. X 2022, 12, 021056. [Google Scholar] [CrossRef]
- Bandt, C. Ordinal Random Processes. Entropy 2025, 27, 610. [Google Scholar] [CrossRef] [PubMed]
- Tyloo, M.; González, J.; Rubido, N. Including the Magnitude Variability of a Signal in the Ordinal Pattern Analysis. Entropy 2025, 27, 840. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adams, M.; Lehnertz, K. Noise Robustness of Transcript-Based Estimators for Properties of Interactions. Entropy 2025, 27, 1067. https://doi.org/10.3390/e27101067
Adams M, Lehnertz K. Noise Robustness of Transcript-Based Estimators for Properties of Interactions. Entropy. 2025; 27(10):1067. https://doi.org/10.3390/e27101067
Chicago/Turabian StyleAdams, Manuel, and Klaus Lehnertz. 2025. "Noise Robustness of Transcript-Based Estimators for Properties of Interactions" Entropy 27, no. 10: 1067. https://doi.org/10.3390/e27101067
APA StyleAdams, M., & Lehnertz, K. (2025). Noise Robustness of Transcript-Based Estimators for Properties of Interactions. Entropy, 27(10), 1067. https://doi.org/10.3390/e27101067





