Analysis of Complex Network Attack and Defense Game Strategies Under Uncertain Value Criterion
Abstract
1. Introduction
2. Basic Model
3. Analysis of Attack and Defense Strategies
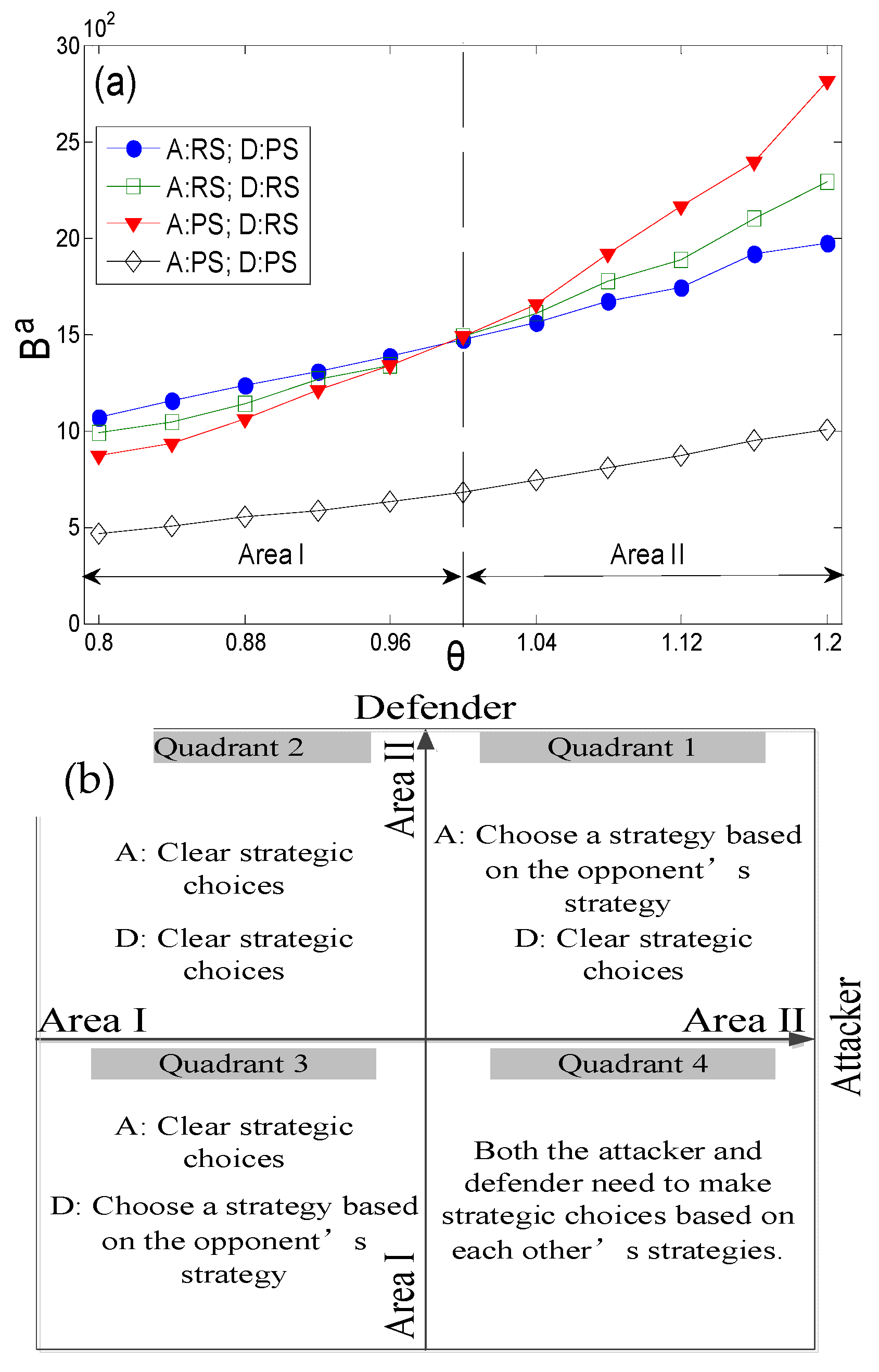
3.1. Analysis of Game-Stable Solutions Under Different Value Coefficients
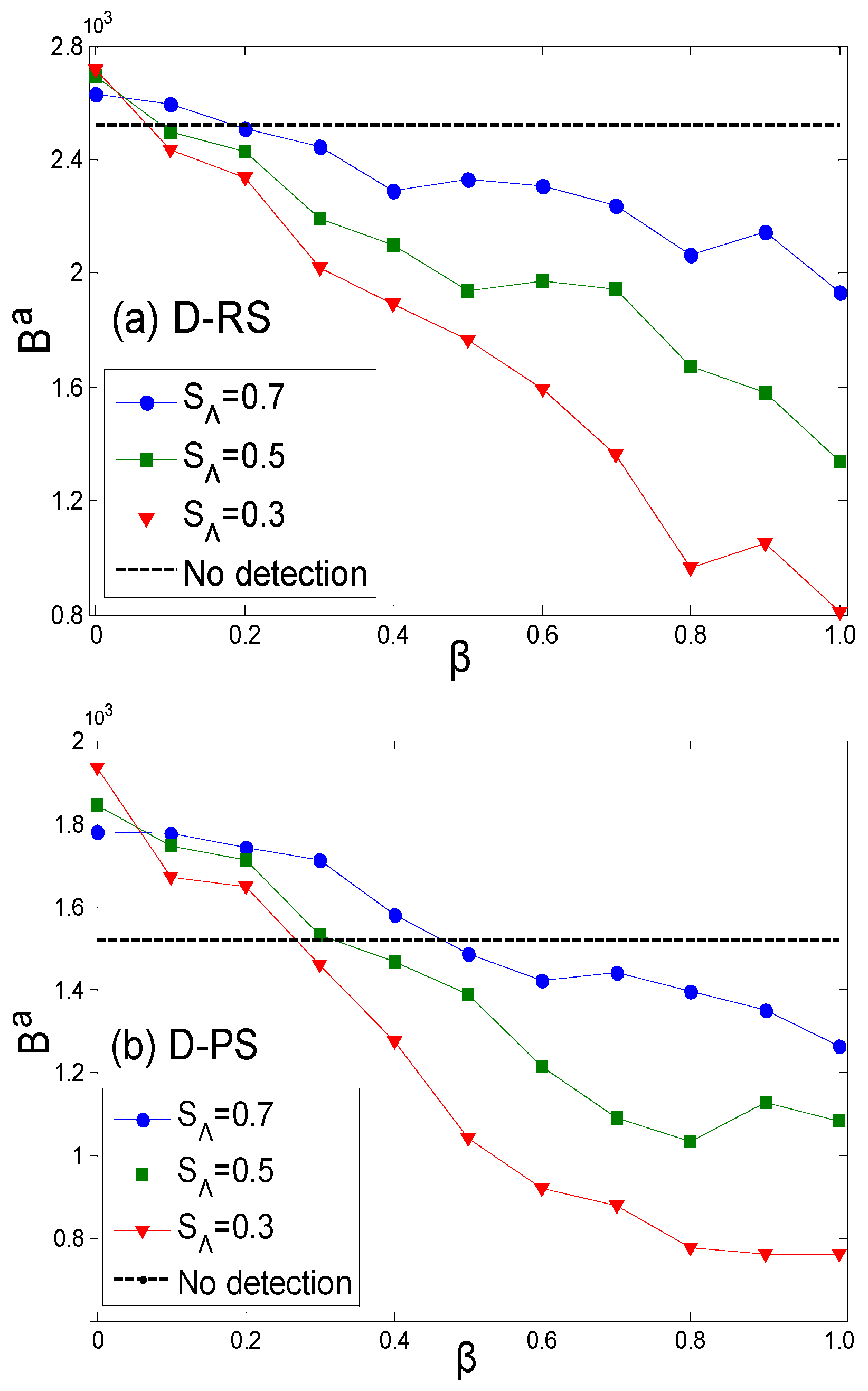
3.2. Decision Analysis Based on Probabilistic Inference Under Uncertain Conditions
- (1)
- The attacker first determines the acceptable security threshold , which represents the level of risk that the attacker can tolerate regarding the defender identifying its detection action. will affect the sample size detected by the attacker; the larger , the fewer nodes will be detected and the lower the accuracy of the attacker’s inference of the defender’s strategy based on the observed results.
- (2)
- Nodes are randomly selected for sequential detection, with the risk of detection behavior being identified by the network denoted as . is the total number of detected nodes, which means that the risk of detection behavior satisfies if and only if condition is satisfied when detecting the -th. is the number of defended nodes among the detected sample. and denote the ability of the network to recognize the attacker’s detection behavior, and they do not directly affect the game results. and only affect the sampling size ( and ) under the constraint of security threshold .
- (3)
- The attacker can calculate the benchmark ratio of defended nodes in the network using the defender’s total defense resources and publicly available/acquired network information. The proportions of nodes defended by the defender under random and preference strategies (denoted as and , respectively) can be obtained by averaging the results from multiple simulations. The proportion of nodes under the random strategy can also be calculated through formula , where is the average degree of the network.
- (4)
- Based on the benchmark ratios and and the sample information and , the conditional probability of the defender adopting a random strategy is . Meanwhile, the conditional probability of adopting a preference strategy is . Here, is the proportion of defended nodes in the sample, and indicates that the attacker is completely unaware of which of the two strategies the defender will employ.
- (5)
- Based on the Bayesian formula, we can calculate the posterior values and using Formulas (1) and (2) and analyze the impact of estimation errors.
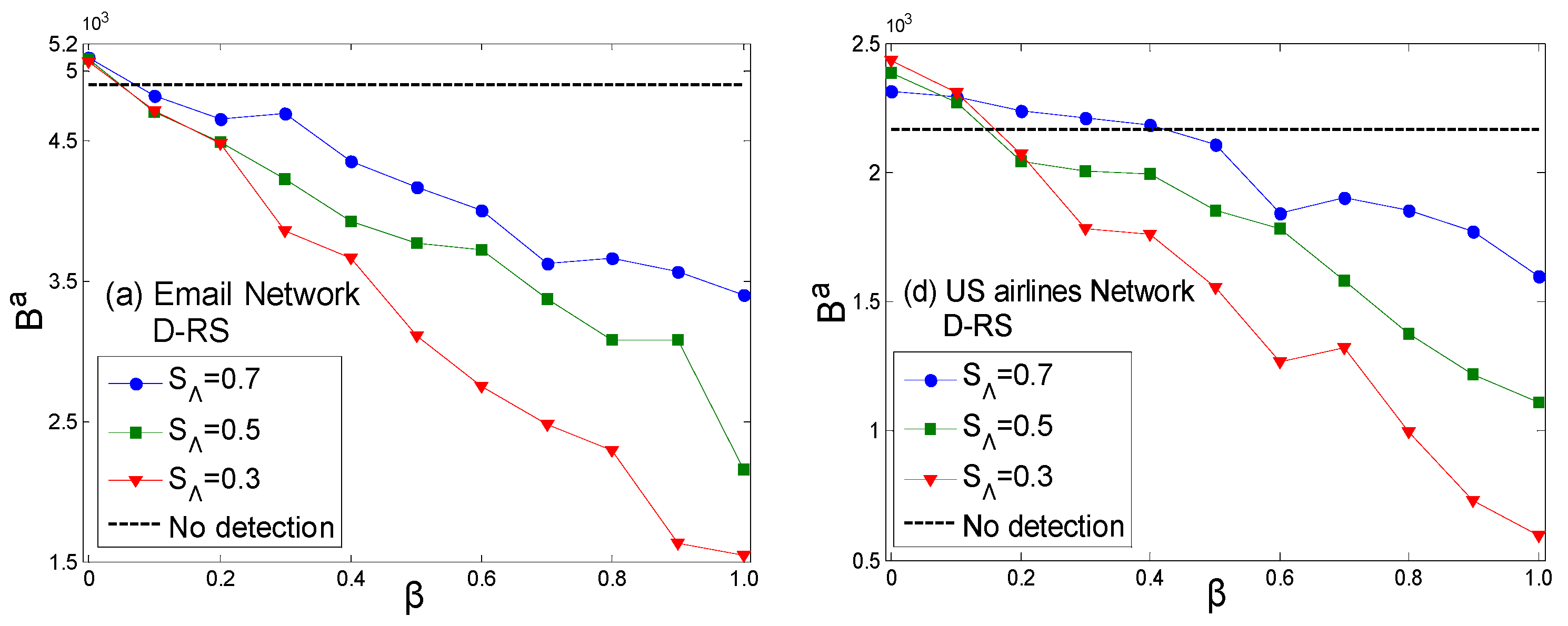
3.3. Verification and Analysis of Real Networks
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jusup, M.; Holme, P.; Kanazawa, K.; Takayasu, M.; Romić, I.; Wang, Z.; Geček, S.; Lipić, T.; Podobnik, B.; Wang, L.; et al. Social physics. Phys. Rep. 2022, 948, 1–148. [Google Scholar] [CrossRef]
- Moteff, J.D. Critical Infrastructures: Background, Policy, and Implementation; DIANE Publishing: Darby, PA, USA, 2010. [Google Scholar]
- Zeng, G.; Li, D.; Guo, S.; Gao, L.; Gao, Z.; Stanley, H.E.; Havlin, S. Switch between critical percolation modes in city traffic dynamics. Proc. Natl. Acad. Sci. USA 2018, 116, 201801545. [Google Scholar] [CrossRef] [PubMed]
- Rosas-Casals, M. Power Grids as Complex Networks: Topology and Fragility. In Proceedings of the 2010 Complexity in Engineering, Rome, Italy, 22–24 February 2010; pp. 21–26. [Google Scholar] [CrossRef]
- Onnela, J.P.; Saramaeki, J.; Hyvoenen, J.; Szabó, G.; Lazer, D.; Kaski, K.; Kertész, K.; Barabási, A.L. Structure and tie strengths in mobile communication networks. Proc. Natl. Acad. Sci. USA 2007, 104, 7332–7336. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.J. The structure and function of complex networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- Committee on Network Science for Future Army Applications, National Research Council. Network Science; National Academies Press: Washington, DC, USA, 2005. [Google Scholar]
- Sandler, T.; Siqueira, K. Games and terrorism: Recent developments. Simul. Gaming 2008, 40, 164–192. [Google Scholar] [CrossRef]
- Tambe, M. Security and Game Theory: Algorithms, Deployed Systems, Lessons Learned; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Hausken, K.; Welburn, J.W.; Zhuang, J. A Review of Attacker-Defender Games and Cyber Security. Games 2024, 15, 1–27. [Google Scholar] [CrossRef]
- Albert, R.; Jeong, H.; Barabasi, A.L. Error and attack tolerance of complex networks. Nature 2000, 406, 378–382. [Google Scholar] [CrossRef]
- Motter, A.E.; Lai, Y.C. Cascade-Based Attacks on Complex Networks. Phys. Rev. E 2003, 66, 065102. [Google Scholar] [CrossRef]
- Li, M.; Liu, R.R.; Lü, L.Y.; Hu, M.B.; Xu, S.; Zhang, Y.C. Percolation on complex networks: Theory and application. Phys. Rep. 2021, 907, 1–68. [Google Scholar] [CrossRef]
- Verma, T.; Russmann, F.; Araújo, N.; Nagler, J.; Herrmann, H. Emergence of core-peripheries in networks. Nat. Commun. 2016, 7, 10441. [Google Scholar] [CrossRef]
- Hunt, K.; Zhuang, J. A review of attacker-defender games: Current state and paths forward. Eur. J. Oper. Res. 2024, 313, 401–417. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.P.; Tan, S.Y.; Deng, Y.; Wu, J. Attacker-defender game from a network science perspective. Chaos 2018, 28, 051102. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Qiao, S.; Deng, Y.; Wu, J. Stackelberg game in critical infrastructures from a network science perspective. Phys. A Stat. Mech. Its Appl. 2019, 521, 705–714. [Google Scholar] [CrossRef]
- He, F.; Zhuang, J.; Rao, N.S.V. Discrete game-theoretic analysis of defense in correlated cyber-physical systems. Ann. Oper. Res. 2020, 294, 741–767. [Google Scholar] [CrossRef]
- Shan, X.J.; Zhuang, J. A game-theoretic approach to modeling attacks and defenses of smart grids at three levels. Reliab. Eng. Syst. Saf. 2020, 195, 106683. [Google Scholar] [CrossRef]
- Chaoqi, F.; Yangjun, G.; Jilong, Z.; Yun, S.; Pengtao, Z.; Tao, W. Attack-defense game for critical infrastructure considering the cascade effect. Reliab. Eng. Syst. Saf. 2021, 216, 107958. [Google Scholar] [CrossRef]
- Chaoqi, F.; Jilong, Z.; Chuhan, Z.; Yuan, B. Analysis of attacker-defender games on interdependent networks. Expert Syst. Appl. 2025, 285, 128057. [Google Scholar] [CrossRef]
- Wu, Y.; Guo, P.; Wang, Y.; Enrico, Z. Attack-defense game modeling framework from a vulnerability perspective to protect critical infrastructure systems. Reliab. Eng. Syst. Saf. 2025, 256, 110740. [Google Scholar] [CrossRef]
- Nagaraja, S.; Anderson, R. Dynamic topologies for robust scale-free networks. In Bio-Inspired Computing and Communication; Springer: Berlin, Germany, 2008; pp. 411–426. [Google Scholar]
- Domingo-Ferrer, J.; González-Nicolás, Ú. Decapitation of networks with and without weights and direction: The economics of iterated attack and defense. Comput. Netw. 2011, 55, 119–130. [Google Scholar] [CrossRef]
- Nystrom, J.K.; Robbins, M.J.; Deckro, R.F.; Morris, J.F. Simulating attacker and defender strategies within a dynamic game on network topology. J. Simul. 2017, 12, 1–25. [Google Scholar] [CrossRef]
- Dong, Y.; Liu, J.; Ren, J.; Li, Z.; Li, W. Attack and Defense Game with Intuitionistic Fuzzy Payoffs in Infrastructure Networks. Tsinghua Sci. Technol. 2025, 30, 384–401. [Google Scholar] [CrossRef]
- Zeng, C.; Ren, B.; Li, M.; Liu, H.; Chen, J. Stackelberg game under asymmetric information in critical infrastructure system: From a complex network perspective. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 083129. [Google Scholar] [CrossRef]
- Wu, D.; Yan, X.; Peng, R.; Wu, S. Risk-attitude-based defense strategy considering proactive strike, preventive strike and imperfect false targets. Reliab. Eng. Syst. Saf. 2020, 196, 106778. [Google Scholar] [CrossRef]
- Zhang, X.; Ding, S.; Ge, B.; Xia, B.; Pedrycz, W. Resource allocation among multiple targets for a defender-attacker game with false targets consideration. Reliab. Eng. Syst. Saf. 2021, 211, 107617. [Google Scholar] [CrossRef]
- Chaoqi, F.; Pengtao, Z.; Lin, Z.; Yangjun, G.; Na, D. Camouflage strategy of a Stackelberg game based on evolution rules. Chaos Solitons Fractals 2021, 153, 111603. [Google Scholar] [CrossRef]
- Keith, A.A.D. Counterfactual regret minimization for integrated cyber and air defense resource allocation. Eur. J. Oper. Res. 2021, 292, 95–107. [Google Scholar] [CrossRef]
- Zhang, X.M.; Han, Q.L.; Ge, X. A novel approach to H_∞ performance analysis of discrete-time networked systems subject to network-induced delays and malicious packet dropouts. Automatica 2022, 136, 110010. [Google Scholar] [CrossRef]
- Gu, X.Q.; Zeng, C.Y.; Xiang, F.T. Applying a Bayesian Stackelberg game to secure infrastructure system: From a complex network perspective. In Proceedings of the 4th International Conference on Automation, Control and Robotics Engineering, Shenzhen, China, 19–21 July 2019; pp. 1–6. [Google Scholar]
- Zeng, C.Y.; Ren, B.A.; Liu, H.F.; Chen, J. Applying the Bayesian Stackelberg active deception game for securing infrastructure networks. Entropy 2019, 21, 909. [Google Scholar] [CrossRef]
- Holme, P.; Kim, B.J.; Yoon, C.N.; Han, S.K. Attack vulnerability of complex networks. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2002, 65, 056109. [Google Scholar] [CrossRef]
- Barabasi, A.L.; Albert, R. Emergence of Scaling in Random Networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
- Available online: https://networkrepository.com/inf.php (accessed on 25 September 2025).
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440. [Google Scholar] [CrossRef]




Attacker | Defender | ||
| Random strategy | Preference strategy | ||
| Random strategy | 985.6, −985.6 | 1064.7, −1064.7 | |
| Preference strategy | 869.3, −869.3 | 465.1, −465.1 | |
Attacker | Defender | ||
| Random strategy | Preference strategy | ||
| Random strategy | 1429.1, −1429.1 | 1470.4, −1470.4 | |
| Preference strategy | 1465.9, −1465.9 | 668.6, −668.6 | |
Attacker | Defender | ||
| Random strategy | Preference strategy | ||
| Random strategy | 2292.2, −2292.2 | 1971.7, −1971.7 | |
| Preference strategy | 2815.5, −2815.5 | 1005.8, −1005.8 | |
Attacker | Defender | ||
| Random strategy | Preference strategy | ||
| Random strategy | 1142.8, −985.6 | 1233.3, −1064.7 | |
| Preference strategy | 1062, −869.3 | 549.4, −465.1 | |
Attacker | Defender | ||
| Random strategy | Preference strategy | ||
| Random strategy | 2292.2, −985.6 | 1971.7, −1064.7 | |
| Preference strategy | 2815.5, −869.3 | 1005.8, −465.1 | |
Attacker | Defender | ||
| Random strategy | Preference strategy | ||
| Random strategy | 1142.8, −1887.5 | 1233.3, −1744.3 | |
| Preference strategy | 1062, −2162.5 | 549.4, −867.7 | |
Attacker | Defender | ||
| Random strategy | Preference strategy | ||
| Random strategy | 2292.2, −1887.5 | 1971.7, −1744.3 | |
| Preference strategy | 2815.5, −2162.5 | 1005.8, −867.7 | |
| Type of Network | RS/PS | S∧ | Sample Size (TT) | Defended Count (Td) |
|---|---|---|---|---|
| Scale-free network | RS | 0.7 | 12.04 | 1.695 |
| 0.5 | 19.17 | 2.755 | ||
| 0.3 | 26.94 | 3.535 | ||
| PS | 0.7 | 17.83 | 2.614 | |
| 0.5 | 28.37 | 3.141 | ||
| 0.3 | 38.8 | 3.88 |
| Network Type | N | <k> | TCA and TCD | PRS | PPS |
|---|---|---|---|---|---|
| Email Network | 1133 | 9.62 | 4500 | 0.4038 | 0.1832 |
| US Airlines Network | 332 | 12.81 | 1800 | 0.38 | 0.102 |
| Random Network | 1000 | 6.62 | 2700 | 0.4038 | 0.377 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, C.; Shi, Z. Analysis of Complex Network Attack and Defense Game Strategies Under Uncertain Value Criterion. Entropy 2025, 27, 1066. https://doi.org/10.3390/e27101066
Fu C, Shi Z. Analysis of Complex Network Attack and Defense Game Strategies Under Uncertain Value Criterion. Entropy. 2025; 27(10):1066. https://doi.org/10.3390/e27101066
Chicago/Turabian StyleFu, Chaoqi, and Zhuoying Shi. 2025. "Analysis of Complex Network Attack and Defense Game Strategies Under Uncertain Value Criterion" Entropy 27, no. 10: 1066. https://doi.org/10.3390/e27101066
APA StyleFu, C., & Shi, Z. (2025). Analysis of Complex Network Attack and Defense Game Strategies Under Uncertain Value Criterion. Entropy, 27(10), 1066. https://doi.org/10.3390/e27101066






