Secure and Efficient Lattice-Based Ring Signcryption Scheme for BCCL
Abstract
1. Introduction
- A TPP model for the BCCL system has been introduced with blockchain and ring signcryption technologies. The blockchain serves as the data-sharing bridge among different cold chain logistics institutions. The ring signcryption serves as the key security mechanism ensuring the protection of logistics information and user privacy during cross-institutional data exchanges within the BCCL system.
- A LRSC scheme has been proposed with lattice theory and a ring mechanism. Lattice theory enables anti-quantum security for the BCCL system, and the ring mechanism protects the signer’s privacy. Meanwhile, the signcryption mechanism effectively saves the algorithm’s execution efficiency.
- Security demonstrations for confidentiality and unforgeability have been established within the framework of the random oracle model. The proposed LRSC scheme captures these two security properties. Meanwhile, the experiment is executed, and the findings demonstrate the efficiency of both the TPP model and the LRSC scheme.
2. Related Work
2.1. BCCL Frameworks
2.2. Privacy-Preserving Mechanisms for BCCL
2.3. Post-Quantum Privacy-Preserving Methods
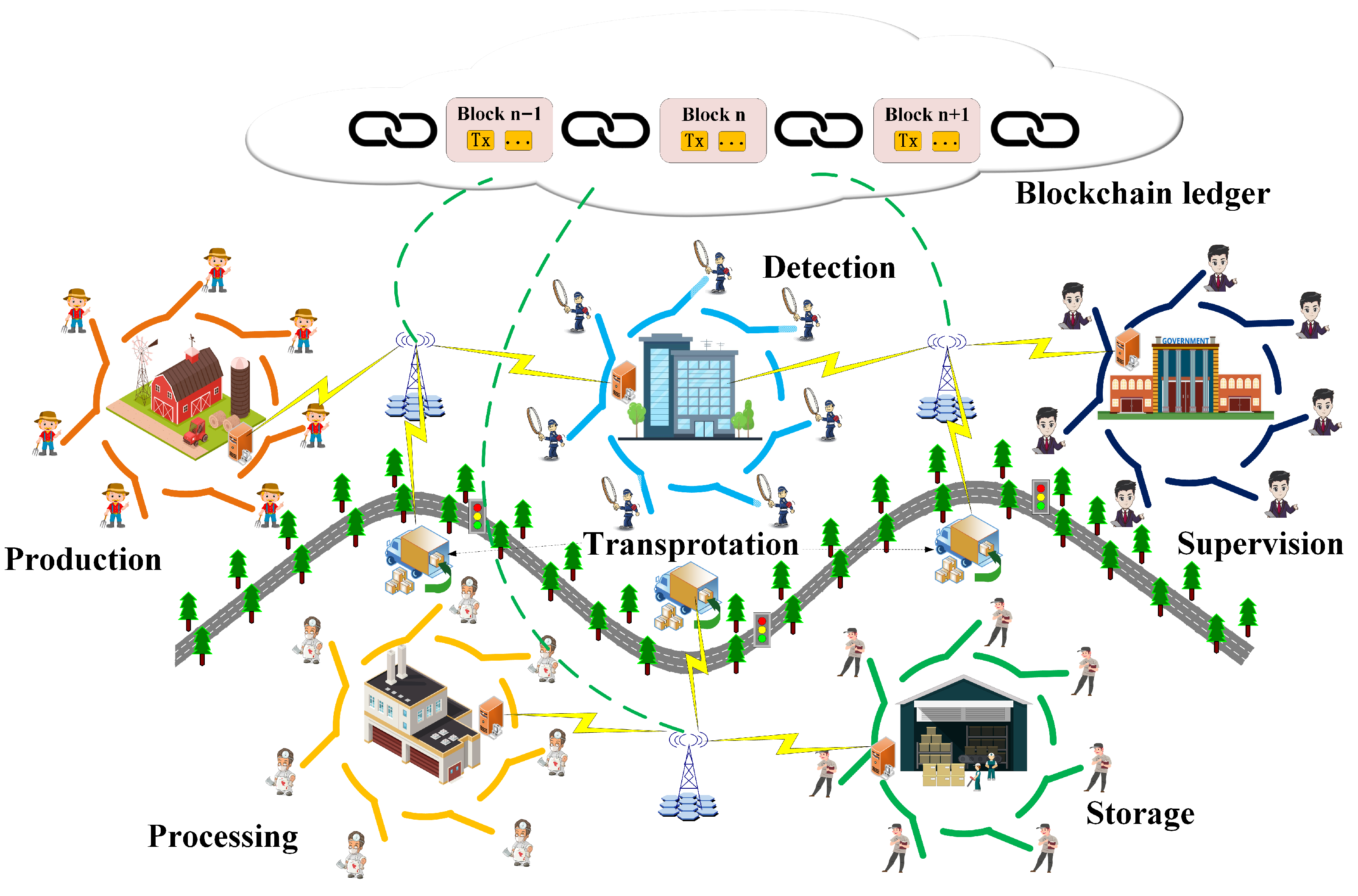
3. TPP Model for BCCL
3.1. Details of TPP Model
- Cold chain institution. Different logistics institutions related to cold chain products, such as production, processing, transportation, detection, storage, and supervision, compose this BCCLS system. They serve as the blockchain nodes to maintain the BCCLS system and take responsibility for the collection, verification, and packaging of data-sharing transactions. Meanwhile, every cold chain institution is a ring. In order to improve transaction efficiency, this model utilizes the LRSC scheme to simultaneously carry out both signature and encryption processes. The ring signature mechanism can select one ring member to represent the ring and perform the signing operation. It can protect the user’s privacy while increasing signature efficiency.
- Cold chain logistics vehicle. When the cold chain products are transmitted among different cold chain institutions, the safety of the transportation process is an important part of ensuring product safety. The vehicle serves as the most important part of the BCCL system, which guarantees the transportation security of cold chain products. Temperature, humidity, route, duration, etc., during transportation are all very important data. The collection, sharing, and storage of these data provide strong evidence for cold chain product security disputes.
- Data-sharing transaction. When the cold chain products arrive at the next institution, they should be safe and qualified. Therefore, the logistics data should be shared and public for every institution and consumer. The data-sharing transaction establishes a data exchange channel with the blockchain. The related transportation data and operation records are collected and formed with transactions, and all these transactions are documented within the blockchain ledger. These records are public and transparent, which provides a secure and traceable mechanism for cold chain product security.
- Blockchain ledger. This ledger records the data-sharing transaction and related operations created during the cold chain products’ transportation. It is the only ledger of the BCCL system, and every cold chain institution retains a copy of this system’s blockchain ledger. When cold chain product disputes occurs, it can find the records about production, transportation, processing, testing, sales, etc. The transparency of records guarantees production security.
3.2. Data Sharing Transaction in BCCL System
- (1)
- Tx. initialization. The operator in the production institution initiates a data-sharing transaction along with the cold chain product transportation process. He first obtains the transaction address from the BCCL system and prepares for this transaction. Here, the related production data and related operations are selected, which serve as the main transaction contents.
- (2)
- Tx. establishment. The transaction operator uploads the production data into the data-sharing transaction and sends it to the next cold chain institution.
- (3)
- Tx. signcryption. Before the sending process, this operator may sign this transaction with his private keys. Based on the LRSC scheme, the system performs both signing and encryption as a signcryption operation, which can effectively reduce the transaction time.
- (4)
- Tx. unsigncryption. The receiver in the next cold chain institution first verifies its validity when he obtains the data-sharing transaction. He performs the unsigncryption operation where the legitimacy of the signature is verified and the transmitted message is decrypted at the same time.
- (5)
- Tx. packaging. The cold chain institution acts as the system maintainer and competes with the bookkeeping rights of the blockchain ledger. Within a fixed period of time, these nodes all collect the published transactions in the BCCL system and package them into a block.
- (6)
- Tx. recording. The nodes obtain accounting rights with a consensus protocol, such as proof of stake (PoS) or delegated proof of stake (DPoS). Then, the node that obtains accounting rights adds the newest block to the blockchain ledger.
4. LRSC Scheme
4.1. Preliminaries
4.2. Details of LRSC Scheme
| Algorithm 1 KeyGen |
|
| Algorithm 2 Signcryption |
|
| Algorithm 3 Unsigncryption |
|
5. Security Analysis
5.1. Correctness
5.2. Confidentiality
- If the pair is found in , returns the stored hash value to ;
- Otherwise, samples a vector uniformly at random, stores in , and returns x to .
- If such an entry is found, returns the values to ;
- Otherwise, samples from the Gaussian distribution and chooses uniformly at random. The challenger then returns to the adversary and records the new entry in .
- If the pair exists, the corresponding symmetric key is returned to ;
- Otherwise, samples uniformly at random from the key space ∑, sets , returns ∂ to , and records the mapping into .
- If such an entry exists, the corresponding hash value is returned to ;
- Otherwise, randomly samples from the coin-flipping-based output space , sets , returns to , and records into .
- If so, it returns the corresponding to ;
- Otherwise, uniformly samples a matrix , records it in , and returns to .
- If , aborts the game;
- Otherwise, it computes the private trapdoor matrix satisfying , stores the tuple in , and returns to .
- If , executes the Algorithm 2 signcryption and returns the resulting ciphertext to ;
- Otherwise, retrieves the key pair from and proceeds to simulate the signcryption process as follows:
- -
- Computes ;
- -
- Computes ;
- -
- Computes ;
- -
- Computes ;
- -
- Computes ;
- -
- Computes ;
- -
- Computes ;
- -
- Computes ;
- -
- Returns ciphertext to .
- If , performs the standard unsigncryption algorithm and returns the result to .
- Otherwise, simulates the process by:
- -
- Computing , and for each component , setting
- -
- Computing ;
- -
- Verifying whether and ;
- -
- Querying the random oracle to get ; if , then is accepted as a valid message; otherwise, ⊥ is output.
- Computes ;
- Selects , computes ;
- Computes ;
- Computes ;
- Computes ;
- Computes ;
- Computes ;
- Computes ;
- Returns ciphertext to .
5.3. Unforgeability
6. Comparison and Performance
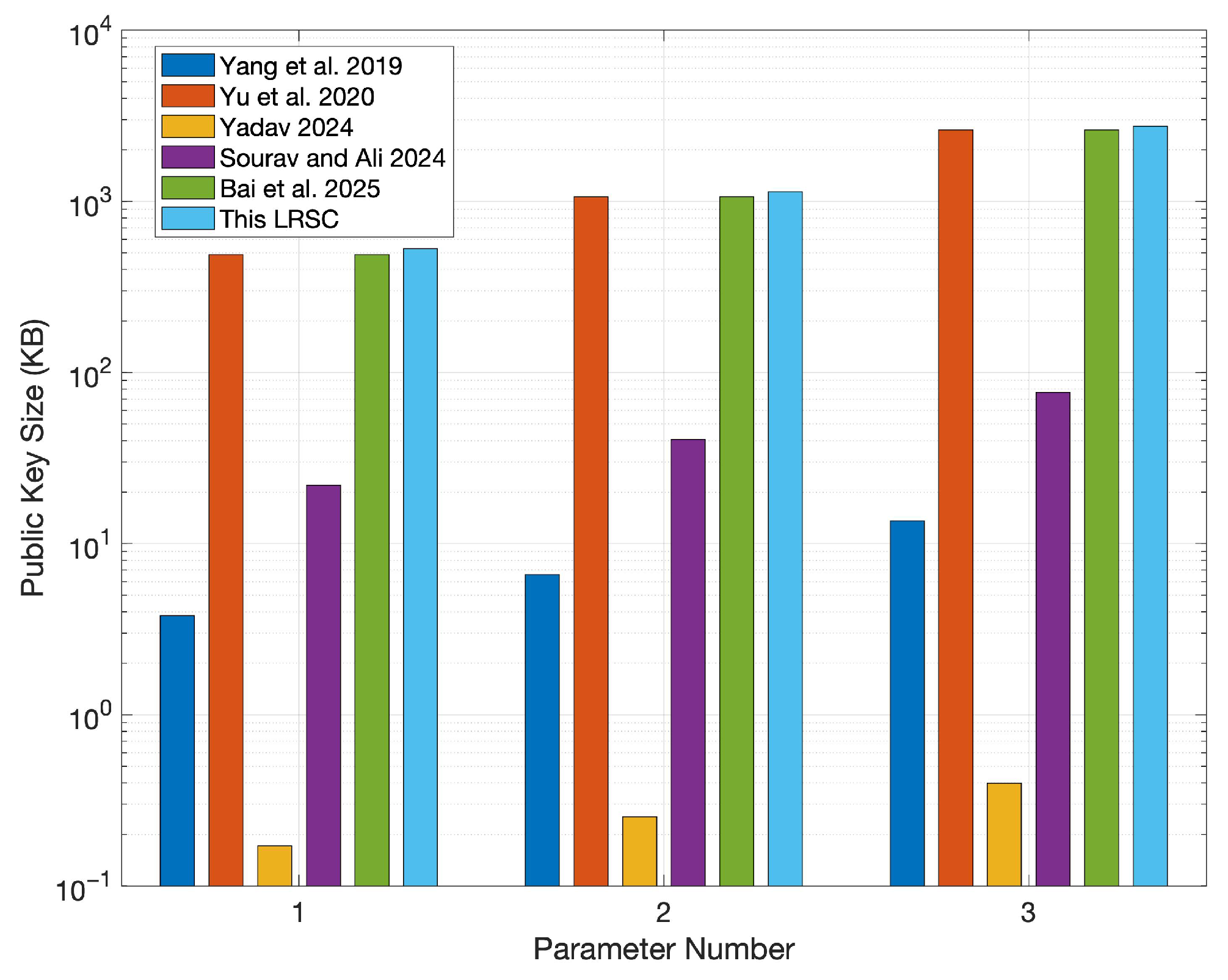
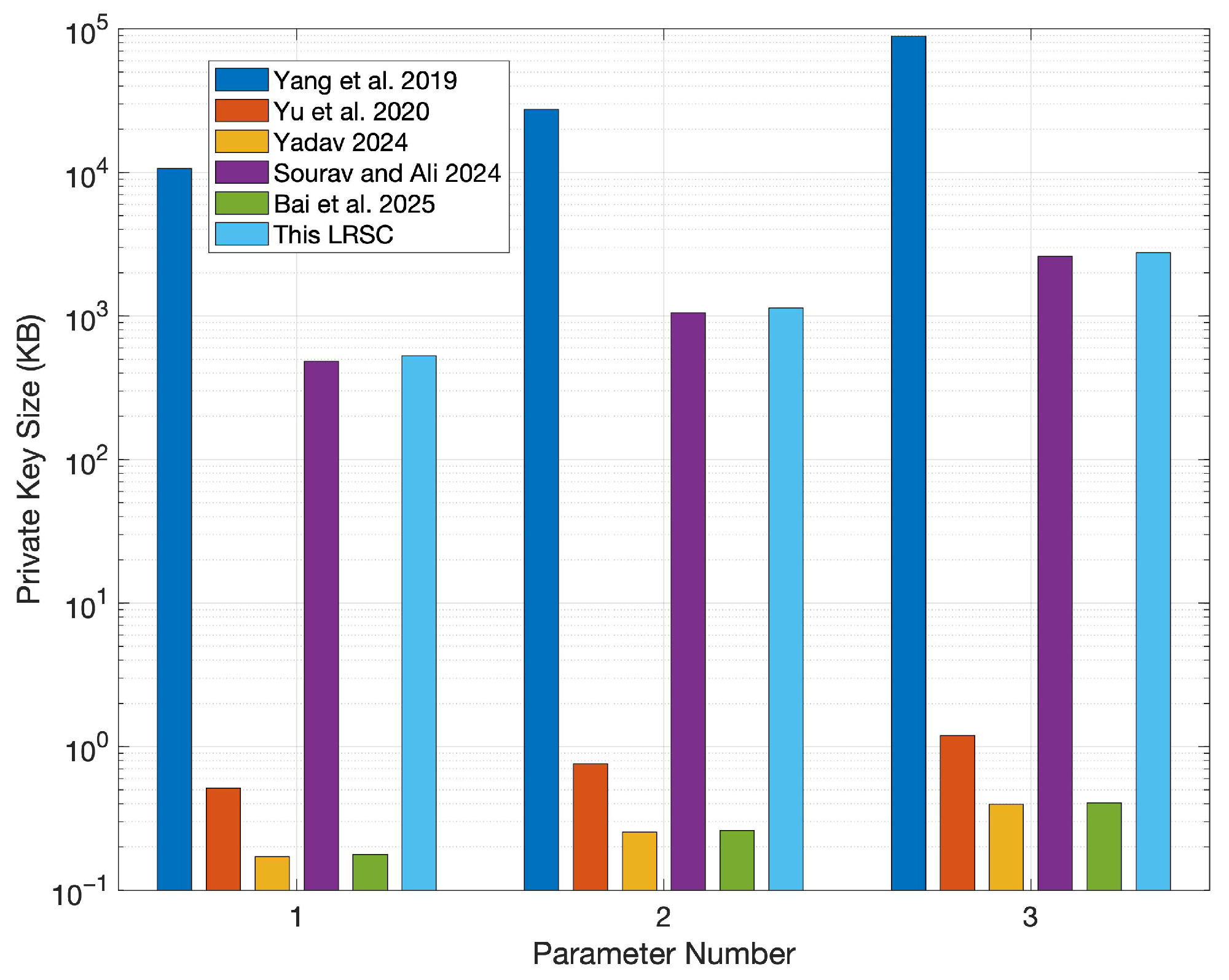
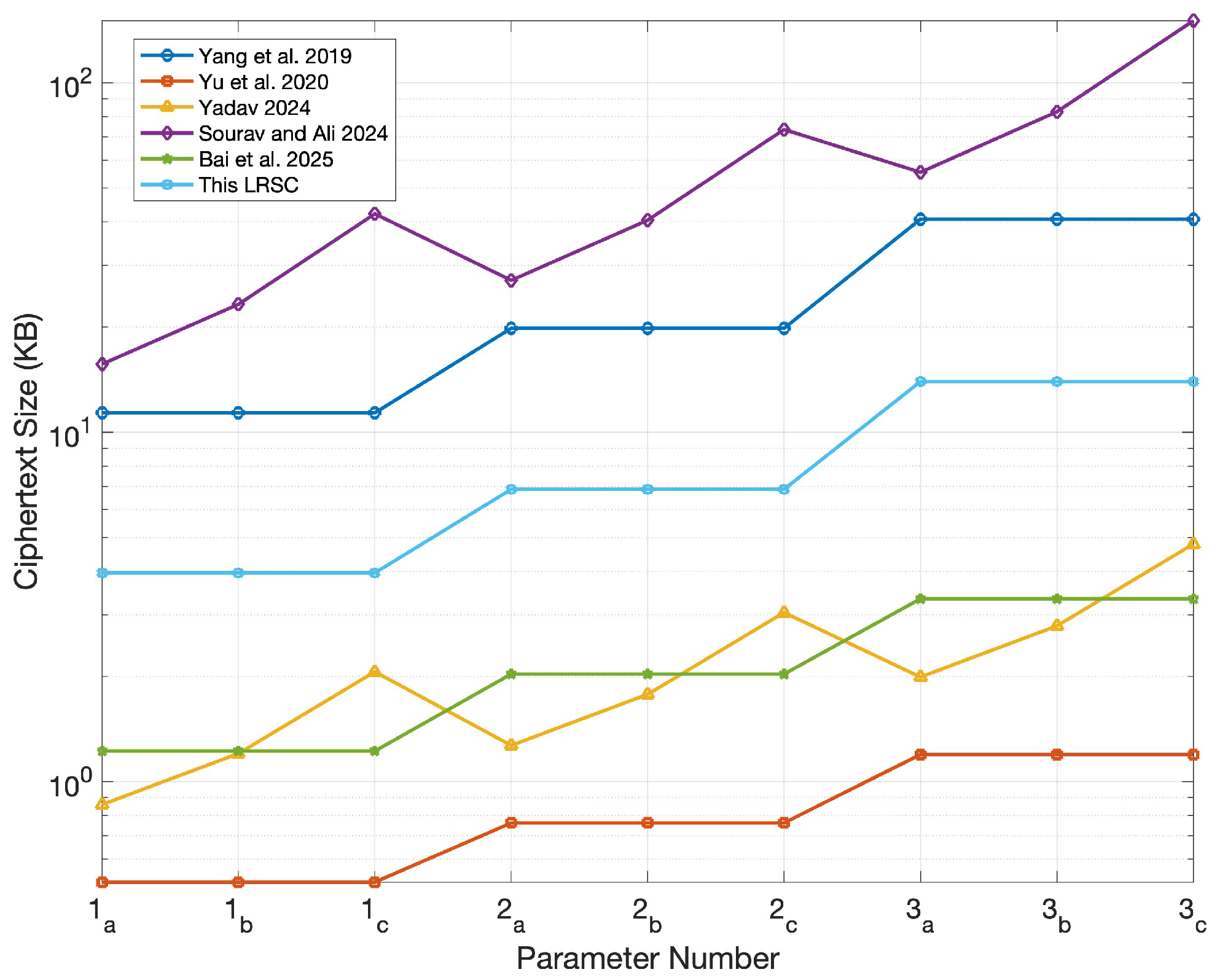
6.1. Comparison of Key and Ciphertext Sizes
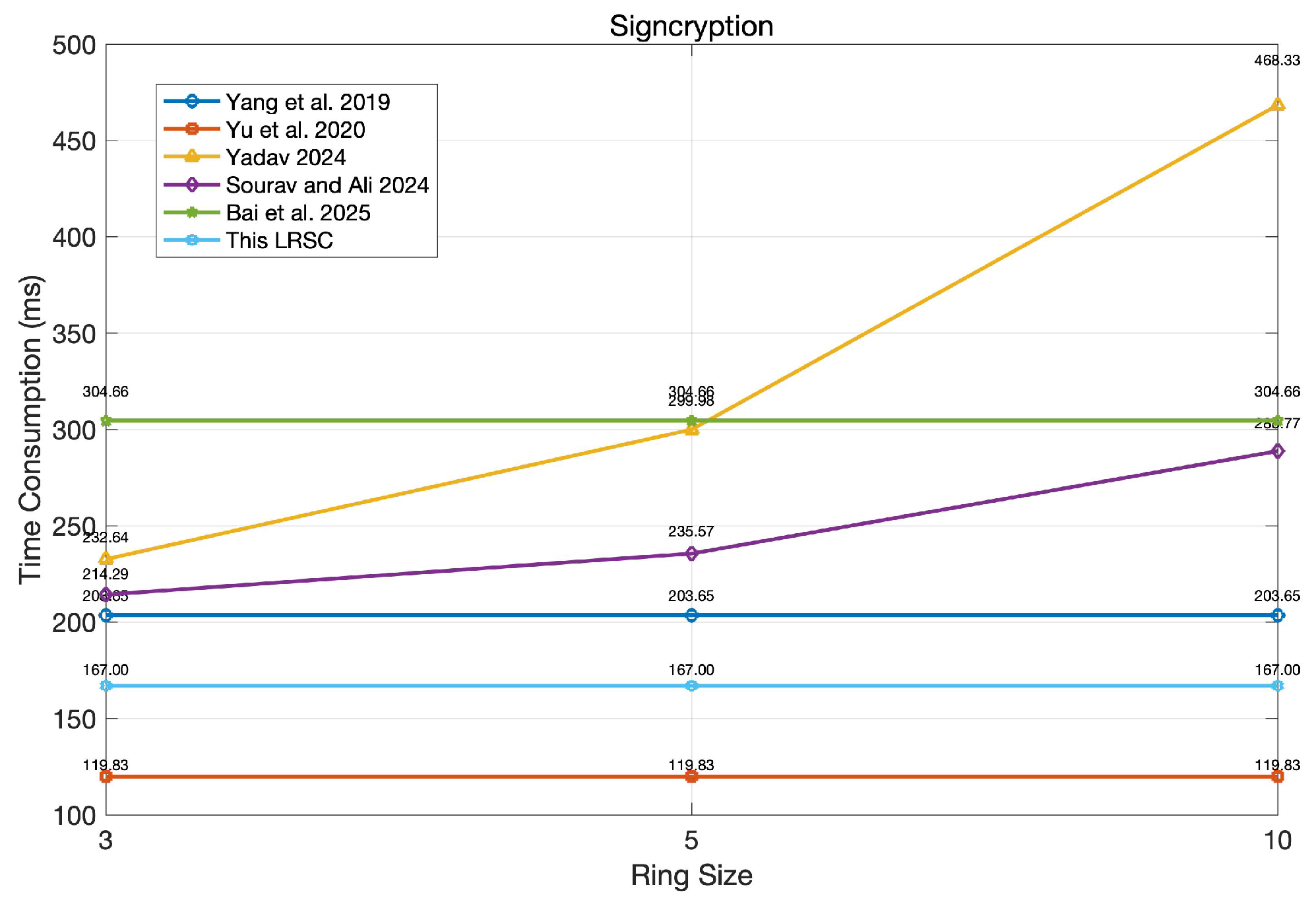
6.2. Performance Evaluation
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yu, M.; Zhang, H.; Ma, J.; Duan, X.; Kang, S.; Li, J. Cold chain logistics supervision of agricultural products supported using internet of things technology. IEEE Internet Things J. 2024, 12, 3502–3511. [Google Scholar] [CrossRef]
- Al-Farsi, S.; Rathore, M.M.; Bakiras, S. Security of blockchain-based supply chain management systems: Challenges and opportunities. Appl. Sci. 2021, 11, 5585. [Google Scholar] [CrossRef]
- Hu, X. Cold chain logistics model of agricultural products based on embedded system and blockchain. Prod. Plan. Control 2022, 1–12. [Google Scholar] [CrossRef]
- Song, H.; Vajdi, A.; Wang, Y.; Zhou, J. Blockchain for consortium: A practical paradigm in agricultural supply chain system. Expert Syst. Appl. 2021, 184, 115425. [Google Scholar] [CrossRef]
- He, M.; Wang, H.; Sun, Y.; Bie, R.; Lan, T.; Song, Q.; Zeng, X.; Pustisĕk, M.; Qiu, Z. T2L: A traceable and trustable consortium blockchain for logistics. Digit. Commun. Netw. 2022, in press. [Google Scholar] [CrossRef]
- Allenbrand, C. Smart contract-enabled consortium blockchains for the control of supply chain information distortion. Blockchain Res. Appl. 2023, 4, 100134. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, Y.; Li, C.; Dong, M.; Huang, M.; Zhang, H.; Ota, K. Privacy-preserving for blockchain-enabled cold-chain logistics system with IoV and linkable ring signature. IEEE Trans. Veh. Technol. 2024, 73, 12585–12596. [Google Scholar] [CrossRef]
- Xiong, R.; Cheng, J.; Dong, X.; Pu, J.; Shan, F. Leveraging consortium blockchain for secure cross-domain data sharing in supply chain networks. IEEE Trans. Serv. Comput. 2025, 18, 897–911. [Google Scholar] [CrossRef]
- Kim, S.; Kim, J.; Kim, D. Implementation of a blood cold chain system using blockchain technology. Appl. Sci. 2020, 10, 3330. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, Y.; Sun, Y. Research on cold chain logistics traceability system of fresh agricultural products based on blockchain. Comput. Intell. Neurosci. 2022, 2022, 1957957. [Google Scholar] [CrossRef]
- Yang, R.; Wakefield, R.; Lyu, S.; Jayasuriya, S.; Han, F.; Yi, X.; Yang, X.; Amarasinghe, G.; Chen, S. Public and private blockchain in construction business process and information integration. Autom. Constr. 2020, 118, 103276. [Google Scholar] [CrossRef]
- Si, Y. Agricultural cold chain logistics mode based on multi-mode blockchain data model. Comput. Intell. Neurosci. 2022, 2022, 8060765. [Google Scholar] [CrossRef]
- Bottoni, P.; Di Ciccio, C.; Pareschi, R.; Tortola, D.; Gessa, N.; Massa, G. Blockchain-as-a-service and blockchain-as-a-partner: Implementation options for supply chain optimization. Blockchain: Res. Appl. 2023, 4, 100119. [Google Scholar] [CrossRef]
- Gao, S.; Zhang, Z.; Li, Q.; Ding, S.; Iu, H.H.C.; Cao, Y.; Xu, X.; Wang, C.; Mou, J. Encrypt a story: A video segment encryption method based on the discrete sinusoidal memristive rulkov neuron. IEEE Trans. Dependable Secur. Comput. 2025, 1–15. [Google Scholar] [CrossRef]
- Gao, S.; Wu, R.; Iu, H.H.C.; Erkan, U.; Cao, Y.; Li, Q.; Toktas, A.; Mou, J. Chaos-based video encryption techniques: A review. Comput. Sci. Rev. 2025, 58, 100816. [Google Scholar] [CrossRef]
- Cha, S.; Baek, S.; Kim, S. Blockchain based sensitive data management by using key escrow encryption system from the perspective of supply chain. IEEE Access 2020, 8, 154269–154280. [Google Scholar] [CrossRef]
- Din, I.U.; Almogren, A.; Han, Z.; Guizani, M. Ensuring privacy and integrity in IoT supply chains through blockchain and homomorphic encryption. IEEE Internet Things J. 2025, 12, 25547–25558. [Google Scholar] [CrossRef]
- Li, C.; Shen, H.; Shi, X.; Liang, H. Quantum secure undeniable signature for blockchain-enabled cold-chain logistics system. Comput. Mater. Contin. 2023, 75, 3941. [Google Scholar] [CrossRef]
- Mouléry, M.; Sanz Sanz, E.; Debolini, M.; Napoléone, C.; Josselin, D.; Mabire, L.; Vicente-Vicente, J.L. Self-sufficiency assessment: Defining the foodshed spatial signature of supply chains for beef in avignon, france. Agriculture 2022, 12, 419. [Google Scholar] [CrossRef]
- Zhan, Q.; Luo, M.; Qiu, M. An efficient multi-mode certificateless ring signcryption scheme in vanets. IEEE Internet Things J. 2024, 11, 33508–33524. [Google Scholar] [CrossRef]
- Zhou, X.; Luo, M.; Qiu, M. A heterogeneous ring signcryption scheme with privacy protection and conditional tracing for smart grid. Comput. Commun. 2024, 228, 107959. [Google Scholar] [CrossRef]
- Wei, J.; Xie, L.; Zhu, Q.; Gao, Y.; Yu, K.; Choo, K.K.R. IDTRSC: ID-based traceable ring signcryption framework for data sharing without key escrow. IEEE Trans. Veh. Technol. 2025, 74, 11207–11220. [Google Scholar] [CrossRef]
- Xiong, F.; Xiao, R.; Ren, W.; Zheng, R.; Jiang, J. A key protection scheme based on secret sharing for blockchain-based construction supply chain system. IEEE Access 2019, 7, 126773–126786. [Google Scholar] [CrossRef]
- Kalyani, D.; Srivani, P.; Pradeep, S. Secured information sharing in supply chain management: Modified data sanitization with optimal key generation via hybrid algorithm. Adv. Eng. Softw. 2022, 173, 103194. [Google Scholar] [CrossRef]
- Vangala, A.; Das, A.K.; Mitra, A.; Das, S.K.; Park, Y. Blockchain-enabled authenticated key agreement scheme for mobile vehicles-assisted precision agricultural IoT networks. IEEE Trans. Inf. Forensics Secur. 2022, 18, 904–919. [Google Scholar] [CrossRef]
- Yang, Z.; Zolanvari, M.; Jain, R. A survey of important issues in quantum computing and communications. IEEE Commun. Surv. Tutor. 2023, 25, 1059–1094. [Google Scholar] [CrossRef]
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 1999, 41, 303–332. [Google Scholar] [CrossRef]
- Grover, L.K. Quantum mechanics helps in searching for a needle in a haystack. Phys. Rev. Lett. 1997, 79, 325. [Google Scholar] [CrossRef]
- Gharavi, H.; Granjal, J.; Monteiro, E. Post-quantum blockchain security for the Internet of Things: Survey and research directions. IEEE Commun. Surv. Tutor. 2024, 26, 1748–1774. [Google Scholar] [CrossRef]
- Sendrier, N. Code-based cryptography: State of the art and perspectives. IEEE Secur. Priv. 2017, 15, 44–50. [Google Scholar] [CrossRef]
- Butin, D. Hash-based signatures: State of play. IEEE Secur. Priv. 2017, 15, 37–43. [Google Scholar] [CrossRef]
- Dey, J.; Dutta, R. Progress in multivariate cryptography: Systematic review, challenges, and research directions. ACM Comput. Surv. 2023, 55, 1–34. [Google Scholar] [CrossRef]
- Nejatollahi, H.; Dutt, N.; Ray, S.; Regazzoni, F.; Banerjee, I.; Cammarota, R. Post-quantum lattice-based cryptography implementations: A survey. ACM Comput. Surv. (CSUR) 2019, 51, 1–41. [Google Scholar] [CrossRef]
- Zheng, Y. Digital signcryption or how to achieve cost (signature & encryption)≪ cost (signature)+ cost (encryption). In Proceedings of the 17th Annual International Cryptology Conference, CRYPTO’97, Santa Barbara, CA, USA, 17–21 August 1997; Springer: Berlin/Heidelberg, Germany, 1997; pp. 165–179. [Google Scholar]
- Ali, R.; Obaidat, M.S. Secure and efficient lattice-based signcryption for blockchain-enabled IoT healthcare. IEEE Trans. Dependable Secur. Comput. 2025, 1–12. [Google Scholar] [CrossRef]
- Xu, S.; Chen, X.; Guo, Y.; Yiu, S.M.; Gao, S.; Xiao, B. Efficient and secure post-quantum certificateless signcryption with linkability for IoMT. IEEE Trans. Inf. Forensics Secur. 2024, 20, 1119–1134. [Google Scholar] [CrossRef]
- Yang, X.; Cao, H.; Li, W.; Xuan, H. Improved lattice-based signcryption in the standard model. IEEE Access 2019, 7, 155552–155562. [Google Scholar] [CrossRef]
- Yu, H.; Bai, L.; Hao, M.; Wang, N. Certificateless signcryption scheme from lattice. IEEE Syst. J. 2020, 15, 2687–2695. [Google Scholar] [CrossRef]
- Yadav, V.K. Anonymous and linkable ring signcryption scheme for location-based services in vanets. Veh. Commun. 2024, 45, 100717. [Google Scholar] [CrossRef]
- Sourav; Ali, R. Lattice-based ring signcryption scheme for smart healthcare management. Clust. Comput. 2024, 27, 14131–14148. [Google Scholar] [CrossRef]
- Bai, Y.; He, D.; Yang, Z.; Luo, M.; Peng, C. Efficient module-lattice-based certificateless online/offline signcryption scheme for internet of medical things. IEEE Internet Things J. 2025, 12, 27350–27363. [Google Scholar] [CrossRef]
- Prajapat, S.; Kumar, D.; Kumar, P.; Das, A.K.; Hossain, M.S. A lattice-based ring signcryption scheme for secure communication in 6G-enabled vehicular ad hoc networks using blockchain. IEEE Trans. Intell. Transp. Syst. 2025, 1–14. [Google Scholar] [CrossRef]
- Micciancio, D.; Regev, O. Lattice-based cryptography. In Post-Quantum Cryptography; Springer: Berlin/Heidelberg, Germany, 2009; pp. 147–191. [Google Scholar]
- Ducas, L.; Durmus, A.; Lepoint, T.; Lyubashevsky, V. Lattice signatures and bimodal Gaussians. In Proceedings of the 33rd Annual International Cryptology Conference, Santa Barbara, CA, USA, 18–22 August 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 40–56. [Google Scholar]
- Bert, P.; Fouque, P.A.; Roux-Langlois, A.; Sabt, M. Practical implementation of ring-SIS/LWE based signature and IBE. In Proceedings of the 9th International Workshop on Post-Quantum Cryptography, PQCrypto 2018, Fort Lauderdale, FL, USA, 9–11 April 2018; Springer International Publishing: Cham, Switzerland, 2018; pp. 271–291. [Google Scholar]
- Micciancio, D.; Mol, P. Pseudorandom knapsacks and the sample complexity of LWE search-to-decision reductions. In Proceedings of the 31st Annual International Cryptology Conference, CRYPTO 2011, Santa Barbara, CA, USA, 14–18 August 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 465–484. [Google Scholar]
- Micciancio, D.; Peikert, C. Trapdoors for lattices: Simpler, tighter, faster, smaller. In Proceedings of the 31st Annual International Conference on the Theory and Applications of Cryptographic Techniques, Cambridge, UK, 15–19 April 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 700–718. [Google Scholar]

| Schemes | Public Key | Private Key | Signature | Ciphertext |
|---|---|---|---|---|
| Yang et al. [37] | ||||
| Yu et al. [38] | ||||
| Yadav [39] | ||||
| Sourav and Ali [40] | ||||
| Bai et al. [41] | ||||
| This LRSC |
| Number | 1 | 2 | 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| n | 128 | 128 | 128 | 160 | 160 | 160 | 192 | 192 | 192 |
| q | |||||||||
| m | 2818 | 2818 | 2818 | 4164 | 4164 | 4164 | 6533 | 6533 | 6533 |
| k | 173 | 173 | 173 | 264 | 264 | 264 | 341 | 341 | 341 |
| r | 3 | 5 | 10 | 3 | 5 | 10 | 3 | 5 | 10 |
| Schemes | Signcryption | Unsigncryption |
|---|---|---|
| Yang et al. [37] | ||
| Yu et al. [38] | ||
| Yadav [39] | ||
| Sourav and Ali [40] | ||
| Bai et al. [41] | ||
| This LRSC |
| Operation | Time Consumption (Times/ms) | Algorithm Description |
|---|---|---|
| 5.32 ms | Matrix–vector multiplication | |
| 14.73 ms | Hash function | |
| 23.03 ms | Gaussian sampling | |
| 35.42 ms | Image sampling |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Duan, P.; Li, C.; Ahmad, H.; Zhang, H. Secure and Efficient Lattice-Based Ring Signcryption Scheme for BCCL. Entropy 2025, 27, 1060. https://doi.org/10.3390/e27101060
Zhang Y, Duan P, Li C, Ahmad H, Zhang H. Secure and Efficient Lattice-Based Ring Signcryption Scheme for BCCL. Entropy. 2025; 27(10):1060. https://doi.org/10.3390/e27101060
Chicago/Turabian StyleZhang, Yang, Pengxiao Duan, Chaoyang Li, Haseeb Ahmad, and Hua Zhang. 2025. "Secure and Efficient Lattice-Based Ring Signcryption Scheme for BCCL" Entropy 27, no. 10: 1060. https://doi.org/10.3390/e27101060
APA StyleZhang, Y., Duan, P., Li, C., Ahmad, H., & Zhang, H. (2025). Secure and Efficient Lattice-Based Ring Signcryption Scheme for BCCL. Entropy, 27(10), 1060. https://doi.org/10.3390/e27101060