Modified Gravity in the Presence of Matter Creation: Scenario for the Late Universe
Abstract
1. Introduction
2. Matter Creation Process
3. Modified Cosmological Dynamics in the Jordan Frame
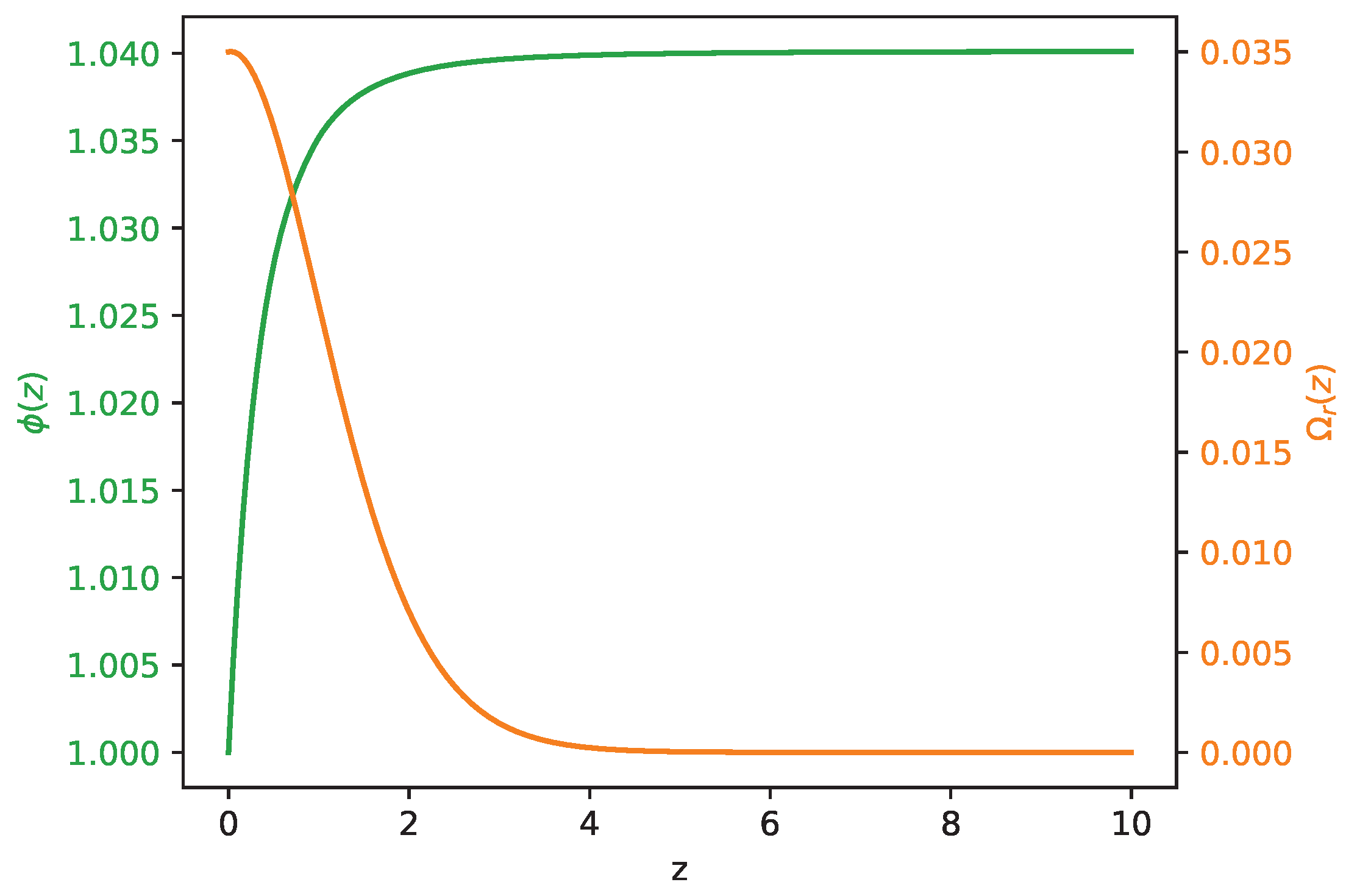
4. Reduced Dynamics
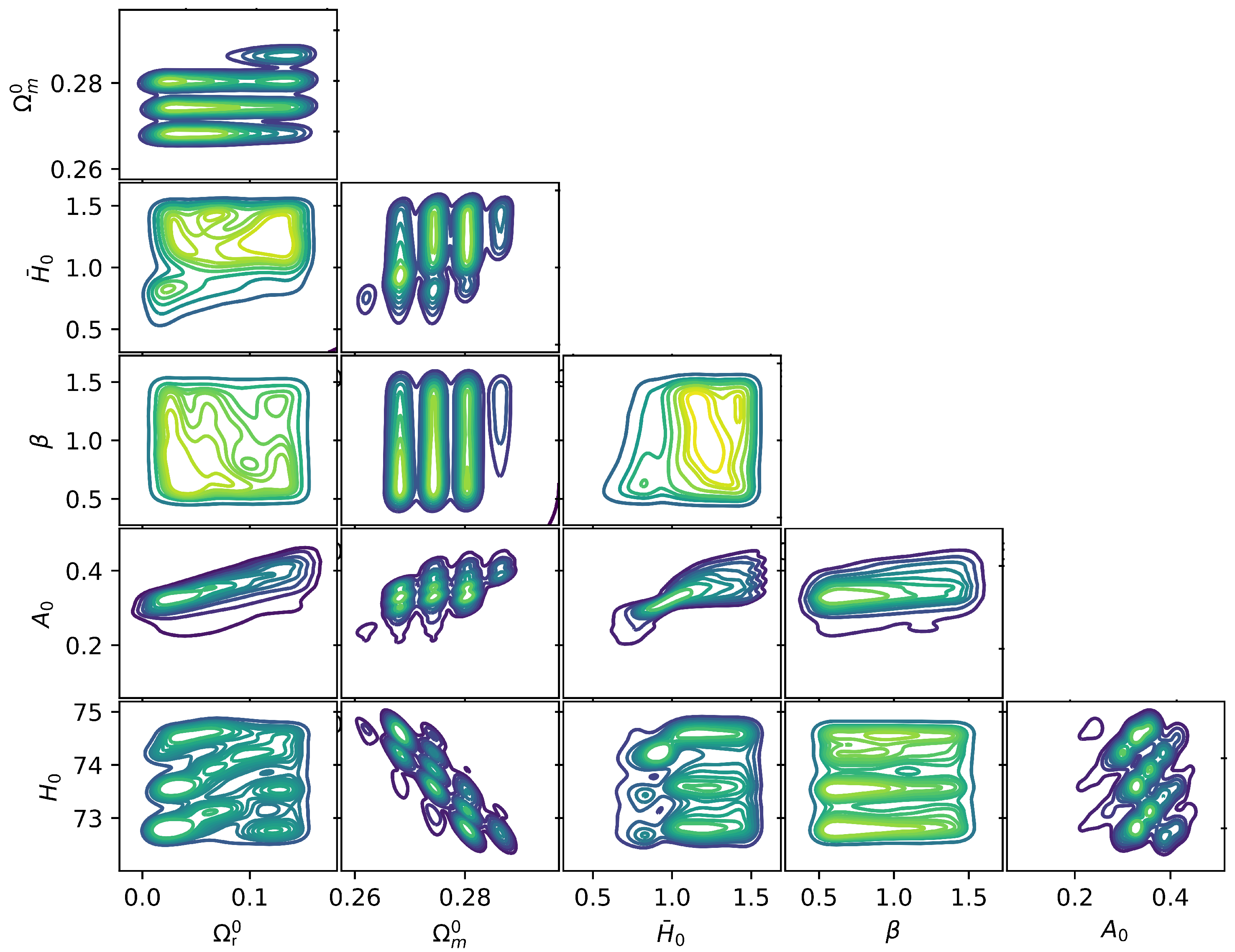
5. Numerical Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Scolnic, D.M.; Brout, D.; Carr, A.; Riess, A.G.; Davis, T.M.; Dwomoh, A.; Jones, D.O.; Ali, N.; Charvu, P.; Chen, R.; et al. The Pantheon+ Analysis: The Full Data Set and Light-curve Release. Astrophys. J. 2022, 938, 113. [Google Scholar] [CrossRef]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Brout, D.; Scolnic, D.; Popovic, B.; Riess, A.G.; Carr, A.; Zuntz, J.; Kessler, R.; Davis, T.M.; Hinton, S.; Jones, D.; et al. The Pantheon+ Analysis: Cosmological Constraints. Astrophys. J. 2022, 938, 110. [Google Scholar] [CrossRef]
- Riess, A.G.; Yuan, W.; Macri, L.M.; Scolnic, D.; Brout, D.; Casertano, S.; Jones, D.O.; Murakami, Y.; Anand, G.S.; Breuval, L.; et al. A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km s−1 Mpc−1 Uncertainty from the Hubble Space Telescope and the SH0ES Team. Astrophys. J. Lett. 2022, 934, L7. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2021, 641, A6, Erratum in Astron. Astrophys. 2021, 652, C4. [Google Scholar] [CrossRef]
- Schiavone, T.; Montani, G.; Bombacigno, F. f(R) gravity in the Jordan frame as a paradigm for the Hubble tension. Mon. Not. RAS 2023, 522, L72–L77. [Google Scholar] [CrossRef]
- Montani, G.; De Angelis, M.; Bombacigno, F.; Carlevaro, N. Metric f(R) gravity with dynamical dark energy as a scenario for the Hubble tension. Mon. Not. RAS 2024, 527, L156–L161. [Google Scholar] [CrossRef]
- Montani, G.; Carlevaro, N.; Dainotti, M.G. Slow-rolling scalar dynamics as solution for the Hubble tension. Phys. Dark Univ. 2024, 44, 101486. [Google Scholar] [CrossRef]
- Adil, S.; Akarsu, Ö.; Di Valentino, E.; Nunes, R.; Özülker, E.; Sen, A.; Specogna, E. Omnipotent dark energy: A phenomenological answer to the Hubble tension. Phys. Rev. D 2024, 109, 023527. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Integral F(R) gravity and saddle point condition as a remedy for the H0-tension. Nucl. Phys. B 2022, 980, 115850. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Sáez-Chillón Gómez, D.; Sharov, G.S. Analyzing the H0 tension in F(R) gravity models. Nucl. Phys. B 2021, 966, 115377. [Google Scholar] [CrossRef]
- Wang, B.; Abdalla, E.; Atrio-Barandela, F.; Pavón, D. Dark matter and dark energy interactions: Theoretical challenges, cosmological implications and observational signatures. Rep. Prog. Phys. 2016, 79, 096901. [Google Scholar] [CrossRef] [PubMed]
- Naidoo, K.; Jaber, M.; Hellwing, W.A.; Bilicki, M. Dark matter solution to the H0 and S8 tensions, and the integrated Sachs-Wolfe void anomaly. Phys. Rev. D 2024, 109, 083511. [Google Scholar] [CrossRef]
- Dainotti, M.; Bargiacchi, G.; Bogdan, M.; Capozziello, S.; Nagataki, S. On the statistical assumption on the distance moduli of Supernovae Ia and its impact on the determination of cosmological parameters. J. High Energy Astrophys. 2024, 41, 30–41. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Bargiacchi, G.; Bogdan, M.; Lenart, A.L.; Iwasaki, K.; Capozziello, S.; Zhang, B.; Fraija, N. Reducing the Uncertainty on the Hubble Constant up to 35% with an Improved Statistical Analysis: Different Best-fit Likelihoods for Type Ia Supernovae, Baryon Acoustic Oscillations, Quasars, and Gamma-Ray Bursts. Astrophys. J. 2023, 951, 63. [Google Scholar] [CrossRef]
- Weinberg, S. Cosmology; OUP Oxford: Oxford, UK, 2008. [Google Scholar]
- Di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the realm of the Hubble tension—a review of solutions. Class. Quant. Grav. 2021, 38, 153001. [Google Scholar] [CrossRef]
- Dainotti, M.G.; De Simone, B.; Schiavone, T.; Montani, G.; Rinaldi, E.; Lambiase, G. On the Hubble constant tension in the SNe Ia Pantheon sample. Astrophys. J. 2021, 912, 150. [Google Scholar] [CrossRef]
- Dainotti, M.G.; De Simone, B.; Schiavone, T.; Montani, G.; Rinaldi, E.; Lambiase, G.; Bogdan, M.; Ugale, S. On the Evolution of the Hubble Constant with the SNe Ia Pantheon Sample and Baryon Acoustic Oscillations: A Feasibility Study for GRB-Cosmology in 2030. Galaxies 2022, 10, 24. [Google Scholar] [CrossRef]
- Xu, B.; Xu, J.; Zhang, K.; Fu, X.; Huang, Q. Model-independent test of the running Hubble constant from the Type Ia supernovae and the Hubble parameter data. Mon. Not. RAS 2024, 530, 5091–5098. [Google Scholar] [CrossRef]
- Krishnan, C.; Colgáin, E.O.; Sheikh-Jabbari, M.M.; Yang, T. Running Hubble Tension and a H0 Diagnostic. Phys. Rev. D 2021, 103, 103509. [Google Scholar] [CrossRef]
- Kazantzidis, L.; Perivolaropoulos, L. Hints of a Local Matter Underdensity or Modified Gravity in the Low z Pantheon data. Phys. Rev. D 2020, 102, 023520. [Google Scholar] [CrossRef]
- Efstathiou, G. To H0 or not to H0? Mon. Not. RAS 2021, 505, 3866–3872. [Google Scholar] [CrossRef]
- Giarè, W. Inflation, the Hubble Tension and Early Dark Energy: An alternative overview. Phys. Rev. D 2024, 109, 123545. [Google Scholar] [CrossRef]
- Vagnozzi, S. Seven Hints That Early-Time New Physics Alone Is Not Sufficient to Solve the Hubble Tension. Universe 2023, 9, 393. [Google Scholar] [CrossRef]
- Vagnozzi, S. New physics in light of the H0 tension: An alternative view. Phys. Rev. D 2020, 102, 023518. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. f(R) theories of gravity. Rev. Mod. Phys. 2010, 82, 451–497. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Montani, G. Influence of particle creation on flat and negative curved FLRW universes. Class. Quantum Gravity 2001, 18, 193–203. [Google Scholar] [CrossRef]
- Calvão, M.O.; Lima, J.A.S.; Waga, I. On the thermodynamics of matter creation in cosmology. Phys. Lett. A 1992, 162, 223–226. [Google Scholar] [CrossRef]
- Erdem, R. Gravitational particle production and the Hubble tension. arXiv 2024, arXiv:2402.16791. [Google Scholar] [CrossRef]
- Nunes, R.C.; Pavón, D. Phantom behavior via cosmological creation of particles. Phys. Rev. D 2015, 91, 063526. [Google Scholar] [CrossRef]
- Nunes, R.C. Gravitationally induced particle production and its impact on structure formation. Gen. Relativ. Gravit. 2016, 48, 107. [Google Scholar] [CrossRef][Green Version]
- Lima, J.A.S.; Graef, L.L.; Pavón, D.; Basilakos, S. Cosmic acceleration without dark energy: Background tests and thermodynamic analysis. J. Cosmol. Astropart. Phys. 2014, 2014, 42. [Google Scholar] [CrossRef]
- Efstathiou, G.; Gratton, S. The evidence for a spatially flat Universe. Mon. Not. RAS 2020, 496, L91–L95. [Google Scholar] [CrossRef]
- Birrell, N.; Davies, P. Quantum Fields in Curved Space; Cambridge University Press: Cambridge, MA, USA, 1982. [Google Scholar]
- Wald, R. Quantum Field Theory in Curved Spacetime and Black Hole Thermodynamics; The University of Chicago Press: Chicago, IL, USA, 1994. [Google Scholar]
- Olmo, G.J. Post–Newtonian constraints on f(R) cosmologies in metric and Palatini formalism. Phys. Rev. D 2005, 72, 083505. [Google Scholar] [CrossRef]
- Brax, P.; van de Bruck, C.; Davis, A.C.; Shaw, D.J. f(R) Gravity and Chameleon Theories. Phys. Rev. D 2008, 78, 104021. [Google Scholar] [CrossRef]
- Alam, S.; Ata, M.; Bailey, S.; Beutler, F.; Bizyaev, D.; Blazek, J.A.; Bolton, A.S.; Brownstein, J.R.; Burden, A.; Chuang, C.H.; et al. The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological analysis of the DR12 galaxy sample. Mon. Not. RAS 2017, 470, 2617–2652. [Google Scholar] [CrossRef]
- Blomqvist, M.; du Mas des Bourboux, H.; Busca, N.G.; de Sainte Agathe, V.; Rich, J.; Balland, C.; Bautista, J.E.; Dawson, K.; Font-Ribera, A.; Guy, J.; et al. Baryon acoustic oscillations from the cross-correlation of Lyα absorption and quasars in eBOSS DR14. Astron. Astrophys. 2019, 629, A86. [Google Scholar] [CrossRef]
- de Sainte Agathe, V.; Balland, C.; du Mas des Bourboux, H.; Busca, N.G.; Blomqvist, M.; Guy, J.; Rich, J.; Font-Ribera, A.; Pieri, M.M.; Bautista, J.E.; et al. Baryon acoustic oscillations at z = 2.34 from the correlations of Lyα absorption in eBOSS DR14. Astron. Astrophys. 2019, 629, A85. [Google Scholar] [CrossRef]
- Hou, J.; Sánchez, A.G.; Ross, A.J.; Smith, A.; Neveux, R.; Bautista, J.; Burtin, E.; Zhao, C.; Scoccimarro, R.; Dawson, K.S.; et al. The completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: BAO and RSD measurements from anisotropic clustering analysis of the quasar sample in configuration space between redshift 0.8 and 2.2. Mon. Not. RAS 2021, 500, 1201–1221. [Google Scholar] [CrossRef]
- Abazajian, K.N. Sterile neutrinos in cosmology. Phys. Rept. 2017, 711, 1–28. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montani, G.; Carlevaro, N.; De Angelis, M. Modified Gravity in the Presence of Matter Creation: Scenario for the Late Universe. Entropy 2024, 26, 662. https://doi.org/10.3390/e26080662
Montani G, Carlevaro N, De Angelis M. Modified Gravity in the Presence of Matter Creation: Scenario for the Late Universe. Entropy. 2024; 26(8):662. https://doi.org/10.3390/e26080662
Chicago/Turabian StyleMontani, Giovanni, Nakia Carlevaro, and Mariaveronica De Angelis. 2024. "Modified Gravity in the Presence of Matter Creation: Scenario for the Late Universe" Entropy 26, no. 8: 662. https://doi.org/10.3390/e26080662
APA StyleMontani, G., Carlevaro, N., & De Angelis, M. (2024). Modified Gravity in the Presence of Matter Creation: Scenario for the Late Universe. Entropy, 26(8), 662. https://doi.org/10.3390/e26080662