Relativistic Heat Conduction in the Large-Flux Regime
Abstract
1. Introduction
2. Mathematical Structure of the GENERIC-Multifluid Theory for Heat Conduction
2.1. Non-Equilibrium Thermodynamics
2.2. Hydrodynamic Constitutive Relations
2.3. Consistency with Relativistic Thermodynamics
2.4. Equations of Motion
3. Evaluation of the Constitutive Relations from Microphysics
3.1. General Strategy
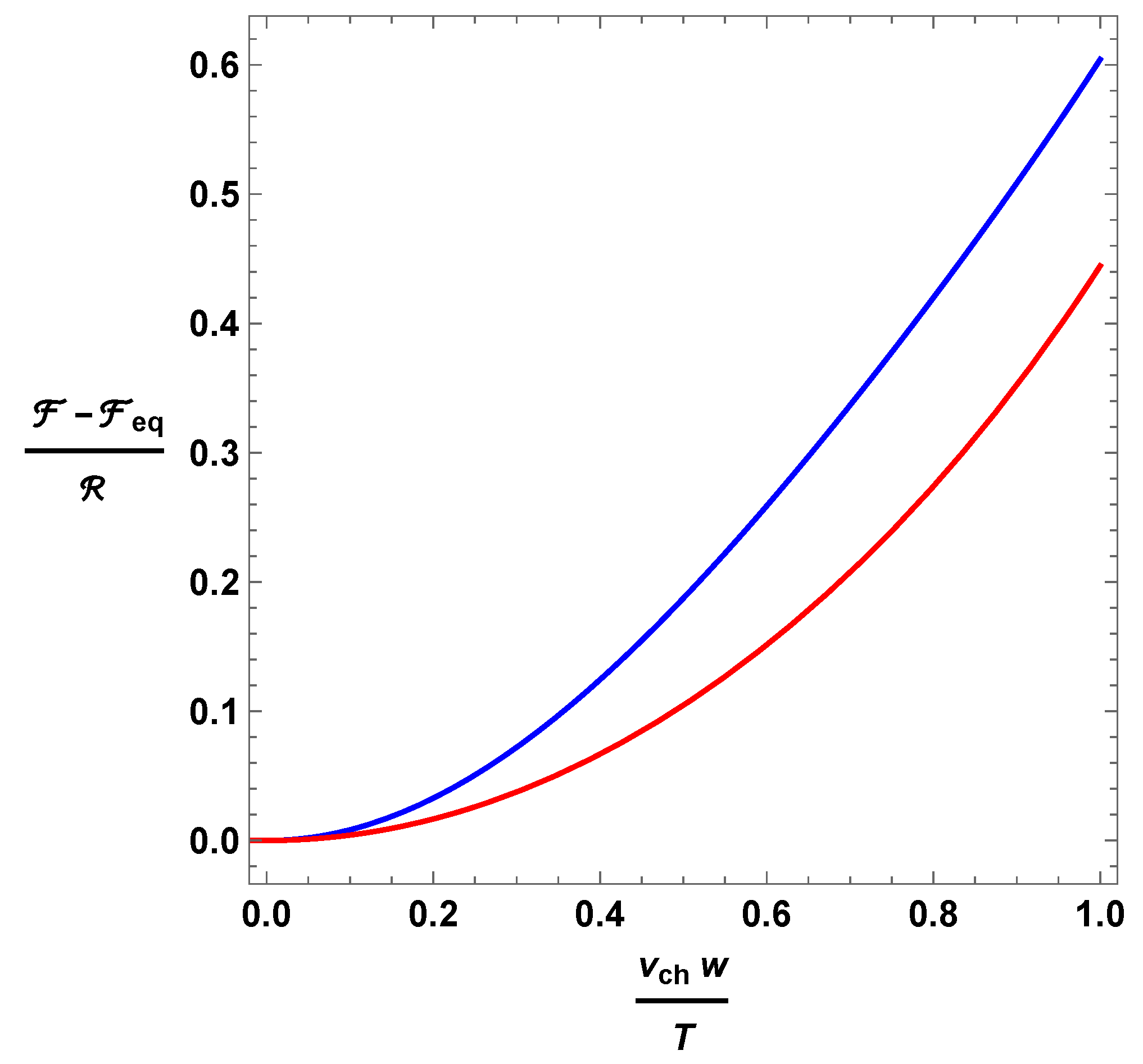
3.2. Two Simple Examples
4. Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Microscopic Derivation of the Toy Model
Appendix A.1. Basic Definitions
Appendix A.2. Non-Equilibrium Temperature
Appendix A.3. Minerbo Closure
Appendix A.4. Levermore Closure
References
- Israel, W.; Stewart, J. Transient relativistic thermodynamics and kinetic theory. Ann. Phys. 1979, 118, 341–372. [Google Scholar] [CrossRef]
- Hiscock, W.A.; Lindblom, L. Stability and causality in dissipative relativistic fluids. Ann. Phys. 1983, 151, 466–496. [Google Scholar] [CrossRef]
- Denicol, G.S.; Niemi, H.; Molnár, E.; Rischke, D.H. Derivation of transient relativistic fluid dynamics from the Boltzmann equation. Phys. Rev. D 2012, 85, 114047. [Google Scholar] [CrossRef]
- Gavassino, L.; Antonelli, M. Relativistic liquids: GENERIC or EIT? Class. Quantum Gravity 2023, 40, 075012. [Google Scholar] [CrossRef]
- Jou, D.; Casas-Vázquez, J.; Lebon, G. Extended Irreversible Thermodynamics. Rep. Prog. Phys. 1999, 51, 1105. [Google Scholar] [CrossRef]
- Cattaneo, C. Sur une Forme de L’équation de la Chaleur Éliminant le Paradoxe d’une Propagation Instantanée. C. R. Acad. Sci. 1958, 247, 431–433. [Google Scholar]
- Denicol, G.S.; Noronha, J.; Niemi, H.; Rischke, D.H. Origin of the relaxation time in dissipative fluid dynamics. Phys. Rev. D 2011, 83, 074019. [Google Scholar] [CrossRef]
- Wagner, D.; Gavassino, L. The regime of applicability of Israel-Stewart hydrodynamics. arXiv 2023, arXiv:2309.14828. [Google Scholar] [CrossRef]
- Frenkel, J. Kinetic Theory of Liquids, 2nd ed.; Dover Publications: New York, NY, USA, 1955. [Google Scholar]
- Baggioli, M.; Vasin, M.; Brazhkin, V.; Trachenko, K. Gapped momentum states. Phys. Rep. 2020, 865, 1–44. [Google Scholar] [CrossRef]
- Gavassino, L. Mapping GENERIC hydrodynamics into Carter’s multifluid theory. arXiv 2023, arXiv:2311.10897. [Google Scholar] [CrossRef]
- Levermore, C.D.; Pomraning, G.C. A flux-limited diffusion theory. ApJ 1981, 248, 321–334. [Google Scholar] [CrossRef]
- Sadowski, A.; Narayan, R.; Tchekhovskoy, A.; Zhu, Y. Semi-implicit scheme for treating radiation under M1 closure in general relativistic conservative fluid dynamics codes. MNRAS 2013, 429, 3533–3550. [Google Scholar] [CrossRef]
- Gavassino, L.; Antonelli, M.; Haskell, B. Multifluid Modelling of Relativistic Radiation Hydrodynamics. Symmetry 2020, 12, 1543. [Google Scholar] [CrossRef]
- Stephanov, M.; Yin, Y. Hydrodynamics with parametric slowing down and fluctuations near the critical point. Phys. Rev. D 2018, 98, 036006. [Google Scholar] [CrossRef]
- Gavassino, L.; Antonelli, M.; Haskell, B. Bulk viscosity in relativistic fluids: From thermodynamics to hydrodynamics. Class. Quantum Gravity 2021, 38, 075001. [Google Scholar] [CrossRef]
- Gavassino, L.; Noronha, J. Relativistic bulk-viscous dynamics far from equilibrium. arXiv 2023, arXiv:2305.04119. [Google Scholar] [CrossRef]
- Strickland, M. Anisotropic Hydrodynamics: Three lectures. Acta Phys. Polon. B 2014, 45, 2355–2394. [Google Scholar] [CrossRef]
- Alqahtani, M.; Nopoush, M.; Strickland, M. Relativistic anisotropic hydrodynamics. Prog. Part. Nucl. Phys. 2018, 101, 204–248. [Google Scholar] [CrossRef]
- Carter, B. Covariant Theory of Conductivity in Ideal Fluid or Solid Media; Springer: Berlin/Heidelberg, Germany, 1989; Volume 1385, p. 1. [Google Scholar] [CrossRef]
- Carter, B. Convective variational approach to relativistic thermodynamics of dissipative fluids. Proc. R. Soc. Lond. Ser. A 1991, 433, 45–62. [Google Scholar] [CrossRef]
- Lopez-Monsalvo, C.S.; Andersson, N. Thermal dynamics in general relativity. Proc. R. Soc. Lond. Ser. A 2011, 467, 738–759. [Google Scholar] [CrossRef]
- Öttinger, H.C. On the structural compatibility of a general formalism for nonequilibrium dynamics with special relativity. Phys. A Stat. Mech. Its Appl. 1998, 259, 24–42. [Google Scholar] [CrossRef]
- Grmela, M.; Öttinger, H.C. Dynamics and thermodynamics of complex fluids. I. Development of a general formalism. Phys. Rev. E 1997, 56, 6620–6632. [Google Scholar] [CrossRef]
- Kovtun, P. First-order relativistic hydrodynamics is stable. J. High Energy Phys. 2019, 2019, 34. [Google Scholar] [CrossRef]
- Gavassino, L.; Antonelli, M. Thermodynamics of uncharged relativistic multifluids. Class. Quantum Gravity 2020, 37, 025014. [Google Scholar] [CrossRef]
- Callen, H.B. Thermodynamics and an Introduction to Thermostatistics, 2nd ed.; Wiley: New York, NY, USA, 1985. [Google Scholar]
- Landau, L.; Lifshitz, E. Statistical Physics; Number v. 5; Elsevier Science: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Olson, T.S.; Hiscock, W.A. Stability, causality, and hyperbolicity in Carter’s “regular” theory of relativistic heat-conducting fluids. Phys. Rev. D 1990, 41, 3687–3695. [Google Scholar] [CrossRef]
- Priou, D. Comparison between variational and traditional approaches to relativistic thermodynamics of dissipative fluids. Phys. Rev. D 1991, 43, 1223–1234. [Google Scholar] [CrossRef] [PubMed]
- van Kampen, N.G. Relativistic Thermodynamics of Moving Systems. Phys. Rev. 1968, 173, 295–301. [Google Scholar] [CrossRef]
- Israel, W. Relativistic Thermodynamics. In E.C.G. Stueckelberg, An Unconventional Figure of Twentieth Century Physics: Selected Scientific Papers with Commentaries; Lacki, J., Ruegg, H., Wanders, G., Eds.; Birkhäuser Basel: Basel, Switzerland, 2009; pp. 101–113. [Google Scholar] [CrossRef]
- Gavassino, L. The zeroth law of thermodynamics in special relativity. Found. Phys. 2020, 50, 1554–1586. [Google Scholar] [CrossRef]
- Gavassino, L. Proving the Lorentz Invariance of the Entropy and the Covariance of Thermodynamics. Found. Phys. 2022, 52, 11. [Google Scholar] [CrossRef]
- Carter, B.; Khalatnikov, I.M. Equivalence of convective and potential variational derivations of covariant superfluid dynamics. Phys. Rev. D 1992, 45, 4536–4544. [Google Scholar] [CrossRef]
- Gavassino, L.; Antonelli, M.; Haskell, B. Extending Israel and Stewart hydrodynamics to relativistic superfluids via Carter’s multifluid approach. Phys. Rev. D 2022, 105, 045011. [Google Scholar] [CrossRef]
- Gavassino, L. Stability and causality of Carter’s multifluid theory. Class. Quantum Gravity 2022, 39, 185008. [Google Scholar] [CrossRef]
- Gavassino, L.; Antonelli, M.; Haskell, B. Thermodynamic Stability Implies Causality. Phys. Rev. Lett. 2022, 128, 010606. [Google Scholar] [CrossRef]
- Gavassino, L. Applying the Gibbs stability criterion to relativistic hydrodynamics. Class. Quantum Gravity 2021, 38, 21LT02. [Google Scholar] [CrossRef]
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics; John Wiley and Sons, Ltd.: Hoboken, NJ, USA, 2014. [Google Scholar]
- Pathria, R.; Beale, P.D. (Eds.) 15-Fluctuations and Nonequilibrium Statistical Mechanics. In Statistical Mechanics, 3rd ed.; Academic Press: Boston, MA, USA, 2011; pp. 583–635. [Google Scholar] [CrossRef]
- Pavelka, M.; Klika, V.; Grmela, M. Time reversal in nonequilibrium thermodynamics. Phys. Rev. E 2014, 90, 062131. [Google Scholar] [CrossRef]
- Gavassino, L. Is Relativistic Hydrodynamics always Symmetric-Hyperbolic in the Linear Regime? arXiv 2022, arXiv:2210.05067. [Google Scholar] [CrossRef]
- Levermore, C. Relating Eddington factors to flux limiters. J. Quant. Spectrosc. Radiat. Transf. 1984, 31, 149–160. [Google Scholar] [CrossRef]
- Minerbo, G.N. Maximum entropy Eddington factors. J. Quant. Spectrosc. Radiat. Transf. 1978, 20, 541–545. [Google Scholar] [CrossRef]
- Levermore, C.D. Chapman–Enskog approach to flux-limited diffusion theory. UCID-18229 1979. [Google Scholar]
- Chapman, S.; Cowling, T.G. The Mathematical Theory of Non-Uniform Gases; Cambridge University Press: Cambridge, UK, 1970. [Google Scholar]
- Tritt, T. Thermal Conductivity: Theory, Properties, and Applications; Kluwer Academic/Plenum Publishers: New York, NY, USA, 2004. [Google Scholar]
- Öttinger, H.C. GENERIC: Review of successful applications and a challenge for the future. arXiv 2018, arXiv:1810.08470. [Google Scholar]
- Chamel, N.; Haensel, P. Entrainment parameters in a cold superfluid neutron star core. Phys. Rev. C 2006, 73, 045802. [Google Scholar] [CrossRef]
- Nakano, E.; Iida, K.; Horiuchi, W. Quasiparticle properties of a single α particle in cold neutron matter. Phys. Rev. C 2020, 102, 055802. [Google Scholar] [CrossRef]
- Liu, H.; Yang, Y.H.; Han, Y.; Chu, P.C. Properties of quark matter and hybrid stars from a quasiparticle model. Phys. Rev. D 2023, 108, 034004. [Google Scholar] [CrossRef]
- Bluhm, M.; Kampfer, B.; Soff, G. The QCD equation of state near T(c) within a quasi-particle model. Phys. Lett. B 2005, 620, 131–136. [Google Scholar] [CrossRef]
- Mykhaylova, V.; Sasaki, C. Impact of quark quasiparticles on transport coefficients in hot QCD. Phys. Rev. D 2021, 103, 014007. [Google Scholar] [CrossRef]
- Li, F.P.; Lü, H.L.; Pang, L.G.; Qin, G.Y. Deep-learning quasi-particle masses from QCD equation of state. Phys. Lett. B 2023, 844, 138088. [Google Scholar] [CrossRef]
- Arteaga, D. Quasiparticle excitations in relativistic quantum field theory. Annals Phys. 2009, 324, 920–954. [Google Scholar] [CrossRef]
- Weinberg, S. Entropy Generation and the Survival of Protogalaxies in an Expanding Universe. ApJ 1971, 168, 175. [Google Scholar] [CrossRef]
- Udey, N.; Israel, W. General relativistic radiative transfer: The 14-moment approximation. MNRAS 1982, 199, 1137–1147. [Google Scholar] [CrossRef]
- Landau, L.; Lifshitz, E.; Pitaevskij, L. Statistical Physics: Part 2: Theory of Condensed State; Landau and Lifshitz Course of Theoretical Physics: Oxford, UK, 1980. [Google Scholar]
- Pitaevskii, L.; Lifshitz, E. Physical Kinetics; Number v. 10; Elsevier Science: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Popov, V. Relativistic Kinetics of Phonon Gas in Superfluids. Gen. Rel. Grav. 2006, 38, 917. [Google Scholar] [CrossRef]
- Cercignani, C.; Kremer, G.M. The Relativistic Boltzmann Equation: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Jaynes, E.T. Information Theory and Statistical Mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Huang, K. Statistical Mechanics, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1987. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gavassino, L. Relativistic Heat Conduction in the Large-Flux Regime. Entropy 2024, 26, 147. https://doi.org/10.3390/e26020147
Gavassino L. Relativistic Heat Conduction in the Large-Flux Regime. Entropy. 2024; 26(2):147. https://doi.org/10.3390/e26020147
Chicago/Turabian StyleGavassino, Lorenzo. 2024. "Relativistic Heat Conduction in the Large-Flux Regime" Entropy 26, no. 2: 147. https://doi.org/10.3390/e26020147
APA StyleGavassino, L. (2024). Relativistic Heat Conduction in the Large-Flux Regime. Entropy, 26(2), 147. https://doi.org/10.3390/e26020147




