Machine Learning Advances in High-Entropy Alloys: A Mini-Review
Abstract
1. Introduction
2. General Model Process
2.1. Data Collection
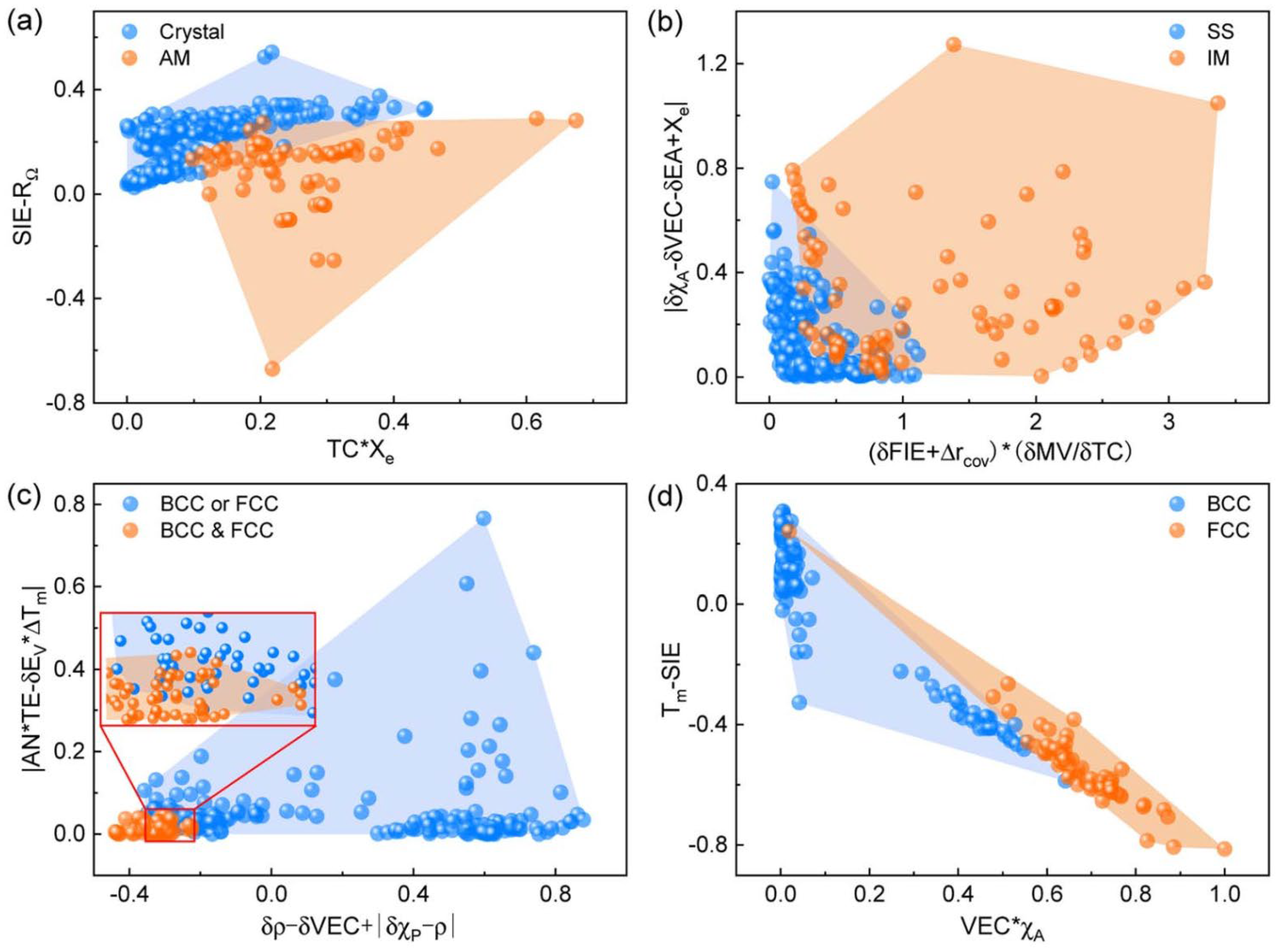
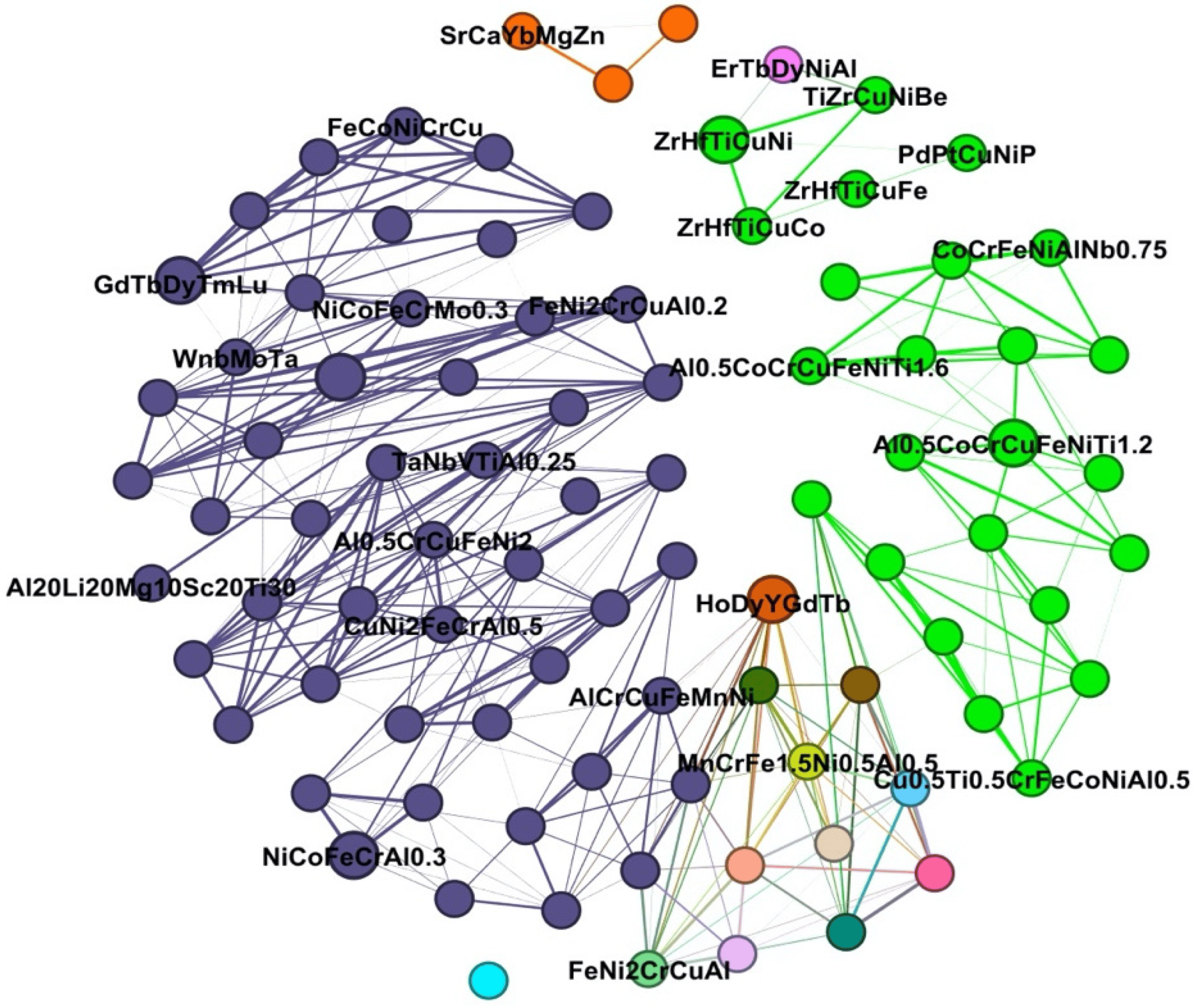
2.2. Descriptor Selection
2.3. Model Selection and Development
2.4. Performance Analysis
3. Special Machine Learning Algorithms
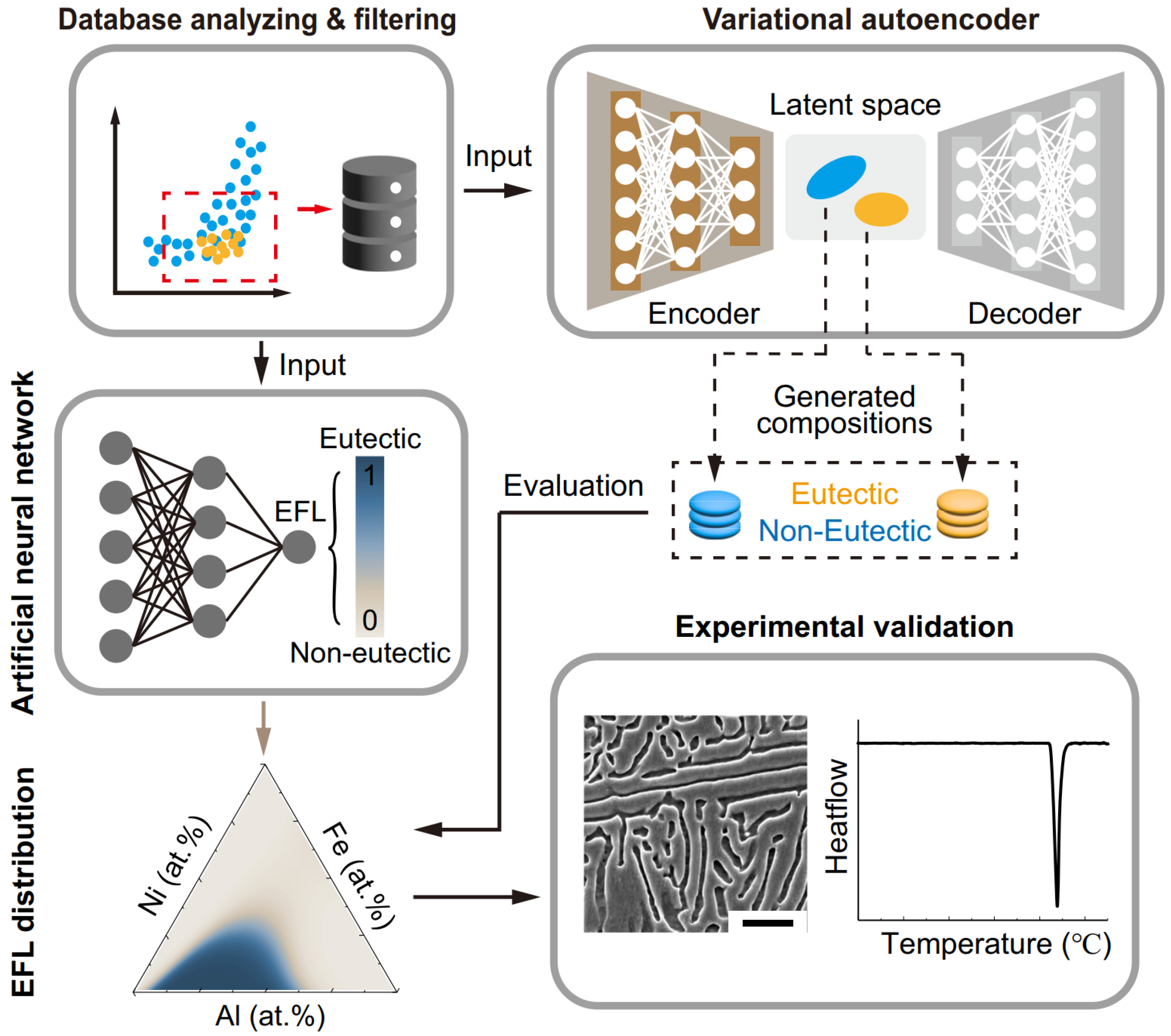
3.1. Generative Models
3.2. Data Augmentation
3.3. Transfer Learning
4. Challenges and Future Directions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| HEA | High-entropy alloys |
| RHEA | Refractory high-entropy alloys |
| SRO | Short-range order |
| LRO | Long-range order |
| DFT | Density functional theory |
| MD | Molecular dynamics |
| CALPHAD | Phase diagram calculation |
| AI | Artificial intelligence |
| EPI | Effective pair interaction |
| SISSO | Sure independence screening and sparsifying operator |
| AM | Amorphous |
| IM | Intermetallic |
| SS | Solid solution |
| BCC | Body-centered-cubic |
| FCC | Face-centered-cubic |
| VASE | Voronoi analysis and Shannon entropy |
| Coefficient of determination | |
| SVM | Support vector machine |
| CART | Classification and regression tree |
| KNN | k-nearest neighbor |
| ANN | Artificial neural network |
| CNN | Convolutional neural network |
| RNN | Recurrent neural network |
| RMSE | Root mean square error |
| GNN | Graph neural network |
| ECNet | Elemental convolution graph neural network |
| SHAP | SHapley Additive exPlanations |
| BD | breakdown |
| t-SNE | t-distributed stochastic neighbor embedding |
| GAN | Generative adversarial network |
| VAE | Variational autoencoder |
References
- Yeh, J.W.; Chen, S.K.; Lin, S.J.; Gan, J.Y.; Chin, T.S.; Shun, T.T.; Tsau, C.H.; Chang, S.Y. Nanostructured high-entropy alloys with multiple principal elements: Novel alloy design concepts and outcomes. Adv. Eng. Mater. 2004, 6, 299–303. [Google Scholar] [CrossRef]
- Cantor, B.; Chang, I.; Knight, P.; Vincent, A. Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. A 2004, 375, 213–218. [Google Scholar] [CrossRef]
- Liu, X.; Xu, P.; Zhao, J.; Lu, W.; Li, M.; Wang, G. Material machine learning for alloys: Applications, challenges and perspectives. J. Alloys Compd. 2022, 921, 165984. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, A.; Suhane, A. A critical review on mechanically alloyed high entropy alloys: Processing challenges and properties. Mater. Res. Express 2022, 9, 052001. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, H.; Fan, Y.; Wei, R.; Zhang, W.; Wang, T.; Zhang, T.; Wu, K.; Li, F.; Guan, S.; et al. Improvement of corrosion resistance and magnetic properties of FeCoNiAl0.2Si0.2 high entropy alloy via rapid-solidification. Intermetallics 2020, 122, 106778. [Google Scholar] [CrossRef]
- Kai, W.; Li, C.; Cheng, F.; Chu, K.; Huang, R.; Tsay, L.; Kai, J. Air-oxidation of FeCoNiCr-based quinary high-entropy alloys at 700–900 C. Corros. Sci. 2017, 121, 116–125. [Google Scholar] [CrossRef]
- Pu, G.; Lin, L.; Ang, R.; Zhang, K.; Liu, B.; Liu, B.; Peng, T.; Liu, S.; Li, Q. Outstanding radiation tolerance and mechanical behavior in ultra-fine nanocrystalline Al1.5CoCrFeNi high entropy alloy films under He ion irradiation. Appl. Surf. Sci. 2020, 516, 146129. [Google Scholar] [CrossRef]
- Lin, Y.; Yang, T.; Lang, L.; Shan, C.; Deng, H.; Hu, W.; Gao, F. Enhanced radiation tolerance of the Ni-Co-Cr-Fe high-entropy alloy as revealed from primary damage. Acta Mater. 2020, 196, 133–143. [Google Scholar] [CrossRef]
- George, E.P.; Raabe, D.; Ritchie, R.O. High-entropy alloys. Nat. Rev. Mater. 2019, 4, 515–534. [Google Scholar] [CrossRef]
- Cantor, B. Multicomponent high-entropy Cantor alloys. Prog. Mater. Sci. 2021, 120, 100754. [Google Scholar] [CrossRef]
- Otto, F.; Yang, Y.; Bei, H.; George, E.P. Relative effects of enthalpy and entropy on the phase stability of equiatomic high-entropy alloys. Acta Mater. 2013, 61, 2628–2638. [Google Scholar] [CrossRef]
- Ma, D.; Grabowski, B.; Körmann, F.; Neugebauer, J.; Raabe, D. Ab initio thermodynamics of the CoCrFeMnNi high entropy alloy: Importance of entropy contributions beyond the configurational one. Acta Mater. 2015, 100, 90–97. [Google Scholar] [CrossRef]
- Senkov, O.; Wilks, G.; Miracle, D.; Chuang, C.; Liaw, P. Refractory high-entropy alloys. Intermetallics 2010, 18, 1758–1765. [Google Scholar] [CrossRef]
- Senkov, O.N.; Wilks, G.B.; Scott, J.M.; Miracle, D.B. Mechanical properties of Nb25Mo25Ta225W25 and V20Nb20Mo20Ta20W20 refractory high entropy alloys. Intermetallics 2011, 19, 698–706. [Google Scholar] [CrossRef]
- Guo, N.; Wang, L.; Luo, L.; Li, X.; Chen, R.; Su, Y.; Guo, J.; Fu, H. Hot deformation characteristics and dynamic recrystallization of the MoNbHfZrTi refractory high-entropy alloy. Mater. Sci. Eng. A 2016, 651, 698–707. [Google Scholar] [CrossRef]
- Shi, Y.; Yang, B.; Xie, X.; Brechtl, J.; Dahmen, K.A.; Liaw, P.K. Corrosion of AlxCoCrFeNi high-entropy alloys: Al-content and potential scan-rate dependent pitting behavior. Corros. Sci. 2017, 119, 33–45. [Google Scholar] [CrossRef]
- Rodriguez, A.A.; Tylczak, J.H.; Gao, M.C.; Jablonski, P.D.; Detrois, M.; Ziomek-Moroz, M.; Hawk, J.A. Effect of molybdenum on the corrosion behavior of high-entropy alloys CoCrFeNi2 and CoCrFeNi2Mo0.25 under sodium chloride aqueous conditions. Adv. Mater. Sci. Eng. 2018, 2018, 3016304. [Google Scholar] [CrossRef]
- Sarkar, S.; Sarswat, P.K.; Free, M.L. Elevated temperature corrosion resistance of additive manufactured single phase AlCoFeNiTiV0.9Sm0.1 and AlCoFeNiV0.9Sm0.1 HEAs in a simulated syngas atmosphere. Addit. Manuf. 2019, 30, 100902. [Google Scholar] [CrossRef]
- Gorr, B.; Mueller, F.; Christ, H.J.; Mueller, T.; Chen, H.; Kauffmann, A.; Heilmaier, M. High temperature oxidation behavior of an equimolar refractory metal-based alloy 20Nb20Mo20Cr20Ti20Al with and without Si addition. J. Alloys Compd. 2016, 688, 468–477. [Google Scholar] [CrossRef]
- Gorr, B.; Schellert, S.; Müller, F.; Christ, H.J.; Kauffmann, A.; Heilmaier, M. Current status of research on the oxidation behavior of refractory high entropy alloys. Adv. Eng. Mater. 2021, 23, 2001047. [Google Scholar] [CrossRef]
- Singh, P.; Smirnov, A.V.; Johnson, D.D. Atomic short-range order and incipient long-range order in high-entropy alloys. Phys. Rev. B 2015, 91, 224204. [Google Scholar] [CrossRef]
- Widom, M. Modeling the structure and thermodynamics of high-entropy alloys. J. Mater. Res. 2018, 33, 2881–2898. [Google Scholar] [CrossRef]
- Oh, H.S.; Kim, S.J.; Odbadrakh, K.; Ryu, W.H.; Yoon, K.N.; Mu, S.; Körmann, F.; Ikeda, Y.; Tasan, C.C.; Raabe, D.; et al. Engineering atomic-level complexity in high-entropy and complex concentrated alloys. Nat. Commun. 2019, 10, 2090. [Google Scholar] [CrossRef]
- Hu, R.; Jin, S.; Sha, G. Application of atom probe tomography in understanding high entropy alloys: 3D local chemical compositions in atomic scale analysis. Prog. Mater. Sci. 2022, 123, 100854. [Google Scholar] [CrossRef]
- Pei, Z.; Li, R.; Gao, M.C.; Stocks, G.M. Statistics of the NiCoCr medium-entropy alloy: Novel aspects of an old puzzle. npj Comput. Mater. 2020, 6, 122. [Google Scholar] [CrossRef]
- George, E.P.; Curtin, W.A.; Tasan, C.C. High entropy alloys: A focused review of mechanical properties and deformation mechanisms. Acta Mater. 2020, 188, 435–474. [Google Scholar] [CrossRef]
- Gludovatz, B.; Hohenwarter, A.; Catoor, D.; Chang, E.H.; George, E.P.; Ritchie, R.O. A fracture-resistant high-entropy alloy for cryogenic applications. Science 2014, 345, 1153–1158. [Google Scholar] [CrossRef]
- Li, Z.; Pradeep, K.G.; Deng, Y.; Raabe, D.; Tasan, C.C. Metastable high-entropy dual-phase alloys overcome the strength–ductility trade-off. Nature 2016, 534, 227–230. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, Y.J.; Lin, J.P.; Chen, G.L.; Liaw, P.K. Solid-solution phase formation rules for multi-component alloys. Adv. Eng. Mater. 2008, 10, 534–538. [Google Scholar] [CrossRef]
- Mak, E.; Yin, B.; Curtin, W. A ductility criterion for bcc high entropy alloys. J. Mech. Phys. Solids. 2021, 152, 104389. [Google Scholar] [CrossRef]
- Sanchez, J.M.; Ducastelle, F.; Gratias, D. Generalized cluster description of multicomponent systems. Phys. A 1984, 128, 334–350. [Google Scholar] [CrossRef]
- Daw, M.S.; Baskes, M.I. Embedded-atom method: Derivation and application to impurities, surfaces, and other defects in metals. Phys. Rev. B 1984, 29, 6443. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Hollingsworth, S.A.; Dror, R.O. Molecular dynamics simulation for all. Neuron 2018, 99, 1129–1143. [Google Scholar] [CrossRef] [PubMed]
- Chang, Y.A.; Chen, S.; Zhang, F.; Yan, X.; Xie, F.; Schmid-Fetzer, R.; Oates, W.A. Phase diagram calculation: Past, present and future. Prog. Mater. Sci. 2004, 49, 313–345. [Google Scholar] [CrossRef]
- Xie, J.; Su, Y.; Zhang, D.; Feng, Q. A vision of materials genome engineering in China. Engineering 2022, 10, 10–12. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Senior, A.W.; Evans, R.; Jumper, J.; Kirkpatrick, J.; Sifre, L.; Green, T.; Qin, C.; Žídek, A.; Nelson, A.W.; Bridgland, A.; et al. Improved protein structure prediction using potentials from deep learning. Nature 2020, 577, 706–710. [Google Scholar] [CrossRef]
- Litjens, G.; Kooi, T.; Bejnordi, B.E.; Setio, A.A.A.; Ciompi, F.; Ghafoorian, M.; Van Der Laak, J.A.; Van Ginneken, B.; Sánchez, C.I. A survey on deep learning in medical image analysis. Med. Image Anal. 2017, 42, 60–88. [Google Scholar] [CrossRef]
- Radovic, A.; Williams, M.; Rousseau, D.; Kagan, M.; Bonacorsi, D.; Himmel, A.; Aurisano, A.; Terao, K.; Wongjirad, T. Machine learning at the energy and intensity frontiers of particle physics. Nature 2018, 560, 41–48. [Google Scholar] [CrossRef]
- Hezaveh, Y.D.; Levasseur, L.P.; Marshall, P.J. Fast automated analysis of strong gravitational lenses with convolutional neural networks. Nature 2017, 548, 555–557. [Google Scholar] [CrossRef] [PubMed]
- Park, C.W.; Kornbluth, M.; Vandermause, J.; Wolverton, C.; Kozinsky, B.; Mailoa, J.P. Accurate and scalable graph neural network force field and molecular dynamics with direct force architecture. npj Comput. Mater. 2021, 7, 73. [Google Scholar] [CrossRef]
- Nyshadham, C.; Rupp, M.; Bekker, B.; Shapeev, A.V.; Mueller, T.; Rosenbrock, C.W.; Csányi, G.; Wingate, D.W.; Hart, G.L. Machine-learned multi-system surrogate models for materials prediction. npj Comput. Mater. 2019, 5, 51. [Google Scholar] [CrossRef]
- Rosenbrock, C.W.; Gubaev, K.; Shapeev, A.V.; Pártay, L.B.; Bernstein, N.; Csányi, G.; Hart, G.L. Machine-learned interatomic potentials for alloys and alloy phase diagrams. npj Comput. Mater. 2021, 7, 24. [Google Scholar] [CrossRef]
- Jia, W.; Wang, H.; Chen, M.; Lu, D.; Lin, L.; Car, R.; Weinan, E.; Zhang, L. Pushing the limit of molecular dynamics with ab initio accuracy to 100 million atoms with machine learning. In Proceedings of the SC20: International Conference for High Performance Computing, Networking, Storage and Analysis, Virtual, 9–19 November 2020; IEEE: New York, NY, USA, 2020; pp. 1–14. [Google Scholar]
- Deringer, V.L.; Bernstein, N.; Csányi, G.; Ben Mahmoud, C.; Ceriotti, M.; Wilson, M.; Drabold, D.A.; Elliott, S.R. Origins of structural and electronic transitions in disordered silicon. Nature 2021, 589, 59–64. [Google Scholar] [CrossRef]
- Yin, S.; Zuo, Y.; Abu-Odeh, A.; Zheng, H.; Li, X.G.; Ding, J.; Ong, S.P.; Asta, M.; Ritchie, R.O. Atomistic simulations of dislocation mobility in refractory high-entropy alloys and the effect of chemical short-range order. Nat. Commun. 2021, 12, 4873. [Google Scholar] [CrossRef]
- Li, X.G.; Chen, C.; Zheng, H.; Zuo, Y.; Ong, S.P. Complex strengthening mechanisms in the NbMoTaW multi-principal element alloy. npj Comput. Mater. 2020, 6, 70. [Google Scholar] [CrossRef]
- Schmidt, J.; Marques, M.R.; Botti, S.; Marques, M.A. Recent advances and applications of machine learning in solid-state materials science. npj Comput. Mater 2019, 5, 83. [Google Scholar] [CrossRef]
- Hart, G.L.; Mueller, T.; Toher, C.; Curtarolo, S. Machine learning for alloys. Nat. Rev. Mater. 2021, 6, 730–755. [Google Scholar] [CrossRef]
- Pei, Z.; Yin, J.; Hawk, J.A.; Alman, D.E.; Gao, M.C. Machine-learning informed prediction of high-entropy solid solution formation: Beyond the Hume-Rothery rules. npj Comput. Mater. 2020, 6, 50. [Google Scholar] [CrossRef]
- Rickman, J.; Chan, H.; Harmer, M.; Smeltzer, J.; Marvel, C.; Roy, A.; Balasubramanian, G. Materials informatics for the screening of multi-principal elements and high-entropy alloys. Nat. Commun. 2019, 10, 2618. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, X.; Bi, S.; Yin, J.; Zhang, G.; Eisenbach, M. Robust data-driven approach for predicting the configurational energy of high entropy alloys. Mater. Design. 2020, 185, 108247. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, J.; Yin, J.; Bi, S.; Eisenbach, M.; Wang, Y. Monte Carlo simulation of order-disorder transition in refractory high entropy alloys: A data-driven approach. Comput. Mater. Sci. 2021, 187, 110135. [Google Scholar] [CrossRef]
- Yin, J.; Pei, Z.; Gao, M.C. Neural network-based order parameter for phase transitions and its applications in high-entropy alloys. Nat. Comput. Sci. 2021, 1, 686–693. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.; Lu, D.; Wang, K. Accelerated discovery of single-phase refractory high entropy alloys assisted by machine learning. Comput. Mater. Sci. 2021, 199, 110723. [Google Scholar] [CrossRef]
- Ha, M.Q.; Nguyen, D.N.; Nguyen, V.C.; Nagata, T.; Chikyow, T.; Kino, H.; Miyake, T.; Denœux, T.; Huynh, V.N.; Dam, H.C. Evidence-based recommender system for high-entropy alloys. Nat. Comput. Sci. 2021, 1, 470–478. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.; Sharma, A.; Singh, P.; Balasubramanian, G.; Johnson, D.D. Accelerating computational modeling and design of high-entropy alloys. Nat. Comput. Sci. 2021, 1, 54–61. [Google Scholar] [CrossRef] [PubMed]
- Rao, Z.; Tung, P.Y.; Xie, R.; Wei, Y.; Zhang, H.; Ferrari, A.; Klaver, T.; Körmann, F.; Sukumar, P.T.; Kwiatkowski da Silva, A.; et al. Machine learning–enabled high-entropy alloy discovery. Science 2022, 378, 78–85. [Google Scholar] [CrossRef]
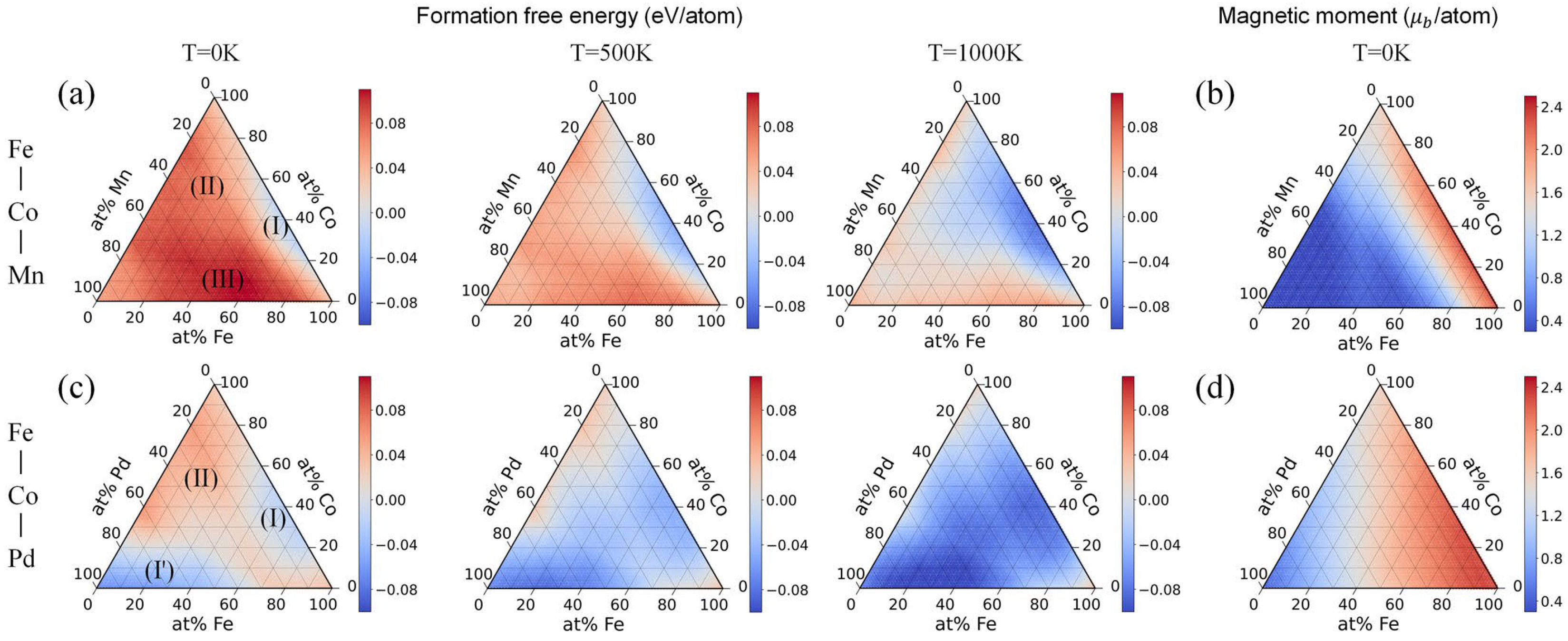
- Tran, N.D.; Saengdeejing, A.; Suzuki, K.; Miura, H.; Chen, Y. Stability and thermodynamics properties of CrFeNiCoMn/Pd high entropy alloys from first principles. J. Phase Equilib. Diffus. 2021, 42, 606–616. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, J.; Eisenbach, M.; Wang, Y. Machine learning modeling of high entropy alloy: The role of short-range order. arXiv 2019, arXiv:1906.02889. [Google Scholar]
- Saal, J.E.; Kirklin, S.; Aykol, M.; Meredig, B.; Wolverton, C. Materials design and discovery with high-throughput density functional theory: The open quantum materials database (OQMD). JOM 2013, 65, 1501–1509. [Google Scholar] [CrossRef]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. [Google Scholar] [CrossRef]
- Curtarolo, S.; Setyawan, W.; Hart, G.L.; Jahnatek, M.; Chepulskii, R.V.; Taylor, R.H.; Wang, S.; Xue, J.; Yang, K.; Levy, O.; et al. AFLOW: An automatic framework for high-throughput materials discovery. Comput. Mater. Sci. 2012, 58, 218–226. [Google Scholar] [CrossRef]
- Talirz, L.; Kumbhar, S.; Passaro, E.; Yakutovich, A.V.; Granata, V.; Gargiulo, F.; Borelli, M.; Uhrin, M.; Huber, S.P.; Zoupanos, S.; et al. Materials Cloud, a platform for open computational science. Sci. Data 2020, 7, 299. [Google Scholar] [CrossRef]
- Villars, P.; Berndt, M.; Brandenburg, K.; Cenzual, K.; Daams, J.; Hulliger, F.; Massalski, T.; Okamoto, H.; Osaki, K.; Prince, A.; et al. The pauling file. J. Alloys Compd. 2004, 367, 293–297. [Google Scholar] [CrossRef]
- Zakutayev, A.; Wunder, N.; Schwarting, M.; Perkins, J.D.; White, R.; Munch, K.; Tumas, W.; Phillips, C. An open experimental database for exploring inorganic materials. Sci. Data 2018, 5, 180053. [Google Scholar] [CrossRef]
- Soedarmadji, E.; Stein, H.S.; Suram, S.K.; Guevarra, D.; Gregoire, J.M. Tracking materials science data lineage to manage millions of materials experiments and analyses. npj Comput. Mater. 2019, 5, 79. [Google Scholar] [CrossRef]
- Pei, Z.; Yin, J. Machine learning as a contributor to physics: Understanding Mg alloys. Mater. Design 2019, 172, 107759. [Google Scholar] [CrossRef]
- Borg, C.K.; Frey, C.; Moh, J.; Pollock, T.M.; Gorsse, S.; Miracle, D.B.; Senkov, O.N.; Meredig, B.; Saal, J.E. Expanded dataset of mechanical properties and observed phases of multi-principal element alloys. Sci. Data 2020, 7, 430. [Google Scholar] [CrossRef]
- Couzinié, J.P.; Senkov, O.; Miracle, D.; Dirras, G. Comprehensive data compilation on the mechanical properties of refractory high-entropy alloys. Data Brief 2018, 21, 1622–1641. [Google Scholar] [CrossRef]
- Gorsse, S.; Nguyen, M.; Senkov, O.N.; Miracle, D.B. Database on the mechanical properties of high entropy alloys and complex concentrated alloys. Data Brief 2018, 21, 2664–2678. [Google Scholar] [CrossRef] [PubMed]
- Gao, M.C.; Zhang, C.; Gao, P.; Zhang, F.; Ouyang, L.; Widom, M.; Hawk, J.A. Thermodynamics of concentrated solid solution alloys. Curr. Opin. Solid State Mater. Sci. 2017, 21, 238–251. [Google Scholar] [CrossRef]
- Kube, S.A.; Sohn, S.; Uhl, D.; Datye, A.; Mehta, A.; Schroers, J. Phase selection motifs in High Entropy Alloys revealed through combinatorial methods: Large atomic size difference favors BCC over FCC. Acta Mater. 2019, 166, 677–686. [Google Scholar] [CrossRef]
- Feng, S.; Zhou, H.; Dong, H. Application of deep transfer learning to predicting crystal structures of inorganic substances. Comput. Mater. Sci. 2021, 195, 110476. [Google Scholar] [CrossRef]
- Zhang, J.; Cai, C.; Kim, G.; Wang, Y.; Chen, W. Composition design of high-entropy alloys with deep sets learning. npj Comput. Mater. 2022, 8, 89. [Google Scholar] [CrossRef]
- Dai, B.; Shen, X.; Wang, J. Embedding learning. J. Am. Stat. Assoc. 2022, 117, 307–319. [Google Scholar] [CrossRef]
- Roy, A.; Balasubramanian, G. Predictive descriptors in machine learning and data-enabled explorations of high-entropy alloys. Comput. Mater. Sci. 2021, 193, 110381. [Google Scholar] [CrossRef]
- Zhang, Y.; Wen, C.; Wang, C.; Antonov, S.; Xue, D.; Bai, Y.; Su, Y. Phase prediction in high entropy alloys with a rational selection of materials descriptors and machine learning models. Acta Mater. 2020, 185, 528–539. [Google Scholar] [CrossRef]
- Ouyang, R.; Curtarolo, S.; Ahmetcik, E.; Scheffler, M.; Ghiringhelli, L.M. SISSO: A compressed-sensing method for identifying the best low-dimensional descriptor in an immensity of offered candidates. Phys. Rev. Mater. 2018, 2, 083802. [Google Scholar] [CrossRef]
- Zhao, S.; Yuan, R.; Liao, W.; Zhao, Y.; Wang, J.; Li, J.; Lookman, T. Descriptors for phase prediction of high entropy alloys using interpretable machine learning. J. Mater. Chem. A 2024, 12, 2807–2819. [Google Scholar] [CrossRef]
- Liu, J.; Wang, P.; Luan, J.; Chen, J.; Cai, P.; Chen, J.; Lu, X.; Fan, Y.; Yu, Z.; Chou, K. VASE: A High-Entropy Alloy Short-Range Order Structural Descriptor for Machine Learning. J. Chem. Theory Comput. 2024. [Google Scholar] [CrossRef] [PubMed]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. Lightgbm: A highly efficient gradient boosting decision tree. Proc. Adv. Neural Inf. Process. Syst. 2017, 30, 52. [Google Scholar]
- Cortes, C. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Loh, W.Y. Classification and regression trees. Wires. Data. Min. Knowl. 2011, 1, 14–23. [Google Scholar] [CrossRef]
- Peterson, L.E. K-nearest neighbor. Scholarpedia 2009, 4, 1883. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Convolutional networks. Deep Learn. 2016, 2016, 330–372. [Google Scholar]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Vaswani, A. Attention is all you need. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2017; pp. 5998–6008. [Google Scholar]
- Wen, C.; Zhang, Y.; Wang, C.; Xue, D.; Bai, Y.; Antonov, S.; Dai, L.; Lookman, T.; Su, Y. Machine learning assisted design of high entropy alloys with desired property. Acta Mater. 2019, 170, 109–117. [Google Scholar] [CrossRef]
- Mehta, P.; Bukov, M.; Wang, C.H.; Day, A.G.; Richardson, C.; Fisher, C.K.; Schwab, D.J. A high-bias, low-variance introduction to machine learning for physicists. Phys. Rep. 2019, 810, 1–124. [Google Scholar] [CrossRef]
- Reiser, P.; Neubert, M.; Eberhard, A.; Torresi, L.; Zhou, C.; Shao, C.; Metni, H.; van Hoesel, C.; Schopmans, H.; Sommer, T.; et al. Graph neural networks for materials science and chemistry. Commun. Mater. 2022, 3, 93. [Google Scholar] [CrossRef] [PubMed]
- Schütt, K.T.; Sauceda, H.E.; Kindermans, P.J.; Tkatchenko, A.; Müller, K.R. Schnet–a deep learning architecture for molecules and materials. J. Chem. Phys. 2018, 148, 241722. [Google Scholar] [CrossRef] [PubMed]
- Xie, T.; Grossman, J.C. Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties. Phys. Rev. Lett. 2018, 120, 145301. [Google Scholar] [CrossRef]
- Chen, C.; Ye, W.; Zuo, Y.; Zheng, C.; Ong, S.P. Graph networks as a universal machine learning framework for molecules and crystals. Chem. Mater. 2019, 31, 3564–3572. [Google Scholar] [CrossRef]
- Ghouchan Nezhad Noor Nia, R.; Jalali, M.; Houshmand, M. A Graph-Based k-Nearest Neighbor (KNN) Approach for Predicting Phases in High-Entropy Alloys. Appl. Sci. 2022, 12, 8021. [Google Scholar] [CrossRef]
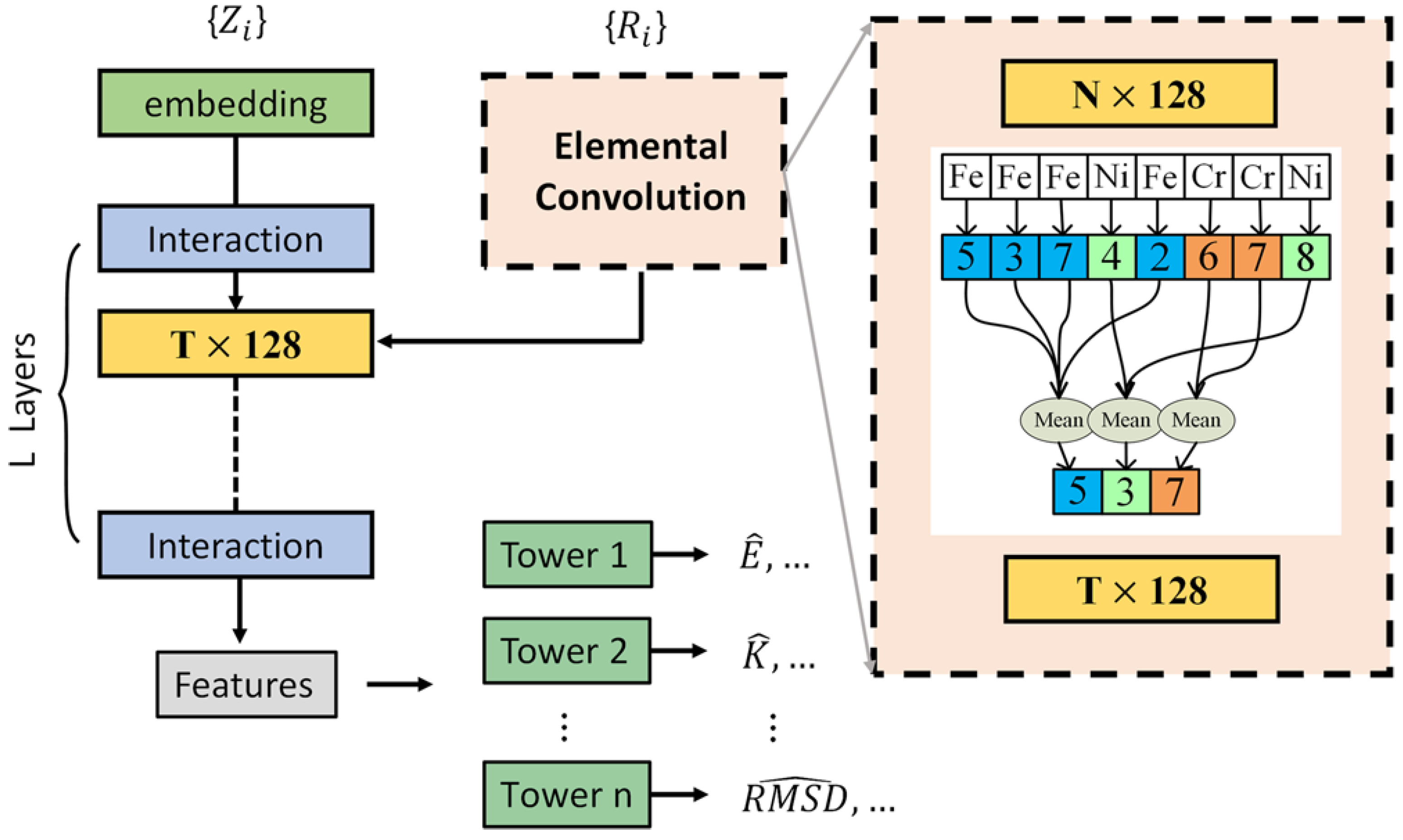
- Wang, X.; Tran, N.D.; Zeng, S.; Hou, C.; Chen, Y.; Ni, J. Element-wise representations with ECNet for material property prediction and applications in high-entropy alloys. npj Comput. Mater. 2022, 8, 253. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, R.; Chen, J.; Rondinelli, J.M.; Chen, W. Do Graph Neural Networks Work for High Entropy Alloys? arXiv 2024, arXiv:2408.16337. [Google Scholar]
- Dong, H.; Shi, Y.; Ying, P.; Xu, K.; Liang, T.; Wang, Y.; Zeng, Z.; Wu, X.; Zhou, W.; Xiong, S.; et al. Molecular dynamics simulations of heat transport using machine-learned potentials: A mini-review and tutorial on GPUMD with neuroevolution potentials. J. Appl. Phys. 2024, 135, 161101. [Google Scholar] [CrossRef]
- Behler, J. Constructing high-dimensional neural network potentials: A tutorial review. Int. J. Quantum Chem. 2015, 115, 1032–1050. [Google Scholar] [CrossRef]
- Bartók, A.P.; Payne, M.C.; Kondor, R.; Csányi, G. Gaussian approximation potentials: The accuracy of quantum mechanics, without the electrons. Phys. Rev. Lett. 2010, 104, 136403. [Google Scholar] [CrossRef]
- Thompson, A.P.; Swiler, L.P.; Trott, C.R.; Foiles, S.M.; Tucker, G.J. Spectral neighbor analysis method for automated generation of quantum-accurate interatomic potentials. J. Comput. Phys. 2015, 285, 316–330. [Google Scholar] [CrossRef]
- Behler, J.; Parrinello, M. Generalized neural-network representation of high-dimensional potential-energy surfaces. Phys. Rev. Lett. 2007, 98, 146401. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Zhang, L.; Han, J.; Weinan, E. DeePMD-kit: A deep learning package for many-body potential energy representation and molecular dynamics. Comput. Phys. Commun. 2018, 228, 178–184. [Google Scholar] [CrossRef]
- Drautz, R. Atomic cluster expansion for accurate and transferable interatomic potentials. Phys. Rev. B 2019, 99, 014104. [Google Scholar] [CrossRef]
- Shapeev, A.V. Moment tensor potentials: A class of systematically improvable interatomic potentials. Multiscale Model. Sim. 2016, 14, 1153–1173. [Google Scholar] [CrossRef]
- Fan, Z.; Zeng, Z.; Zhang, C.; Wang, Y.; Song, K.; Dong, H.; Chen, Y.; Ala-Nissila, T. Neuroevolution machine learning potentials: Combining high accuracy and low cost in atomistic simulations and application to heat transport. Phys. Rev. B 2021, 104, 104309. [Google Scholar] [CrossRef]
- Fan, Z.; Wang, Y.; Ying, P.; Song, K.; Wang, J.; Wang, Y.; Zeng, Z.; Xu, K.; Lindgren, E.; Rahm, J.M.; et al. GPUMD: A package for constructing accurate machine-learned potentials and performing highly efficient atomistic simulations. J. Chem. Phys. 2022, 157, 114801. [Google Scholar] [CrossRef]
- Mirzoev, A.; Gelchinski, B.; Rempel, A. Neural Network Prediction of Interatomic Interaction in Multielement Substances and High-Entropy Alloys: A Review. In Doklady Physical Chemistry; Springer: Berlin/Heidelberg, Germany, 2022; Volume 504, pp. 51–77. [Google Scholar]
- Kostiuchenko, T.; Körmann, F.; Neugebauer, J.; Shapeev, A. Impact of lattice relaxations on phase transitions in a high-entropy alloy studied by machine-learning potentials. npj Comput. Mater. 2019, 5, 55. [Google Scholar] [CrossRef]
- Körmann, F.; Kostiuchenko, T.; Shapeev, A.; Neugebauer, J. B2 ordering in body-centered-cubic AlNbTiV refractory high-entropy alloys. Phys. Rev. Mater. 2021, 5, 053803. [Google Scholar] [CrossRef]
- Byggmästar, J.; Nordlund, K.; Djurabekova, F. Modeling refractory high-entropy alloys with efficient machine-learned interatomic potentials: Defects and segregation. Phys. Rev. B 2021, 104, 104101. [Google Scholar] [CrossRef]
- Gubaev, K.; Ikeda, Y.; Tasnádi, F.; Neugebauer, J.; Shapeev, A.V.; Grabowski, B.; Körmann, F. Finite-temperature interplay of structural stability, chemical complexity, and elastic properties of bcc multicomponent alloys from ab initio trained machine-learning potentials. Phys. Rev. Mater. 2021, 5, 073801. [Google Scholar] [CrossRef]
- Pandey, A.; Gigax, J.; Pokharel, R. Machine learning interatomic potential for high-throughput screening of high-entropy alloys. JOM 2022, 74, 2908–2920. [Google Scholar] [CrossRef]
- Song, K.; Zhao, R.; Liu, J.; Wang, Y.; Lindgren, E.; Wang, Y.; Chen, S.; Xu, K.; Liang, T.; Ying, P.; et al. General-purpose machine-learned potential for 16 elemental metals and their alloys. Nat. Commun. 2024, 15, 10208. [Google Scholar] [CrossRef]
- Wu, L.; Li, T. A machine learning interatomic potential for high entropy alloys. J. Mech. Phys. Solids 2024, 187, 105639. [Google Scholar] [CrossRef]
- Ferrari, A.; Körmann, F.; Asta, M.; Neugebauer, J. Simulating short-range order in compositionally complex materials. Nat. Comput. Sci. 2023, 3, 221–229. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Jin, X.; Zhao, W.; Li, T. Intricate short-range order in GeSn alloys revealed by atomistic simulations with highly accurate and efficient machine-learning potentials. Phys. Rev. Mater. 2024, 8, 043805. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Mizutani, U. The Hume-Rothery rules for structurally complex alloy phases. In Surface Properties and Engineering of Complex Intermetallics; World Scientific: Singapore, 2010; pp. 323–399. [Google Scholar]
- Lundberg, S. A unified approach to interpreting model predictions. arXiv 2017, arXiv:1705.07874. [Google Scholar]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 11. [Google Scholar]
- Lee, S.Y.; Byeon, S.; Kim, H.S.; Jin, H.; Lee, S. Deep learning-based phase prediction of high-entropy alloys: Optimization, generation, and explanation. Mater. Design 2021, 197, 109260. [Google Scholar] [CrossRef]
- Lee, K.; Ayyasamy, M.V.; Delsa, P.; Hartnett, T.Q.; Balachandran, P.V. Phase classification of multi-principal element alloys via interpretable machine learning. npj Comput. Mater. 2022, 8, 25. [Google Scholar] [CrossRef]
- Wong, T.T.; Yang, N.Y. Dependency analysis of accuracy estimates in k-fold cross validation. IEEE Trans. Knowl. Data Eng. 2017, 29, 2417–2427. [Google Scholar] [CrossRef]
- Oh, S.H.V.; Yoo, S.H.; Jang, W. Small dataset machine-learning approach for efficient design space exploration: Engineering ZnTe-based high-entropy alloys for water splitting. npj Comput. Mater. 2024, 10, 166. [Google Scholar] [CrossRef]
- Li, Z.; Nash, W.; O’Brien, S.; Qiu, Y.; Gupta, R.; Birbilis, N. cardiGAN: A generative adversarial network model for design and discovery of multi principal element alloys. J. Mater. Sci. Technol. 2022, 125, 81–96. [Google Scholar] [CrossRef]
- Chen, Z.; Shang, Y.; Liu, X.; Yang, Y. Accelerated discovery of eutectic compositionally complex alloys by generative machine learning. npj Comput. Mater. 2024, 10, 204. [Google Scholar] [CrossRef]
- Harshvardhan, G.; Gourisaria, M.K.; Pandey, M.; Rautaray, S.S. A comprehensive survey and analysis of generative models in machine learning. Comput. Sci. Rev. 2020, 38, 100285. [Google Scholar]
- Fuhr, A.S.; Sumpter, B.G. Deep generative models for materials discovery and machine learning-accelerated innovation. Front. Mater. 2022, 9, 865270. [Google Scholar] [CrossRef]
- Zhou, Z.; Shang, Y.; Liu, X.; Yang, Y. A generative deep learning framework for inverse design of compositionally complex bulk metallic glasses. npj Comput. Mater. 2023, 9, 15. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Pinheiro Cinelli, L.; Araújo Marins, M.; Barros da Silva, E.A.; Lima Netto, S. Variational autoencoder. In Variational Methods for Machine Learning with Applications to Deep Networks; Springer: Berlin/Heidelberg, Germany, 2021; pp. 111–149. [Google Scholar]
- Rezende, D.; Mohamed, S. Variational inference with normalizing flows. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; PMLR: New York, NY, USA, 2015; pp. 1530–1538. [Google Scholar]
- Yang, L.; Zhang, Z.; Song, Y.; Hong, S.; Xu, R.; Zhao, Y.; Zhang, W.; Cui, B.; Yang, M.H. Diffusion models: A comprehensive survey of methods and applications. Acm Comput. Surv. 2023, 56, 1–39. [Google Scholar] [CrossRef]
- Ye, Y.; Li, Y.; Ouyang, R.; Zhang, Z.; Tang, Y.; Bai, S. Improving machine learning based phase and hardness prediction of high-entropy alloys by using Gaussian noise augmented data. Comput. Mater. Sci. 2023, 223, 112140. [Google Scholar] [CrossRef]
- Chen, C.; Zhou, H.; Long, W.; Wang, G.; Ren, J. Phase prediction for high-entropy alloys using generative adversarial network and active learning based on small datasets. Sci. China Technol. Sci. 2023, 66, 3615–3627. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2009, 22, 1345–1359. [Google Scholar] [CrossRef]



| Model | SVM | KNN | ANN |
| RMSE * | 82 | 69 | 65 |
| Augmented Data | RMSE in Test Set * | RMSE in Validation Set * |
|---|---|---|
| Row Data | 58.1 | 44.4 |
| 2 × Row Data | 42.8 | 40.5 |
| Low noise enhanced | 42.8 | 40.1 |
| Middle noise enhanced | 43.2 | 39.6 |
| High noise enhanced | 43.7 | 40.0 |
| 3 × Row Data | 39.0 | 41.5 |
| Low + middle noise enhanced | 39.8 | 41.0 |
| Low + high noise enhanced | 40.0 | 40.7 |
| Middle + high noise enhanced | 40.9 | 40.5 |
| 4 × Row Data | 30.2 | 43.1 |
| Low + middle + high noise enhanced | 31.1 | 41.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Ni, J. Machine Learning Advances in High-Entropy Alloys: A Mini-Review. Entropy 2024, 26, 1119. https://doi.org/10.3390/e26121119
Sun Y, Ni J. Machine Learning Advances in High-Entropy Alloys: A Mini-Review. Entropy. 2024; 26(12):1119. https://doi.org/10.3390/e26121119
Chicago/Turabian StyleSun, Yibo, and Jun Ni. 2024. "Machine Learning Advances in High-Entropy Alloys: A Mini-Review" Entropy 26, no. 12: 1119. https://doi.org/10.3390/e26121119
APA StyleSun, Y., & Ni, J. (2024). Machine Learning Advances in High-Entropy Alloys: A Mini-Review. Entropy, 26(12), 1119. https://doi.org/10.3390/e26121119






