Quantum Control Design by Lyapunov Trajectory Tracking and Optimal Control
Abstract
1. Introduction
2. Control Law Design
2.1. Quantum System Described by Schrödinger Equation (TDSE)
2.2. Lyapunov Control Design
2.3. Examples and Simulations
3. A Spin-1/2 Particle System
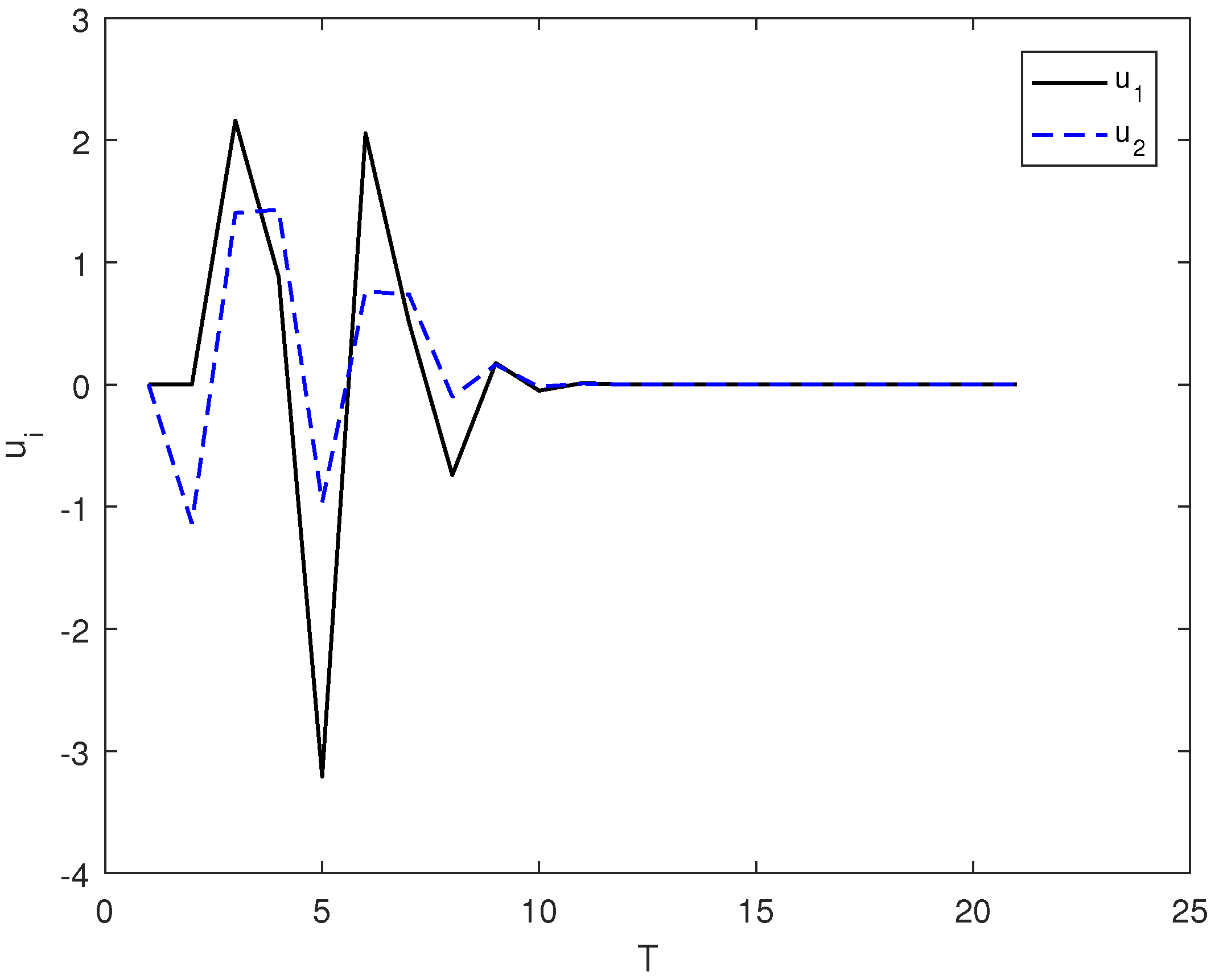
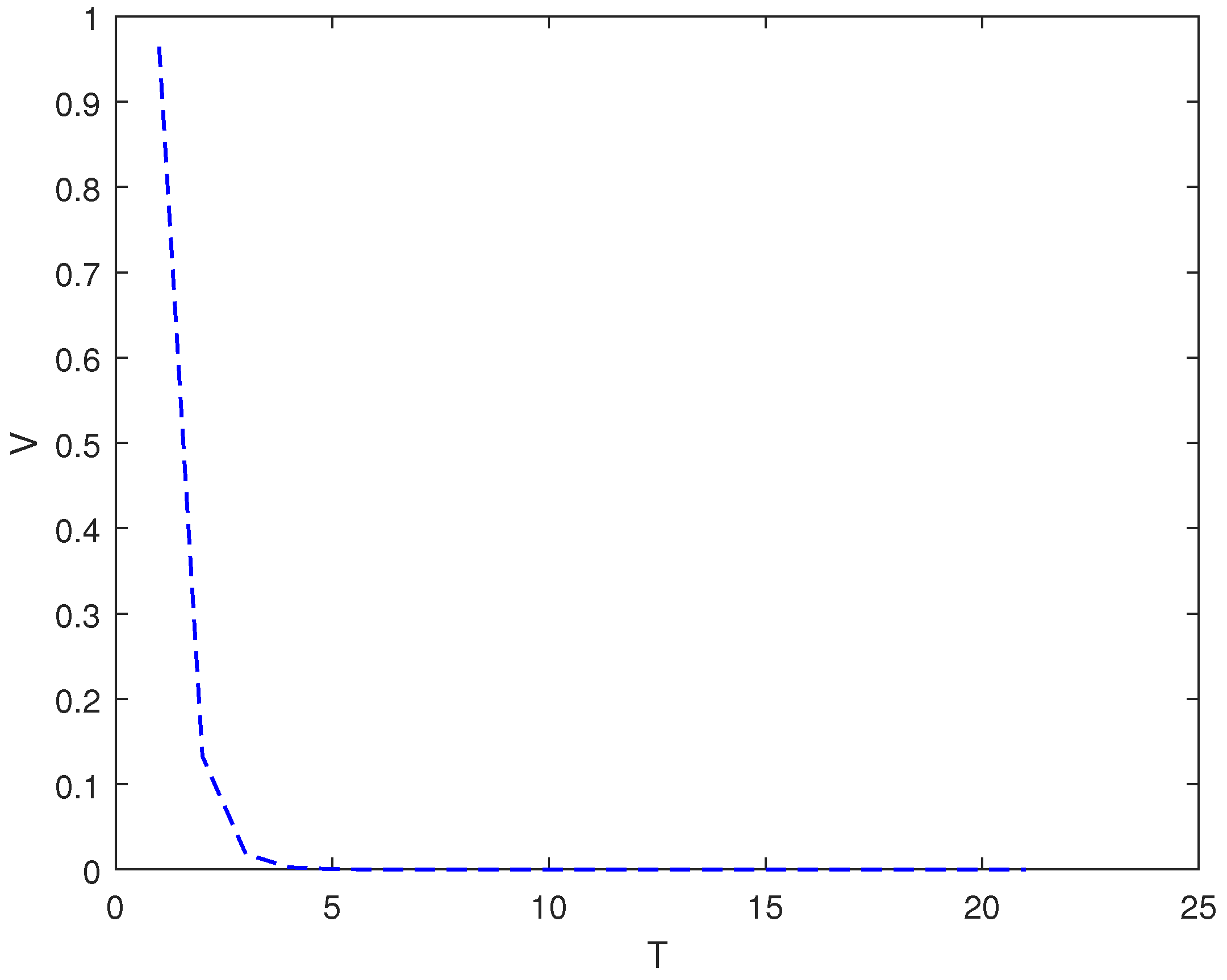
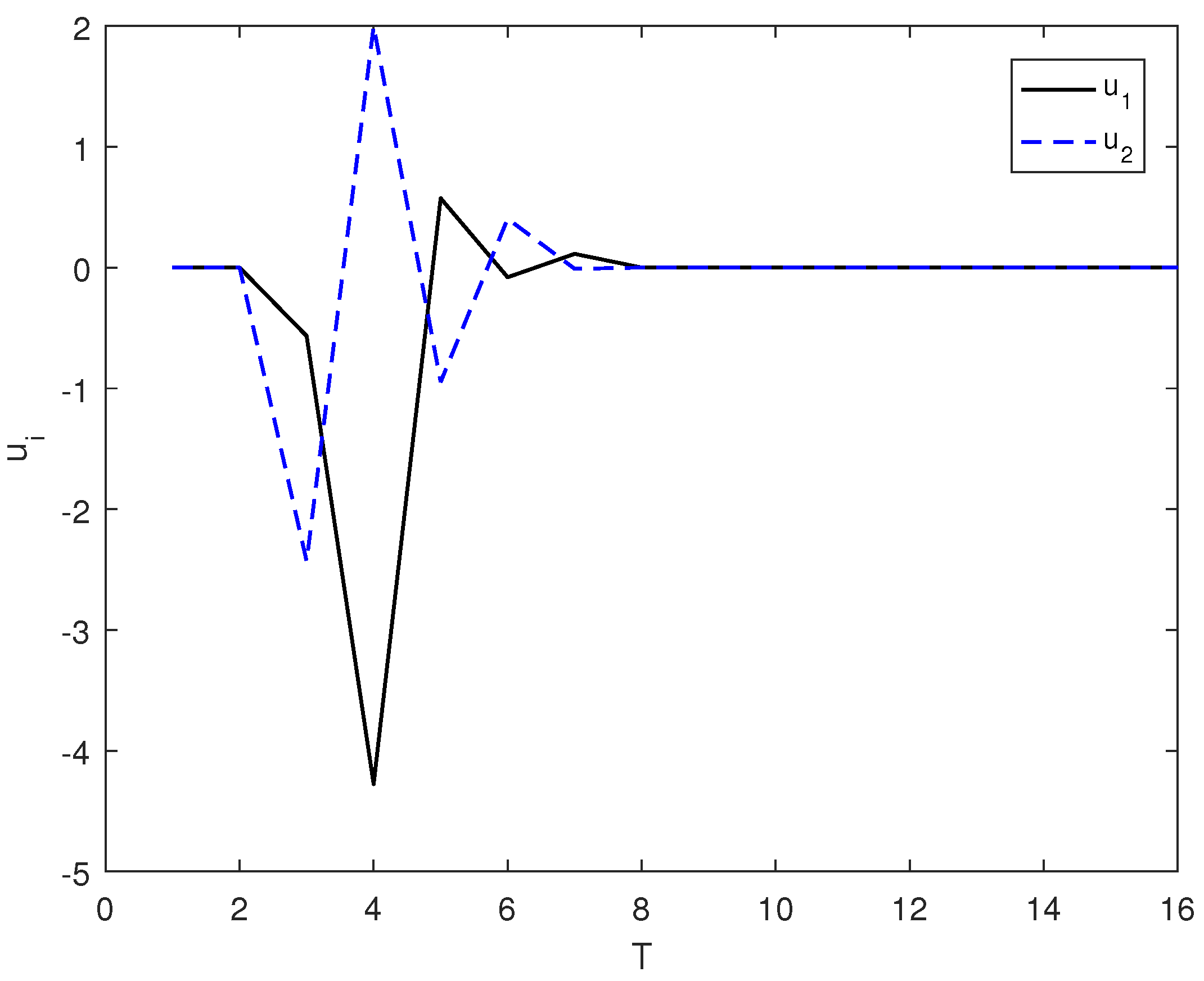
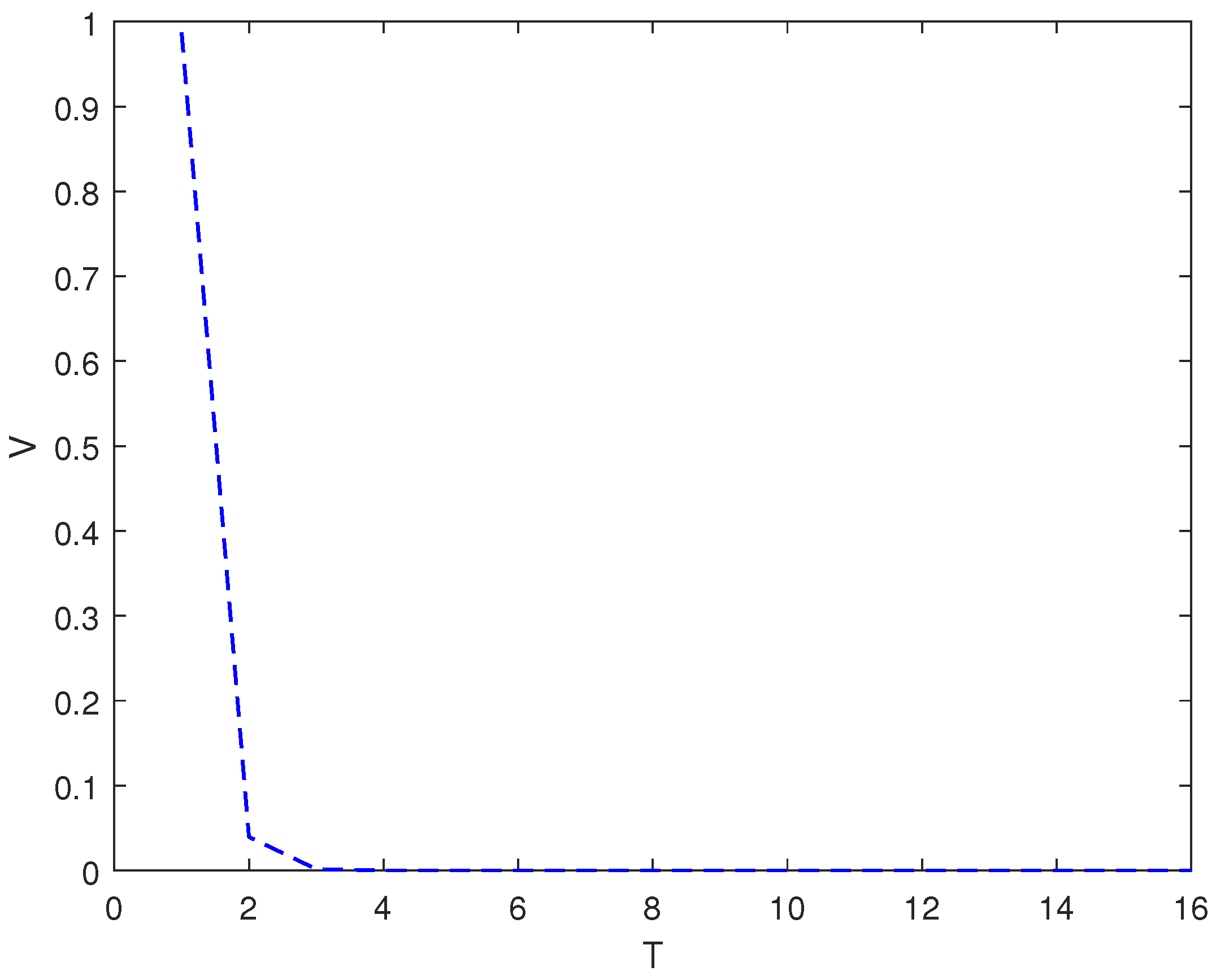
3.1. Simulation Experiment
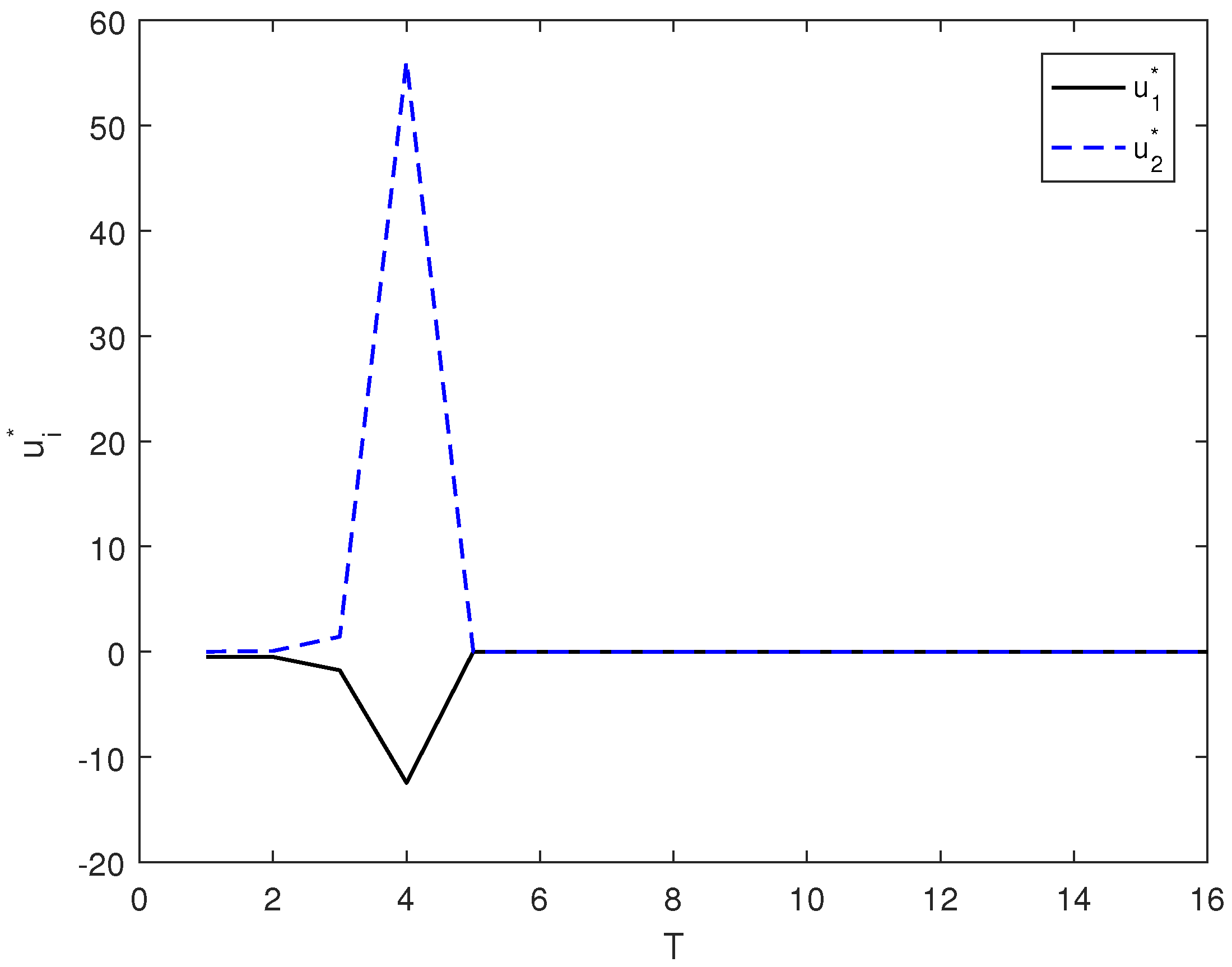
3.2. Optimal Control
3.2.1. Selection of Optimal Control Law
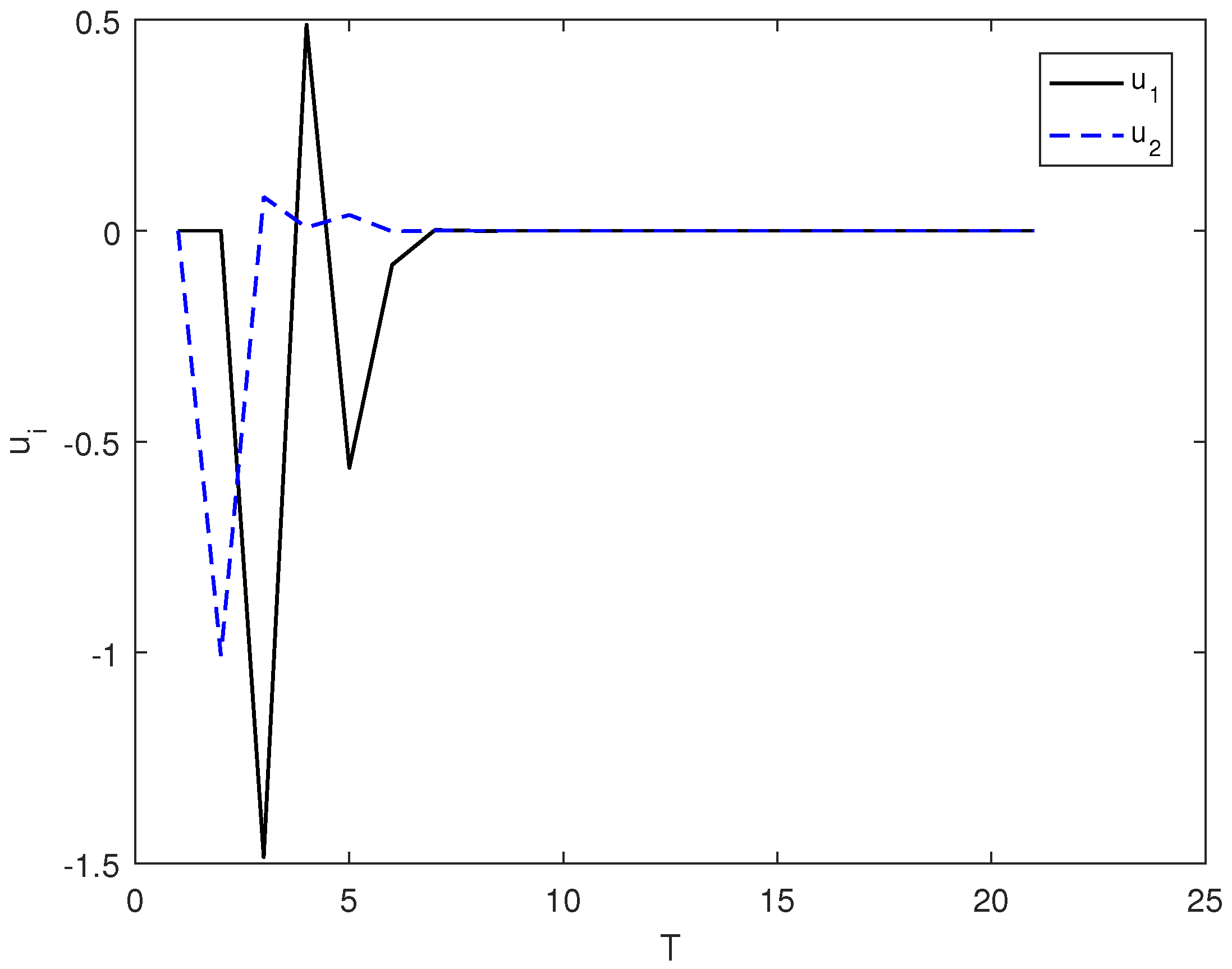
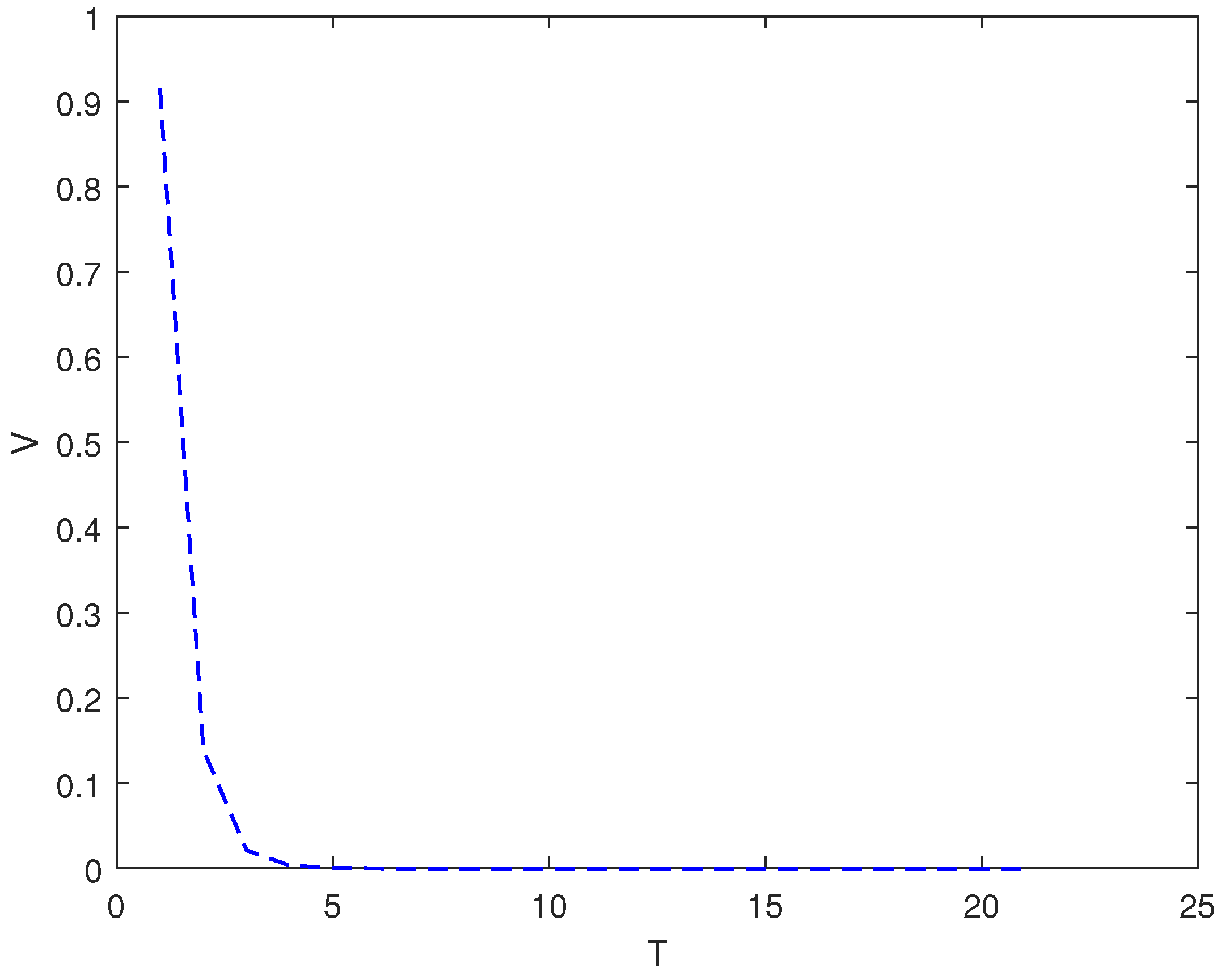
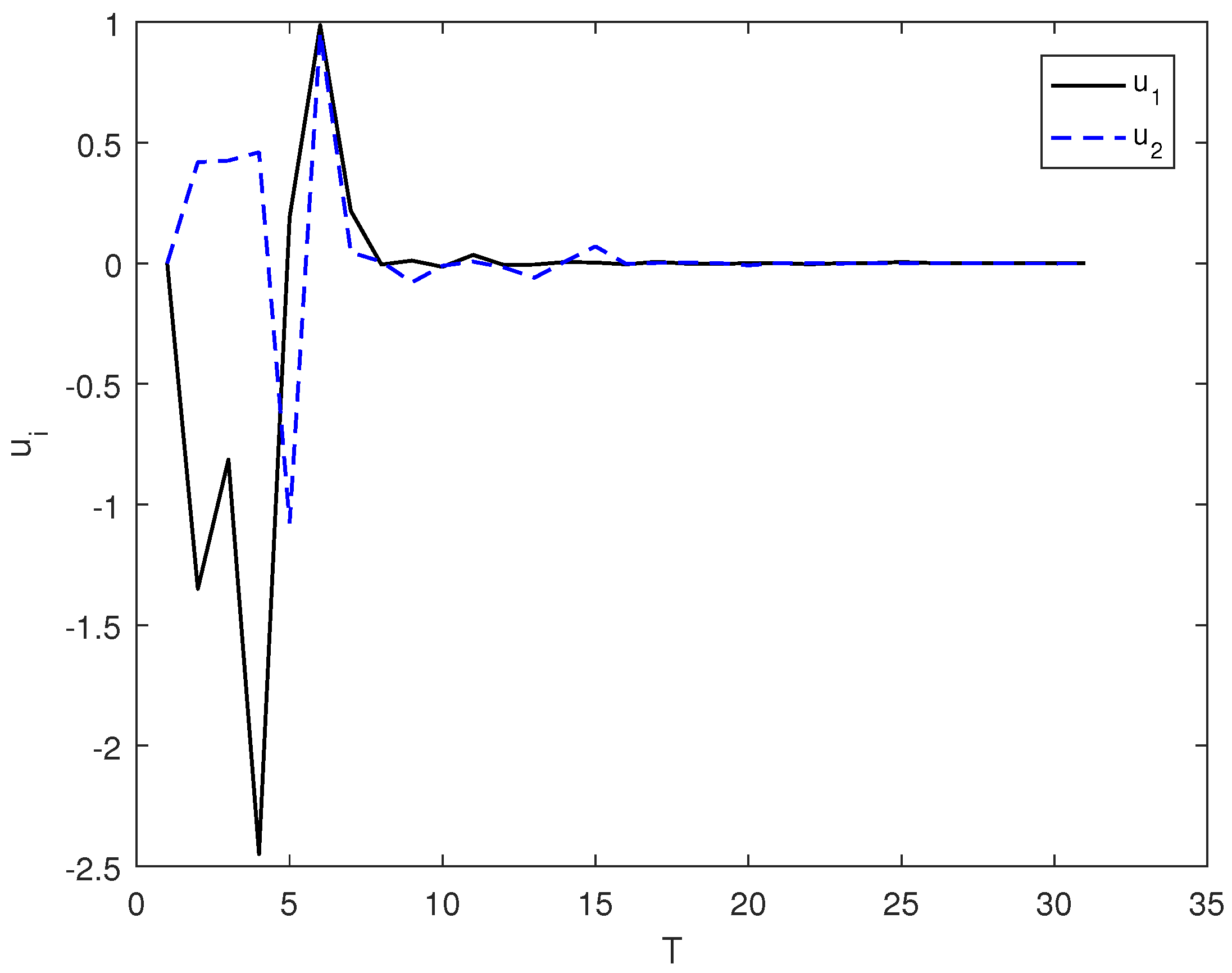
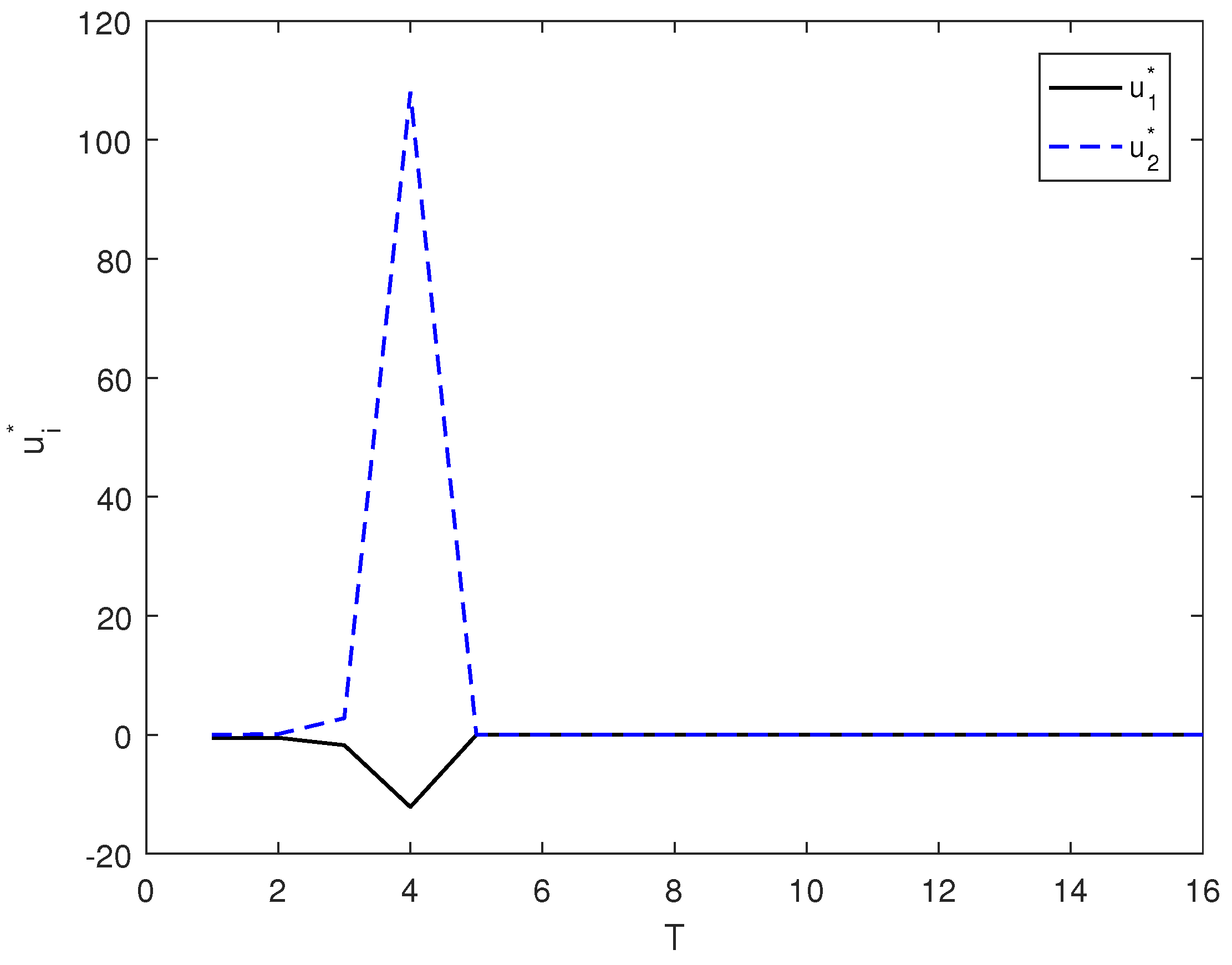
3.2.2. Optimal Control of a Spin-1/2 Particle System
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Timothy, H.B. Blackbody radiation in classical physics: A historical perspective. Am. J. Phys. 2018, 86, 495–509. [Google Scholar]
- Don, S.L.; William, R.S. Adiabatic invariance and its application to Wien’s complete displacement law of blackbody radiation. Am. J. Phys. 2024, 86, 132–139. [Google Scholar]
- Gkourmpis, A. A demonstration of the photoelectric effect with sunlight. Phys. Teach. 2023, 61, 710–711. [Google Scholar] [CrossRef]
- Lou, C.G.; Dai, J.L.; Wang, Y.X.; Zhang, Y.; Li, Y.F.; Liu, X.L.; Ma, Y.F. Highly sensitive light-induced thermoelastic spectroscopy oxygen sensor with co-coupling photoelectric and thermoelastic effect of quartz tuning fork. Photoacoustics 2023, 31, 100515. [Google Scholar] [CrossRef]
- Hsieh, S.S.; Katsuyuki, T. Spectral information content of Compton scattering events in silicon photon counting detectors. Med. Phys. 2024, 51, 2386–2397. [Google Scholar] [CrossRef]
- Bornikov, K.A.; Volobuev, I.P.; Popov, Y.V. Notes on Inverse Compton Scattering. Mosc. Univ. Phys. Bull. 2023, 78, 453–459. [Google Scholar] [CrossRef]
- Ikuta, R. Wave-particle duality of light appearing in an intensity interferometric scenario. Opt. Express 2022, 30, 46972–46981. [Google Scholar] [CrossRef] [PubMed]
- Elinor, Z.H.; Yonatan, D. Signature of Quantum Coherence in the Exciton Energy Pathways of the LH2 Photosynthetic Complex. ACS Omega 2023, 8, 38871–38878. [Google Scholar]
- Daniel, L.; Martin, H.G. Making and breaking bonds with absolutely localized molecular orbitals: An energy-decomposition analysis for bonded interactions. Abstr. Pap. Am. Chem. Soc. 2016, 251. [Google Scholar]
- Peirce, A.; Dahleh, M.; Rabitz, H. Optimal control of quantum-mechanical systems: Existence, numerical approximation, and applications. Phys. Rev. A Gen. Phys. 1988, 37, 4950–4964. [Google Scholar] [CrossRef]
- Albertini, F.; D’Alessandro, D. Control of a two-level quantum system in a coherent feedback scheme. Phys. A Math. Theor. 2013, 46, 045301-1–045301-8. [Google Scholar] [CrossRef]
- Stefanatos, D.; Paspalakis, E. A shortcut tour of quantum control methods for modern quantum technologies. Europhys. Lett. 2020, 132, 60001. [Google Scholar] [CrossRef]
- Koch, C.P.; Boscain, U.; Calarco, T.; Dirr, G.; Filipp, S.; Glaser, S.J.; Kosloff, R.; Montangero, S.; Schulte-Herbrüggen, T.; Sugny, D.; et al. Quantum optimal control in quantum technologies. Strategic report on current status, visions and goals for research in Europe. EPJ Quantum Technol. 2022, 9, 19. [Google Scholar] [CrossRef]
- Khaneja, N.; Brockett, R.; Glaser, S.J. Time optimal control in spin systems. Phys. Rev. A 2001, 63, 032308. [Google Scholar] [CrossRef]
- Cong, S. Control of Quantum Systems: Theory and Methods; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Kuang, S.; Cong, S. Lyapunov control methods of closed quantum systems. Automatica 2008, 44, 98–108. [Google Scholar] [CrossRef]
- Wang, X.; Schirmer, S. Analysis of Lyapunov method for control of quantum states. IEEE Trans. Autom. Control 2010, 55, 2259–2270. [Google Scholar] [CrossRef]
- Grivopoulos, S.; Bamieh, B. Lyapunov-based control of quantum systems. In Proceedings of the 42nd IEEE Conference on Decision and Control, Maui, HI, USA, 9–12 December 2003; pp. 434–438. [Google Scholar]
- Coron, J.M.; Grigoriu, A.; Lefter, C.; Turinici, G. Quantum control design by Lyapunov trajectory tracking for dipole and polarizability coupling. New J. Phys. 2009, 11, 105034. [Google Scholar] [CrossRef]
- Bose, S.S.C.; Alfurhood, B.S.; Flammini, F.; Natarajan, R.; Jaya, S.S. Decision Fault Tree Learning and Differential Lyapunov Optimal Control for Path Tracking. Entropy 2023, 25, 443. [Google Scholar] [CrossRef]
- Byoungsoo, L.; Walter, J.G. Aeroassisted orbital maneuvering using Lyapunov optimal feedback control. J. Guid. Control Dyn. 2012, 12, 237–242. [Google Scholar]
- Rush, D.R.; Gordon, G.P.; Hanspeter, S.; John, L.J. Lyapunov Optimal Saturated Control for Nonlinear Systems. J. Guid. Control Dyn. 2012, 20, 1083–1088. [Google Scholar]
- Jouili, K.; Madani, A. Nonlinear Lyapunov Control of a Photovoltaic Water Pumping System. Energies 2023, 16, 2241. [Google Scholar] [CrossRef]
- Yang, Z.; Yang, J.; Chao, S.; Zhao, C.; Peng, R.; Zhou, L. Simultaneous ground-state cooling of identical mechanical oscillators by Lyapunov control. Opt. Express 2022, 30, 20135–20148. [Google Scholar] [CrossRef] [PubMed]
- Kuang, S.; Guan, X.K. Robustness of continuous non-smooth finite-time Lyapunov control for two-level quantum systems. IET Control Theory Appl. 2020, 14, 2449–2454. [Google Scholar] [CrossRef]
- Hou, S.C.; Yi, X.X. Quantum Lyapunov control with machine learning. Quantum Inf. Process. 2020, 19, 8. [Google Scholar] [CrossRef]
- Guan, X.K.; Kuang, S.; Lu, X.J.; Yan, J.Z. Lyapunov Control of High-Dimensional Closed Quantum Systems Based on Particle Swarm Optimization. IEEE Access 2020, 8, 49765–49774. [Google Scholar] [CrossRef]
- Aleksandrov, A.; Efimov, D.; Dashkovskiy, S. On input to state stability Lyapunov functions for mechanical systems. Int. J. Robust Nonlinear Control 2022, 33, 2902–2912. [Google Scholar] [CrossRef]
- Mirrahimi, M.; Rouchon, P.; Turinici, G. Lyapunov control of bilinear Schrödinger equations. Automatica 2005, 41, 1987–1994. [Google Scholar] [CrossRef]
- Yu, G.H.; Yang, H.L. Quantum control based on three forms of Lyapunov functions. Chin. Phys. B 2024, 33, 040201. [Google Scholar] [CrossRef]
- Benallou, A.; Mellichamp, D.A.; Seborg, D.E. Optimal stabilizing controllers for bilinear systems. Int. J. Control 1988, 48, 1487–1501. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Cong, S. Optimal quantum control based on Lyapunov stability theorem. J. Univ. Sci. Technol. China 2008, 38, 331–336. [Google Scholar]
- Franco, B.; Stefano, M. Set-Theoretic Methods in Control; Birkhäuser: Cham, Switzerland, 2019; pp. 143–146. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Yu, G.; Ivanov, I.G. Quantum Control Design by Lyapunov Trajectory Tracking and Optimal Control. Entropy 2024, 26, 978. https://doi.org/10.3390/e26110978
Yang H, Yu G, Ivanov IG. Quantum Control Design by Lyapunov Trajectory Tracking and Optimal Control. Entropy. 2024; 26(11):978. https://doi.org/10.3390/e26110978
Chicago/Turabian StyleYang, Hongli, Guohui Yu, and Ivan Ganchev Ivanov. 2024. "Quantum Control Design by Lyapunov Trajectory Tracking and Optimal Control" Entropy 26, no. 11: 978. https://doi.org/10.3390/e26110978
APA StyleYang, H., Yu, G., & Ivanov, I. G. (2024). Quantum Control Design by Lyapunov Trajectory Tracking and Optimal Control. Entropy, 26(11), 978. https://doi.org/10.3390/e26110978





